Computational Investigation on Cracking Behaviors of AerMet 100

Abstract

AerMet 100 exhibits excellent mechanical properties, proven in previous studies; however, defects may greatly influence the mechanical behavior during the service of the material, which serves as one of the major challenges in the wider application of the material. To quantify the crack evolution process, the in-plane type I crack propagation behavior is comprehensively investigated based on the extended finite element method (XFEM). The crack growth is characterized in terms of the extracted crack propagation angle, stress intensity factor (SIF) in the crack tip, and stress field profiles during the crack propagation process. An extrapolation method is adopted to calculate the SIF, followed by a series of parametric studies on the influence of the governing factors, i.e., initial crack length, initial crack location, initial crack angle, and the crack number through numerical investigation. It is found that the crack propagation angle enlarges monotonously with the increase of the initial crack location, the initial crack length, and the crack number, increases slowly with the growth of initial crack angle, and rapidly enlarges in reverse at about 45°. The SIF in Mode I, K_Id, gradually decreases with the increase of the initial crack location and the crack number, and nearly keeps steady when the initial crack length and initial crack angle varies. Results provide further understanding of the failure and fracture behavior of AerMet 100 and guide the future application and design of the structures.

1. Introduction

With the impressing need for ultra-high strength with high fracture strain metallic materials in both civil and national defense applications, AerMet 100 steel proves to be an excellent and promising candidate, with a fracture toughness 130 $\mathrm{MPa}\cdot \sqrt{\mathrm{m}}$ [1], ultimate strength~2 GPa [2] and corrosion-fatigue fracture resistance 50 $\mathrm{MPa}\cdot \sqrt{\mathrm{m}}$ [3], to substitute 300 M steel for landing gears for aircraft in astronautics engineering to the framework of bicycles in the sports industry [4]. The excellent mechanical behaviors of AerMet 100 were comprehensively investigated through its microscopic property [5], micro-component [6], and microstructure [7]. Recently, due to the dynamic mechanical loading during the engineering application in nature, the dynamic mechanical behaviors of AerMet 100 were explored by using the SHPB (Split Hopkinson Pressure Bar) [8,9,10]. The results showed a significant strain rate-strengthening effect in which the yield strength increased by 30%, and the ultimate strength had an increase of about 35%, as the strain rate varied from 0.001 s⁻¹ to 4200 s⁻¹. Furthermore, a parameterized Johnson–Cook model based on the SHPB tests was established and discussed. That the strain rate intensifies the mechanism was revealed by the SEM evidence [8]. These pioneering research efforts not only lay a solid foundation to understand the dynamic mechanical behavior of AerMet 100, but further draws interest to revealing the mechanical behavior with initial cracks in the structure made by AerMet 100.

On the other hand, crack initiation and propagation have long been an important issue for the structural material, which may usually cause catastrophic consequences [11]. Successful attempts have been made through elaborately designed experiments such as motors [12], welds [13], and blades [14]. An alternative way to study the cracking problem is numerical simulation. Several new numerical methods are put forward to solve the singularity dilemma within the crack tip. Hu et al. [15] obtained crack growth and debonding development in CFRP-strengthened cracked steel plates through the boundary element method. Thiyahuddin et al. [16] investigated the fluid–structure interaction effect under vehicular impact using the mesh-less method. Recently, a popular simulation method to describe the crack growth behavior is XFEM (extended finite element method), where the simulation results showed satisfactory consistency with experimental values [13,17,18,19,20,21,22]. Jena et al. [17] accurately captured the singularity at the crack tip during semipermeable crack propagation using XFEM. Xiao et al. [18] proposed a B-spline ruled surface algorithm, which was applied to modeling arbitrary 3D crack propagation in the context of the improved XFEM. It had been proved to possess both efficiency and accuracy by comparing with the experimental records. The fracture behavior of human cortical bone was also successfully simulated by Yadav et al. [22]. They reported that the severe stress intensity factor could be attributed to the presence of small microcracks around the major crack tip. To assess the stress intensity in the crack tip, the exploration method was adopted by Kamaya, which showed its accuracy in describing the fracture behavior of the cracked components [23], avoiding the re-meshing problem [24]. In fact, XFEM has become an effective tool to study the interfacial cracking problem in the bi-material as well as multi-crack stress mode, which are highly complicated in theoretical analysis [25,26,27].

However, investigations about the crack initiation and propagation problem in AerMet 100, an ultra-strong and tough metallic material with strain-rate dependency, are still lacking, which hinders the material’s further application in critical mechanical parts. To fill in this gap, in this paper, a 3D plate model is established with XFEM to quantitatively study cracking behaviors. The strain rate-dependent constitutive material description is based on our previous paper [8], and an extrapolation method is adopted to calculate SIF in the crack tip. Under uniaxial tensile loads, the numerical crack growth models with different initial crack length, different initial crack location, different initial crack angle and different crack numbers are developed, while the crack propagation angle and SIF during crack propagation are recorded, respectively. Further, a series of comprehensive parametric studies are conducted to explore the influence of the initial crack length, location, angle, and number on the cracking propagation behavior.

2. Methods

2.1. Microstructure of AerMet 100 Steel

A microscopic photo demonstrating the microstructure of AerMet 100 steel is obtained through the optical microscope. The microstructure of AerMet 100 is typical for ultra-high strength steel, with a large amount of martensite (brighter grains) and tiny amounts of residual austenite (darker grains), as shown in Figure 1a. The martensite demonstrates small and dense laths, which direct differently and distribute uniformly, contributing greatly to the high strength of AerMet 100 steel.

Additionally, the quasi-static tensile fractography of AerMet 100 steel is obtained through SEM (Figure 1b), where a clear necking-down zone could be observed. With the color dark and no metallic luster, the fracture surface is flat and full of fibroid grain, implying the macroscopic ductile fracture. The fracture consists of dimples of various sizes, with sunken bottoms and bulged edges. The deep and uniform dimples suggest the fine plasticity of AerMet 100 steel.

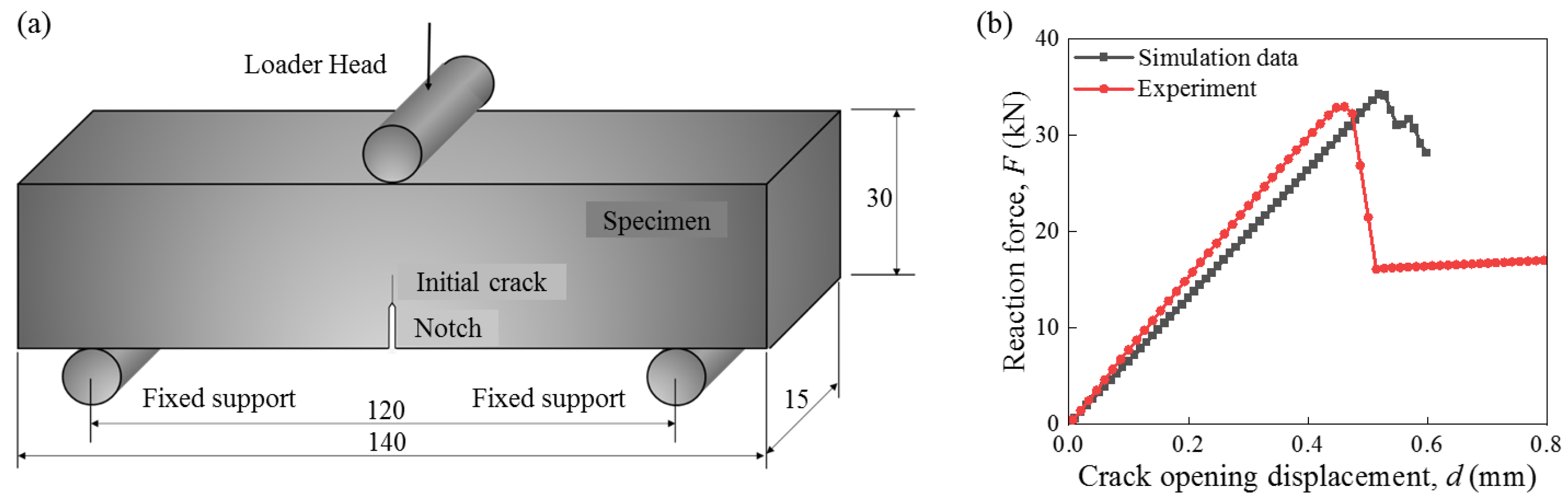
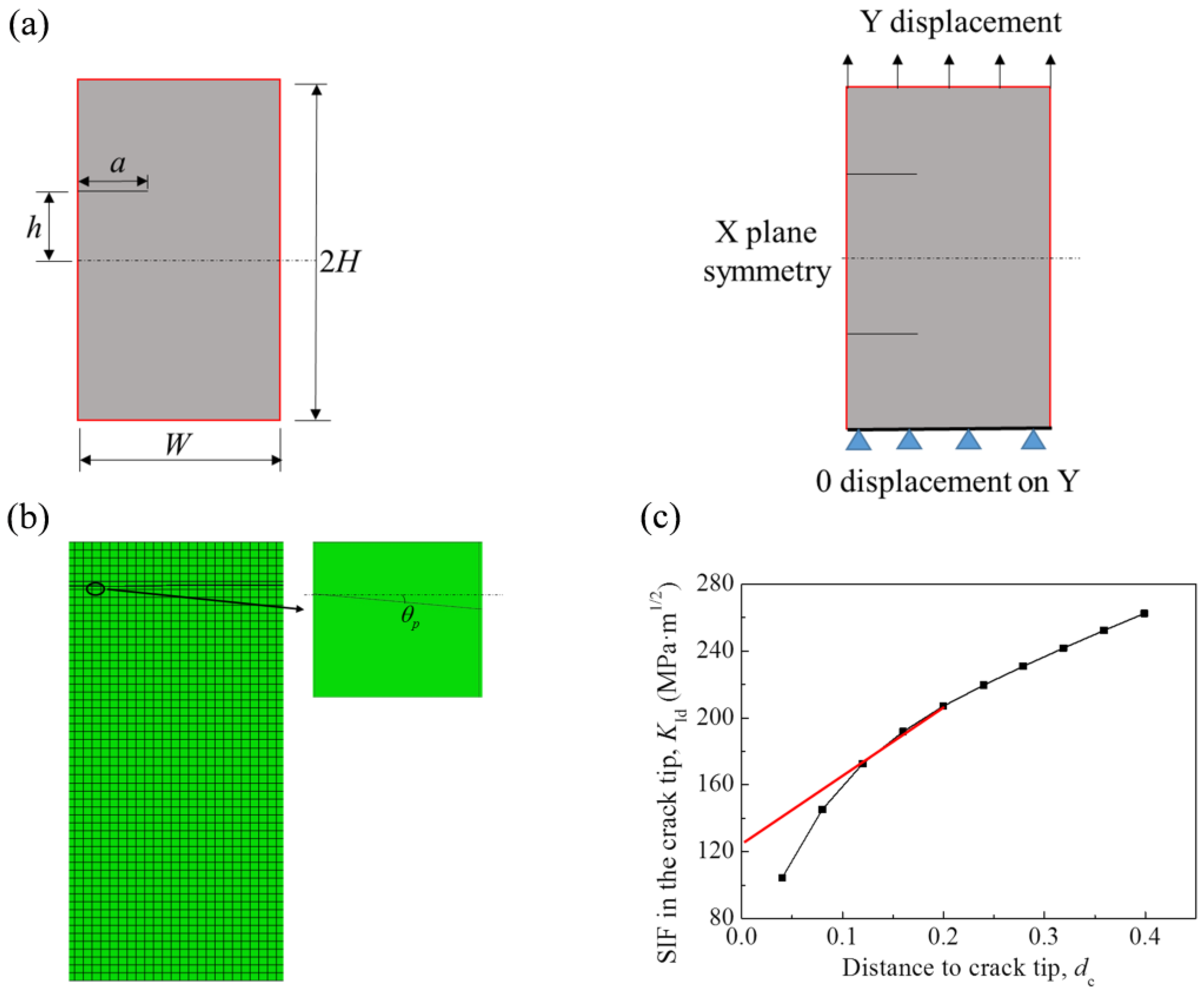
2.2. Modeling

A summary of basic mechanical properties of AerMet 100 is summarized in Ref. [8] and listed in

Table 1. A summary of basic mechanical properties of AerMet 100 steel.

Material Parameter	Young’s Modulus, E (GPa)	Yield Strength, σe (MPa)	Ultimate Strength, σu (MPa)	Density, ρ (kg/m3)	Poisson’s Ratio, μ	Elongation, η
Value	187.20	1724.51	1986.9	7.8 × 103	0.35	0.166

.

A simplified Johnson–Cook constitutive model of AerMet 100 is fitted based on a series of quasi-static and dynamic experiments. The formula demonstrates as follows:

$$\sigma =(A+B{\epsilon }^n)(1+C\ln {\dot{\epsilon }}^{*})$$

(1)

where $\sigma$ represent the stress; A is the yield stress of AerMet 100; B, n, and C are material constants; $\epsilon$, $\dot{\epsilon }$ and ${\dot{\epsilon }}^{*}$ means the equivalent plastic strain, the strain rate and dimensionless plastic strain rate expressed as $\dot{\epsilon }/{\dot{\epsilon }}_0$ for ${\dot{\epsilon }}_0=0.001{\mathrm{s}}^{-1}$. The value of A, B, n, and C are presented in

Table 2. The value of material constants in Johnson-Cook model.

Material Parameters	A	B	n	C	${\dot{\mathit{\epsilon }}}_0$ (s−1)
Value	1724.51	90.92	0.002	0.018	0.001

.

To investigate the crack growth in AerMet 100 steel, a standard three-point bending test of AerMet 100 steel is conducted according to ASTM E 1820 [28] to obtain the plane strain fracture toughness, i.e., the critical stress intensity factor K_IC for the opening model (model I) of loading.

The specimen, with a length 150 mm, height 30 mm, and thickness 15 mm, is firstly notched through the wire electrical discharge machining and then cracked by using the fatigue testing machine (Figure 2a). The notch is 2 mm wide and 10 mm high with a triangle-shaped top. The initial crack in the specimen is 5 mm long. Both the notch and crack are in the middle of the specimen in terms of the transverse direction.

The specimen is placed horizontally on two fixed supports with a distance 120 mm, and then deforms under the pressure of the loader head, which gradually lowers down at the speed of 5 mm/sec, regarded as the quasi-static loading [8]. The reaction force on the loader head and the crack opening displacement are recorded (Figure 2b).

The critical stress intensity factor in the mode I fracture type K_IC can be obtained through the following calculation [28]:

$$K_{\mathrm{{\rm I}}\mathrm{C}}=\left(\frac{F_{\mathrm{Q}}S}{{(B{B}_{\mathrm{N}})}^{\frac{1}{2}}{D}^{\frac{3}{2}}}\right)\times f\left(\frac{a}{D}\right)$$

(2)

$$f\left(\frac{a}{D}\right)=3{(\frac{a}{D})}^{\frac{1}{2}}[1.99-(\frac{a}{D})(1-\frac{a}{D})]\times \frac{[2.15-3.93(\frac{a}{D})+2.70{(\frac{a}{D})}^2]}{2(1+2\frac{a}{D}){(1-\frac{a}{D})}^{\frac{3}{2}}}$$

(3)

where F_Q is the maximum reaction force on the loader head; S is the support span; B and B_N are the specimen thickness and the effective specimen thickness, respectively, and B_N = B if there are no side grooves; a represents the length of the initial crack and D indicates the specimen height.

The test result shows K_IC = 150 $\mathrm{MPa}\cdot \sqrt{\mathrm{m}}$. The critical fracture energy G_IC could be calculated according to the Irwin relationship for plane strain case [29]:

$$G_{\mathrm{{\rm I}}\mathrm{C}}=\frac{K_{\mathrm{{\rm I}}\mathrm{C}}}{E}(1-{\mu }^2)$$

(4)

where E is Young’s modulus, and μ is the Poisson ratio.

In XFEM computation, a propagation criterion is set as the crack propagation occurs with the maximum principal strain of 0.01. The damage evolution method based on the energy with linear softening is adopted in the simulation. To avoid the errors that may happen in the calculation based on the 2D elements and simulate the real-world processes in engineering in a more accurate method, a 3D finite element plate model is established with a width of 10 mm, height of 20 mm, and thickness of 0.1 mm in Cartesian coordinates (Figure 3a), where W represents the width and 2H represent the height, respectively. For simplicity, dimensionless initial crack location and initial crack length are adopted, i.e., $h_i=\frac{h}{H}$ and $l_i=\frac{a}{W}$, respectively. Note that adequate plate area should be given to ensure the propagation of cracks and to avoid the boundary effect. In this study, the maximum l_i is taken as 0.3, and the maximum h_i is taken as 0.8.

Mesh sensitivity analysis is first carried out prior to the parametric calculation, due to the correct size of the elements as well as the type of element, and its numerical formulation is used to ensure good results and the lowest computational cost [30,31]. The liner shape of elements is preferred in this study [32]. The element size has been determined as 0.25 mm × 0.25 mm × 0.1 mm after a sensitivity analysis was conducted. The maximum aspect ratio in this XFE model is 2.50, and the Jacobian rate of all the elements is 1.00. An 8-node linear brick, reduced integration, hourglass control (C3D8R) and small-deformation Lagrangian formulation are adopted in this research.

The crack initiation problem can be described and simplified as a half model of a thin plate with an inner crack. In the XFE model with a preset crack, X-plane symmetry boundary condition has been applied on the left side of the XFE model, which makes the displacements of nodes on the left boundary restricted in the X-plane. The displacement in Y direction of nodes in the bottom surface is fixed as 0 and the displacement in Y direction of the top surface gradually reaches 2 mm under tension (Figure 3a).

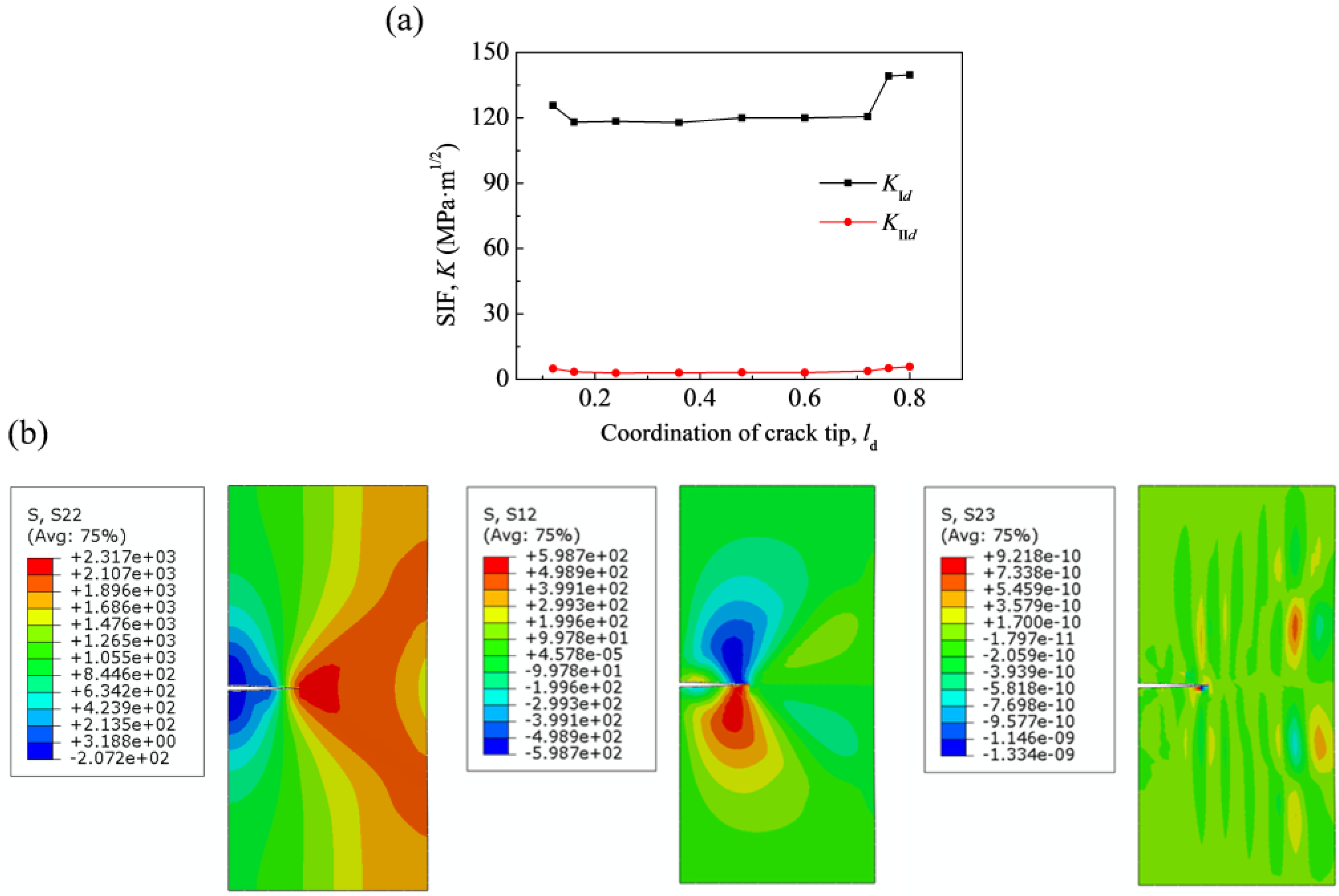
2.3. Computational Method of Crack Propagation Angle and SIF

The suggested fracture mode is proven to be opening-mode (mode I) dominant such that the crack propagation angle ${\theta }_p$ and stress intensity factor (SIF), namely K_Id, are selected to study the influence of governing parameters in the simulation. The crack propagation angle is defined as between the propagated crack in the first element and horizon line, illustrated in Figure 3b.

According to the fundamentals in elasticity, the stress singularity of r^−1/2 is around the crack tip. Thus, the SIF is adopted instead and described as follows [33]:

$$K_{\mathrm{{\rm I}}}=\underset{r\to 0}{\lim }\left[{\sigma }_{22}(r,\theta =0)\sqrt{2\pi r}\right]$$

(5)

$$K_{\mathrm{II}}=\underset{r\to 0}{\lim }\left[{\sigma }_{12}(r,\theta =0)\sqrt{2\pi r}\right]$$

(6)

$$K_{\mathrm{III}}=\underset{r\to 0}{\lim }\left[{\sigma }_{23}(r,\theta =0)\sqrt{2\pi r}\right]$$

(7)

where K_I, K_II and K_III represent the SIFs in the opening mode (mode I), in-plane shearing mode (mode II), and anti-plane shearing mode (mode III), respectively. ${\sigma }_{22}$, ${\sigma }_{12}$ and ${\sigma }_{23}$ are the stress components normal to the crack propagation direction, locally perpendicular to the crack edge and tangent to the crack edge, respectively. r means the distance to the crack tip and $\theta$ represents the angle between the crack propagation direction and the line connecting the crack tip and the point. Due to the unavailability of the stress in the crack tip, an extrapolation method is adopted to calculate K_Id, K_IId and K_IIId in the crack tip and elaborated as follows.

It is straightforward to obtain the stress components ${\sigma }_{22i}$, ${\sigma }_{12i}$ and ${\sigma }_{23i}$ (i = 1, 2, 3) and coordinates of the points r_i in front of the crack tip. Therefore, the SIFs in those points can be obtained as follows:

$$K_{\mathrm{{\rm I}}}{}_{\mathrm{d}i}={\sigma }_{22i}\sqrt{2\pi r_i}$$

(8)

$$K_{\mathrm{II}}{}_{\mathrm{d}i}={\sigma }_{12i}\sqrt{2\pi r_i}$$

(9)

$$K_{\mathrm{III}}{}_{\mathrm{d}i}={\sigma }_{23i}\sqrt{2\pi r_i}$$

(10)

Assume that the relationship between r_i and K_jdi, where j represents for I, II and III, can be described in a linear equation. Least square method is adopted to fit the data pair of (r_i, K_jdi). Accordingly, the SIFs in the crack tip can be calculated in the following equation:

$$K_{\mathrm{{\rm I}}}{}_{\mathrm{d}}\approx \frac{{\displaystyle \sum r_i}{\displaystyle \sum r_i}{K}_{{\rm I}\mathrm{d}i}-{\displaystyle \sum r_i^2}{\displaystyle \sum K_{{\rm I}\mathrm{d}i}}}{{({\displaystyle \sum r_i})}^2-N{\displaystyle \sum r_i^2}}$$

(11)

$$K_{\mathrm{II}}{}_{\mathrm{d}}\approx \frac{{\displaystyle \sum r_i}{\displaystyle \sum r_i}{K}_{\mathrm{II}}{{}_{\mathrm{d}}}_i-{\displaystyle \sum r_i^2}{\displaystyle \sum K_{\mathrm{II}}{{}_{\mathrm{d}}}_i}}{{({\displaystyle \sum r_i})}^2-N{\displaystyle \sum r_i^2}}$$

(12)

$$K_{\mathrm{III}}{}_{\mathrm{d}}\approx \frac{{\displaystyle \sum r_i}{\displaystyle \sum r_i}{K}_{\mathrm{IIId}i}-{\displaystyle \sum r_i^2}{\displaystyle \sum K_{\mathrm{IIId}i}}}{{({\displaystyle \sum r_i})}^2-N{\displaystyle \sum r_i^2}}$$

(13)

where N is the number of the points selected to calculate K_Id, K_IId and K_IIId.

To verify the accuracy of the suggested extrapolation method, a similar finite model under 2000 MPa tensile pressure with the same size as the previous model pressure is established. Figure 3c demonstrates ten selected points in front of the crack tip and the data (r_i, K_Idi). The calculation results are compared with the typical computation formula as [33]:

$$K_{\mathrm{{\rm I}}}{}_{\mathrm{d}}=\sigma \sqrt{\pi a}\sqrt{\frac{2W}{\pi a}\tan \frac{\pi a}{2W}}$$

(14)

where $\sigma$ represents the tensile pressure; W denotes the width of the half model, and a is the crack length.

The stresses within the vicinity of the crack tip are extremely high and calculated incorrectly in the FE analysis. Thus, the first two points, whose K_Ids obviously do not stand in a line with the following points (Figure 3c), are excluded when calculating the stress intensity factor in the crack tip; similar methods are adopted in Refs. [34,35].

To obtain an accurate calculation, 4 different methods to select the extrapolation are compared to calculate the K_Id.

• Method 1: 10 points in front of the crack tip are selected;
• Method 2: the first 2 points are excluded, but the remaining 8 points are selected;
• Method 3: the first 3 points are selected;
• Method 4: the first 2 points are excluded, but the consecutive 3 points are selected.

The computational results are listed in

Table 3. Comparison of the calculation results for four different methods.

Method	1	2	3	4	Computation Formula
Result Value (MPa·m1/2)	114.41	141.16	72.39	121.77	123.5

. In comparison, Method 4 obviously possesses a better accuracy than other methods; thus, it is adopted in the later discussion.

3. Results

3.1. Propagation Behavior of Typical In-Plane Crack

When the initial crack length l_i equals 0.1 at h_i = 0, the crack grows along the middle line, and there is no deflection in the crack path. Based on the extrapolation method, the SIFs, i.e., K_Id, K_IId, and K_IIId in the crack tip in the crack propagation process could be calculated. K_IIId stays at zero during the crack propagation (Figure 4a). Obviously, K_Id is larger than K_IId and K_IIId, evidenced by the stress contours of S₂₂, S_12, and S₂₃ in the crack propagation process, with S₂₂ much bigger than S₁₂ and S₂₃ (Figure 4b), where S₂₂, S₁₂ and S₂₃ correspond to ${\sigma }_{22}$, ${\sigma }_{12}$ and ${\sigma }_{23}$. The result implies that the fracture mode in this process could be regarded as the opening mode such that only K_Id would be discussed in the following study. In addition, K_Id shows a bigger value at the beginning and approaching the end while staying stable in the propagation process due to the boundary effect.

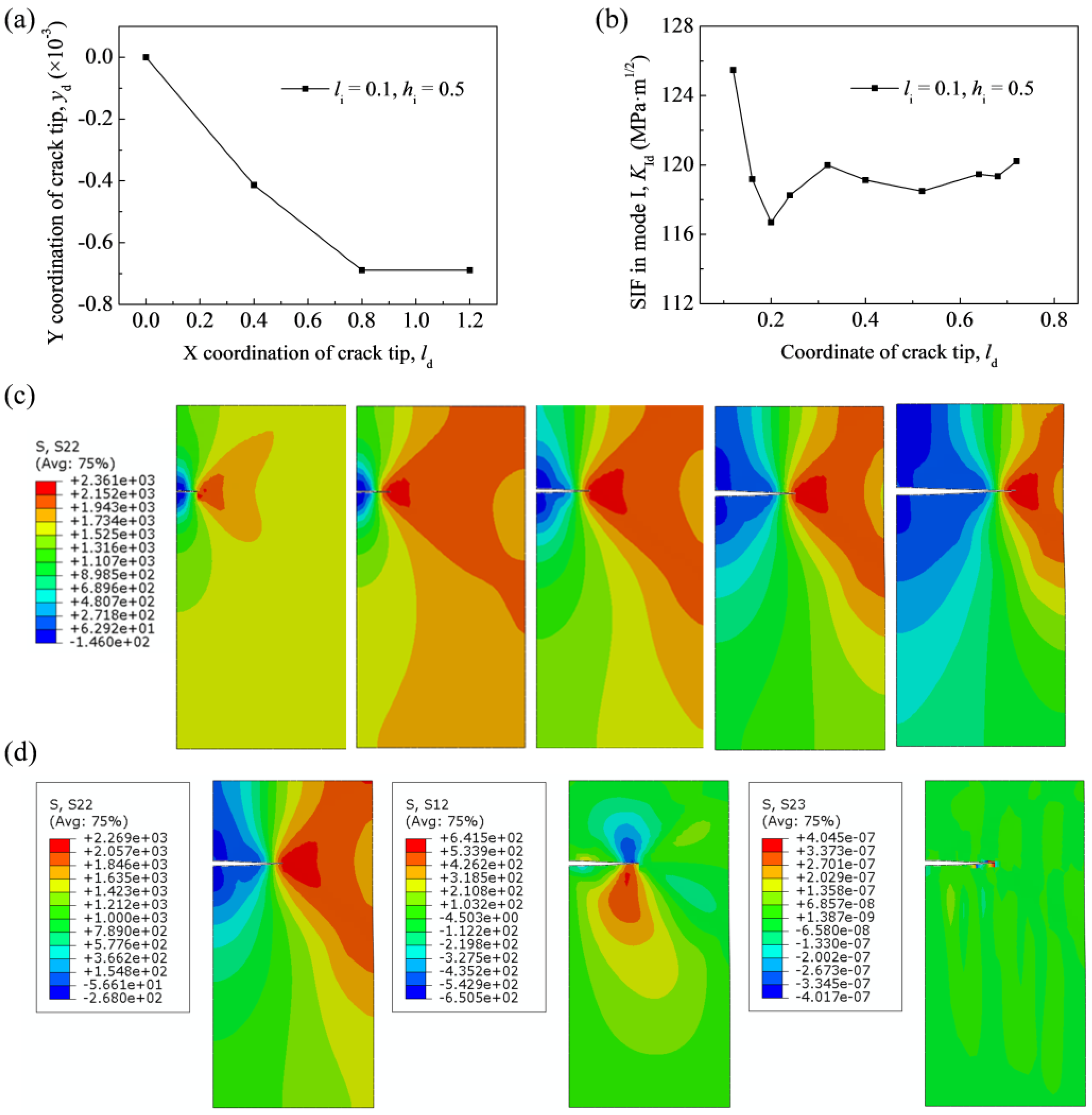
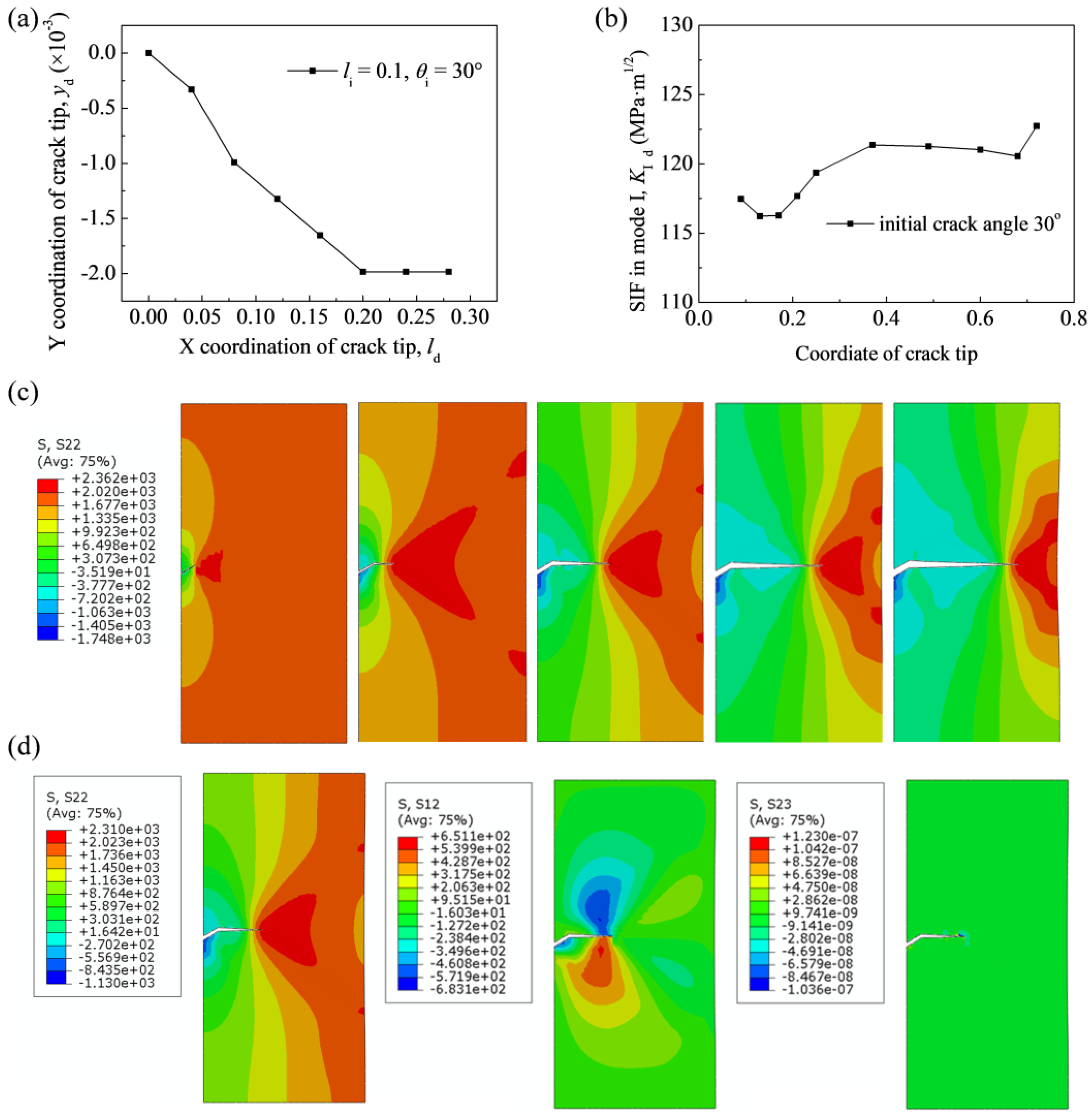
3.2. Propagation Behavior of Crack with an Offset

If the crack is offset, namely h_i > 0, there is a turning in the crack path and the crack propagation angle shows an inward tendency. The crack propagation path shows an exponential decline from the beginning of the crack propagation process when h_i = 0.5 and l_i = 0.1 (Figure 5a). The stress contours in the crack propagation process are presented in Figure 5c, where the stress distribution in front of the crack tip shows more severe asymmetry at the beginning of the crack propagation caused by the offset of the crack location. Additionally, the fracture mode could be regarded as mode I, since S₂₂ is much larger than S₁₂ and S₂₃ (Figure 5d). The boundary effect also exerts a nontrivial influence on K_Id in the propagation process of the crack with an offset recorded (Figure 5b).

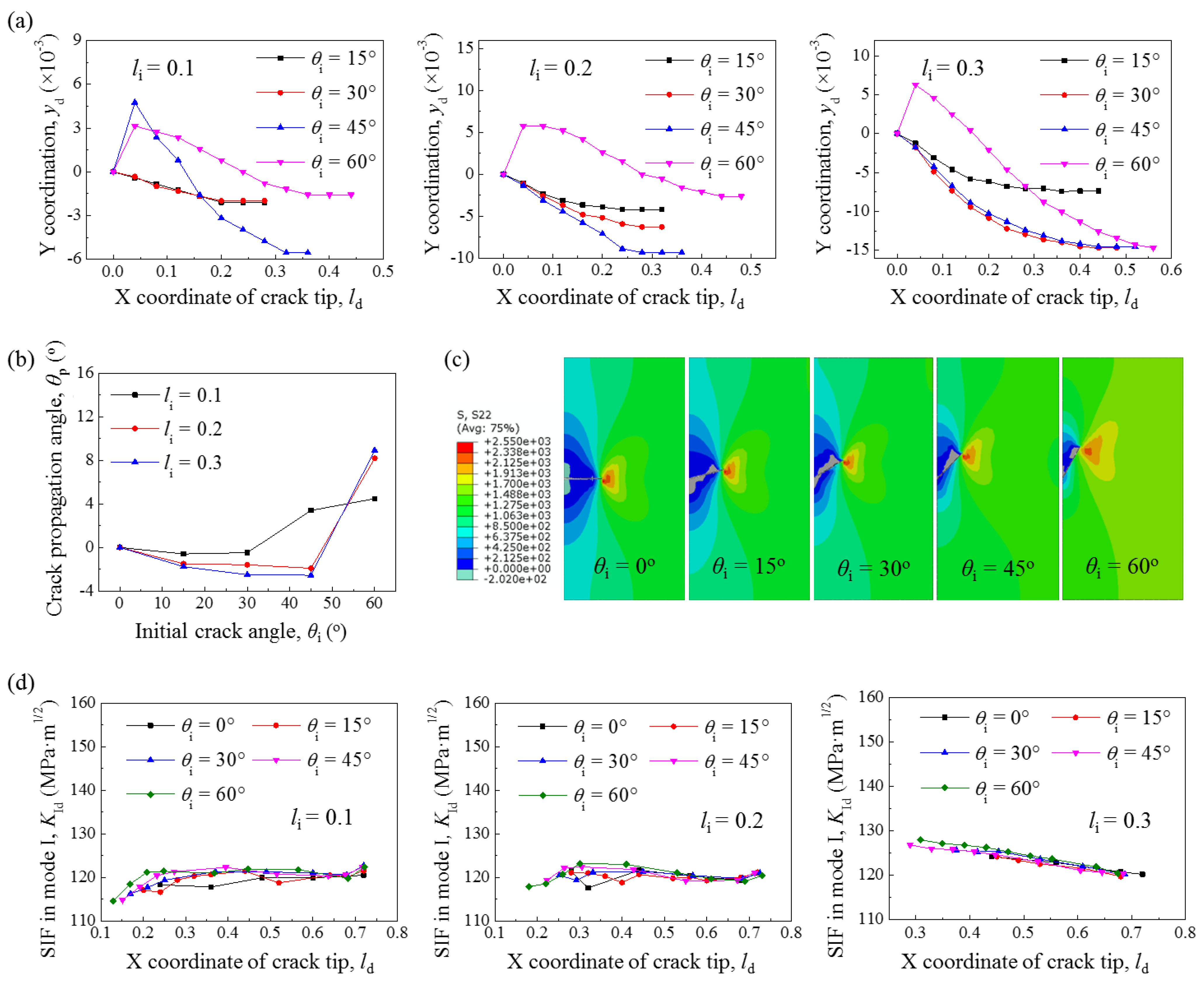
3.3. Propagation Behavior of Crack with an Initial Angle

It is possible that the crack is not always parallel to the plate boundary in real engineering applications. When the crack starts to propagate, its path deflects inward, and the Y coordinate of the crack tip gradually declines in an exponent shape (Figure 6a). The stress contour in front of the crack tip is more asymmetric in the beginning (Figure 6c). One may observe that S₂₂ is far larger than S₁₂ and S₂₃ (Figure 6d), indicating a mode I fracture. K_Id in the propagation process exhibits a plateau stage in the whole process, without the beginning and the end section (Figure 6b).

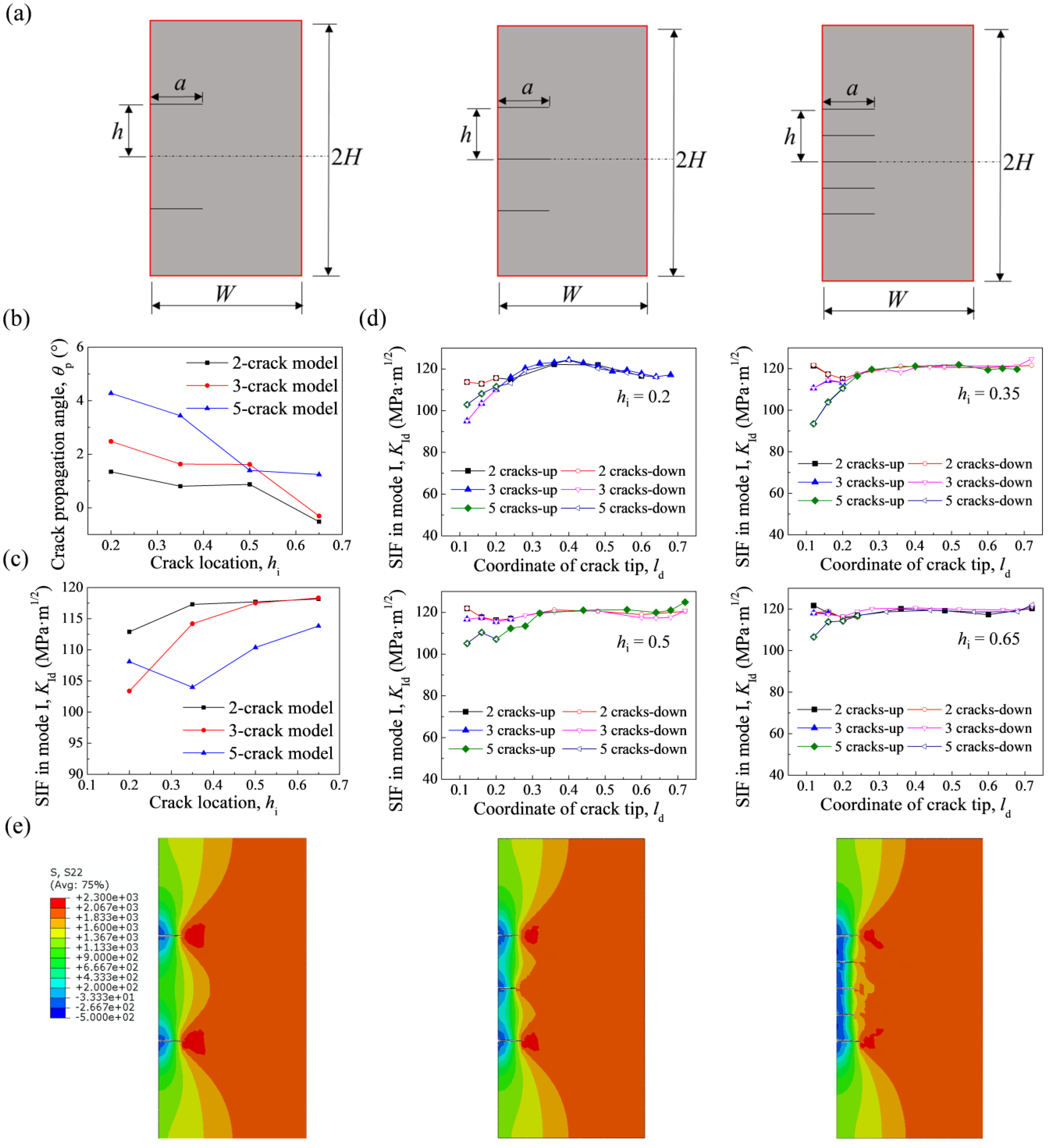
3.4. Propagation Behavior of Multi-Crack

The existence of multi-cracks imposes significant influence on the crack propagation process. In the two-crack model with l_i = 0.1 and h_i = 0.5, two cracks would not propagate simultaneously after some time due to the residual numerical error accumulation during the propagation process. Thus, only the beginning section is taken into consideration when two cracks propagate simultaneously. An outward deflection is observed and the Y coordinate of the crack tip shows a gradual increase (Figure 7a). The decrease of the deflection angle could also be explained based on the stress distribution in the stress contour, which is more asymmetric in the beginning than in the later propagation process (Figure 7c). Mode I fracture is observed since S₂₂ is larger than S₁₂ and S₂₃ (Figure 7d). A steady plateau of K_Id is observed in the beginning, followed by a sharp increase in the end of the crack propagation procedure (Figure 7b). The sharp surge of K_Id in the end may be attributed to the influence of the boundary effect.

4. Discussion

4.1. Influence of Initial Crack Length

The crack propagation angle of the initial crack length in the range from 0.1 to 0.3 shows a significant increase trend when the crack location h_i increases from 0 to 0.8 (Figure 8a). All cracks show an inward tendency, becoming closer to the middle line when h_i > 0 (Figure 8a). Straightforwardly, the line with a shorter initial crack length stays consistently higher, which means a smaller crack propagation angle than that of a longer initial crack length. The influence of l_i can be attributed to the change in the stress field. When the initial crack starts to propagate when l_i equals 0.1, 0.2, and 0.3 at crack location 0.5, the asymmetry of the stress contour in front of the crack tip on the plate determines the value of the crack propagation direction (Figure 8b). This also changes with the increase in initial crack length and the crack location.

For a brief comparison, only the plateau stage in the line describing K_Ids in the crack propagation process is selected, and all stress contours are normalized. K_Id in the crack tip nearly keeps steady in the crack propagation process when the initial crack length ranges from 0.04 to 0.2 (Figure 8c), indicating the initial crack length has little influence on K_Id, which could also be verified through the stress contour (Figure 8d). The distribution stress contour and K_Ids calculated at the first and the last two points change dramatically because of the boundary effect and may result in a comparatively large error in reflecting the real stress state at the crack tip. If the first two points are excluded, K_Ids in Figure 4a, Figure 5d, Figure 6c and Figure 8d fluctuate around an average value, with the difference less than 4%, which is within the error tolerance of the FE method and K_Ids could be regarded as remaining stable in the propagation process.

4.2. Influence of Crack Location

The crack propagation angle gradually becomes larger as the crack location changes from 0 to 0.8 in the crack length range l_i from 0.1 to 0.3 (Figure 9a). The crack propagation stays zero when h_i = 0. The crack propagation angles increase from 0 to 1.86°, 3.89°, and 5.39°, respectively, in three lines of different crack lengths as h_i increases from 0 to 0.8. The responsible reason should be the influence of h_i on the change of stress distribution. Clearly, the asymmetry of the stress contour in front of the crack tip shows an increase with the increase of the crack location, namely the value of h_i (Figure 9b).

As h_i increases, K_Id exhibits a smaller value consistently than that of a smaller crack location (Figure 9c), which could be attributed to the change of the stress distribution in front of the crack tip. The observed high stress region in red color declines gradually as the crack location increases, leading to a smaller value of K_Id.

4.3. Influence of Initial Crack Angle

In the FE model with different initial crack angles, the locations of all cracks tip experience an exponential decline and finally stay steady at a certain value (Figure 10a). The crack inclines inward gradually with the initial angle, while after reaching its lowest point, the inward crack propagation angle starts to increase and finally changes to an outward angle (Figure 10b). The combination of the change of the X and Y coordinates of the initial crack tip and the stress field in the plate model dominate the crack path, further evidenced by stress contour change (Figure 10c) with the initial crack angle ranging from 0° to 60° when l_i = 0.3. In general, K_Id of different initial crack angles is seldom influenced by the initial angle since the stress field does not change much (Figure 10d).

4.4. Influence of Crack Number

To investigate the crack propagation behavior in AerMet 100 plate model, models with two cracks, three cracks or five cracks are established (Figure 11a). Cracks distribute systematically about the middle line of the model. The initial crack length l_i = 0.1 for all models, and the outer crack location h_i ranges from 0.2 to 0.65. The crack propagation angle increases with the number of cracks at each h_i (Figure 11b). The K_Ids in two outer cracks in all models, namely the upper and the lower, are calculated and compared to figure out the influence of the crack number (Figure 11c). As K_Ids in the upper and lower cracks stay nearly the same; for a brief comparison, the second points in all lines are selected out. Generally, when the crack tip propagates to the same location, the K_Id in the model with fewer cracks expresses a higher value (Figure 11d). Both the effects on the crack propagation angle and the K_Id can be explained through the change of stress contours (Figure 11e) when the crack tip propagates to 0.16 at crack location 0.35. The stress distribution exhibits a more severe asymmetry in front of the upper and the lower cracks, leading to a bigger crack propagation angle. On the other hand, the high-stress region shows an obvious decrease as the crack number increases, which contributes to the declination of K_Id.

5. Conclusions

The crack propagation behavior of AerMet 100 plays a critical role in the engineering application of the material in heavy load-bearing structures and mechanical parts, and single-crack problems, with or without inclination, and multi-crack problems are constant threats in practical engineering. In this paper, a 1/2 model of AerMet 100 plate with in-plane crack was established, and its typical crack propagation behavior was obtained through XFEM. Correspondingly, the physical variables were summarized and extracted based on the suggested extrapolation method. Then, the crack propagation behaviors in the AerMet 100 plate model with varied initial crack lengths, locations, angles, and numbers were investigated. Some conclusions about the research content of this paper were obtained:

• The crack propagation angle showed a significant increasing trend when the initial crack length and the initial crack location increased, which could be attributed to the asymmetry of the stress contour in front of the crack tip.
• The initial crack length had little influence on K_Id, while K_Id exhibited a smaller value as the crack location increased casing the declined of the stress level.
• The inward crack propagation angle slowly increased and finally turned into an outward angle until the initial crack angle reached about 45°, while K_Id rarely changed.
• More cracks in the model would enhance the deflection in the propagation process and lead to a smaller K_Id value in the crack tip.

The results may lay a solid foundation for the study of the crack propagation behavior of AerMet 100, subject to mechanical loadings, and enable theoretical predictions for the mode I cracking behaviors of the AerMet 100 plate.