Modeling and Simulation Investigations on Microstructure Evolution during Additive Manufacturing of AlSi10Mg Alloy
Abstract
:1. Introduction
2. Model Description and Experimental Procedure
2.1. Solute Distribution
2.2. Interface Growth Kinetics
2.3. Nucleation Mechanism
2.4. Simulation Parameters and Experimental Methods
3. Results and Discussion
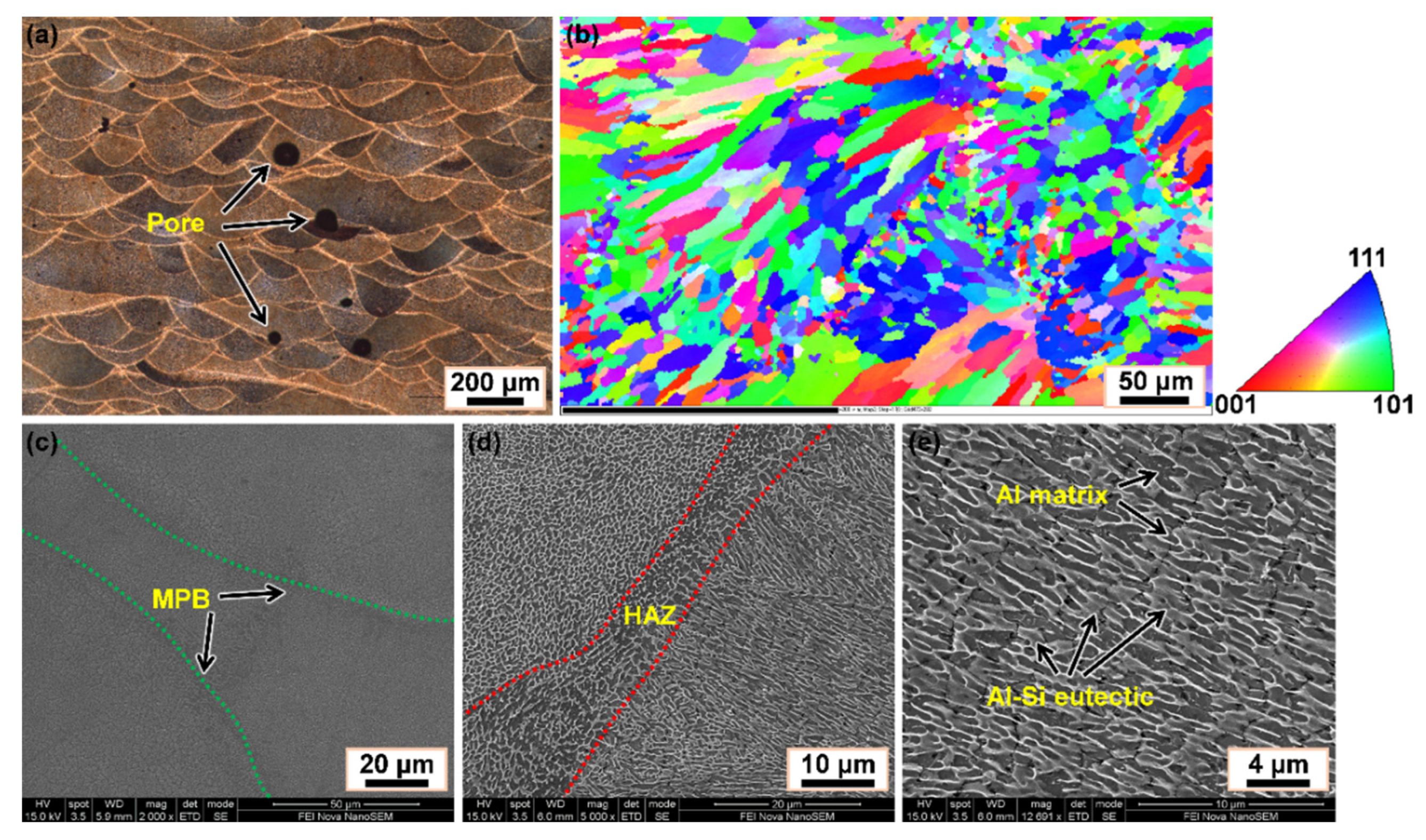
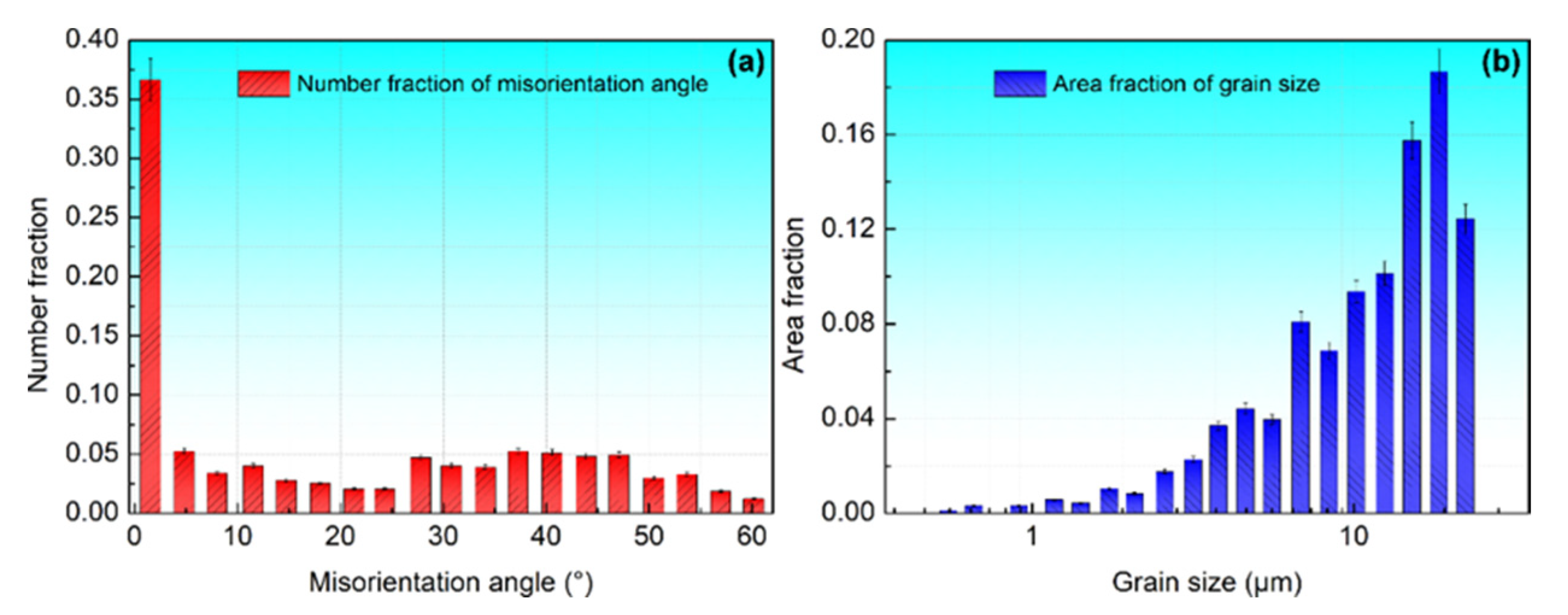
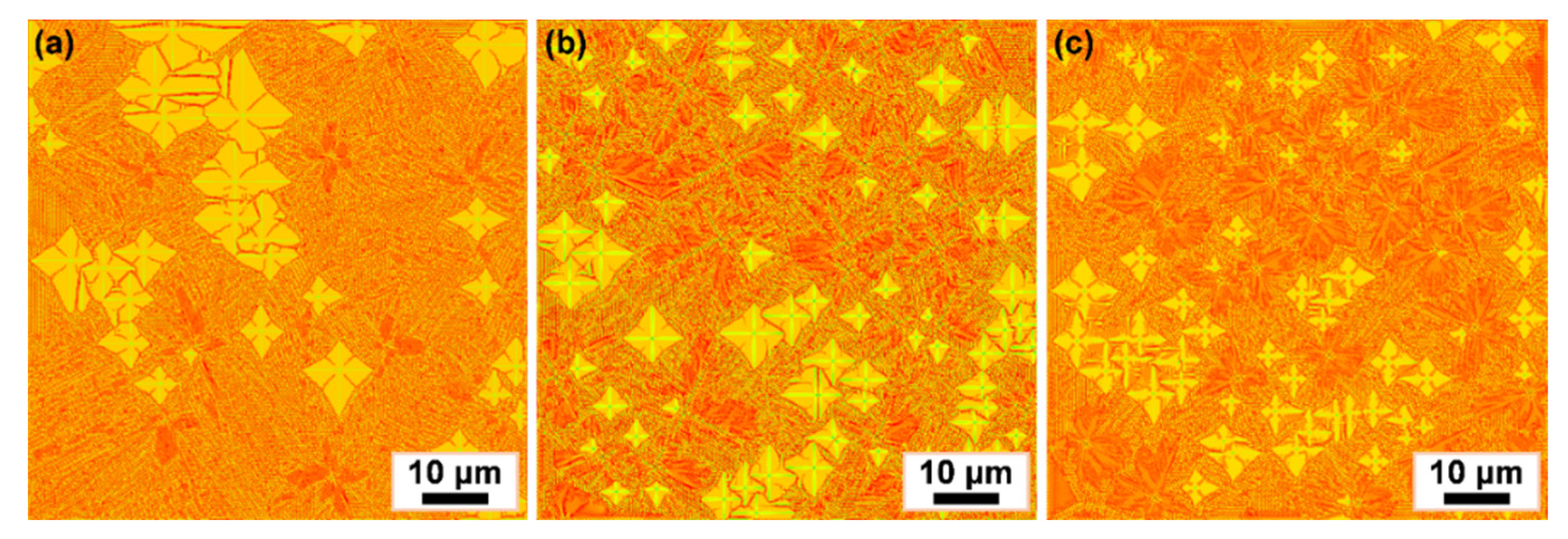
3.1. Experimental Observation of Microstructures
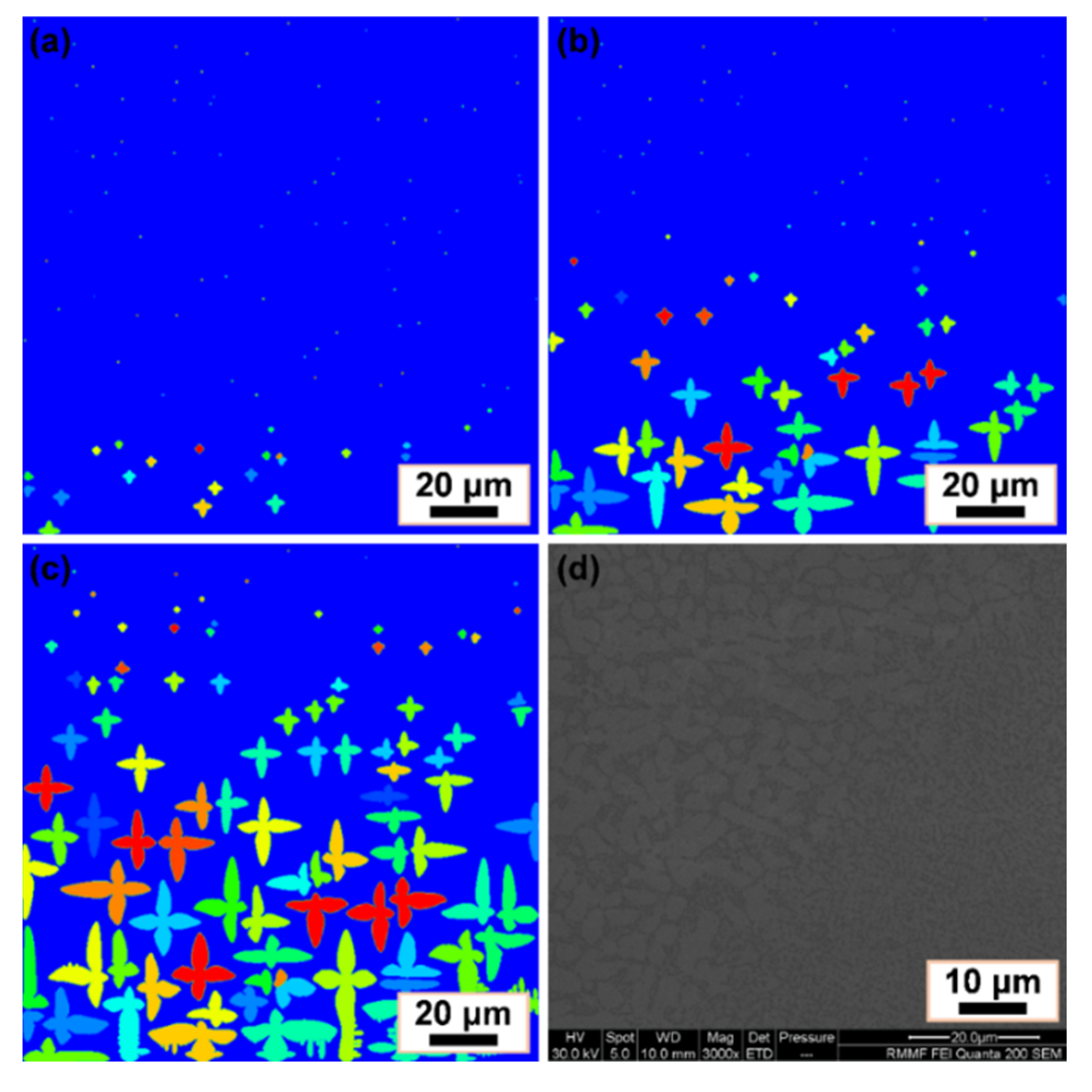
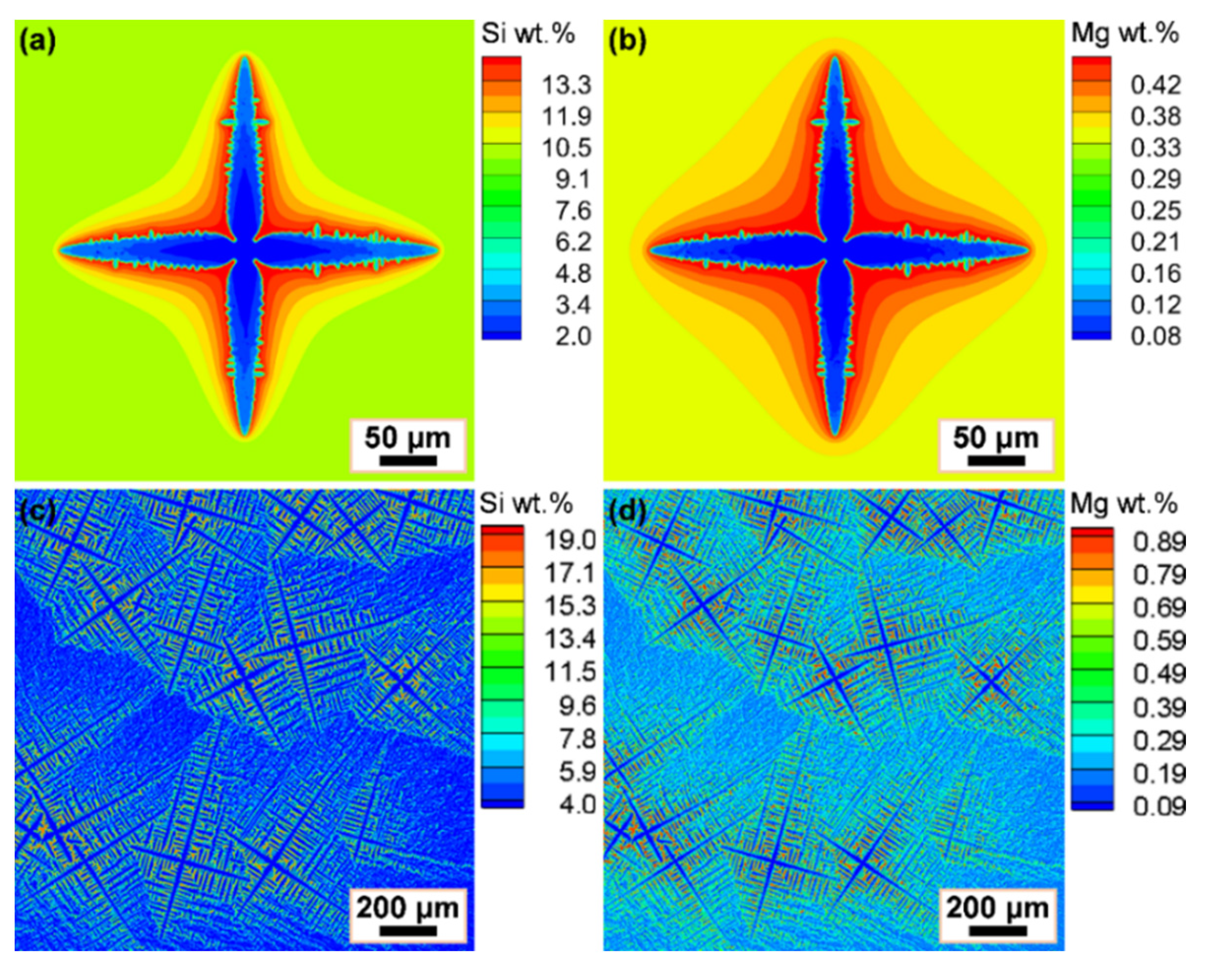
3.2. Dendrite Growth of AlSi10Mg Ternary Alloy
3.3. Simulation of Al-Si Eutectic Evolution
4. Conclusions
- (1)
- An integrated primary dendrite and eutectic evolution model based on the CA-FD method, taking account of solute distribution, growth kinetics and nucleation mechanism, was developed. The proposed model would be helpful for describing the time-dependent dendrite and eutectic growth during the nonequilibrium solidification process and understanding the microstructure evolution of Al-Si system alloys. However, the presented model is also preliminary and simplified, and there are some restrictions, such as not considering the influence of fluid flow and gravity, which need to be further refined in the future work.
- (2)
- Dendrite growth of AlSi10Mg alloy was simulated by the proposed model and various gradients initialized to imitate real heat transfer in the melt pool during SLM. The experimental dendrites obtained by SEM presented good agreement with the simulation. Single and multi-equiaxed dendritic morphologies of AlSi10Mg ternary alloy were simulated, and it was found that solute diffusion had a significant influence on dendrite growth. The influence of cooling rate on dendrite characteristics was further investigated, and the results indicated that dendrites were refined with the increasing of the cooling rates.
- (3)
- The Al-Si eutectic evolution in AlSi10Mg alloy was simulated, and corresponding experimental validation was also carried out, and both of them agreed reasonably well. Finally, the proposed model was applied to investigate the effect of undercooling on eutectic morphology, and simulations with the eutectic undercooling of 5 K, 15 K and 20 K were performed. The simulated results revealed that Al-Si eutectic morphologies were sensitive to the eutectic undercooling such that a higher eutectic undercooling can refine the eutectic microstructure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Starke, E.A., Jr.; Staley, J.T. Application of modern aluminum alloys to aircraft. Prog. Aerosp. Sci. 1996, 32, 131–172. [Google Scholar] [CrossRef]
- Miller, W.S.; Zhuang, L.; Bottema, J.; Wittebrood, A.J.; De Smet, P.; Haszler, A.; Vieregge, A. Recent development in aluminium alloys for the automotive industry. Mater. Sci. Eng. A 2000, 280, 37–49. [Google Scholar] [CrossRef]
- Dursun, T.; Soutis, C. Recent developments in advanced aircraft aluminium alloys. Mater. Des. 2014, 56, 862–871. [Google Scholar] [CrossRef]
- Javidani, M.; Larouche, D. Application of cast Al-Si alloys in internal combustion engine components. Int. Mater. Rev. 2014, 59, 132–158. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.; Hu, J. Recent advances in the development of aerospace materials. Prog. Aerosp. Sci. 2018, 97, 22–34. [Google Scholar] [CrossRef]
- Kempen, K.; Thijs, L.; Van Humbeeck, J.; Kruth, J.P. Processing AlSi10Mg by selective laser melting: Parameter optimisation and material characterization. Mater. Sci. Technol. 2015, 31, 917–923. [Google Scholar] [CrossRef]
- Paoletti, C.; Santecchia, E.; Cabibbo, M.; Cerri, E.; Spigarelli, S. Modelling the creep behavior of an AlSi10Mg alloy produced by additive manufacturing. Mater. Sci. Eng. A 2021, 799, 140138. [Google Scholar] [CrossRef]
- Li, W.; Li, S.; Liu, J.; Zhang, A.; Zhou, Y.; Wei, Q.; Yan, C.; Shi, Y. Effect of heat treatment on AlSi10Mg alloy fabricated by selective laser melting: Microstructure evolution, mechanical properties and fracture mechanism. Mater. Sci. Eng. A 2016, 663, 116–125. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, C.; Zhou, X.; Shen, Z.; Liu, W. Microstructure of selective laser melted AlSi10Mg alloy. Mater. Des. 2019, 168, 107677. [Google Scholar] [CrossRef]
- Wu, J.; Wang, X.; Wang, W.; Attallah, M.M.; Loretto, M.H. Microstructure and strength of selectively laser melted AlSi10Mg. Acta Mater. 2016, 117, 311–320. [Google Scholar] [CrossRef]
- Dasgupta, R. Property improvement in Al-Si alloys through rapid solidification processing. J. Mater. Process. Technol. 1997, 72, 380–384. [Google Scholar] [CrossRef]
- Shabestari, S.G.; Moemeni, H. Effect of copper and solidification conditions on the microstructure and mechanical properties of Al-Si-Mg alloys. J. Mater. Process. Technol. 2004, 153–154, 193–198. [Google Scholar] [CrossRef]
- Reed, N.; Wang, W.; Essa, K.; Attallah, M.M. Selective laser melting of AlSi10Mg alloy: Process optimization and mechanical properties development. Mater. Des. 2015, 65, 417–424. [Google Scholar] [CrossRef] [Green Version]
- Guo, M.; Sun, M.; Huang, J.; Pang, S. A comparative study on the microstructures and mechanical properties of Al-10Si-0.5Mg alloys prepared under different conditions. Metals 2022, 142, 2010142. [Google Scholar] [CrossRef]
- Martin, J.H.; Yahata, B.D.; Hundley, J.M.; Mayer, J.A.; Schaedler, T.A.; Pollock, T.M. 3D printing of high-strength aluminium alloys. Nature 2017, 549, 365–369. [Google Scholar] [CrossRef]
- Panwisawas, C.; Tang, Y.T.; Reed, R.C. Metal 3D printing as a disruptive technology for superalloys. Nat. Commun. 2020, 11, 2327. [Google Scholar] [CrossRef] [PubMed]
- Zinoviev, A.; Zinovieva, O.; Ploshikhin, V.; Romanova, V.; Balokhonov, R. Evolution of grain structure during laser additive manufacturing. Simulation by a cellular automata method. Mater. Des. 2016, 106, 321–329. [Google Scholar] [CrossRef]
- Lian, Y.; Gan, Z.; Yu, C.; Kats, D.; Liu, W.K.; Wagner, G.J. A cellular automaton finite volume method for microstructure evolution during additive manufacturing. Mater. Des. 2019, 169, 107672. [Google Scholar] [CrossRef]
- Xiong, F.; Huang, C.; Kafka, O.L.; Lian, Y.; Yan, W.; Chen, M.; Fang, D. Grain growth prediction in selective electron beam melting of Ti-6Al-4V with a cellular automaton method. Mater. Des. 2021, 199, 109410. [Google Scholar] [CrossRef]
- Sahoo, S.; Chou, K. Phase-field simulation of microstructure evolution of Ti-6Al-4V in electron beam additive manufacturing process. Addit. Manuf. 2016, 9, 14–24. [Google Scholar] [CrossRef]
- Lu, L.; Sridhar, N.; Zhang, Y. Phase field simulation of powder bed-based additive manufacturing. Acta Mater. 2018, 144, 801–809. [Google Scholar] [CrossRef]
- Yang, M.; Wang, L.; Yan, W. Phase-field modeling of grain evolutions in additive manufacturing from nucleation, growth, to coarsening. Npj Comput. Mater. 2021, 7, 56. [Google Scholar] [CrossRef]
- Chadwick, A.F.; Voorhees, P.W. The development of grain structure during additive manufacturing. Acta Mater. 2021, 211, 116862. [Google Scholar] [CrossRef]
- Rai, A.; Markl, M.; Körner, C. A coupled cellular automaton-lattice boltzmann model for grain structure simulation during additive manufacturing. Comput. Mater. Sci. 2016, 124, 37–48. [Google Scholar] [CrossRef]
- Akram, J.; Chalavadi, P.; Pal, D.; Stucker, B. Understanding grain evolution in additive manufacturing through modeling. Addit. Manuf. 2018, 21, 255–268. [Google Scholar] [CrossRef]
- Zinovieva, O.; Zinoviev, A.; Ploshikhin, V. Three-dimensional modeling of the microstructure evolution during metal additive manufacturing. Comput. Mater. Sci. 2018, 141, 207–220. [Google Scholar] [CrossRef]
- Lian, Y.; Lin, S.; Yan, W.; Liu, W.K.; Wagner, G.J. A parallelized three-dimensional cellular automaton model for grain growth during additive manufacturing. Comput. Mech. 2018, 61, 543–558. [Google Scholar] [CrossRef]
- Shi, R.; Khairallah, S.A.; Roehling, T.T.; Heo, T.W.; McKeown, J.T.; Matthews, M.J. Microstructural control in metal laser powder bed fusion additive manufacturing using laser beam shaping strategy. Acta Mater. 2020, 184, 284–305. [Google Scholar] [CrossRef]
- Mohebbi, M.S.; Ploshikhin, V. Implementation of nucleation in cellular automaton simulation of microstructural evolution during additive manufacturing of Al alloys. Addit. Manuf. 2020, 36, 101726. [Google Scholar] [CrossRef]
- Rappaz, M.; Gandin, C.A. Probabilistic modelling of microstructure formation in solidification processes. Acta Metall. Mater. 1993, 41, 345–360. [Google Scholar] [CrossRef]
- Wang, W.; Lee, P.D.; McLean, M. A model of solidification microstructures in nickel-based superalloys: Predicting primary dendrite spacing selection. Acta Mater. 2003, 51, 2971–2987. [Google Scholar] [CrossRef]
- Yan, X.; Xu, Q.; Liu, B. Numerical simulation of dendrite growth in nickel-based superalloy and validated by in-situ observation using high temperature confocal laser scanning microscopy. J. Cryst. Growth 2017, 479, 22–33. [Google Scholar] [CrossRef]
- Bayat, M.; Dong, W.; Thorborg, J.; To, A.C.; Hattel, J.H. A review of multi-scale and multi-physics simulations of metal additive manufacturing processes with focus on modeling strategies. Addit. Manuf. 2021, 47, 102278. [Google Scholar] [CrossRef]
- Chen, R.; Xu, Q.; Liu, B. Modeling of aluminum-silicon irregular eutectic growth by cellular automaton model. China Foundry 2016, 13, 114–122. [Google Scholar] [CrossRef] [Green Version]
- Dahle, A.K.; Nogita, K.; Zindel, J.W.; Mcdonald, S.D.; Hogan, L.M. Eutectic nucleation and growth in hypoeutectic Al-Si alloys at different strontium levels. Metall. Mater. Trans. 2001, 32, 949–960. [Google Scholar] [CrossRef]
- Nafisi, S.; Ghomashchi, R.; Vali, H. Eutectic nucleation in hypoeutectic Al-Si alloys. Mater. Charact. 2008, 59, 1466–1473. [Google Scholar] [CrossRef]
- Sun, Y.; Pang, S.; Liu, X.; Yang, Z.; Sun, G. Nucleation and growth of eutectic cell in hypoeutectic Al-Si alloy. Trans. Nonferr. Metal. Soc. 2011, 21, 2186–2191. [Google Scholar] [CrossRef]
- Zhu, M.F.; Hong, C.P. Modeling of microstructure evolution in regular eutectic growth. Phys. Rev. B 2002, 66, 155428. [Google Scholar] [CrossRef]
- Xiong, S.; Wu, M. Experimental and modeling studies of the lamellar eutectic growth of Mg-Al alloy. Metall. Mater. Trans. A 2012, 43, 208–218. [Google Scholar] [CrossRef]
- Ye, H. An overview of the development of Al-Si-alloy based material for engine applications. J. Mater. Eng. Perform. 2003, 12, 288–297. [Google Scholar] [CrossRef]
- Paul, M.J.; Liu, Q.; Best, J.P.; Li, X.P.; Kruzic, J.J.; Ramamurty, U.; Gludovatz, B. Fracture resistance of AlSi10Mg fabricated by laser powder bed fusion. Acta Mater. 2021, 211, 116869. [Google Scholar] [CrossRef]
- Xiong, Z.; Liu, S.; Li, S.; Shi, Y.; Yang, Y.; Misra, R.D.K. Role of melt pool boundary condition in determining the mechanical properties of selective laser melting AlSi10Mg alloy. Mater. Sci. Eng. A 2019, 740–741, 148–156. [Google Scholar] [CrossRef]
- Yan, X.; Xu, Q.; Tian, G.; Liu, Q.; Hou, J.; Liu, B. Multi-scale modeling of liquid-metal cooling directional solidification and solidification behavior of nickel-based superalloy casting. J. Mater. Sci. Technol. 2021, 67, 36–49. [Google Scholar] [CrossRef]
- Chen, R.; Xu, Q.; Liu, B. Cellular automaton simulation of three-dimensional dendrite growth in Al-7Si-Mg ternary aluminum alloys. Comput. Mater. Sci. 2015, 105, 90–100. [Google Scholar] [CrossRef] [Green Version]
- Ao, X.; Xia, H.; Liu, J.; He, Q.; Lin, S. A numerical study of irregular eutectic in Al-Si alloys under a large undercooling. Comput. Mater. Sci. 2021, 186, 110049. [Google Scholar] [CrossRef]
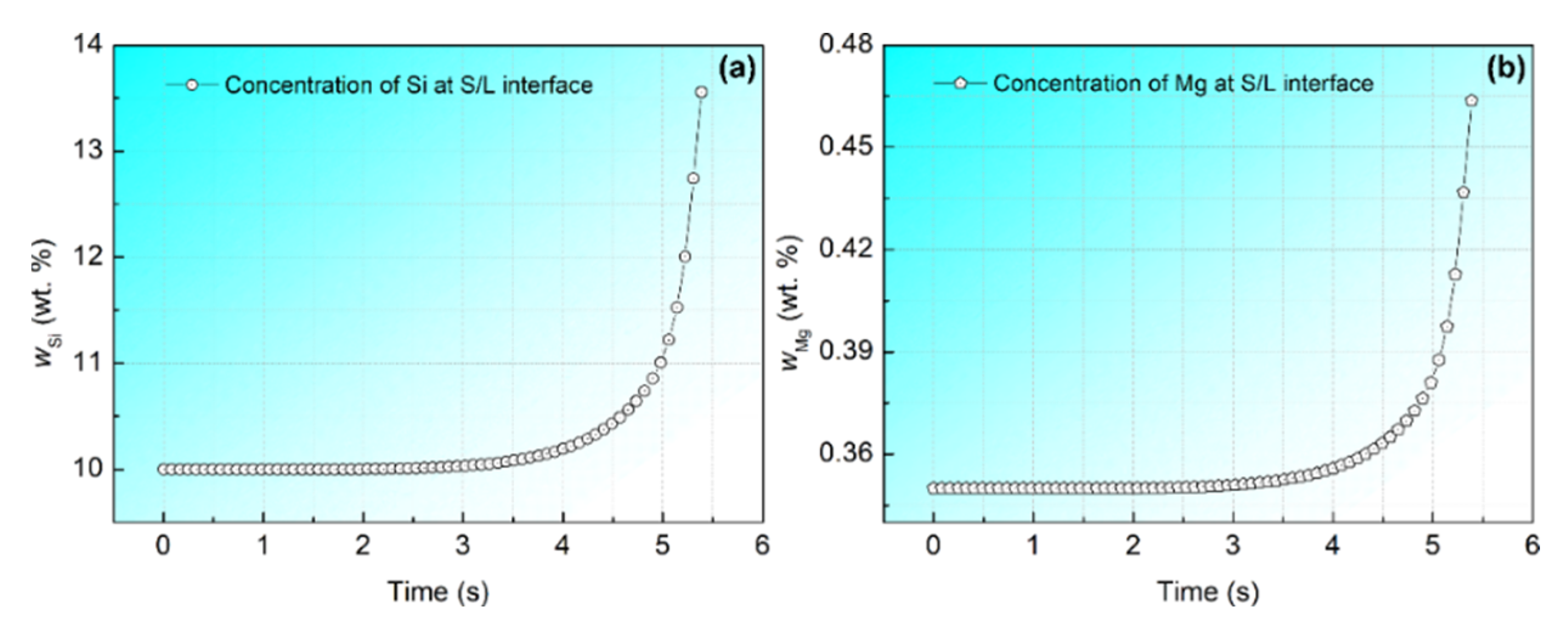


| Parameter (Unit) | Value | Reference |
|---|---|---|
| Liquidus temperature TL (K) | 873 | [29] |
| Eutectic temperature TE (K) | 850 | [40] |
| Eutectic composition wE′ (wt.%) | 12.6 | [40] |
| Solubility in α-phase wα0 (wt.%) | 1.65 | [34] |
| Solubility in β-phase wβ0 (wt.%) | 77.5 | [34] |
| Liquidus slope of α-phase mα (K/wt.%) | −6.83 | [29] |
| Liquidus slope of β-phase mβ (K/wt.%) | 17.5 | [34] |
| Liquid diffusion coefficient DL (m2/s) | 2.4 × 10−9 | [29] |
| Solid diffusion coefficient DS (m2/s) | 3.0 × 10−12 | [34] |
| Gibbs–Thomson coefficient of α-phase Γα (m·K) | 2.4 × 10−7 | [29] |
| Gibbs–Thomson coefficient of β-phase Γβ (m·K) | 1.7 × 10−7 | [34] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Yang, X.; Tian, G.; Sun, D.; Liu, S.; Xiong, Z.; Wen, Z.; Xu, Q. Modeling and Simulation Investigations on Microstructure Evolution during Additive Manufacturing of AlSi10Mg Alloy. Metals 2022, 12, 1711. https://doi.org/10.3390/met12101711
Yan X, Yang X, Tian G, Sun D, Liu S, Xiong Z, Wen Z, Xu Q. Modeling and Simulation Investigations on Microstructure Evolution during Additive Manufacturing of AlSi10Mg Alloy. Metals. 2022; 12(10):1711. https://doi.org/10.3390/met12101711
Chicago/Turabian StyleYan, Xuewei, Xuemei Yang, Guoqiang Tian, Dejian Sun, Shilong Liu, Zhihui Xiong, Zhenhua Wen, and Qingyan Xu. 2022. "Modeling and Simulation Investigations on Microstructure Evolution during Additive Manufacturing of AlSi10Mg Alloy" Metals 12, no. 10: 1711. https://doi.org/10.3390/met12101711
APA StyleYan, X., Yang, X., Tian, G., Sun, D., Liu, S., Xiong, Z., Wen, Z., & Xu, Q. (2022). Modeling and Simulation Investigations on Microstructure Evolution during Additive Manufacturing of AlSi10Mg Alloy. Metals, 12(10), 1711. https://doi.org/10.3390/met12101711








