Effect of Al Content on the Microstructural and Grain Growth Kinetics of Magnesium Alloys

Abstract

In order to control the grain size in thermomechanical processing, the grain growth behavior of hot extruded Mg–xAl–1Zn (x = 3, 6, 9) alloys and their relationship with second phase particles and solutes were investigated. The growth rate of AZ61 is greater than that of AZ31 and AZ91 at 300 °C, 350 °C, 400 °C, and 450 °C under isothermal annealing. The average grain growth exponents n of Mg–xAl–1Zn (x = 3, 6, 9) alloys were 2.26, 2.33, and 2.53 at 300–400 °C, respectively. The deviation from the theoretical value of 2 was attributed to the hindrance of grain boundary migration of Al-rich second phase particles and solute Al. Microscopic observations show that the grain size of the annealed samples is closely related to the shape, volume fraction, size, and distribution position of the second phase particles. Significantly, the pinning effect is stronger for lamellar and network-like second phase particles. In addition, the pinning effect of Al-rich second phase particles plays a more important role in grain refinement than the dragging of solute Al. The growth of abnormal grains in the microstructure is attributed to the high energy difference between the preferentially oriented $<11\overline{2}0>$ grains and the surrounding grains, which drives the grain boundaries to overcome the same pinning force of the second phase particles.

1. Introduction

Magnesium (Mg) alloys are widely used in transportation because of their excellent specific strength and specific stiffness. However, Mg alloys have a hexagonal close-packed (hcp) structure with a limited number of slip systems, which result in their poor formability at room temperature. Grain refinement is one of the effective strategies to improve the poor formability of Mg alloys [1,2,3,4,5]. Thus, in order to maintain a thermally stable fine-grained structure, controlling the grain size is essential.

For some applications, thermomechanical processing is followed by various annealing schedules, during which grain growth is inevitable. So far, the grain growth behavior of Mg alloys and its key influencing factors (such as temperature, microstructure, second phase particles, solute, and texture) have been extensively explored, in which the second phase particles and solute are induced by the alloying elements. Early study found that the activation energy of grain growth kinetics of hot-rolled AZ31 Mg alloy is lower than that of pure Mg, which is attributed to its special microstructure [6]. Wang et al. [7] investigated the growth kinetics of bulk AZ31 magnesium alloy grains prepared by hot pressing, isothermal, and isochronous annealing treatments. Mohseni et al. [8] investigated the growth kinetics of hot-rolled AZ61 Mg alloy under different annealing conditions. The results show that the second phase particles during annealing can obtain fine and uniform grain size. Chang and Wu et al. [9,10] examined the effects of the second phase particle morphology, volume fraction, and size on grain growth by a phase field method, and small needle-like second phase particles can effectively slow down grain growth. Apparently, the second phase particles induced by alloying elements have a significant influence on the grain growth of Mg alloys.

The effect of alloying elements on grain growth is not only the pinning of second phase particles but also the dragging of solute [8,11,12,13]. Solute atoms affect grain growth by diffusion rate in the matrix, which is controlled by atomic radius, mass, and lattice type [14]. Ganeshan [15] and Shewmon [16] et al. studied the self-diffusion coefficients of magnesium using theoretical calculations of first principles and the continuous sectioning method with a radiotracer, respectively. The results show that the self-diffusion coefficient along the c-axis is smaller than the self-diffusion coefficient of Mg perpendicular to the c-axis. Moreau et al. [17] performed a diffusion couple study using pure Mg and Mg–Al alloys to determine the Al diffusion coefficient in hcp polycrystalline Mg. Das et al. [18] used Mg–Zn and Mg–Al diffusion coupling experiments and found that the solute (Zn and Al) diffusion coefficients in Mg crystals increase elliptically from the direction perpendicular to the basal plane toward the basal plane. Das et al. [19] found that Zn has a low diffusion rate in Mg alloys in diffusion coupling experiments of Mg single crystals. Subsequently, Jin et al. [11] demonstrated in Mg–6Zn samples that the solute Zn dragging effect reduces the migration rate at grain boundaries and limits grain growth. The grain growth is influenced by the alloying elements, which results in two modes: normal grain growth (NGG) and abnormal grain growth (AGG) [20]. Alili et al. [21] found that only NGG occurred in AZ91 magnesium alloy after annealing at 450 °C for 36 h, which must be caused by a strong effect of solutes (Zener Drag) or precipitates. Bhattacharyya et al. [22] studied the grain growth kinetics and texture evolution of the AZ31B Mg alloy during annealing at 260 to 450 °C in the AZ31B Mg alloy. The AGG was produced and attributed to solute and pinning of the second phase particles. However, the above studies mainly focused on the grain growth of Mg alloys with single element content. The effect of changes in the second phase and solute distribution induced by different Al contents on the grain growth of Mg alloys is not clear.

In this paper, the variation of the average grain size of Mg–xAl–1Zn (x = 3, 6, 9) alloys with annealing conditions is measured and quantitatively described. In addition, the distribution of second phase particles (morphology, size, volume fraction) and solutes are measured and their relationship with grain growth is discussed. These results can better understand the grain growth behavior in Mg–Al alloys.

2. Experiment

The 1 mm thick Mg–xAl–1Zn (x = 3, 6, 9) alloys plates were prepared by direct casting and subsequent hot extrusion. The chemical composition of the plates examined by X-ray Fluorescence is listed in

Table 1. Chemical composition of AZ31, AZ61, and AZ91 alloys.

Material	Chemical Composition (wt.%)
	Al	Zn	Mn	Si	Mg
AZ31	2.90	0.80	0.27	0.07	Bal.
AZ61	6.53	0.47	0.27	0.02	Bal.
AZ91	8.70	0.82	0.27	0.02	Bal.

. Samples with the sizes of 10 mm × 10 mm × 1 mm were cut from the sheets by wire electrical discharge machining. These samples were subsequently heat treated at 300 °C, 350 °C, 400 °C, and 450 °C for 12, 24, 48, 72 h, respectively, followed by air cooling to systematically examine the evolution of the microstructure.

The surfaces of the extruded and annealed samples were polished to a mirror finish with SiC paper (600/1000/2500). After that, the samples were etched with picric acid solution (1 g picric acid, 1 mL acetic acid, 2 mL distilled water, 20 mL anhydrous ethanol) for 10 s at room temperature. Research planes (RD plane, the normal of plane is rolling direction) of samples were observed by LEICA DM2500M Optical microscope (Leica, Wetzlar, Germany). The grain size measurements were performed according to the Nano Measurer 1.2 software (Fudan University, Shanghai, China), and the histogram was plotted by Origin 2018 64 Bit software (9.50.00, OriginLab, Northampton, MA, USA), where the average size of each grain was measured considering about 250 grains. The second phase particles were characterized by HITACHI S-3700N emission scanning electron microscope (Hitachi, Tokyo, Japan) combined with energy dispersive spectroscopy (EDS). The size and volume fraction of the second phase particles were obtained by using the linear intercept method and Image Tool analysis software (6.00.0000, Media Cybernetics, Inc., Rockville, MD, USA), respectively. The polished samples were electropolished in AC2 solution (800 mL ethanol, 100 mL propanol, 18.5 mL distilled water, 10 g hydroxyquinoline, 75 g citric acid, 41.5 g sodium thiocyanate, 15 mL perchloric acid) at 20 V and 0.15 A for 50 s, before Oxford Symmetry S2 electron back scattered diffraction (EBSD) prior to characterization. The grain orientation of the sample was examined by EBSD with a data acquisition step of 1 μm and the scan area was determined based on the observed area.

3. Results and Discussion

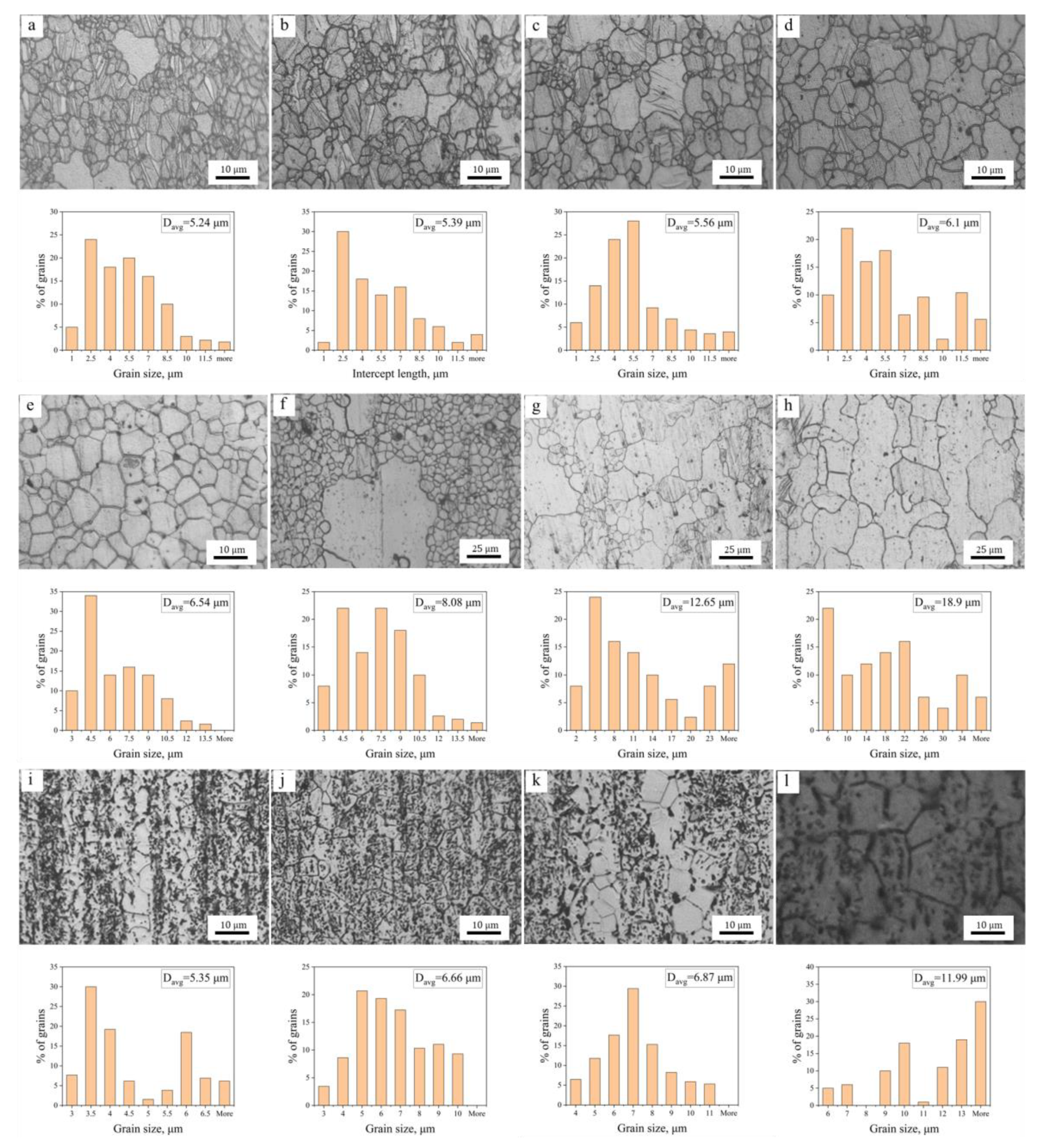
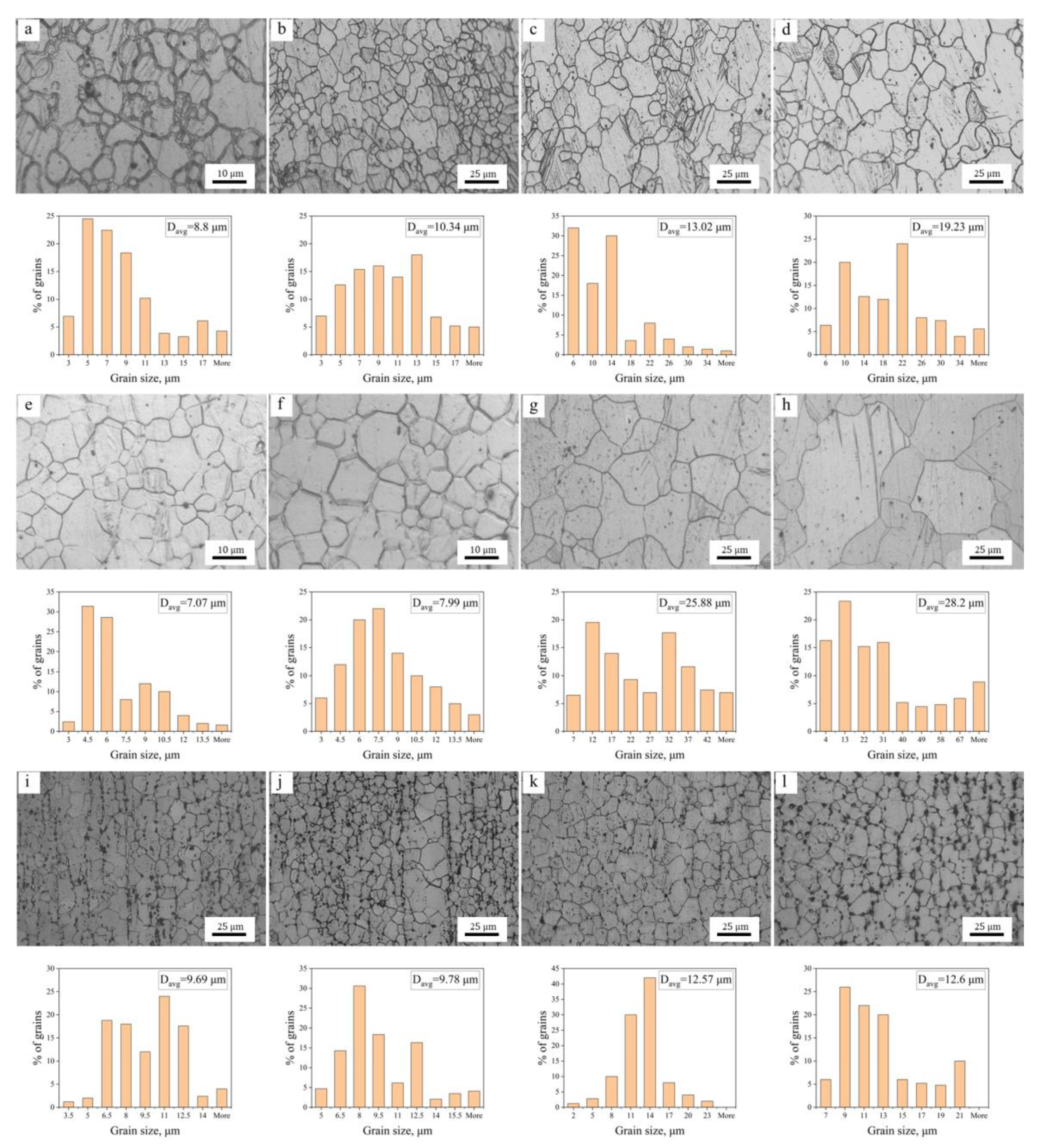
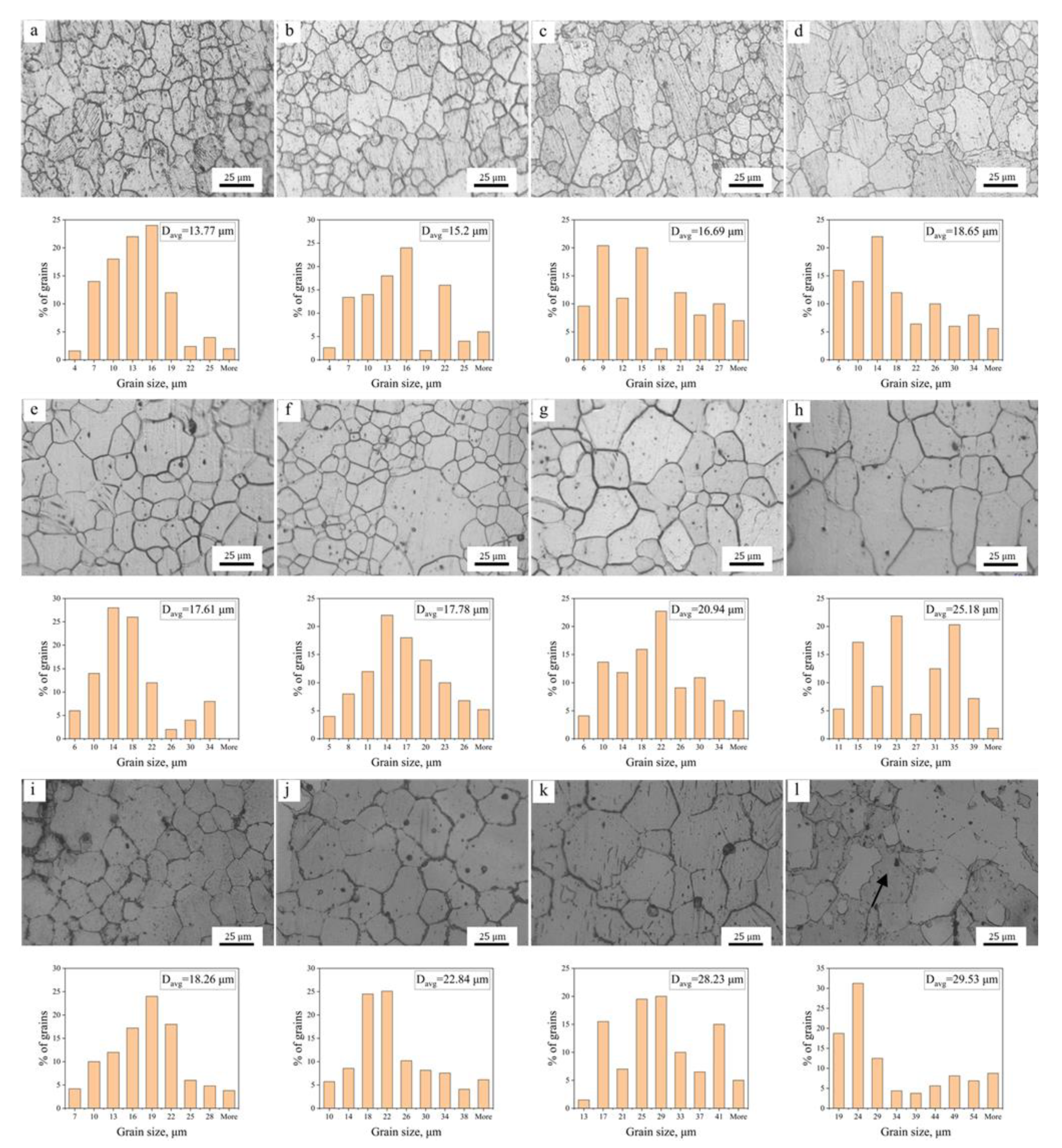
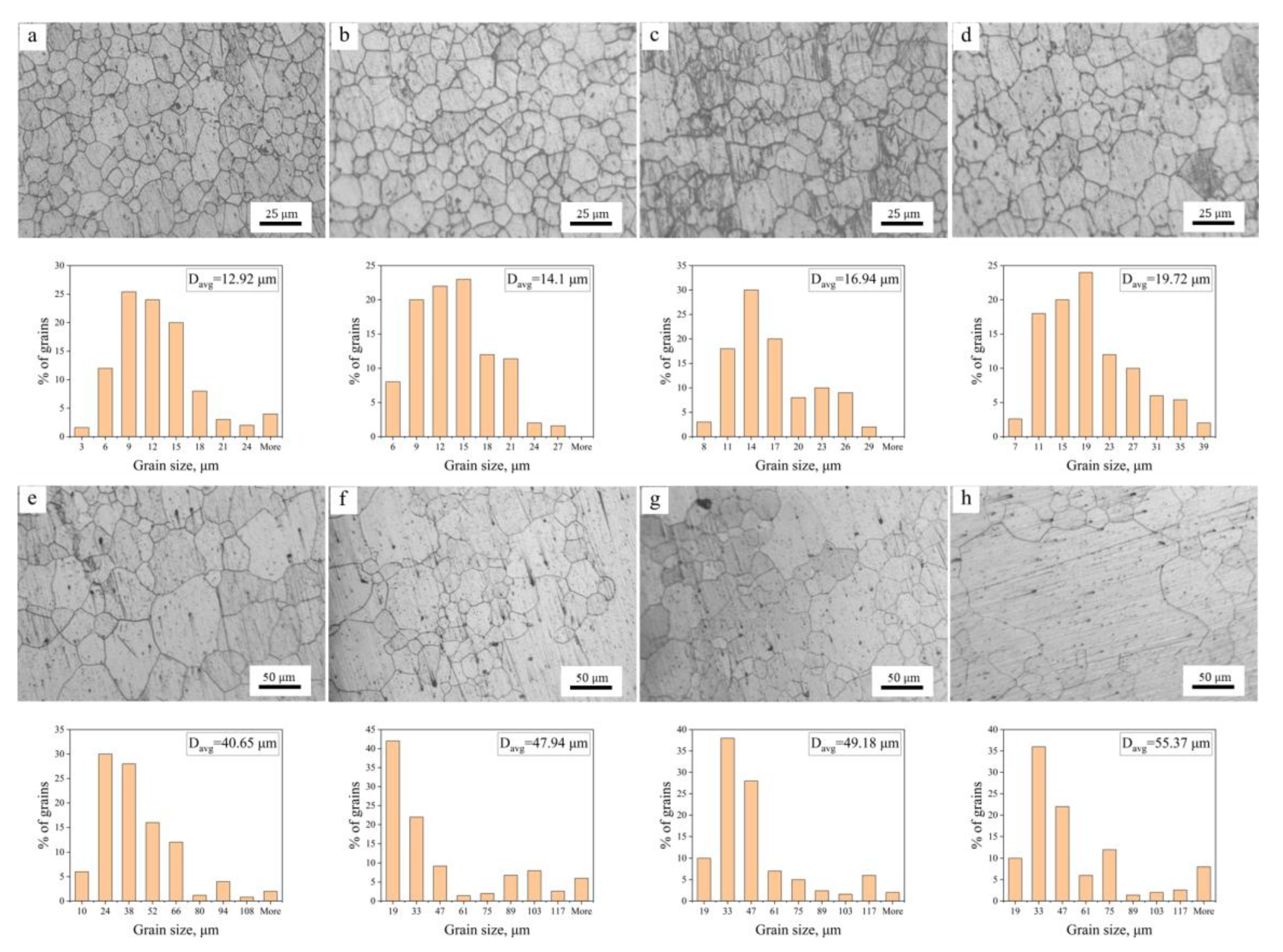
3.1. Influence of Al Content on Grain Growth

3.1.1. The Hot-Extruded State

As shown in Figure 1a–c, the extruded AZ31 exhibits an inhomogeneous microstructure with an average grain size of 5.0 µm. The extruded Mg alloys (AZ61, AZ91) are characterized in structure as an equiaxed microstructure with average grain sizes of 5.6 μm and 8.4 μm, respectively. SEM examination revealed the presence of a small amount of second phase particles in the extruded AZ31 and AZ61. The volume fractions of the second phase were 1.3% and 1.5%. With the increase in Al content, the volume fraction of the second phase in the extruded AZ91 increased to 4.0%, which tended to precipitate to grain boundaries, seen in Figure 1d–f. The EDS analysis revealed that the second phase particles pinned to the grain boundaries were rich in Al, as shown in Figure 1g–i. Similar results were obtained by repeating this analysis for many second phase particles.

3.1.2. Microstructure Evolution during Annealing

The microstructure evolutions of AZ31, AZ61, and AZ91 alloys during annealing at 300 °C are shown in Figure 2. A large quantity of small, recrystallized grains exist in AZ31, which reduces and grows as the annealing progresses, as shown in Figure 2a–d. It is evident that different degrees of growth are observed in the abnormal grains of AZ61 annealed at 300 °C for 24 h and 48 h. The histogram of grain size distribution changes significantly with increasing annealing time, which clearly infers the transition from NGG to AGG with an annealing time of 48 h from the appearance of a bimodal distribution, as shown in Figure 2e–h. Additionally, the NGG behavior of AZ31 and AZ91 was dominant in all annealing conditions. The grain size of AZ91 before annealing for 48 h is smaller than the initial grain size, as shown in Figure 2i–l. This should be attributed to the fact that the second phase particles can also induce recrystallization nucleation by strain localization near the particles, and inhibit grain growth with Zener pinning.

Previous studies have shown that AGG appears when NGG is inhibited by second phase particles [23,24]. Therefore, the AZ61 sample annealed for 48 h was selected for more detailed experiments. The SEM micrograph of this sample is shown in Figure 3. As indicated by the black arrows in Figure 3a, the size of the abnormal grain is 3.8 times larger than that of normal grains, and most of the second phase particles are granulated and distributed at grain boundaries. According to statistics, the granular second phase particles of size 1.1 ± 0.6 µm were directly pinned on the grain boundaries. Smaller second phase particles (<0.5 µm) aggregate near the grain boundaries, as shown in Figure 3b. Overall, the precipitation of the second phase on the grain boundaries leads to the pinning effect and inhibits further grain growth. The distribution of second phase particles may be a key factor of AGG.

The microstructures evolutions of AZ31, AZ61, and AZ91 alloys during annealing at 350 °C are shown in Figure 4. As can be seen, the grain sizes of AZ31 and AZ91 conform to Gaussian distribution, which indicates NGG. The AGG of AZ61 leads to an abnormal increase in the average grain size at 48 h and 72 h. This particular annealing condition creates heterogeneous microstructure with a few abnormally grown grains. The precipitate content of AZ91 decreases significantly with increasing temperature. The precipitate distribution changes from diffuse distribution to accumulation at grain boundaries, which slows down the grain growth rate. The histograms of all three alloys with increasing annealing time showed that the grains tended to coarsen.

The microstructures evolutions of AZ31, AZ61, and AZ91 alloys during annealing at 400 °C is shown in Figure 5. With the increase in temperature, the grains of the three alloys grow normally and the number of second phase particles decreases significantly. The microstructure of supersaturated AZ91 is consisted mainly of Mg solid solution (bright phase) and Al-rich precipitated phase (dark phase, as indicated by the black arrow) annealed at 400 °C for 72 h, as shown in Figure 5l.

In order to directly compare the grain growth of the studied alloys, the grain growth parameter P_G was introduced [25]:

$$P_G=(D-D_0)/D_0$$

(1)

where D is the average grain size after specific annealing conditions, and D₀ is the initial average grain size (μm). The P_G parameters of the studied alloy are shown in Figure 6. At an annealing temperature of 300 °C, AZ61 has the maximum P_G value in each annealing temperature examined. This means that the grain growth rate of AZ61 is greater than that of AZ31 and AZ91. This is attributed to the varying degrees of recrystallized grains surrounding the normally growing grains in AZ31 during the annealing process, which causes the decrease in the grain growth rate. The rapid grain growth of AZ61 depends on AGG. For AZ91, the second phase particles precipitate and then dissolve as the annealing temperature increases. The pinning of the second phase particles changes from a diffuse distribution in the matrix to aggregation at the grain boundaries, and finally the excessive dissolution of Al leads to severe solute dragging effects. These factors lead to the lowest grain growth rate of AZ91.

The microstructures evolutions of AZ31, AZ61 alloys during annealing at 450 °C are shown in Figure 7. It can be seen that the microstructure of AZ31 at 450 °C is relatively homogeneous, and the number of fine recrystallized grains is reduced. However, the grain growth of AZ61 alloy is dominated by AGG at increasing temperatures. This indicates that the dissolution of the second phase particles increases the driving force of grain growth, and the abnormal grains can continue to grow, which is mainly at the expense of engulfing normal grains. The relationship between the average grain size and annealing time of AZ31, AZ61, and AZ91 at all temperatures investigated in this study is shown in Figure 8. Their average grain size varies in a range of 5~19.7 μm, 5.7~55.4 μm, 8.4~29.5 μm, respectively. It is known that the grain size increases with time under isothermal annealing conditions, but the grain growth rate decreases due to the decrease in internal stress. The grains are pinned by the second phase, resulting in abnormal growth of AZ61 at 350 °C for 48 h, and the grain growth rate is much greater than that of the previous time period. For alloys with different Al contents, the annealing process is accompanied by the dissolution and precipitation of the second phase. The grain growth of Mg–xAl–1Zn (x = 3, 6, 9) alloys are influenced by different concentrations of solute atoms and second phase particles with different sizes, shapes, and distribution positions.

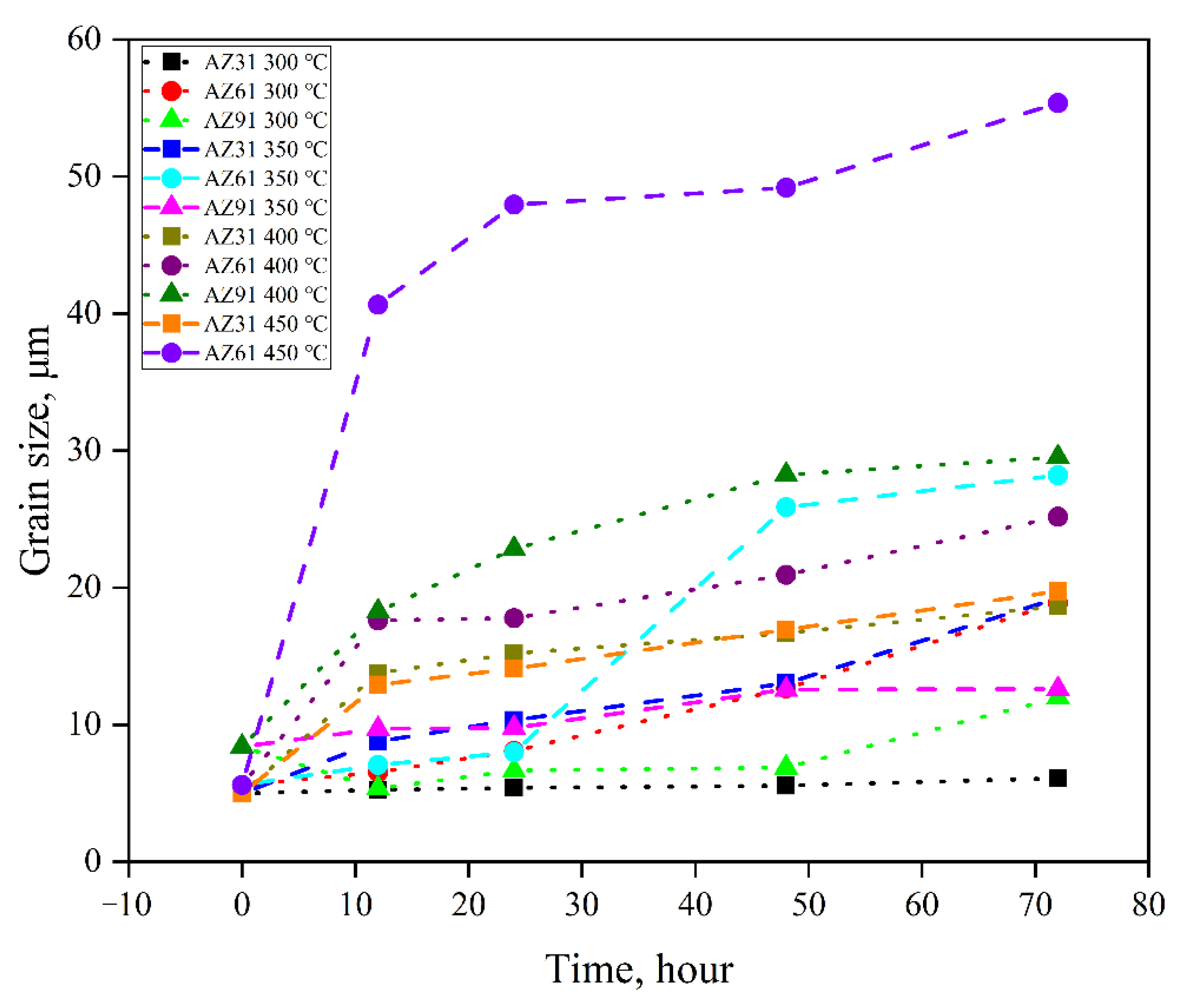
3.2. Grain Growth Kinetics

It is necessary to establish a mathematical model of grain growth for understanding grain growth behavior of AZ31, AZ61, and AZ91 Mg alloys. The kinetic curves and activation energy of the grain growth Q at different annealing times for all of the temperatures investigated in this study can be seen in Figure 9. The nonlinear Hillert equation is chosen to describe the growth kinetics of grains [10,11]:

$$(D_n-D_0^n)=k_{0}t\exp (-Q/RT)$$

(2)

where D is the average grain size after annealing (μm), D₀ is the initial average grain size (μm), n is the grain growth exponent, k₀ is the constant, t is the annealing time (h), Q is the activation energy of grain growth (KJ/mol), R is the general gas constant, and T is the annealing temperature (K).

$$K=k_0\exp (-Q/RT)$$

(3)

To determine the values of n and Q, Equation (3) is differentiated and taken in logarithmic form:

$$\ln (D_n-D_0^n)=\ln k+\ln t$$

(4)

According to Equation (3), when the annealing temperature is constant, the logarithm of $D_n-D_0^n$ is linearly related to the logarithm of K; thus, the value of n can be determined by least squares linear regression. The determined value of n is substituted into Equation (1), and finally the value of grain growth activation energy Q at a specific temperature and time is obtained.

The values of the fitting parameters are shown in

Table 2. The values of the fitted parameters n, and K for Mg–xAl–1Zn (x = 3, 6, 9) alloys at different annealing conditions.

Annealing Temperature/°C	nAZ31	KAZ31	nAZ61	KAZ61	nAZ91	KAZ91
300	2.1	0.3	2.0	0.6	2.2	1.7
350	2.0	2.9	2.0	1.2	2.0	1.5
400	2.7	84.6	3.0	2.4 × 102	3.4	1.7 × 103
450	4.0	2.1 × 103	2.8	1.5 × 103	-	-

. It is noted that the average grain growth exponent n of AZ31 and AZ61 Mg alloys is 2.7 and 2.4 at 300–450 °C, respectively. Due to the limited data collected for AZ91 at 450 °C, the average grain growth exponent n of AZ91 magnesium alloy at 300–400 °C is 2.5. The real n of AZ31, AZ61, and AZ91 Mg alloys are all larger than the theoretical n = 2 [10]. The possible impact of anisotropy on boundary energy and mobility is enhanced. Such a high value of n is suggestive of grain growth stagnation, which could be attributed to second phase particles exerting a drag force on the boundaries and pinning the microstructure. Indeed, Figure 8 shows that the grain size vs. time curves are quite flat after a rapid increase in grain size at short durations. This is particularly obvious at lower temperatures, while the grain growth curves appear more parabolic as the temperature increases, particularly in AZ61 and AZ91 Mg alloys. The linear fits suggest that the process is indeed thermally activated, and the activation energy Q is 204.1 KJ/mol, 166.1 KJ/mol, and 215.6 KJ/mol, which is larger than the grain boundary diffusion energy (92 KJ/mol) and bulk diffusion energy (135 kJ/mol) in Mg [14]. The range of values obtained for these Mg alloys suggests that the activation energy may depend upon the composition (impurity levels) and the initial conditions (microstructure, vacancy content, etc.).

Contrary to AZ31 and AZ61 Mg alloys, AZ91 did not undergo considerable grain growth at 300 °C and 350 °C. This must be caused by a strong effect of solutes (Zener Drag) or precipitates, which were more present in AZ91 than AZ31 and AZ61 Mg alloys. After annealing at 400 °C, most of precipitate was dissolved, and the remaining uneven particles distribution hindered NGG in AZ91 Mg alloy. It is worth mentioning that the n value and Q of AZ61 are smaller than those of AZ31 and AZ91Mg alloys. This is because the grains can continue to grow by AGG in AZ61 Mg alloy when the NGG is limited.

AGG is impossible in an ideal microstructure because grain growth is driven only by capillary forces and has a uniform grain boundary energy and mobility. In such case, a large grain would grow at a slower rate and would eventually be joined by the initial fine-grained matrix. In fact, conditions leading to AGG have been identified, including: i. evolution of initial textures/textures; ii. coarsening and interaction of the second phase [19]; iii. formation of high-angle grain boundaries; iv. evolution of the average sub-grain misorientation [20]. For example, it can result from the presence of a strong initial crystallographic texture [21]. This is because grains with similar orientation have low-angle (i.e., low-energy and low-mobility) boundaries between them, which results in reduced driving pressure, thus lowering the growth rates of normal grains. However, abnormal grains tend to have a higher orientation gradient than the initial grains, which causes the driving force of AGG to not decrease. This AGG can lead to pronounced changes in texture, as well as altering the grain growth kinetics, leading to a lower value of n [22]. Additionally, as the present study concerns AZ31, AZ61, and AZ91 Mg alloys, the pinning of solute and second phase particles are important for grain growth. The coarsening and interaction of the second phase particles with the grain boundaries may be responsible for the occurrence of AGG in AZ61 alloy. It was shown that the addition of 6% Al content at the appropriate temperature promoted grain growth by reducing the grain growth activation energy to a certain extent by AGG. As the annealing temperature increases from 300 °C to 450 °C, it is expected that the mobility of the dislocations will increase and that they will be absorbed by the grain boundaries. The grains with less residual stored energy would overcome the pinning of the second phase to grow at the expense of grain with high stored energy.

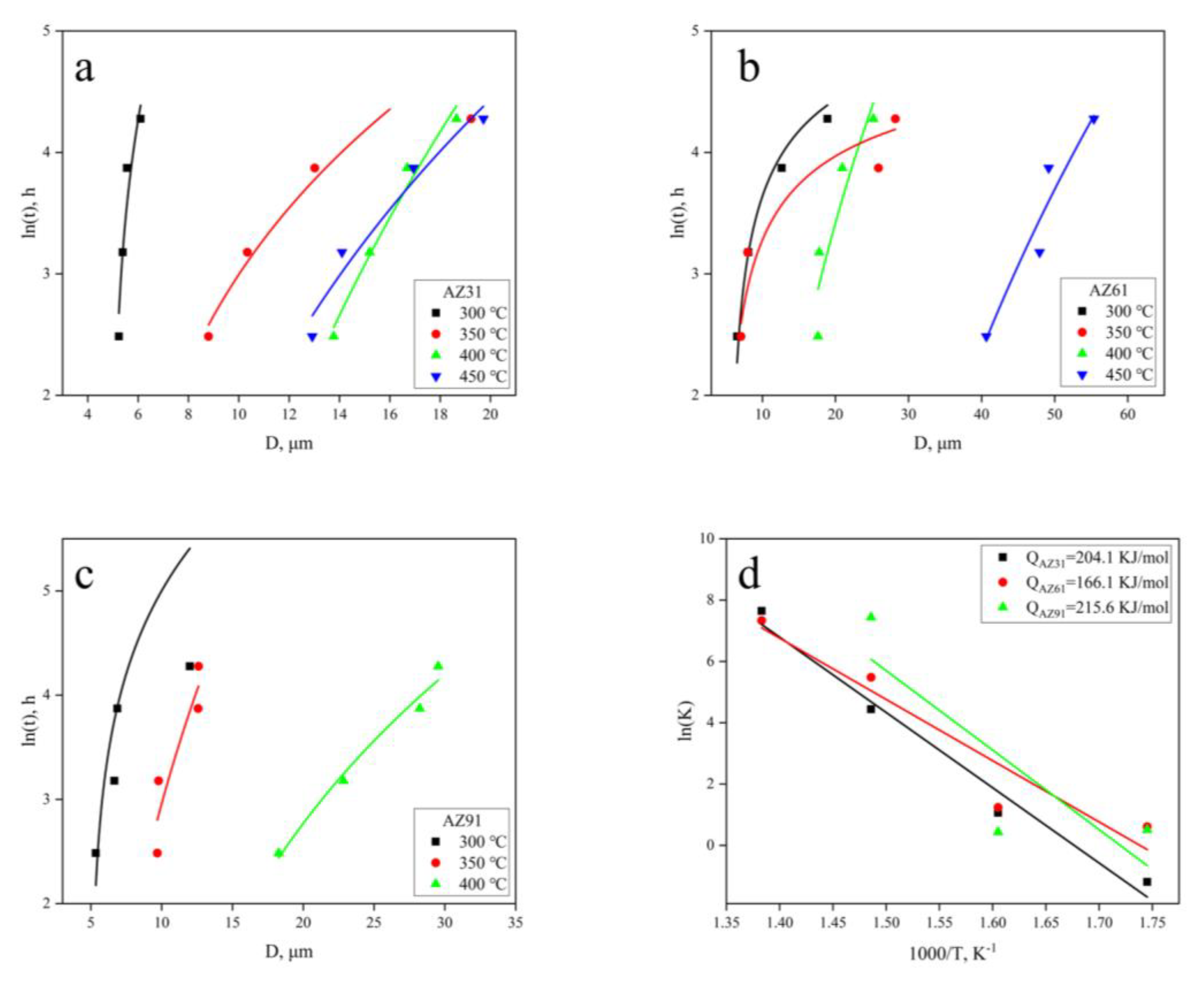
3.3. Deviation of Grain Growth Exponent n

In the present study, AZ91 was burned for a long annealing time at 450 °C. Therefore, the study temperature was controlled between 300 °C and 400 °C. The average values of n of AZ31, AZ61, and AZ91 annealed at 300–400 °C were 2.26, 2.33, and 2.53, respectively. The average value of n increased with the increase in Al content. The results of previous studies have shown that the n-values of Mg alloys are between 2 and 5 [6,26,27,28]. Deviations in n values are attributed to a non-homogeneous microstructure, Al-rich second phase, solute Al, specific grain orientation, and the influence of other factors on grain growth. In the previous sections, the microstructural evolutions of Mg alloys under different annealing conditions were analyzed in detail. In the next section, the distribution of the second phase particles and solute Al are measured, and their influence on the grain growth behavior is discussed in detail.

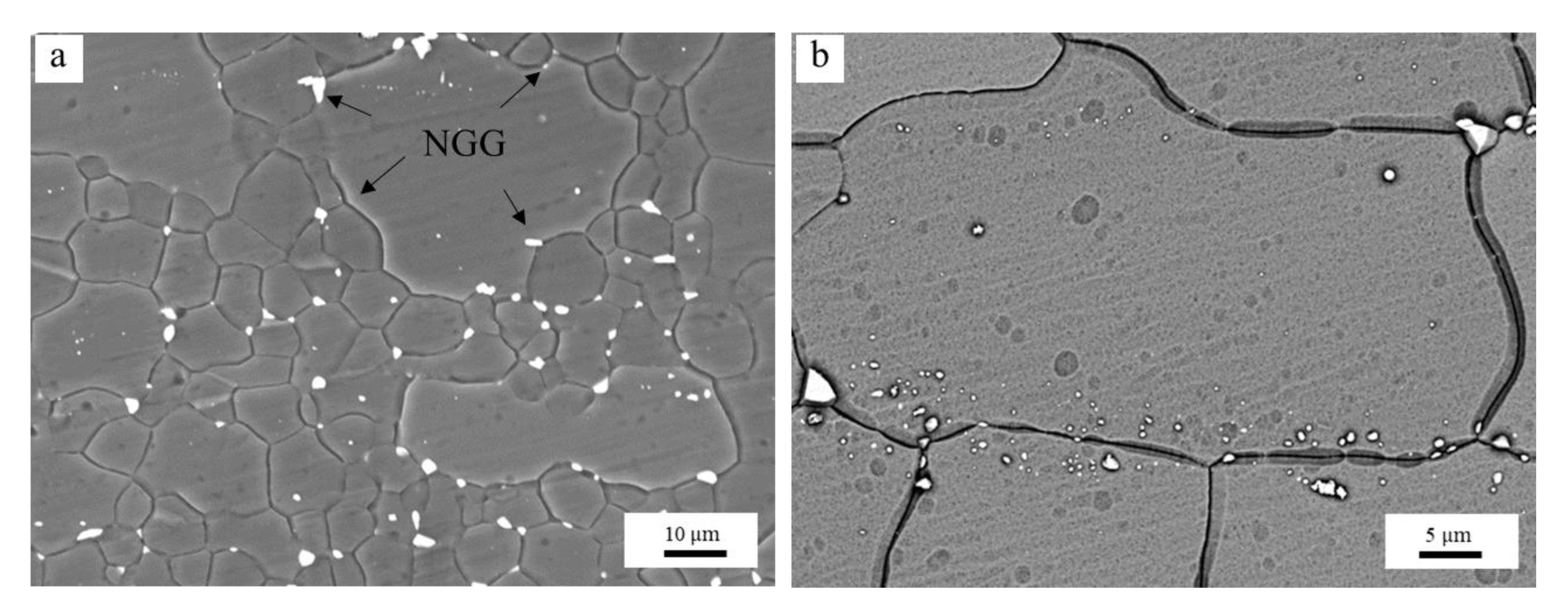
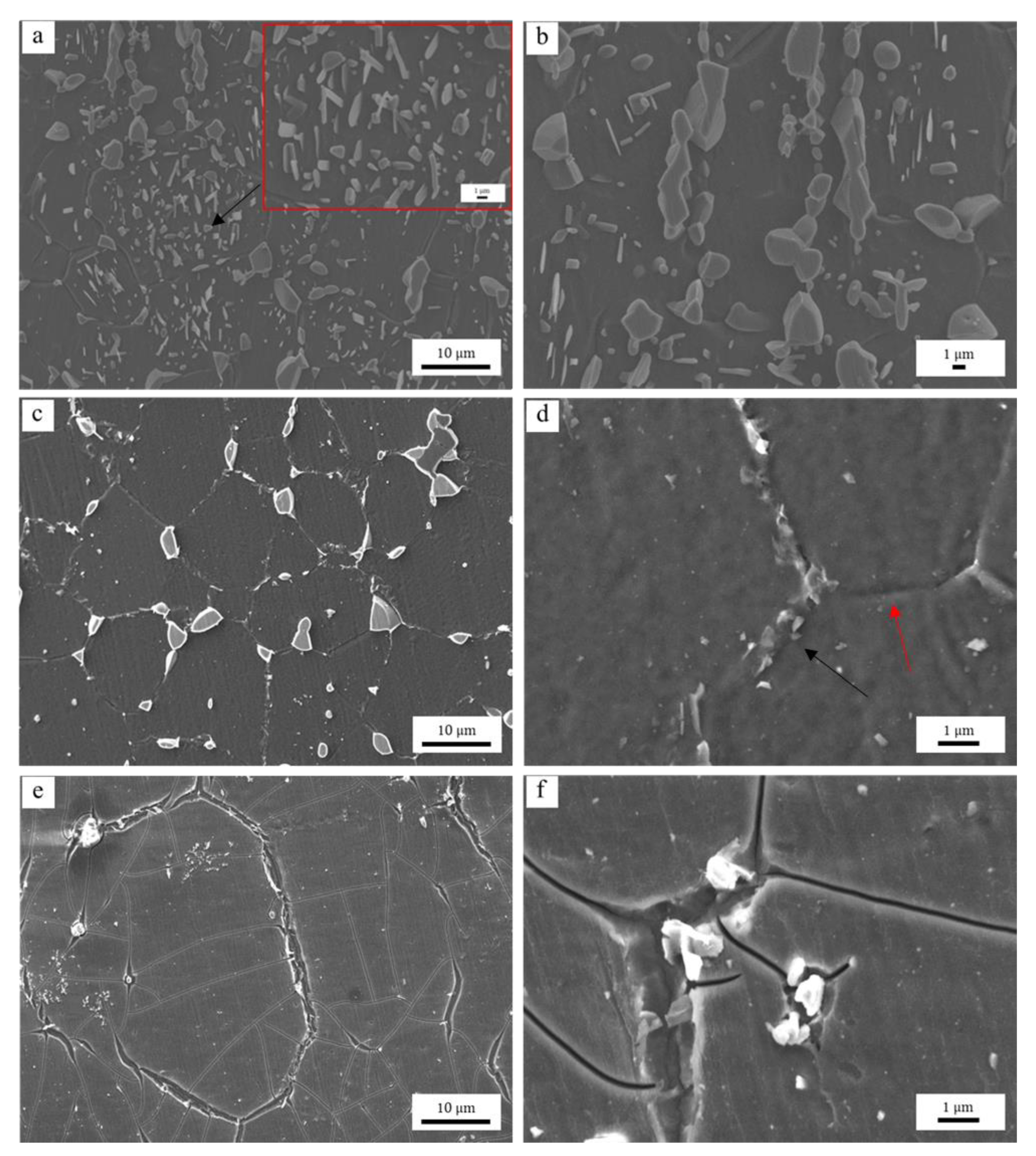
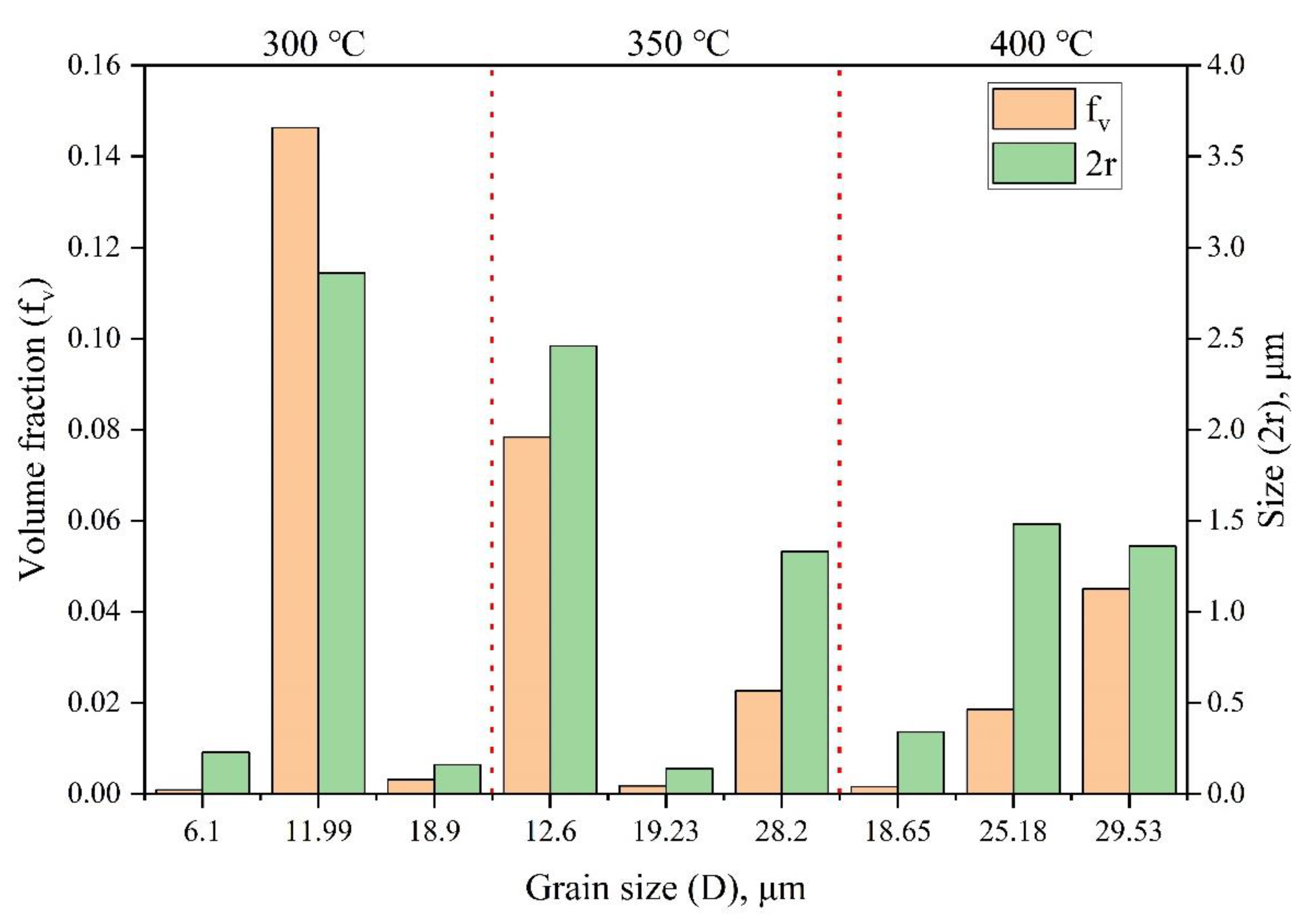
3.4. Second Phase and Solute Effects Influences Grain Growth

3.4.1. Effects of the Al-Rich Second Phase

The SEM images of the initial AZ31, AZ61, and AZ91 alloy sheets are shown in Figure 10. The second phase particles near the grain boundaries directly affect the grain boundary migration, further characterizing the grain boundaries. As can be seen from Figure 10a,b and Figure 1d, small amounts of second phase particles of the sub-micron scale (100–200 nm) and micro scale (1–5 μm) size are distributed in AZ31 Mg alloy. No clear second phase particles were observed at the grain boundaries. The volume fraction of the second phase particles in the initial AZ61 is only 0.2% more than that in AZ31. This means that the amount of the second phase particles is almost independent of the increase in the Al content in the initial Mg–Al alloy sheets (Al content < 6%). In addition to the spherical second phase particles, lamellar second phase particles are embedded at the grain boundaries of AZ61 (Figure 10c,d). The grain boundary would absorb a large amount of Al atoms to form the grain boundary phase (GBP) in AZ91, as shown in Figure 10e,f. The distribution of GBP is random, which may be related to the random distribution of grains with different orientations, which is to be further elucidated.

The size and volume fraction of second phase particles of Mg–xAl–1Zn alloys were evaluated by SEM. Figure 11 shows the SEM images of AZ31 captured at 300 °C, 350 °C and 400 °C at different magnifications. It can be seen that only a small amount of randomly distributed second phase particles are presented in AZ31. As the annealing temperature increases, most of the micro scale second phase particles of AZ31 dissolve in size to the sub-micron scale (100–300 nm). Figure 11a,b shows that the volume fraction of the second phase is 0.09%, and the second phase particles at the grain boundaries are spherical in AZ31 annealed at 300 °C for 72 h. The second phase was precipitated by increasing the temperature to 350 °C and 400 °C, and the volume fraction of the second phase was 0.18% and 0.16%, respectively, as shown in Figure 11c,e. In general, the grain size increases with increasing temperature when the volume fraction of the second phase is similar. The grain size decreases instead when the annealing temperature increases from 350 °C to 400 °C, and the average size of the second phase particles on the grain boundaries increases from 140 nm to 340 nm. This is attributed to the small size of the second phase particles in Figure 11d, which has a weak pinning effect on the grain boundaries. The large lamellar second phase particles in Figure 11f severely pin the grain boundaries, preventing the grain boundaries from straightening and inhibiting the grain growth. The magnitude of the interaction between the second phase particles and the grain boundaries can be approximated as [29]:

$$v=m\cdot (p-p_z)=m\cdot (p-3\mathsf{\gamma }{f}_v/2r)$$

(5)

where v is the GB migration rate, m is the intrinsic mobility of the boundary, p is the driving pressure, p_z is the pinning pressure, γ is the GB energy, ∂ is a small geometric constant and f_v and r are the volume fraction and radius of the dispersed second phase particles, respectively. Due to grain growth, the value of the driving pressure gradually decreases to the pinning pressure, and the grain growth stagnates at the limit value D_glim as:

$$D_{\mathrm{glim}}=4\partial r/3f_v$$

(6)

The SEM images of AZ61 captured at 300 °C, 350 °C, and 400 °C at different magnifications are shown in Figure 12. At an annealing temperature of 300 °C, the second phase particles dissolved with a volume fraction of 0.31% in AZ61, which was similar to the behavior of the second phase particles in AZ31, as shown in Figure 12a,b. The grain size of AZ31 was smaller than that of AZ61 due to the presence of a large number of fine recrystallized grains in AZ31. Figure 12c,d shows the normal and abnormal grain growth of AZ61 at 350 °C, which led to an increase in the average grain size growth rate. The volume fraction of second phase particles in the abnormal grain regions (2.17%) is lower than that in the normal grain regions (2.34%), which may be attributed to the reduced grain boundary area of AGG and the lack of pinning sites for the dissolution of large second phase particles. The majority of the second phase particles within the abnormal grains are smaller than 0.5 µm, and the size of the second phase particles pinned at the grain boundaries is 0.5–3 µm. The large granular second phase particles presenting near the grain boundaries (as shown by black arrows in Figure 12c) are the residues in the abnormal grains after engulfing the normal grains, which dissolve with increasing annealing time. Significantly, this dissolution of second phase particles occurs only in abnormal grains. The second phase particles are preferentially distributed at trigonal grain boundaries in normal grains, and second phase particles are present in small amounts of the lamellar form (as shown by red circles in Figure 12d) in addition to granular form. When the annealing temperature increased from 350 °C to 400 °C, the volume fraction of second phase particles decreased to 1.85%, and the second phase particles (long-axis size of 1.5–6.5 μm) tended to be distributed along the grain boundaries in the form of lamellae. The abnormal grains disappeared, and the average grain size decreased from 28.2 µm to 25.18 µm. This means that lamellar second phase particles can inhibit AGG and contribute to grain refinement.

In fact, the morphology of the second phase particles in AZ Mg alloys can be quite complex, ranging from granular to rod-like and network-like morphology [30,31,32]. At present, there are few reports on lamellar second phase particles in AZ Mg alloys. The pinning effect depends on the interaction between the second phase particles and grain boundaries. The morphology of the second phase particles leads to different contact patterns between the second phase particles and the grain boundaries. Thus, different morphologies of second phase particles have different pinning effects on grain boundaries. Previous studies have shown that deviations of the aspect ratio of second phase particles from 1 lead to an increase in the pinning effect [9,33]. This means that the lamellar second phase particles have a stronger pinning effect on the grain boundaries than the rod and granular forms.

The SEM images of AZ91 taken at 300 °C, 350 °C, and 400 °C at different magnifications are shown in Figure 13. Different from AZ31 and AZ61, the second phase particles in AZ91 preferentially precipitated at an annealing temperature of 300 °C with a volume fraction of 14.63%. The rod-like and lamellar second phase particles dominate in the grains, and the granular second phase particles larger than 2 μm are distributed at the grain boundaries, as shown in Figure 13a,b. When the annealing temperature is increased to 350 °C, most of the second phase particles are distributed on the grain boundaries, forming the continuous network as shown in Figure 13c,d. The volume fraction of second phase particles decreases to 7.84%, and the average grain size increases slightly by 0.61 µm. The results indicate that the network-like second phase particles have a stronger pinning effect on the grain boundaries. The network-like second phase particles were also observed in Mg–Al–Ca–Mn alloys and Mg–Gd–Zn alloys [34,35]. The formation of network-like second phase particles is due to the increase in the number of second phase particles and their distribution along the grain boundaries. The network-like morphology greatly increases the interaction of the second phase particles with the grain boundaries and strongly pins the grain boundaries.

As shown by the red and black arrows in Figure 13d, the segregation of fine second phase particles has a special preference due to the anisotropy of the grain boundaries. This result may lead to the continued migration of certain grain boundaries lacking pinning forces. As shown in Figure 13e, when the annealing temperature is 400 °C, a large number of second phase particles dissolve and the volume fraction decreases to 4.51%. The grain boundaries are rich in second phase particles, and a large number of intracrystalline or intergranular cracks are caused by second phase particles (Figure 13f).

The initial hypothesis was that cracks could be etched out, which might exist as low-angle grain boundaries or sub-grain boundaries in the grains. The relationship between the cracks and grain boundaries in AZ91 was investigated by EBSD. The inverse pole figure (IPF) maps and the substructure distribution maps of AZ91 annealed at 400 °C for 72 h are shown in Figure 14. The correlation between cracks and low-angle grain boundaries is not found in Figure 14a. As shown in Figure 14b, the annealed microstructure is mostly recrystallized tissue with a small amount of substructure, where the deformed tissue may have been introduced during the treatment of the specimen. It is obvious that the substructure is not related to the crack distribution. This indicates that the cracks produced by solute supersaturated AZ91 under high temperature annealing do not affect the grain boundary structure.

In order to further illustrate the effect of the dissolution and precipitation behavior of the second phase on grain growth in Mg–xAl–1Zn (x = 3, 6, 9) alloys, the relationship between the average grain size and the average size and volume fraction of the second phase particles is shown in Figure 15 with the parameters in

Table 3. The values of the average grain size (D), volume fraction (f_v), and average size (2r) of the second phase particles for Mg–xAl–1Zn (x = 3, 6, 9) alloys at different annealing conditions. In which, only the average size of the second phase particles at the grain boundaries is counted.

Annealing Temperature/°C	D, (μm)			fv			2r, (μm)
	AZ31	AZ61	AZ91	AZ31	AZ61	AZ91	AZ31	AZ61	AZ91
Initial	4.98	5.66	8.42	1.30%	1.50%	4.00%	0.7	1.32	0.87
300	6.1	18.9	11.99	0.09%	0.31%	14.63%	0.23	0.16	2.86
350	19.23	28.2	12.6	0.18%	2.26%	7.84%	0.14	1.33	2.46
400	18.65	25.18	29.53	0.16%	1.85%	4.51%	0.34	1.48	1.36

. Theoretically, according to the Equation (6), the grain size increases with increasing second phase particles’ size (2r) and decreases with increasing second phase particles’ volume fraction (f_v). As shown in Figure 15, AZ31 with the smallest second phase particle size at the grain boundaries tends to have the smallest grain size. This is because the fine second phase particles are more effective in inhibiting the growth of recrystallized grains. The volume fraction of second phase particles does not correlate well with grain size. In fact, the complexity of the morphology of the second phase particles significantly affects the magnitude of the pinning force acting on the moving grain boundaries. When the annealing temperature is 400 °C, the strong pinning effect of the lamellar second phase particles at the grain boundaries leads to a decrease in grain size of AZ31 and AZ61. For AZ91, in addition to the granular second phase particles similar to AZ61, a network-like grain boundary phase is presented at an annealing temperature of 350 °C. This results in a small grain size of AZ91. Among all the results, AZ91 has the largest grain size at 400 °C annealing conditions, which may be related to the diffusion of solute Al in the Mg matrix.

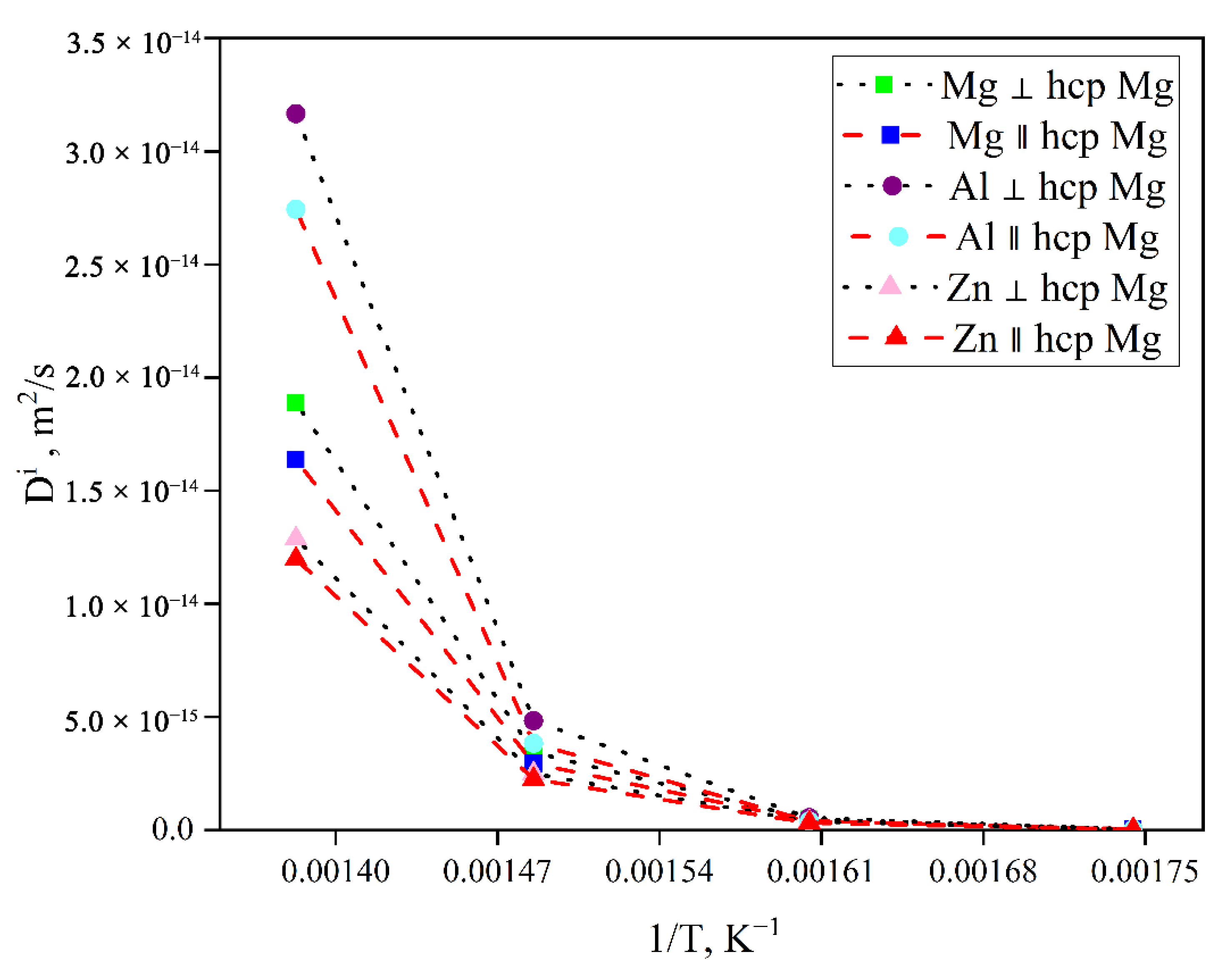
3.4.2. Effects of Solute Al

Solute resistance greatly affects grain growth. The diffusion velocity of solute atoms in the matrix is controlled by their radius, mass, and lattice type. For Mg with a hcp crystal structure (c/a ratio = 1.6236), the diffusion of solute atoms in the hcp–Mg matrix is anisotropic [14,36]. This means that the diffusion coefficients (D_diff) of solute atoms along or perpendicular to the c-axis are different. The following relationship is used to calculate the anisotropic solute atoms diffusion coefficient [19,25,37]:

$$D_{\perp \mathrm{hcp}-\mathrm{Mg}}^{\mathrm{Mg}}=1.75\times {10}^{-4}\exp (-137,979/RT)$$

$$D_{\parallel \mathrm{hcp}-\mathrm{Mg}}^{\mathrm{Mg}}=1.78\times {10}^{-4}\exp (-138,943/RT)$$

$$D_{\perp \mathrm{hcp}-\mathrm{Mg}}^{\mathrm{Al}}=3.1\times {10}^{-3}\exp (-152,154/RT)$$

$$D_{\parallel \mathrm{hcp}-\mathrm{Mg}}^{\mathrm{Al}}=8.7\times {10}^{-3}\exp (-159,221/RT)$$

$$D_{\perp \mathrm{hcp}-\mathrm{Mg}}^{\mathrm{Zn}}=4.98\times {10}^{-5}\exp (-132,725/RT)$$

$$D_{\parallel \mathrm{hcp}-\mathrm{Mg}}^{\mathrm{Zn}}=7.33\times {10}^{-5}\exp (-135,488/RT)$$

The solute atoms diffusion coefficients of Mg, Al, and Zn in hcp–Mg along or perpendicular to the c-axis are shown in Figure 16. For Mg–xAl–1Zn (x = 3, 6, 9) alloys, the solute atoms are mainly Al and Zn. As seen in Figure 16, the solute atoms diffusion coefficients: $D_{\mathrm{hcp}-\mathrm{Mg}}^{\mathrm{Al}}>D_{\mathrm{hcp}-\mathrm{Mg}}^{\mathrm{Mg}}>D_{\mathrm{hcp}-\mathrm{Mg}}^{\mathrm{Zn}}$. The diffusion coefficient of solute Al is larger than the self-diffusion coefficient of Mg, which implies that solute Al hardly hinders the migration of grain boundaries during grain growth. Though the diffusion coefficient of Zn atoms is lower than the self-diffusion coefficient of Mg, their volume fractions is very low, and the drag effect can also be neglected.

In order to examine the influence of solute distribution on grain growth, the concentration of solute Al within abnormal and normal grains was measured. As shown in Figure 17, no specific concentration distribution of solute Al was found except for the Al-rich second phase particles, and the three linear EDSs had similar results. The solute Al has a sufficiently high diffusion rate, which is greater than the grain boundary migration rate, thus allowing solute Al to agglomerate at the grain boundaries during grain growth (As shown by Figure 16). According to the Mg–Al binary phase diagram [38], α-Mg phase (solid solution of Al in Mg) and Mg₁₇Al₁₂ eutectoids occurred during solidification. The second phase particles at line 1 may be the Mg₁₇Al₁₂ phase. The homogeneous distribution of solute Al indicates that it is not the cause of AGG. The pinning effect of second phase particles is more effective than solute dragging effect in grain refinement.

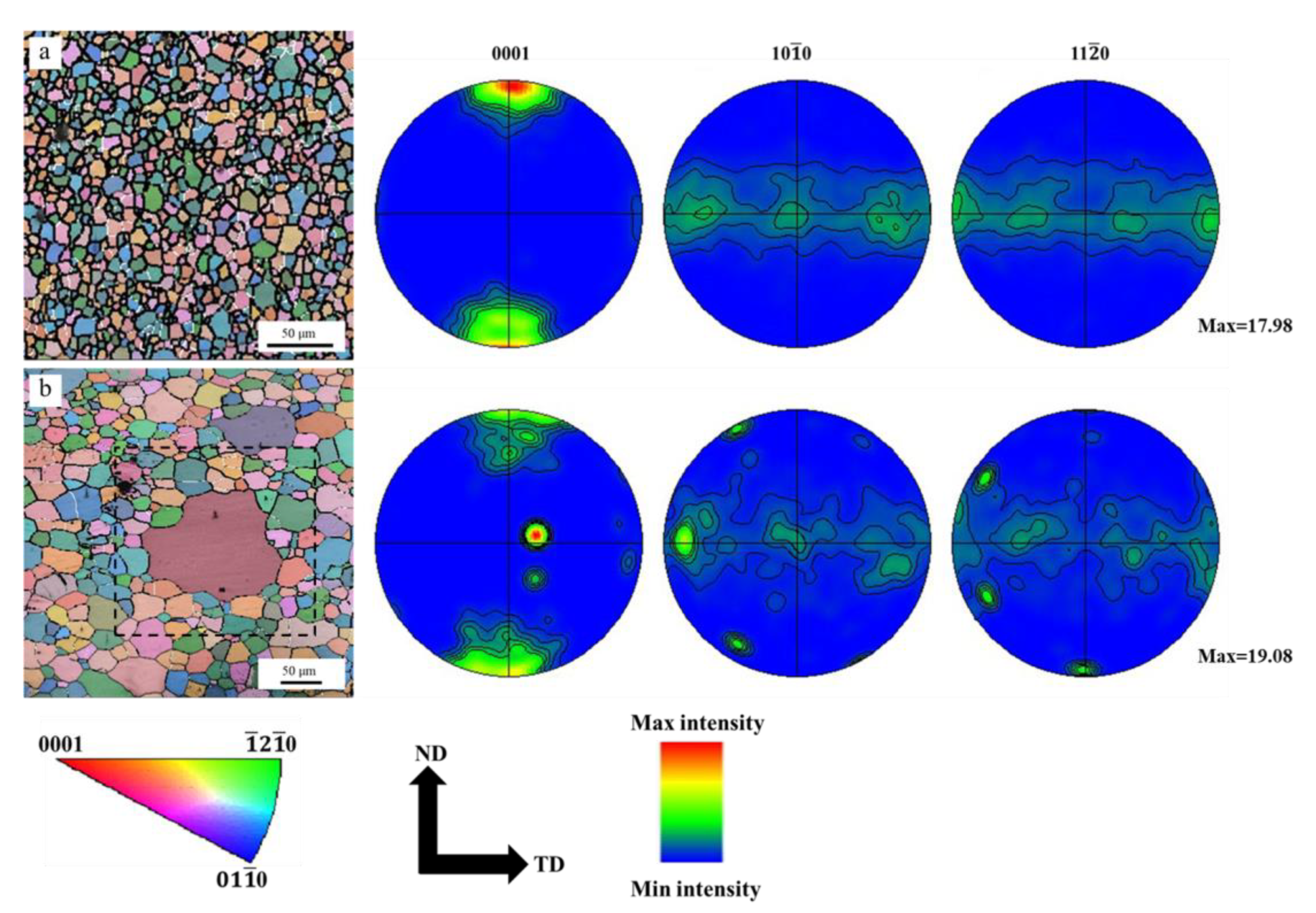
3.5. Texture Selection and Oriented Preferential Growth

The addition of alloying elements (especially rare earth elements) to create solute drag in Mg alloys can improve textures [39,40]. The LM model of equilibrium segregation to grain boundaries predicts that Al and Zn will not strongly segregate to grain boundaries [41]. This is consistent with the experimentally observed behavior of solute Al, which also indicates that solute Al cannot produce effective texture change in Mg alloys.

As shown in Figure 18, there was AGG and the significant changes in the texture after annealing at 350 °C for 72 h in AZ61. The orientation of the abnormal grain is ND//$<11\overline{2}0>$ in Figure 18b, and the directions of TD and ED are $<10\overline{1}0>$ and $<0001>$ deviate by 18°, respectively, which is consistent with the preferred orientation of Mg alloys in previous studies [42,43,44]. The texture changes its basal texture deflection from ND to ED direction, $<11\overline{2}0>$ type texture deflection from the TD to ND direction, and $<10\overline{1}0>$ type texture intensity increases in the TD direction. The results indicate that the AGG leads to changes in texture. Tang et al. [42] found that that the formation of abnormal grains was attributed to the inhomogeneous distribution of precipitates and the preferential growth of certain grains. In our study, Figure 12c,d shows that the grain boundaries of the abnormal grains do not lack the pinning of the second phase particles, and the large number of diffuse second phase particles within the abnormal grains are products of the migration of the grain boundaries. Figure 19 shows the microstructure and misorientation distribution of the enlarged view of the rectangular region in Figure 18. The growth of the abnormal grains is completely surrounded by the high-angle grain boundaries, and the misorientation of 68% grain boundaries is greater than 60°, as shown in Figure 19a,b. The high-angle grain boundaries represent high mobility, which implies that abnormal grains have growth advantages in annealing. The kernel average misorientation (KAM) map of abnormal and normal grains is shown in Figure 19c. It can be seen that the KAM value of the normal grain region is larger than that of the abnormal grains, which means there are more dislocations and strain energy in the normal grains, which provides the driving force for the growth of the abnormal grains. Therefore, it can be concluded that the energy difference between abnormal grains with high-angle grain boundaries and normal grains drives the growth of abnormal grains to overcome the pinning of second phase particles.

3.6. Mechanical Properties

In polycrystalline materials, the microhardness (H_V) can be related to the average grain size (D) through the Hall-Petch relationship [45]:

$$H_V=H_0+k{D}^{-1/2}$$

(7)

where H₀ is the frictional stress, indicating the total resistance to dislocation movement by the lattice, and k is a constant for measuring the relative hardening of the grain boundaries. This equation is used only in the case of single-phase materials and average grain size. The microhardness of Mg–xAl–1Zn (x = 3, 6, 9) alloys as a function of grain size is shown in Figure 20. It can be seen that Equation (7) is applicable to this grain range (5.0 to 55.4 µm) of Mg–xAl–1Zn (x = 3, 6, 9) alloys. This also indicates that the addition of alloying elements and the control of grain growth have a great influence on the mechanical properties of the material. Compared with grain size, the addition of Al elements has a greater effect on the mechanical properties of Mg alloys, and the effect of grain size on mechanical properties decreases with the addition of Al elements.

4. Conclusions

In this paper, the effect of second phase particles and solutes on grain growth in hot extruded Mg–xAl–1Zn (x = 3, 6, 9) alloys is discussed. The main results are as follows:

(1)

The average grain size of hot extruded Mg–xAl–1Zn (x = 3, 6, 9) alloys increases with an increasing annealing temperature and holding time under isothermal annealing treatment. The growth rate of AZ61 is greater than that of AZ31 and AZ91, which is attributed to the fact that AZ31 has a large number of recrystallized grains at all annealing conditions, which significantly reduces the growth rate of grains. The AZ91 obtains the lowest growth rate by the pinning of the second phase and dragging of the solute.

(2)

The average grain growth exponent n of hot extruded Mg–xAl–1Zn (x = 3, 6, 9) alloys increases with increasing Al content. The n values are 2.26, 2.33, and 2.53, respectively, which are greater than the theoretical value of 2. This deviation is related to the presence of Al-rich second phase particles and solute Al. The activation energy Q values are 204.4 KJ/mol, 166.1 KJ/mol, and 215.6 KJ/mol. The Q values of AZ61 are lower than those of AZ31 and AZ91. This is due to the AGG, which reduces the grain growth activation energy of the system.

(3)

The pinning of lamellar and networked second phase particles at grain boundaries in hot extruded Mg–xAl–1Zn (x = 3, 6, 9) alloys is greater than that in spherical and granular forms. The distribution of solute Al in the alloy is homogeneous. Moreover, the pinning of Al-rich second phase particles is more effective than the dragging of solute Al during grain refinement.

(4)

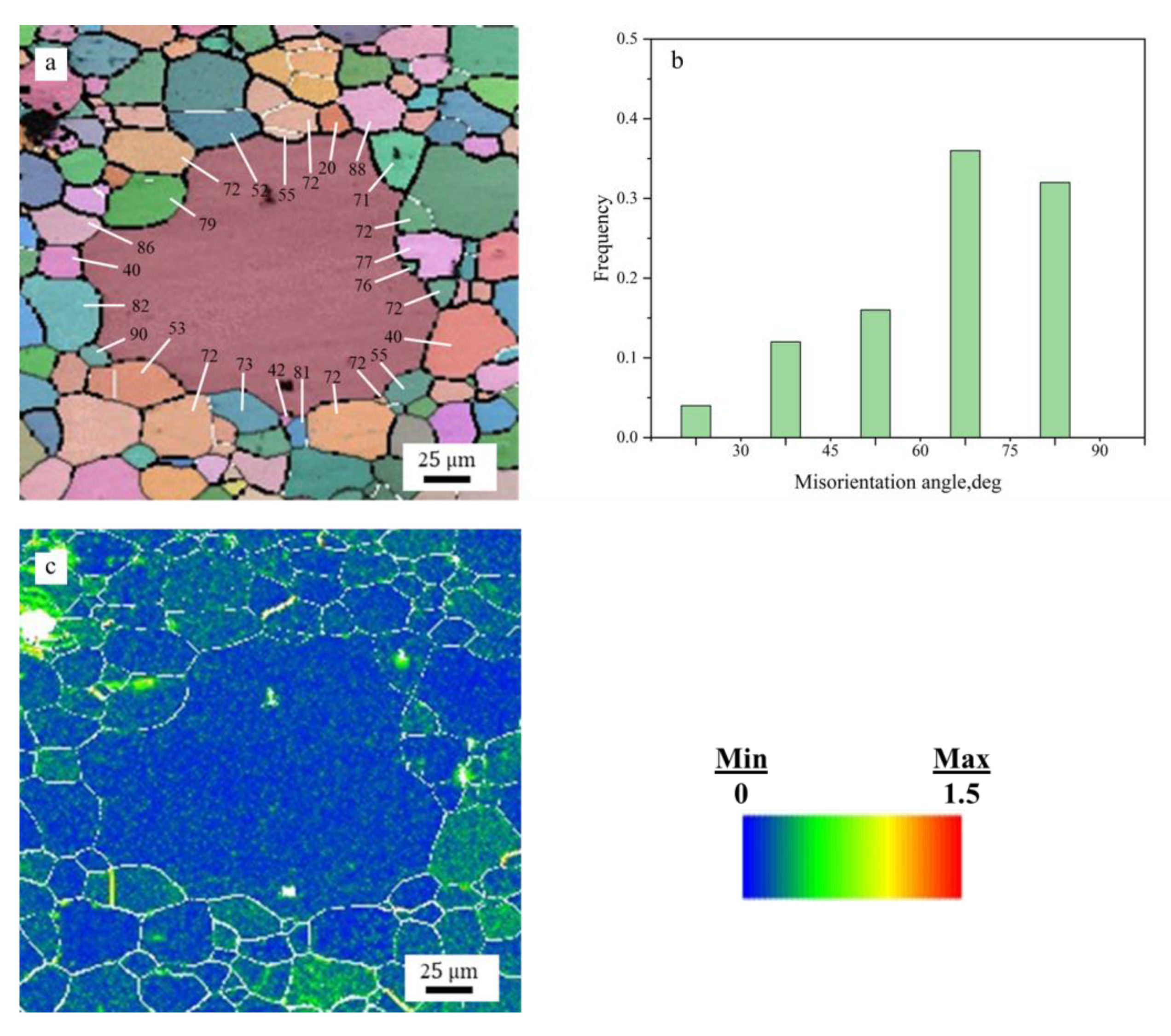
The AGG in hot extruded Mg–xAl–1Zn (x = 3, 6, 9) alloys is not caused by the inhomogeneous distribution of the second phase particles, but by the high energy difference between the preferentially oriented $<11\overline{2}0>$ abnormal grains and the surrounding grains, which drives the grain boundaries to overcome the same pinning forces and continue to migrate.