Metal Crystal/Polycrystal Plasticity and Strengths
Abstract
:1. Introduction
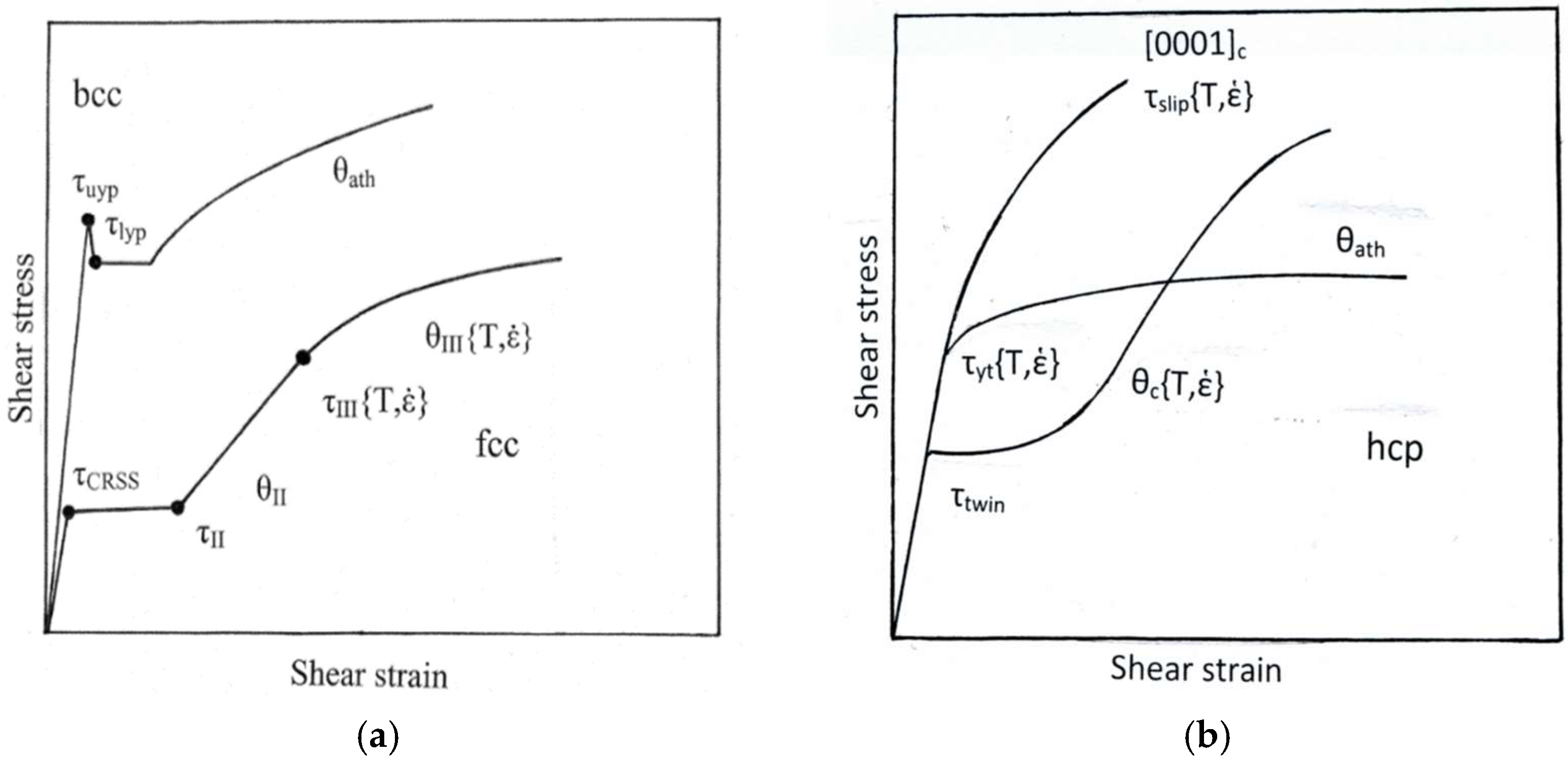
2. Stress–Strain Characterizations of Fcc, Bcc and Hcp Metal Deformations
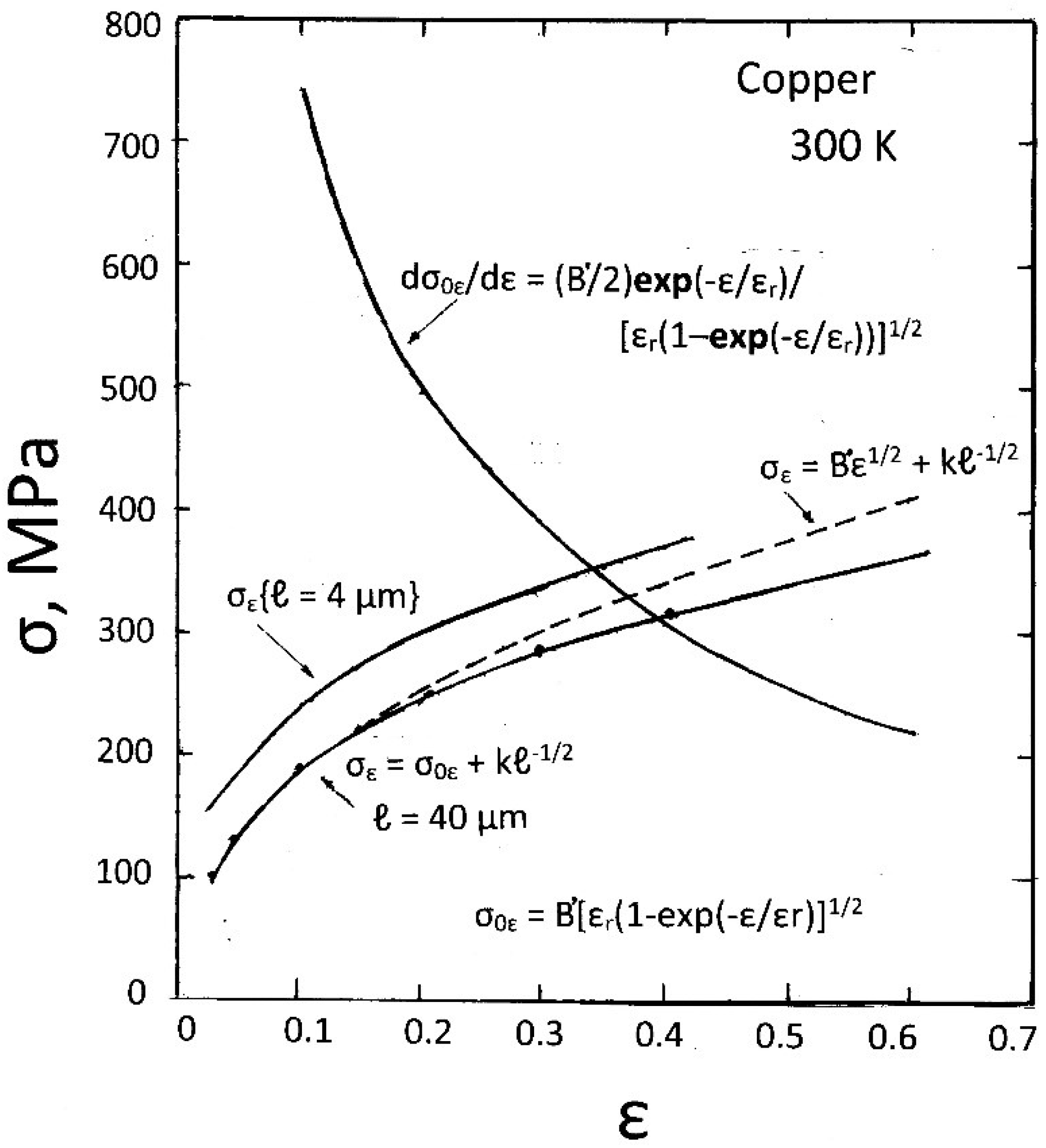
3. Dislocation Interactions/Reactions
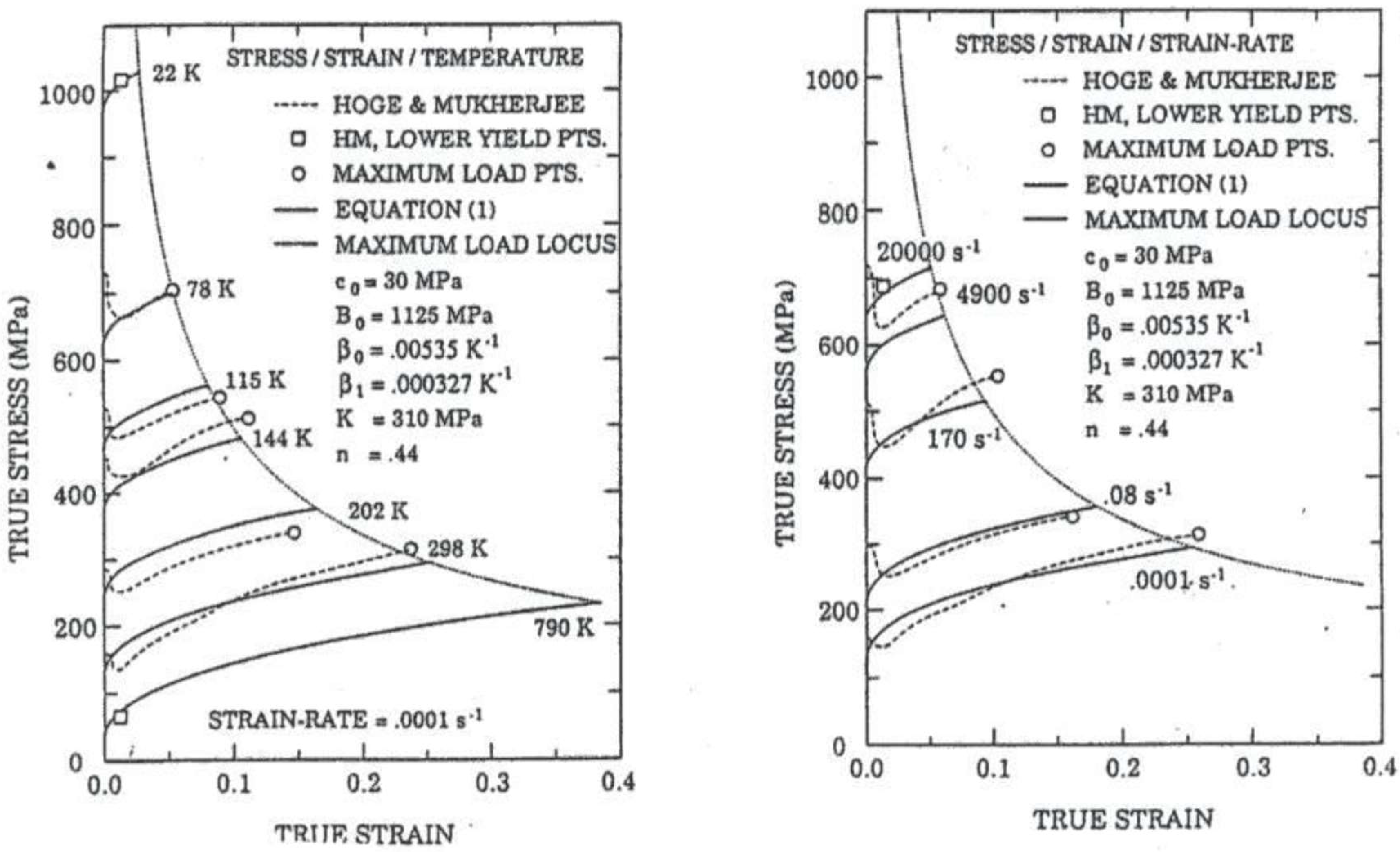
4. Strain Hardening and (Tensile) Plastic Instability
5. Plastic Instability for the Bcc Case
6. Discussion
7. Summary
Funding
Acknowledgments
Conflicts of Interest
References
- Taylor, G.I. The Mechanism of Plastic Deformation of Crystals. Part I. Theoretical. Proc. R. Soc. Lond. 1934, 145, 362–387. [Google Scholar]
- Nabarro, F.R.N.; Basinski, Z.S.; Holt, D.B. The plasticity of pure single crystals. Adv. Phys. 1964, 13, 193–323. [Google Scholar] [CrossRef]
- Pande, C.S. Strain hardening in FCC metals and alloys. Mater. Sci. Eng. 2001, A309–A310, 328–330. [Google Scholar] [CrossRef]
- Cottrell, A.H. Commentary: A brief review on work hardening. Dislocations Solids 2002, 11, vii–xvii. [Google Scholar]
- Zepeda-Ruiz, L.A.; Stukowski, A.; Oppelstrup, T.; Bertin, N.; Barton, N.A.; Freitas, R.; Bulatov, V.V. Atomic insights into metal hardening. Nat. Mater. 2021, 5, 315–320. [Google Scholar] [CrossRef]
- Hirsch, P.B.; Horne, R.W.; Whelan, M.J. Direct observations of the arrangement and motion of dislocations in aluminum. Philos. Mag. 1956, 1, 677–684, reprinted in Special Issue: 50 years of TEM of dislocations, Philos. Mag. 2006, 86, 4553–4572. [Google Scholar]
- Mott, N.F. The Work Hardening of Metals. Trans. TMS-AIME 1960, 218, 962–968. [Google Scholar]
- Armstrong, R.W. Plasticity: Grain Size Effects III. In Reference Module in Materials Science and Materials Engineering; Hashmi, S., Ed.; Elsevier: Oxford, UK, 2016; pp. 1–23. [Google Scholar]
- Armstrong, R.W.; Li, Q.-Z. Dislocation mechanisms of high-rate deformations. Metall. Mater. Trans. A 2014, 46A, 4438–4453. [Google Scholar]
- Kurukuri, S.; Worswick, M.J.; Tari, D.G.; Misra, R.K.; Carter, J.T. Rate sensitivity and tension-compression asymmetry in AZ31B magnesium alloy sheet. Philos. Trans. R. Soc. A 2014, 372, 20130216. [Google Scholar] [CrossRef] [Green Version]
- Xie, Q.; Zhu, Z.; Kang, G.; Yu, C. Crystal plasticity-based impact dynamic constitutive model of magnesium alloy. Int. J. Mech. Sci. 2016, 119, 107–113. [Google Scholar] [CrossRef]
- Conrad, H.; Armstrong, R.W.; Wiedersich, H.; Schoeck, G. Thermally-activated Glide in Magnesium Crystals from 4 2 to 420 K. Philos. Mag. 1961, 6, 177–188. [Google Scholar] [CrossRef]
- Frank, F.C.; Nicholas, J.F. Stable dislocations in the common crystal lattices. Philos. Mag. 1953, 44, 1213–1235. [Google Scholar] [CrossRef]
- Hirth, J.P. On dislocation reactions in the fcc lattice. J. Appl. Phys. 1961, 32, 700–706. [Google Scholar] [CrossRef]
- Hansen, N. Effect of grain size and strain on the tensile flow stress of aluminum at room temperature. Acta Metall. 1977, 25, 863–869. [Google Scholar] [CrossRef]
- Hansen, N.; Ralph, B. The Strain and Grain Size Dependence of the Flow Stress of Copper. Acta Metall. 1982, 30, 411–417. [Google Scholar] [CrossRef]
- Hall, E.O. The deformation and ageing of mild steel: Discussion of results. Proc. Phys. Soc. Lond. B 1951, 64, 747–753. [Google Scholar] [CrossRef]
- Petch, N.J. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Zerilli, F.J.; Armstrong, R.W. Dislocation-mechanics–based constitutive equations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef] [Green Version]
- Zerilli, F.J. Dislocation mechanics based constitutive relations. Metall. Mater. Trans. A. 2004, 35A, 2547–2555. [Google Scholar] [CrossRef]
- Zerilli, F.J.; Armstrong, R.W. Description of tantalum deformation behavior by dislocation mechanics based constitutive relations. J. Appl. Phys. 1990, 68, 1580–1591. [Google Scholar] [CrossRef]
- Hoge, K.G.; Mukherjee, A.K. Temperature and strain rate dependence of flow stress of tantalum. J. Mater. Sci. 1977, 12, 1666–1672. [Google Scholar] [CrossRef]
- Peeters, B.; Bacroix, B.; Teodosiu, C.; Van Houtte, P.; Aernoudt, E. Work-Hardening/Softening Behavior of BCC Polycrystals during Changing Strain Paths: II. TEM Observations of Dislocation Sheets in an IF Steel during Two-Stage Strain Paths and Their Representation in Terms of Dislocation Densities. Acta Mater. 2001, 49, 1621–1632. [Google Scholar] [CrossRef]
- De Messemaeker, J.; Verlinden, B.; Van Humbeeck, J. On the strength of boundaries in submicron IF steel. Mater. Lett. 2004, 58, 3782–3786. [Google Scholar] [CrossRef]
- Madec, R.; Kubin, L.P. Dislocation strengthening in FCC metals and in BCC metals at high temperatures. Acta Mater. 2017, 126, 166–173. [Google Scholar] [CrossRef]
- Messner, M.C.; Rhee, M.; Arsenlis, A.; Barton, N.R. A crystal plasticity model for slip in hexagonal close packed metals based on discrete dislocation simulations. Model. Simul. Mater. Sci. Eng. 2017, 25, 044001. [Google Scholar] [CrossRef]
- Mishra, A.; Alankar, A. Revisiting dislocation reactions and their role in uniaxial deformation of copper single crystal micro-pillars. Model. Simul. Mater. Sci. Eng. 2019, 27, 055010. [Google Scholar] [CrossRef]
- Li, Z.; Cui, Y.; Yan, W.; Zhang, D.; Fang, Y.; Chen, Y.; Yu, Q.; Wang, G.; Ouyang, H.; Fan, C.; et al. Enhanced strengthening and hardening via self-stabilized dislocation network in additively manufactured metals. Mater. Today 2021, 50, 79–88. [Google Scholar] [CrossRef]
- Muñoz, J.A.; Higuera, O.F.; Cabrera, J.M. Microstructural and mechanical study in the plastic zone of ARMCO iron processed by ECAP. Mater. Sci. Eng. A 2017, 697, 24–26. [Google Scholar] [CrossRef] [Green Version]
- Brown, L.M. Unifying concepts in dislocation plasticity. Philos. Mag. 2005, 85, 2989–3001. [Google Scholar] [CrossRef]
- Brown, L.M. Constant intermittent flow of dislocations: Central problems in plasticity. Mater. Sci. Tech. 2012, 28, 1209–1232. [Google Scholar] [CrossRef]
- Alhafez, I.A.; Ruestes, C.J.; Bringa, E.M.; Urbassek, H.M. Influence of pre-existing plasticity on nano-indentation—An atomistic analysis of the dislocation fields produced. J. Mech. Phys. Sol. 2019, 132, 103674. [Google Scholar]
- Goel, S.; Cross, G.; Stukowski, A.; Gamsjäger, E.; Beake, B.; Agrawal, A. Designing nanoindentation simulation studies by appropriate indenter choices: Case study on single crystal tungsten. Comput. Mater. Sci. 2018, 152, 196–210. [Google Scholar] [CrossRef] [Green Version]
- Armstrong, R.W.; Elban, W.L. Dislocation Reaction Mechanism for Enhanced Strain Hardening in Crystal Nano-indentations. Crystals 2020, 10, 9. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Armstrong, R.W. Metal Crystal/Polycrystal Plasticity and Strengths. Metals 2022, 12, 2070. https://doi.org/10.3390/met12122070
Armstrong RW. Metal Crystal/Polycrystal Plasticity and Strengths. Metals. 2022; 12(12):2070. https://doi.org/10.3390/met12122070
Chicago/Turabian StyleArmstrong, Ronald W. 2022. "Metal Crystal/Polycrystal Plasticity and Strengths" Metals 12, no. 12: 2070. https://doi.org/10.3390/met12122070
APA StyleArmstrong, R. W. (2022). Metal Crystal/Polycrystal Plasticity and Strengths. Metals, 12(12), 2070. https://doi.org/10.3390/met12122070