An Improvement in Constrained Studded Pressing for Producing Ultra-Fine-Grained Copper Sheet
Abstract
:1. Introduction
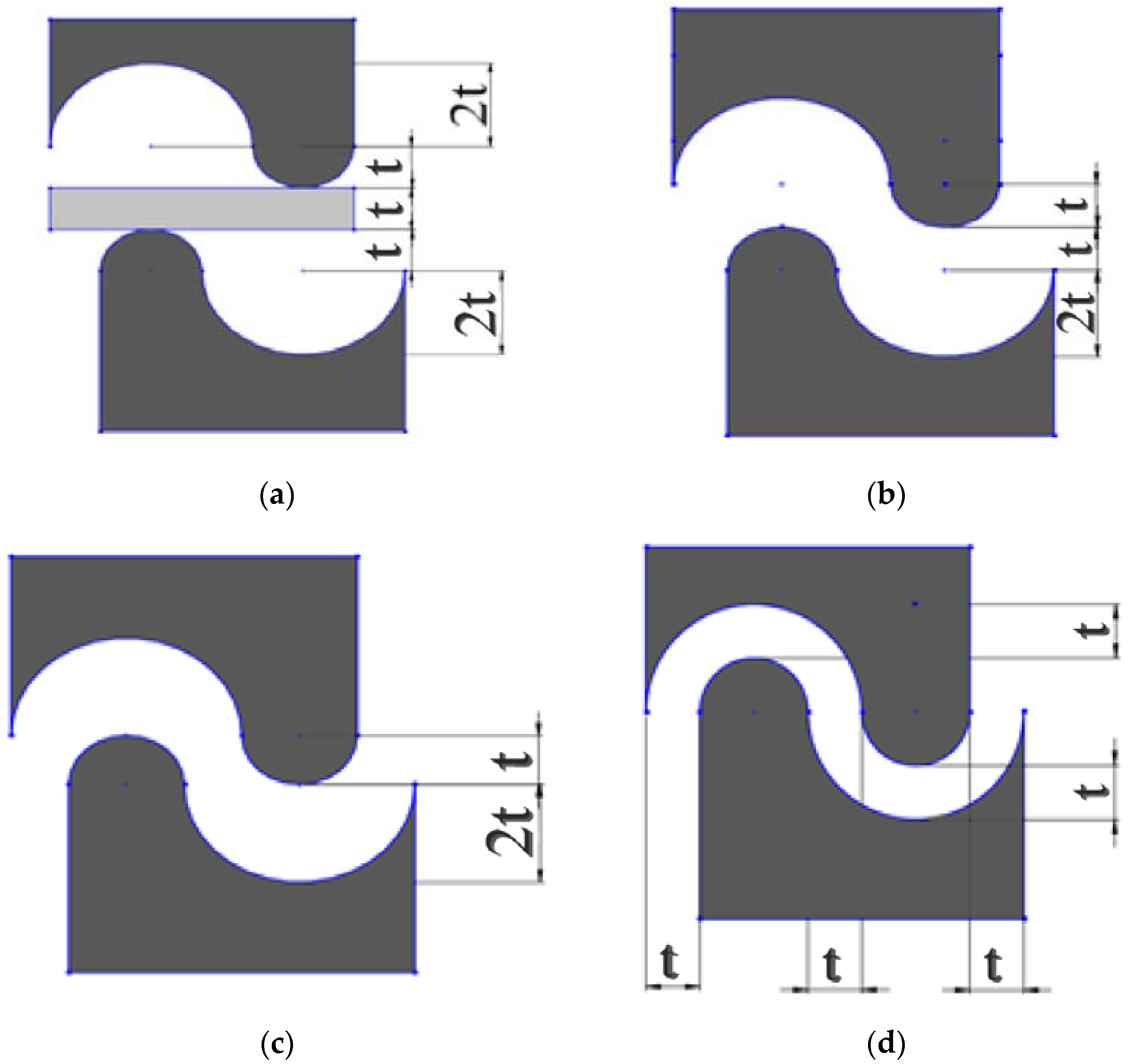
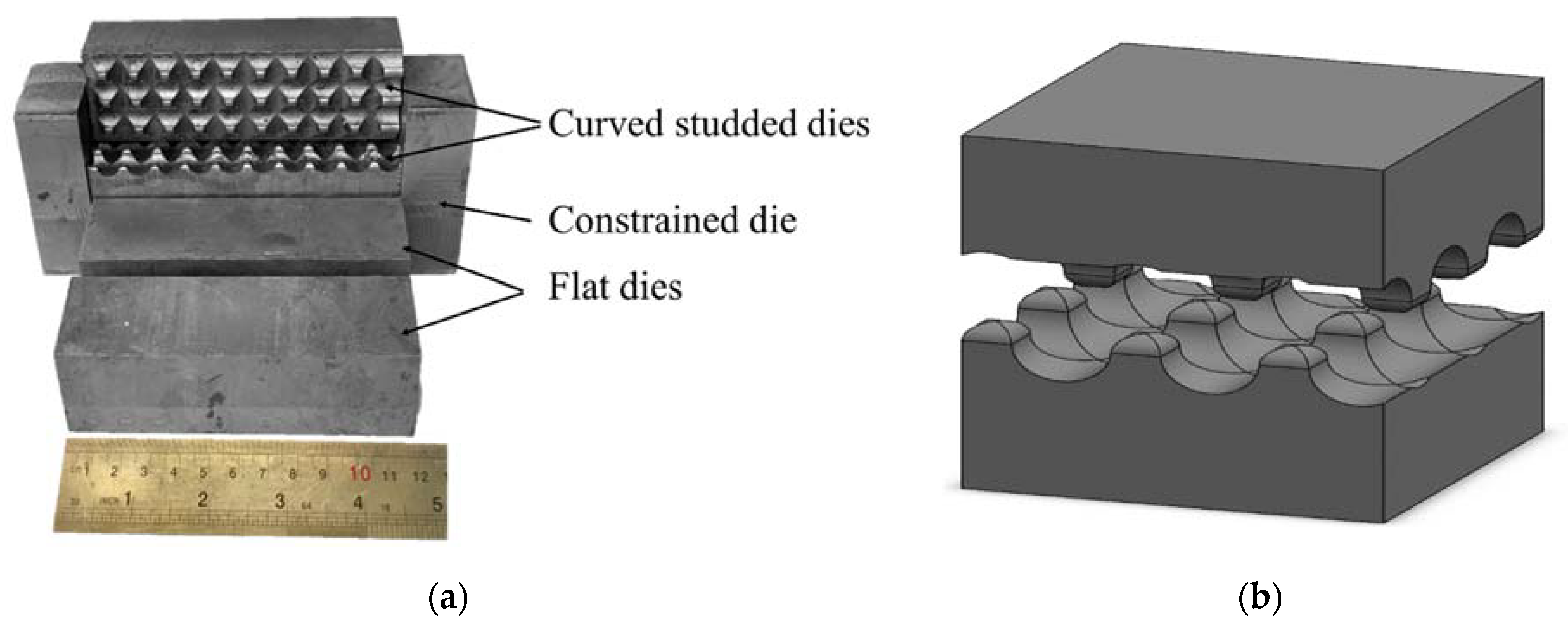
2. Illustration of the Proposed Die Design
3. Experimental Procedures
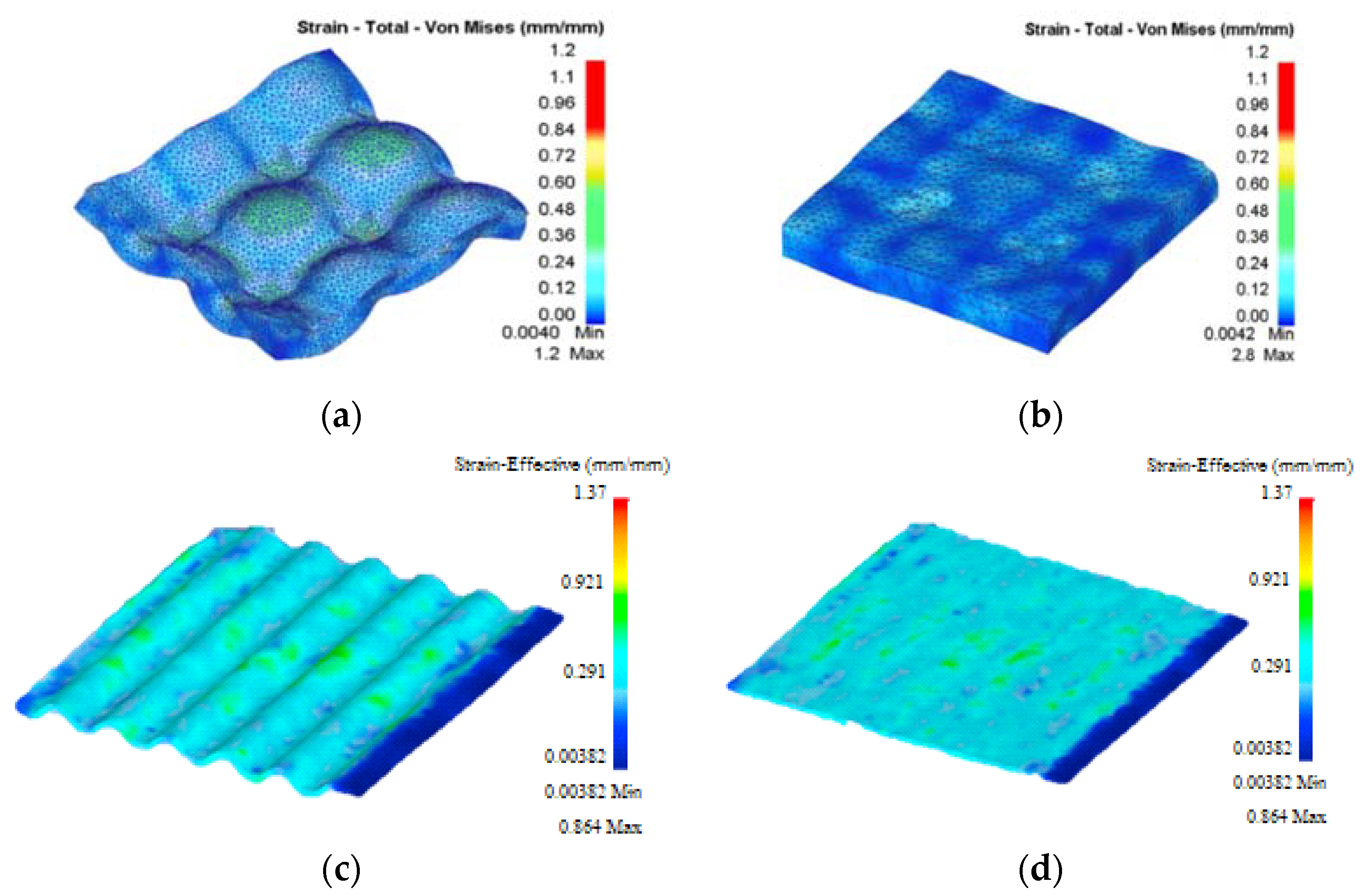
4. Finite Element Simulation
Effective Plastic Strain Analysis
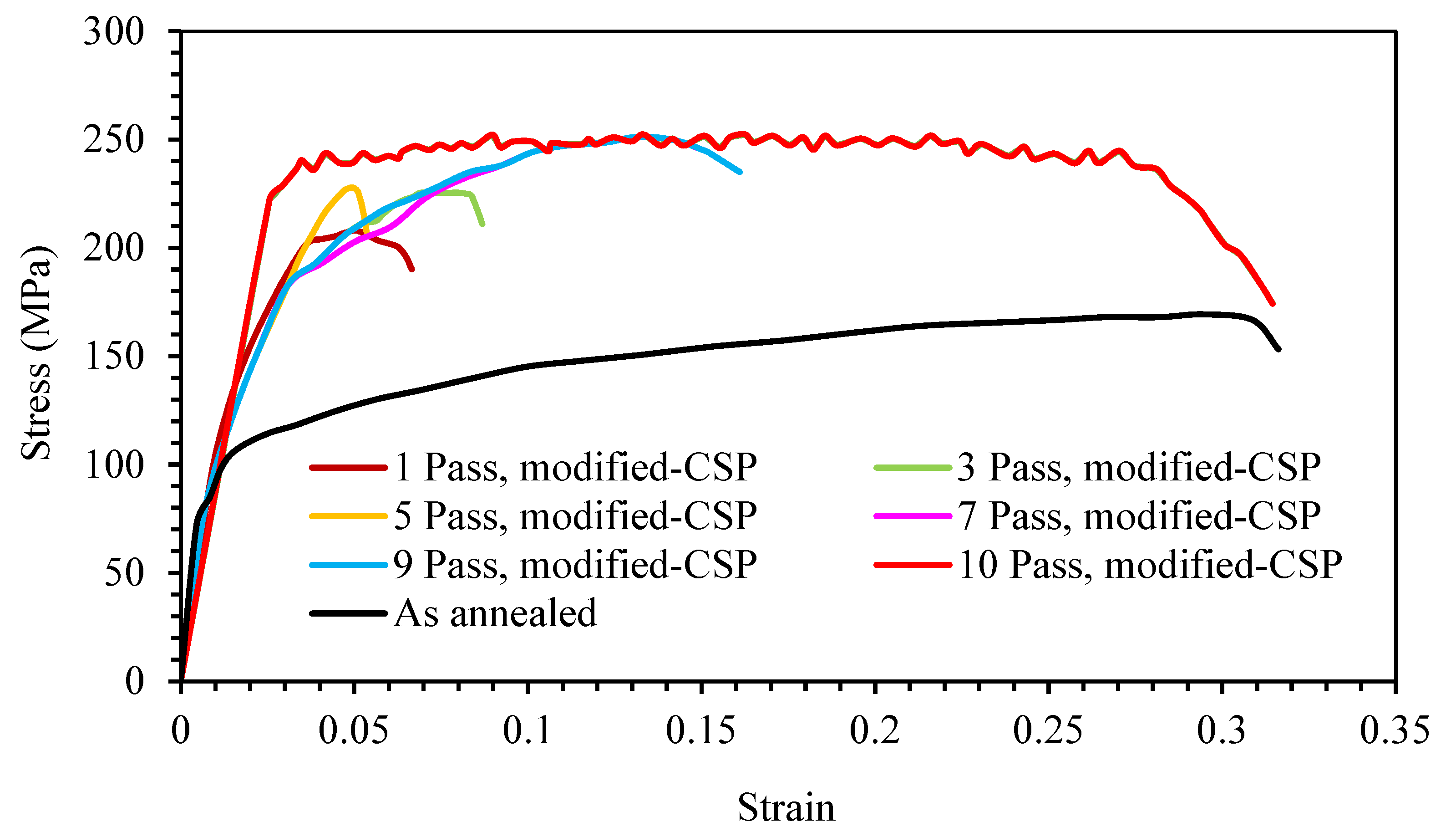
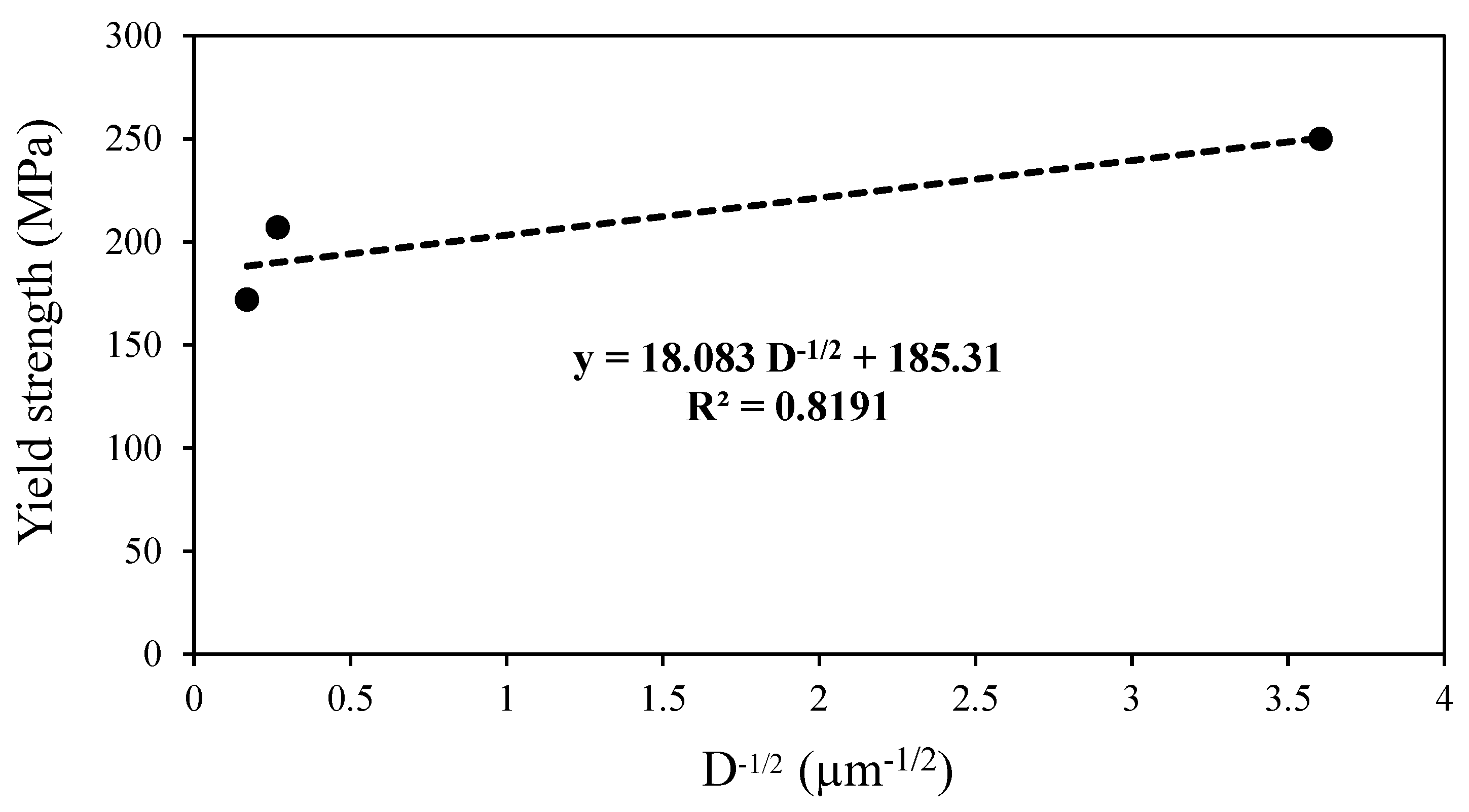
5. Tensile Properties
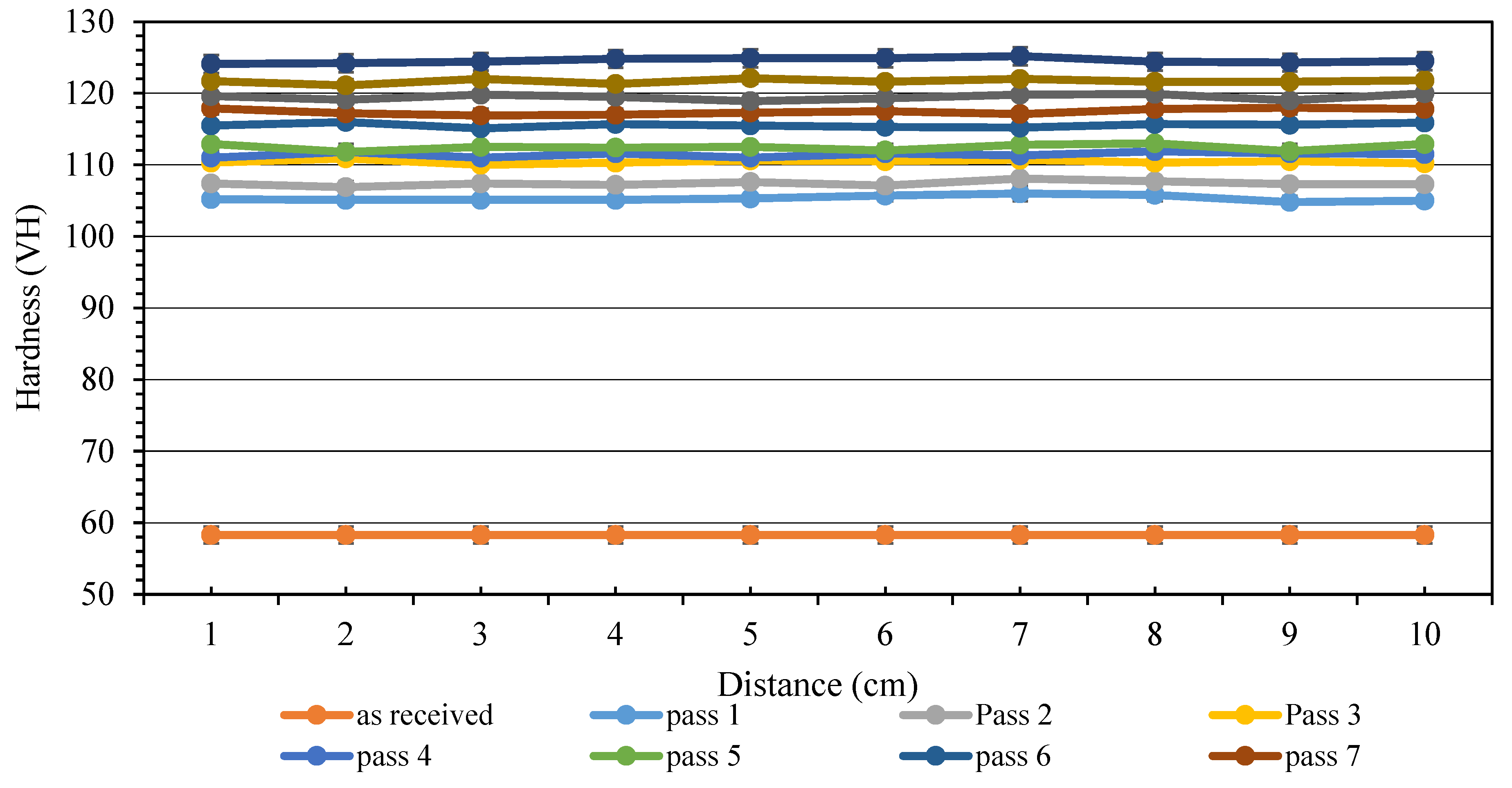
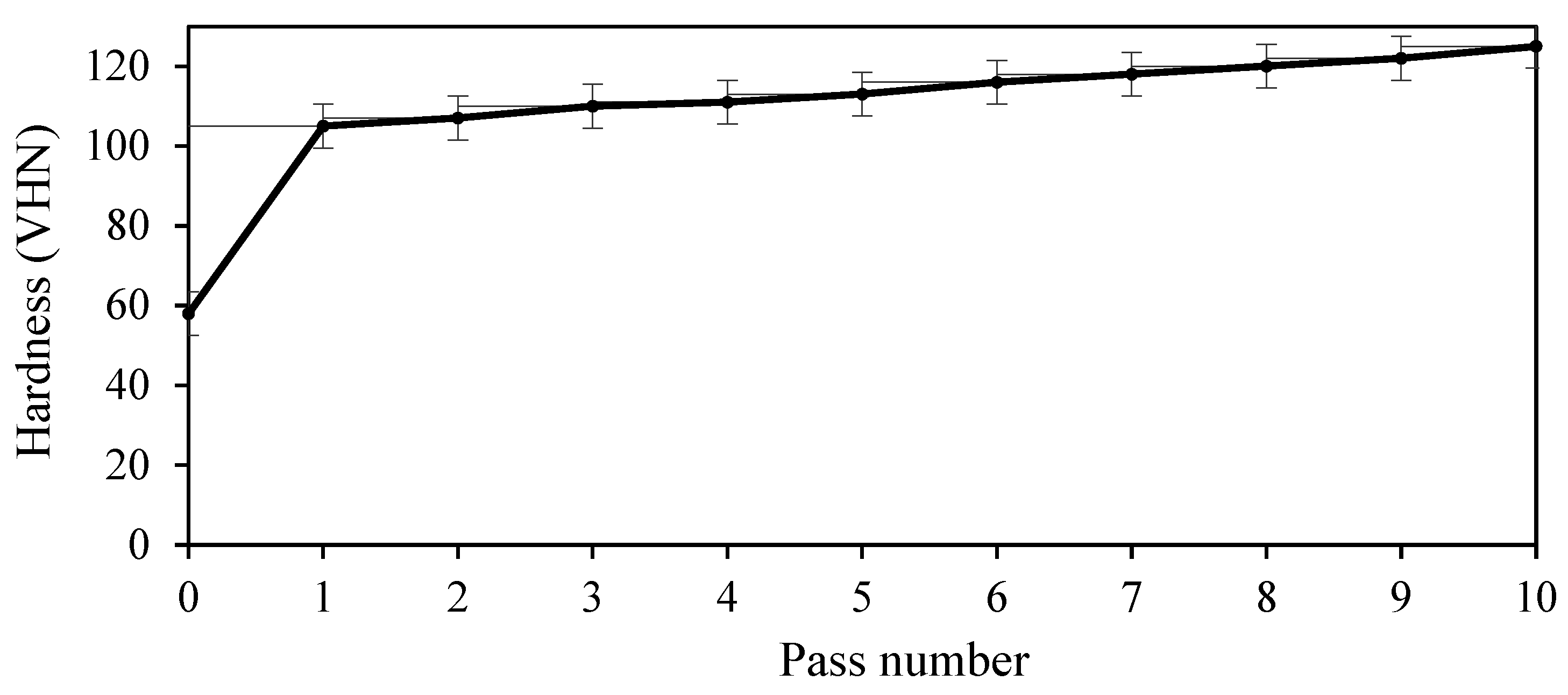
5.1. Hardness Measurement
5.2. Force Analysis
6. Microstructural Evolution
7. Conclusions
- Due to the use of asymmetric semicircle studs in modified-CSP, the maximum groove depth can be up to three times the sheet thickness, which can impose a higher strain in each pass than CSP.
- Due to alternation of the deformation mechanism from slip to twinning, serration was observed in the strain-stress curves of the tenth pass of the modified-CSP sample.
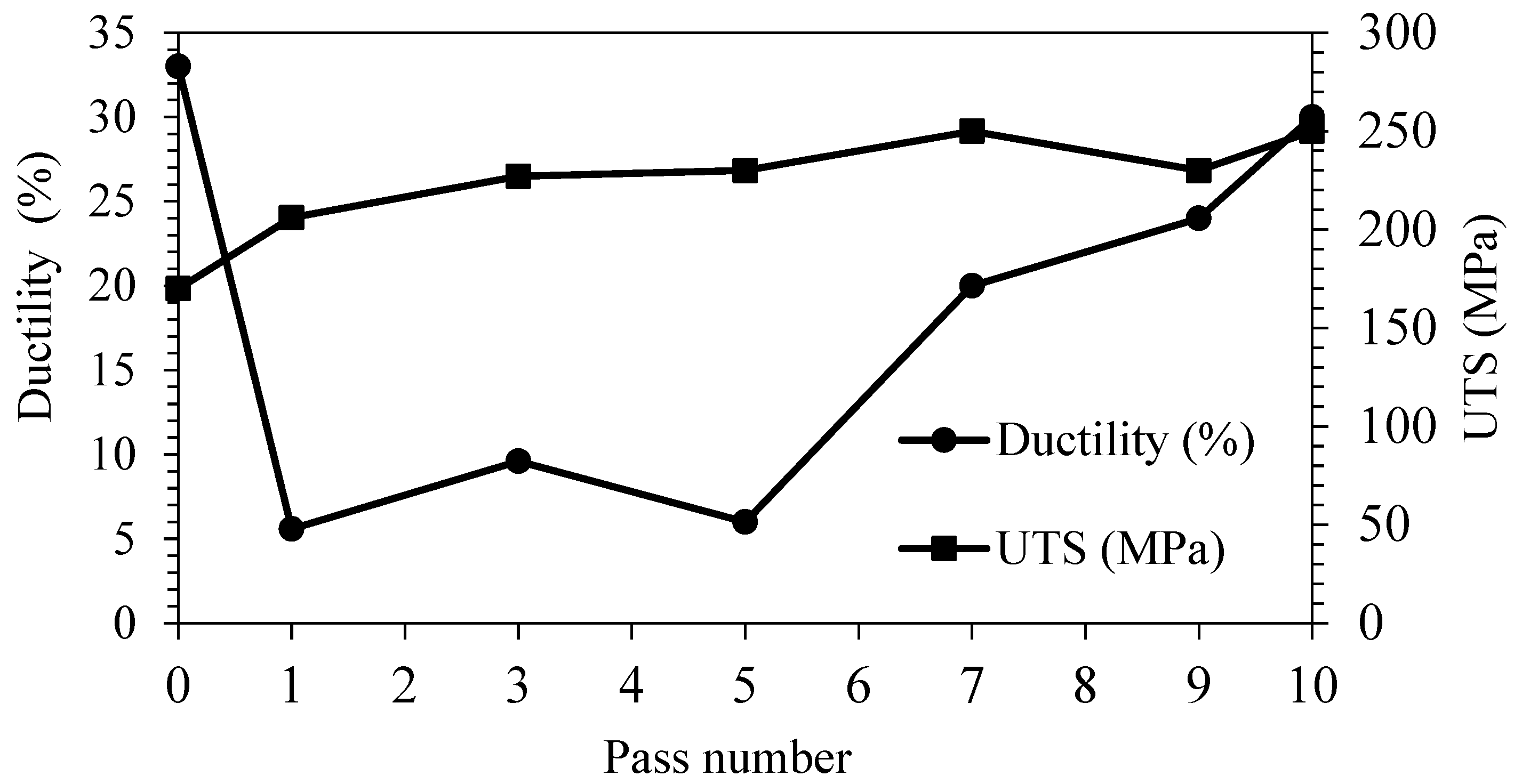
- In the first pass, the average hardness for the annealed sample increased sensitively from 58.4 Vickers to 105.3 Vickers.
- By applying extreme strain, the grains were refined in the first pass. Twins bands were also formed. Simultaneous formation of bimodal grains and the twins bands has increased the strength and ductility of the sample in the tenth pass.
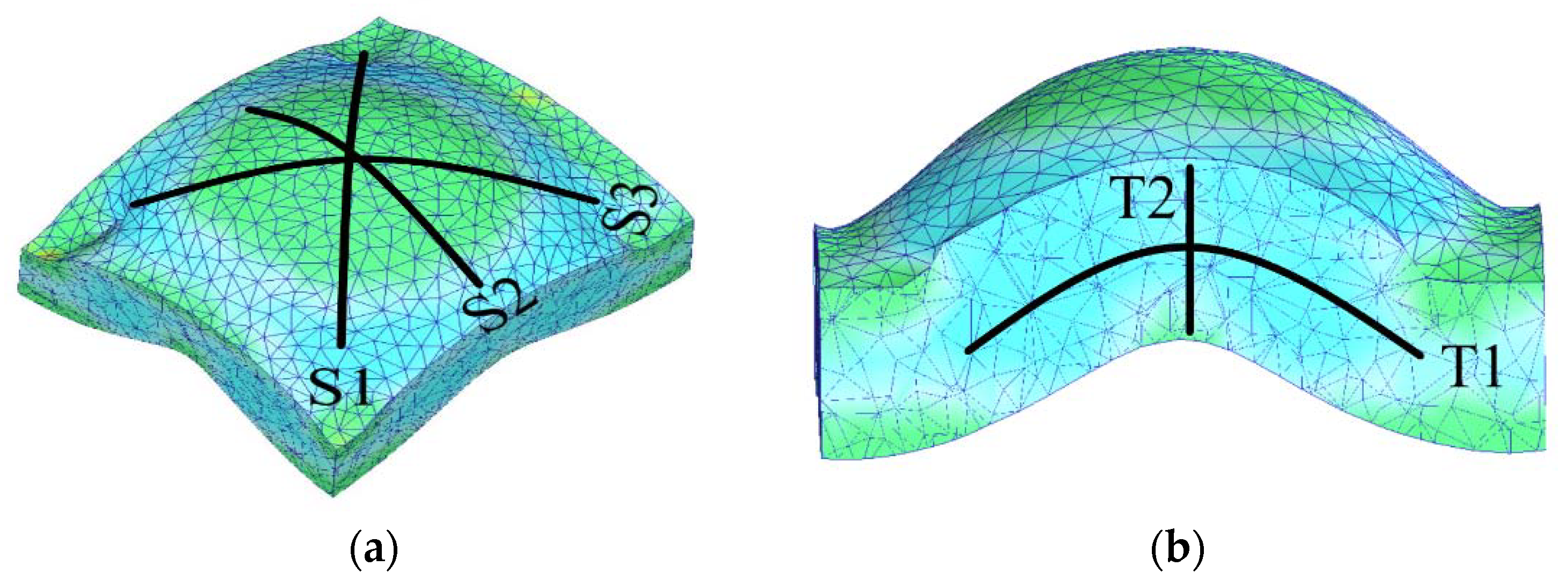
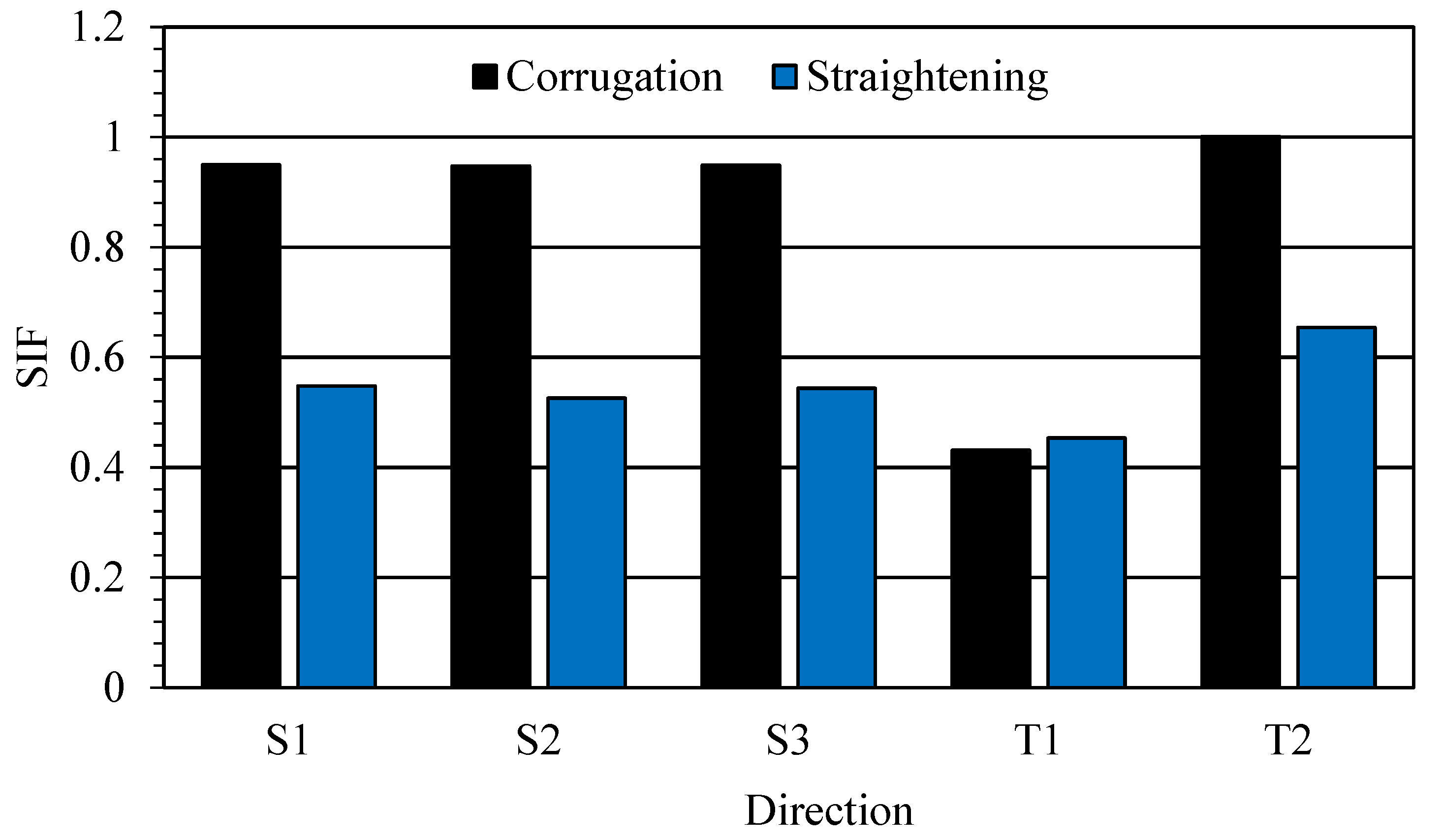
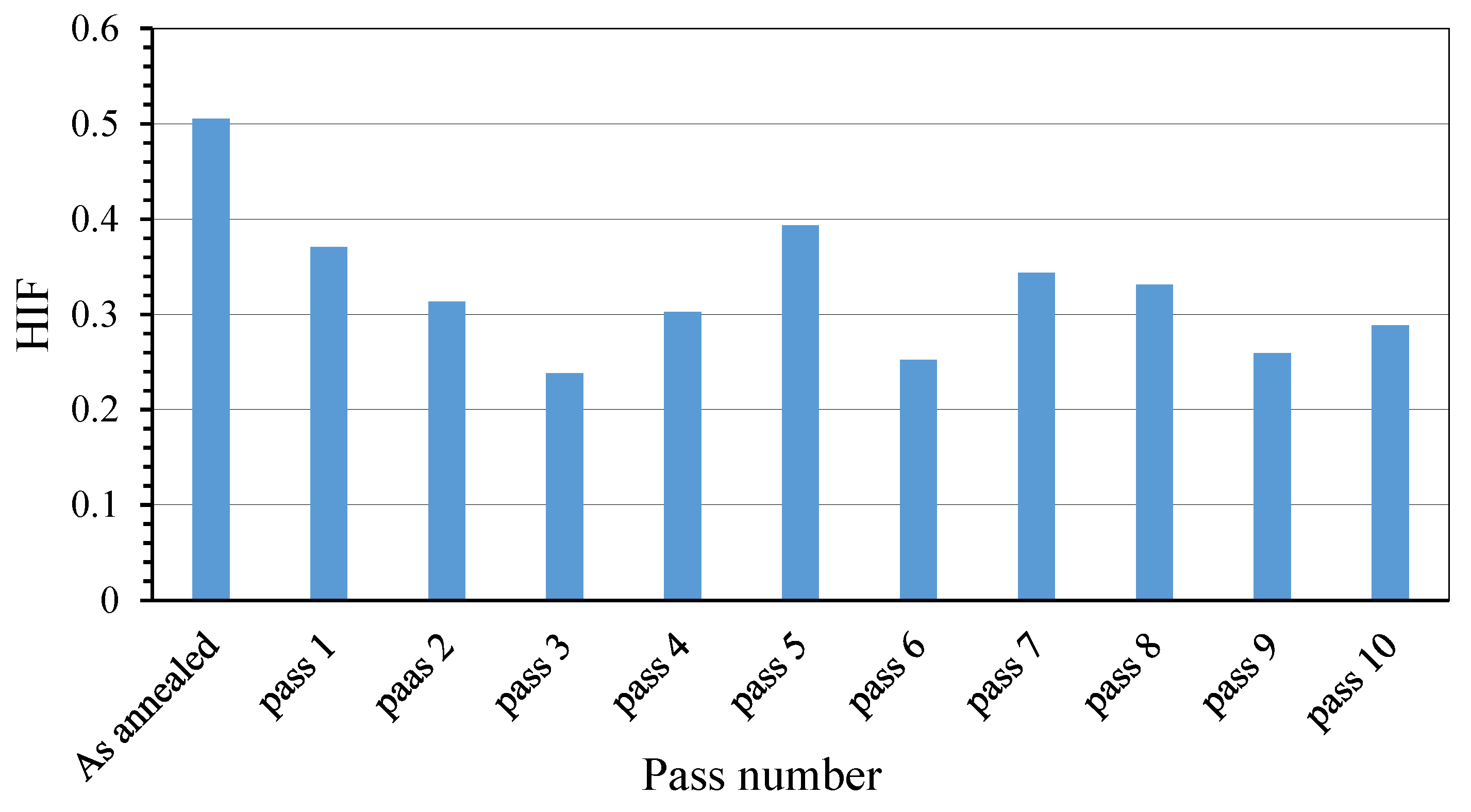
- SIF and HIF have a similar trend. At the end of the process, the SIF and HIF values on the surface are minimized, indicating the effect of the curved surface geometry and the reduction of the sharp edge effects of CGP dies. Noteworthy, the SIF in the center of the sheet thickness (direction T1) is lower than other directions.
- The load-die stroke diagram of CGP and modified-CSP includes three transition steps. CGP has several drastic conversion steps, whereas for modified-CSP the transition steps are quite uniform. In modified-CSP, the load-die stroke diagram increases almost uniformly due to elimination of interface region of the studs and the gradual engagement of dies with the sheet.
- In the modified-CSP dies, by eliminating the sharp edges, surface cracks will be less likely to form and the produced samples will have a greater tensile toughness.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Asano, M.; Yuasa, M.; Miyamoto, H.; Tanaka, T.; Erdogan, C.; Yalçinkaya, T. Potential of High Compressive Ductility of Ultrafine Grained Copper Fabricated by Severe Plastic Deformation. Metals 2020, 10, 1503. [Google Scholar] [CrossRef]
- Wang, Z.; Guan, Y.; Li, L.; Zhu, L. The Fracture Behavior and Thermal Stability of Commercially Pure Nickel Sheets Processed by Constrained Groove Pressing. Metals 2019, 9, 1047. [Google Scholar] [CrossRef] [Green Version]
- Saito, Y.; Tsuji, N.; Utsunomiya, H.; Sakai, T.; Hong, R.G. Ultra-fine grained bulk aluminum produced by accumulative roll-bonding (ARB) process. Scripta Mater. 1998, 39, 1221–1227. [Google Scholar] [CrossRef]
- Zhu, Y.T.; Jiang, H.; Huang, J.; Lowe, T.C. A new route to bulk nanostructured metals. Metall. Mater. Trans. A 2001, 32, 1559–1562. [Google Scholar] [CrossRef]
- Shin, D.H.; Park, J.-J.; Kim, Y.-S.; Park, K.-T. Constrained groove pressing and its application to grain refinement of aluminum. Mater. Sci. Eng. A 2002, 328, 98–103. [Google Scholar] [CrossRef]
- Gupta, A.K.; Maddukuri, T.S.; Singh, S.K. Constrained groove pressing for sheet metal processing. Prog. Mater. Sci. 2016, 84, 403–462. [Google Scholar] [CrossRef]
- Thangapandian, A.N.; Prabu, S.B.; Padmanabhan, K.A. On the Role of Experimental Variables in the Repetitive Corrugation and Straightening of an Al-Mg Alloy. Procedia Eng. 2017, 207, 1457–1462. [Google Scholar] [CrossRef]
- Wang, Z.S.; Guan, Y.J.; Zhong, C.K. Effects of friction on constrained groove pressing of pure Al sheets. Adv. Mater. Res. 2014, 926–930, 81–84. [Google Scholar] [CrossRef]
- Mohammadi Aghbolagh, V.; Alimirzaloo, V.; Khamedi, R. Constrained groove pressing process of Al/Cu bimetal sheet. Mater. Manuf. Process. 2020, 35, 130–141. [Google Scholar] [CrossRef]
- Sajadi, A.; Ebrahimi, M.; Djavanroodi, F. Experimental and numerical investigation of Al properties fabricated by CGP process. Mater. Sci. Eng. A 2012, 552, 97–103. [Google Scholar] [CrossRef]
- Kumar, S.; Hariharan, K.; Digavalli, R. Hybrid optimization of die design in constrained groove pressing. Mater. Manuf. Processes 2020, 35, 687–699. [Google Scholar] [CrossRef]
- Torkestani, A.; Dashtbayazi, M. A new method for severe plastic deformation of the copper sheets. Mater. Sci. Eng. A 2018, 737, 236–244. [Google Scholar] [CrossRef]
- Ezequiel, M.; Figueroa, I.A.; Elizalde, S.; Cabrera, J.M.; Braham, C.; Morin, L.; Gonzalez, G. Numerical and experimental study of a 5754-aluminum alloy processed by heterogeneous repetitive corrugation and straightening. J. Mater. Res. Technol. 2020, 9, 1941–1947. [Google Scholar] [CrossRef]
- Torkestani, A.; Dashtbayazi, M.R. On the evaluation of the constrained studded pressing method for producing nanocrystalline copper sheets. Int. J. Mater. Res. 2020, 111, 594–599. [Google Scholar] [CrossRef]
- Asgari, M.; Honarpisheh, M.; Mansouri, H. Experimental and Numerical Investigation of Mechanical Properties in the Ultrasonic Assisted constraint groove pressing process of copper sheets. J. Ultrafine Grained Nanostructured Mater. 2020, 53, 48–59. [Google Scholar] [CrossRef]
- Keyvani, A.; Naseri, M.; Imantalab, O.; Gholami, D.; Babaei, K.; Fattahalhosseini, A. Microstructural characterization and electrochemical behavior of nano/ ultrafine grained pure copper through constrained groove pressing (CGP). J. Mater. Res. Technol. 2021, 11, 1918–1931. [Google Scholar] [CrossRef]
- Wang, Z.S.; Guan, Y.J.; Song, L.B.; Liang, P. Finite Element Analysis and Deformation Homogeneity Optimization of Constrained Groove Pressing. Appl. Mech. Materials. 2013, 278–280, 505–513. [Google Scholar] [CrossRef]
- Liu, J.; Chen, C.; Xu, Y.; Wu, S.; Wang, G.; Wang, H.; Fang, Y.; Meng, L. Deformation twinning behaviors of the low stacking fault energy high-entropy alloy: An in-situ TEM study. Scr. Mater. 2017, 137, 9–12. [Google Scholar] [CrossRef]
- Meyers, M.A.; Mishra, A.; Benson, D.J. Mechanical properties of nanocrystalline materials. Prog. Mater. Sci. 2006, 51, 427–556. [Google Scholar] [CrossRef]
- Mohammed, A.A.; El-Danaf, E.A.; Radwan, A.-K.A. Equivalent twinning criteria for FCC alloys under uniaxial tension at high temperatures. Mater. Sci. Eng. A 2007, 457, 373–379. [Google Scholar] [CrossRef]
- Brechtl, J.; Chen, S.; Lee, C.; Shi, Y.; Feng, R.; Xie, X.; Hamblin, D.; Coleman, A.M.; Straka, B.; Shortt, H.; et al. A review of the serrated-flow phenomenon and its role in the deformation behavior of high-entropy alloys. Metals 2020, 10, 1101. [Google Scholar] [CrossRef]
- Tabin, J.; Skoczen, B.; Bielski, J. Strain localization during discontinuous plastic flow at extremely low temperatures. Int. J. Solids Struct. 2016, 97, 593–612. [Google Scholar] [CrossRef]
- Gubicza, J.; Chinh, N.Q.; Krallics, G.; Schiller, I.; Ungár, T. Microstructure of ultrafine-grained fcc metals produced by severe plastic deformation. Curr. Appl. Phys. 2006, 6, 194–199. [Google Scholar] [CrossRef]
- An, X.H.; Lin, Q.Y.; Wu, S.D.; Zhang, Z.; Figueiredo, R.B.; Gao, N.; Langdon, T.G. The influence of stacking fault energy on the mechanical properties of nanostructured Cu and Cu–Al alloys processed by high-pressure torsion. Scr. Mater. 2011, 64, 954–957. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Estrin, Y.; Horita, Z.; Langdon, T.G.; Zehetbauer, M.J.; Zhu, Y. Producing bulk ultrafine-grained materials by severe plastic deformation: Ten years later. JOM 2016, 68, 1216–1226. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Meng, X.; Li, Y.; Mao, D.; Wan, L.; Huang, Y. Insight into ultra-refined grains of aluminum matrix composites via deformation-driven metallurgy. Compos. Commun. 2021, 26, 100776. [Google Scholar] [CrossRef]
- Bacca, M.; Hayhurst, D.R.; McMeeking, R.M. Continuous dynamic recrystallization during severe plastic deformation. Mech. Mater. 2015, 90, 148–156. [Google Scholar] [CrossRef] [Green Version]
- Krishnaiah, A.; Chakkingal, U.; Venugopal, P. Production of ultrafine grain sizes in aluminium sheets by severe plastic deformation using the technique of groove pressing. Scr. Mater. 2005, 52, 1229–1233. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, Y.; Guan, M.; Meng, X.; Xie, Y. Grain Refinement in Surficial Cryogenic Grinding. Metall. Mater. Trans. A 2020, 51, 3349–3353. [Google Scholar] [CrossRef]
- Lee, H.-W.; Yoo, J.-H.; Kwon, Y.-C.; Kang, J.-H. Calculation Method for Cold Flow Stress of Al6082 Based on Tensile Test and Compression Test Results. Int. J. Precis. Eng. Manuf. 2021, 22, 1337–1344. [Google Scholar] [CrossRef]
- Borhani, M.; Djavanroodi, F. Rubber pad-constrained groove pressing process: Experimental and finite element investigation. Mater. Sci. Eng. A 2012, 546, 1–7. [Google Scholar] [CrossRef]
- Shirdel, A.; Khajeh, A.; Moshksar, M. Experimental and finite element investigation of semi-constrained groove pressing process. Mater. Des. 2010, 31, 946–950. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Langdon, T.G. Principles of equal-channel angular pressing as a processing tool for grain refinement. Prog. Mater. Sci. 2006, 51, 881–981. [Google Scholar] [CrossRef]


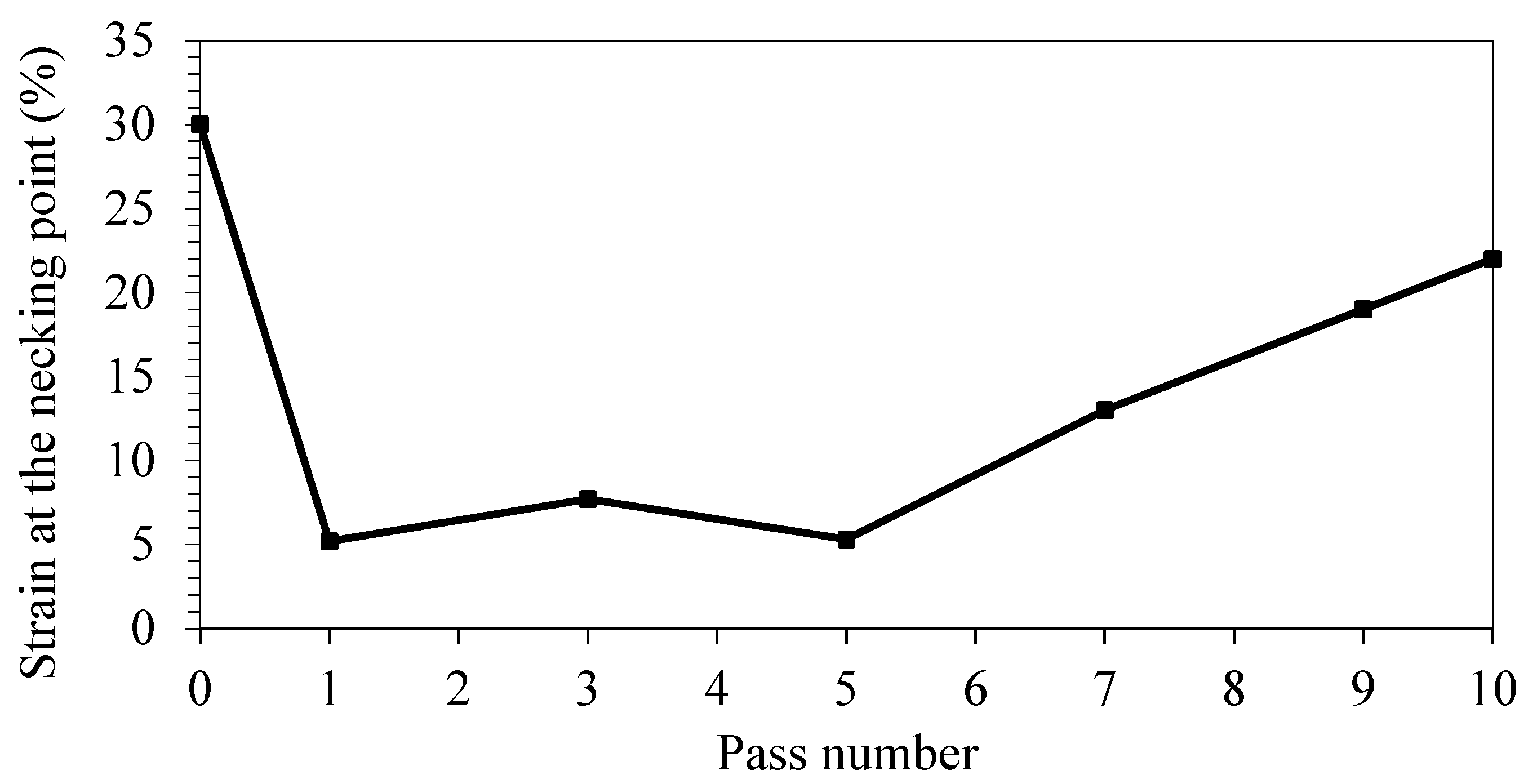





| Material | Density (kg/m3) | Young Modulus (MPa) | Poisson Ratio |
|---|---|---|---|
| Copper | 8.93 | 125,000 | 0.34 |
| Material | A (MPa) | B (MPa) | c | n | m | T Melt (K) |
|---|---|---|---|---|---|---|
| Copper | 90 | 292 | 0.025 | 0.31 | 1.09 | 1356 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaykha, M.M.; Dashtbayazi, M.R. An Improvement in Constrained Studded Pressing for Producing Ultra-Fine-Grained Copper Sheet. Metals 2022, 12, 193. https://doi.org/10.3390/met12020193
Kaykha MM, Dashtbayazi MR. An Improvement in Constrained Studded Pressing for Producing Ultra-Fine-Grained Copper Sheet. Metals. 2022; 12(2):193. https://doi.org/10.3390/met12020193
Chicago/Turabian StyleKaykha, Mohammad M., and Mohammad R. Dashtbayazi. 2022. "An Improvement in Constrained Studded Pressing for Producing Ultra-Fine-Grained Copper Sheet" Metals 12, no. 2: 193. https://doi.org/10.3390/met12020193
APA StyleKaykha, M. M., & Dashtbayazi, M. R. (2022). An Improvement in Constrained Studded Pressing for Producing Ultra-Fine-Grained Copper Sheet. Metals, 12(2), 193. https://doi.org/10.3390/met12020193





