Taylor Impact Tests with Copper Cylinders: Experiments, Microstructural Analysis and 3D SPH Modeling with Dislocation Plasticity and MD-Informed Artificial Neural Network as Equation of State
Abstract
:1. Introduction
2. Materials and Methods
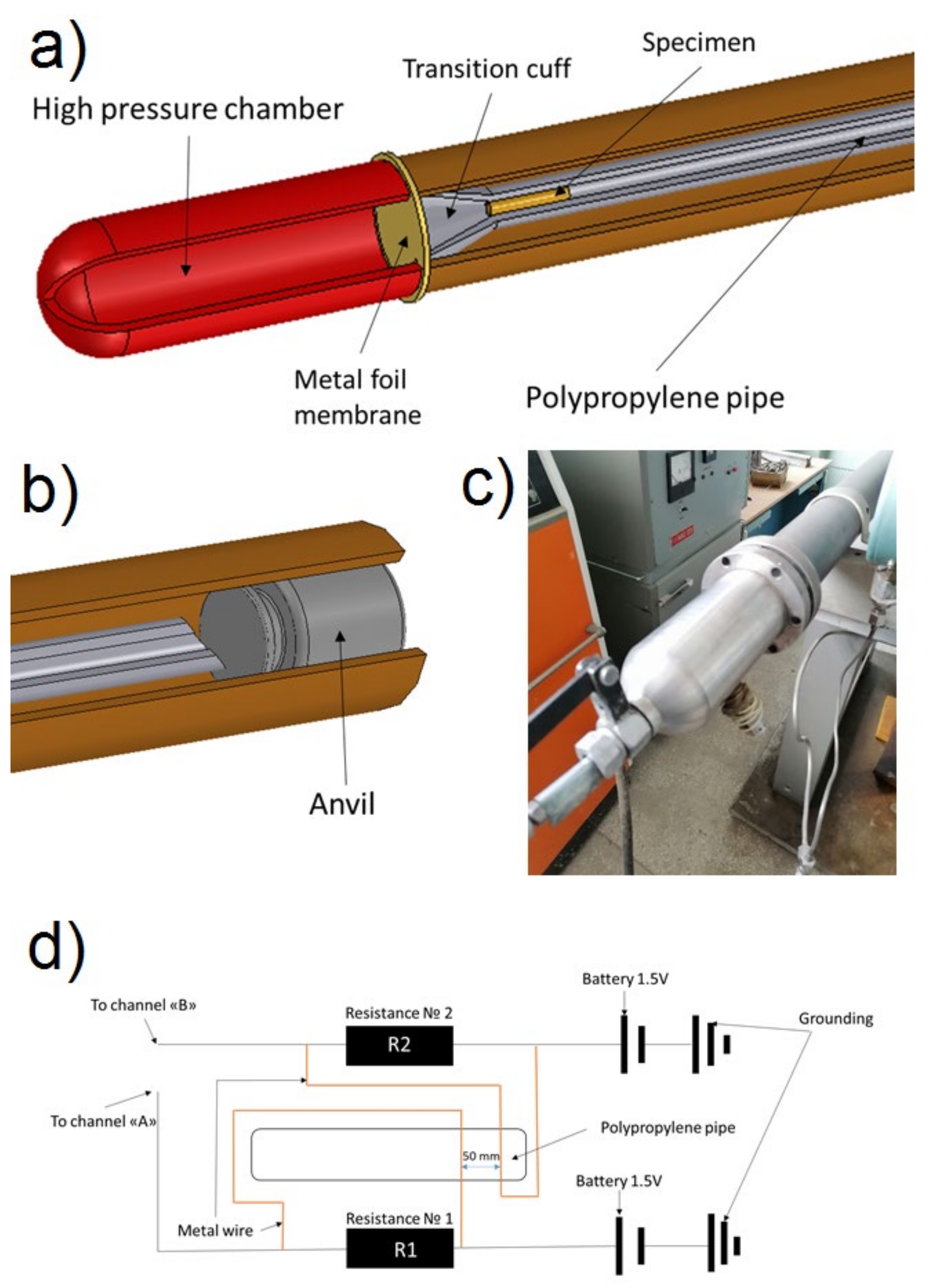
2.1. Material, Specimens and Gas Gun Launcher
2.2. Dislocation Plasticity Model
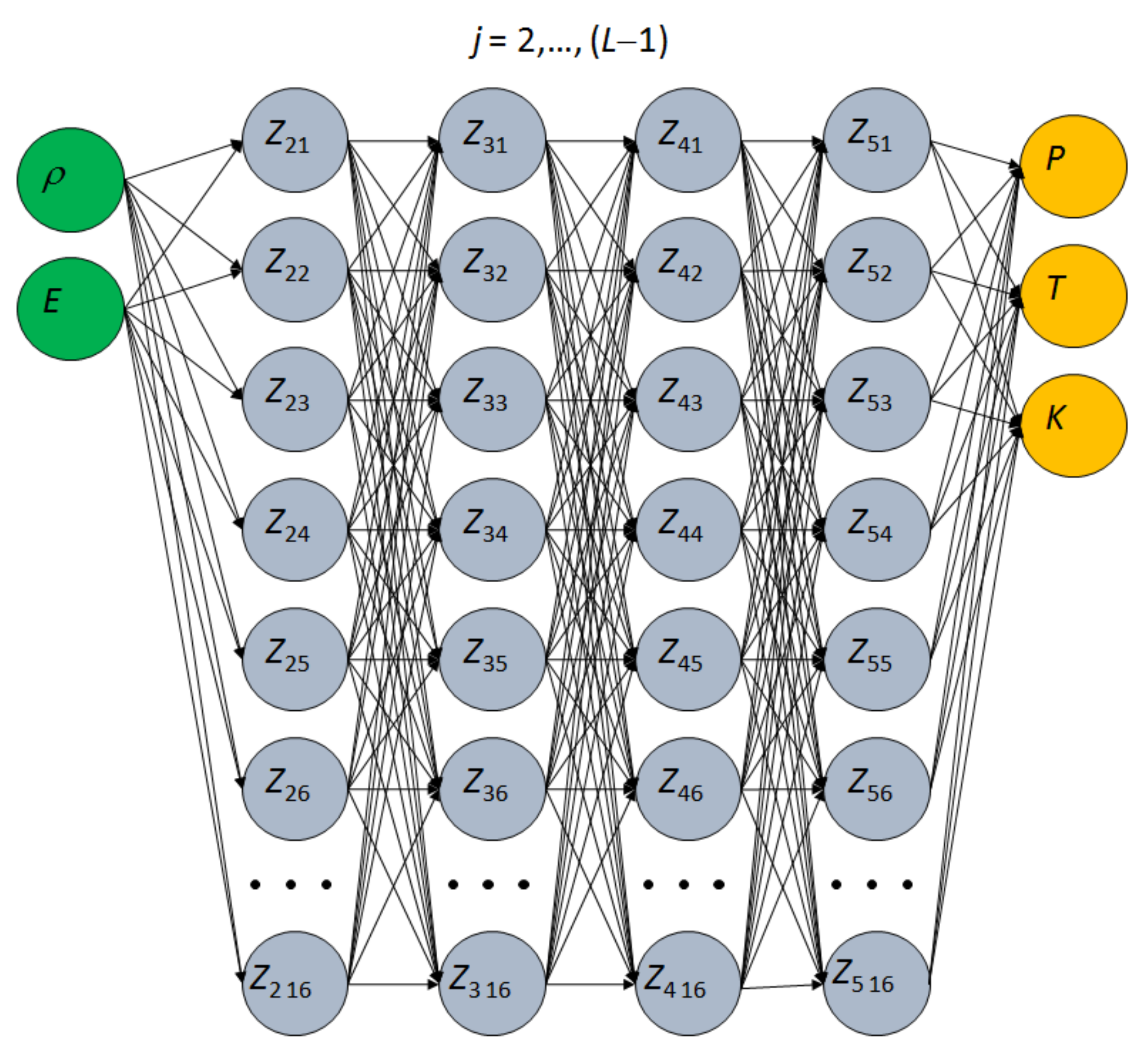
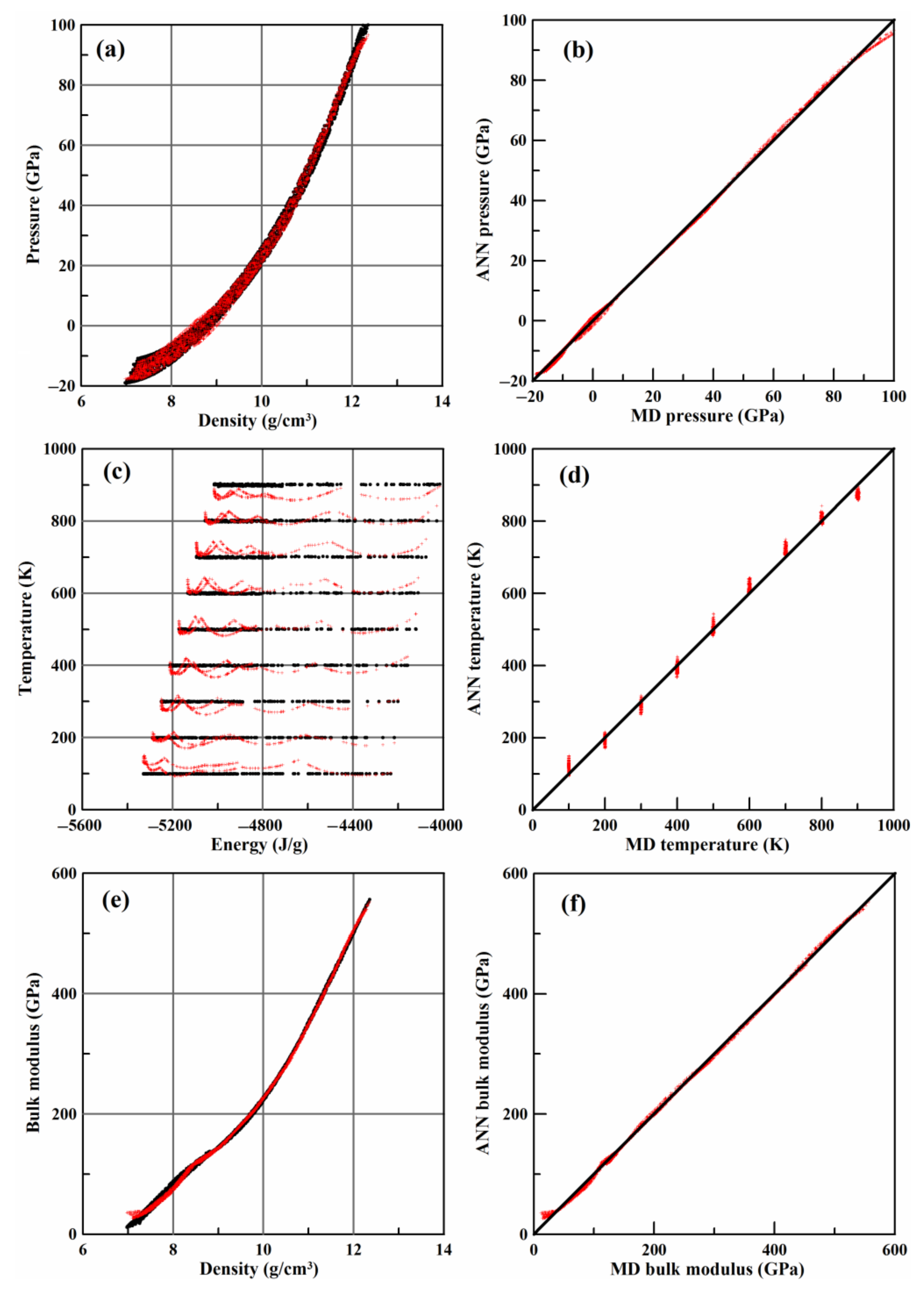
2.3. Equation of State in the Form of the Molecular Dynamics (MD)-Informed Artificial Neural Network (ANN)
2.4. Numerical Scheme of the Smoothed Particle Hydrodynamics (SPH)
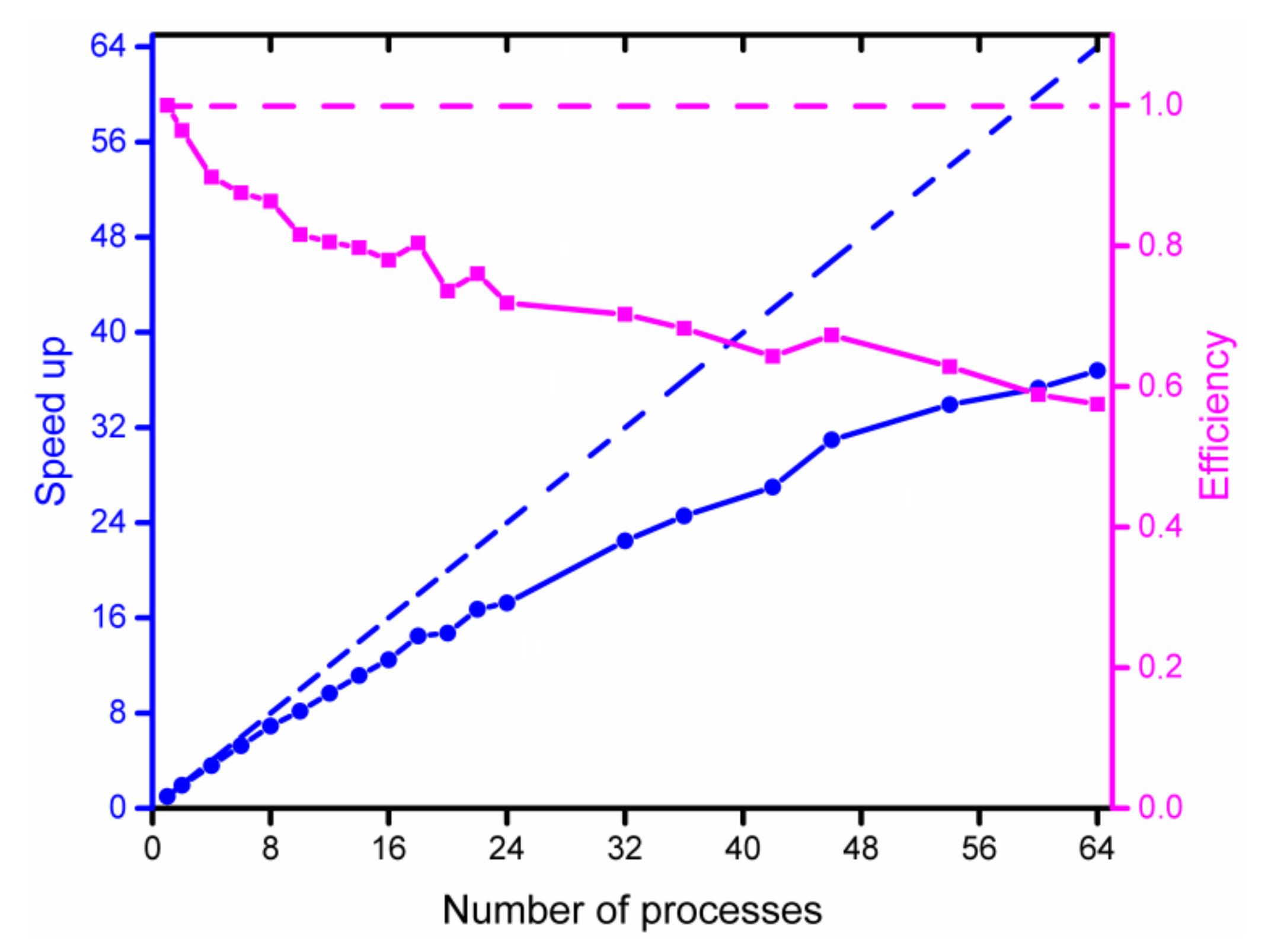
2.5. Parallel Algorithm
3. Results
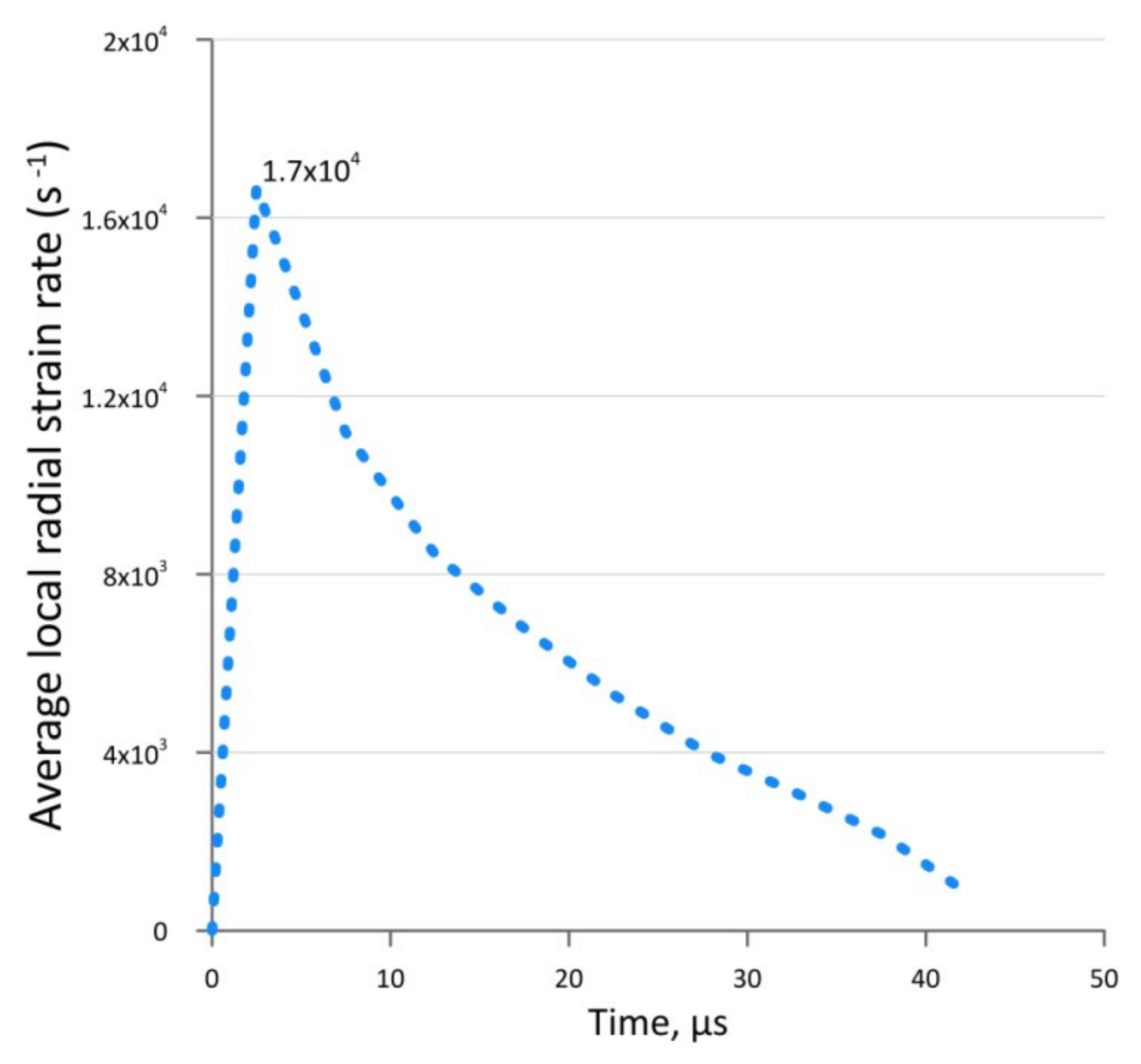
3.1. Results of Experiments
3.2. Microstructural Analysis
3.3. Results of Numerical Modeling in Comparison with Experiment
3.4. Determination of Optimal Coefficients for the Numerical Scheme of Elastic-Plastic Deformations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Raw Data of Experiment in Comparison with Modeling
| Impact Velocity (m/s) | Initial Length (mm) | Final Length (mm) | Initial Diameter (mm) | Final Diameter (mm) | ||||
|---|---|---|---|---|---|---|---|---|
| Experiment | Model | Experiment | Model | Experiment | Model | Experiment | Model | |
| 37.8 | 40.0 | 40.2 | 39.65 | 39.207 | 8.00 | 8.00 | 8.32 | 8.738 |
| 48.5 | 39.35 | 38.693 | 8.62 | 8.928 | ||||
| 76.3 | 38.63 | 37.114 | 9.35 | 9.475 | ||||
| 84.7 | 38.03 | 36.586 | 9.68 | 9.646 | ||||
| 86.9 | 36.93 | 36.445 | 9.516 | 9.693 | ||||
| 87 | 37.54 | 36.439 | 9.72 | 9.693 | ||||
| 87.7 | 37.72 | 36.394 | 9.91 | 9.703 | ||||
| 92.6 | 37.49 | 36.078 | 9.84 | 9.805 | ||||
| 113.6 | 31.3 | 31.4 | 28.75 | 27.249 | 9.683 | 10.195 | ||
Appendix B. Structure of File with Parameters of ANN for Equation of State
| Parameter | Value |
|---|---|
| Number of inputs | 2 |
| Inputs | |
| Number of outputs | 3 |
| Outputs |
References
- Kanel, G.I.; Razorenov, S.V.; Baumung, K.; Singer, J. Dynamic yield and tensile strength of aluminum single crystals at temperatures up to the melting point. J. Appl. Phys. 2001, 90, 136–143. [Google Scholar] [CrossRef]
- Winey, J.M.; LaLone, B.M.; Trivedi, P.B.; Gupta, Y.M. Elastic wave amplitudes in shock-com- pressed thin polycrystalline aluminum samples. J. Appl. Phys. 2009, 106, 073508. [Google Scholar] [CrossRef]
- Gurrutxaga-Lerma, B.; Shehadeh, M.A.; Balint, D.S.; Dini, D.; Chen, L.; Eakins, D.E. The effect of temperature on the elastic precursor decay in shock loaded FCC aluminium and BCC iron. Int. J. Plast. 2017, 96, 135–155. [Google Scholar] [CrossRef]
- Saveleva, N.V.; Bayandin, Y.V.; Savinykh, A.S.; Garkushin, G.V.; Razorenov, S.V.; Naimark, O.B. The formation of elastoplastic fronts and spall fracture in amg6 alloy under shock-wave loading. Tech. Phys. Lett. 2018, 44, 823–826. [Google Scholar] [CrossRef]
- Gnyusov, S.F.; Rotshtein, V.P.; Mayer, A.E.; Rostov, V.V.; Gunin, A.V.; Khishchenko, K.V.; Levashov, P.R. Simulation and experimental investigation of the spall fracture of 304L stainless steel irradiated by a nanosecond relativistic high-current electron beam. Int. J. Fract. 2016, 199, 59–70. [Google Scholar] [CrossRef]
- Gnyusov, S.F.; Rotshtein, V.P.; Mayer, A.E.; Astafurova, E.G.; Rostov, V.V.; Gunin, A.V.; Maier, G.G. Comparative study of shock-wave hardening and substructure evolution of 304L and Hadfield steels irradiated with a nanosecond relativistic high-current electron beam. J. Alloys Compd. 2017, 714, 232–244. [Google Scholar] [CrossRef]
- Baumung, K.; Bluhm, H.J.; Goel, B.; Hoppé, P.; Karow, H.U.; Rusch, D.; Fortov, V.E.; Kanel, G.I.; Razorenov, S.V.; Utkin, A.V.; et al. Shock-wave physics exper- iments with high-power proton beams. Laser Part Beams 1996, 14, 181–209. [Google Scholar] [CrossRef]
- Baumung, K.; Bluhm, H.; Kanel, G.I.; Müller, G.; Razorenov, S.V.; Singer, J.; Utkin, A.V. Tensile strength of five metals and alloys in the nanosecond load duration range at normal and elevated temperatures. Int. J. Impact. Eng. 2001, 25, 631–639. [Google Scholar] [CrossRef]
- Moshe, E.; Eliezer, S.; Dekel, E.; Ludmirsky, A.; Henis, Z.; Werdiger, M.; Goldberg, I.B. An increase of the spall strength in aluminum, copper, and Metglas at strain rates larger than 107 s−1. J. Appl. Phys. 1998, 83, 4004. [Google Scholar] [CrossRef] [Green Version]
- Krasyuk, I.K.; Pashinin, P.P.; Semenov, A.Y.; Khishchenko, K.V.; Fortov, V.E. Study of extreme states of matter at high energy densities and high strain rates with powerful lasers. Laser Phys. 2016, 26, 094001. [Google Scholar] [CrossRef] [Green Version]
- Ashitkov, S.I.; Komarov, P.S.; Struleva, E.V.; Agranat, M.B.; Kanel, G.I. Mechanical and optical properties of vanadium under shock picosecond loads. JETP Lett. 2015, 101, 276–281. [Google Scholar] [CrossRef]
- Kanel, G.I.; Zaretsky, E.B.; Razorenov, S.V.; Ashitkov, S.I.; Fortov, V.E. Unusual plasticity and strength of metals at ultra-short load durations. Phys. Usp. 2017, 60, 490–508. [Google Scholar] [CrossRef] [Green Version]
- Zuanetti, B.; McGrane, S.D.; Bolme, C.A.; Prakash, V. Measurement of elastic precursor decay in pre-heated aluminum films under ultra-fast laser generated shocks. J. Appl. Phys. 2018, 123, 195104. [Google Scholar] [CrossRef] [Green Version]
- Bilalov, D.A.; Sokovikov, M.A.; Chudinov, V.V.; Oborin, V.A.; Bayandin, Y.V.; Terekhina, A.I.; Naimark, O.B. Numerical simulation and experimental study of plastic strain lo- calization under the dynamic loading of specimens in conditions close to a pure shear. J. Appl. Mech. Tech. Phys. 2018, 59, 1179–1188. [Google Scholar] [CrossRef]
- Nie, H.; Suo, T.; Wu, B.; Li, Y.; Zhao, H. A versatile split Hopkinson pressure bar using electromagnetic loading. Int. J. Impact Eng. 2018, 116, 94–104. [Google Scholar] [CrossRef]
- Nguyen, T.; Fensin, S.J.; Luscher, D.J. Dynamic crystal plasticity modeling of single crystal tantalum and validation using Taylor cylinder impact tests. Int. J. Plast. 2021, 139, 102940. [Google Scholar] [CrossRef]
- Grässel, O.; Krüger, L.; Frommeyer, G.; Meyer, L.W. High strength Fe-Mn-(Al, Si) TRIP/TWIP steels development–properties–application. Int. J. Plast. 2000, 16, 1391–1409. [Google Scholar] [CrossRef]
- Taylor, G.I. The use of flat-ended projectiles for determining dynamic yield stress. I. Theoretical considerations. Proc. R. Soc. Lond. Ser. A 1948, 194, 289–299. [Google Scholar] [CrossRef]
- Whiffin, A.C. The use of flat-ended projectiles for determining dynamic yield stress. II. Tests on various metallic materials. Proc. R. Soc. Lond. Ser. A 1948, 194, 300–322. [Google Scholar] [CrossRef] [Green Version]
- Carrington, W.E.; Gayler, M.L.V. The use of flat-ended projectiles for determining dynamic yield stress III. Changes in microstructure caused by deformation under impact at high-striking velocities. Proc. R. Soc. Lond. Ser. A 1948, 194, 323–331. [Google Scholar] [CrossRef] [Green Version]
- Khayer Dastjerdi, A.; Naghdabadi, R.; Arghavani, J. An energy-based approach for analysis of dynamic plastic deformation of metals. Int. J. Mech. Sci. 2013, 66, 94–100. [Google Scholar] [CrossRef]
- Gao, C.; Iwamoto, T. Finite element analysis on a newly-modified method for the Taylor impact test to measure the stress-strain curve by the only single test using pure aluminum. Metals 2018, 8, 642. [Google Scholar] [CrossRef] [Green Version]
- Rakvåg, K.G.; Børvik, T.; Westermann, I.; Hopperstad, O.S. An experimental study on the deformation and fracture modes of steel projectiles during impact. Mater. Des. 2013, 51, 242–256. [Google Scholar] [CrossRef] [Green Version]
- Borodin, E.N.; Mayer, A.E. Structural model of mechanical twinning and its application for modeling of the severe plastic deformation of copper rods in Taylor impact tests. Int. J. Plast. 2015, 74, 141–157. [Google Scholar] [CrossRef]
- Volkov, G.A.; Bratov, V.A.; Borodin, E.N.; Evstifeev, A.D.; Mikhailova, N.V. Numerical simulations of impact Taylor tests. J. Phys. Conf. Ser. 2020, 1556, 012059. [Google Scholar] [CrossRef]
- Zhang, L.; Pellegrino, A.; Townsend, D.; Petrinic, N. Thermomechanical constitutive behaviour of a near 𝛼 titanium alloy over a wide range of strain rates: Experiments and modelling. Int. J. Mech. Sci. 2021, 189, 105970. [Google Scholar] [CrossRef]
- Rakvåg, K.G.; Børvik, T.; Hopperstad, O.S. A numerical study on the deformation and fracture modes of steel projectiles during Taylor bar impact tests. Int. J. Solids Struct. 2014, 51, 808–821. [Google Scholar] [CrossRef] [Green Version]
- Moćko, W.; Janiszewski, J.; Radziejewska, J.; Gra¸zka, M. Analysis of deformation history and damage initiation for 6082-T6 aluminium alloy loaded at classic and symmetric Taylor impact test conditions. Int. J. Impact. Eng. 2015, 75, 203–213. [Google Scholar] [CrossRef]
- Xiao, X.; Mu, Z.; Pan, H.; Lou, Y. Effect of the Lode parameter in predicting shear cracking of 2024-T351 aluminum alloy Taylor rods. Int. J. Impact. Eng. 2018, 120, 185–201. [Google Scholar] [CrossRef]
- Piao, M.J.; Huh, H.; Lee, I.; Park, L. Characterization of hardening behaviors of 4130 Steel, OFHC Copper, Ti6Al4V alloy considering ultra-high strain rates and high temperatures. Int. J. Mech. Sci. 2017, 131, 1117–1129. [Google Scholar] [CrossRef]
- Kanel, G.I.; Savinykh, A.S.; Garkushin, G.V.; Razorenov, S.V. Effects of temperature on the flow stress of aluminum in shock waves and rarefaction waves. J. Appl. Phys. 2020, 127, 035901. [Google Scholar] [CrossRef]
- Zaretsky, E.B.; Kanel, G.I. Response of copper to shock-wave loading at temperatures up to the melting point. J. Appl. Phys. 2013, 114, 083511. [Google Scholar] [CrossRef]
- Kanel, G.I.; Savinykh, A.S.; Garkushin, G.V.; Razorenov, S.V. Effects of temperature and strain on the resistance to high-rate deformation of copper in shock waves. J. Appl. Phys. 2020, 128, 115901. [Google Scholar] [CrossRef]
- Kuksin, A.Y.; Stegailov, V.V.; Yanilkin, A.V. Molecular-dynamics simulation of edge-dislocation dynamics in aluminum. Dokl. Phys. 2008, 53, 287–291. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Kuksin, A.Y.; Mayer, A.E.; Yanilkin, A.V. Plastic deformation under high-rate loading: The multiscale approach. Phys. Solid State 2010, 52, 1386–1396. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E. Influence of local stresses on motion of edge dislocation in aluminum. Int. J. Plast. 2018, 101, 170–187. [Google Scholar] [CrossRef]
- Austin, R.A.; McDowell, D.L. A dislocation-based constitutive model for viscoplastic deformation of fcc metals at very high strain rates. Int. J. Plast. 2011, 27, 1–24. [Google Scholar] [CrossRef]
- Barton, N.R.; Bernier, J.V.; Becker, R.; Arsenlis, A.; Cavallo, R.; Marian, J.; Rhee, M.; Park, H.-S.; Remington, B.A.; Olson, R.T. A multiscale strength model for extreme loading conditions. J. Appl. Phys. 2011, 109, 073501. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E.; Yalovets, A.P. Dislocation based high-rate plasticity model and its application to plate-impact and ultra-short electron irradiation simulations. Int. J. Plast. 2011, 27, 1294–1308. [Google Scholar] [CrossRef]
- Luscher, D.J.; Mayeur, J.R.; Mourad, H.M.; Hunter, A.; Kenamond, M.A. Coupling continuum dislocation transport with crystal plasticity for application to shock loading conditions. Int. J. Plast. 2016, 76, 111–129. [Google Scholar] [CrossRef] [Green Version]
- Khishchenko, K.V.; Mayer, A.E. High- and low-entropy layers in solids behind shock and ramp compression waves. Int. J. Mech. Sci. 2021, 189, 105971. [Google Scholar] [CrossRef]
- Lim, H.; Carroll, J.D.; Battaile, C.C.; Chen, S.R.; Moore, A.P.; Lane, J.M.D. Anisotropy and strain localization in dynamic impact experiments of tantalum single crystals. Sci. Rep. 2018, 8, 5540. [Google Scholar] [CrossRef] [Green Version]
- Mayer, A.E.; Khishchenko, K.V.; Levashov, P.R.; Mayer, P.N. Modeling of plasticity and fracture of metals at shock loading. J. Appl. Phys. 2013, 113, 93508. [Google Scholar] [CrossRef]
- Yao, S.L.; Pei, X.Y.; Yu, J.D.; Bai, J.S.; Wu, Q. A dislocation-based explanation of quasi-elastic release in shock-loaded aluminum. J. Appl. Phys. 2017, 121, 035101. [Google Scholar] [CrossRef] [Green Version]
- Yao, S.; Pei, X.; Yu, J.; Wu, Q. Scale dependence of thermal hardening of fcc metals under shock loading. J. Appl. Phys. 2020, 128, 0026226. [Google Scholar] [CrossRef]
- Popova, T.V.; Mayer, A.E.; Khishchenko, K.V. Evolution of shock compression pulses in polymethylmethacrylate and aluminum. J. Appl. Phys. 2018, 123, 235902. [Google Scholar] [CrossRef]
- Selyutina, N.; Borodin, E.N.; Petrov, Y.; Mayer, A.E. The definition of characteristic times of plastic relaxation by dislocation slip and grain boundary sliding in copper and nickel. Int. J. Plast. 2016, 82, 97–111. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Pan, W.; Li, D.; Tartakovsky, A.M.; Ahzi, S.; Khraisheh, M.; Khaleel, M. A new smoothed particle hydrodynamics non-Newtonian model for friction stir welding: Process modeling and simulation of microstructure evolution in a magnesium alloy. Int. J. Plast. 2013, 48, 189–204. [Google Scholar] [CrossRef]
- Li, X.; Roth, C.C.; Mohr, D. Machine-learning based temperature- and rate-dependent plasticity model: Application to analysis of fracture experiments on DP steel. Int. J. Plast. 2019, 118, 320–344. [Google Scholar] [CrossRef]
- Islam, M.R.I.; Chakraborty, S.; Shaw, A. On consistency and energy conservation in smoothed particle hydrodynamics. Int. J. Numer. Methods Eng. 2018, 116, 601–632. [Google Scholar] [CrossRef]
- Jordan, B.; Gorji, M.B.; Mohr, D. Neural network model describing the temperature- and rate-dependent stress-strain response of polypropylene. Int. J. Plast. 2020, 135, 102811. [Google Scholar] [CrossRef]
- Gorji, M.B.; Mozaffar, M.; Heidenreich, J.N.; Cao, J.; Mohr, D. On the potential of recurrent neural networks for modeling path dependent plasticity. J. Mech. Phys. Solids 2020, 43, 103972. [Google Scholar] [CrossRef]
- Bonatti, C.; Mohr, D. Neural network model predicting forming limits for Bi-linear strain paths. Int. J. Plast. 2021, 137, 102886. [Google Scholar] [CrossRef]
- Grachyova, N.A.; Lekanov, M.V.; Mayer, A.E.; Fomin, E.V. Application of neural networks for modeling shock-wave processes in aluminum. Mech. Solids 2021, 56, 326–342. [Google Scholar] [CrossRef]
- Mayer, A.E.; Krasnikov, V.S.; Pogorelko, V.V. Dislocation nucleation in Al single crystal at shear parallel to (111) plane: Molecular dynamics simulations and nucleation theory with artificial neural networks. Int. J. Plast. 2021, 139, 102953. [Google Scholar] [CrossRef]
- Fortov, V.E.; Khishchenko, K.V.; Levashov, P.R.; Lomonosov, I.V. Wide-range multi-phase equations of state for metals. Nucl. Instrum. Methods Phys. Res. A 1998, 415, 604–608. [Google Scholar] [CrossRef]
- Borodin, E.N.; Mayer, A.E. Localization of plastic flow at dynamic channel angular pressing. Tech. Phys. 2013, 58, 1159–1163. [Google Scholar] [CrossRef]
- Mayer, A.E.; Borodin, E.N.; Mayer, P.N. Localization of plastic flow at high-rate simple shear. Int. J. Plast. 2013, 51, 188–199. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E. Modeling of plastic localization in aluminum and Al–Cu alloys under shock loading. Mater. Sci. Eng. A 2014, 619, 354–363. [Google Scholar] [CrossRef]
- Bai, Y.; Dodd, B. Shear Localization: Occurrence Theories and Applications; Pergamon Press: Oxford, UK, 1992. [Google Scholar]
- Wright, T. The Physics and Mathematics of Adiabatic Shear Bands; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Walley, S.M. Shear localization: A historical overview. Metall. Mater. Trans. A 2007, 38, 2629–2654. [Google Scholar] [CrossRef]
- Shockey, D.A.; Murr, L.E.; Staudhammer, K.P.; Meyers, M.A. (Eds.) Metallurgical Applications of Shock-Wave and High-Strain-Rate Phenomena; Marcel-Dekker: New York, NY, USA, 1986; pp. 633–656. [Google Scholar]
- Shahan, A.R.; Taheri, A.K. Adiabatic shear bands in titanium and titanium alloys: A critical review. Mater. Res. Bull. 1993, 14, 243–250. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, J.; Bai, Y.; Meyers, M.A. Shear localization in dynamic deformation: Microstructural evolution. Metall. Mater. Trans. A 2008, 39, 811–843. [Google Scholar] [CrossRef]
- Tresca, H. On further application of the flow of solids. Proc. Inst. Mech. Eng. 1878, 30, 301–345. [Google Scholar] [CrossRef]
- Massey, H.F. The flow of metals during forging. Trans. Manch. Eng. Assoc. 1921, 21–66. [Google Scholar]
- Johnson, W.; Baraya, G.L.; Slater, R.A.C. On heat lines or lines of thermal discontinuity. Int. J. Mech. Sci. 1964, 6, 409–414. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Kuropatenko, V.F. New models of continuum mechanics. J. Eng. Phys. Thermophys. 2011, 84, 77–99. [Google Scholar] [CrossRef]
- Mayer, A.E.; Krasnikov, V.S.; Pogorelko, V.V. Homogeneous nucleation of dislocations in copper: Theory and approximate description based on molecular dynamics and artificial neural networks. 2022; submitted. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity. Course of Theoretical Physics, 7; Pergamon: New York, NY, USA, 1986. [Google Scholar]
- Hirth, J.P.; Lothe, J. Theory of Dislocations; Wiley & Sons: New York, NY, USA, 1982. [Google Scholar]
- Dudorov, A.E.; Mayer, A.E. The equations of the dynamics and kinetics of dislocations at high strain rate plastic deformation. CSU Bull. Phys. 2011, 39, 48–56. (In Russian) [Google Scholar]
- Mayer, A.E.; Krasnikov, V.S. Molecular dynamics investigation of dislocation slip in pure metals and alloys. In Proceedings of the Second International Conference on Theoretical, Applied and Experimental Mechanics, ICTAEM 2019, Corfu, Greece, 23–26 June 2019; Volume 8, pp. 59–64. [Google Scholar] [CrossRef]
- Franciosi, P. The concepts of latent hardening and strain hardening in metallic single crystals. Acta Metall. 1985, 33, 1601–1612. [Google Scholar] [CrossRef]
- Devincre, B.; Kubin, L.; Hoc, T. Physical analyses of crystal plasticity by DD simulations. Scr. Mater. 2006, 54, 741–746. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Apostol, F.; Mishin, Y. Interatomic potential for the Al-Cu system. Phys. Rev. B 2011, 83, 054116. [Google Scholar] [CrossRef] [Green Version]
- Thompson, A.P.; Plimpton, S.J.; Mattson, W. General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions. J. Chem. Phys. 2009, 131, 154107. [Google Scholar] [CrossRef] [Green Version]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: https://www.deeplearningbook.org/ (accessed on 30 December 2021).
- Nielsen, M. Neural Networks and Deep Learning. 2019. Available online: http://neuralnetworksanddeeplearning.com (accessed on 30 December 2021).
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- Monaghan, J.J. An introduction to SPH. Comput. Phys. Commun. 1998, 48, 89–96. [Google Scholar] [CrossRef]
- Marrone, S.; Di Mascio, A.; Le Touzé, D. Coupling of Smoothed Particle Hydrodynamics with Finite Volume method for free-surface flows. J. Comput. Phys. 2016, 310, 161–180. [Google Scholar] [CrossRef]
- Popov, G.; Mastorakis, N.; Mladenov, V. Calculation of the acceleration of parallel programs as a function of the number of threads. In Proceedings of the ICCOMP’10: 14th WSEAS International Conference on Computers: Part of the 14th WSEAS CSCC Multiconference—V. II, Corfu, Greece, 23–25 July 2010; pp. 411–414. [Google Scholar]
- Rodgers, D.P. Improvements in multiprocessor system design. ACM SIGARCH Comput. Archit. News 1985, 13, 225–231. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Modell. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Foster, J.T.; Chen, W.; Luk, V.K. Dynamic crack initiation toughness of 4340 steel at constant loading rates. Eng. Fract. Mech. 2011, 78, 1264–1276. [Google Scholar] [CrossRef]
- Zhou, L.; Zhu, Z.; Dong, Y.; Niu, C. Investigation of dynamic fracture properties of multi-crack tunnel samples under impact loads. Theor. Appl. Fract. Mech. 2020, 109, 102733. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, Z.; Zhou, L.; Gao, W.; Dong, Y.; Niu, C.; Ai, T. Study the effect of circular hole on dynamic fracture properties of cracked PMMA specimen under impact loads. Int. J. Impact. Eng. 2021, 156, 103948. [Google Scholar] [CrossRef]
- Sitek, W.; Trzaska, J. Practical aspects of the design and use of the artificial neural networks in materials engineering. Metals 2021, 11, 1832. [Google Scholar] [CrossRef]
- Reséndiz-Flores, E.O.; Altamirano-Guerrero, G.; Costa, P.S.; Salas-Reyes, A.E.; Salinas-Rodríguez, A.; Goodwin, F. Optimal design of hot-dip galvanized DP steels via artificial neural networks and multi-objective genetic optimization. Metals 2021, 11, 578. [Google Scholar] [CrossRef]
- Ishihara, K.; Kitagawa, H.; Takagishi, Y.; Meshii, T. Application of an artificial neural network to develop fracture toughness predictor of ferritic steels based on tensile test results. Metals 2021, 11, 1740. [Google Scholar] [CrossRef]
- Khan, A.S.; Liu, J.; Yoon, J.W.; Nambori, R. Strain rate effect of high purity aluminum single crystals: Experiments and simulations. Int. J. Plast. 2015, 67, 39–52. [Google Scholar] [CrossRef]
- Khan, A.S.; Liu, J. A deformation mechanism based crystal plasticity model of ultrafine-grained/nanocrystalline FCC polycrystals. Int. J. Plast. 2016, 86, 56–69. [Google Scholar] [CrossRef]
- Mayer, A.E.; Lekanov, M.V.; Gracheva, N.A.; Fomin, E.V. Machine-learning-based model of elastic-plastic deformation of copper for application to shock wave problem. Metals 2022, 12. submitted. [Google Scholar]







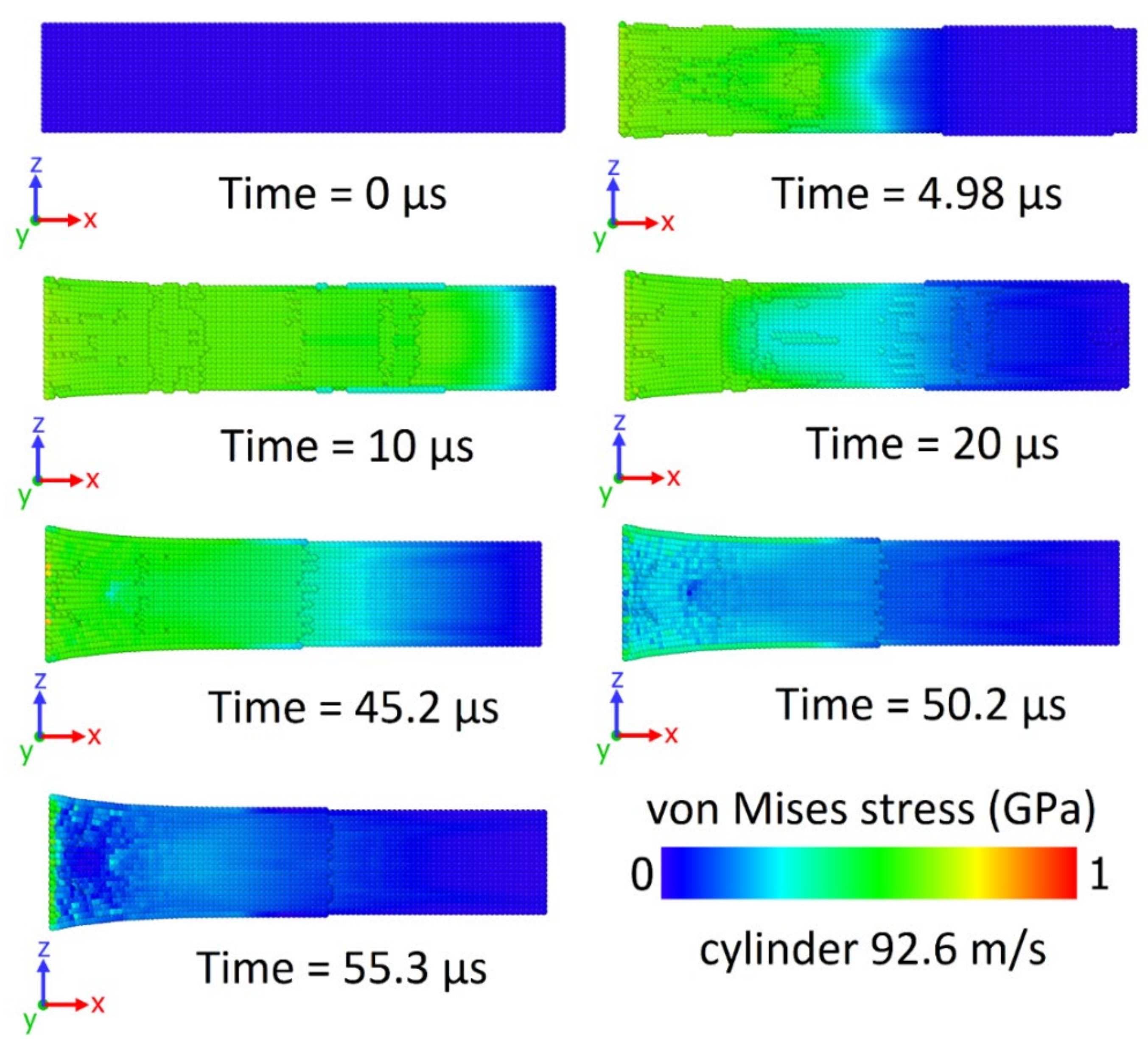
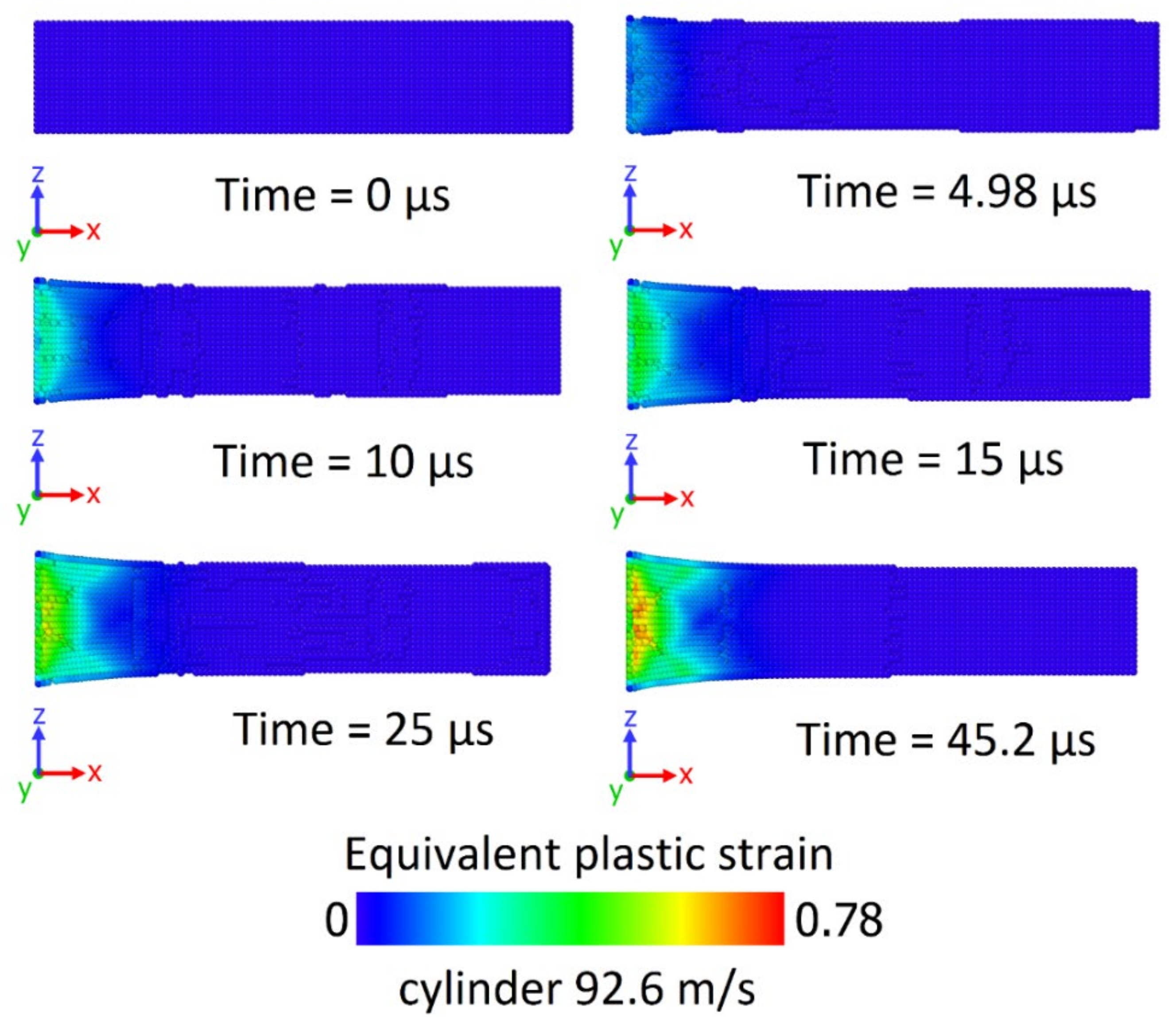




| Parameter | Value |
|---|---|
| [Pa × s] | |
| 0.34 | |
| [MPa] | 30 |
| 3 | |
| [m/s] | 2 |
| [J−1] | 7.8 × 1016 |
| 5 | |
| 0.1 | |
| [m−2] | 1011 |
| [m−2] | 1011 |
| [m−2] | 1013 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodionov, E.S.; Lupanov, V.G.; Gracheva, N.A.; Mayer, P.N.; Mayer, A.E. Taylor Impact Tests with Copper Cylinders: Experiments, Microstructural Analysis and 3D SPH Modeling with Dislocation Plasticity and MD-Informed Artificial Neural Network as Equation of State. Metals 2022, 12, 264. https://doi.org/10.3390/met12020264
Rodionov ES, Lupanov VG, Gracheva NA, Mayer PN, Mayer AE. Taylor Impact Tests with Copper Cylinders: Experiments, Microstructural Analysis and 3D SPH Modeling with Dislocation Plasticity and MD-Informed Artificial Neural Network as Equation of State. Metals. 2022; 12(2):264. https://doi.org/10.3390/met12020264
Chicago/Turabian StyleRodionov, Egor S., Victor G. Lupanov, Natalya A. Gracheva, Polina N. Mayer, and Alexander E. Mayer. 2022. "Taylor Impact Tests with Copper Cylinders: Experiments, Microstructural Analysis and 3D SPH Modeling with Dislocation Plasticity and MD-Informed Artificial Neural Network as Equation of State" Metals 12, no. 2: 264. https://doi.org/10.3390/met12020264







