Calculation of T_c of Superconducting Elements with the Roeser–Huber Formalism

Abstract

The superconducting transition temperature, $T_c$, can be calculated for practically all superconducting elements using the Roeser–Huber formalism. Superconductivity is treated as a resonance effect between the charge carrier wave, i.e., the Cooper pairs, and a characteristic distance, x, in the crystal structure. To calculate $T_c$ for element superconductors, only x and information on the electronic configuration is required. Here, we lay out the principles to find the characteristic lengths, which may require us to sum up the results stemming from several possible paths in the case of more complicated crystal structures. In this way, we establish a non-trivial relation between superconductivity and the respective crystal structure. The model enables a detailed study of polymorphic elements showing superconductivity in different types of crystal structures like Hg or La, or the calculation of $T_c$ under applied pressure. Using the Roeser–Huber approach, the structure-dependent different $T_c$’s of practically all superconducting elements can nicely be reproduced, demonstrating the usefulness of this approach offering an easy and relatively simple calculation procedure, which can be straightforwardly incorporated in machine-learning approaches.

1. Introduction

We use the Roeser–Huber formalism [1,2,3,4] to calculate the superconducting transition temperature, $T_c$, of the superconducting elements in ambient conditions as well as under pressure. Up to now, there are 53 superconducting elements known (in ambient conditions and under pressure, [5,6]), and three more are superconductors under special conditions (i.e., in thin film form (Cr), after irradiation (Pd), or C in several modifications [7], e.g., diamond films, alkali-doped fullerene, and carbon nanotubes). A periodic table of the elements with the $T_c$-data from the literature is presented in Figure 1. From all reviews and teaching books covering this field [6,7,8,9,10,11,12,13], it is clear that there is no simple relation between $T_c$ and the respective crystal structure. Moreover, some elements are polymorphic superconductors with different crystal structures, e.g., La, Hg and Ga, and some elements show changes of the crystal structure under pressure (e.g., Fe becomes superconducting under pressure in the non-magnetic phase (hexgonally close-packed (hcp) $ϵ$-Fe phase) [14,15,16]). Commonly, bandstructure calculations are performed to obtain $T_c$ requiring many parameters (see, e.g., Refs. [17,18]) and using given crystal structures as a base, which is, however, not straightforward to enable comparison of a large variety of elements and different crystal structures. Thus, a relatively simple calculation procedure like the Roeser–Huber formalism, which requires only knowledge of the crystal structure and the basic electronic configuration with no free parameters, has clear advantages when being incorporated as a test in machine learning approaches to find new superconducting materials [19,20,21], because there is only a limited number of crystal structures to be considered.

2. Principles of the Model

The basic idea of the Roeser–Huber formalism is the view of superconductivity being a resonance effect between the charge carrier wave (Cooper pairs with the de Broglie wavelength, ${\lambda }_{cc}$) moving through the crystal lattice and a characteristic distance, x, within the crystal unit cell. Interpreting the superconducting transition in a resistance measurement of a superconductor as an integrated resonance curve helps to visualize this resonance effect. The resistance data reflect the material properties and the microstructure (e.g., grain boundaries), but the superconducting transition itself is only due to the Cooper pairs. Of course, their underlying properties are influenced by the band structure configuration of the material. As discussed in Refs. [22,23], the mass of the Cooper pairs is given by $2·m_e$ with $m_e$ being the free electron mass. The characteristic distance, x, which can be deduced from the crystal unit cell as an interatomic distance being different for various possible directions, and some knowledge about the electronic structure of the material are sufficient to calculate $T_c$, based on the particle-in-box (PiB) principle [24]. As described already in Refs. [3,25], the Roeser–Huber formula is given as

$${\Delta }_{\left(0\right)\mathrm{ges}}=\frac{h^2}{2M_{\mathrm{L}}}·\left(\sum _{R_1}^{R_n}\frac{1}{{\left(2x_{R_i}\right)}^2}·n_0^{2/3}·\frac{n_{2R_i}}{n_{1R_i}}\right)=\pi k_B{T}_{c\left(0\right)},$$

(1)

with ${\Delta }_{\left(0\right)}$ describing the lowest level energy of the PiB. h denotes the Planck constant, $k_B$ the Boltzmann constant, $M_{\mathrm{L}}$ is a parameter with the unit of a mass, and the sum is taken for all possible directions, $R_i$, as explained below. For all unit cells of metallic elemental superconductors, there are no 2D-like superconducting planes, thus $n_0$ (describing the number of superconducting planes of 2D superconductors) is set to $n_0=$ 1. The interatomic distance x now depends on each crystallographic direction (which will be called superconducting path hereafter), $R_i$, and the two correction factors, $n_1$ and $n_2$, the determination of which is discussed below.

Following the work of Moritz [25], there are four important points to be considered when calculating $T_c$ for metallic elements:

(i)

The distance x corresponds to an interatomic distance similar to the PiB approach applied in [1]. The distance x is obtained from possible symmetric paths (also called superconducting directions in the following) for the movement of the charge carrier wave within the crystal structure, as discussed below. The crystallographic data come from respective databases [26,27], which is an important issue for application of the Roeser–Huber formalism in machine-learning calculation approaches.

(ii)

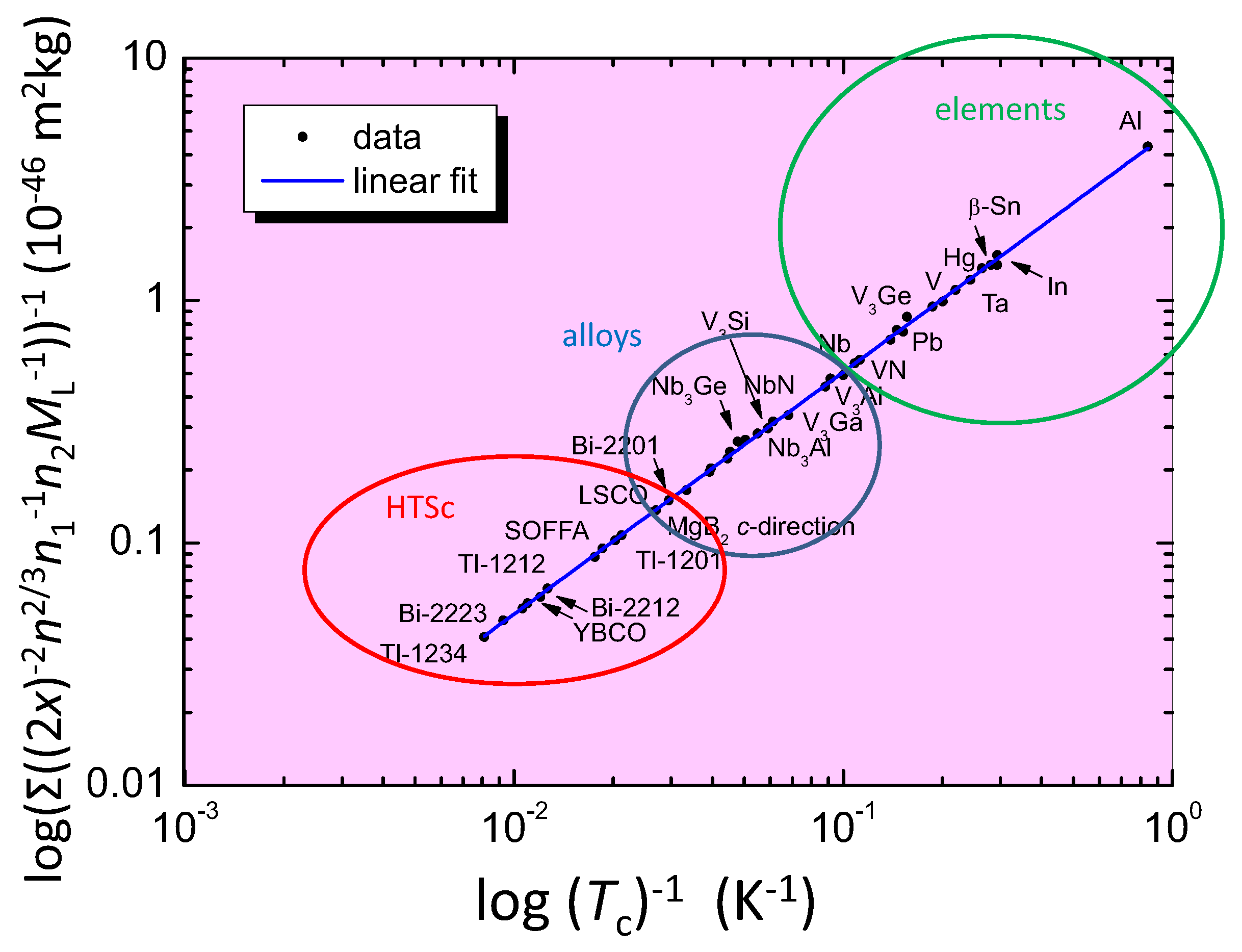
The parameter $M_{\mathrm{L}}$ for high-$T_c$ superconductor (HTSc) compounds was taken as 2$m_e$. For element superconductors, $M_{\mathrm{L}}=\eta ·m_e$ is much higher as all the phononic interactions (Fermi temperature, Debye temperature, effective mass, charge carrier density) are incorporated in the parameter $\eta$. In a first approximation, $\eta ·m_e\sim$1900, which corresponds closely to the mass of a proton ($m_p/m_e=$ 1836.15). Regarding the location of metallic superconductors in a Uemura plot ($T_c$ as function of the Fermi temperature, $T_F=(m^{*}·v_F^2)/\left(2k_B\right)$ [28,29] and $v_F$ denoting the Fermi velocity, m* is the effective mass) in the lower right corner with $T_F\sim$ 10${}^4$… 10${}^5$ K, the high value for $\eta$ is reasonable. This significant difference between elemental metallic superconductors and the HTSc materials was also pointed out by Emery and Kievelson [30] mentioning the substantial phase rigidity of the superconducting state in, e.g., lead at all temperatures below $T_c$.

(iii)

A first correction factor is required to account for more complex crystal structures. Atoms being close to a superconducting direction may have an influence on the moving charge carriers via the phonon interaction. Therefore, the number of atoms passed within a unit cell is counted. This correction was originally added to the parameter $M_L$ via:

$$M_L=\frac{N_L}{N_{\mathrm{atoms}}}·m_p,$$

(2)

which we keep here for consistency. Regarding the definition of $\eta$ given above, the relation $N_L/N_{\mathrm{atoms}}$ is thus incorporated in $\eta$. Here, $N_L$ represents the number of the charge carriers and $N_{\mathrm{atoms}}$ denotes the number of the near, passed atoms along each superconducting path. A correction factor $n_1$ can be then defined as $n_1=N_L/N_{\mathrm{atoms}}$. In case there are no (near) passed atoms, then $n_1=$ 1.

As the symmetry of the superconducting path plays an important role for our considerations, the passed atoms must be symmetrically arranged along the superconducting path, as otherwise the charge carriers would be not in phase due to the unsymmetric forces. This implies that superconductivity cannot exist in directions with unsymmetrically arranged passed atoms. As test for the influence of the passed atoms, we define a relation $l/x$, with l being a distance perpendicular to the direction of the moving charge carriers. If $l/x\le$ 0.5, the passed atoms show an influence on the superconductivity and must be counted in $N_{\mathrm{atoms}}$. Here, it is important to point out that $N_L$ and $N_{\mathrm{atoms}}$ are not free parameters, but are given from the respective crystal structure being investigated. A special case for determining $N_L$ will be encountered for hcp Fe under pressure as discussed below.

(iv)

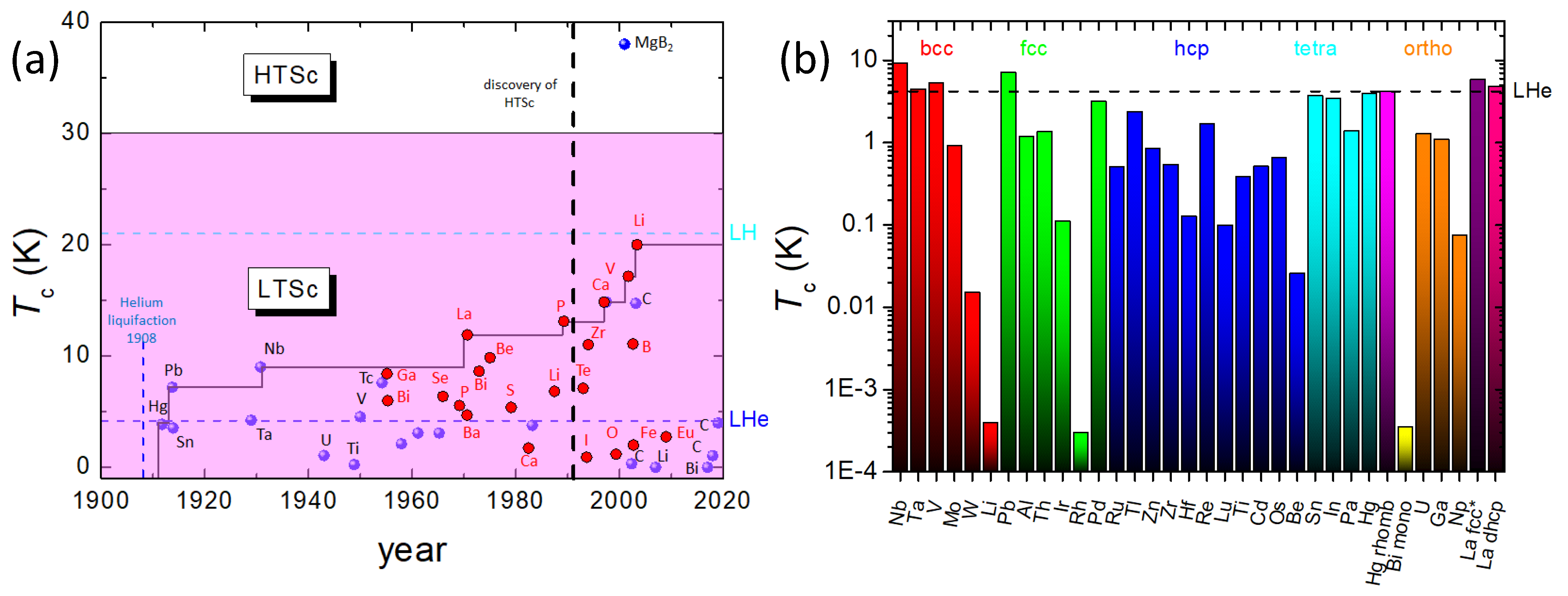
A second correction factor is necessary to account for anisotropic superconductivity, which can even lead to so-called multimode superconductivity. The factor $n_2$ gives a relation between the specific directions for the charge carrier wave, $R_i$, in the given crystal structure. The energy ${\Delta }_{\left(0\right)}$ and the transition temperature $T_{c\left(0\right)}$ are then calculated for each existing superconducting path $R_i$, and the results must be summed up according to Equation (1). If one of the directions $R_i$ gives a reasonable value for $T_c\left(R_i\right)$ to compare with the experimentally determined $T_c$, this direction is taken as the superconducting path. However, the $T_c\left(R_i\right)$-values of the other directions and the complete sum of all $T_c\left(R_i\right)$ may also have important implications as, e.g., in the case of Al, which was discussed in Ref. [3], the experimental value of $T_c$ is reached with 2 of the possible 4 directions in the fcc structure, but the total sum of all 4 directions is strikingly close to the increased $T_c$, when measuring thin films. A similar situation is given for the energies, ${\Delta }_{\left(0\right)}\left(R_i\right)$. ${\Delta }_{\left(0\right)}\left(R_i\right)$ may be compared to the pairing energy or energy gap as determined experimentally. Thus, all ${\Delta }_{\left(0\right)}\left(R_i\right)$- and $T_c\left(R_i\right)$-values must be calculated for a given material. For most elemental superconductors, $n_2=$ 1, in contrast to the metallic alloys Nb${}_3$Sn or MgB${}_2$, where superconducting directions can exist several times within one unit cell, as already discussed in Ref. [3].

The Roeser–Huber formalism (1) does not contain any free parameters, as all the required inputs are given via the crystal unit cell (i.e., x and $N_{\mathrm{atoms}}$) and $N_L$ from the basic electronic configuration of the material. It must be noted here that the Roeser–Huber formalism does not describe how the Cooper pairs are formed, and so it is not possible to determine if a given material is a superconductor. However, regarding the limits of the parameter $\eta$ (${\eta }_{\min }=$ 2, and ${\eta }_{max}$ is set by the demand of the BCS-theory that the effective charge carrier mass, $m^{*}$ cannot be smaller than $m^{*}<0.1m_e$ for isotropic, spherical Fermi surfaces [31]), one may deduce a possibility to judge if superconductivity for a given material and crystal structure exists. This will be elaborated in future works.

3. Results and Discussion

Figure 1 presents the periodic table of the superconducting elements. Thirty-three of them are superconductors in ambient conditions with the reported $T_c$-values ranging between 0.00053 K (Bi) to 9.2 K (Nb). Under applied high pressures, 20 more elements become superconductors, and the $T_c$-values can be as high as 20 K (Li), and also several non-metals (O, P, S, Br, I) were found to supercoduct as well. Finally, three elements (C, Cr and Pd) are superconductors in ambient conditions, but only under special conditions—C in several modifications (alkali-doped C${}_{60}$, carbon nanotubes, diamond) having also different values of $T_c$, Cr only as thin film material and Pd only after irradiation with He⁺-ions [32].

In Figure 2a, $T_c$ is plotted versus the year of discovery. Up to 1950, only superconductors at ambient conditions were known. In 1970, the measured $T_c$ of La under pressure exceeded the first time the ambient $T_c$ of Nb, and after the discovery of the HTSc materials, the high-pressure experiments were extended to find elements with even much higher $T_c$-values up to 20 K (Li). Figure 2b presents a logarithmic plot of $T_c$ in relation to the respective crystal structure (body-centered cubic (bcc), face-centered cubic (fcc), hexagonally close-packed (hcp), tetragonal (tetra), monoclinic (mono), orthorhombic (ortho), fcc* and double hexagonally close-packed (dhcp)), and it is obvious that there is no direct and simple relation between $T_c$ and the crystal structures. For example, the highest $T_c$ is obtained for bcc Nb, but bcc Li shows the second-lowest $T_c$ at ambient conditions. Figure 2b indicates that similar behavior holds for all other crystal lattice types as well. Thus, the link between crystal structure and $T_c$, if existing, must be a much more subtle and non-trivial one.

Exactly this task is fulfilled by the Roeser–Huber formalism, establishing a non-trivial relation between $T_c$ and the given crystal structures. For a successful application of the Roeser–Huber formalism, one needs the information of the possible crystal structures, and about the electronic configuration to count $N_L$ (similar to the valence electron count used by Matthias [9]) and the number of passed (or near) atoms, $N_{\mathrm{atoms}}$ (as determined from the given crystal structure using the relation $l/x<$0.5.

In Ref. [2], $T_c$ of the elements Nb, V, Ta (bcc) and Hg (rhombohedral) were calculated introducing the procedure. In [3], the calculation of Pb and Al (fcc) and Sn (tetragonal) was presented. As an example, here the two most interesting cases of the polymorphic elements La and Hg will be discussed, where two different crystal structures exist with different $T_c$-values.

Figure 3 presents all the crystal structures, which need to be calculated for this purpose. For $\alpha$-Hg, the details of the crystal structure and the calculation steps were already presented in Ref. [2]. The structure is rhombohedral, being a simple cubic cell with the angles $\alpha =\beta =\gamma =$ 70.52${}^{\circ }$. $\beta$-Hg is tetragonal, and more precisely, tetragonal bcc with $a=b\ne c$ and having an atom in the center of the unit cell. The crystal structure fcc* is unique to the rare earth elements La, Ce and Yb [33]. Indeed, in the [111]-direction, the structure is similar to the standard fcc one, only the number of atoms involved is different. The dhcp-structure is the common one for most of the rare earth elements, and is treated here the first time. Both fcc* and dhcp structures are derivatives of the hcp structure as indicated with letters A–C.

The case of the rhombohedral Hg ($\alpha$-Hg) is simple. All distances between the atoms correspond to a, and all 3 rhombohedral directions are equal. There is only one possible superconducting path along a, which fulfills the symmetry condition. The calculation yields one value for $T_{c\left(0\right)}=$ 4.175 K, which corresponds well to the tabulated $T_{\exp }$ of 4.15 K [7]. In the case of the tetragonal Hg ($\beta$-Hg) [34], there are three possible superconducting paths like in the standard bcc structure, each with an own energy ${\Delta }_{\left(0\right)}$ and $T_{c\left(0\right)}$.

(1)

along the space diagonal via the central atom. Thus, x is the half of this distance, so $x=\sqrt{2·a^2+c^2}/2$ and $N_{\mathrm{atoms}}=$ 1.

(2)

corresponds to the crystal edge along a, so $x=a$ and $N_{\mathrm{atoms}}=$ 1.

(3)

along the diagonal in the top/bottom plane with $x=\sqrt{a^2+c^2}$ and $N_{\mathrm{atoms}}=$ 4, i.e., the other two atoms in this plane and the central atoms (one of the given cell and the one of the cell below) are close enough to have an influence on the superconducting path.

See also the Supplementary Material for drawings of each superconducting direction.

Table 1. The crystal parameters a and c, the direction number, the distance x, $N_L$, $N_{\mathrm{atoms}}$, $M_{\mathrm{L}}$, the calculated energies and the calculated $T_{c\left(0\right)}$ for Hg (rhombohedral $\alpha$-Hg and tetragonal bcc $\beta$-Hg) and La (fcc* and dhcp).

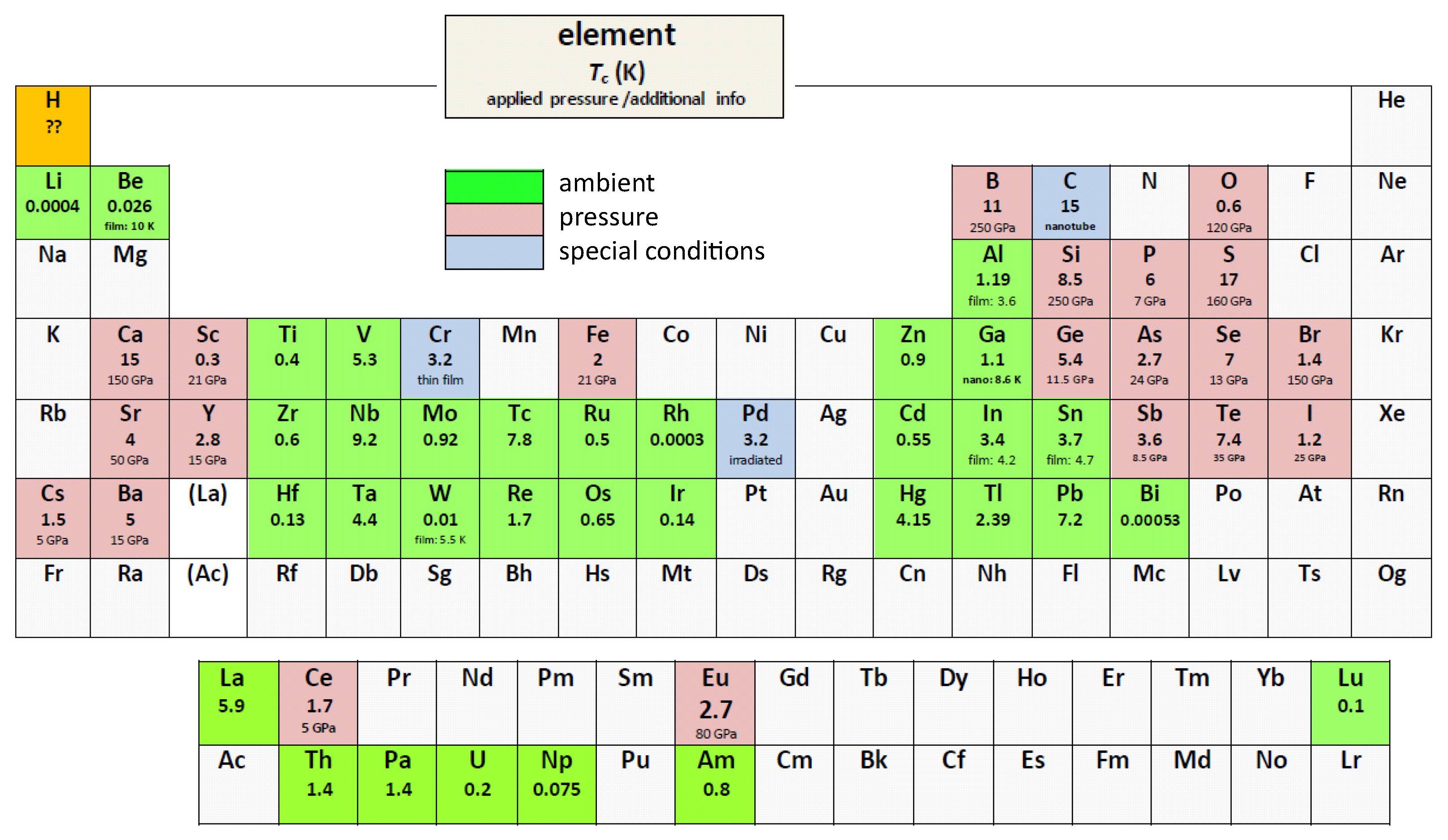
Element	Structure	a (nm)	c (nm)	Number	x (nm)	${\mathit{N}}_{\mathit{L}}$	${\mathit{N}}_{\mathbf{atoms}}$	${\mathit{M}}_{\mathbf{L}}(1/{\mathit{m}}_{\mathit{p}})$	${\mathbf{\Delta }}_{\left(0\right)}$ (10${}^{-22}$ J)	${\mathit{T}}_{\mathit{c}\left(0\right)}$ (K)
Hg	rhomb.	0.3005	—	(1)	0.308	2	1	2	1.811	4.175
Hg	tetra	0.3995	0.2825	(1)	0.3158	2	1	2	1.644	3.792
Hg	tetra			(2)	0.3995	2	1	2	1.028	2.37
Hg	tetra			(3)	0.4893	2	4	0.5	2.741	6.32
La	fcc*	0.3660	1.214	(1)	1.214	2	6	3	0.667	1.539
				(2)	0.366	2	1	0.5	1.225	2.824
				(3)	0.6339	2	2	1	0.816	1.882
La	dchp	0.3772	1.214	(1)	0.6072	2	3	1.5	1.335	3.078
				(2)	0.3772	2	1	0.5	1.153	2.658
				(3)	0.6533	2	2	1	0.769	1.772

presents the details of the superconducting paths fulfilling the symmetry condition together with the calculations performed.

Here, one can see that direction (1) yields $T_{c\left(0\right)}=$ 3.792 K, which again fits closely to the tabulated value of 3.95 K [7]. For the comparison of the calculated and the experimental $T_c$-values, one must note that the Roeser–Huber approach requires $T_c^{\mathrm{MF}}$ (the mean-field $T_c$ corresponding to the maximum of the derivative dR/dT). This is not always the case concerning various literature data, where often $T_{c,\mathrm{onset}}$ or 50 % of the normal-state resistivity are given as $T_c$. Therefore, the small deviations obtained may stem from this problem.

In the case of La, there are two crystal structures which are both unique to the rare-earth materials, fcc* and double hexagonally close-packed (dhcp) [33]. Figure 3 shows that for both structures, the hexagonal top and bottom layers labeled A are the same like in the hcp structure. In fcc*, there are more atoms as in the conventional fcc structure, but some of the possible superconducting paths are basically the same, except that we have to account for the near atoms. Therefore, both systems have three possible paths for superconductivity, which fulfill the condition of symmetry. For dhcp La, the superconducting paths are:

(1)

Along the c-axis in the center of the structure with $x=c/2$, and $N_{\mathrm{atoms}}$ counts to 3.

(2)

Oriented along the edge with $x=a$ ($N_{\mathrm{atoms}}=$1), and

(3)

In the plane between 2 not neighboring atoms with $x=\sqrt{3}a$ and $N_{\mathrm{atoms}}=$ 2.

For fcc* La, paths (2) and (3) are the same as before, and path (1) takes the length $x=c$ with $N_{\mathrm{atoms}}=$ 6. Table 1 gives the results of the calculations.

The experimental $T_c$ of dhcp La is 4.8 K, and $T_c$ of the fcc*-La is 6 K [6,8]. Looking at Table 1 reveals that we must combine at least two directions to reach the experimental value, e.g., (1) + (3) or (2) + (3) for dhcp with (1) + (3) yielding 4.85 K, and for fcc ^*, even all three directions must contribute to reach the experimental value with the sum yielding 6.245 K. Given the large experimental variation of $T_c$ reported [8], this is again a perfect coincidence.

As an example for an element being superconducting under applied pressure, we have chosen the hcp $ϵ$-Fe, which is nonmagnetic [15]. Therefore, superconductivity may develop in this specific crystal structure. The properties of hcp Fe were discussed in the work by Roth [16], using all available information from the literature. To obtain reasonable values for comparison with the experimentally measured $T_c$-values, it is important that also the crystallographic data under pressure are available. For hcp iron, one can find two equations describing the lattice parameters under pressure, determined using x-ray diffraction techniques [35]:

$$a^{\mathrm{hcp}}=2.523{\left(1+\frac{p}{32.5}\right)}^{-0.033}$$

(3)

and

$${\left(\frac{c}{a}\right)}^{\mathrm{hcp}}=1.603\pm 0.001.$$

(4)

Using Equations (3) and (4), one can determine the proper crystal parameters at the given applied pressure. Following Shimizu et al. [14], the maximum $T_c$ of 2 K is reached at a pressure of 21 GPa. Fe has the electron configuration [Ar] 3d⁶ 4s², so in total 8 electrons in the outer shell. Fe can have oxidation states from −2 to 7. As Fe also has a specific resistance below 10⁻⁸ Ωm, it is reasonable to consider all eight outer electrons like in the e/a-count by Matthias [9] being involved in superconductivity. The hcp structure (see Figure 3) has basically the same superconducting paths as the dhcp structure discussed before, that is,

(1)

Along the c-axis in the center of the structure with $x=c$, and $N_{\mathrm{atoms}}=$ 3.

(2)

Oriented along the edge with $x=a$ ($N_{\mathrm{atoms}}=$1), and

(3)

In the top/bottom plane between two not-neighboring atoms with $x=\sqrt{3}a$ and $N_{\mathrm{atoms}}=$ 2.

With this information, $T_c$ can now be calculated as summarized in

Table 2. The crystal parameters a and c, the direction number, the distance x, $N_L$, $N_{\mathrm{atoms}}$, $M_{\mathrm{L}}$, the calculated energies and the calculated $T_{c\left(0\right)}$ for $ϵ$-Fe under a pressure of 21 GPa [14] and 22.2 GPa [36].

Element	Structure	a (nm)	c (nm)	Number	x (nm)	${\mathit{N}}_{\mathit{L}}$	${\mathit{N}}_{\mathbf{atoms}}$	${\mathit{M}}_{\mathbf{L}}(1/{\mathit{m}}_{\mathit{p}})$	${\mathbf{\Delta }}_{\left(0\right)}$ (10${}^{-22}$ J)	${\mathit{T}}_{\mathit{c}\left(0\right)}$ (K)
Fe	hcp	0.2482	3.978	(1)	0.3978	8	3	0.375	0.778	1.7926
	21 GPa			(2)	0.2482	8	1	0.125	0.666	1.5349
				(3)	0.4299	8	2	0.25	0.444	1.0233
Fe	hcp	0.2480	3.9755	(1)	0.3976	8	3	0.375	0.7785	1.7949
	22.2 GPa			(2)	0.2480	8	1	0.125	0.6685	1.5374
				(3)	0.4295	8	2	0.25	0.4446	1.025

.

Now, we have to realize that the value for $T_c$ of 2 K reported is the onset temperature of superconductivity, and the transition width is quite broad [14], so $T_c^{\mathrm{MF}}$ is much smaller, possibly between 1.5 and 1.7 K, as the full resistance curve at 21 GPa is not published in [14]. In [36], the high-pressure experiments on Fe were repeated and the highest $T_c^{\mathrm{onset}}$ with 2.5 K was obtained at 22.2 GPa. Here, the complete resistance curve is published showing a broad superconducting transition with $\Delta T_c=$ 1.5 K, yielding $T_c^{\mathrm{MF}}=$ 1.64 K. Thus, the calculated values of direction (1) or (2) give a good representation of the situation with only a small error margin. To summarize this, it is possible to calculate the $T_c$ of elements under pressure using the Roeser–Huber formalism, provided that experimental crystallographic data are available.

Finally, Figure 4 presents the Roeser–Huber plot with many calculated superconducting materials, high-$T_c$ superconductors (HTSc, marked with a red circle), metallic alloys (blue circle) and elements (green circle). Practically all superconducting elements can be calculated using the Roeser–Huber formalism with only small error margins. The only exceptions are the very low-$T_c$ materials Li, Be and Bi, where the low values of $T_c$ can only be reproduced with an adaptation of $\eta$, which is due to either an extremely small charge carrier mass (Li, Be) or a large electron mean free path (Bi). In contrast, the Roeser–Huber formalism works well to calculate the respective $T_c$-values of the same materials under applied pressure. A very important point is here that all the data of $T_c$ obtained fall on a common, straight line (blue), which follows the equation for a particle in a box [24] with the slope $h^2/\left(2\pi k_B\right)=$ 5.061 × 10${}^{-45}$ m ${}^2$ kg K. This result enables the Roeser–Huber formalism to act as a test for given predictions of $T_c$, e.g., for the case of metallic hydrogen as was done recently in Ref. [37].

4. Conclusions

To conclude, we have presented $T_c$-calculations of two polymorphic superconducting elements (Hg, La) using the Roeser–Huber formalism and for $ϵ$-Fe (hcp) under pressure. The principles of this formalism enable to reproduce the different $T_c$-values of various crystal structures of the same elements, which directly proofs the validity of the concept. This will enable us to apply this formalism for the prediction of $T_c$ of still unknown superconducting materials, e.g., in machine learning approaches.