Strain-Controlled Fatigue Behavior of a Nodular Cast Iron in Real Off-Highway Axles: Effects of Casting Skin and Strain Ratio
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specimens’ Position
2.2. Metallographic Analyses and Hardness Measurements on the Axle
2.3. Static and Fatigue Testing: Parameters and Specimens’ Geometry
3. Results
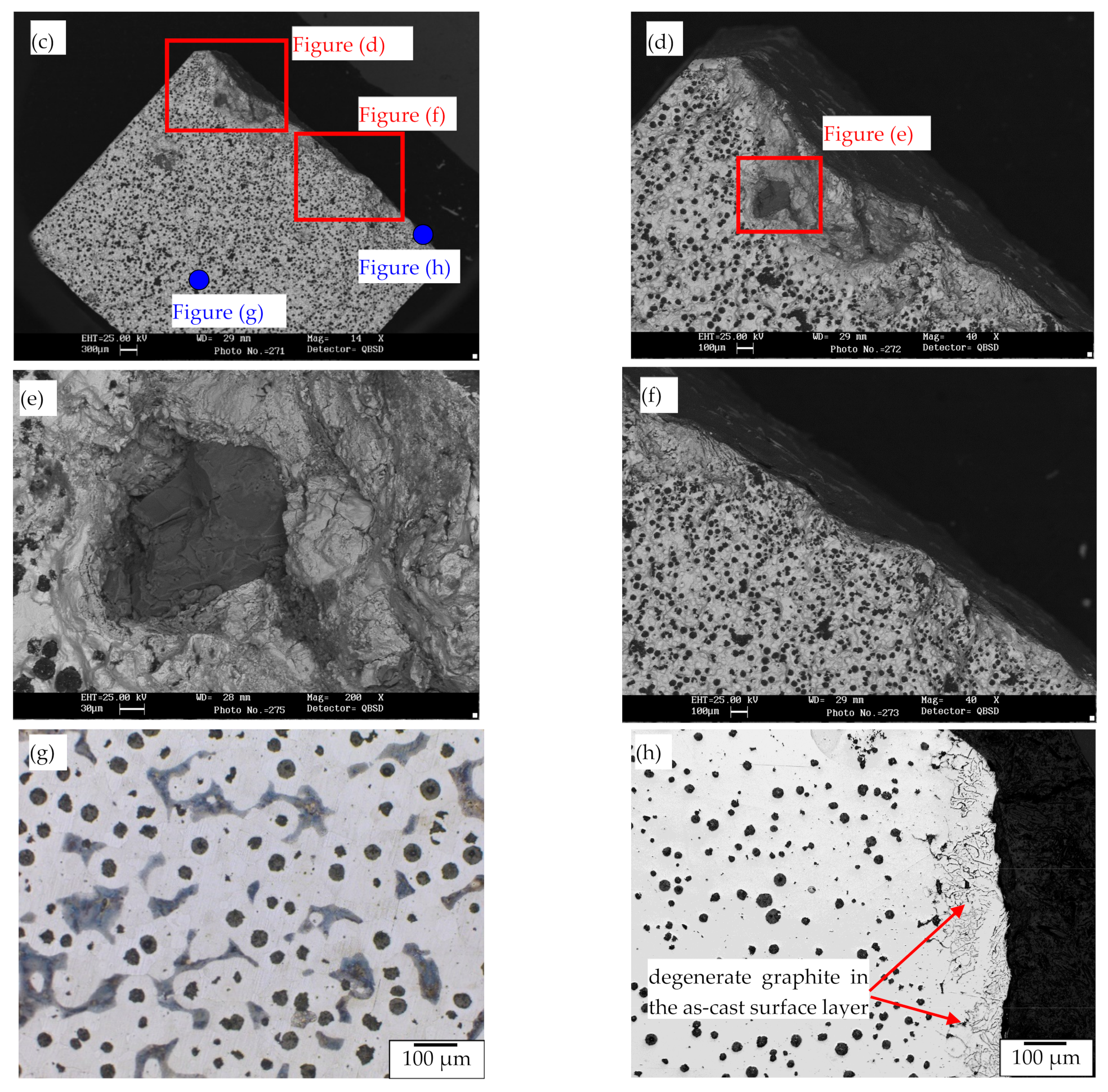
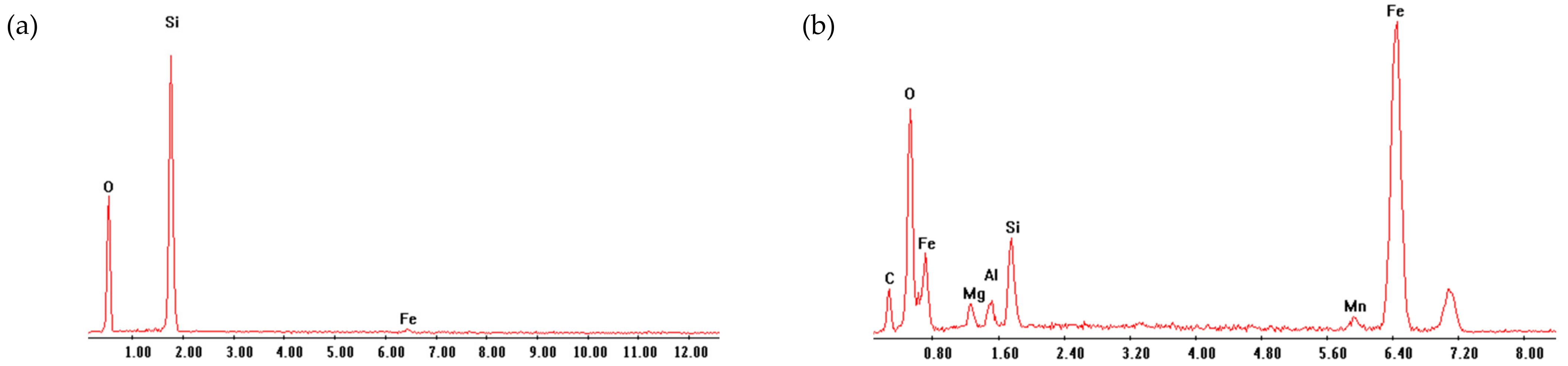
3.1. Metallographic Analyses and Hardness Measurements on the Tested Samples
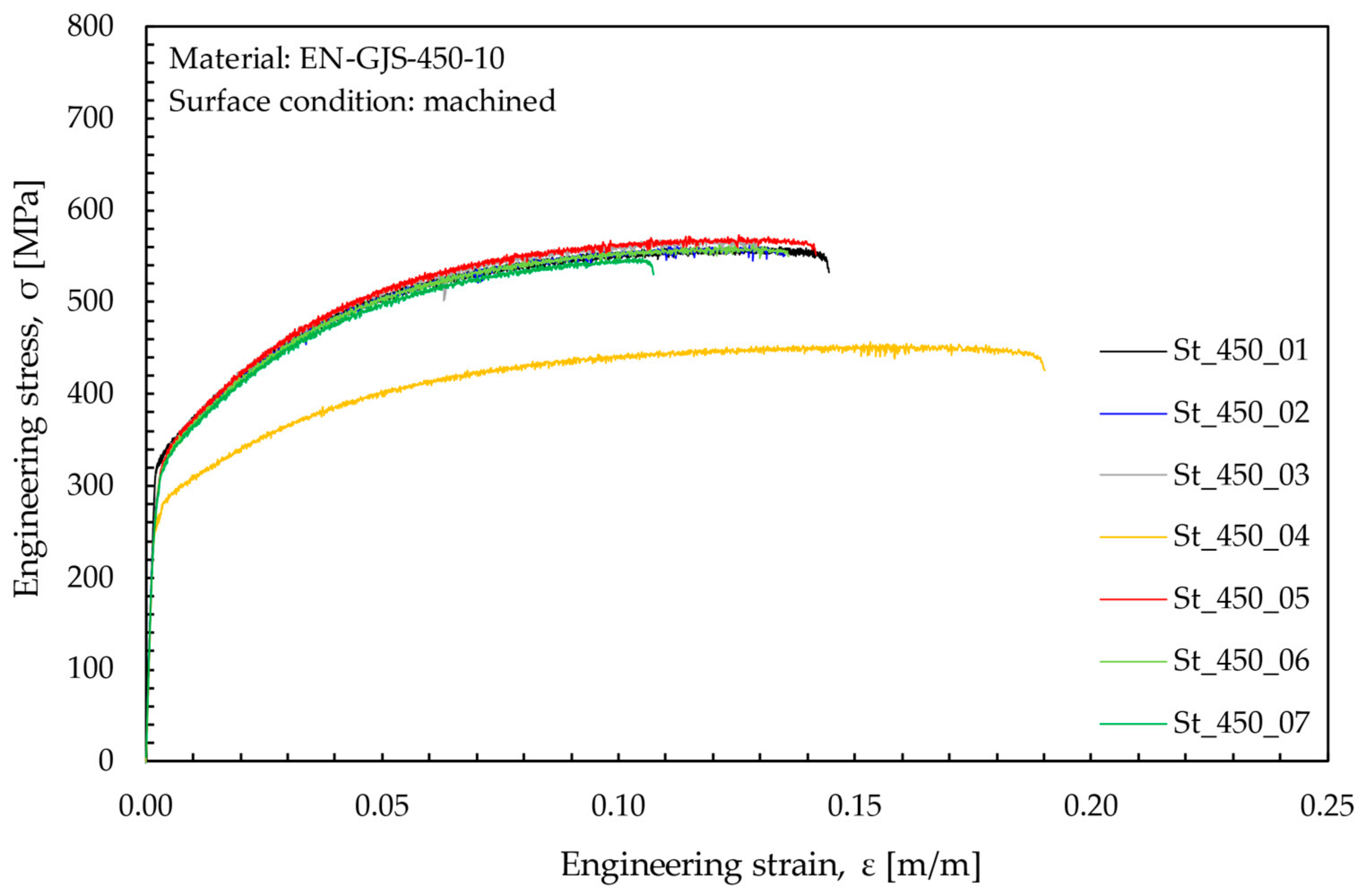
3.2. Static Tensile Test Results
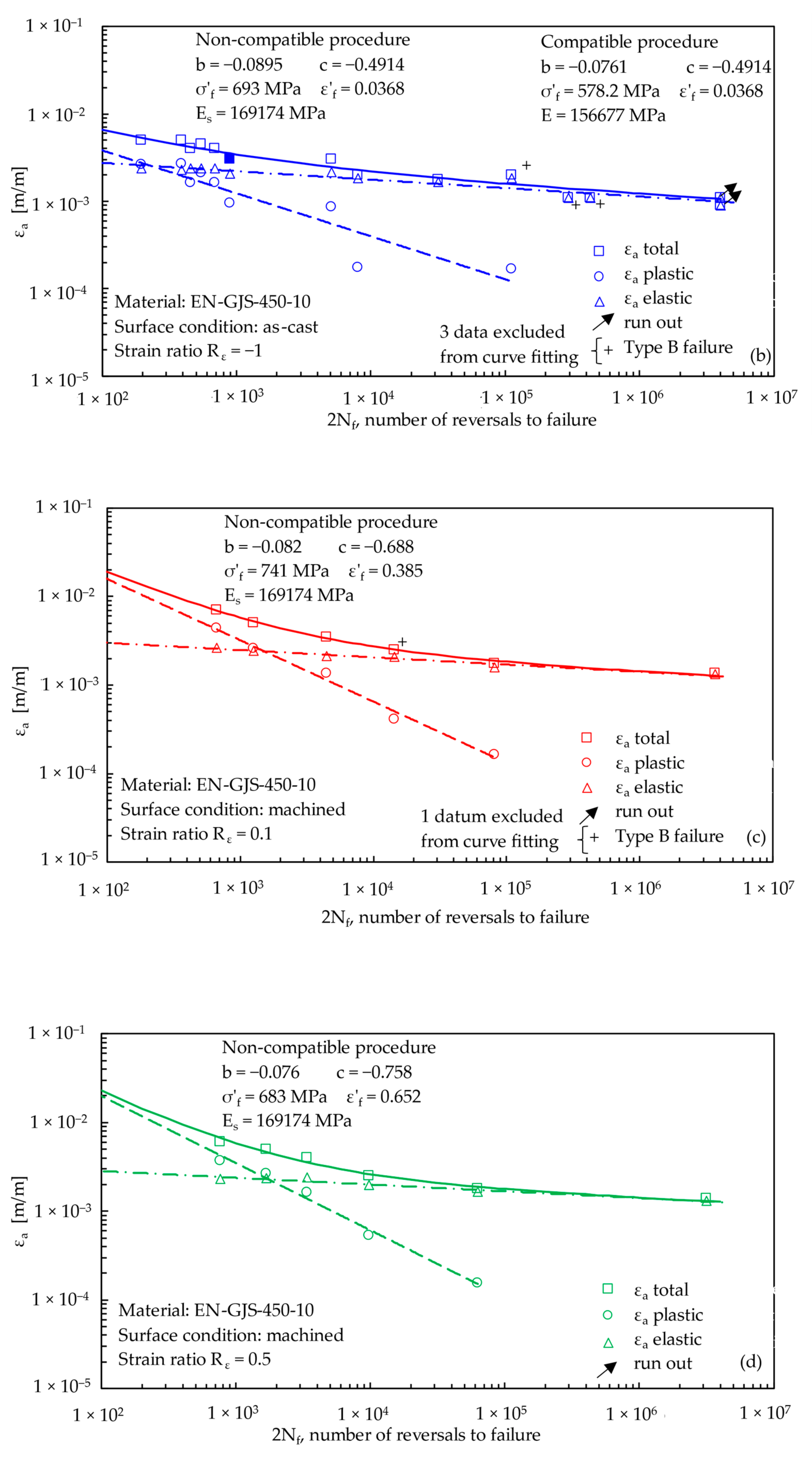
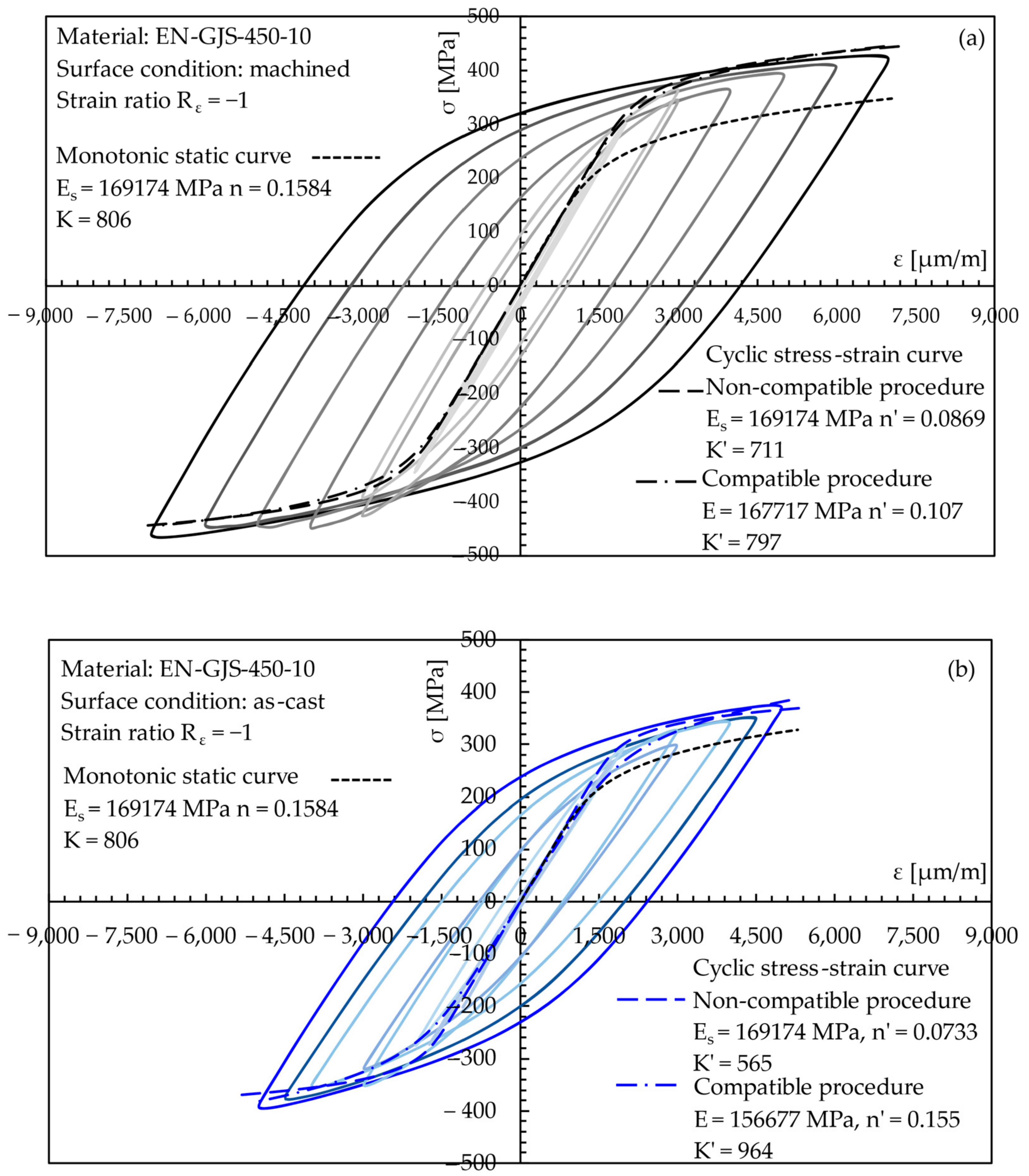
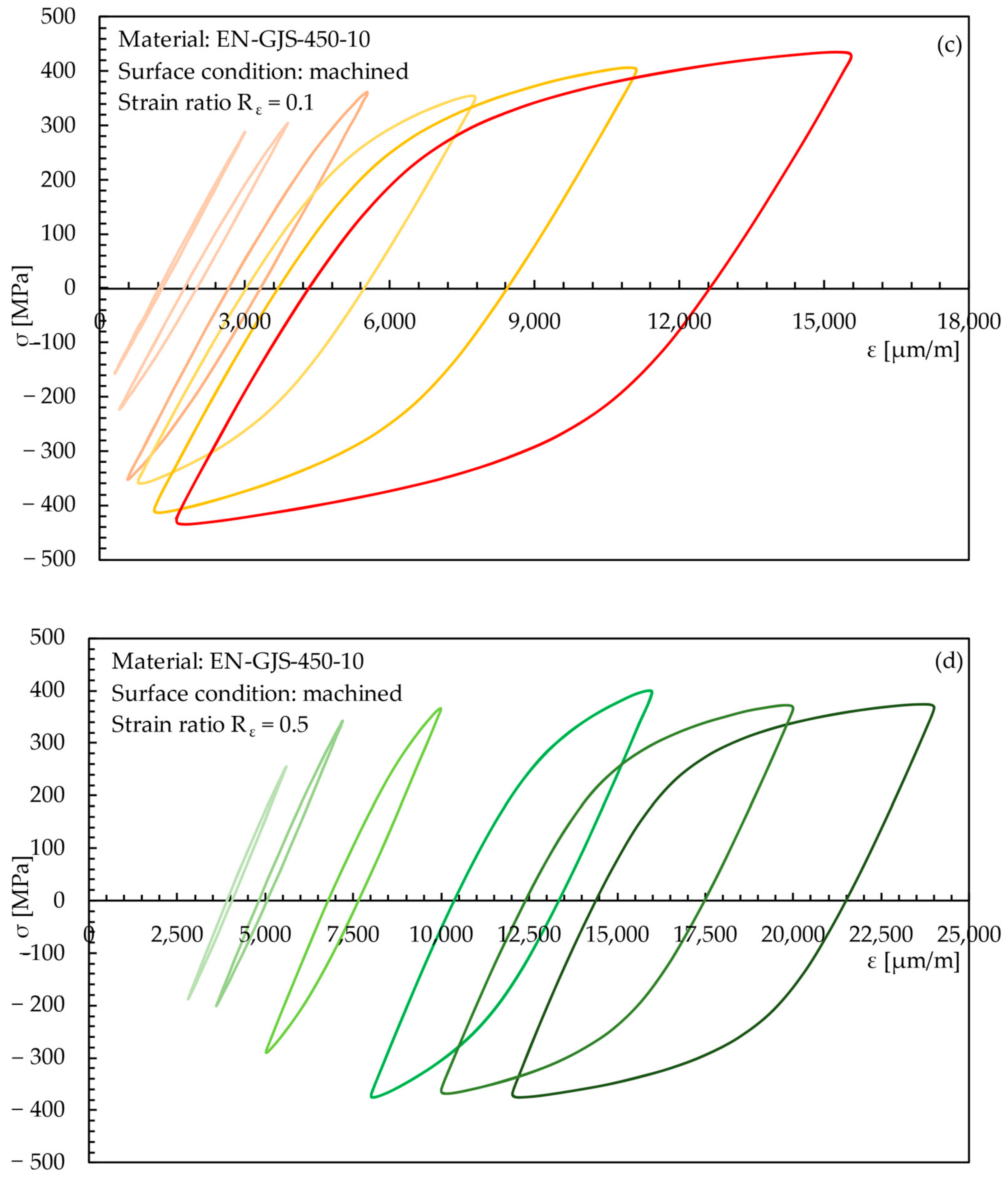
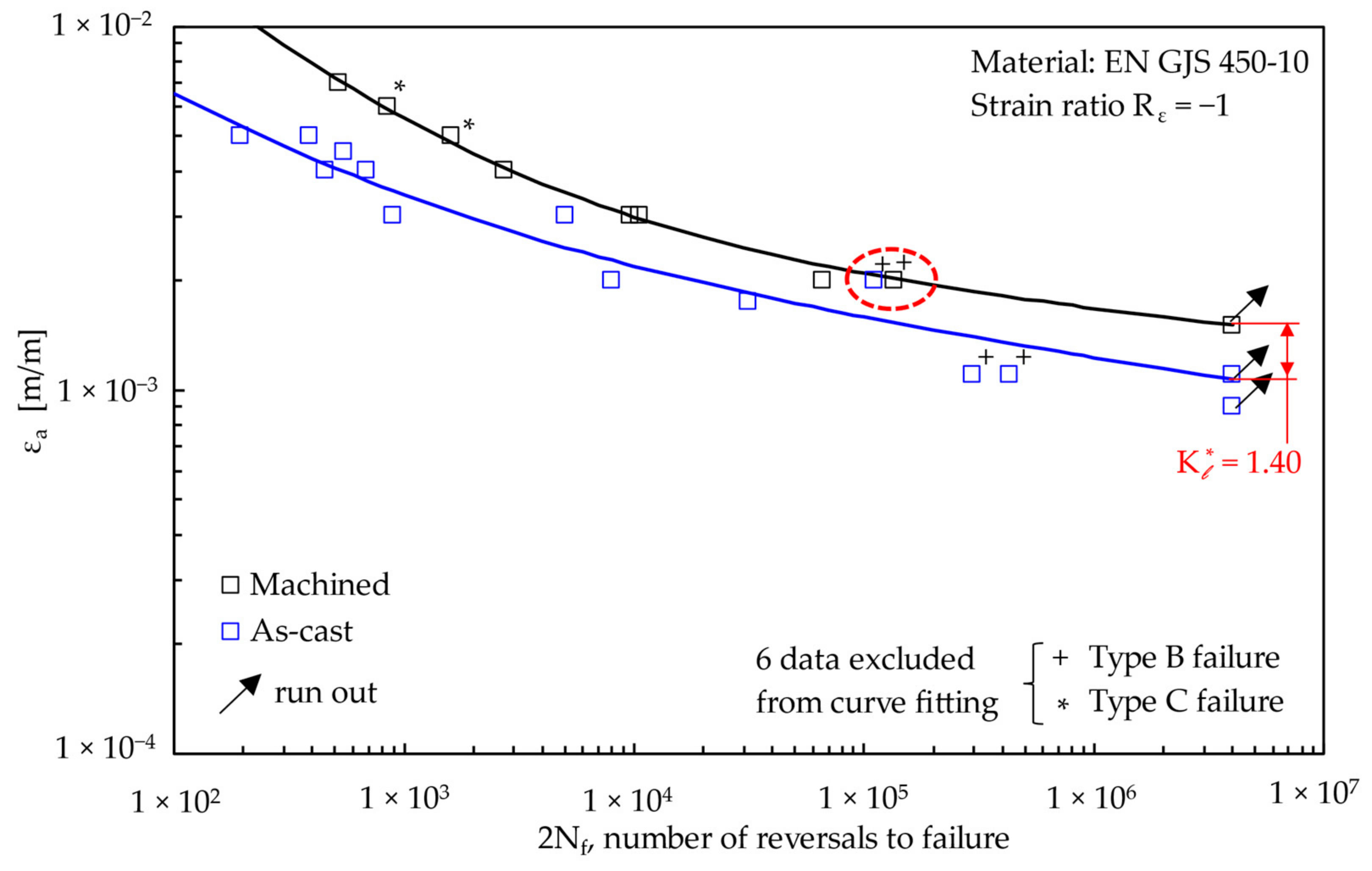
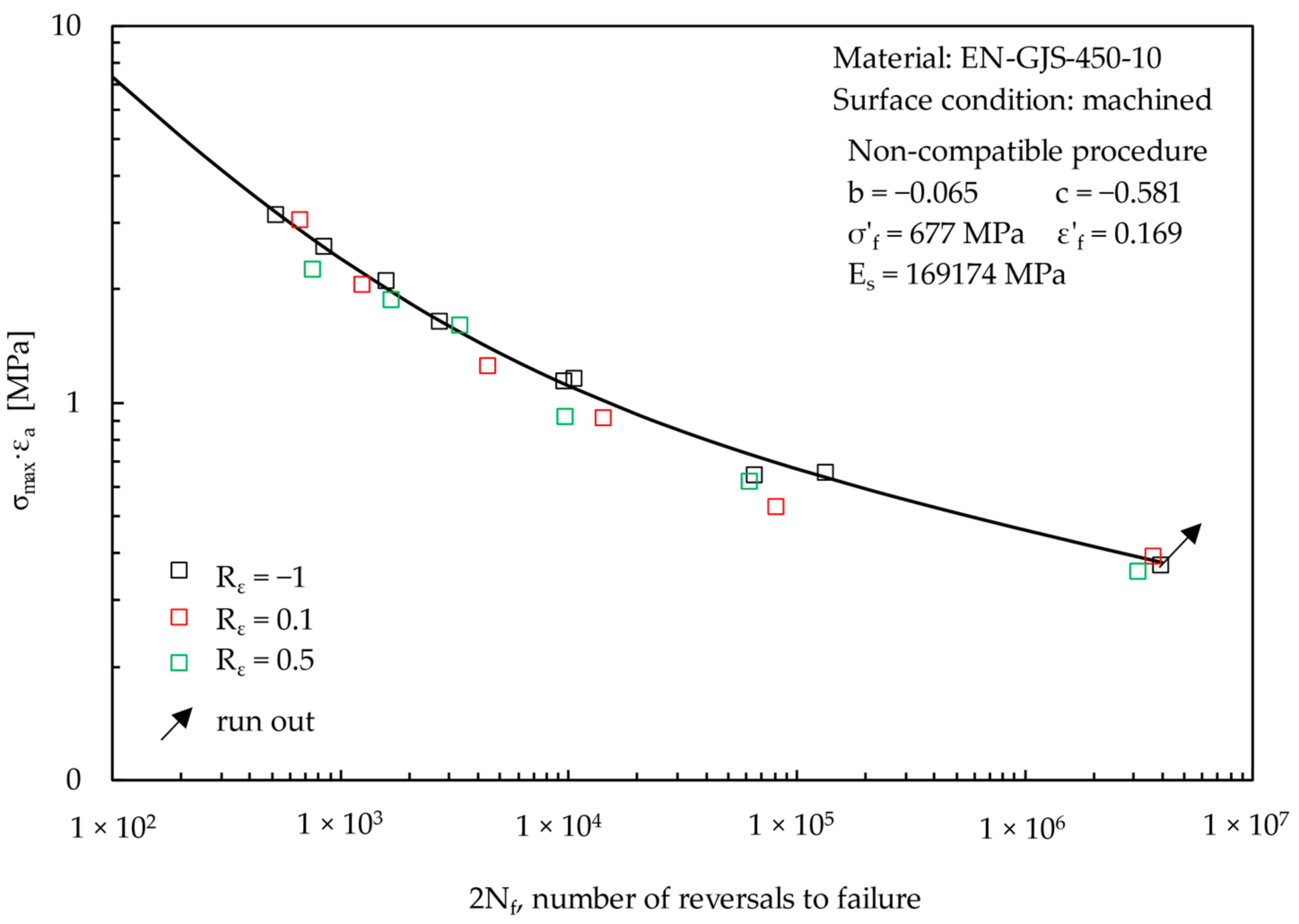
3.3. Strain-Controlled Fatigue Test Results
3.4. Failure Location and Fracture Surface Analyses
4. Discussion
- the higher roughness of as-cast surface as compared to the machined one;
- the presence of defects underneath the as-cast surface.
5. Conclusions
- The analysed EN-GJS-450-10 has graphite nodules with regular spheroidal shape dispersed in a matrix consisting of 50% ferrite and 50% pearlite. Specimens tested under static tensile loading exhibited an almost flat fracture surface and provided a proof stress σp,02 equal to 328 MPa, an ultimate tensile strength σR equal to 538 MPa, and an elongation after fracture A% and a reduction of area Z% equal to 12.9% and 10%, respectively.
- Concerning the fatigue behaviour, the experimental data were fitted by the Manson–Coffin equation according to the common practice, as well as to a recent procedure, which assures, strictly speaking, the compatibility conditions between stress-strain-life data.
- The analysis of the half fatigue life hysteresis loops shows that the stress ratio Rσ was different from the nominal strain ratio Rε. In particular, it ranged between -1.36 and −0.76 when Rε = −1, between −1.02 and −0.55 when Rε = 0.1, and between −1 and −0.59 when Rε = 0.5. Moreover, the comparison of the cyclic stress-strain curve with the monotonic static curve highlighted that the tested material exhibited a hardening behavior.
- The analysis of the fracture surfaces shows that machined specimens exhibited crack initiation from the surface, while as-cast specimens failed in most cases from the as-cast surface or from sub-surface defects, such as silicon oxides. A reduction coefficient Kl* has been defined to account for the high-cycle downgrading effect of the casting skin. At 2Nf = 4∙106 reversals to failure and with reference to a strain ratio Rε = −1, Kl* was equal to 1.40.
- Finally, it has been observed that the higher the strain ratio, the shorter the fatigue life for a given strain amplitude. Experimental fatigue data generated from machined specimens tested under different strain ratios, from −1 to 0.5, have been successfully correlated by using a Smith–Watson–Topper (SWT) expression, previously fitted only on experimental results relevant to Rε = −1.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Borsato, T.; Berto, F.; Ferro, P.; Carollo, C. Effect of in-mould inoculant composition on microstructure and fatigue behaviour of heavy section ductile iron castings. Procedia Struct. Integr. 2016, 2, 3150–3157. [Google Scholar] [CrossRef]
- Konečná, R.; Kokavec, M.; Nicoletto, G. Surface conditions and the fatigue behavior of nodular cast iron. Procedia Eng. 2011, 10, 2538–2543. [Google Scholar] [CrossRef] [Green Version]
- Benam, A.S. Effect of Shot Peening on the High-Cycle Fatigue Behavior of High-Strength Cast Iron with Nodular Graphite. Met. Sci. Heat Treat. 2017, 58, 568–571. [Google Scholar] [CrossRef]
- Meyer, N.; Fatemi, A.; McCutcheon, S.; Havard, B.; Fairchilds, W. Fatigue Behavior of Cast Iron Including Mean Stress Effects. SAE Int. J. Mater. Manuf. 2015, 8, 425–434. [Google Scholar] [CrossRef]
- Shirani, M.; Härkegård, G. Large scale axial fatigue testing of ductile cast iron for heavy section wind turbine components. Eng. Fail. Anal. 2011, 18, 1496–1510. [Google Scholar] [CrossRef]
- Shirani, M.; Härkegård, G. Fatigue life distribution and size effect in ductile cast iron for wind turbine components. Eng. Fail. Anal. 2011, 18, 12–24. [Google Scholar] [CrossRef]
- Clement, P.; Angeli, J.P.; Pineau, A. Short crack behaviour in nodular cast iron. Fatigue Fract. Eng. Mater. Struct. 1984, 7, 251–265. [Google Scholar] [CrossRef]
- Agha, H.Y.; Beranger, A.-S.; Billardon, R.; Hild, F. High-cycle fatigue behaviour of spheroidal graphite cast iron. Fatigue Fract. Eng. Mater. Struct. 1998, 21, 287–296. [Google Scholar] [CrossRef] [Green Version]
- Yamabe, J.; Kobayashi, M. Influence of casting surfaces on fatigue strength of ductile cast iron. Fatigue Fract. Eng. Mater. Struct. 2006, 29, 403–415. [Google Scholar] [CrossRef]
- Zambrano, H.R.; Härkegård, G.; Stärk, K.F. Fracture toughness and growth of short and long fatigue cracks in ductile cast iron EN-GJS-400-18-LT. Fatigue Fract. Eng. Mater. Struct. 2011, 35, 374–388. [Google Scholar] [CrossRef] [Green Version]
- Shirani, M.; Härkegård, G.; Morin, N. Fatigue life prediction of components made of spheroidal graphite cast iron. Procedia Eng. 2010, 2, 1125–1130. [Google Scholar] [CrossRef] [Green Version]
- Nadot, Y. Influence of casting defects on the fatigue limit of nodular cast iron. Int. J. Fatigue 2004, 26, 311–319. [Google Scholar] [CrossRef]
- SAE J 1099; Technical Report on Low Cycle Fatigue Properties: Ferrous and Non Ferrous Materials. SAE International: Warrendale, PA, USA, 2002.
- Petrenec, M.; Tesařová, H.; Beran, P.; Šmíd, M.; Roupcová, P. Comparison of low cycle fatigue of ductile cast irons with different matrix alloyed with nickel. Procedia Eng. 2010, 2, 2307–2316. [Google Scholar] [CrossRef] [Green Version]
- Šamec, B.; Potrč, I.; Šraml, M. Low cycle fatigue of nodular cast iron used for railway brake discs. Eng. Fail. Anal. 2011, 18, 1424–1434. [Google Scholar] [CrossRef]
- Meneghetti, G.; Ricotta, M.; Masaggia, S.; Atzori, B. Comparison of the low-cycle and medium-cycle fatigue behaviour of ferritic, pearlitic, isothermed and austempered ductile irons. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 913–929. [Google Scholar] [CrossRef]
- Boonmee, S.; Stefanescu, D.M. Effect of Casting Skin on Fatigue Properties of CG Iron. Int. J. Met. 2013, 7, 15–26. [Google Scholar] [CrossRef]
- Nasu, S.; Fujita, S.; Furusato, N.; Yamada, S.; Hiratsuka, S. Effect of Casting Skin Condition on Fatigue Strength of Gray Cast Iron. Int. J. Met. 2016, 11, 155–161. [Google Scholar] [CrossRef]
- Rehmer, B.; Skrotzki, B.; Glaubitz, S. Influence of casting skin on the fatigue lifetime of ferritic ductile cast iron. Mater. Test. 2016, 59, 5–10. [Google Scholar] [CrossRef]
- Nain, P.K.S. The Effect of Remaining Casting Skin on Cast Iron Components Fatigue Strength. Int. J. Eng. Res. Comput. Sci. Eng. 2017, 4, 157–165. [Google Scholar]
- Gróza, M.; Váradi, K. Fatigue Design of Ferritic-Pearlitic Nodular Cast Iron Components with Surface Discontinuities. Stroj. Vestn. J. Mech. Eng. 2018, 64, 373–382. [Google Scholar] [CrossRef] [Green Version]
- Lundberg, M.; Peng, R.L.; Ahmad, M.; Bäckström, D.; Vuoristo, T.; Johansson, S. Fatigue Strength of Machined and Shot Peened Grey Cast Iron. Adv. Mater. Res. 2014, 891–892, 30–35. [Google Scholar] [CrossRef]
- Bergner, K.; Bleicher, C.; Wagener, R. Influence of remaining casting skin on the fatigue strength of cast iron components. Procedia Struct. Integr. 2019, 18, 792–801. [Google Scholar] [CrossRef]
- Bergner, K.; Hesseler, J.; Bleicher, C. Fatigue analysis of cast iron components considering the influence of casting skin. Procedia Struct. Integr. 2019, 19, 140–149. [Google Scholar] [CrossRef]
- Anca, D.; Chisamera, M.; Stan, S.; Stan, I.; Riposan, I. Sulfur and Oxygen Effects on High-Si Ductile Iron Casting Skin Formation. Coatings 2020, 10, 618. [Google Scholar] [CrossRef]
- Dowling, N.E. Mechanical Behavior of Materials—Engineering Methods for Deformation, Fracture and Fatigue, 4th ed.; Pearson: Harlow, UK, 2013. [Google Scholar]
- Sonsino, C.M. Light-weight design chances using high-strength steels. Mater. Werkst. 2007, 38, 9–22. [Google Scholar] [CrossRef]
- Hübner, P.; Pusch, G.; Krodel, L. Fatigue Behaviour of Cast Iron with Globular Graphite. Adv. Eng. Mater. 2004, 6, 541–544. [Google Scholar] [CrossRef]
- Bleicher, C.; Wagener, R.; Kaufmann, H.; Melz, T. Fatigue strength of nodular cast iron with regard to heavy-wall applications. Mater. Test. 2015, 57, 723–731. [Google Scholar] [CrossRef]
- Bleicher, C.; Wagener, R.; Kaufmann, H.; Melz, T. Influence of Different Load Histories on the Cyclic Material Behavior of Nodular Cast Iron for Thick-Walled Application. In Proceedings of the International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017. [Google Scholar]
- Heinrietz, A.; Hesseler, J. An approach for the fatigue estimation of porous cast iron based on non-destructive testing results. MATEC Web Conf. 2014, 12, 05001. [Google Scholar] [CrossRef] [Green Version]
- ISO/TR 945-3:2016; Microstructure of Cast Irons, Part1: Graphite Classification by Visual Analysis. International Organization for Standardization (ISO): Geneva, Switzerland, 2016.
- ISO 6506-1:2014; Metallic Materials—Brinell Hardness Test. International Organization for Standardization (ISO): Geneva, Switzerland, 2014.
- ISO 6892-1:2016; Metallic Materials—Tensile Testing. International Organization for Standardization (ISO): Geneva, Switzerland, 2016.
- ISO 12106:2017; Metallic Materials—Fatigue Testing—Axial-Strain-Controlled Method. International Organization for Standardization (ISO): Geneva, Switzerland, 2017.
- ASTM E 606-04; Standard Practice for Strain-Controlled Fatigue Testing. ASTM International: West Conshohocken, PA, USA, 2004.
- EN 1563:2018; Founding—Spheroidal Graphite Cast Irons. European Standard, 2018. Available online: https://standards.iteh.ai/catalog/standards/cen/e04bc999-3e91-4f24-855b-06dd6cf1d728/en-1563-2018 (accessed on 10 January 2022).
- Toktaş, G.; Tayanç, M.; Toktaş, A. Effect of matrix structure on the impact properties of an alloyed ductile iron. Mater. Charact. 2006, 57, 290–299. [Google Scholar] [CrossRef]
- Aristizabal, R.; Druschitz, A.; Druschitz, E.; Bragg, R.; Hubbard, C.; Watkins, T.; Ostrander, M. Intercritically Austempered Ductile Iron. In Proceedings of the American Foundry Society Transactions, Schaumburg, IL, USA, 5–8 April 2011; pp. 1–6. [Google Scholar]
- Durmuş, A.; Aydın, H.; Tutar, M.; Bayram, A.; Yiğit, K. Effect of the microstructure on the notched tensile strength of as-cast and austempered ductile cast irons. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 226, 2214–2229. [Google Scholar] [CrossRef]
- Angella, G.; Donnini, R.; Ripamonti, D.; Górny, M.; Zanardi, F. The Role of Microstructure on the Tensile Plastic Behaviour of Ductile Iron GJS 400 Produced through Different Cooling Rates—Part II: Tensile Modelling. Metals 2019, 9, 1019. [Google Scholar] [CrossRef] [Green Version]
- Basquin, O.H. The exponential law of endurance tests. Am. Soc. Test Mater. Proc. 1910, 10, 625–630. [Google Scholar]
- Manson, S.S. Behavior of Materials under Conditions of Thermal Stress. Report No. NACA TN-2933; Nasa: Washington, DC, USA, 1945. [Google Scholar]
- Coffin, L.F. A study of the effect of cyclic thermal stresses on a ductile metal. Trans. ASME 1954, 76, 931–950. [Google Scholar]
- Morrow, J. Cyclic Plastic Strain Energy and Fatigue of Metals. In Internal Friction, Damping, and Cyclic Plasticity; ASTM International: West Conshohocken, PA, USA, 1965; pp. 43–45. [Google Scholar]
- Niesłony, A.; El Dsoki, C.; Kaufmann, H.; Krug, P. New method for evaluation of the Manson–Coffin–Basquin and Ramberg–Osgood equations with respect to compatibility. Int. J. Fatigue 2008, 30, 1967–1977. [Google Scholar] [CrossRef]
- Atzori, B.; Meneghetti, G.; Ricotta, M. A Three Dimensional Graphical Aid for Fatigue Data Analysis. Key Eng. Mater. 2011, 488–489, 755–758. [Google Scholar] [CrossRef]
- Williams, C.; Lee, Y.-L.; Rilly, J. A practical method for statistical analysis of strain–life fatigue data. Int. J. Fatigue 2002, 25, 427–436. [Google Scholar] [CrossRef]
- ASTM E739-10 (2010); Standard Practice for Statistical Analysis of Linear or Linearized Stress-Life (S-N) and Strain-Life (ε-N) Fatigue Data. ASTM International: West Conshohocken, PA, USA, 2015.
- Smith, R.; Watson, P.; Topper, T. A stress–strain function for the fatigue of metal. J. Mater. 1970, 5, 767–778. [Google Scholar]
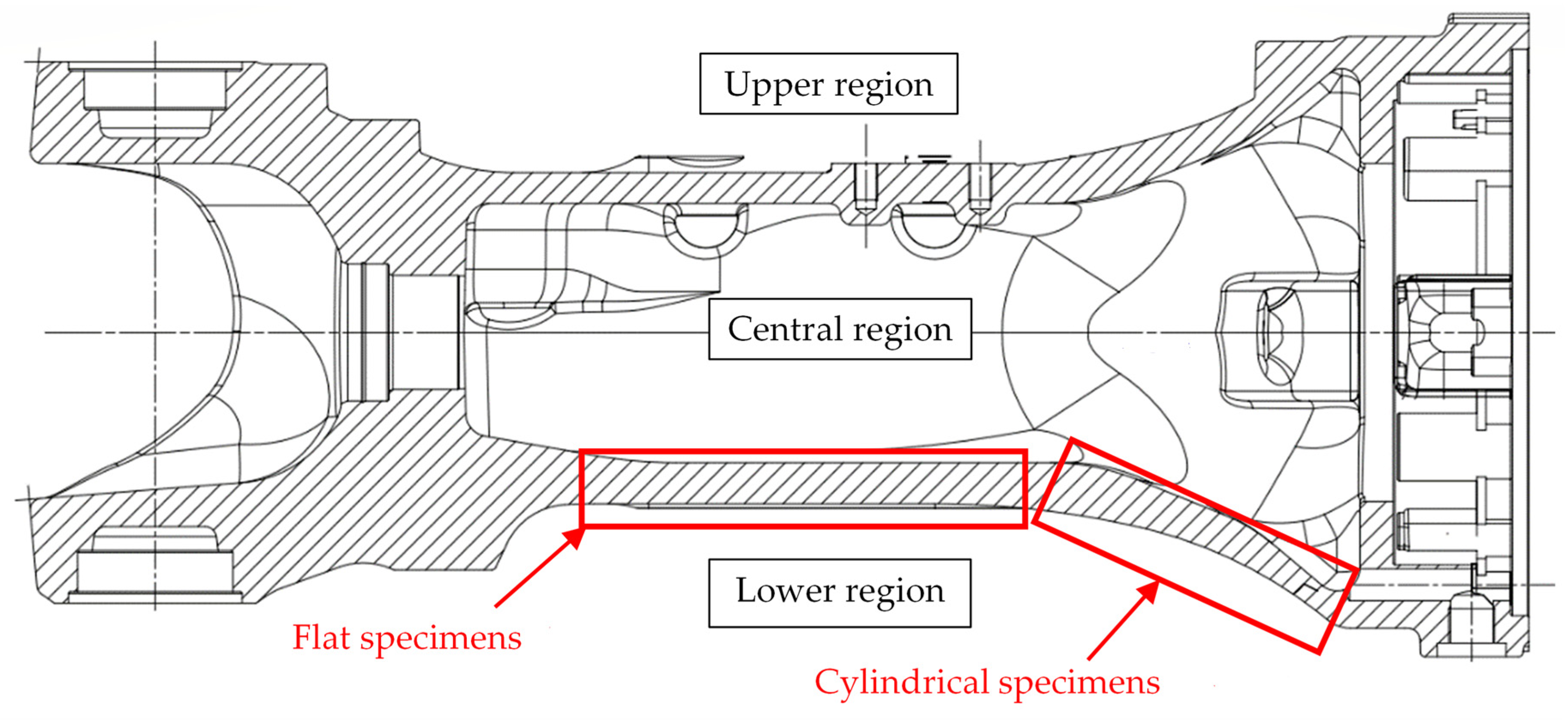
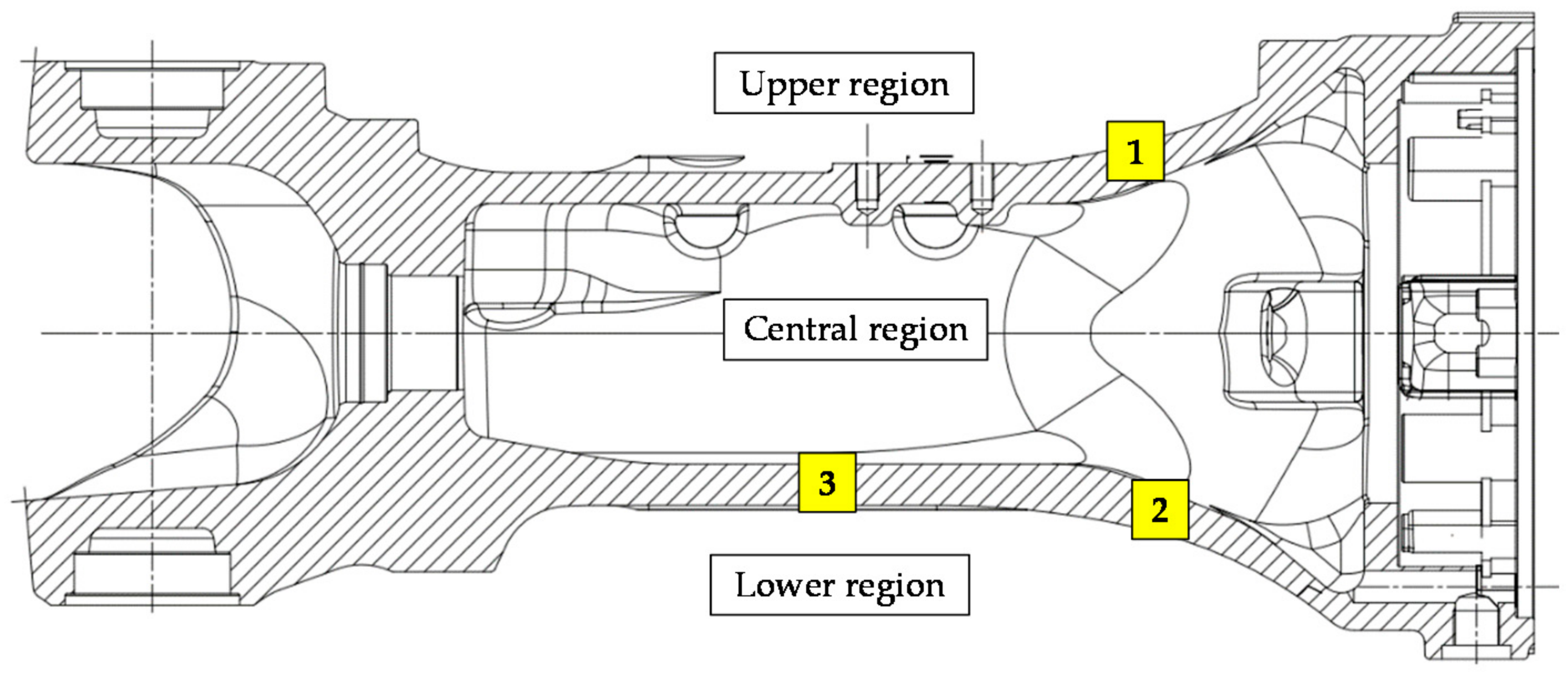

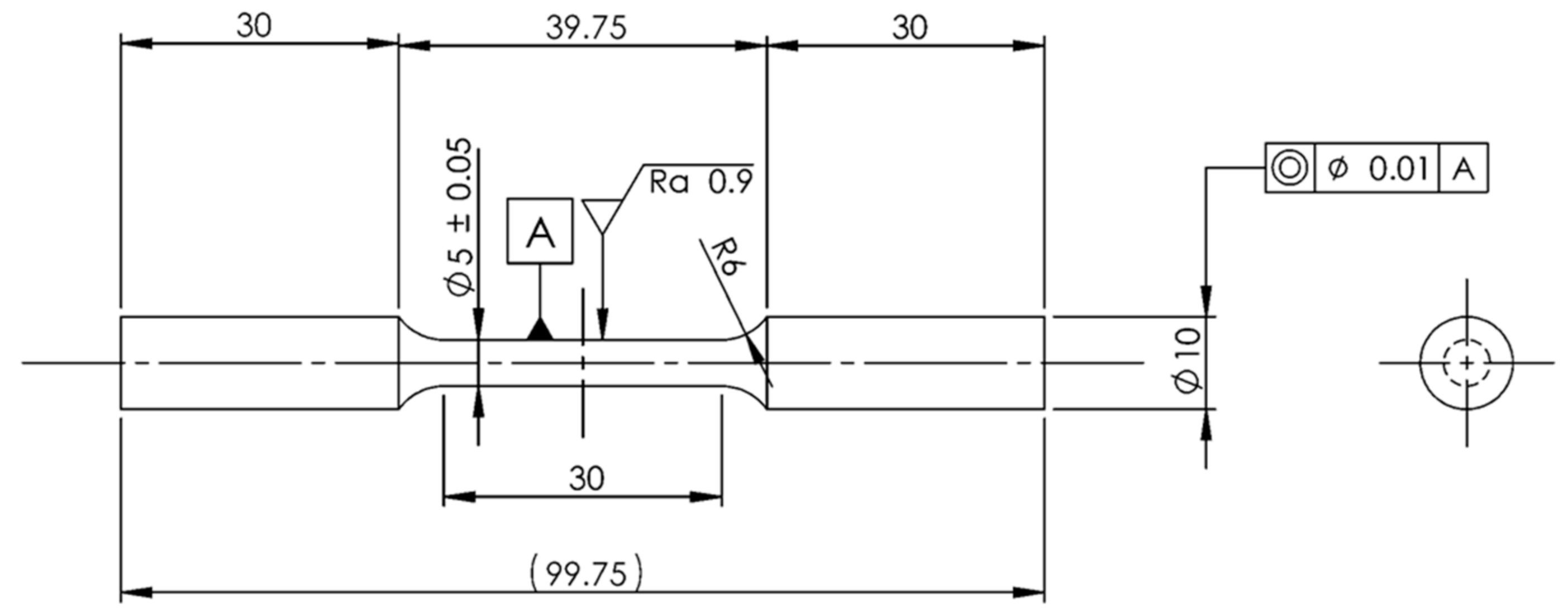

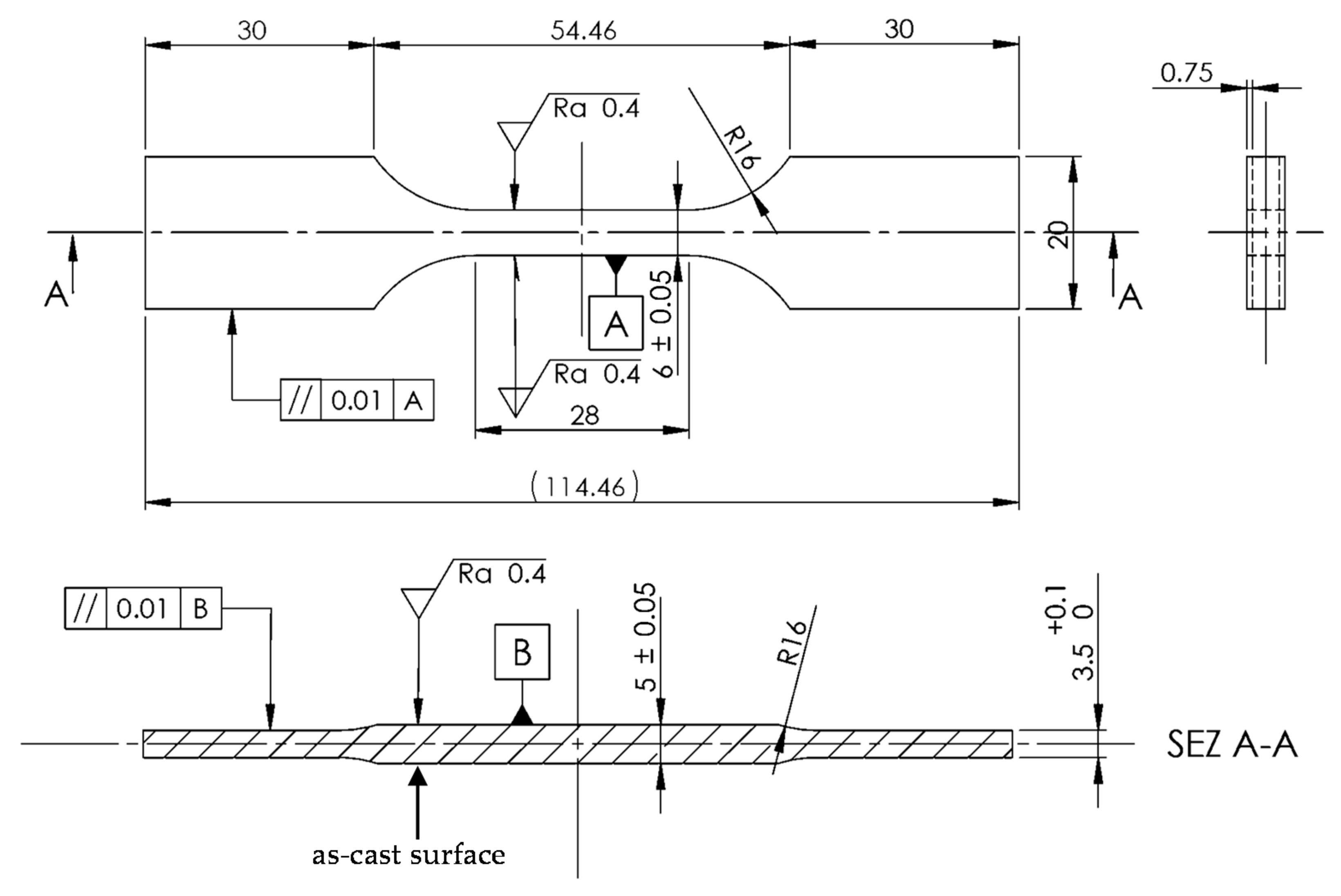









| Region | Shape # and Size * of Graphite Nodules | Matrix Composition |
|---|---|---|
| 1 | VI-7 Spheroidal graphite | ferritic (50%)–pearlitic (50%) |
| 2 | VI-6/7 Spheroidal graphite | ferritic (50%)–pearlitic (50%) |
| 3 | VI-7 Spheroidal graphite | ferritic (50%)–pearlitic (50%) |
| Region | HBW—Test 1 | HBW—Test 2 | HBW—Test 3 | HBW—Average | HBW—Standard Deviation |
|---|---|---|---|---|---|
| 1 | 182 | 182 | 183 | 182.3 | 0.577 |
| 2 | 182 | 184 | 183 | 183.0 | 1.000 |
| 3 | 185 | 187 | 187 | 186.3 | 1.155 |
| Material | Raw Component | Specimen Surface | Test | Specimen Geometry | Rε | N° Tests | f [Hz] | Rate [mm/min] | Failure Criterion |
|---|---|---|---|---|---|---|---|---|---|
| EN-GJS-450-10 | Off-highway axle | machined | Static | Figure 4 | n.a. | 7 | n.a. | 0.5 | separation |
| Fatigue * | Figure 5 | −1 0.1 0.5 | 10 6 6 | 0.2–18 0.2–15 0.2–15 | n.a. n.a. n.a. | separation separation separation | |||
| as-cast | Fatigue * | Figure 6 | −1 | 15 | 0.2–18 | n.a. | separation |
| Material | Raw Component | Pearlite Content | HBW |
|---|---|---|---|
| EN-GJS-450-10 | off-highway axle | 20–50% | 170–206 |
| Material | Raw Component | Parameter | Es | σp0.2 | σR | A | Z | K | n |
|---|---|---|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (MPa) | (%) | (%) | (MPa) | (/) | |||
| EN-GJS-450-10 | off-highway axle | Average value | 169,174 | 328 | 563 | 12.9 | 10 | 806 | 0.1584 |
| Standard deviation | 2383 | 4 | 9 | 1.3 | 1 | 26 | 0.0113 |
| Material | Raw Component | Specimen Surface | Test | Rε | N° Tests | Type A | Type B | Type C | Run Out |
|---|---|---|---|---|---|---|---|---|---|
| EN-GJS-450-10 | off-highway axle | machined | Static | n.a. | 7 | 6 | 0 | 1 | n.a. |
| Fatigue * | −1 0.1 0.5 | 10 6 6 | 6 5 6 | 1 1 0 | 2 0 0 | 1 0 0 | |||
| as-cast | Fatigue * | −1 | 14 | 9 | 3 | 0 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scacco, F.; Campagnolo, A.; Franceschi, M.; Meneghetti, G. Strain-Controlled Fatigue Behavior of a Nodular Cast Iron in Real Off-Highway Axles: Effects of Casting Skin and Strain Ratio. Metals 2022, 12, 426. https://doi.org/10.3390/met12030426
Scacco F, Campagnolo A, Franceschi M, Meneghetti G. Strain-Controlled Fatigue Behavior of a Nodular Cast Iron in Real Off-Highway Axles: Effects of Casting Skin and Strain Ratio. Metals. 2022; 12(3):426. https://doi.org/10.3390/met12030426
Chicago/Turabian StyleScacco, Federico, Alberto Campagnolo, Mattia Franceschi, and Giovanni Meneghetti. 2022. "Strain-Controlled Fatigue Behavior of a Nodular Cast Iron in Real Off-Highway Axles: Effects of Casting Skin and Strain Ratio" Metals 12, no. 3: 426. https://doi.org/10.3390/met12030426
APA StyleScacco, F., Campagnolo, A., Franceschi, M., & Meneghetti, G. (2022). Strain-Controlled Fatigue Behavior of a Nodular Cast Iron in Real Off-Highway Axles: Effects of Casting Skin and Strain Ratio. Metals, 12(3), 426. https://doi.org/10.3390/met12030426









