Measuring the Depth of Subsurface Defects in Additive Manufacturing Components by Laser-Generated Ultrasound
Abstract
:1. Introduction
2. Experimental Setup
3. Method
3.1. Velocity Dispersion of the Lamb Waves
- —wave number along the horizontal direction of the sample
- b—1/2 sample thickness
- —angular frequency
- —longitudinal wave velocity
- —shear wave velocity
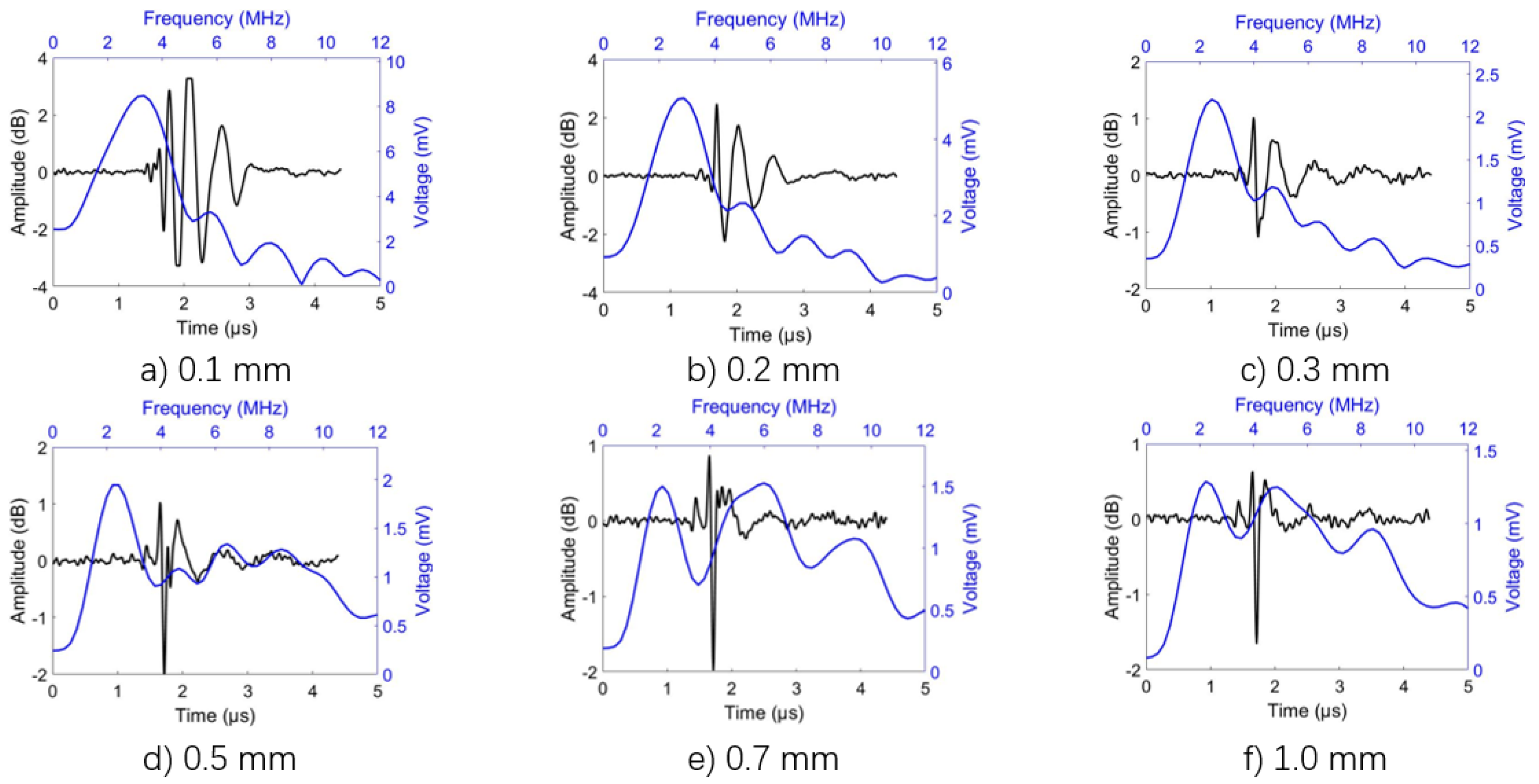
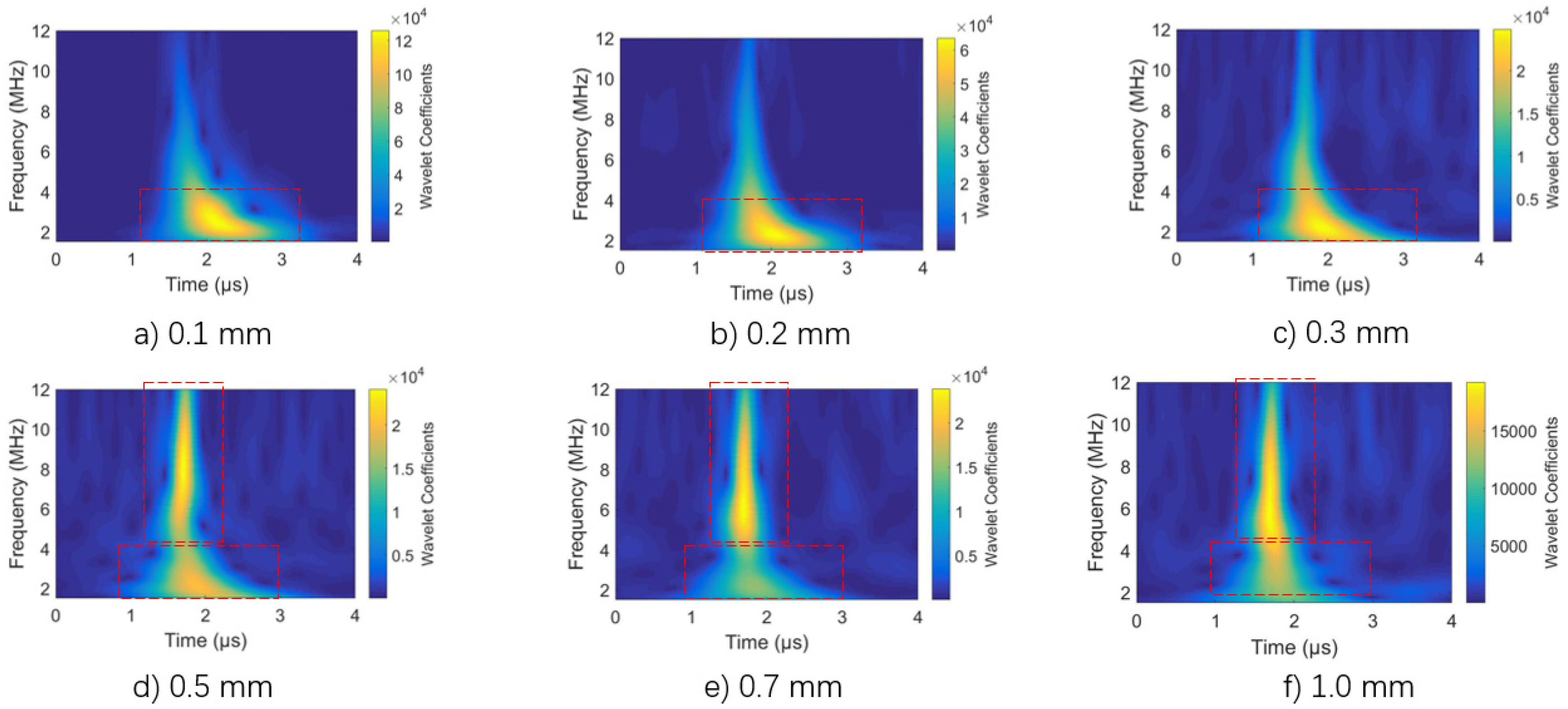
3.2. Time and Frequency Measurement by Wavelet-Transform
3.3. Velocity Calculation
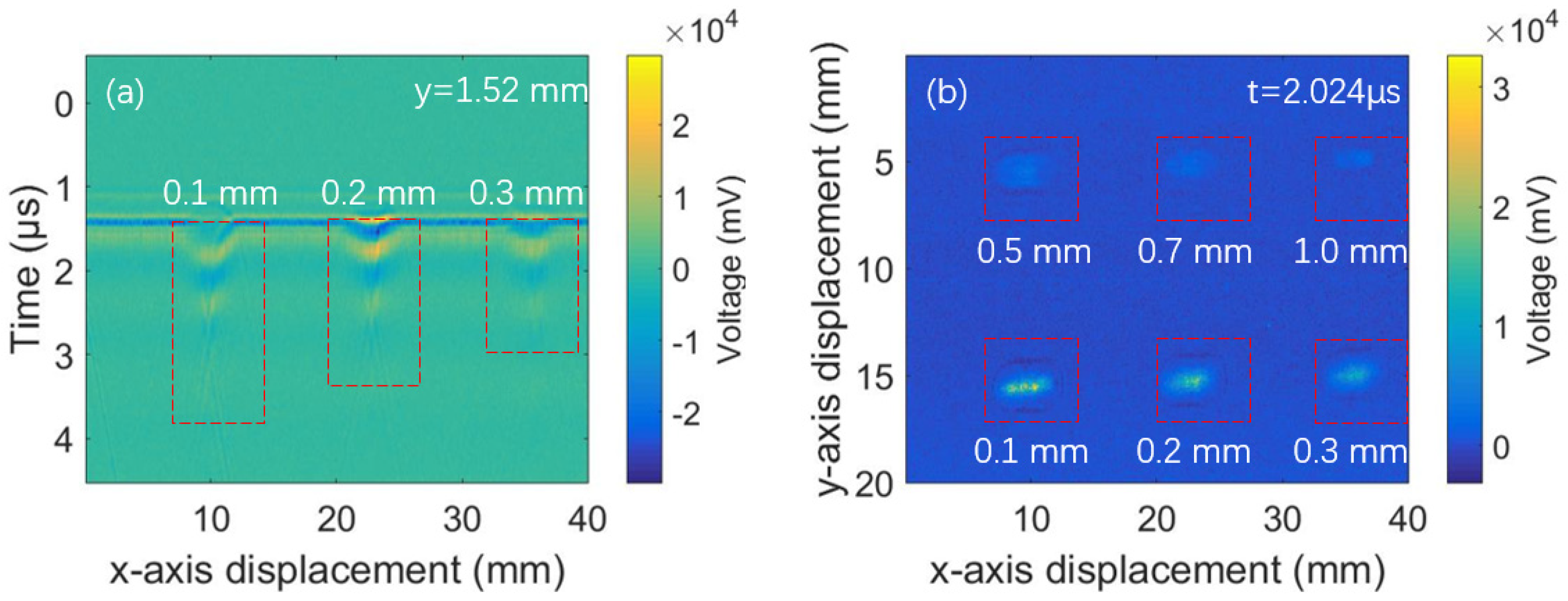
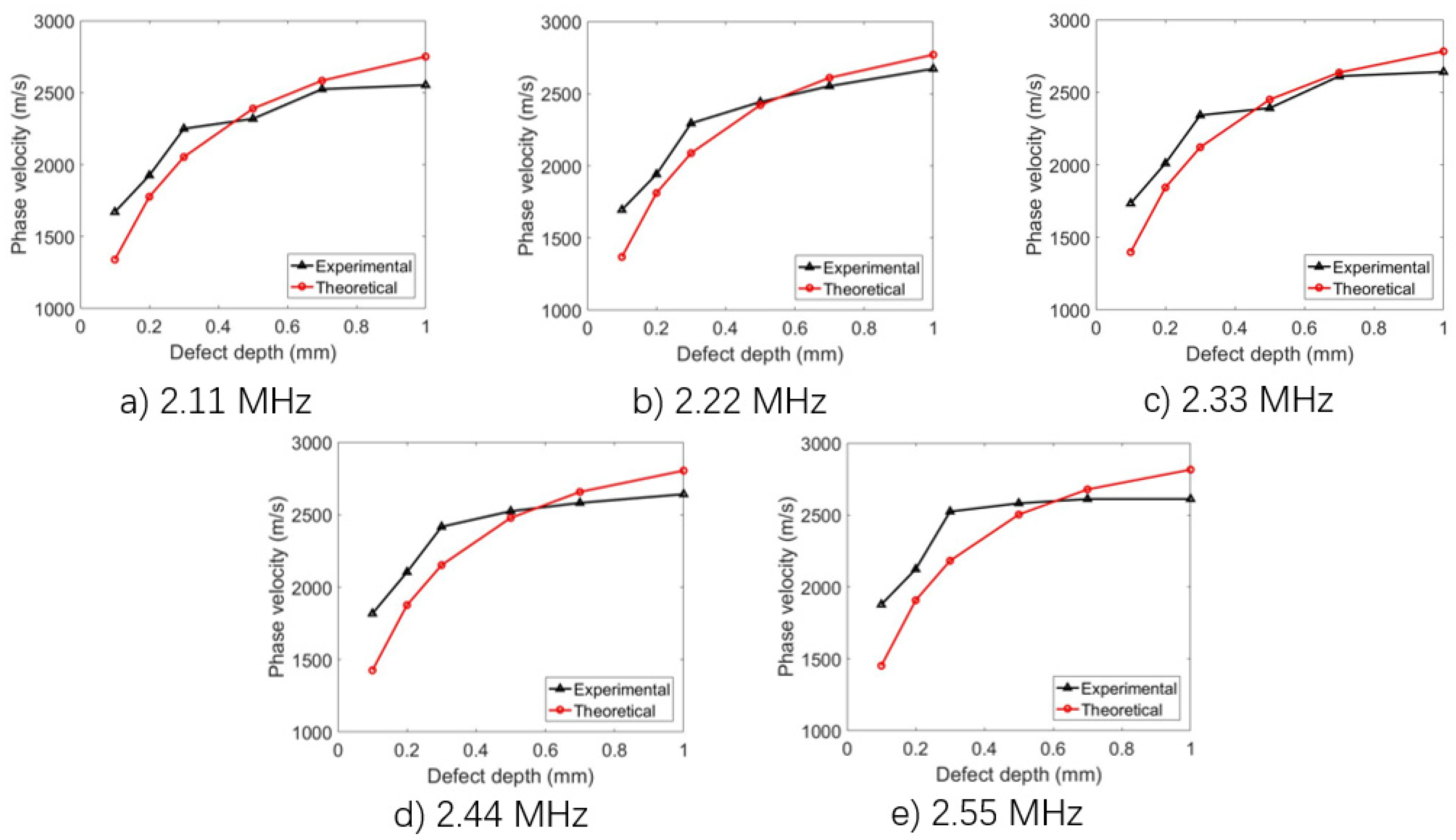
4. Results and Discussion
5. Conclusions
- (1)
- The mode-conversion is attributed to the velocity dispersion of the LGU. The central frequency and propagation velocity of the laser-induced surface wave are changed as the depth of the defects change.
- (2)
- The measured result of defect depth is very close to the theoretical value with a fitting coefficient of 0.98. The recommended defect depth range for accurate measurement is suggested to be lower than 0.8 mm, which is enough to meet the inspection layers thickness of AM methods, such as the selective melting method.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Martin, J.H.; Yahata, B.D.; Hundley, J.M.; Mayer, J.; Schaedler, T.A.; Pollock, T.M. 3D printing of high-strength aluminium alloys. Nature 2017, 549, 365–369. [Google Scholar] [CrossRef]
- Ma, Y.; Hu, Z.; Tang, Y.; Ma, S.; Chu, Y.; Li, X.; Luo, W.; Guo, L.; Zeng, X.; Lu, Y. Laser opto-ultrasonic dual detection for simultaneous compositional, structural, and stress analyses for wire + arc additive manufacturing. Addit. Manuf. 2020, 31, 100956. [Google Scholar] [CrossRef]
- Gisario, A.; Kazarian, M.; Martina, F.; Mehrpouya, M. Metal additive manufacturing in the commercial aviation industry: A review. J. Manuf. Syst. 2019, 53, 124–149. [Google Scholar] [CrossRef]
- Du, W.; Bai, Q.; Wang, Y.; Zhang, B. Eddy current detection of subsurface defects for additive/subtractive hybrid manufacturing. Int. J. Adv. Manuf. Technol. 2018, 95, 3185–3195. [Google Scholar] [CrossRef]
- Zhang, J.; Qin, X.; Yuan, J.; Wang, X.; Zeng, Y. The extraction method of laser ultrasonic defect signal based on EEMD. Opt. Commun. 2021, 484, 126570. [Google Scholar] [CrossRef]
- Davis, G.; Nagarajah, R.; Palanisamy, S.; Rashid, R.A.R.; Rajagopal, P.; Balasubramaniam, K. Laser ultrasonic inspection of additive manufactured components. Int. J. Adv. Manuf. Technol. 2019, 102, 2571–2579. [Google Scholar] [CrossRef]
- Lu, J.; Hou, R.; Chen, J.; Shao, H.; Ni, X. A new detection technique for laser-generated Rayleigh wave pulses. Opt. Commun. 2001, 11, S312–S316. [Google Scholar] [CrossRef]
- Zeng, Y.; Wang, X.; Qin, X.; Hua, L.; Xu, M. Laser Ultrasonic inspection of a Wire + Arc Additive Manufactured (WAAM) sample with artificial defects. Ultrasonics 2021, 110, 106273. [Google Scholar] [CrossRef]
- Wang, C.; Sun, A.; Yang, X.; Ju, B.-F.; Pan, Y. Laser-generated Rayleigh wave for width gauging of subsurface lateral rectangular defects. J. Appl. Phys. 2018, 124, 065104. [Google Scholar] [CrossRef]
- Chen, D.; Lv, G.; Guo, S.; Zuo, R.; Liu, Y.; Zhang, K.; Su, Z.; Feng, W. Subsurface defect detection using phase evolution of line laser-generated Rayleigh waves. Opt. Laser Technol. 2020, 131, 106410. [Google Scholar] [CrossRef]
- Zeng, W.; Zou, X.; Yao, F. Finite element simulation of phased array laser-generated surface acoustic wave for identification surface defects. Optik 2020, 224, 165733. [Google Scholar] [CrossRef]
- Gao, F.; Zhou, H.; Huang, C. Defect detection using the phased-array laser ultrasonic crack diffraction enhancement method. Opt. Commun. 2020, 474, 126070. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, K.; Zhou, J.; Sun, G.; Wang, J. Application of laser ultrasonic technique for non-contact detection of structural surface-breaking cracks. Opt. Laser Technol. 2015, 73, 173–178. [Google Scholar] [CrossRef]
- Hayashi, Y.; Ogawa, S.; Cho, H.; Takemoto, M. Non-contact estimation of thickness and elastic properties of metallic foils by the wavelet transform of la-ser-generated Lamb waves. NDT E Int. 1999, 32, 21–27. [Google Scholar] [CrossRef]
- Sun, H.; Xu, B.; Xu, G.; Xu, C. Study on laser-generated Lamb waves propagation in viscoelastic and anisotropic plate. Chin. Opt. Lett. 2010, 8, 776–779. [Google Scholar] [CrossRef]
- Benmeddour, F.; Grondel, S.; Assaad, J.; Moulin, E. Study of the fundamental Lamb modes interaction with asymmetrical discontinuities. NDT E Int. 2008, 41, 330–340. [Google Scholar] [CrossRef]
- Benmeddour, F.; Grondel, S.; Assaad, J.; Moulin, E. Study of the fundamental Lamb modes interaction with symmetrical notches. NDT E Int. 2008, 41, 1–9. [Google Scholar] [CrossRef]
- Lee, B.C.; Staszewski, W.J. Lamb wave interaction with structural defects: Modeling and simulations. In Proceedings of the Smart Structures and Materials 2003: Modeling, Signal Processing, and Control, San Diego, CA, USA, 3–6 March 2003; Volume 5049, pp. 146–155. [Google Scholar] [CrossRef]
- Wooh, S.C.; Veroy, K. Time-frequency analysis of broadband dispersive waves using the wavelet transform. In Proceedings of the 26th Annual Review of Progress in Quantitative Nondestructive Evaluation, Montreal, QC, Canada, 25–30 July 1999; pp. 831–838. [Google Scholar]
- Mostafapour, A.; Davoodi, S. Continuous leakage location in noisy environment using modal and wavelet analysis with one AE sensor. Ultrasonics 2015, 62, 305–311. [Google Scholar] [CrossRef]
- Gur, B.; Niezrecki, C. Autocorrelation based denoising of manatee vocalizations using the undecimated discrete wavelet transform. J. Acoust. Soc. Am. 2007, 122, 188–199. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Lin, G.; Wu, L.; Cheng, Y. Speckle filtering of medical ultrasonic images using wavelet and guided filter. Ultrasonics 2016, 65, 177–193. [Google Scholar] [CrossRef]
- Praveen, A.; Vijayarekha, K.; Abraham, S.T.; Venkatraman, B. Signal quality enhancement using higher order wavelets for ultrasonic TOFD signals from austenitic stainless steel welds. Ultrasonics 2013, 53, 1288–1292. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Zhang, J.; Li, X.; Yuan, S.; Ma, G.; Xue, Z.; Jing, X.; Cao, J. Intelligent denoise laser ultrasonic imaging for inspection of selective laser melting components with rough surface. NDT E Int. 2022, 125, 102548. [Google Scholar] [CrossRef]
- Moser, F.; Jacobs, L.J.; Qu, J. Modeling elastic wave propagation in waveguides with the finite element method. NDT E Int. 1999, 32, 225–234. [Google Scholar] [CrossRef]

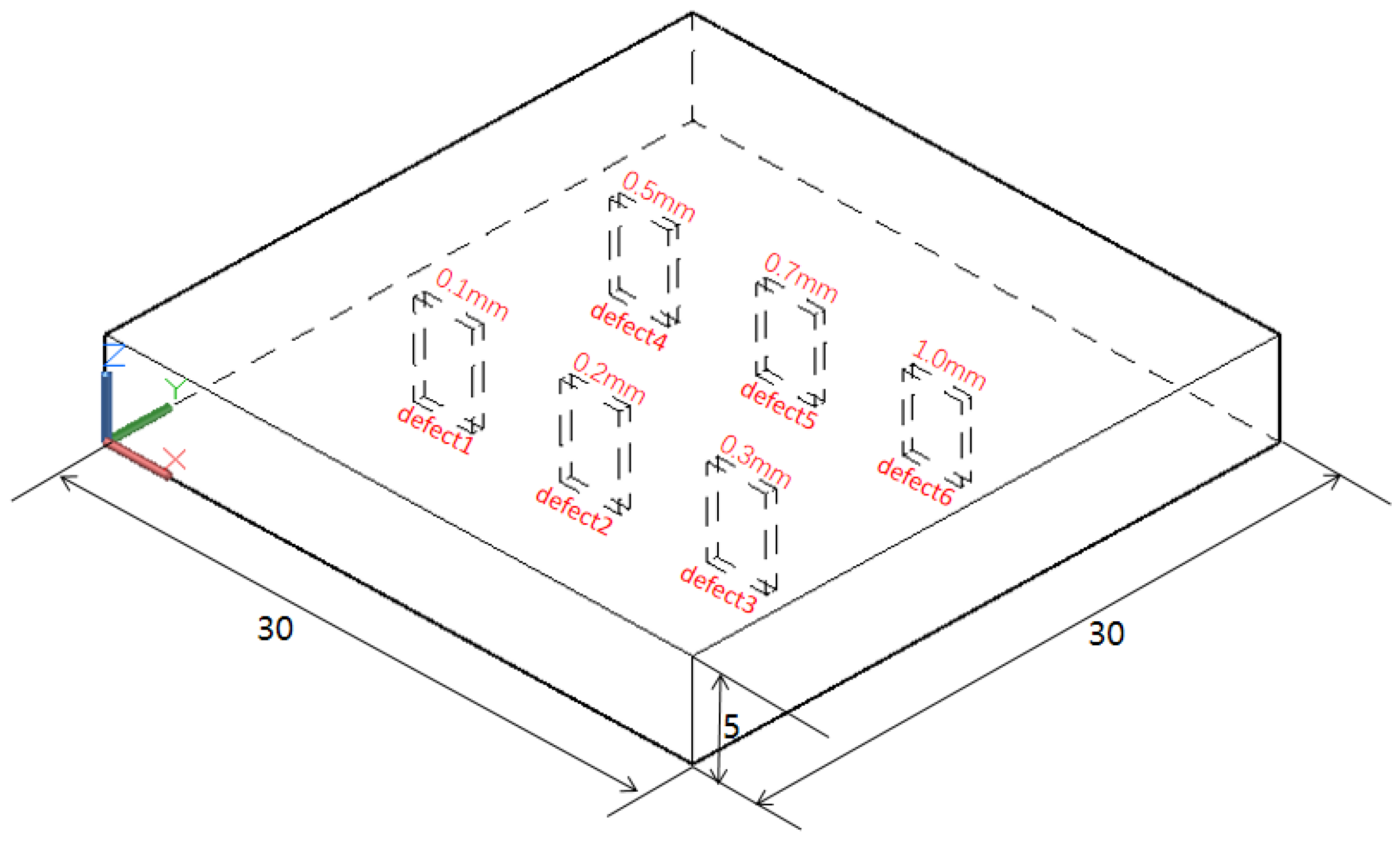



| Parameter | Wavelength/(nm) | Laser Coefficient of Sample (A) | Spot Diameter (d)/(μm) | Pulse Energy (e)/(mJ) |
|---|---|---|---|---|
| Value | 1064 | 0.1 | 150 | 2 |
| Parameter | )/(m/s) | |||
|---|---|---|---|---|
| Value | 5880 | 3230 | 2990 | 450 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, Z.; Xu, W.; Peng, Y.; Wang, M.; Pelenovich, V.; Yang, B.; Zhang, J. Measuring the Depth of Subsurface Defects in Additive Manufacturing Components by Laser-Generated Ultrasound. Metals 2022, 12, 437. https://doi.org/10.3390/met12030437
Xue Z, Xu W, Peng Y, Wang M, Pelenovich V, Yang B, Zhang J. Measuring the Depth of Subsurface Defects in Additive Manufacturing Components by Laser-Generated Ultrasound. Metals. 2022; 12(3):437. https://doi.org/10.3390/met12030437
Chicago/Turabian StyleXue, Zhixiang, Wanli Xu, Yunchao Peng, Mengmeng Wang, Vasiliy Pelenovich, Bing Yang, and Jun Zhang. 2022. "Measuring the Depth of Subsurface Defects in Additive Manufacturing Components by Laser-Generated Ultrasound" Metals 12, no. 3: 437. https://doi.org/10.3390/met12030437
APA StyleXue, Z., Xu, W., Peng, Y., Wang, M., Pelenovich, V., Yang, B., & Zhang, J. (2022). Measuring the Depth of Subsurface Defects in Additive Manufacturing Components by Laser-Generated Ultrasound. Metals, 12(3), 437. https://doi.org/10.3390/met12030437






