Investigation on the Cause-Effect Relationships between the Process Parameters and the Resulting Geometric Properties for Wire-Based Coaxial Laser Metal Deposition
Abstract
:1. Introduction
1.1. Directed Energy Deposition Processes
1.2. State of the Art
1.2.1. Process Development for LMD with Lateral Wire Feeding
1.2.2. Process Development for LMD with Coaxial Wire Feeding
1.3. Problem Statement
1.4. Objectives and Approach
2. Materials, Systems and Methods
2.1. Materials
2.2. Systems
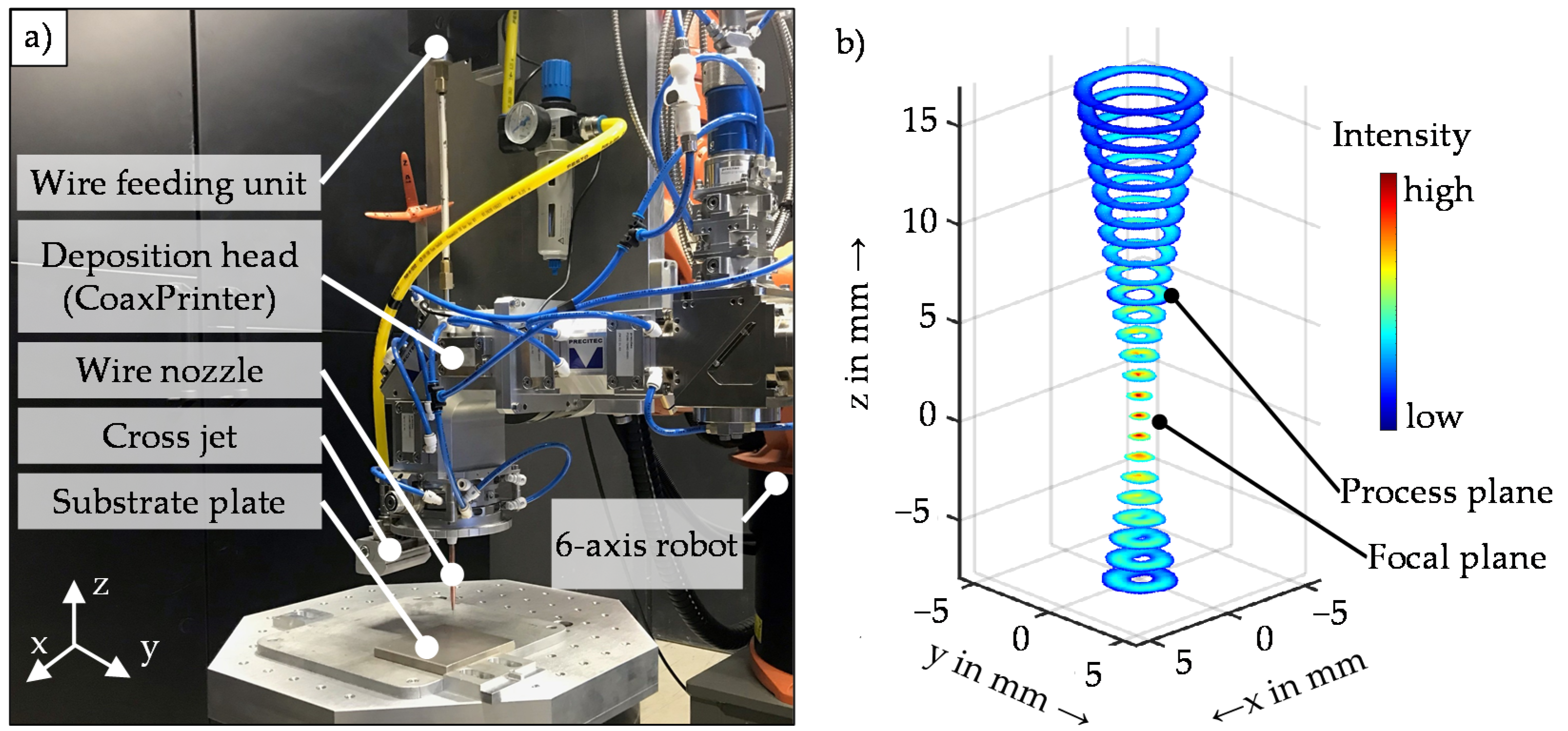
2.2.1. Laser Metal Deposition System
2.2.2. Optical Measurement
2.3. Methods
2.3.1. Theoretical Considerations
2.3.2. Experimental Procedure
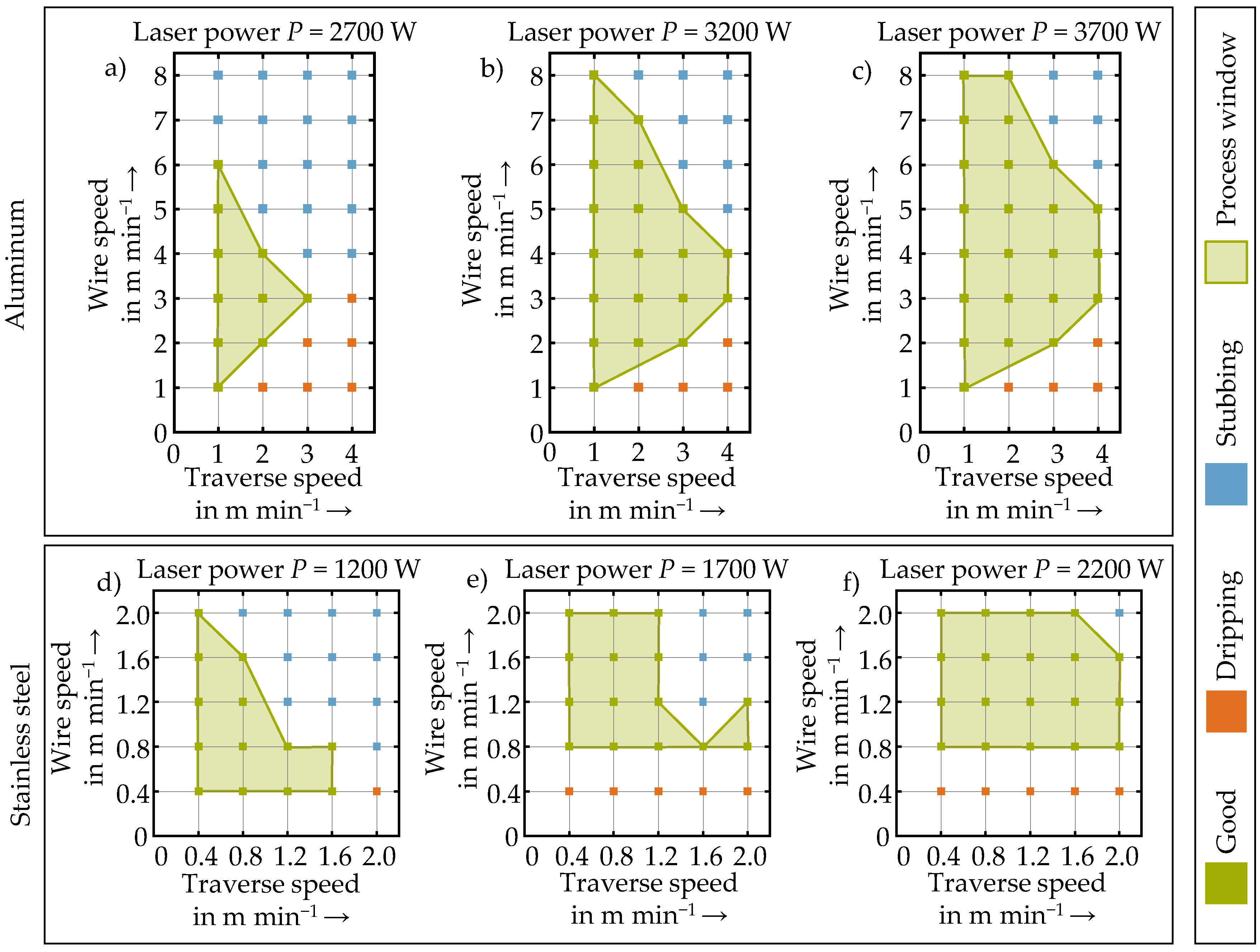
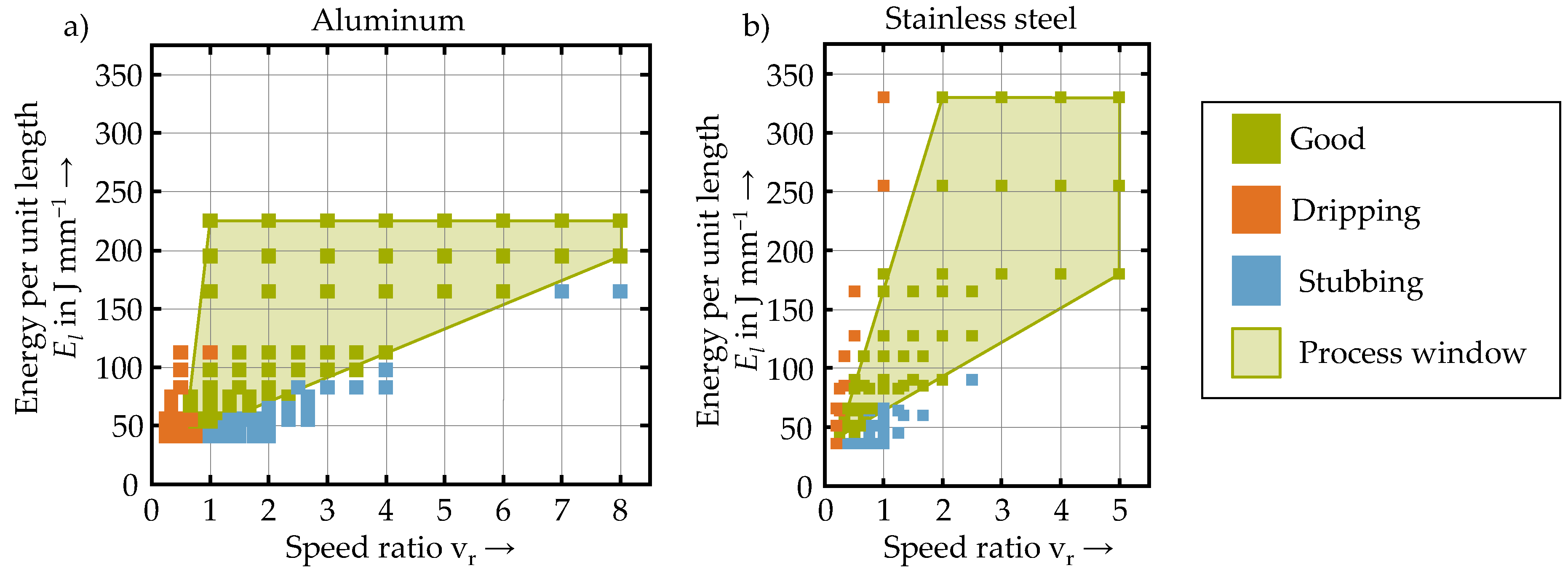
Process Window
Regression Analysis
Height Increment
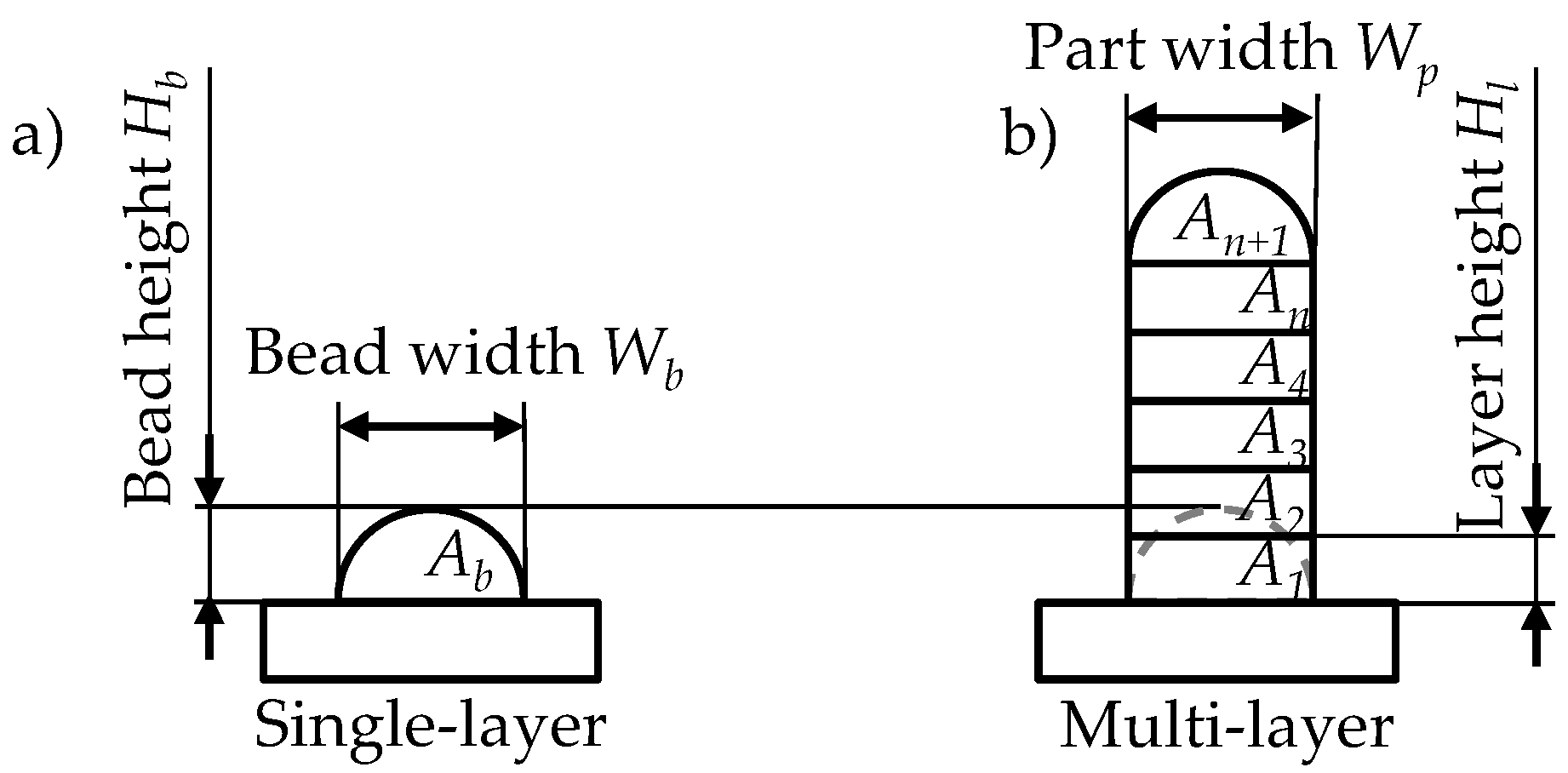
2.3.3. Bead Analysis
3. Results and Discussion
3.1. Process Windows
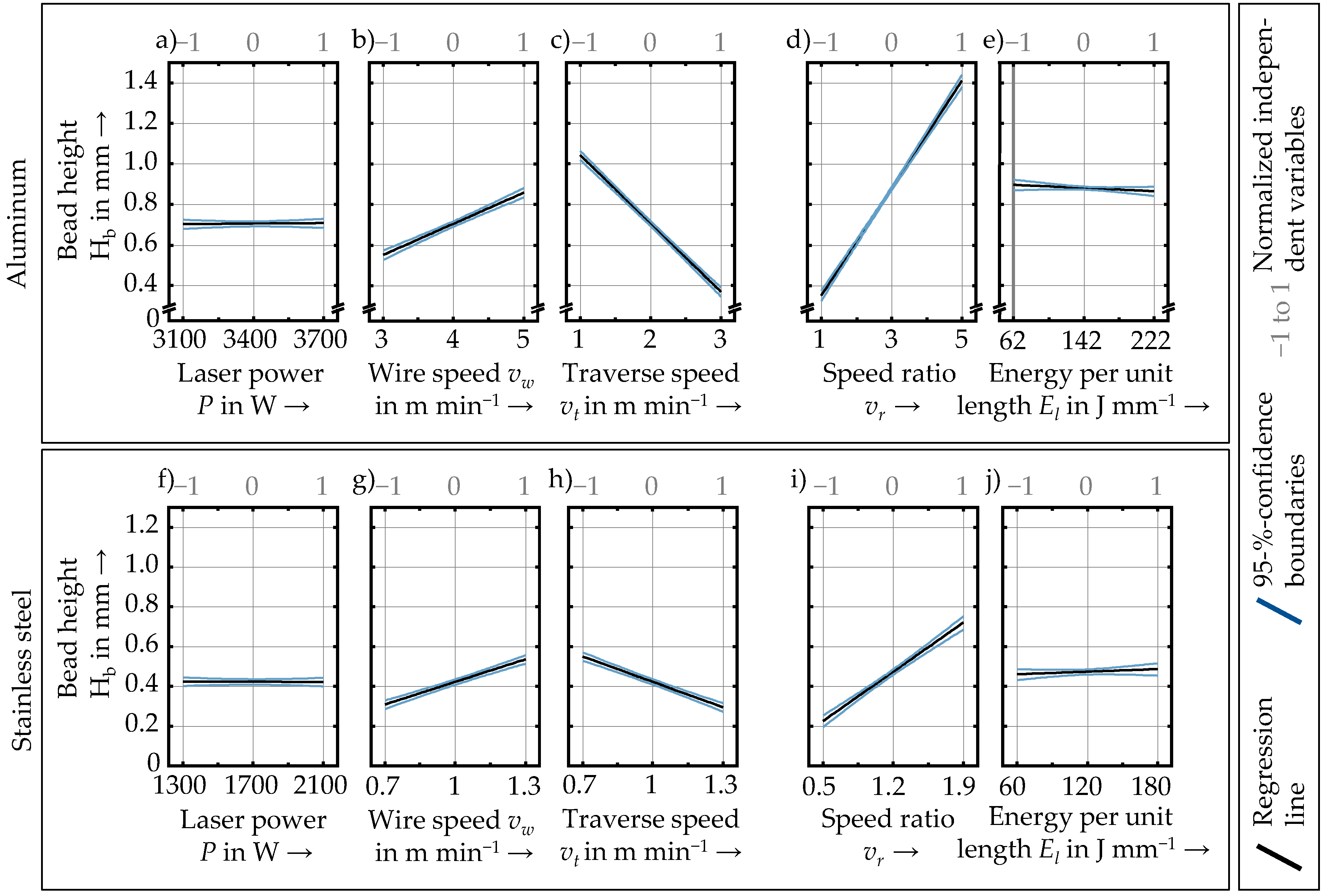
3.2. Regression Analysis
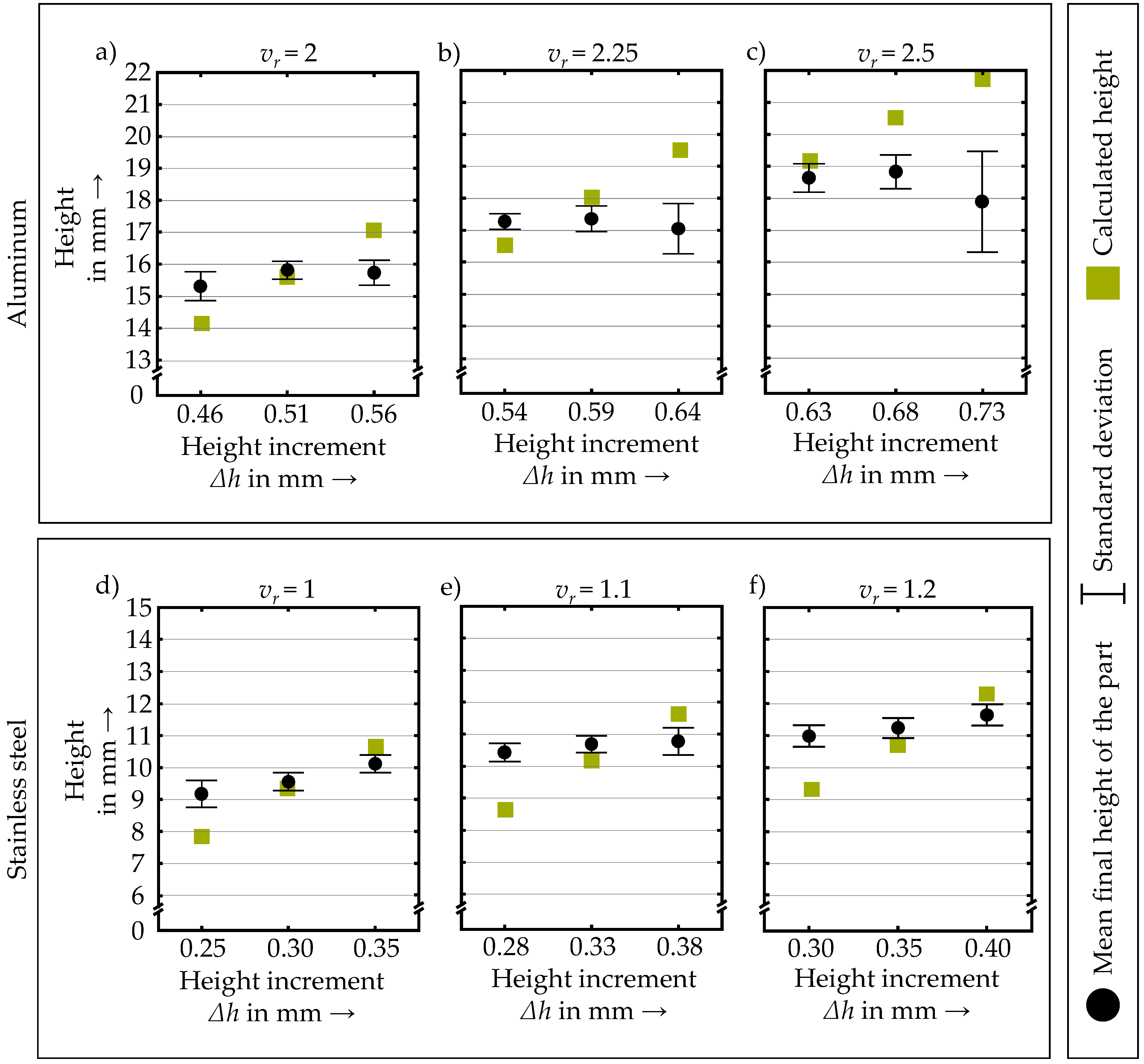
3.3. Height Increment
4. Conclusions and Outlook
- A suitable combination between the speed ratio and the energy per unit length plays a crucial role in establishing a defect-free process. Therefore, these parameters offer a material-independent valid alternative to the more widely used parameters of the laser power, wire speed, and traverse speed for process development. For both materials, the minimal amount of energy per unit length for a defect-free process was 50 J mm−1. Due to the lower melting temperature of aluminum, a defect-free process could only be achieved using speed ratios above 1, while lower speed ratios resulted in a defect-free process with stainless steel.
- The correlation between process parameters and the bead width and height for both investigated materials can be approximated by linear models.
- Independent of the used material, the following observations regarding the influence of parameter variations within the respective process windows on the bead height and width were made:
- ○
- The bead height increases with higher wire speeds and speed ratios, decreases for higher traverse speeds, and is not affected by the laser power nor the energy per unit length.
- ○
- The bead width increases with a higher laser power and energy per unit length, decreases with higher traverse speeds, and is marginally affected by the wire speed. A higher speed ratio leads to narrower beads for aluminum and wider beads for stainless steel.
- The height increment required for a layer-wise additive process can be chosen based on the presented formula that uses the dimensions of the wire, the speed ratio, and the width of single beads.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Dependent Variable | Material | R2 of the Model | SSR | SSE | Independent Variable | Variable Value | Standard Error | p-Value |
|---|---|---|---|---|---|---|---|---|
| Height | Aluminum | 0.92 | 8.57 | 0.69 | P | 7.75 × 10−6 | 3.17 × 10−5 | 0.81 |
| vt | −0.34 | 9.51 × 10−3 | 1.06 × 10−65 | |||||
| vw | 0.15 | 9.51 × 10−3 | 4.61 × 10−32 | |||||
| 0.98 | 9.10 | 0.15 | vr | 0.26 | 6.77 × 10−3 | 6.39 × 10−71 | ||
| El | −0.19 × 10−3 | 0.14 × 10−3 | 0.18 | |||||
| Stainless steel | 0.94 | 0.53 | 0.02 | P | −2.25 × 10−6 | 1.96 × 10−5 | 0.90 | |
| vt | −0.42 | 0.03 | 3.97 × 10−14 | |||||
| vw | 0.38 | 0.03 | 4.42 × 10−13 | |||||
| 0.95 | 0.53 | 0.02 | vr | 0.35 | 0.02 | 1.65 × 10−15 | ||
| El | 0.21 × 10−3 | 0.21 × 10−3 | 0.33 | |||||
| Width | Aluminum | 0.84 | 6.10 | 1.11 | P | 0.22 × 10−3 | 4.04 × 10−3 | 1.53 × 10−7 |
| vt | −0.30 | 0.01 | 7.62 × 10−50 | |||||
| vw | −0.018 | 0.01 | 0.14 | |||||
| 0.87 | 6.30 | 0.91 | vr | −0.05 | 0.02 | 1.87 × 10−3 | ||
| El | 5.53 × 10−3 | 0.35 × 10−3 | 3.18 × 10−3 | |||||
| Stainless steel | 0.67 | 0.93 | 0.37 | P | 0.17 × 10−3 | 7.56 × 10−5 | 0.03 | |
| vt | −0.70 | 0.10 | 4.41 × 10−7 | |||||
| vw | 0.17 | 0.10 | 0.11 | |||||
| 0.68 | 0.93 | 0.38 | vr | 0.22 | 0.07 | 8.92 × 10−3 | ||
| El | 3.50 × 10−3 | 0.83 × 10−3 | 0.27 × 10−3 |

References
- Sames, W.J.; List, F.A.; Pannala, S.; Dehoff, R.R.; Babu, S.S. The metallurgy and processing science of metal additive manufacturing. Int. Mater. Rev. 2016, 61, 315–360. [Google Scholar] [CrossRef]
- Gu, D.D.; Meiners, W.; Wissenbach, K.; Poprawe, R. Laser additive manufacturing of metallic components: Materials, processes and mechanisms. Int. Mater. Rev. 2012, 57, 133–164. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Ding, D.; Pan, Z.; Cuiuri, D.; Li, H. Wire-feed additive manufacturing of metal components: Technologies, developments and future interests. Int. J. Adv. Manuf. Technol. 2015, 81, 465–481. [Google Scholar] [CrossRef]
- Maderieta, M.; Leunda, J.; Garmendia, I.; Soriano, C. Compartive study of laser metal deposition (LMD) of coaxial wire and powder in the manufacture of Ti-6AL-4V structures. DYNAII 2020, 95, 376–379. [Google Scholar] [CrossRef]
- Dass, A.; Moridi, A. State of the Art in Directed Energy Deposition: From Additive Manufacturing to Materials Design. Coatings 2019, 9, 418. [Google Scholar] [CrossRef] [Green Version]
- Syed, W.U.H.; Li, L. Effects of wire feeding direction and location in multiple layer diode laser direct metal deposition. Appl. Surf. Sci. 2005, 248, 518–524. [Google Scholar] [CrossRef]
- Shakhverdova, I.; Nowotny, S.; Thieme, S.; Kubisch, F.; Beyer, E.; Leyens, C. Coaxial Laser Wire Deposition. J. Phys. Conf. Ser. 2018, 1109, 12026. [Google Scholar] [CrossRef]
- Pajukoski, H.; Näkki, J.; Thieme, S.; Tuominen, J.; Nowotny, S.; Vuoristo, P. High performance corrosion resistant coatings by novel coaxial cold- and hot-wire laser cladding methods. J. Laser Appl. 2016, 28, 12011. [Google Scholar] [CrossRef]
- Bambach, M.; Sizova, I.; Silze, F.; Schnick, M. Comparison of laser metal deposition of Inconel 718 from powder, hot and cold wire. Procedia CIRP 2018, 74, 206–209. [Google Scholar] [CrossRef]
- Du, F.; Zhu, J.; Ding, X.; Zhang, Q.; Ma, H.; Yang, J.; Cao, H.; Ling, Z.; Wang, G.; Duan, X.; et al. Dimensional characteristics of Ti-6Al-4V thin-walled parts prepared by wire-based multi-laser additive manufacturing in vacuum. Rapid Prototyp. J. 2019, 25, 849–856. [Google Scholar] [CrossRef]
- Lammers, M.; Biester, K.; Schwarz, N.; Hermsdorf, J.; Kaierle, S.; Ahlers, H. Automatic changing of weld deposit for additive manufacturing of hybrid metal-glass components using direct laser deposition. In Proceedings of the Lasers in Manufacturing Conference 2021, Munich, Germany, 21–24 June 2021. [Google Scholar]
- Kelbassa, J.; Gasser, A.; Bremer, J.; Pütsch, O.; Poprawe, R.; Henrich Schleifenbaum, J. Equipment and process windows for laser metal deposition with coaxial wire feeding. J. Laser Appl. 2019, 31, 22320. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Jeromen, A.; Levy, G.; Fujishima, M.; Govekar, E. Annular Laser Beam Cladding Process Feasibility Study. Phys. Procedia 2016, 83, 647–656. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Kong, F.; Shi, S.; Kovacevic, R. Study of a hollow laser beam for cladding. Int. J. Adv. Manuf. Technol. 2014, 73, 147–159. [Google Scholar] [CrossRef]
- Govekar, E.; Jeromen, A.; Kuznetsov, A.; Kotar, M.; Kondo, M. Annular laser beam based direct metal deposition. Procedia CIRP 2018, 74, 222–227. [Google Scholar] [CrossRef]
- Nowotny, S.; Scharek, S.; Beyer, E.; Richter, K.-H. Laser Beam Build-Up Welding: Precision in Repair, Surface Cladding, and Direct 3D Metal Deposition. J. Therm. Spray. Tech. 2007, 16, 344–348. [Google Scholar] [CrossRef]
- Abioye, T.E.; Medrano-Tellez, A.; Farayibi, P.K.; Oke, P.K. Laser metal deposition of multi-track walls of 308LSi stainless steel. Mater. Manuf. 2017, 32, 1660–1666. [Google Scholar] [CrossRef]
- Medrano, A.; Folkes, J.; Segal, J.; Pashby, I. Fibre laser metal deposition with wire: Parameters study and temperature monitoring system. In Proceedings of the XVII International Symposium on Gas Flow, Chemical Lasers, and High-Power Lasers, Lisboa, Portugal, 15–19 September 2008. [Google Scholar]
- Oliari, S.H.; D’Oliveira, A.S.C.M.; Schulz, M. Additive Manufacturing of H11 with Wire-Based Laser Metal Deposition. Soldag. Insp. 2017, 22, 466–479. [Google Scholar] [CrossRef] [Green Version]
- Akbari, M.; Ding, Y.; Kovacevic, R. Process Development for a Robotized Laser Wire Additive Manufacturing. In Proceedings of the ASME 2017, Los Angeles, CA, USA, 3–9 November 2017. [Google Scholar]
- Silva, A.D.; Wang, S.; Volpp, J.; Kaplan, A.F.H. Vertical laser metal wire deposition of Al-Si alloys. Procedia CIRP 2020, 94, 341–345. [Google Scholar] [CrossRef]
- Froend, M.; Riekehr, S.; Kashaev, N.; Klusemann, B.; Enz, J. Process development for wire-based laser metal deposition of 5087 aluminium alloy by using fibre laser. J. Manuf. Process. 2018, 34, 721–732. [Google Scholar] [CrossRef]
- Valentin, M.; Arnaud, C.; Kling, R. Additive manufacturing by wire based laser metal deposition. In Proceedings of the Laser 3D Manufacturing VI, San Francisco, CA, USA, 5–7 February 2019. [Google Scholar]
- Barroi, A.; Hermsdorf, J.; Kaierle, S.; Overmeyer, L. Influence of scan width and wire feed speed on seam geometry and the substrate surface in laser wire cladding. In Proceedings of the International Congress on Applications of Lasers & Electro-Optics ICALEO®, San Diego, CA, USA, 16–20 October 2016. [Google Scholar]
- Hu, R.; Luo, M.; Liu, T.; Liang, L.; Huang, A.; Trushnikov, D.; Karunakaran, K.P.; Pang, S. Thermal fluid dynamics of liquid bridge transfer in laser wire deposition 3D printing. Sci. Technol. Weld. Join. 2019, 24, 401–411. [Google Scholar] [CrossRef]
- Shaikh, M.O.; Chen, C.-C.; Chiang, H.-C.; Chen, J.-R.; Chou, Y.-C.; Kuo, T.-Y.; Ameyama, K.; Chuang, C.-H. Additive manufacturing using fine wire-based laser metal deposition. Rapid Prototyp. J. 2019, 26, 473–483. [Google Scholar] [CrossRef]
- Caiazzo, F. Additive manufacturing by means of laser-aided directed metal deposition of titanium wire. Int. J. Adv. Manuf. Technol. 2018, 96, 2699–2707. [Google Scholar] [CrossRef] [Green Version]
- Mok, S.H.; Bi, G.; Folkes, J.; Pashby, I. Deposition of Ti–6Al–4V using a high power diode laser and wire, Part I: Investigation on the process characteristics. Surf. Coat. Technol. 2008, 202, 3933–3939. [Google Scholar] [CrossRef]
- Huang, W.; Chen, S.; Xiao, J.; Jiang, X.; Jia, Y. Laser wire-feed metal additive manufacturing of the Al alloy. Opt. Laser Technol. 2021, 134, 106627. [Google Scholar] [CrossRef]
- Demir, A.G. Micro laser metal wire deposition for additive manufacturing of thin-walled structures. Opt. Lasers Eng. 2018, 100, 9–17. [Google Scholar] [CrossRef]
- Mbodj, N.G.; Abuabiah, M.; Plapper, P.; El Kandaoui, M.; Yaacoubi, S. Bead Geometry Prediction in Laser-Wire Additive Manufacturing Process Using Machine Learning: Case of Study. Appl. Sci. 2021, 11, 11949. [Google Scholar] [CrossRef]
- Motta, M.; Demir, A.G.; Previtali, B. High-speed imaging and process characterization of coaxial laser metal wire deposition. Addit. Manuf. 2018, 22, 497–507. [Google Scholar]
- Kotar, M.; Fujishima, M.; Levy, G.; Govekar, E. Initial transient phase and stability of annular laser beam direct wire deposition. CIRP Ann. 2019, 68, 233–236. [Google Scholar] [CrossRef]
- Wang, Y.K.; Shi, S.H.; Fu, G.Y.; Li, C.S. Research on the Key Process Parameters in Direct Laser Deposition Using Coaxial Inside-Beam Wire Feeding. Appl. Mech. Mater. 2010, 43, 401–404. [Google Scholar]
- Shi, J.; Zhu, P.; Fu, G.; Shi, S. Geometry characteristics modeling and process optimization in coaxial laser inside wire cladding. Opt. Laser Technol. 2018, 101, 341–348. [Google Scholar] [CrossRef]
- Kelbassa, J.; Biber, A.; Wissenbach, K.; Loosten, J.H.; Gasser, A.; Pütsch, O.; Loosen, P.; Schleifenbaum, J. Influence of focal length on the laser metal deposition process with coaxial wire feeding. In Proceedings of the High-Power Laser Materials Processing: Applications, Diagnostics, and Systems VIII, San Francisco, CA, USA, 2–7 February 2019. [Google Scholar]
- Ji, S.; Liu, F.; Shi, T.; Fu, G.; Shi, S. Effects of Defocus Distance on Three-Beam Laser Internal Coaxial Wire Cladding. Chin. J. Mech. Eng. 2021, 34, 1–22. [Google Scholar] [CrossRef]
- Govekar, E.; Kuznetsov, A.; Jerič, A. Drop on demand generation from a metal wire by means of an annular laser beam. J. Mater. Process. Technol. 2016, 227, 59–70. [Google Scholar] [CrossRef] [Green Version]
- Kotar, M.; Govekar, E. The influence of the workpiece illumination proportion in annular laser beam wire deposition process. Procedia CIRP 2018, 74, 228–232. [Google Scholar] [CrossRef]
- Donadello, S.; Motta, M.; Demir, A.G.; Previtali, B. Coaxial laser triangulation for height monitoring in laser metal deposition. Procedia CIRP 2018, 74, 144–148. [Google Scholar] [CrossRef]
- Becker, D.; Boley, S.; Eisseler, R.; Stehle, T.; Möhring, H.-C.; Onuseit, V.; Hoßfeld, M.; Graf, T. Influence of a closed-loop controlled laser metal wire deposition process of S Al 5356 on the quality of manufactured parts before and after subsequent machining. Prod. Eng. Res. Dev. 2021, 15, 489–507. [Google Scholar] [CrossRef]
- Garmendia, I.; Pujana, J.; Lamikiz, A.; Madarieta, M.; Leunda, J. Structured light-based height control for laser metal deposition. J. Manuf. Process. 2019, 42, 20–27. [Google Scholar] [CrossRef]
- Wu, M.J.; Shi, S.H.; Fu, G.Y.; Liu, Y. Process Parameters Control of Deposition of Hollow Cylindrical Part with Internal Wire Feeding through a Hollow Laser Beam. Appl. Mech. Mater. 2013, 419, 305–309. [Google Scholar] [CrossRef]
- Leyens, C.; Beyer, E. Innovations in laser cladding and direct laser metal deposition. In Laser Surface Engineering; Lawrence, J., Waugh, D.G., Eds.; Woodhead Publishing: Sawston, Cambridge, UK, 2015; pp. 181–192. [Google Scholar]
- Townsend, A.; Senin, N.; Blunt, L.; Leach, R.K.; Taylor, J.S. Surface texture metrology for metal additive manufacturing: A review. Precis. Eng. 2016, 46, 34–47. [Google Scholar] [CrossRef] [Green Version]
- Nagalingam, A.P.; Vohra, M.S.; Kapur, P.; Yeo, S.H. Effect of Cut-Off, Evaluation Length, and Measurement Area in Profile and Areal Surface Texture Characterization of As-Built Metal Additive Manufactured Components. Appl. Sci. 2021, 11, 5089. [Google Scholar] [CrossRef]
- Flores, J.O.N.; Garmendia Saez, I.; Cabanes Axpe, I. Thermal monitoring and control by infrared camera in the manufacture of parts with laser metal deposition. DYNAII 2020, 95, 360–364. [Google Scholar] [CrossRef]




| Alloy | Part | Alloying Elements by Mass Percentage |
|---|---|---|
| AISI 304 | Substrate | C ≤ 0.07; Si ≤ 1.00; Mn ≤ 2.00; P ≤ 0.50; S ≤ 0.02; Cr 17.50–19.50; Ni 8.00–10.50 |
| AISI 316L | Wire | C ≤ 0.03; Si 0.65–1.20; Mn 1.00–2.50; P ≤ 0.03; S ≤ 0.02; Cr 18.00–20.00; Ni 11.00–14.00 |
| AlSi1MgMn | Substrate | Si 0.70–1.30; Fe ≤ 0.50; Cu ≤ 0.10; Mn 0.40–1.00; Mg 0.60–1.20; Cr 0.20; Zn 0.20; Ti 0.10 |
| AlMg4,5MnZr | Wire | Si ≤ 0.25; Fe ≤ 0.40; Cu ≤ 0.05; Mn 0.70–1.10; Mg 4.50–5.20; Cr 0.05–0.25; Zn 0.25; Ti ≤ 0.15; Zr 0.10–0.20 |
| Material | Laser Power in W | Wire Speed in m min−1 | Traverse Speed in m min−1 |
|---|---|---|---|
| Aluminum | 2700; 3200; 3700 | 1–8; in 1 m min−1 steps | 1–4; in 1 m min−1 steps |
| Stainless steel | 1200; 1700; 2200 | 0.4–2.0; in 0.4 m min−1 steps | 0.4–2.0; in 0.4 m min−1 steps |
| Material | Laser Power in W | Wire Speed in m min−1 | Traverse Speed in m min−1 |
|---|---|---|---|
| Aluminum | 3100; 3250; 3400; 3550; 3700 | 3; 3.5; 4; 4.5; 5 | 1; 1.5; 2; 2.5; 3; 3.5; 4 |
| Stainless steel | 1300; 1700; 2100 | 0.7; 1; 1.3 | 0.7; 1; 1.3 |
| Material | Laser Power in W | Laser Power Decay Strategy | Speed Ratio | Height Increment in mm |
|---|---|---|---|---|
| Aluminum | 3700 | −150 W for each layer from layer 4 to layer 9 | 2.0 | 0.46; 0.51; 0.56 |
| 2.25 | 0.54; 0.59; 0.64 | |||
| 2.5 | 0.63; 0.68; 0.73 | |||
| Stainless steel | 1500 | −25 W for each layer from layer 4 to layer 9 | 1.0 | 0.25; 0.30; 0.35 |
| 1.1 | 0.28; 0.33; 0.38 | |||
| 1.2 | 0.30; 0.35; 0.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zapata, A.; Bernauer, C.; Stadter, C.; Kolb, C.G.; Zaeh, M.F. Investigation on the Cause-Effect Relationships between the Process Parameters and the Resulting Geometric Properties for Wire-Based Coaxial Laser Metal Deposition. Metals 2022, 12, 455. https://doi.org/10.3390/met12030455
Zapata A, Bernauer C, Stadter C, Kolb CG, Zaeh MF. Investigation on the Cause-Effect Relationships between the Process Parameters and the Resulting Geometric Properties for Wire-Based Coaxial Laser Metal Deposition. Metals. 2022; 12(3):455. https://doi.org/10.3390/met12030455
Chicago/Turabian StyleZapata, Avelino, Christian Bernauer, Christian Stadter, Cara G. Kolb, and Michael F. Zaeh. 2022. "Investigation on the Cause-Effect Relationships between the Process Parameters and the Resulting Geometric Properties for Wire-Based Coaxial Laser Metal Deposition" Metals 12, no. 3: 455. https://doi.org/10.3390/met12030455
APA StyleZapata, A., Bernauer, C., Stadter, C., Kolb, C. G., & Zaeh, M. F. (2022). Investigation on the Cause-Effect Relationships between the Process Parameters and the Resulting Geometric Properties for Wire-Based Coaxial Laser Metal Deposition. Metals, 12(3), 455. https://doi.org/10.3390/met12030455






