A Study of Physical Modeling and Mathematical Modeling on Inclusion Behavior in a Planar Flow Casting Process
Abstract
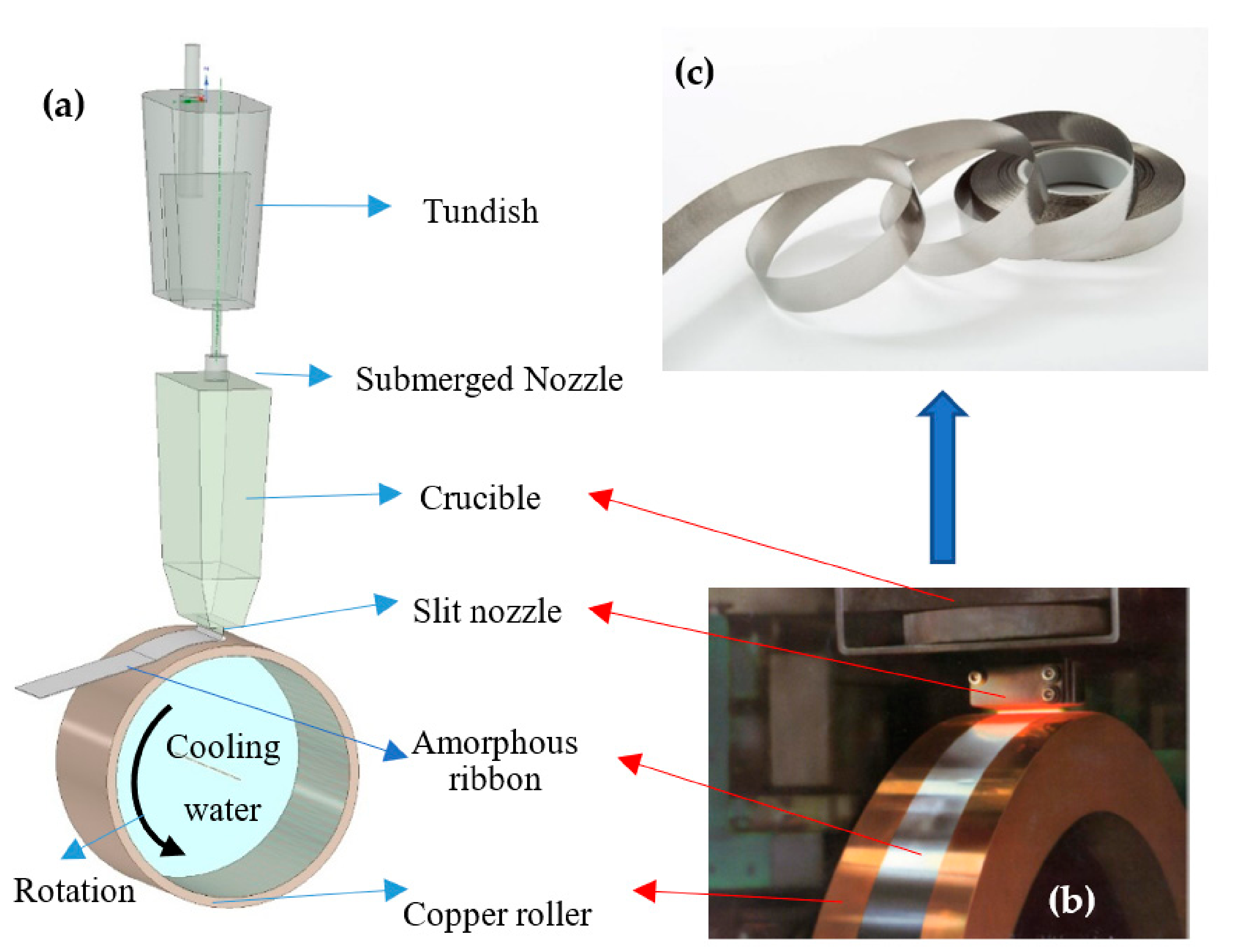
:1. Introduction
- Inclusions in the molten master alloy. In the manufacturing process, the inclusion particles in the molten alloy can collide into nodules on the inner wall during a long casting cycle, especially at the nozzle slit with the width of 0.2–1 mm, which could form scratches or defects on the amorphous ribbon and decrease the corrosion resistance performance, even causing serious nozzle slit clogging, interrupting production [8,9,10,11].
- The homogenization of flow field and melt temperature in the long-term and continuous production process. The superheat of melt affects the ribbon’s quality and production to a large extent [8,9,10,11]. Excessively high superheat could lower the cooling rate, in which case, the amorphous structure would not form. On the contrary, the low melt temperature could lead to an abnormal temperature gradient of melt in the nozzle slit and the puddle [1,12,13].
- Applying Lorenz force to control the flow and inclusions behavior. It has been reported that an electromagnetic braking field can be employed to adjust the melt flow, temperature distribution, inclusion floating, and solidification, improving the product quality by enhancing the stability and continuity in the continuous casting process [14,15,16,17].
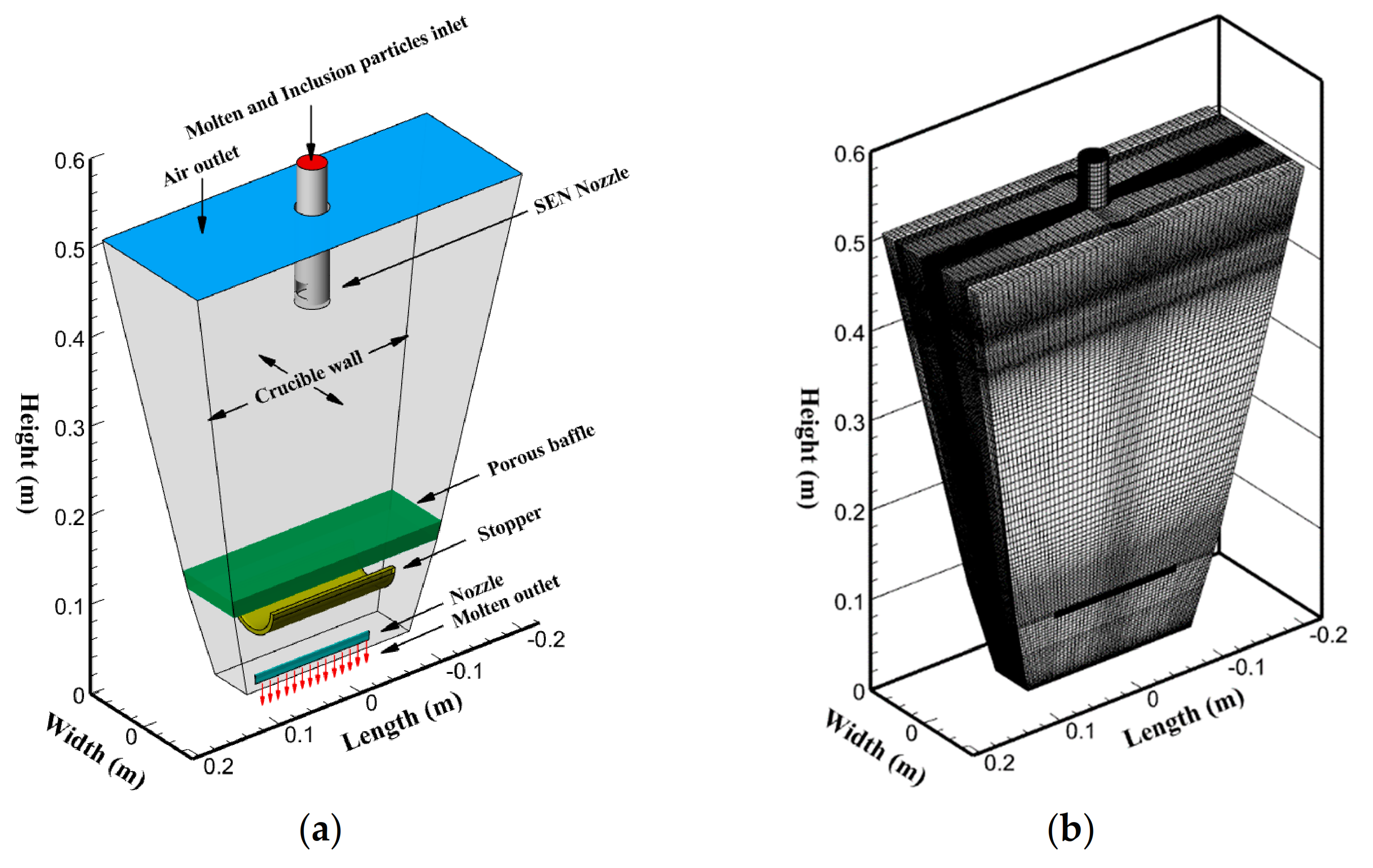
2. Model Description
3. Results and Discussion
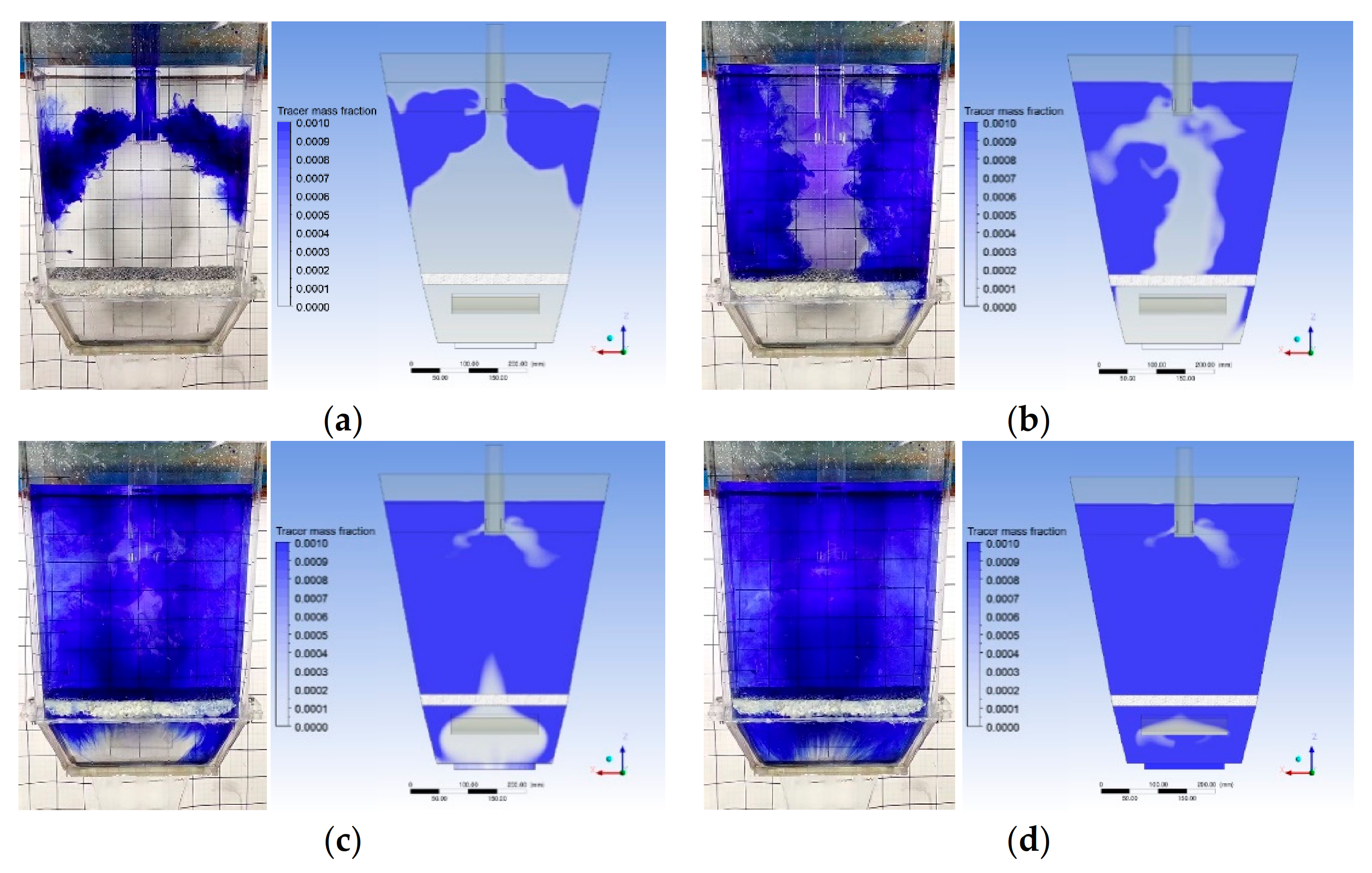
3.1. Model Validation
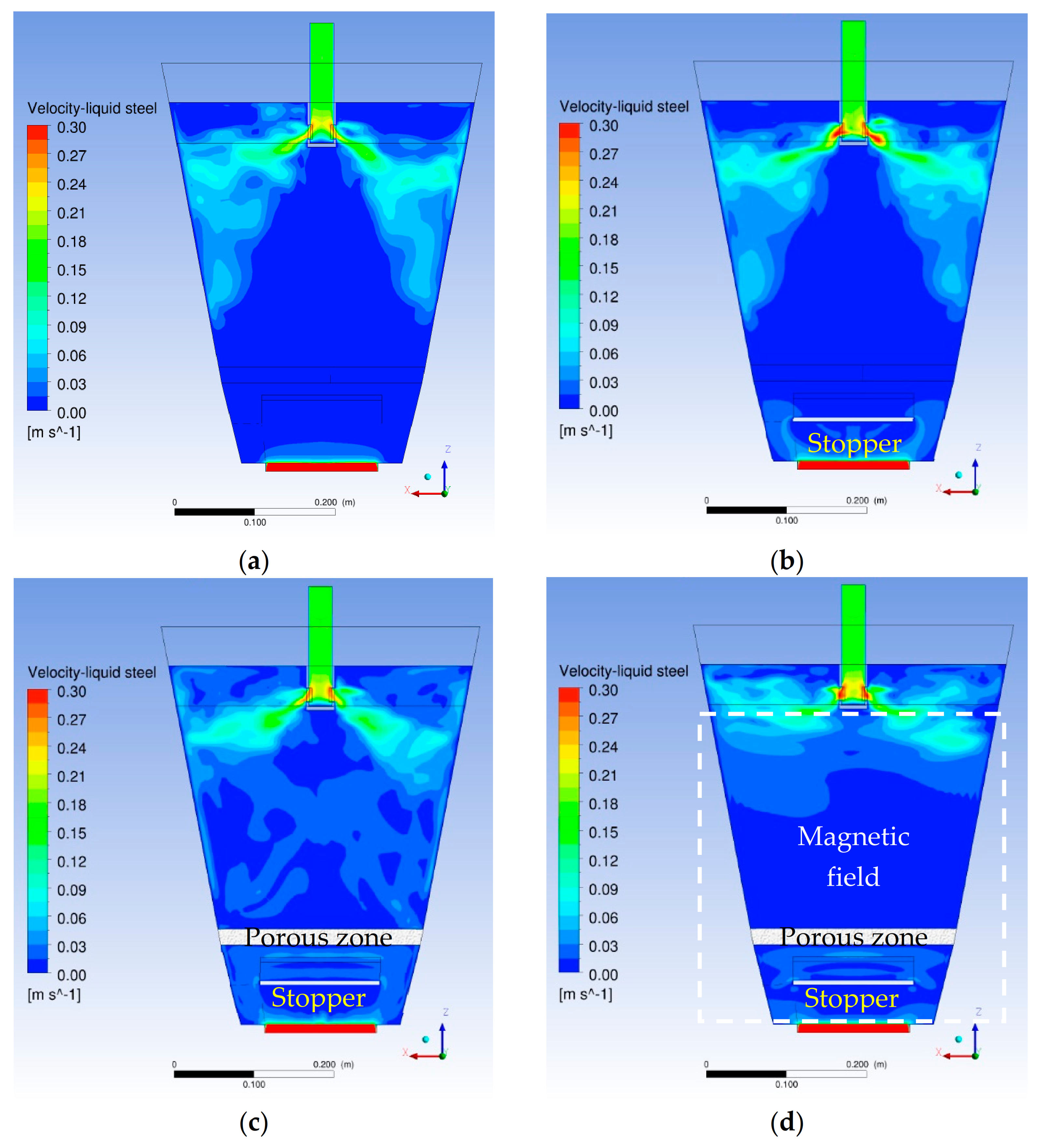
3.2. Flow Field Distribution
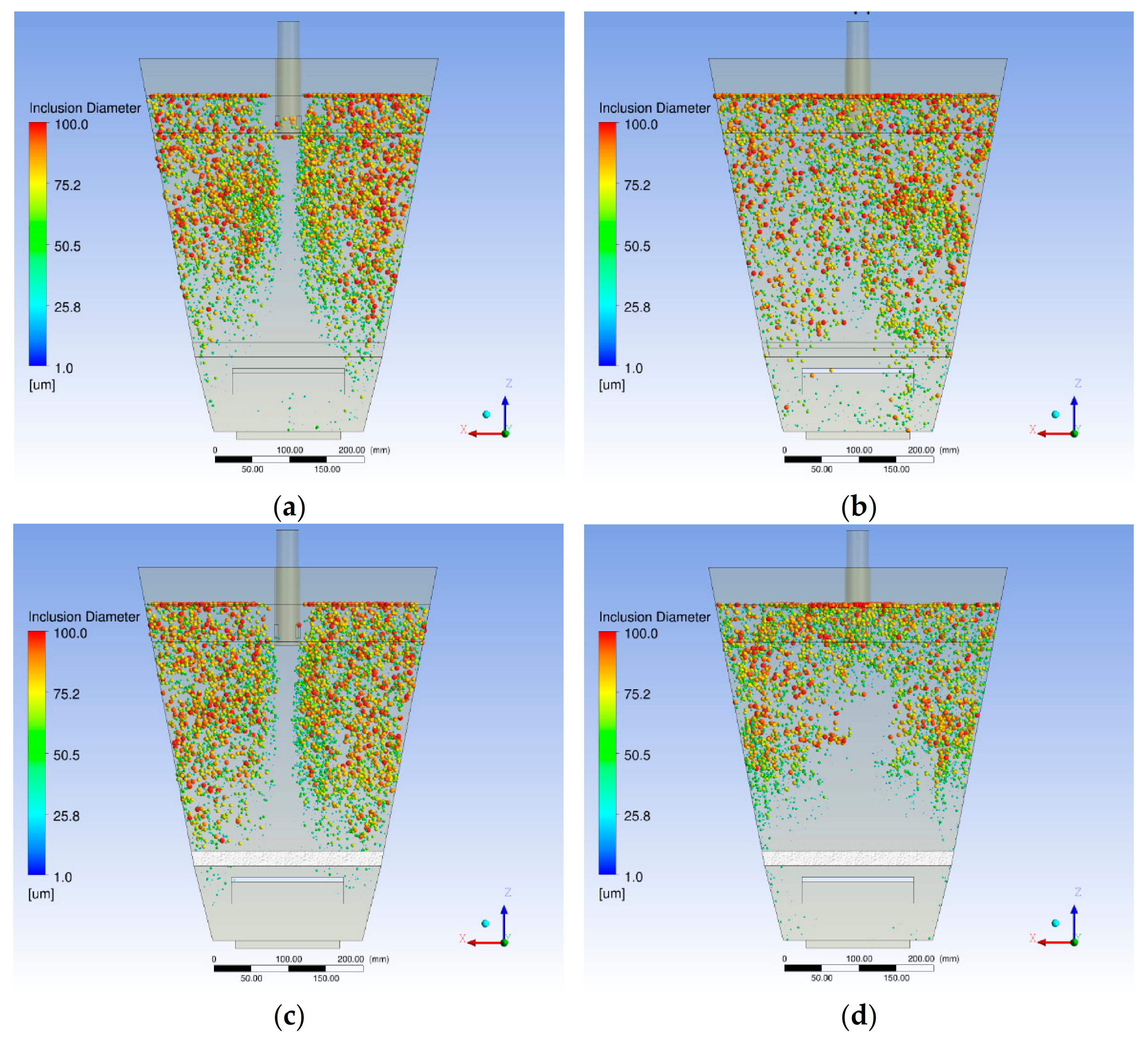
3.3. Inclusion Behavior and Removal Ratio
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lavernia, E.J.; Srivatsan, T.S. The rapid solidification processing of materials: Science, principles, technology, advances, and applications. J. Mater. Sci. 2010, 45, 287–325. [Google Scholar] [CrossRef]
- Shibuya, K. Production and Magnetic-Properties of Fe-B-Si Amorphous Alloy Ribbons: A Review. Mater. Sci. Eng. A 1994, 181, 1435–1439. [Google Scholar] [CrossRef]
- Jacobson, L.A.; McKittrick, J. Rapid solidification processing. Mater. Sci. Eng. R 1994, 11, 355–408. [Google Scholar] [CrossRef]
- Gutierrez, E.M.; Szekely, J. A mathematical model of the planar flow melt spinning process. Met. Mater. Trans. A 1986, 17, 695–703. [Google Scholar] [CrossRef]
- Takeshita, K.; Shingu, P.H. An Analysis of the Ribbon Formation Process by the Single Roller Rapid Solidification Technique. Trans. Jpn. Inst. Met. 1983, 24, 529–536. [Google Scholar] [CrossRef] [Green Version]
- Yu, H. A fluid mechanics model of the planar flow melt spinning process under low reynolds number conditions. Met. Mater. Trans. A 1987, 18, 557–563. [Google Scholar] [CrossRef]
- Geoffroy, O. Soft Nanocrystalline Alloys (Melt Spun). In New Magnetic Materials and Their Functions” and Workshop on Advanced Magnetic Materials, Cluj-Napoca, Romania, 9–18 September 2007; STUDIA UNIVERSITATIS: Cluj-Napoca, Romania, 2007; p. 49. [Google Scholar]
- Li, B.-S.; Chen, W.-Z.; Zhao, Y.-L.; Zhao, P. Evolution and control of nonmetallic inclusions in FeSiB alloy. J. Iron Steel Res. Int. 2020, 27, 588–597. [Google Scholar] [CrossRef]
- Zuo, Y.; Wang, S.L.; Huang, Y.; Wang, S.X. Corrosion Resistance of Fe-Based Bulk Amorphous Alloy with Sulfide Inclusion. In Chinese Materials Conference; Springer Science and Business Media LLC.: Singapore, 2018; pp. 309–318. [Google Scholar]
- Cox, B.L. Planar-Flow Melt Spinning: Process Dynamics and Defect Formation. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 2011. [Google Scholar]
- Su, Y.-G.; Chen, F.; Wu, C.-Y.; Chang, M.-H.; Chung, C.-A. Effects of Manufacturing Parameters in Planar Flow Casting Process on Ribbon Formation and Puddle Evolution of Fe–Si–B Alloy. ISIJ Int. 2015, 55, 2383–2390. [Google Scholar] [CrossRef] [Green Version]
- Byrne, C.J.; Kueck, A.M.; Baker, S.P.; Steen, P.H. In situ manipulation of cooling rates during planar-flow melt spinning processing. Mater. Sci. Eng. A 2007, 459, 172–181. [Google Scholar] [CrossRef]
- Kramer, M.; Mecco, H.; Dennis, K.; Vargonova, E.; McCallum, R.; Napolitano, R.E. Rapid solidification and metallic glass formation—Experimental and theoretical limits. J. Non-Cryst. Solids 2007, 353, 3633–3639. [Google Scholar] [CrossRef]
- Yu, H.; Wang, B.; Li, H.; Li, J. Influence of electromagnetic brake on flow field of liquid steel in the slab continuous casting mold. J. Mater. Process. Technol. 2008, 202, 179–187. [Google Scholar]
- Cho, S.-M.; Thomas, B.G. Electromagnetic Forces in Continuous Casting of Steel Slabs. Metals 2019, 9, 471. [Google Scholar] [CrossRef] [Green Version]
- Vakhrushev, A.; Kharicha, A.; Liu, Z.; Wu, M.; Ludwig, A.; Nitzl, G.; Tang, Y.; Hackl, G.; Watzinger, J. Electric Current Distribution During Electromagnetic Braking in Continuous Casting. Met. Mater. Trans. A 2020, 51, 2811–2828. [Google Scholar] [CrossRef]
- Bichi, A.; Smith, W.; Wissink, J. Solidification and downstream meniscus prediction in the planar-flow spin casting process. Chem. Eng. Sci. 2008, 63, 685–695. [Google Scholar] [CrossRef]
- Bussmann, M.; Mostaghimi, J.; Kirk, D.; Graydon, J. A numerical study of steady flow and temperature fields within a melt spinning puddle. Int. J. Heat Mass Transf. 2002, 45, 3997–4010. [Google Scholar] [CrossRef]
- Wu, S.; Chen, C.; Hwang, W.; Yang, C. Analysis for melt puddle in the planar flow casting process—A mathematical modelling study. Appl. Math. Model. 1992, 16, 394–403. [Google Scholar] [CrossRef]
- Chen, C.-W.; Hwang, W.-S. A Modified Free Surface Treatment for the Modeling of Puddle Formation in Planar Flow Casting Process. ISIJ Int. 1995, 35, 393–401. [Google Scholar] [CrossRef]
- Chen, C.-W.; Hwang, W.-S. A three-dimensional fluid flow model for puddle formation in the single-roll rapid solidification process. Appl. Math. Model. 1995, 19, 704–712. [Google Scholar] [CrossRef]
- Su, Y.-G.; Chen, F.; Chang, C.-M.; Wu, C.-Y.; Chang, M.-H.; Chung, C.-A. Tuning the Planar-Flow Melt-Spinning Process Subject to Operability Conditions. JOM 2014, 66, 1277–1286. [Google Scholar] [CrossRef]
- Su, Y.-G.; Chen, F.; Wu, C.-Y.; Chang, M.-H. Simulation for the Effect of Wetting Conditions of Melt Puddle on the Fe–Si–B Ribbon Alloy in the Planar-Flow Melt-Spinning Process. ISIJ Int. 2017, 57, 100–106. [Google Scholar] [CrossRef] [Green Version]
- Majumdar, B.; Sowjanya, M.; Srinivas, M.; Babu, D.A.; Reddy, T.K.K. Issues on Puddle Formation During Rapid Solidification of Fe–Si–B–Nb–Cu Alloy Using Planar Flow Melt Spinning Process. Trans. Indian Inst. Met. 2012, 65, 841–847. [Google Scholar] [CrossRef]
- Sowjanya, M.; Reddy, T.K.K. Cooling wheel features and amorphous ribbon formation during planar flow melt spinning process. J. Mater. Process. Technol. 2014, 214, 1861–1870. [Google Scholar] [CrossRef]
- Liu, H.; Chen, W.; Qiu, S.; Liu, G. Numerical Simulation of Initial Development of Fluid Flow and Heat Transfer in Planar Flow Casting Process. Met. Mater. Trans. A 2009, 40, 411–429. [Google Scholar] [CrossRef]
- Liu, H.; Chen, W.; Chen, Y.; Liu, G. Thermal Deformation Analysis of the Rotating Roller in Planar Flow Casting Process. ISIJ Int. 2010, 50, 1431–1440. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; He, C. Three-dimensional transient temperature analysis of cooling roller for preparing amorphous ribbon. J. Non-Crystalline Solids 2018, 481, 276–281. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; He, C. Temperature and Thermal Expansion Analysis of the Cooling Roller Based on the Variable Heat Flux Boundary Condition. JOM 2018, 70, 855–860. [Google Scholar] [CrossRef]
- Ansys, I. Ansys Fluent Theory Guide Version; RANSYS Inc.: Canonsburg, PA, USA, 2019; pp. 193–195. [Google Scholar]
- Chaudhary, R.; Ji, C.; Thomas, B.; Vanka, S.P. Transient Turbulent Flow in a Liquid-Metal Model of Continuous Casting, Including Comparison of Six Different Methods. Met. Mater. Trans. A 2011, 42, 987–1007. [Google Scholar] [CrossRef]
- Gregorc, J.; Kunavar, A.; Šarler, B. RANS versus Scale Resolved Approach for Modeling Turbulent Flow in Continuous Casting of Steel. Metals 2021, 11, 1140. [Google Scholar] [CrossRef]
- Li, D.; Lu, Z. The effects of aging on the cyclical thermal shock response of a copper-beryllium alloy as a substrate of cooling wheel in planar flow casting process. Mater. Res. Express 2020, 7, 116511. [Google Scholar] [CrossRef]
- Andrzejewski, P.; Köhler, K.-U.; Pluschkell, W. Model investigations on the fluid flow in continuous casting moulds of wide dimensions. Steel Res. 1992, 63, 242–246. [Google Scholar] [CrossRef]
- Jin, X.; Chen, D.; Xie, X.; Shen, J.; Long, M. Investigation on Water Model for Fluid Flow in Slab Continuous Casting Mold with Consideration of Solidified Process. Steel Res. Int. 2013, 84, 31–39. [Google Scholar] [CrossRef]
- Jin, X.; Chen, D.F.; Zhang, D.J.; Xie, X.; Bi, Y.Y. Water model study on fluid flow in slab continuous casting mould with solidified shell. Ironmak. Steelmak. 2011, 38, 155–159. [Google Scholar] [CrossRef]
- Zhang, M.; Gu, H.; Huang, A.; Zhu, H.; Deng, C. Physical and mathematical modeling of inclusion removal with gas bottom-blowing in continuous casting tundish. J. Min. Met. Sect. B Met. 2011, 47, 37–44. [Google Scholar] [CrossRef]
- Liu, Z.; Li, B. Transient motion of inclusion cluster in vertical-bending continuous casting caster considering heat transfer and solidification. Powder Technol. 2016, 287, 315–329. [Google Scholar] [CrossRef]
- Zhang, K.-T.; Liu, J.-H.; Cui, H. Effect of Flow Field on Surface Slag Entrainment and Inclusion Adsorption in a Continuous Casting Mold. Steel Res. Int. 2019, 91, 2. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Water density (kg·m−3) | 998.2 |
| Water viscosity (Pa·s) | 0.001003 |
| Melt density (kg·m−3) | 7100 |
| Melt viscosity (Pa·s) | 0.0042 |
| Melt electrical conductivity (S·m−1) | 8.33 × 106 |
| Melt magnetic permeability (H·m−1) | 1.257 × 10−6 |
| Air density (kg·m−3) | 1.225 |
| Air viscosity (Pa·s) | 1.894 × 10−5 |
| Inclusion particle density (kg·m−3) | 2872 |
| Inclusion particle mass flow rate (kg·s−1) | 0.0002 |
| Boundary Conditions and Initial Conditions | Mass Fraction of Liquid | Mass and Momentum |
|---|---|---|
| Molten and inclusion particles inlet | ||
| Air outlet | ||
| SEN Nozzle wall | - | |
| Crucible wall | - | |
| Porous baffle | - | |
| Stopper wall | - | |
| Nozzle wall | - | |
| Molten outlet | ||
| Molten level | - | |
| Magnetic field | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Qiu, H.; He, Z.; Yu, Y.; Liu, H. A Study of Physical Modeling and Mathematical Modeling on Inclusion Behavior in a Planar Flow Casting Process. Metals 2022, 12, 606. https://doi.org/10.3390/met12040606
Liu Y, Qiu H, He Z, Yu Y, Liu H. A Study of Physical Modeling and Mathematical Modeling on Inclusion Behavior in a Planar Flow Casting Process. Metals. 2022; 12(4):606. https://doi.org/10.3390/met12040606
Chicago/Turabian StyleLiu, Yu, Hao Qiu, Zixu He, Yue Yu, and Heping Liu. 2022. "A Study of Physical Modeling and Mathematical Modeling on Inclusion Behavior in a Planar Flow Casting Process" Metals 12, no. 4: 606. https://doi.org/10.3390/met12040606
APA StyleLiu, Y., Qiu, H., He, Z., Yu, Y., & Liu, H. (2022). A Study of Physical Modeling and Mathematical Modeling on Inclusion Behavior in a Planar Flow Casting Process. Metals, 12(4), 606. https://doi.org/10.3390/met12040606






