Effect of Transverse Restraint on Welding Residual Stress in V-Groove Butt Welding
Abstract
:1. Introduction
2. Comparison of Two-Dimensional (2D) to Three-Dimensional (3D) Thermal Elastic–Plastic Analyses and Experiment
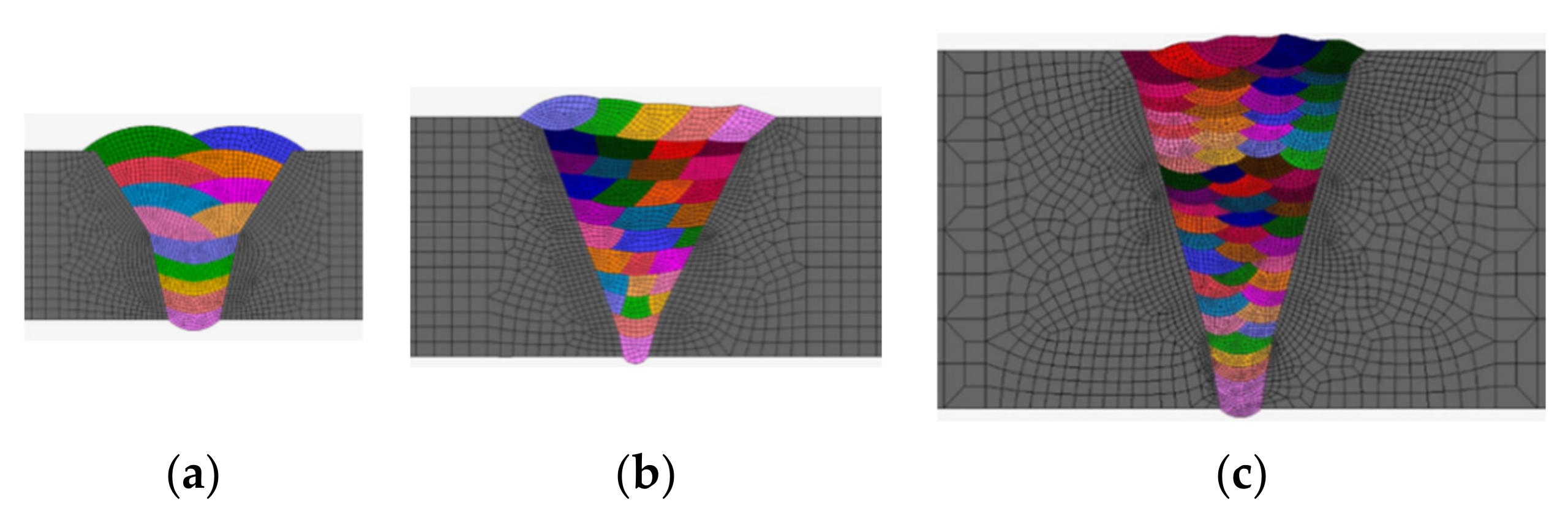
2.1. Experiment and Analysis Model
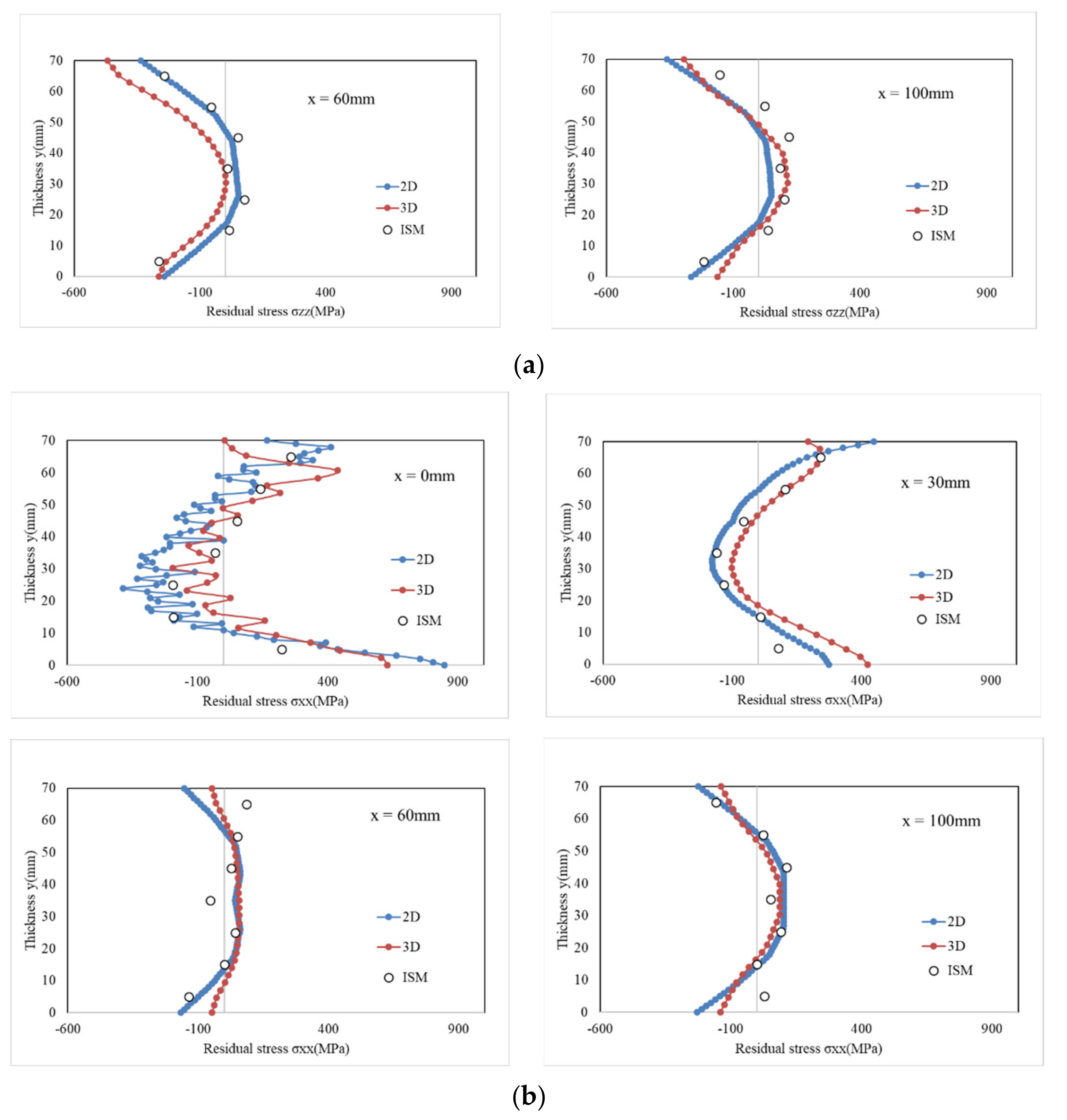
2.2. Comparison of Welding Residual Stress Obtained Using FE Analysis and ISM
3. Effect of Restraint on Residual Stress
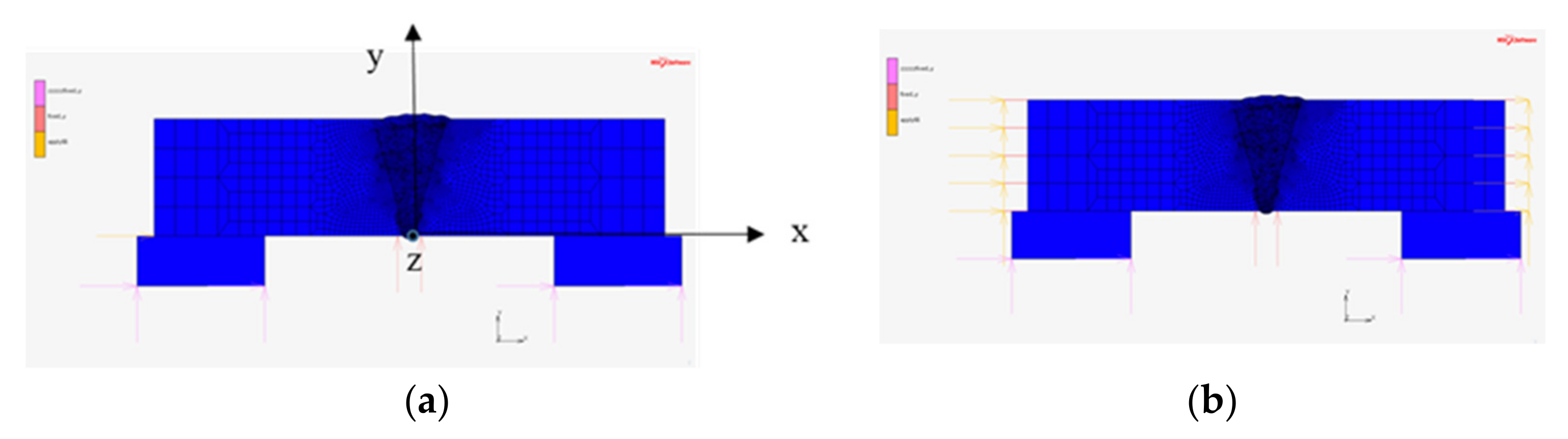
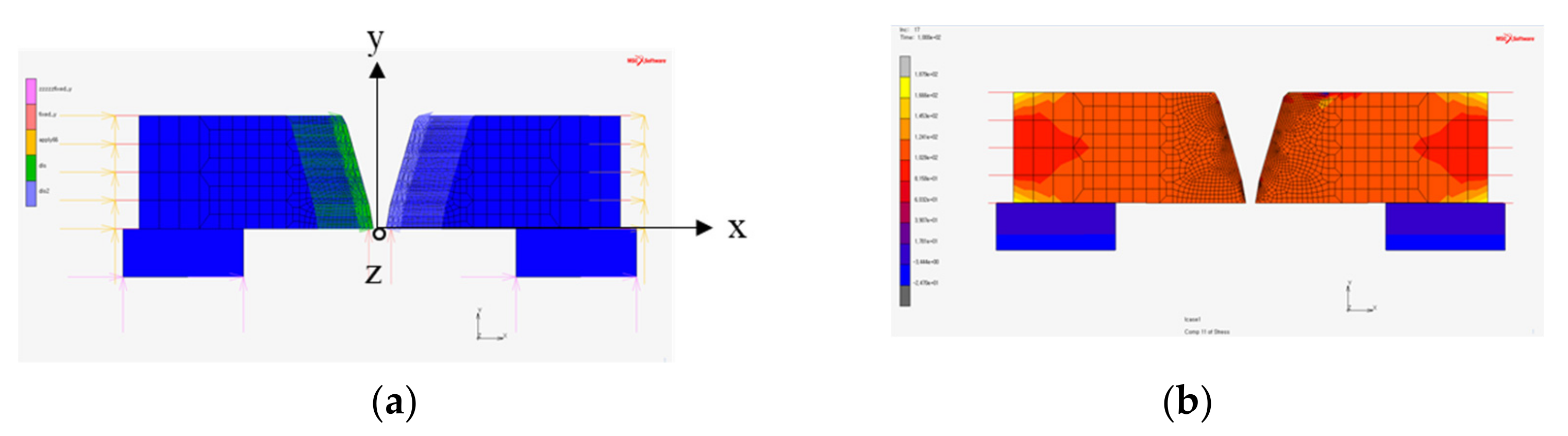
3.1. Model for Restraint Calculation
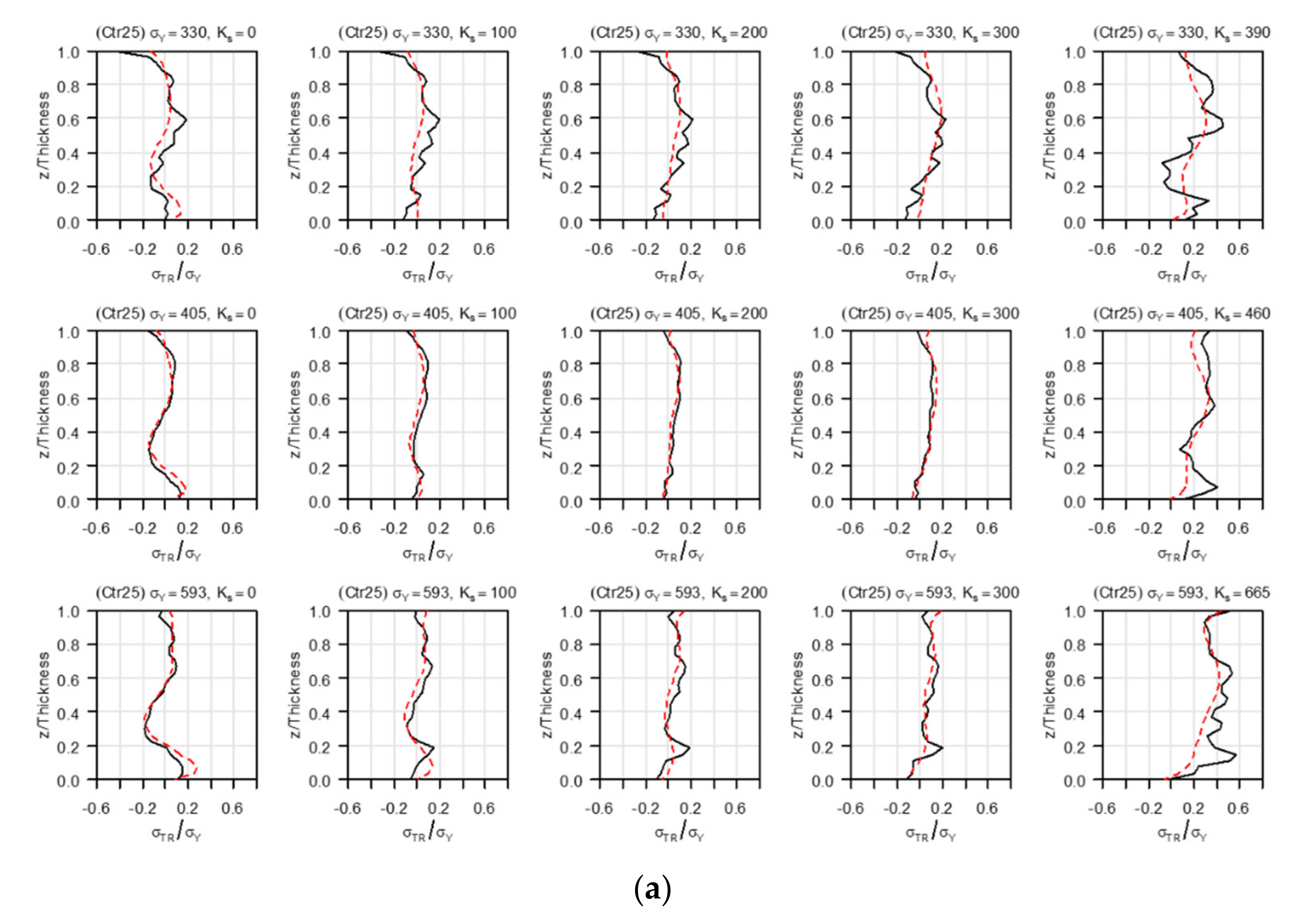
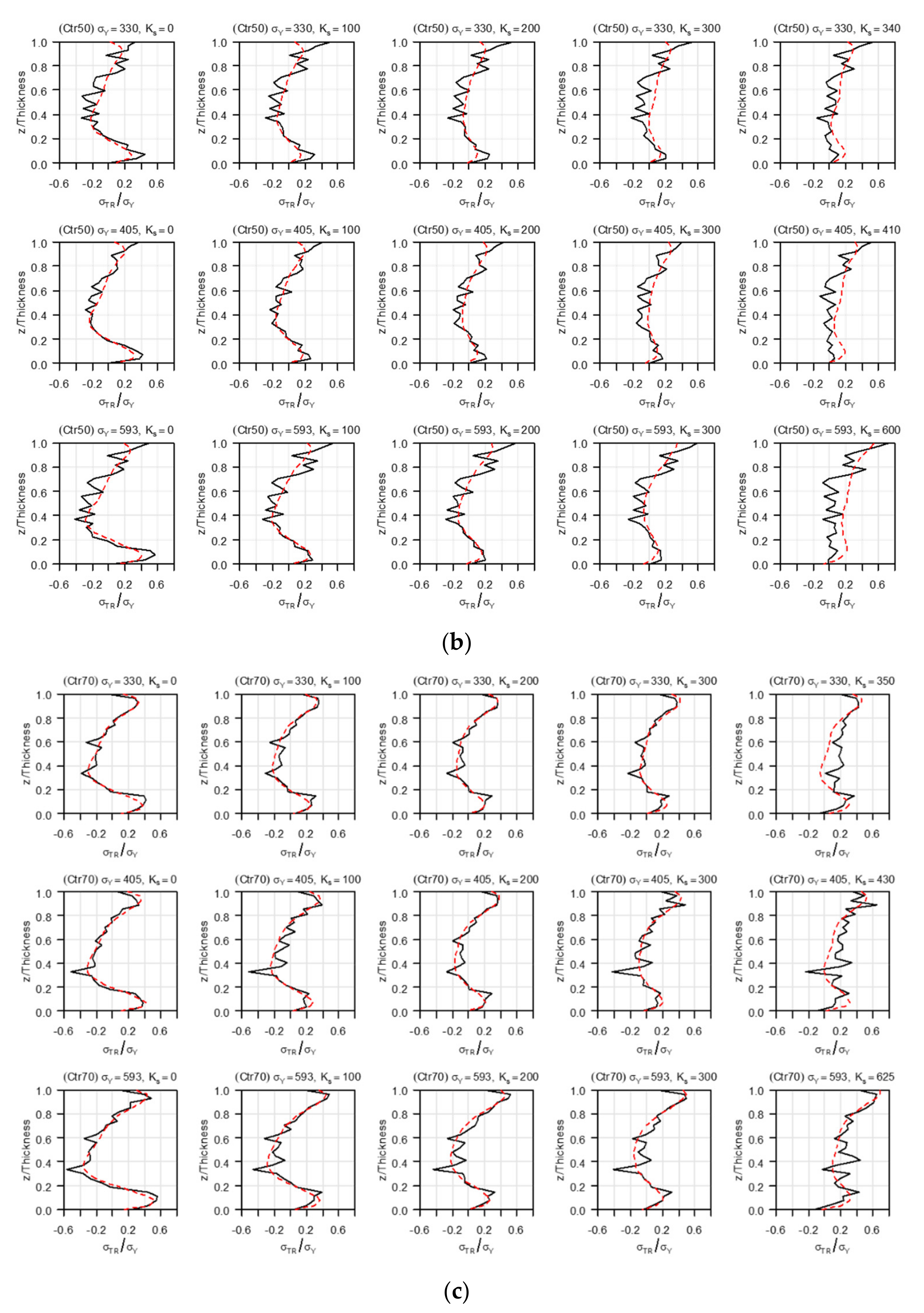
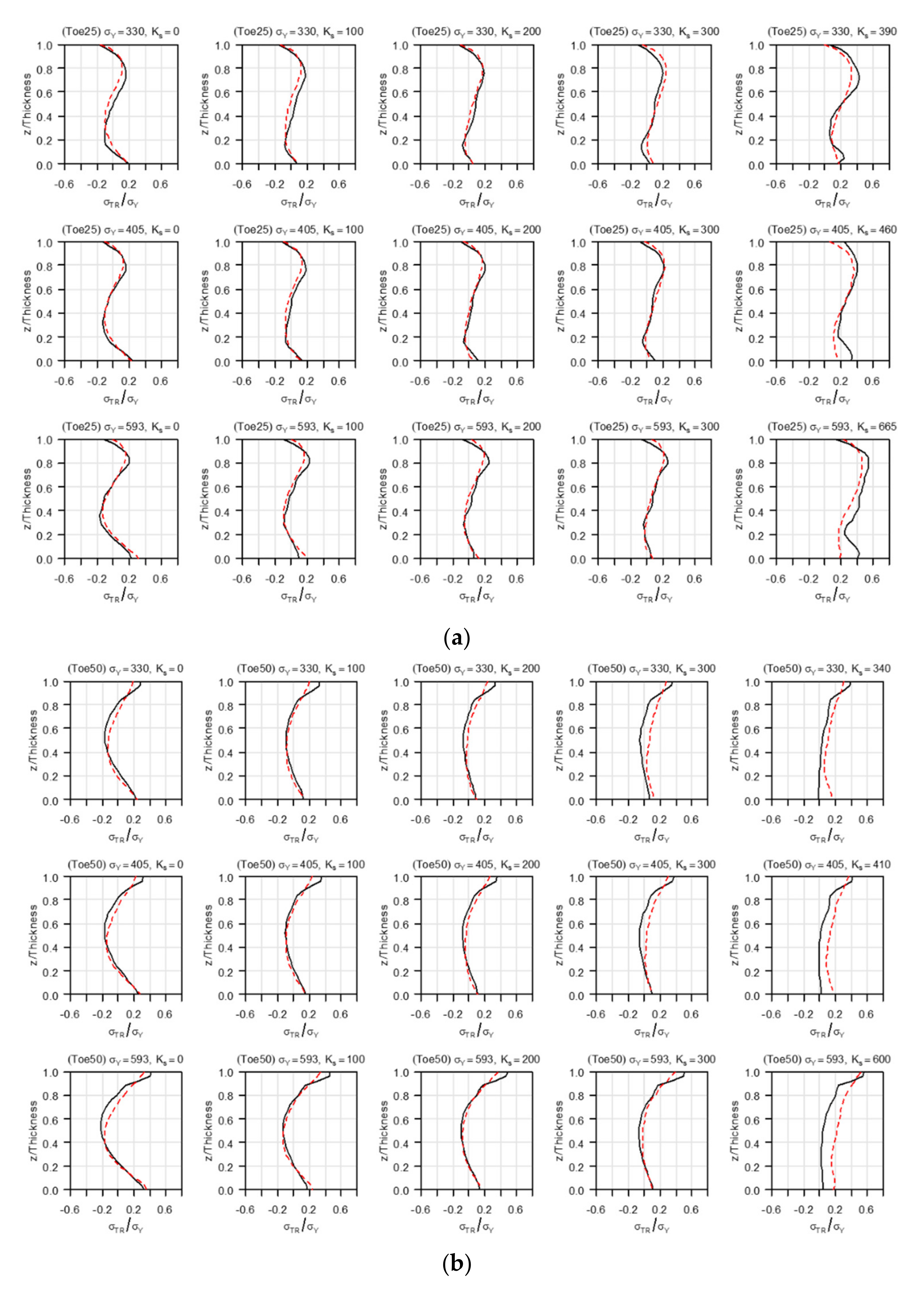
3.2. Effect of Restraint on Residual Welding Stress
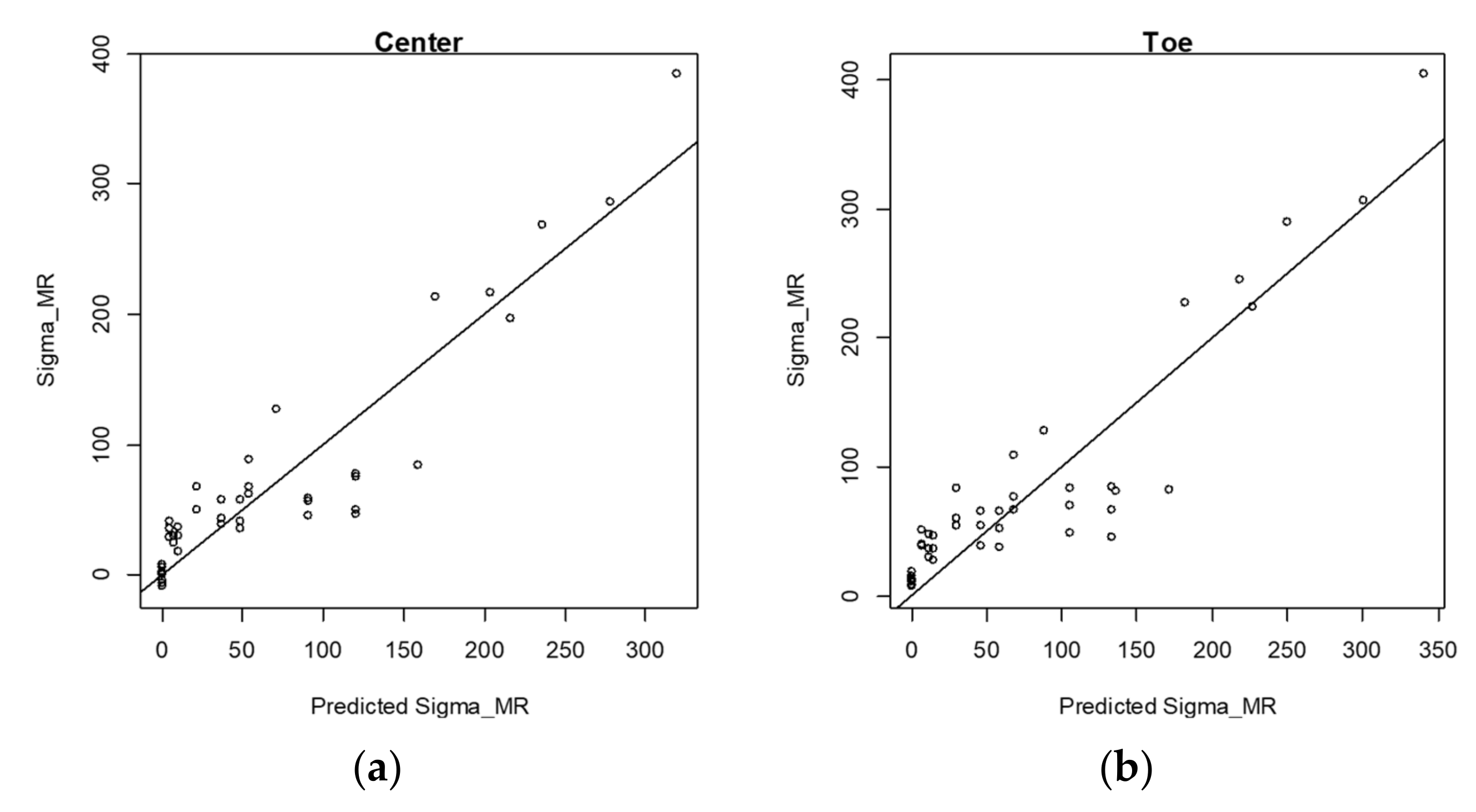
3.3. Prediction Equation and Discussion
4. Conclusions
- In this study, a 2D thermal elastic–plastic analysis that could minimize the analysis time was performed instead of a 3D thermal elastic–plastic analysis. The results of the 2D thermal elastic–plastic analysis were verified by comparing them with the results measured by the intrinsic strain diagram method and 3D thermal elastic–plastic analysis.
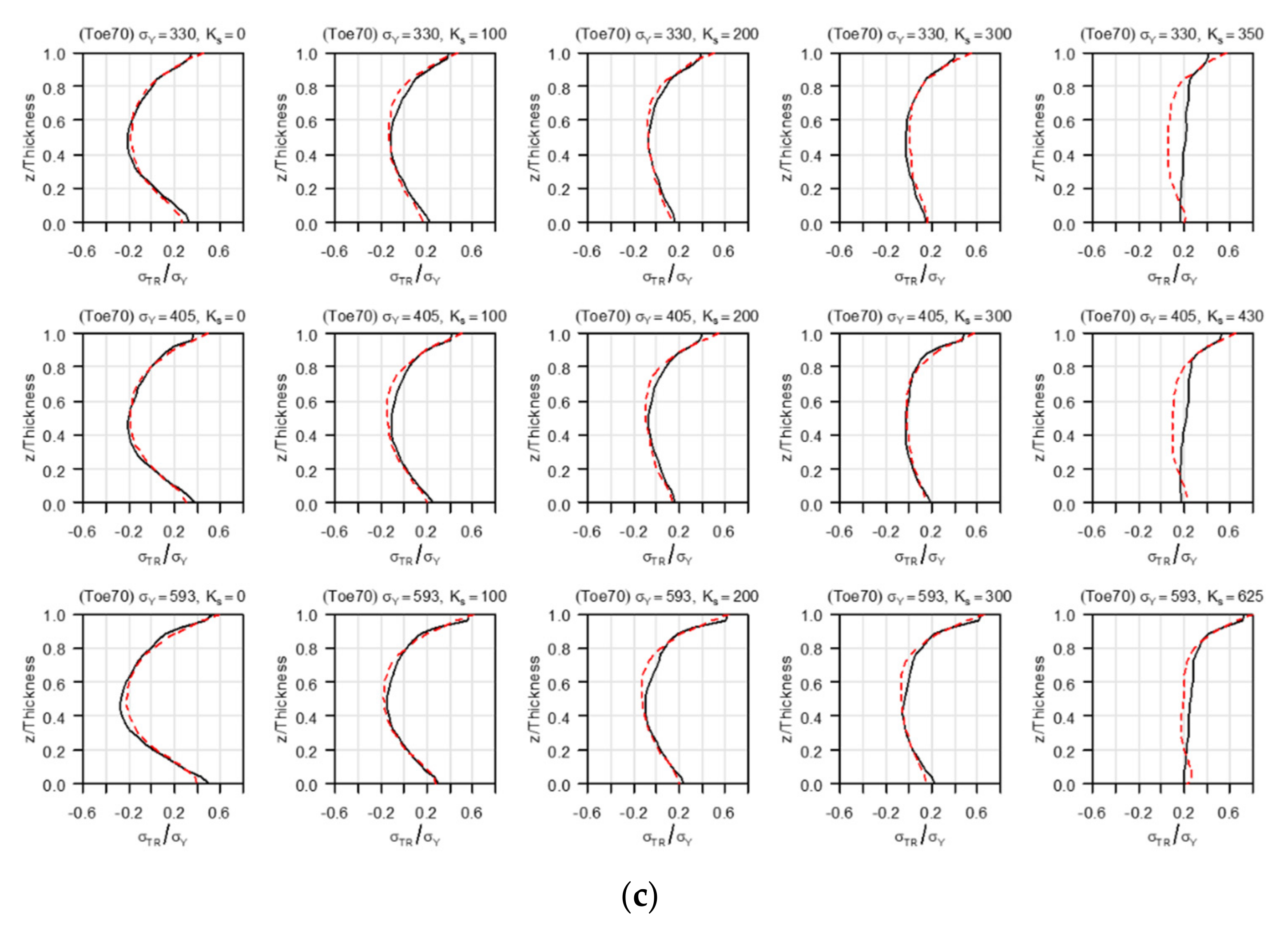
- The transverse restraint did not affect the magnitude and distribution of the residual stress in the weld line direction. However, the restraint conditions affected the size and distribution of the residual stress in the direction perpendicular to the weld line.
- Owing to the transversal restraint, the residual stress in the direction perpendicular to the weld line moved from the tensile to the compression direction in the first layer of the weld and moved in the tensile direction in the middle and final layers of the weld owing to the restraint. The change in residual stress was the largest in the middle of the weld.
- The magnitude of the yield stress of the member and the degree of restraint did not affect the overall shape of the residual stress distribution in the direction perpendicular to the weld line. Except for the final weld layer, most of the residual stress was less than half of the yield stress. However, under extreme constraint conditions (>300 MPa/mm), the residual stress exhibited an overall increase.
- The residual stress prediction formula according to the restraint was derived through regression analysis to predict the residual stress in the thickness direction at the center of the weld and the weld toe. The reliability analysis of the prediction results yielded the RMSEs of 101.6 and 55.93 for the welding center and the toe, respectively, and R2 of 72.12 and 86.19%, respectively. Moreover, high correlation between the thermal elastic–plastic analysis value and the predicted value was confirmed.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Masubuchi, K. Analysis of Welded Structures: Residual Stresses, Distortion, and Their Consequences; Elsevier: New York, NY, USA, 2013; Volume 33. [Google Scholar]
- Kihara, H.; Kusuda, T.; Iida, K.; Maeda, T.; Matsuoka, T. Effect of residual stresses on the behavior of brittle fracture propagation. J. Zosen Kiokai 1960, 108, 385–393. [Google Scholar] [CrossRef] [Green Version]
- An, G.B.; Woo, W.; Park, J.U.; Em, V. Comparison of crack-arrest fracture toughness between low and high heat-input thick weld specimens. Int. J. Fract. 2015, 194, 197–203. [Google Scholar] [CrossRef]
- Hadley, I.; Smith, S. Effects of Mechanical Loading on Residual Stress and Fracture: Part II—Validation of the BS 7910:2013 Rules. In Proceedings of the ASME 2014 Pressure Vessels and Piping Conference, Anaheim, CA, USA, 20–24 July 2014; Volume 1. Codes and Standards. [Google Scholar]
- Ueda, Y.; Yamakawa, T. Analysis of thermal elastic-plastic stress and strain during welding by finite element method. Jpn. Weld. Soc. Trans. 1971, 2, 90–100. [Google Scholar]
- Shibahara, M.; Ikushima, K. Development of analytical method for welding mechanics using idealized explicit FEM. Trans. JWRI 2010, 39, 384–386. [Google Scholar]
- Ueda, Y.; Kim, Y.C.; Yuan, M.G. A predicting method of welding residual stress using source of residual stress (report I): Characteristics of inherent strain (source of residual stress)(mechanics, strength & structural design). Trans. JWRI 1989, 18, 135–141. [Google Scholar]
- Luo, Y.; Murakawa, H.; Ueda, Y. Prediction of welding deformation and residual stress by elastic FEM based on inherent strain (report I): Mechanism of inherent strain production (mechanics, strength & structure design). Trans. JWRI 1997, 26, 49–57. [Google Scholar]
- Ma, N. An accelerated explicit method with a two-stage computation scheme for transient thermal stress and welding deformation. Trans. JWRI 2015, 44, 31–40. [Google Scholar]
- Dong, P.; Brust, F. Welding residual stresses and effects on fracture in pressure vessel and piping components: A millennium review and beyond. J. Press. Vessel. Technol. 2000, 122, 329–338. [Google Scholar] [CrossRef]
- Ha, Y.S.; Cho, S.H.; Jang, T.W. Development of welding distortion analysis method using residual strain as boundary condition. Mater. Sci. Forum 2008, 580–582, 649–654. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Hossain, S.; Truman, C.E.; Smith, D.J.; Pavier, M.J. A new procedure to measure near yield residual stresses using the deep hole drilling technique. Exp. Mech. 2009, 49, 595–604. [Google Scholar] [CrossRef]
- Woo, W.; An, G.; Kingston, E.; De Wald, A.; Smith, D.; Hill, M.R. Through-thickness distributions of residual stresses in two extreme heat-input thick welds: A neutron diffraction, contour method and deep hole drilling study. Acta Mater. 2013, 61, 3564–3574. [Google Scholar] [CrossRef]
- Ueda, Y.; Yuan, M. Prediction of residual stresses in butt welded plates using inherent strains. J. Eng. Mater. Technol. 1993, 115, 417–423. [Google Scholar] [CrossRef]
- Park, J.-U.; An, G.; Woo, W.; Choi, J.-H.; Ma, N. Residual stress measurement in an extra thick multi-pass weld using initial stress integrated inherent strain method. Mar. Struct. 2014, 39, 424–437. [Google Scholar] [CrossRef]
- Dong, P.; Hong, J.K. Analysis of IIW X/XV RSDP Phase I Round-Robin Residual Stress Results. Weld World 2002, 46, 24–31. [Google Scholar] [CrossRef]
- Janosch, J.J. IIW “Round Robin” Protocol for 3-Dimensional Welding Residual Stress and Distortion Prediction, IIW Doc. X/XIII/XV-RSDP-75-03; International Institude of Welding’s Report; International Institude: Paris, France, 2003. [Google Scholar]
- BMI. Investigation of Weld Residual Stresses and Local Post-Weld Heat Treatment; PVRC: Hong Kong, 2002. [Google Scholar]
- Wiesner, C.; Maddox, S.; Xu, W.; Webster, G.; Burdekin, F.; Andrews, R.; Harrison, J. Engineering critical analyses to BS 7910—the UK guide on methods for assessing the acceptability of flaws in metallic structures. Int. J. Press. Vessel. Pip. 2000, 77, 883–893. [Google Scholar] [CrossRef]
- Watanabe, M.; Satoh, K. Research on Intensity of Restraint and Reaction Stress in Welded Joints. J. Zosen Kiokai 1961, 1961, 349–358. [Google Scholar] [CrossRef]
- Watanabe, M.; Takagi, O.; Satoh, K.; Aso, F. External constraint and shrinkage of butt-welded joints in the erection of assemblies on building way. J. Zosen Kiokai 1958, 1958, 191–200. [Google Scholar] [CrossRef]
- Park, J.U.; An, G.; Woo, W. The effect of initial stress induced during the steel manufacturing process on the welding residual stress in multi-pass butt welding. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 129–140. [Google Scholar] [CrossRef]
- Park, J.; An, G.; Kim, S. The Effect of Welding-Pass Grouping on the Prediction Accuracy of Residual Stress in Multipass Butt Welding. Math. Probl. Eng. 2017, 2017, 7474020. [Google Scholar] [CrossRef]
- Satoh, K.; Ueda, Y.; Kihara, H. Recent trend of researches on restraint stresses and strains for weld cracking. Trans. JWRI 1972, 1, 53–68. [Google Scholar]
- Satoh, K. An analytical approach to the problem of restraint intensity in slit weld. Trans. JWRI 1972, 1, 69–76. [Google Scholar]
- Shin, S.-B.; Lee, D.-J.; Park, D.-H. A study on the evaluation of transverse residual stress at the multi-pass FCA butt weldment using FEA. J. Weld. Join. 2010, 28, 26–32. [Google Scholar] [CrossRef] [Green Version]
- Commission of design, analyses and structural strength of welded structures. Standardization for Temperature Distribution Prediction of the Arc Weld using FEA. Int. J. Korean Weld. Soc. 2005, 23, 497–503.
- Ikushima, K.; Shibahara, M. Large-scale non-linear analysis of residual stresses in multi-pass pipe welds by idealized explicit FEM. Weld. World 2015, 59, 839–850. [Google Scholar] [CrossRef]
- Goldak, J.; Chakravarti, A.; Bibby, M. A new finite element model for welding heat sources. Metall. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]

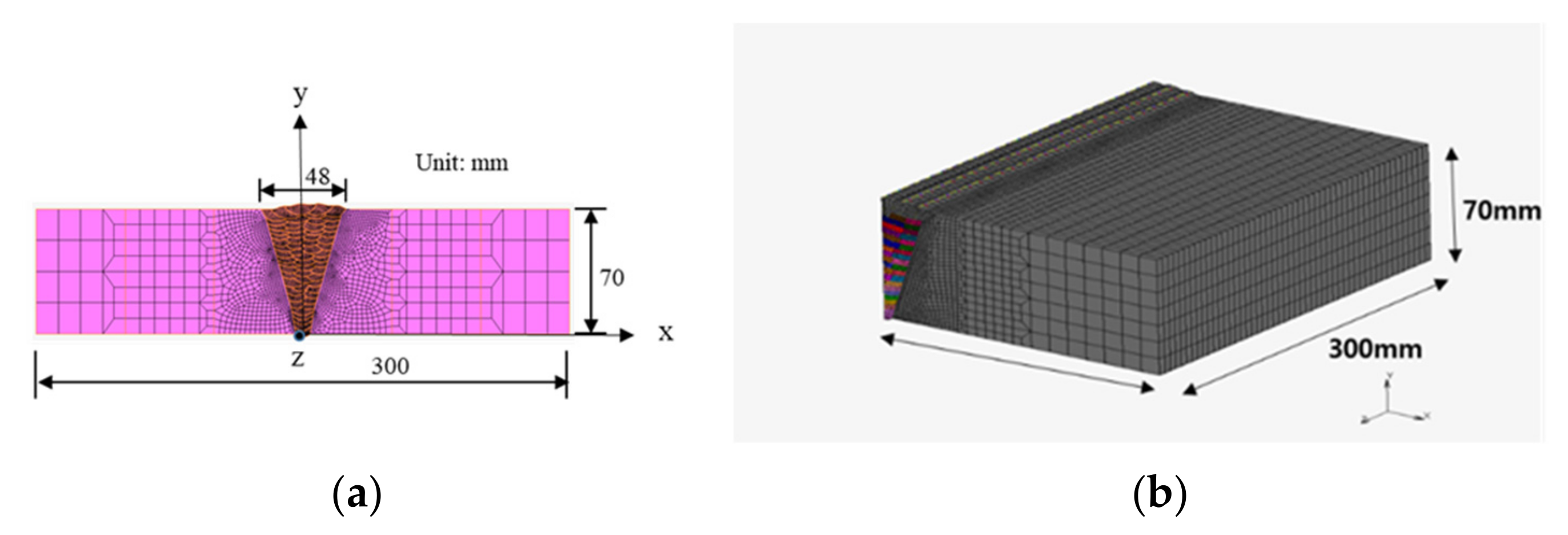

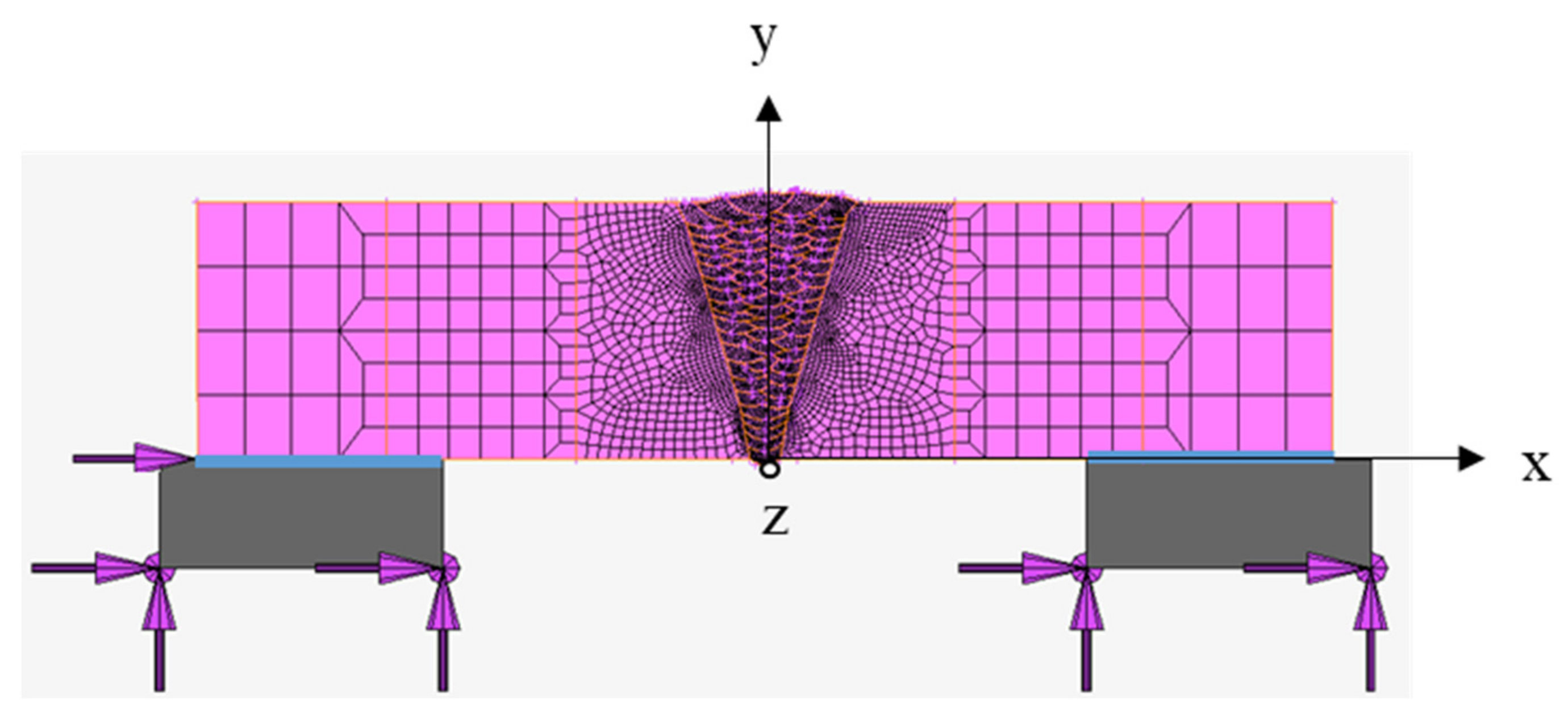
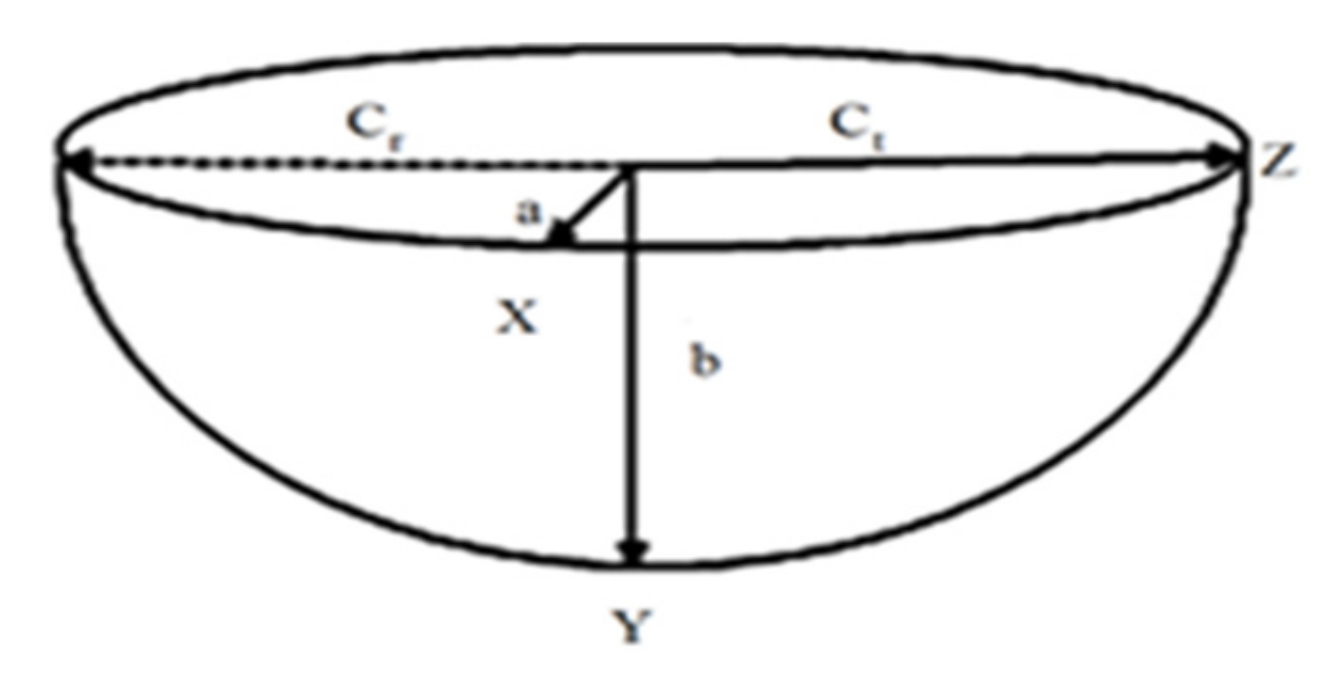
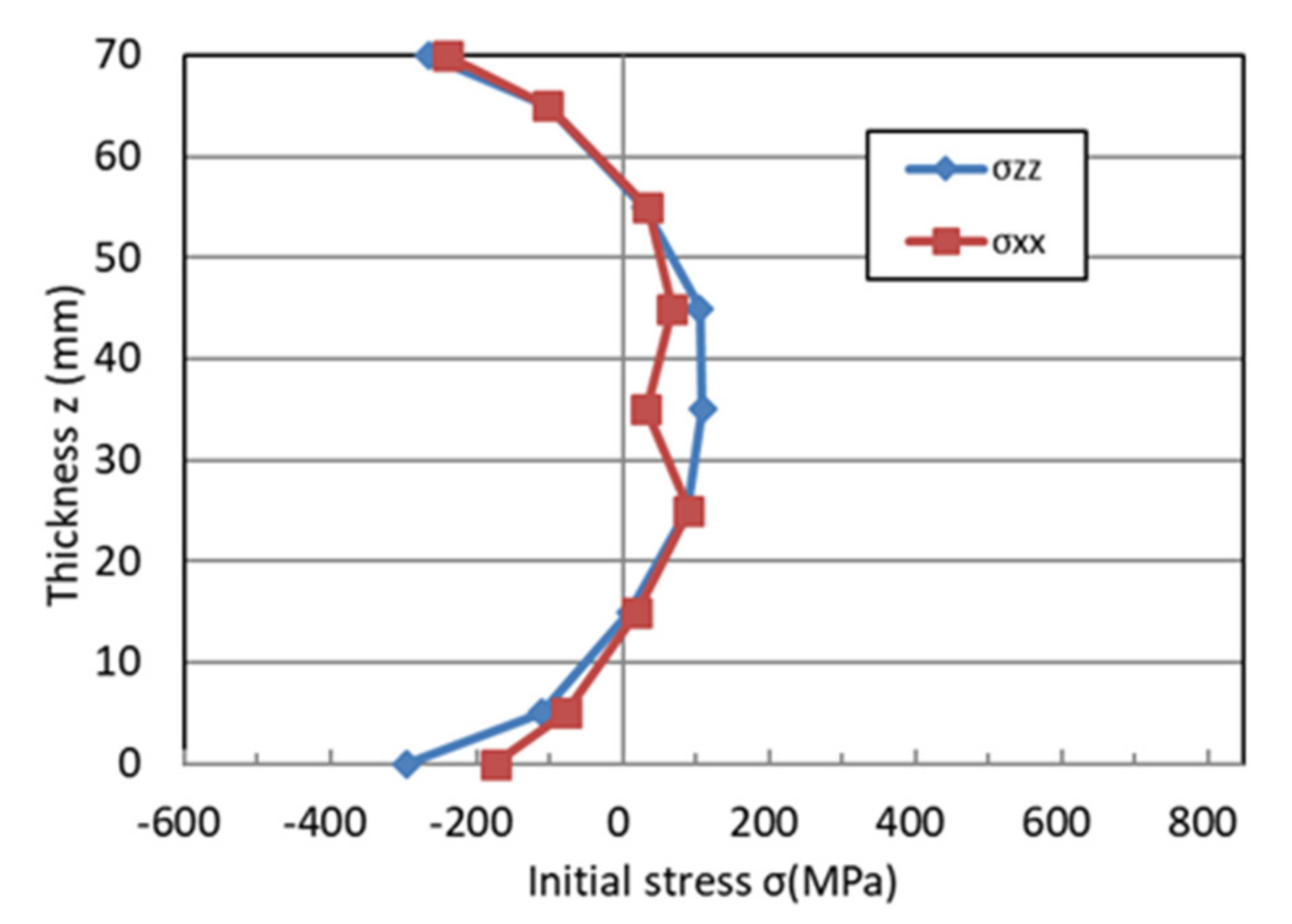


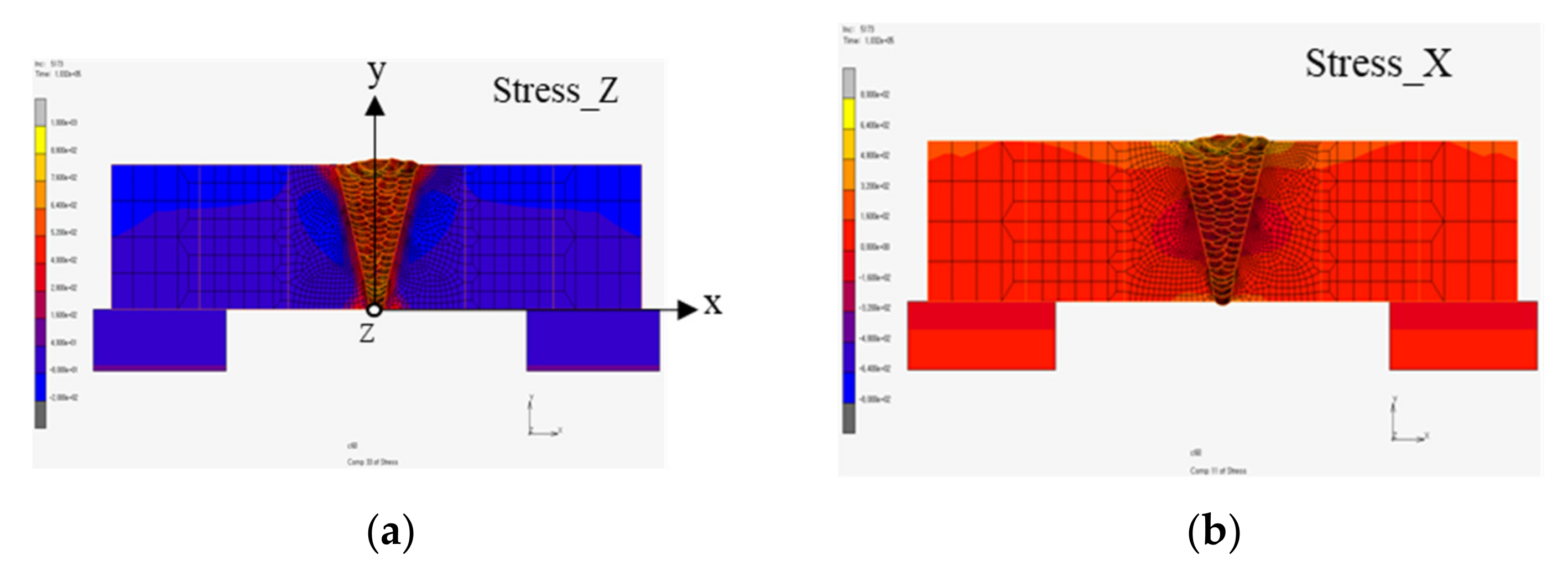

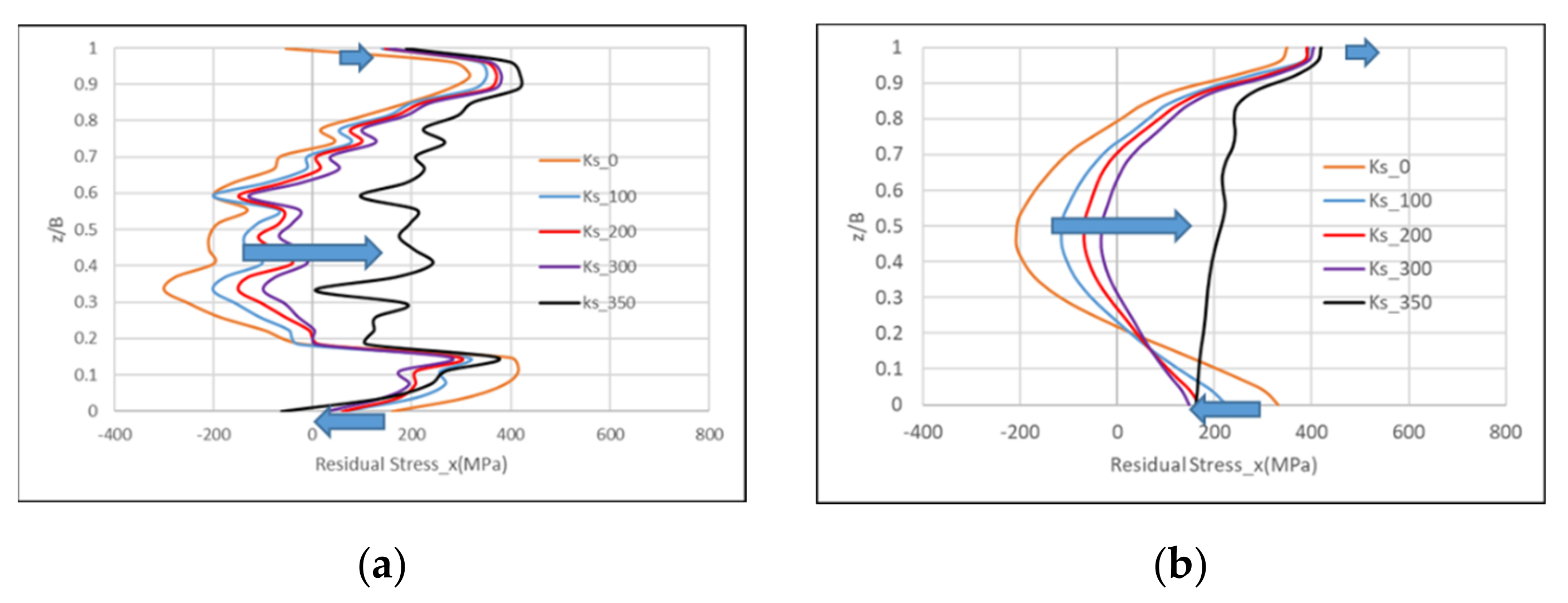
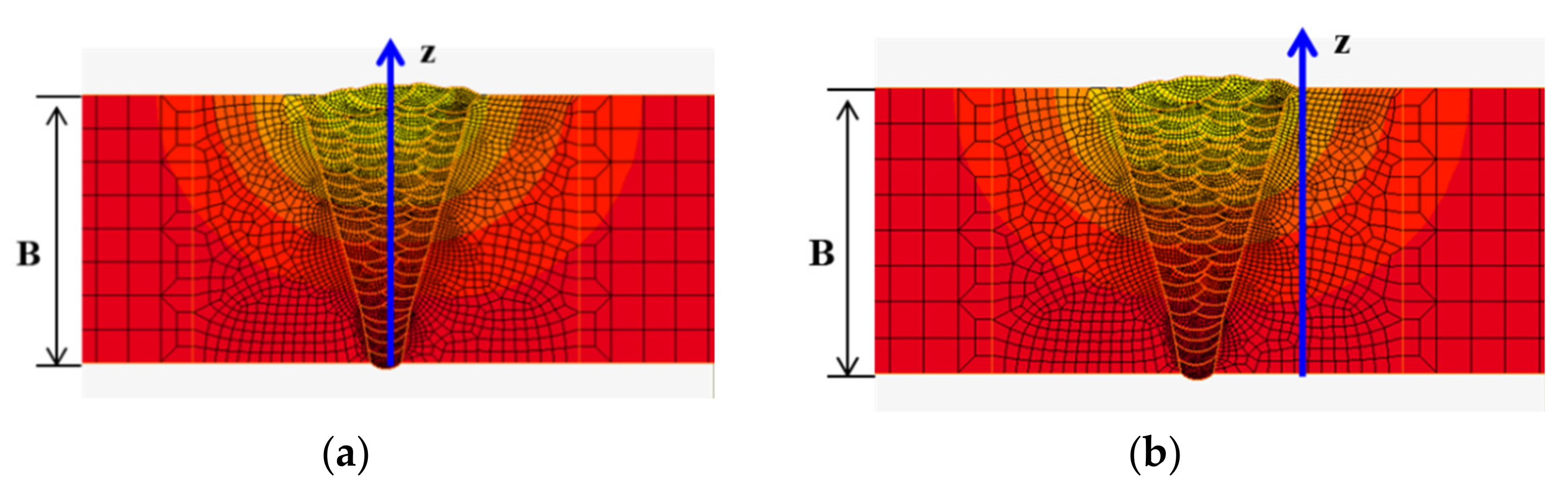
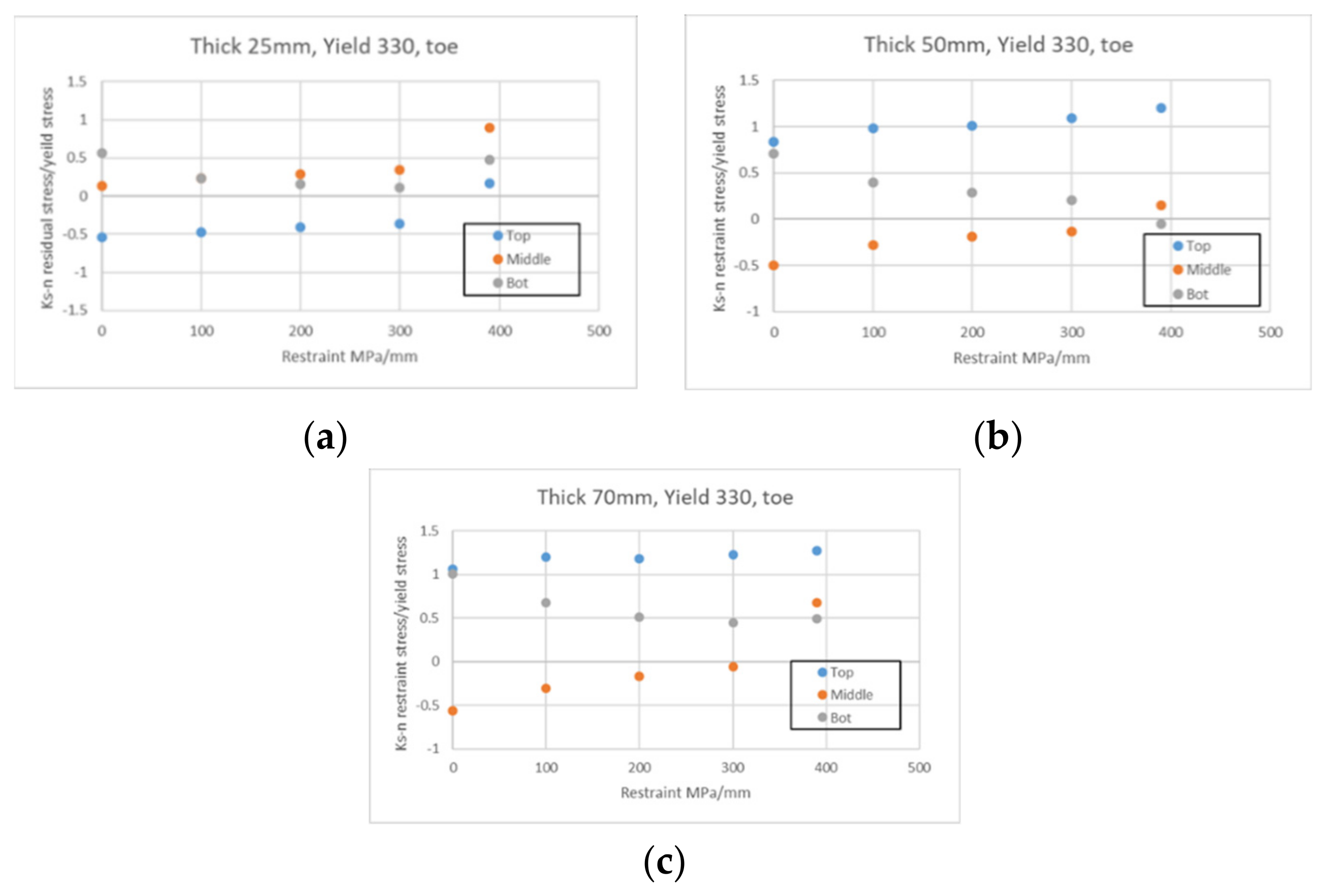

| Items | Base Materials | Welding Consumables |
|---|---|---|
| EH40 TMCP | SF-36E | |
| Yield strength (MPa) | 500 | 570 |
| Tensile strength (MPa) | 604 | 610 |
| Young’s modulus (GPa) | 206 | 206 |
| Elongation (%) | 21 | 29 |
| Poisson’s ratio | (0.28) | (0.28) |
| Welding Process | Heat Input | Consumables | Shield Gas | Current | Voltage | Speed | Pass/Layer |
|---|---|---|---|---|---|---|---|
| FCAW | 15–17 kJ/cm | SF-36E (NSSW) | 100% CO2 | 255 A | 32 V | 30 CPM | 60/21 |
| Thickness (mm) | Yield Stress (MPa) | Constraint Change (MPa/mm) |
|---|---|---|
| 25 | 330 | 0, 100, 200, 300, 390 |
| 405 | 0, 100, 200, 300, 460 | |
| 590 | 0, 100, 200, 300, 665 | |
| 50 | 330 | 0, 100, 200, 300, 340 |
| 405 | 0, 100, 200, 300, 410 | |
| 590 | 0, 100, 200, 300, 600 | |
| 70 | 330 | 0, 100, 200, 300, 350 |
| 405 | 0, 100, 200, 300, 430 | |
| 590 | 0, 100, 200, 300, 625 | |
| Total number of analysis cases: 45 | ||
| Thickness | Welding Process | Heat Input | Consumables | Shield Gas | Current | Voltage | Speed | Pass/Layer |
|---|---|---|---|---|---|---|---|---|
| 25 | FCAW | 15–17 kJ/cm | SF-36E (NSSW) | 100% CO2 | 255 A | 32 V | 30 CPM | 13/9 |
| 50 | 34/11 |
| Position | Center | Toe |
|---|---|---|
| −1.3675 (sd = 0.2370) | −1.1396 (sd = 0.2168) | |
| 2.2306 (sd = 0.2366) | 2.0167 (sd = 0.2170) | |
| RMSE | 32.8728 | 36.8211 |
| Predicted | 85.49% | 83.89% |
| Estimation Models | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 0 | 22.08 | 0.07 | −0.87 | 1.38 | 0.90 | |
| 1 | −4598.95 | 12.97 | −31.56 | 56.16 | 147.73 | |
| 2 | 35,584.71 | −117.31 | 396.62 | −662.19 | −1570.34 | |
| 3 | −109,133.50 | 371.10 | −1527.09 | 2564.27 | 5836.57 | |
| 4 | 175,217.08 | −545.76 | 2640.39 | −4468.19 | −10,392.73 | |
| 5 | −144,638.02 | 381.81 | −2137.07 | 3626.75 | 8957.90 | |
| 6 | 47,074.16 | −102.27 | 660.05 | −1117.86 | −2974.11 | |
| RMSE | 101.6 | Predicted | 72.12% | |||
| Estimation Models | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 0 | −13.47 | 0.49 | −1.35 | 2.24 | 1.74 | |
| 1 | −2876.10 | 1.77 | −1.89 | 8.73 | 27.15 | |
| 2 | 20,692.62 | −37.21 | 74.52 | −149.30 | −270.15 | |
| 3 | −62,617.81 | 135.84 | −264.05 | 536.06 | 852.59 | |
| 4 | 98,247.37 | −218.60 | 386.07 | −822.92 | −1353.47 | |
| 5 | −72,824.16 | 167.78 | −261.56 | 584.72 | 1012.13 | |
| 6 | 18,725.59 | −49.53 | 68.39 | −159.07 | −256.52 | |
| RMSE | 55.93 | Predicted | 86.19% | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; An, G.; Ma, N.; Kim, S. Effect of Transverse Restraint on Welding Residual Stress in V-Groove Butt Welding. Metals 2022, 12, 654. https://doi.org/10.3390/met12040654
Park J, An G, Ma N, Kim S. Effect of Transverse Restraint on Welding Residual Stress in V-Groove Butt Welding. Metals. 2022; 12(4):654. https://doi.org/10.3390/met12040654
Chicago/Turabian StylePark, Jeongung, Gyubaek An, Ninshu Ma, and Seongjoon Kim. 2022. "Effect of Transverse Restraint on Welding Residual Stress in V-Groove Butt Welding" Metals 12, no. 4: 654. https://doi.org/10.3390/met12040654
APA StylePark, J., An, G., Ma, N., & Kim, S. (2022). Effect of Transverse Restraint on Welding Residual Stress in V-Groove Butt Welding. Metals, 12(4), 654. https://doi.org/10.3390/met12040654






