Microstructural Impact on Fatigue Crack Growth Behavior of Alloy 718
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experiments
3. Results
3.1. Threshold of Stress Intensity Factor Range for Fatigue Growth
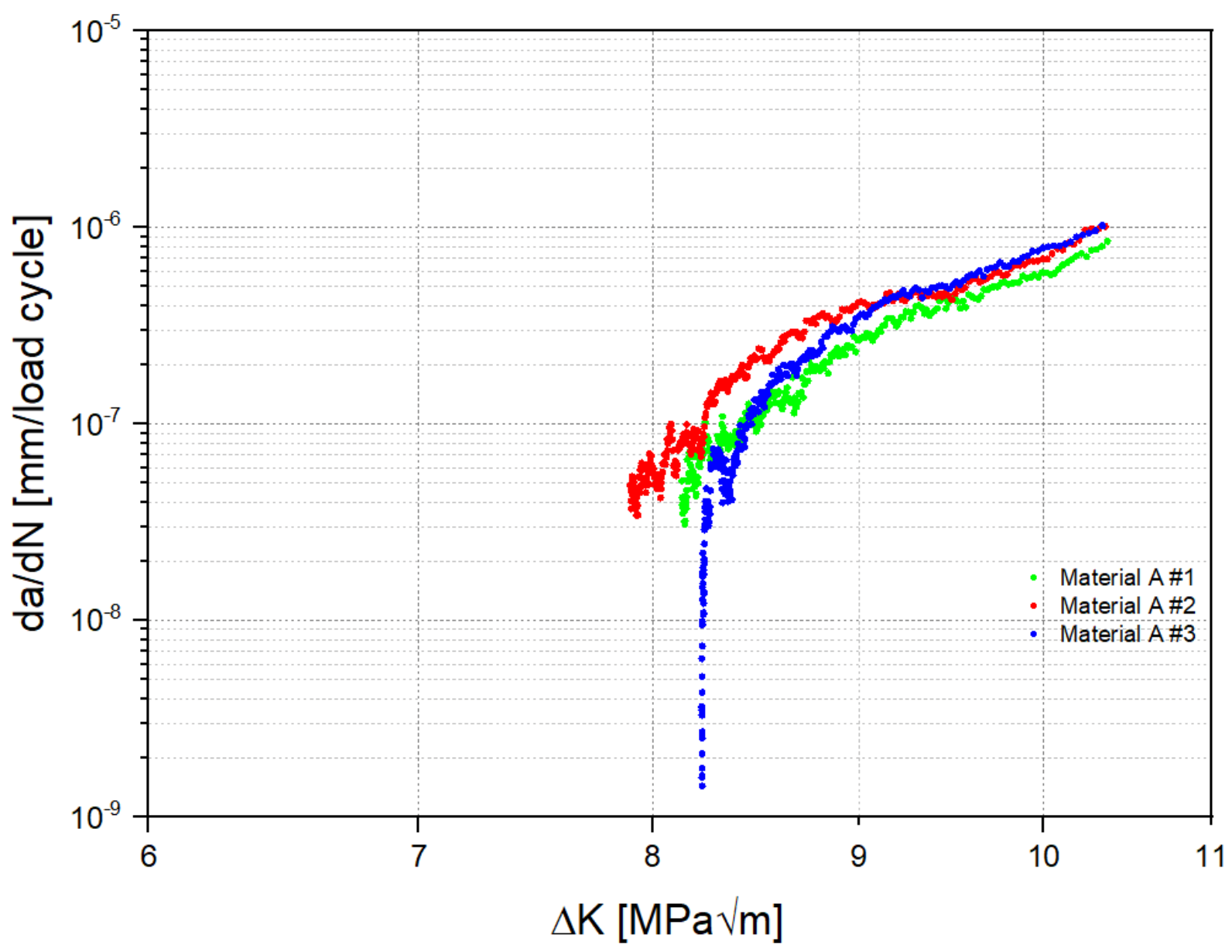
3.1.1. Material A
3.1.2. Material B
3.1.3. Material C
3.1.4. Material D
3.2. Fractography
3.3. Fracture Toughness
3.4. Modelling Approach
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Konečná, R.; Kunz, L.; Nicoletto, G.; Bača, A. Long fatigue crack growth in Inconel 718 produced by selective laser melting. Int. J. Fatigue 2016, 92, 2. [Google Scholar] [CrossRef]
- Wang, Z.; Guan, K.; Gao, M.; Li, X.; Chen, X.; Zeng, X. The microstructure and mechanical properties of deposited-IN718 by selective laser melting. J. Alloy Compd. 2012, 513, 518–523. [Google Scholar] [CrossRef]
- Amato, K.N.; Gaytan, S.M.; Murr, L.E.; Martinez, E.; Shindo, P.W.; Hernandez, J.; Collins, S.; Medina, F. Microstructures and mechanical behavior of Inconel 718 fabricated by selective laser melting. Acta Mater. 2012, 60, 2229–2239. [Google Scholar] [CrossRef]
- Kruth, J.-P.; Levy, G.; Klocke, F.; Childs, T.H.C. Consolidation phenomena in laser and powder-bed based layered manufacturing. CIRP Ann. 2007, 56, 730–759. [Google Scholar] [CrossRef]
- Murr, L.E.; Martinez, E.; Gaytan, S.M.; Ramirez, D.A.; Machado, B.I.; Shindo, P.W.; Martinez, J.L.; Medina, F.; Wooten, J.; Ciscel, D.; et al. Microstructural Architecture, Microstructures, and Mechanical Properties for a Nickel-Base Superalloy Fabricated by Electron Beam Melting. Met. Mater. Trans. A 2011, 42, 3491–3508. [Google Scholar] [CrossRef] [Green Version]
- Mercer, C.; Soboyejo, A.B.O.; Soboyejo, W.O. Micromechanisms of fatigue crack growth in a forged Inconel 718 nickel-based superalloy. Mater. Sci. Eng. A 1999, 270, 308–322. [Google Scholar] [CrossRef]
- Clavel, M.; Pineau, A. Frequency and wave-form effects on the fatigue crack growth behavior of alloy 718 at 298 K and 823 K. Met. Trans. A 1978, 9, 471–480. [Google Scholar] [CrossRef]
- Clavel, M.; Pineau, A. Fatigue behaviour of two nickel-base alloys I: Experimental results on low cycle fatigue, fatigue crack propagation and substructures. Mater. Sci. Eng. 1982, 55, 157–171. [Google Scholar] [CrossRef]
- Chen, X.; Lin, Y.C.; Chen, M.; Li, H.; Wen, D.; Zhang, J.; He, M. Microstructural evolution of a nickel-based superalloy during hot deformation. Mater. Des. 2015, 77, 41–49. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, K.; Zhou, H.; Lu, Z.; Zhao, C.; Yang, X. Effect of strain rate on microstructure evolution of a nickel-based superalloy during hot deformation. Mater. Des. 2015, 80, 51–62. [Google Scholar] [CrossRef]
- Sommitsch, C.; Mitter, W. On modelling of dynamic recrystallisation of fcc materials with low stacking fault energy. Acta Mater. 2006, 54, 357–375. [Google Scholar] [CrossRef]
- Gruber, C.; Raninger, P.; Stanojevic, A.; Godor, F.; Rath, M.; Kozeschnik, E.; Stockinger, M. Simulation of Dynamic and Meta-Dynamic Recrystallization Behavior of Forged Alloy 718 Parts Using a Multi-Class Grain Size Model. Materials 2020, 14, 111. [Google Scholar] [CrossRef] [PubMed]
- Pokluda, J.; Pippan, R. Analysis of roughness-induced crack closure based on asymmetric crack-wake plasticity and size ratio effect. Mater. Sci. Eng. A 2007, 462, 355–358. [Google Scholar] [CrossRef]
- Pippan, R.; Hohenwarter, A. Fatigue crack closure: A review of the physical phenomena. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 471–495. [Google Scholar] [CrossRef] [PubMed]
- Pippan, R.; Riemelmoser, F.O.; Weinhandl, H.; Kreuzer, H. Plasticity-induced crack closure under plane-strain conditions in the near-threshold regime. Philos. Mag. A 2009, 82, 3299–3309. [Google Scholar] [CrossRef]
- ASTM E8/E8M-13a; Standard Test Methods for Tension Testing of Metallic Materials. American Society for Testing and Materials: West Conshohocken, PA, USA, 2013.
- ASTM E399–20a; Standard Test Method for Linear-Elastic Plane-Strain Fracture Toughness of Metallic Materials. American Society for Testing and Materials: West Conshohocken, PA, USA, 2020.
- Maierhofer, J.; Kolitsch, S.; Pippan, R.; Gänser, H.P.; Madia, M.; Zerbst, U. The cyclic R-curve—Determination, problems, limitations and application. Eng. Fract. Mech. 2018, 198, 45–64. [Google Scholar] [CrossRef]
- ISO 12108:2018; Metallic Materials—Fatigue Testing—Fatigue Crack Growth Method. International Organization for Standardization: Geneva, Switzerland, 2018.
- Ashby, M.F. Materials Selection in Mechanical Design, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2016. [Google Scholar]
- Rielli, V.V.; Godor, F.; Gruber, C.; Stanojevic, A.; Oberwinkler, B.; Primig, S. Effects of processing heterogeneities on the micro- to nanostructure strengthening mechanisms of an alloy 718 turbine disk. Mater. Des. 2021, 212, 110295. [Google Scholar] [CrossRef]
- Maierhofer, J.; Gänser, H.P.; Pippan, R. Crack closure and retardation effects—Experiments and modelling. Procedia Struct. Integr. 2017, 4, 19–26. [Google Scholar] [CrossRef]
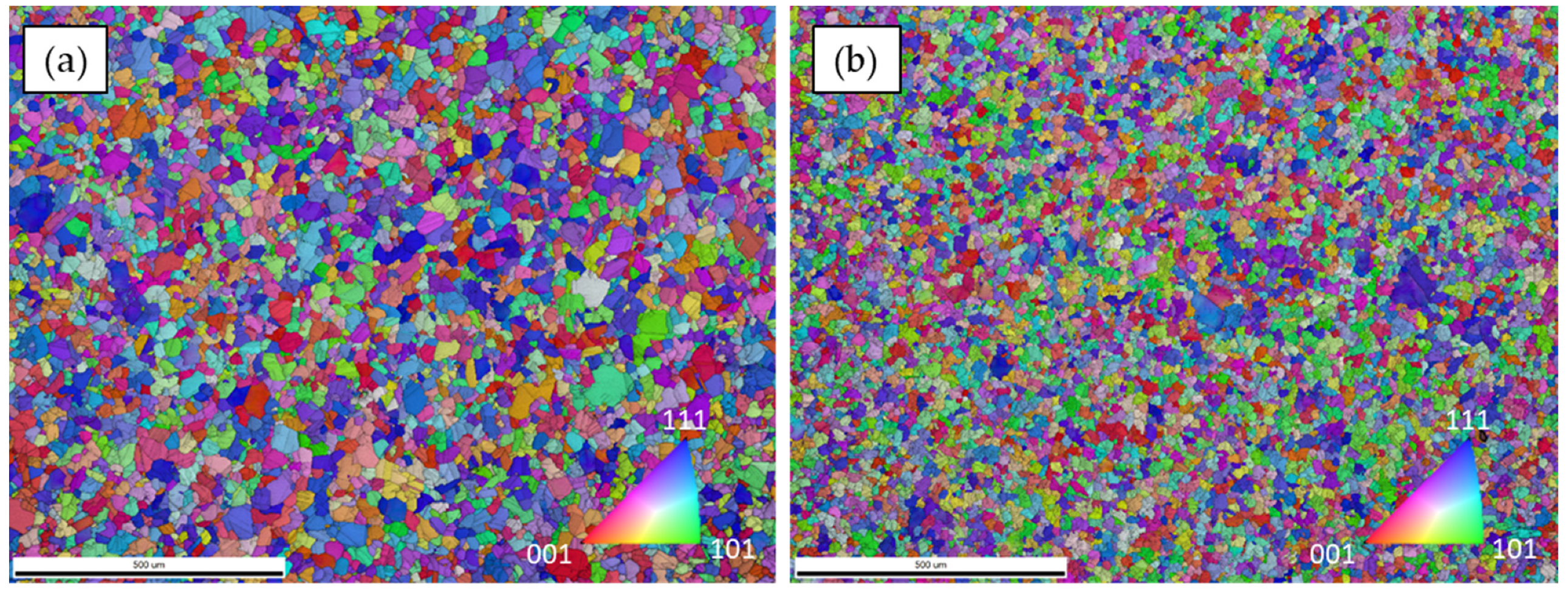








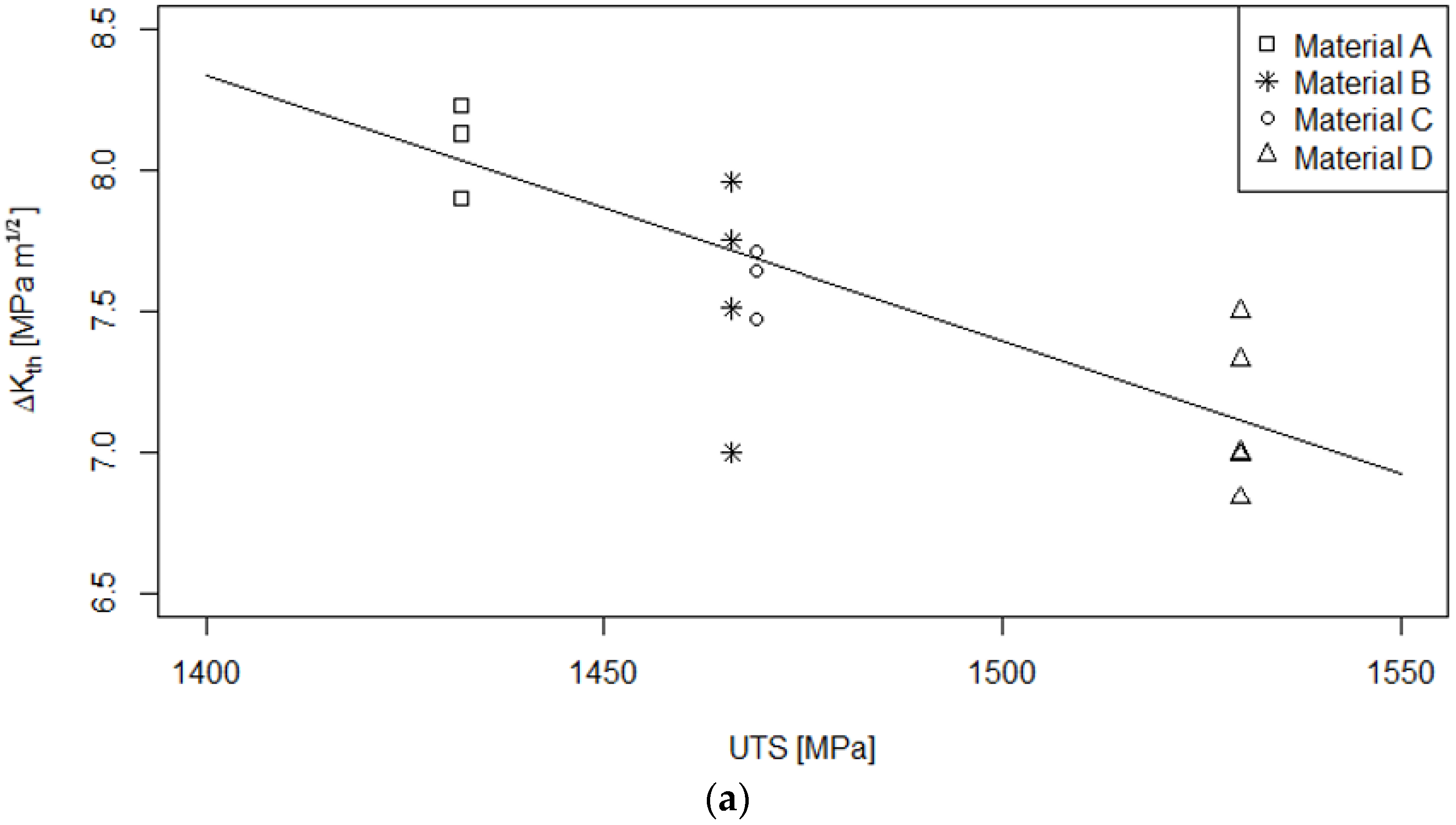
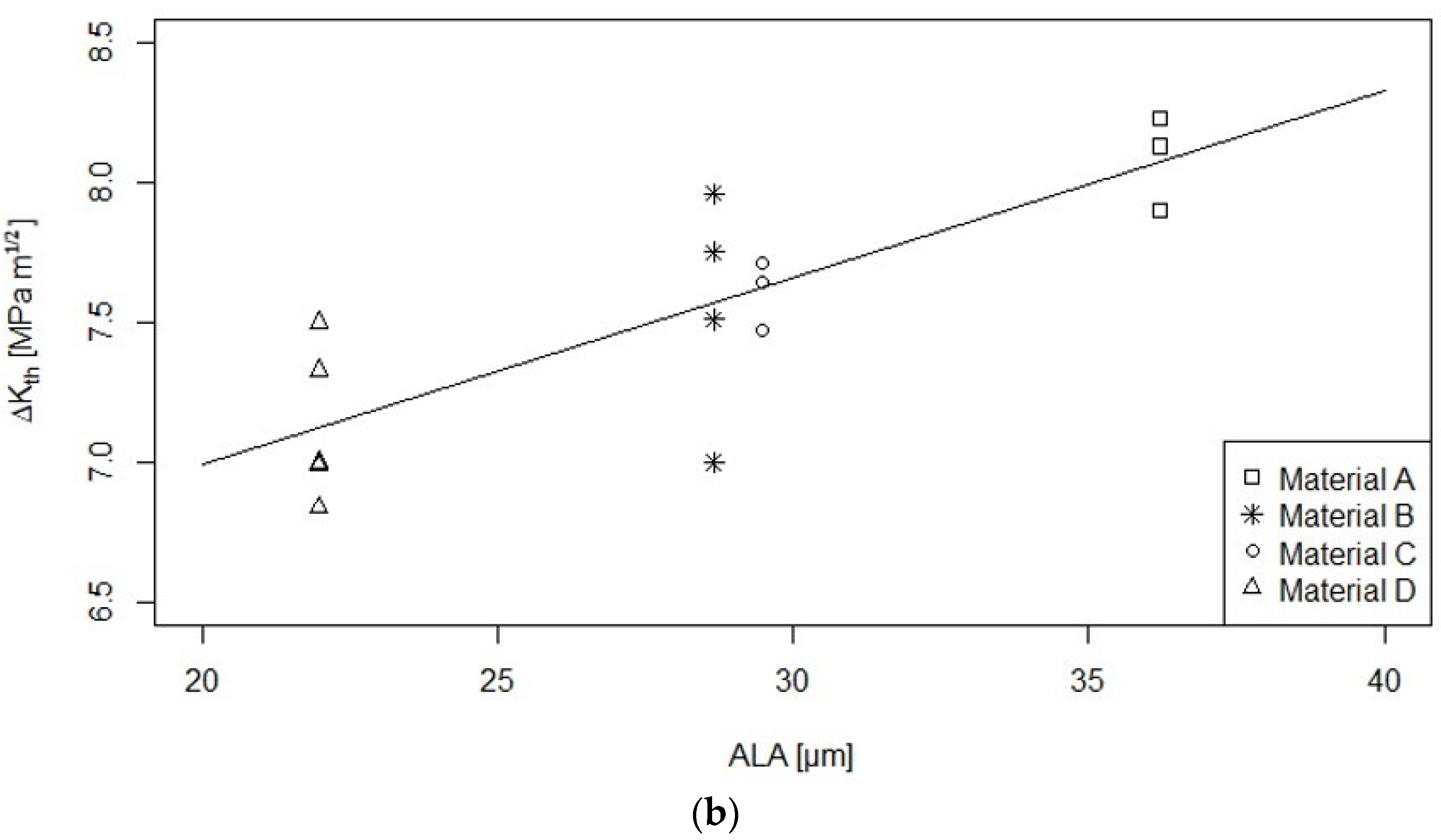
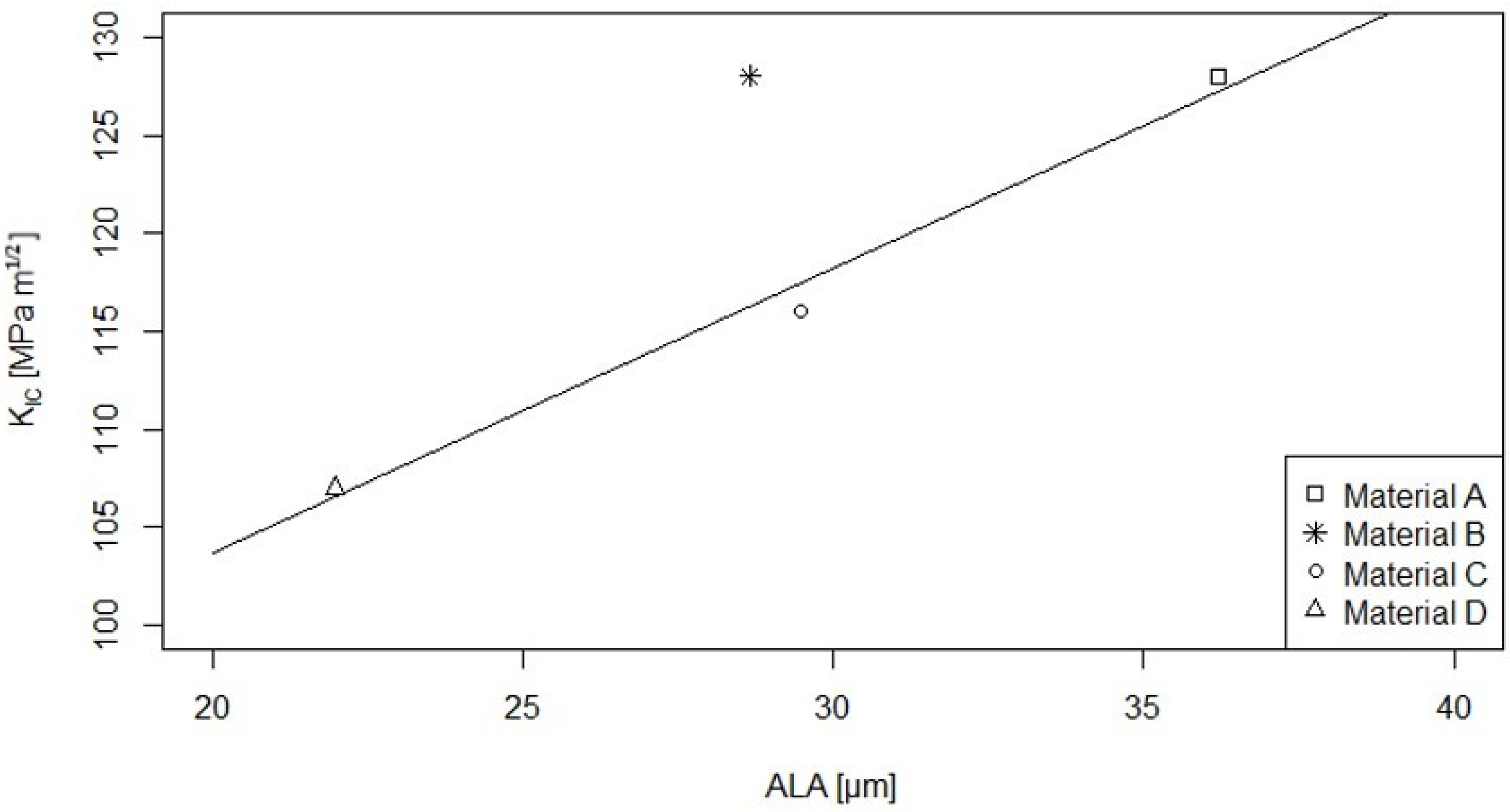

| Material | ECD [µm] | ALA [µm] | Rp0.2 [MPa] | UTS [MPa] | KIC [MPa√m] | Validity |
|---|---|---|---|---|---|---|
| Material A | 11.83 | 36.20 | 1237 | 1432 | 128 | not valid |
| Material B | 9.29 | 28.66 | 1274 | 1466 | 128 | not valid |
| Material C | 9.99 | 29.48 | 1174 | 1469 | 116 | not valid |
| Material D | 7.67 | 21.97 | 1390 | 1530 | 107 | valid |
| Material | ΔKth [MPa√m] | C [-] | m [-] |
|---|---|---|---|
| Material A #1 | 8.13 | 7.41 × 10−14 | 6.91 |
| Material A #2 | 7.90 | 1.20 × 10−13 | 6.77 |
| Material A #3 | 8.23 | 8.91 × 10−14 | 6.94 |
| Material B #1 | 7.96 | 6.92 × 10−14 | 6.96 |
| Material B #2 | 7.75 | 9.55 × 10−14 | 6.90 |
| Material B #3 | 7.51 | 1.29 × 10−12 | 6.13 |
| Material B #4 | 7.00 | 2.69 × 10−12 | 5.92 |
| Material C #1 | 7.71 | 3.89 × 10−16 | 9.59 |
| Material C #2 | 7.47 | 8.51 × 10−15 | 8.25 |
| Material C #3 | 7.64 | 5.13 × 10−15 | 8.37 |
| Material D #1 | 7.00 | 2.75 × 10−13 | 7.11 |
| Material D #2 | 7.50 | 4.07 × 10−15 | 8.81 |
| Material D #3 | 6.99 | 2.24 × 10−14 | 8.13 |
| Material D #4 | 6.84 | 2.75 × 10−16 | 9.96 |
| Material D #5 | 7.33 | 4.90 × 10−16 | 9.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gruber, C.; Raninger, P.; Maierhofer, J.; Gänser, H.-P.; Stanojevic, A.; Hohenwarter, A.; Pippan, R. Microstructural Impact on Fatigue Crack Growth Behavior of Alloy 718. Metals 2022, 12, 710. https://doi.org/10.3390/met12050710
Gruber C, Raninger P, Maierhofer J, Gänser H-P, Stanojevic A, Hohenwarter A, Pippan R. Microstructural Impact on Fatigue Crack Growth Behavior of Alloy 718. Metals. 2022; 12(5):710. https://doi.org/10.3390/met12050710
Chicago/Turabian StyleGruber, Christian, Peter Raninger, Jürgen Maierhofer, Hans-Peter Gänser, Aleksandar Stanojevic, Anton Hohenwarter, and Reinhard Pippan. 2022. "Microstructural Impact on Fatigue Crack Growth Behavior of Alloy 718" Metals 12, no. 5: 710. https://doi.org/10.3390/met12050710
APA StyleGruber, C., Raninger, P., Maierhofer, J., Gänser, H.-P., Stanojevic, A., Hohenwarter, A., & Pippan, R. (2022). Microstructural Impact on Fatigue Crack Growth Behavior of Alloy 718. Metals, 12(5), 710. https://doi.org/10.3390/met12050710







