Numerical Simulation of 50 mm 316L Steel Joint of EBW and Its Experimental Validation

Abstract

The 316L thick plate electron beam welding (EBW) has been widely used in fusion test reactor manufacturing. Therefore, the numerical simulation of the 50 mm 316L austenitic stainless steel by two heat sources and experimental on microstructure and residual stress have been studied in this article. In the simulation study, the traditional heat source model (3D Gaussian heat source) and composite heat source (double ellipsoid heat source superimposed on the 3D Gaussian heat source) were proposed to simulate the welding of local joint. Weld cross-section, temperature curve, and residual stress after welding obtained by simulations were investigated. The experimental study involved residual stress tests and microstructure analysis. It turned out that the result of the composite heat source was closer to the actual joint. The residual stress distribution of simulation was validated and in accordance with experimental measurement. Moreover, the microstructures were studied by electro backscattered diffraction (EBSD) and compared with the temperature curve. The formation mechanism of microstructural heterogeneity was caused mainly by different thermal cycles at different positions of the thick plate. The top of the joint was more prone to stress concentration.

1. Introduction

Energy resource is one of the central issues of the world today [1]. The controlled fusion is promising energy in the future, one promising and key path to realize it is through a magnetically confined device Tokamak. The Chinese Fusion Engineering Test Reactor (CFETR) is the next generation of all superconducting tokamak independently developed by China. The research and development (R&D) of the CFETR 1/8 vacuum vessel (VV) aimed to verify the engineering feasibility of the large-scale complex double-layer structure manufacturing are under development [2,3].

In the production of the VV, welding is the most important essential technology. Due to electron beam welding (EBW) having the advantages of high-power density, high efficiency, low deformation, and great depth-to-width ratio [4,5], it has been used in the VV port stubs manufacturing. The quality of welded joint is the key index of the VV manufacturing. However, the thick plate welding has led to a barrage of problems for quality control, including through-thickness microstructure and mechanical properties and theirs variation. It is very difficult to analyze the relationship between the nonuniform temperature field, stress–strain field and microstructure of the 50 mm joints of EBW. Thus, it is essential to establish the appropriate finite element analysis model for the 50 mm thick plate EBW simulation to perform further investigation and reduce the time and economic costs, also provide theoretical basis and experimental data for welding simulation of the large-scale complex double-layer structure.

The simulation and experiment for thick austenitic stainless steel have been advancing. Previous research has shown the through thickness microstructure and mechanical properties for thick austenitic stainless steel evaluated by microstructural analysis and mechanical tests (e.g., Xia, 2019 [6]; Alali, 2017 [7]). Moreover, there is a large volume of published studies describing the numerical simulation of the EBW (e.g., Chiumenti, 2016 [8]; Bonakdar, 2017 [9]), most studies focused on the verification of simulation stress and deformation after welding with experiments. So far, however, there has been little discussion about the relationship between the simulated thermal cycle curve and microstructure at different positions.

In this paper, the thermo–mechanical finite element (FE) simulation and experiments of 50 mm 316L stainless steel plate welded by EBW were performed. The objective of this paper was to reveal the mechanism of microstructure variation through thickness by the combination of acceptable simulation results and metallurgy analysis, and then verify the simulation accuracy.

2. Methodology

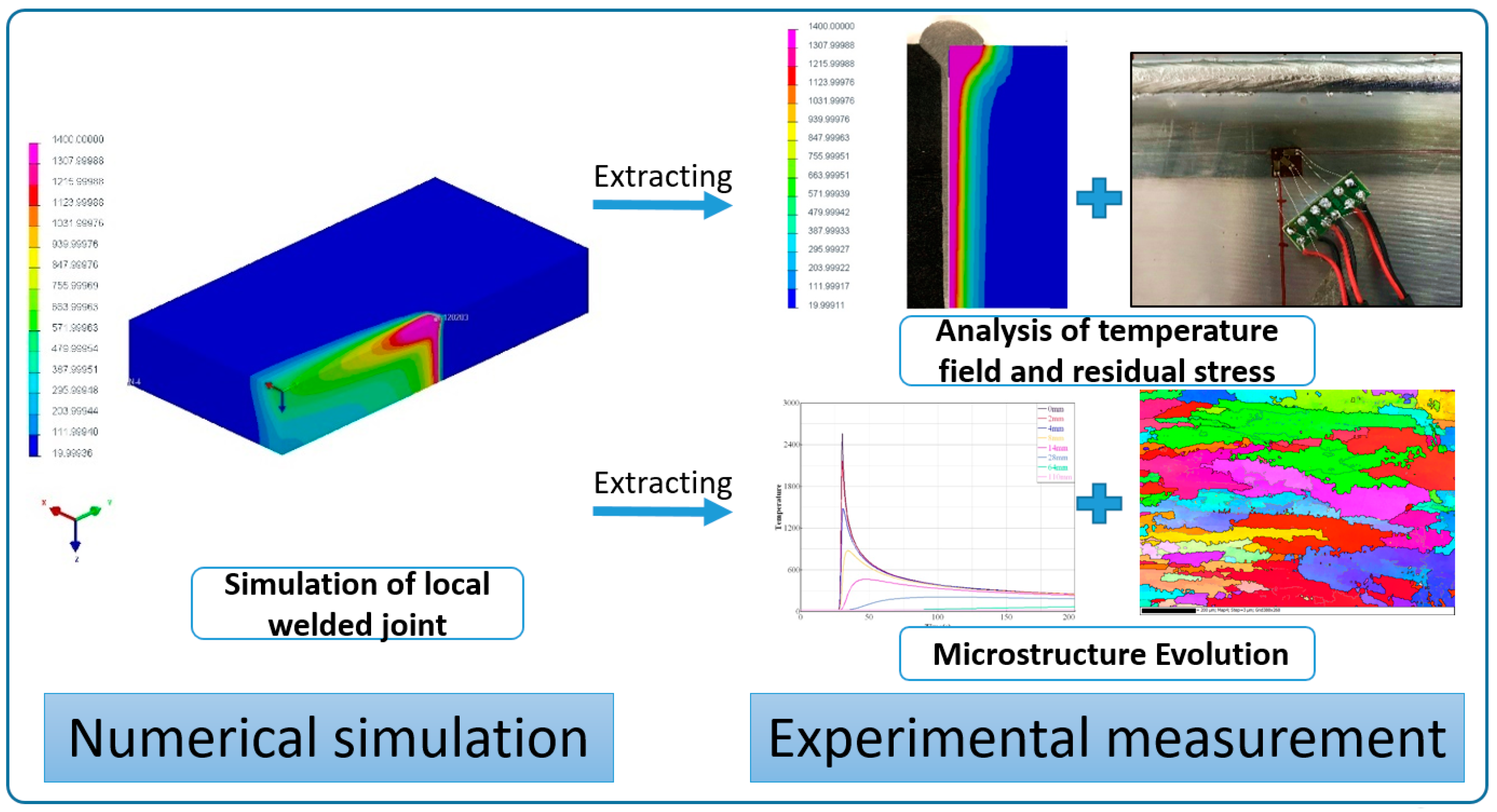
The technology roadmap is presented in Figure 1. Two key parts: numerical simulation and experimental measurements were investigated.

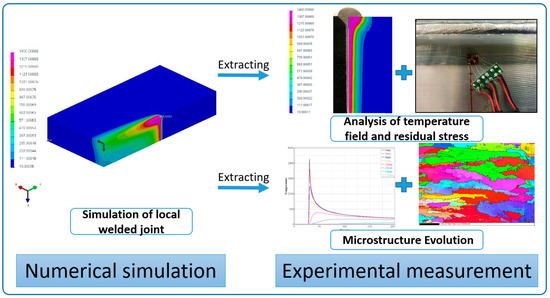
Figure 1. Technology roadmap.

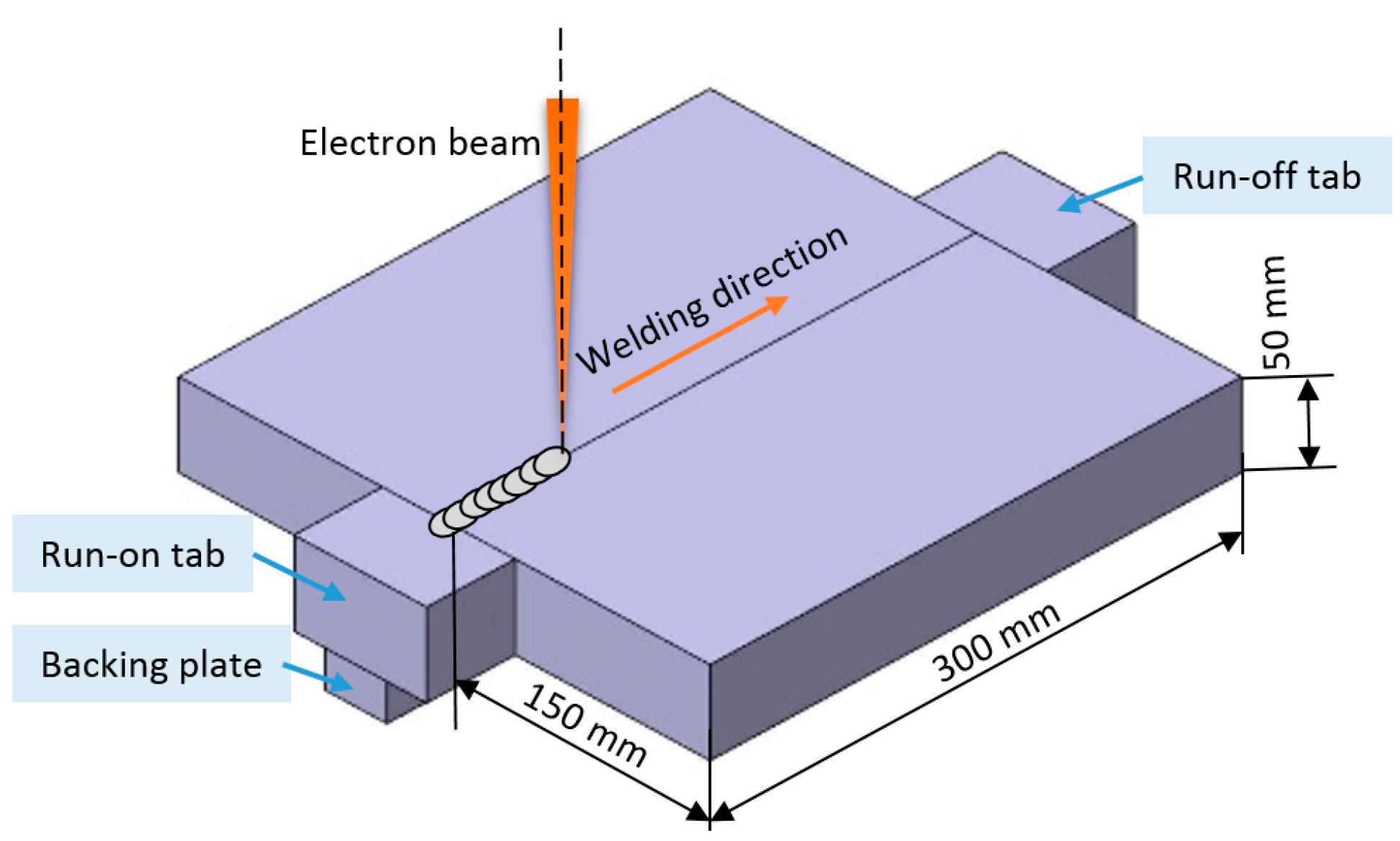
The dimensions of the two ASTM A240/A240M-14 316L stainless steel plates for butt welding were 300 mm × 150 mm × 50 mm shown in Figure 2. The chemical compositions obtained by spectroscopic analysis are presented in Table 1. Before welding, the 316L plates oil and oxide scale should be removed. During the assembly process, the plates should be closely matched to ensure that the assembly clearance is less than 0.2 mm. A universal type ZD150-60C CV66M vacuum electron beam machine was applied to the welding test. The electron beam machine system contains several main components: electron gun (G600KM, Steigerwald Strahltechnik GmbH (SST), Maisach, Germany), high-voltage power supply (HCV-150kV/60kW, SST, Maisach, Germany), 66 m² vacuum chamber and its workbench.

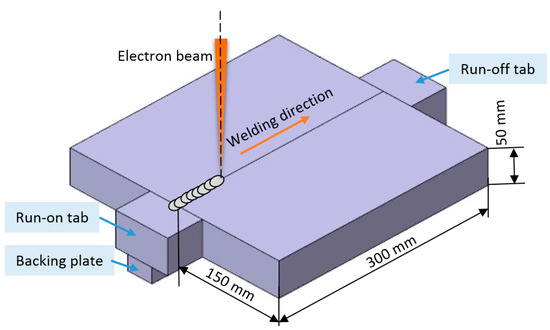
Figure 2. Schematic diagram: the dimensions of test plate, EBW welding direction.

Table 1. The chemical composition of base metals (wt%). Reprinted from Ref. [6].

Element	Cr	Ni	Mo	Mn	Si	Cu	P	C	N	S	Fe
wt%	16.31	10.12	2.04	1.36	0.50	0.3	0.032	0.012	0.027	0.004	rest

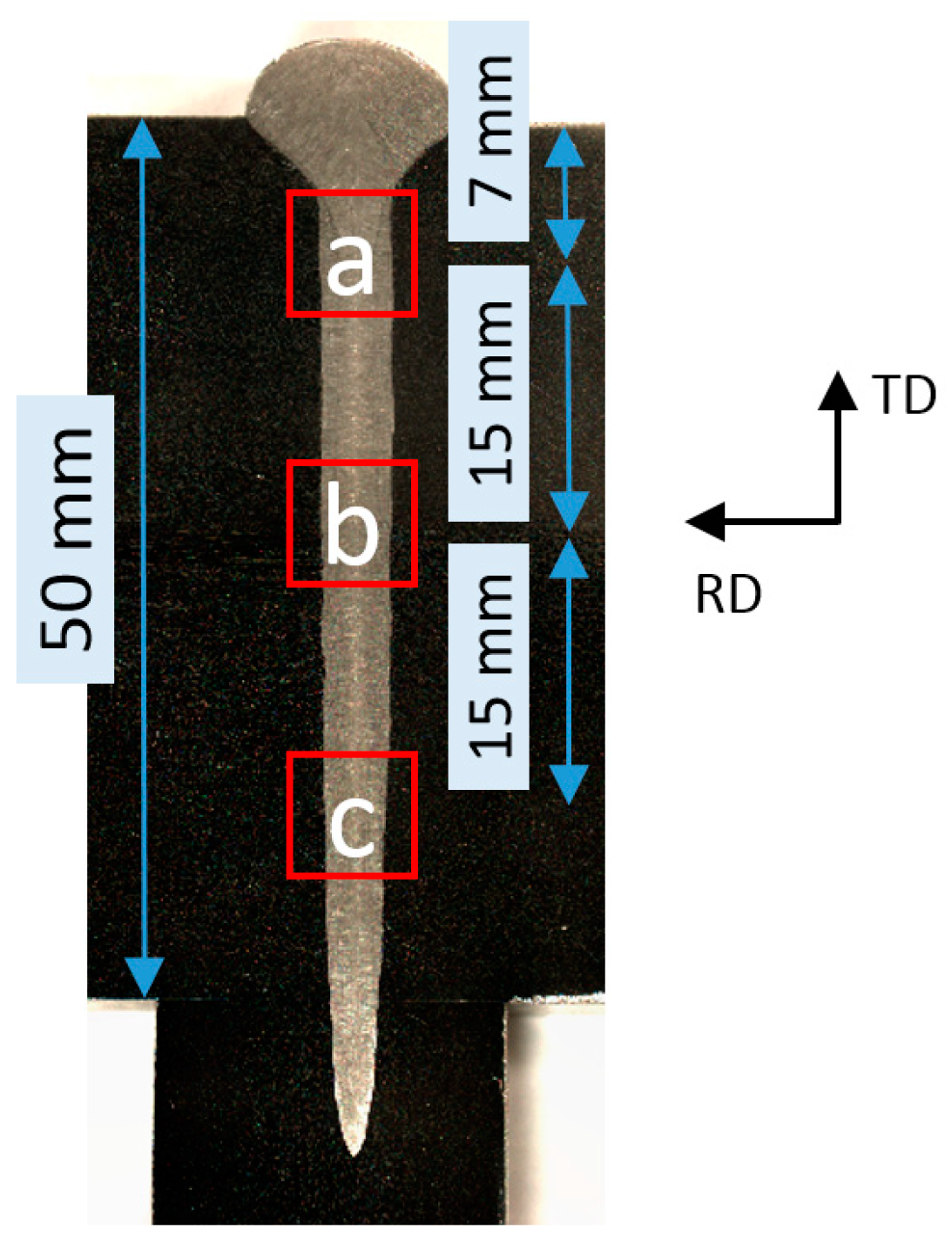
The welding parameters are given in Table 2. The weld cross-section of the test plates was taken in the middle of the weld by using wire-electrode cutting. The polished samples were etched in oxalic acid. The sampling method of the electron backscattered diffraction (EBSD) samples is shown in Figure 3. The upper, middle, and lower samples were taken from the weld cross-section. The microscope analysis was performed using a SIGMA300 (Zeiss, Jena, Germany) field emission scanning electron microscope (SEM) with OXFORD C-NANO EBSD (OXFORD instruments, Oxford, Britain). The hole-drilling technique was used in determining the local residual stresses on the welding plate’s surface.

Table 2. Welding parameters.

Voltage Ua (kV)	Beam Current Ib (mA)	Focusing Lens Current If (mA)	Velocity v (mm/s)	Working Distance (mm)	Welding Attitude	Working Pressure of the Electron Beam Machine Chamber (mbar)
150	140	2407	5	440	horizontal	1.7 × 10−4

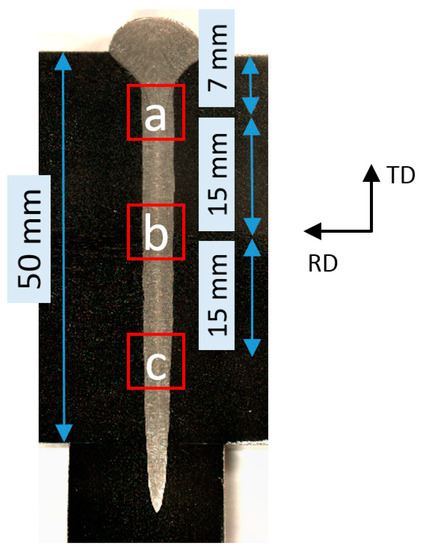
Figure 3. Schematic diagram: sampling location of the EBSD samples (a, b, c), sample placement direction (TD, RD).

In this paper, a three-dimensional finite element method was built. Based on SYSWELD 2019 software (Framatome, Courbevoie, France), thermo–mechanical uncoupled analyses of the 50 mm 316L EBW have been simulated.

3. Simulation of Local Welded Joint

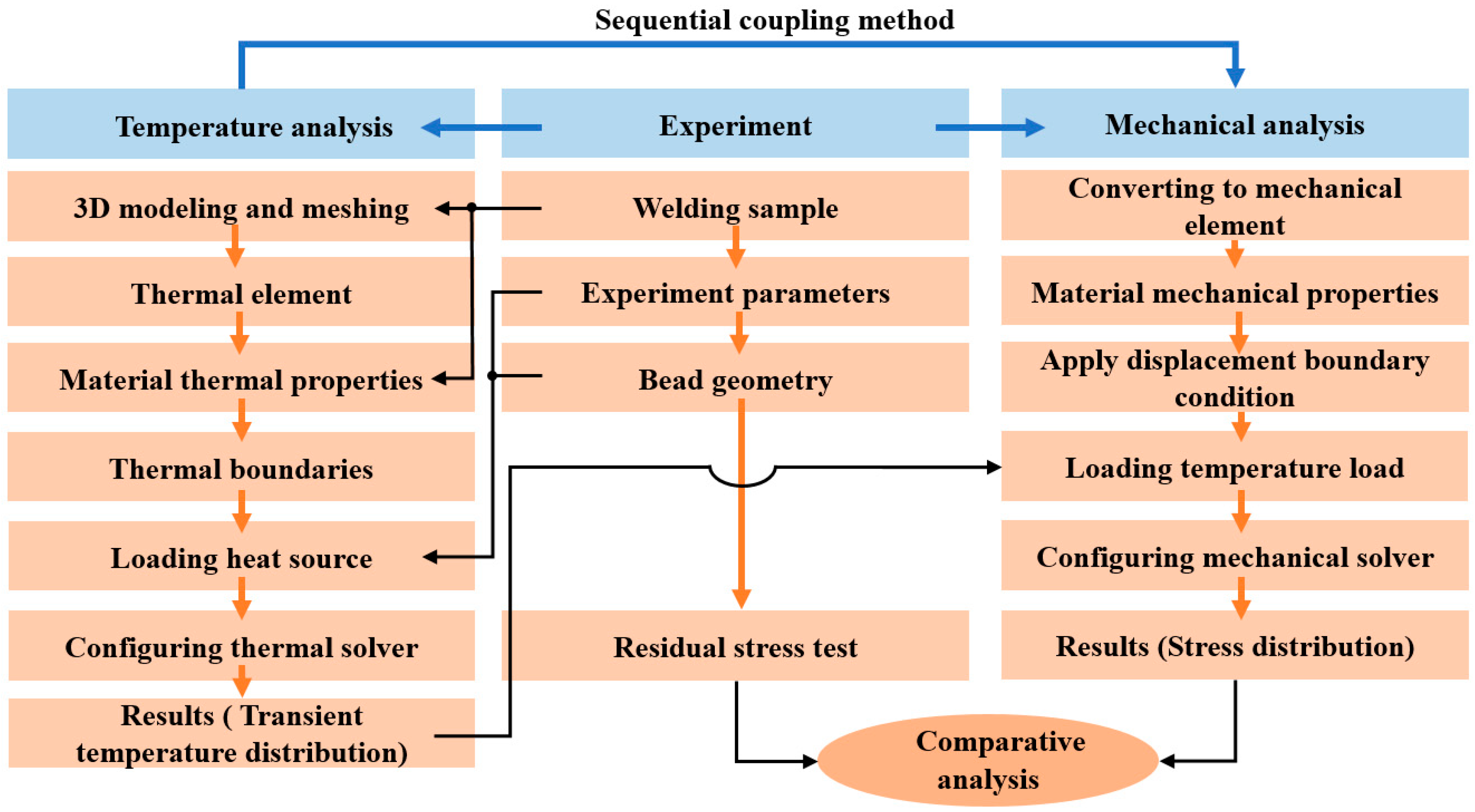
Figure 4 presents the simulation calculation flow of the local welded joint, proposed by Lin Chen [10] and Rong [11]. The simulation parameters were based on the test results, and the accuracy of the simulation results was proved by test results. In this paper, thermal elasto-plastic [12] FE simulation is used to analyze the temperature field and the residual stresses of the thick plates induced by welding.

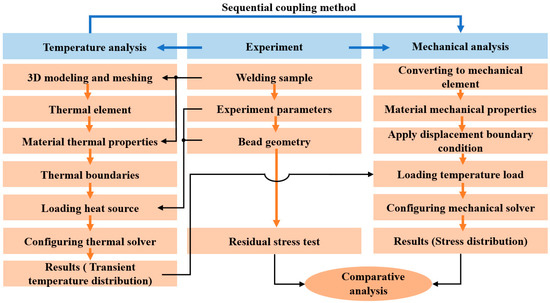
Figure 4. Simulation framework of thermo–mechanical FE simulation. Reprinted from refs. [10,11].

3.1. The Thermal Elastoplastic Theory

This method mainly considered the following four fundamental relations: the strain displacement relation, the stress–strain relation, the equilibrium relation, and the boundary condition relation.

3.1.1. Stress–Strain Relation

The stress–strain relationship of elastic and plastic materials is expressed as follows [13,14,15]:

$$\left\{\mathrm{d}\sigma \right\}=\left[D\right]\left\{\mathrm{d}\epsilon \right\}-\left\{C\right\}\mathrm{d}T$$

(1)

where $\left[D\right]$ is the elastic or plastic matrix, $\left\{C\right\}$ is the temperature-dependent vector.

In the elastic zone:

$$\left[D\right]={\left[D\right]}_e$$

(2)

$$\left\{C\right\}={\left\{C\right\}}_e={\left[D\right]}_e\left(\left\{\alpha \right\}+\frac{\partial {\left[D\right]}_e^{-1}}{\partial T}\left\{\sigma \right\}\right)$$

(3)

where $\alpha$ is the linear expansion coefficient, $T$ is the temperature.

In the plastic zone:

$$\left\{D\right\}={\left\{D\right\}}_e-{\left[D\right]}_e\left\{\frac{\partial f}{\partial \sigma }\right\}{\left\{\frac{\partial f}{\partial \sigma }\right\}}^T{\left[D\right]}_e/S$$

(4)

$$\left\{C\right\}={\left\{C\right\}}_{ep}={\left[D\right]}_{ep}\left(\left\{\alpha \right\}+\frac{\partial {\left[D\right]}_e^{-1}}{\partial T}\left\{\sigma \right\}\right)-{\left[D\right]}_e\left\{\frac{\partial f}{\partial \sigma }\right\}\left\{\frac{\partial f_0}{\partial T}\right\}/S$$

(5)

$$S={\left\{\frac{\partial f}{\partial \sigma }\right\}}^{\tau }{\left[D\right]}_e\left\{\frac{\partial f}{\partial \sigma }\right\}+{\left\{\frac{\partial f_0}{\partial {\epsilon }_p}\right\}}^{\tau }\left\{\frac{\partial f}{\partial \sigma }\right\}$$

(6)

where $f$ is yield function and $f_0$ is yield stress function.

3.1.2. Balance Equation

Considering a certain element of the structure, the equilibrium equations are written as: [13,14,15]

$${\left\{\mathrm{d}F\right\}}^e+{\left\{\mathrm{d}R\right\}}^e={\left[K\right]}^e{\left\{\mathrm{d}\delta \right\}}^e$$

(7)

$${\left[K\right]}^e={{\displaystyle \int }\left[B\right]}^T\left[D\right]\left[B\right]\mathrm{d}V$$

(8)

$${\left\{\mathrm{d}R\right\}}^e={{\displaystyle \int }\left[B\right]}^T\left\{C\right\}\mathrm{d}T\mathrm{d}V$$

(9)

where ${\left\{\mathrm{d}F\right\}}^e$ is an increment of the nodal force, ${\left\{\mathrm{d}R\right\}}^e$ is an increment of of thermal load, ${\left\{\mathrm{d}\delta \right\}}^e$ is displacement increment, ${\left[K\right]}^e$ is element stiffness matrix, $\left[B\right]$ is the matrix of connection strain, and node displacement increment.

$\left[D\right]$ and $\left\{C\right\}$ in Equations (8) and (9) can be substituted by ${\left[D\right]}_e$ and ${\left\{C\right\}}_e$ or ${[D]}_{ep}$ and ${\left\{C\right\}}_{ep}$ in Section 3.1.1. The equilibrium equation of the entire component is obtained as follow:

$$\left[K\right]\left\{\mathrm{d}\delta \right\}=\left\{\mathrm{d}F\right\}$$

(10)

where $\left[K\right]$ is total stiffness matrix, $\left\{\mathrm{d}F\right\}$ is total load vector, are presented as follows:

$$\left[K\right]={{\displaystyle \sum \left[K\right]}}^e$$

(11)

$$\left\{\mathrm{d}F\right\}={\displaystyle \sum \left({\left\{\mathrm{d}F\right\}}^e+{\left\{\mathrm{d}R\right\}}^e\right)}$$

(12)

3.1.3. Solution Procedure

Firstly, the temperature increment is loaded into the elements which divided by the component. The displacement increment of each node $\left\{\mathrm{d}\delta \right\}$ can be solved according to the temperature increment. Thus, the strain increment ${\left\{\mathrm{d}\epsilon \right\}}^e$ can be obtained by the following formula [13,14,15]:

$${\left\{\mathrm{d}\epsilon \right\}}^e=\left[B\right]{\left\{\mathrm{d}\delta \right\}}^e$$

(13)

The stress increment can be estimated by the relationship between stress and strain, and the dynamic stress–strain change and the final deformation after welding is determined.

3.2. Geometry Model

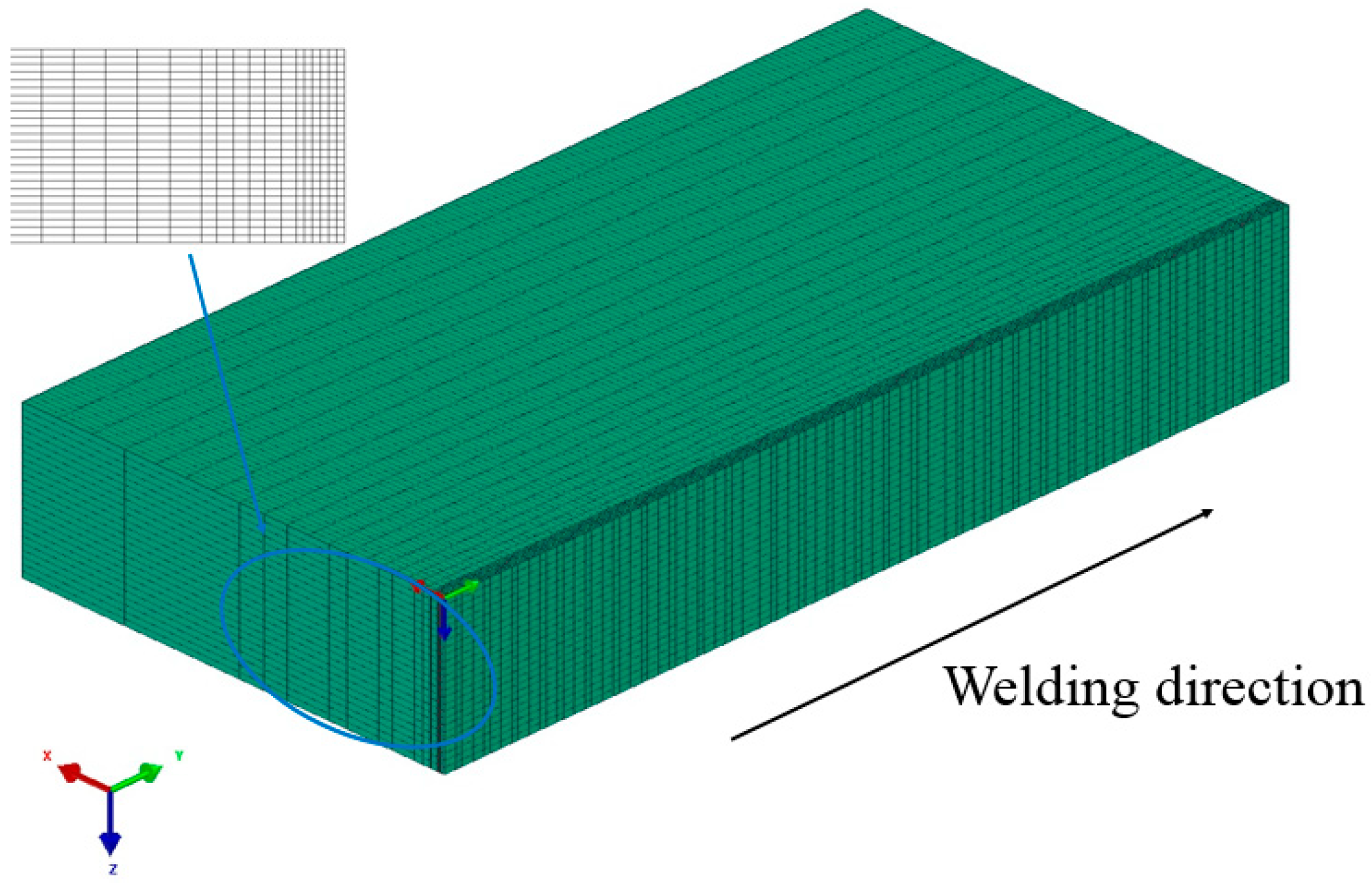
The two plates were symmetrical along the welding line, to be simplified into a half model for meshing and analysis. In the region near the welding zone, the fine grid blocks have been adopted, other regions using the nonuniform upscaling method, as shown in Figure 5. The entire model consisted of 117,780 nodes, 108,705 solid elements, and the weld length was 300 mm. The X and Y directions are defined as plate width direction and welding direction, respectively.

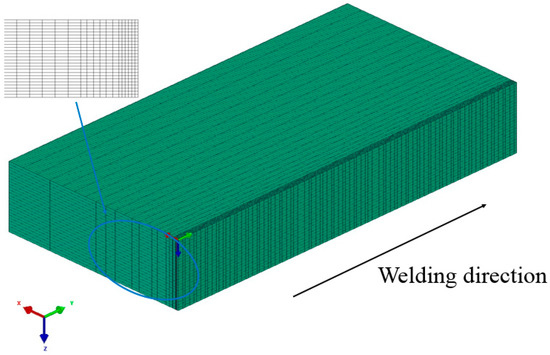
Figure 5. Finite element meshing for the local welded joint.

3.3. Heat Source Model

Welding deformation trend, deformation degree, tensile strength, and crack sensitivity were the most concerned targets in actual production, and most of the targets were closely related to material properties and temperature thermal cycle curve of the welding process. Therefore, the accuracy of the welding thermal cycle curve was the prerequisite to ensure the reliability of other simulation results.

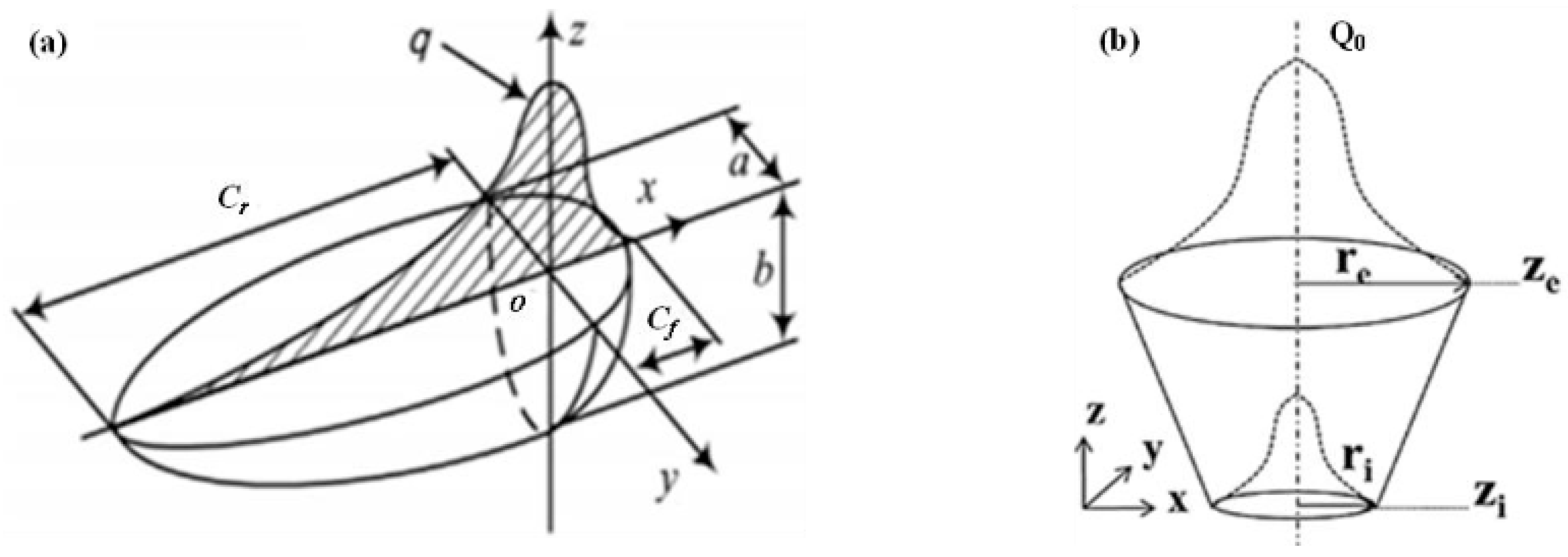
The 50 mm austenitic stainless steel EBW butt joint was obtained by a single pass. Considering the effect of the EBW keyhole, the traditional heat source model (3D Gaussian heat source) [16] and composite heat source (double ellipsoid heat source superimposed on 3D Gaussian heat source) [10,17] were investigated in this study, as presented in Figure 6b and Figure 7 respectively.

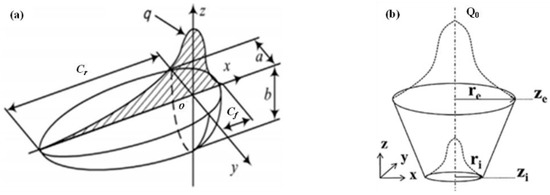
Figure 6. Traditional heat source model: (a) double ellipsoid heat source, (b) 3D Gaussian heat source. Reproduced from [16,18], with permission from Ji-Jun Xin, 2022.

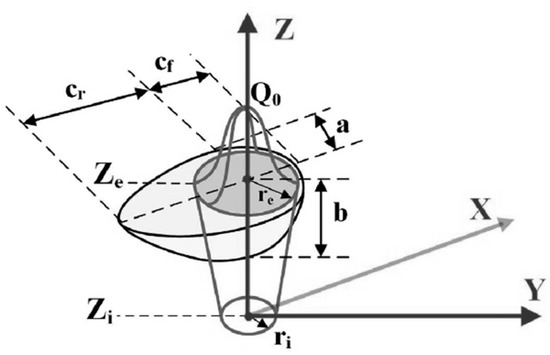
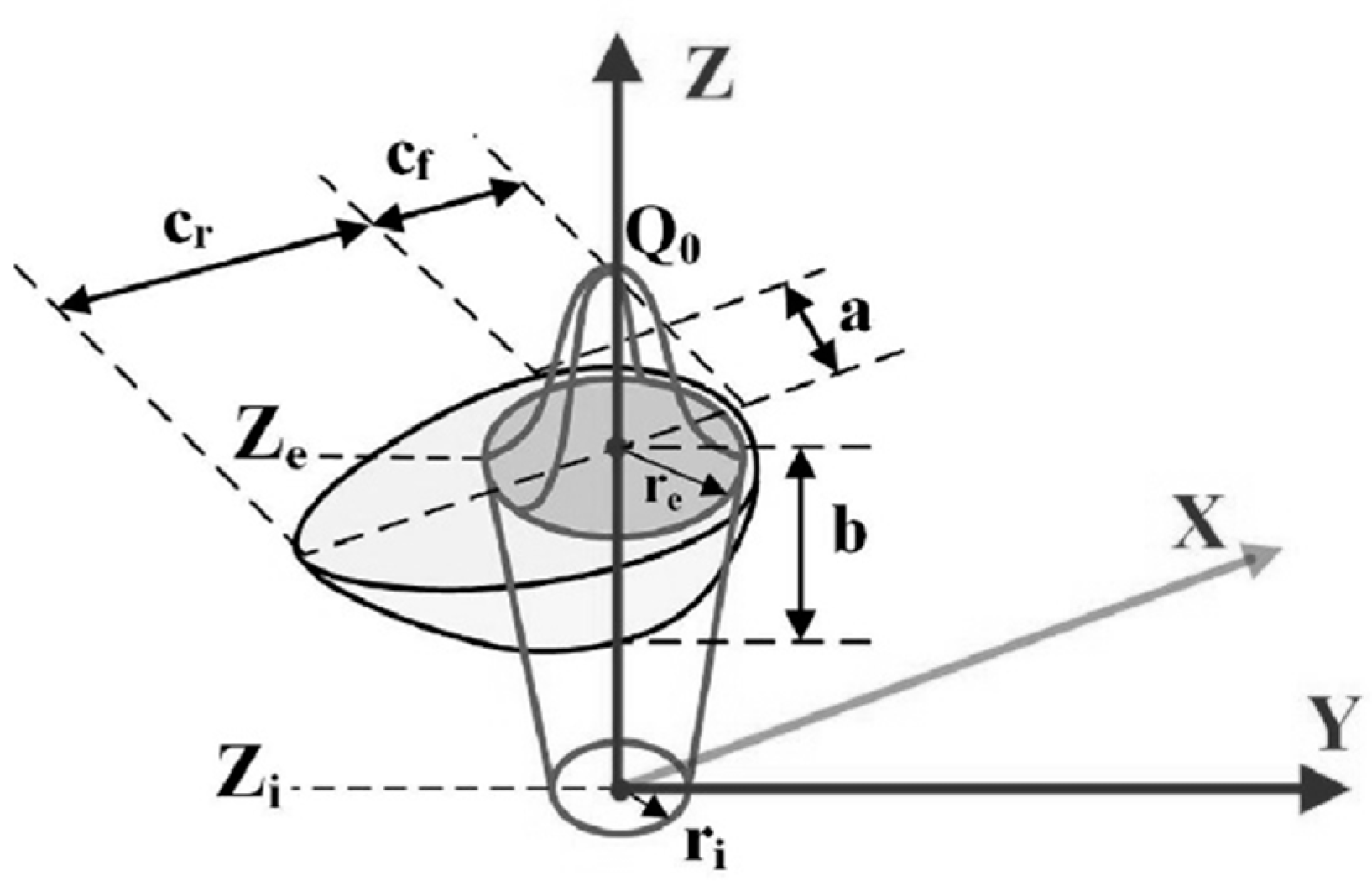
Figure 7. Composite heat source (double ellipsoid heat source superimposed on 3D Gaussian heat source). Reproduced from [10], with permission from Elsevier, 2019.

Assuming that the double ellipsoid heat source energy is $Q_{v1}$, the 3D Gaussian heat source energy is $Q_{v2}$ in Figure 7, then the heat flux distribution in the front half ellipsoid of the double ellipsoid heat source model can be expressed by the following formula [16]:

$$q_f(x,y,z)=\frac{6\sqrt{3}{f}_f{Q}_{v1}}{ab{c}_f\pi \sqrt{\pi }}\exp \left(-\frac{3x^2}{c_f{}^2}-\frac{3y^2}{a^2}-\frac{3z^2}{b^2}\right),x\ge 0$$

(14)

The heat flux distribution in the back half ellipsoid of the double ellipsoid heat source model is:

$$q_r(x,y,z)=\frac{6\sqrt{3}{f}_r{Q}_{v1}}{ab{c}_r\pi \sqrt{\pi }}\exp \left(-\frac{3x^2}{c_r{}^2}-\frac{3y^2}{a^2}-\frac{3z^2}{b^2}\right),x<0$$

(15)

The heat input of the front half ellipsoid in the double ellipsoid heat source model is:

$$\begin{array}{l}2{\int }_0^{\infty }{q}_f(x,y,z)dxdydz\\ =2\frac{6\sqrt{3}\left(f_f{Q}_{v1}\right)}{ab{c}_f\pi \sqrt{\pi }}{\int }_0^{\infty }\exp \left(-\frac{3x^2}{c_f{}^2}\right)dx{\int }_0^{\infty }\exp \left(-\frac{3y^2}{a^2}\right)dy{\int }_0^{\infty }\exp \left(-\frac{3z^2}{b^2}\right)dz\\ =2\times \frac{6\sqrt{3}\left(f_f{Q}_{v1}\right)}{ab{c}_f\pi \sqrt{\pi }}\times \frac{c_f}{\sqrt{3}}\frac{\sqrt{\pi }}{2}\times \frac{a}{\sqrt{3}}\frac{\sqrt{\pi }}{2}\times \frac{b}{\sqrt{3}}\frac{\sqrt{\pi }}{2}\\ =\frac{1}{2}\left(f_f{Q}_{v1}\right)\end{array}$$

(16)

Similarly, the heat input of the back half ellipsoid in the double ellipsoid heat source model is:

$$\begin{array}{l}2{\int }_0^{\infty }{q}_r(x,y,z)dxdydz\\ =\frac{1}{2}\left(f_r{Q}_{v1}\right)\end{array}$$

(17)

where $a$, $b$, $c_f$ and $c_r$ are shape parameters of the double ellipsoid heat source model, $f_f$ and $f_r$ are heat flux distribution coefficient of front and back ellipsoids, in addition, $f_f+f_r=2$. During the EBW welding process, the focal position is in the 1/3 of the thickness for 50 mm thick plate. Set $a$ and $b$ to 4 mm and 16 mm, respectively.

As presented in Figure 6b, the heat flux distribution of the 3D Gaussian heat source model can be expressed by the following formula [18]:

$$q\left(r,z\right)=\frac{9Q_{v2}{e}^3}{\pi \left(e^3-1\right)}\times \frac{1}{\left(z_e-z_i\right)\left(r_e{}^2+r_e{r}_i+r_i{}^2\right)}\exp \left(-\frac{3r^2}{r_o{}^2}\right)$$

(18)

$$r_0=r_0(z)=r_i+\left(r_e-r_i\right)\frac{z-z_i}{z_e-z_i}$$

(19)

where $z_e$ and $z_i$ are Z coordinate of the upper and lower surface of the welding plate, $r_e$ and $r_i$ are heat flux distribution radius of upper and lower surfaces. Geometric parameters of heat source are repeatedly modified in accordance with the prospective target, finally set $r_e$ and $r_i$ to 6 mm and 3 mm, respectively.

Figure 7 illustrates the composite heat source, the heat input can be shown as follows:

$$Q_R=Q_{v1}+Q_{v2}$$

(20)

3.4. Material Properties and Boundary Condition

The testing coupon was made of austenitic steel 316L, with a density at room temperature of 7.98 × 10³ kg/m³ and a specific heat capacity of 0.502 J/(g·K). During the welding simulation, as physical and mechanical properties of materials and material properties at a high temperature need to be taken into account. Table 3 provides the thermophysical properties of 316L at a high temperature. The thermophysical properties are obtained through JMatPro (Sente Software, Guildford, UK).

Table 3. The thermophysical properties of 316L at high temperature.

Temperature (°C)	Thermal Conductivity	Specific Heat (J/g·K)	Density (kg/m3)	Coefficient of Thermal Expansion (10−6 mm/K)	Elastic Modulus (GPa)	Poisson’s Ratio	Yield Strengths (MPa)	Tensile Strengths Limit (MPa) (1% Strain)
20	13.31	0.470	7966	15.24	195.1	0.267	278	325
200	16.33	0.508	7893	16.43	185.7	0.290	193	226
400	19.47	0.550	7814	17.44	172.6	0.322	154	180
600	22.38	0.592	7724	18.21	155.0	0.296	141	165
800	25.07	0.634	7630	18.83	131.4	0.262	130	153
900	26.33	0.655	7583	19.11	116.8	0.24	86	100
1000	27.53	0.676	7535	19.38	100.1	0.229	45	53
1100	28.67	0.698	7486	19.66	81.1	0.223	22	23
1200	29.76	0.719	7436	19.95	59.5	0.223	13	15
1420	31.95	0.765	7320	20.7	2.0	0.223	3	3.3
1460	320	0.765	7320	20.7	2.0	0.223	3	3.3

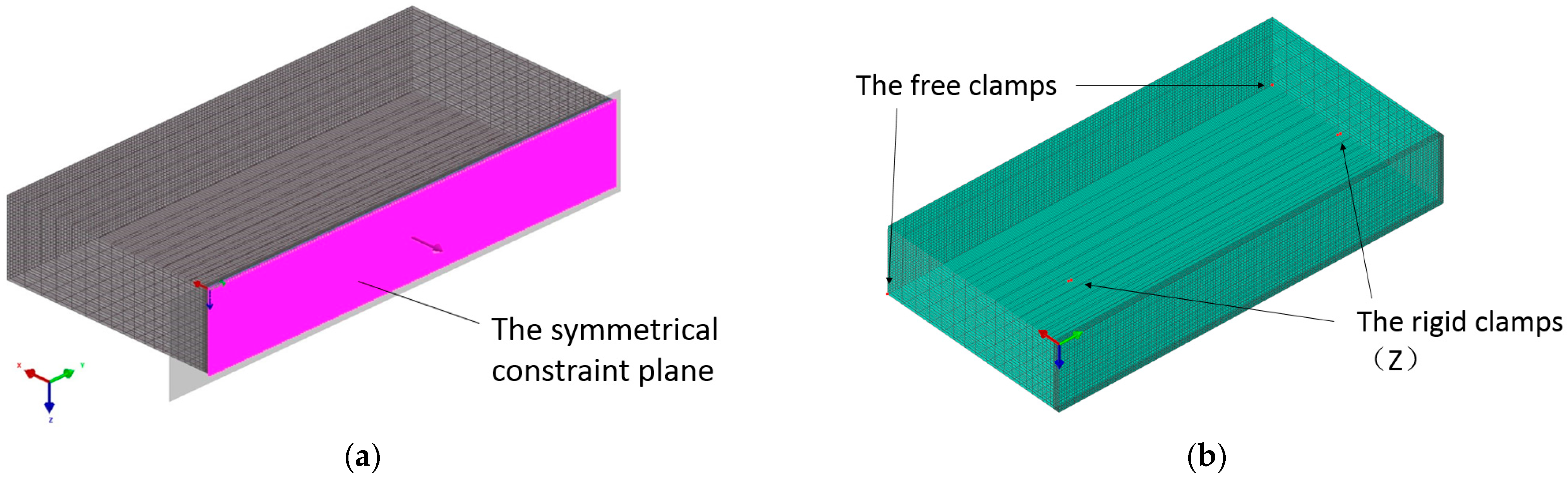
It can be seen from Figure 8a that the weld center plane along the weld direction and perpendicular to the upper surface of the plate was defined as the symmetrical constraint plane in welding simulation settings. The clamping position depends on the actual welding conditions, show as Figure 8b. The initial temperature was 20 °C. It was assumed that the convection loss was 0 W/m² in the vacuum. The heat density of the heat source was loaded on the solid element, while the surface effect element was used to consider the boundary radiation condition.

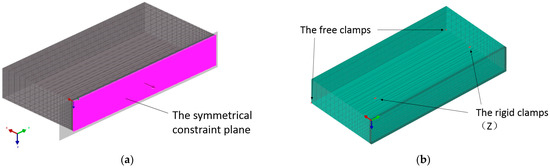
Figure 8. The constraints for the simulation: (a) symmetric constraint settings for simulation of local welded joint, (b) clamping positions for free clamps and rigid clamps.

Thermal radiation loss was carried out by use of Stefan–Boltzmann’s Law, and radiation heat transfer density can be expressed as:

$$q=\sigma \epsilon (T^4-T_{\alpha }{}^4)$$

(21)

where $\sigma$ is constant, $\epsilon$ is surface radiation efficiency and the empirical values of 0.8, $T_{}$ is workpiece temperature, $T_{\alpha }$ is ambient temperature.

3.5. Simulation Result

3.5.1. Temperature Field Simulation Results

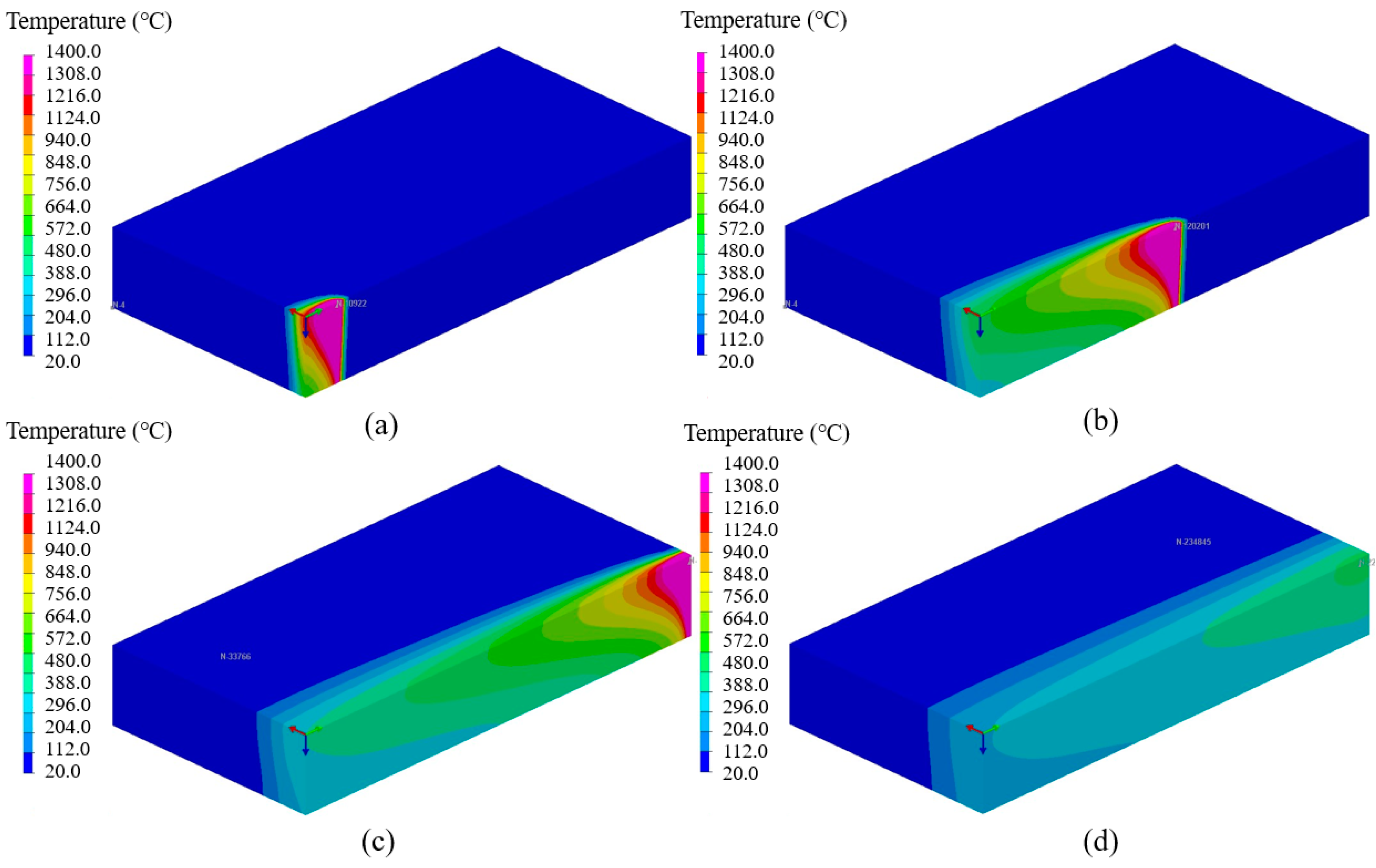
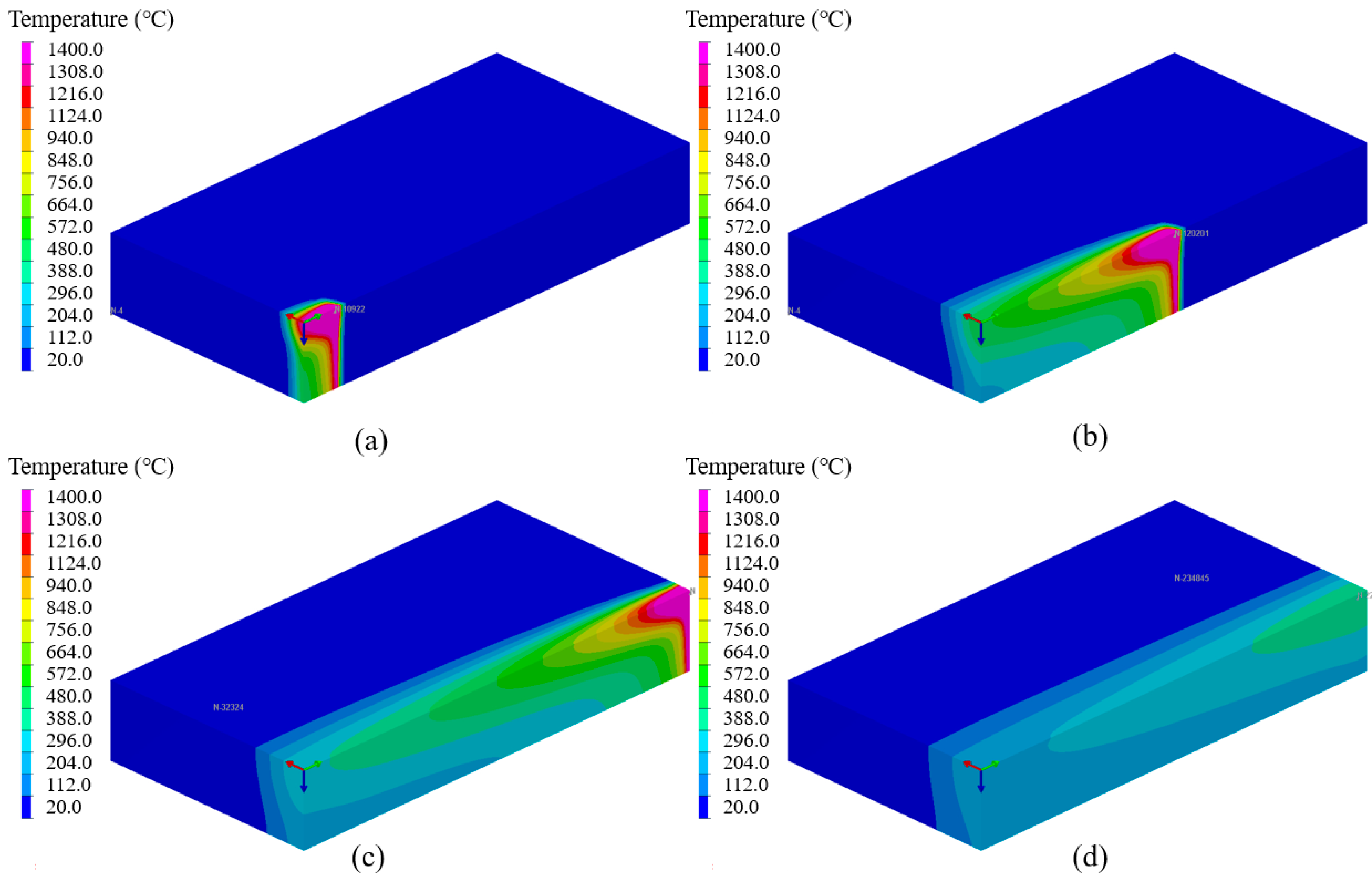
Figure 9 and Figure 10 are the transient temperature contours results of the 3D Gaussian heat source and composite heat source model after welding for 5, 30, 60, and 100 s, respectively. The upper temperature limited set as 1400 °C, which was the austenitic stainless steel melting point, and the purple part in the temperature field results was the metal melting state, namely the weld pool. It can be seen that after the heat source started to move, the temperature at the heat source center on the test plate rose sharply to above the boiling point temperature, the temperature around the weld rose unevenly, and the weld depth was deepening. With the heat source moving, the electron beam just penetrated the plate, and the molten pool reached a quasi-stationary state. With the heat source away, the temperature of the test plate decreased rapidly, and the molten metal solidified to the weld.

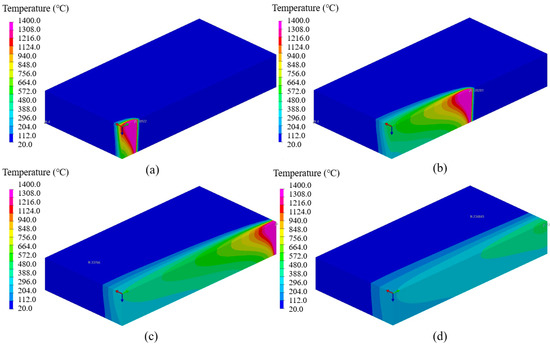
Figure 9. The simulated transient temperature contours using 3D Gaussian heat source at different times: (a) 5 s, (b) 30 s, (c) 60 s, (d) 100 s.

Figure 10. The simulated transient temperature contours using a composite heat source at different times: (a) 5 s, (b) 30 s, (c) 60 s, (d) 100 s.

The density of isotherms can reflect the temperature gradient on the test panel. It can be seen from Figure 9 that the 3D Gaussian heat source had dense isotherms and a large temperature gradient in front of the heat source but sparse isotherms and a slight temperature gradient behind the heat source. The weld pool was cone-shaped in the cross-section of the weld center. In conclusion, the energy distribution of the electron beam was concentrated, forming a circle of long oval isotherms near the center, and the weld pool and heat-affected zone were narrow.

It is apparent from Figure 10 that the simulation results of the composite heat source are similar to those of the 3D Gaussian heat source. The isotherms in front of the heat source were dense, but the difference between them was that the bottom of the molten pool was narrow, the weld seam was nail shaped, and the top was relatively wide. The weld pool morphology simulated by the composite heat source was more consistent with the actual electron beam weld forming mechanism. That was when the electron beam moved, the keyhole also moved with the beam current, the metal in front of the keyhole continuously melted and evaporated rapidly under the heating effect of the keyhole and the molten metal moved backward along both sides of the keyhole under the action of steam. Finally, a weld formed with the heat source away. A circle of long oval isotherms was formed near the center, and the weld pool and heat-affected zone were narrow. The simulation results of the composite heat source had a strong energy concentration characteristics and could better reflect the EBW keyhole compared with the 3D Gaussian heat source.

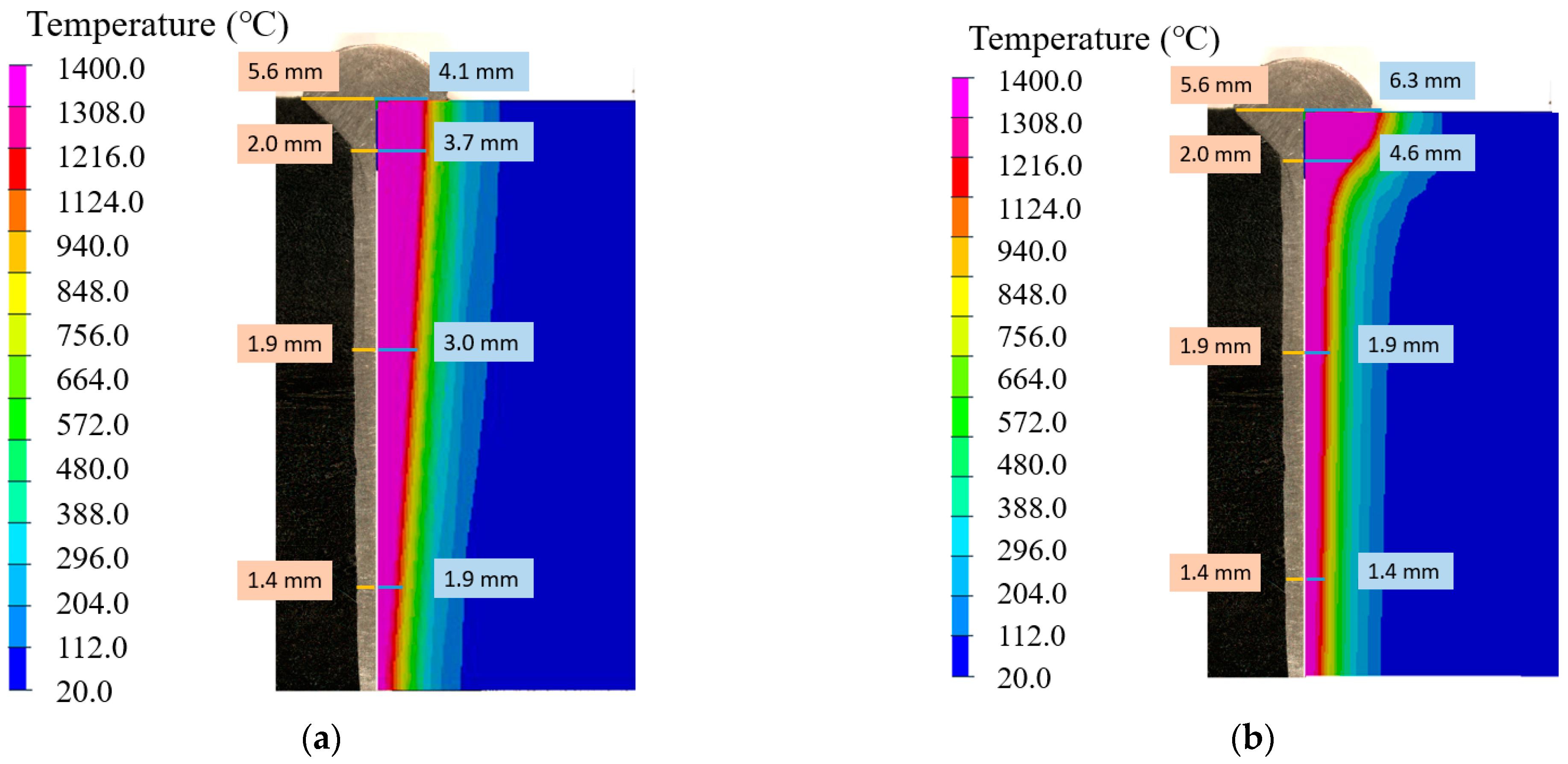
Figure 11 compares the cross-section temperature contour maps of the two simulation results with the actual weldment. The temperature above 1400 °C in the figure (purplish-red in the figure) was the simulated weld pool profile, indicated that the composite heat source calculated weld pool was funnel-shaped, which was consistent with the actual weld morphology. In summary, the simulation result of the composite heat source was more reliable than the 3D Gaussian heat source.

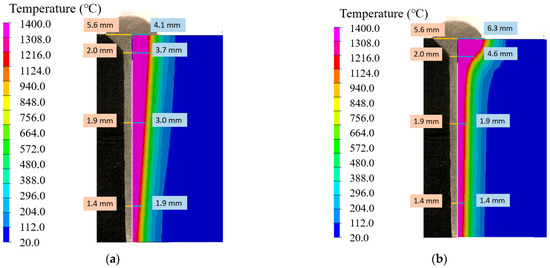
Figure 11. Comparison between simulation and experiment on weld cross-section using: (a) 3D Gaussian heat source, (b) composite heat source.

3.5.2. Extraction of Welding Thermal Cycle Curve

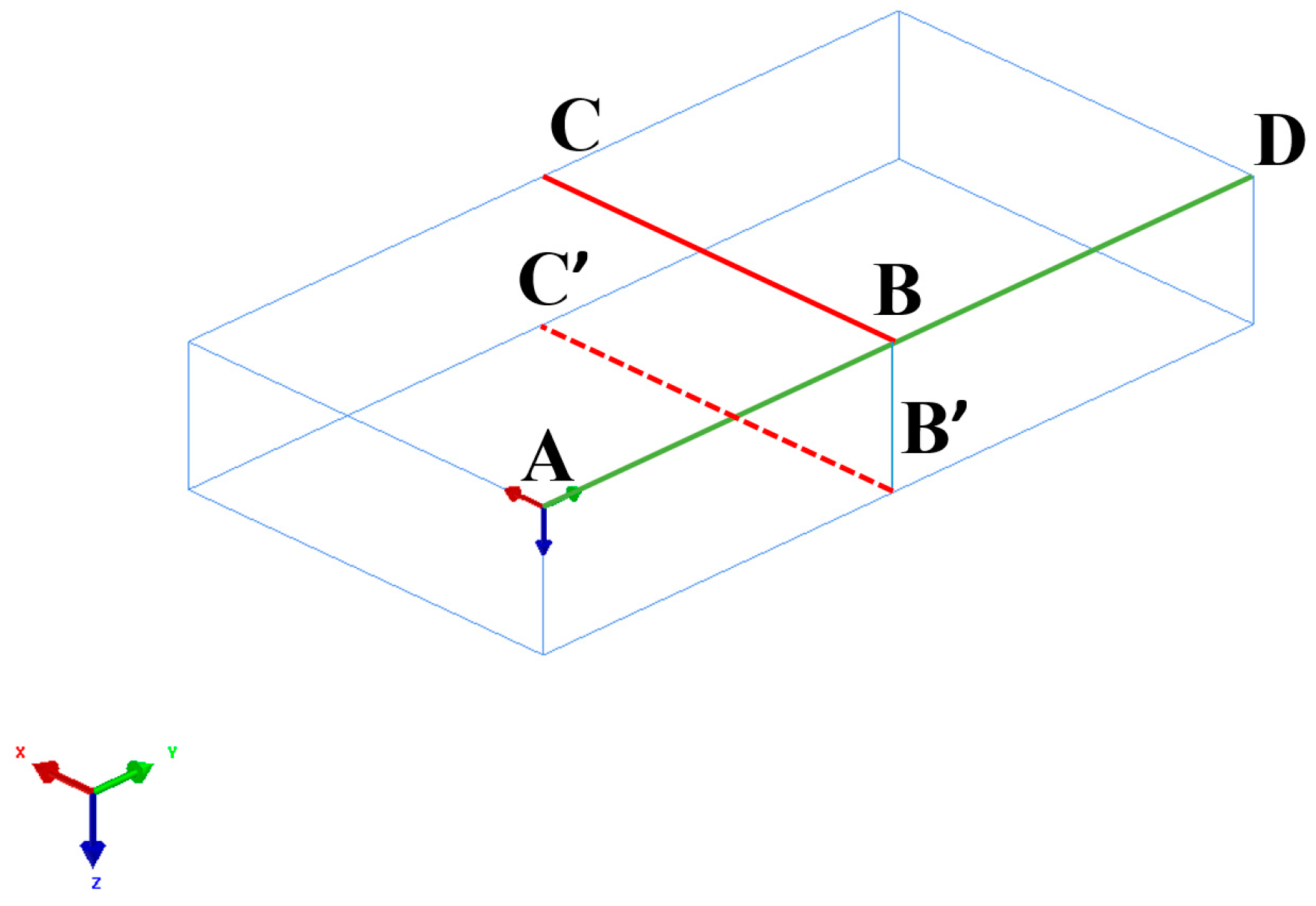
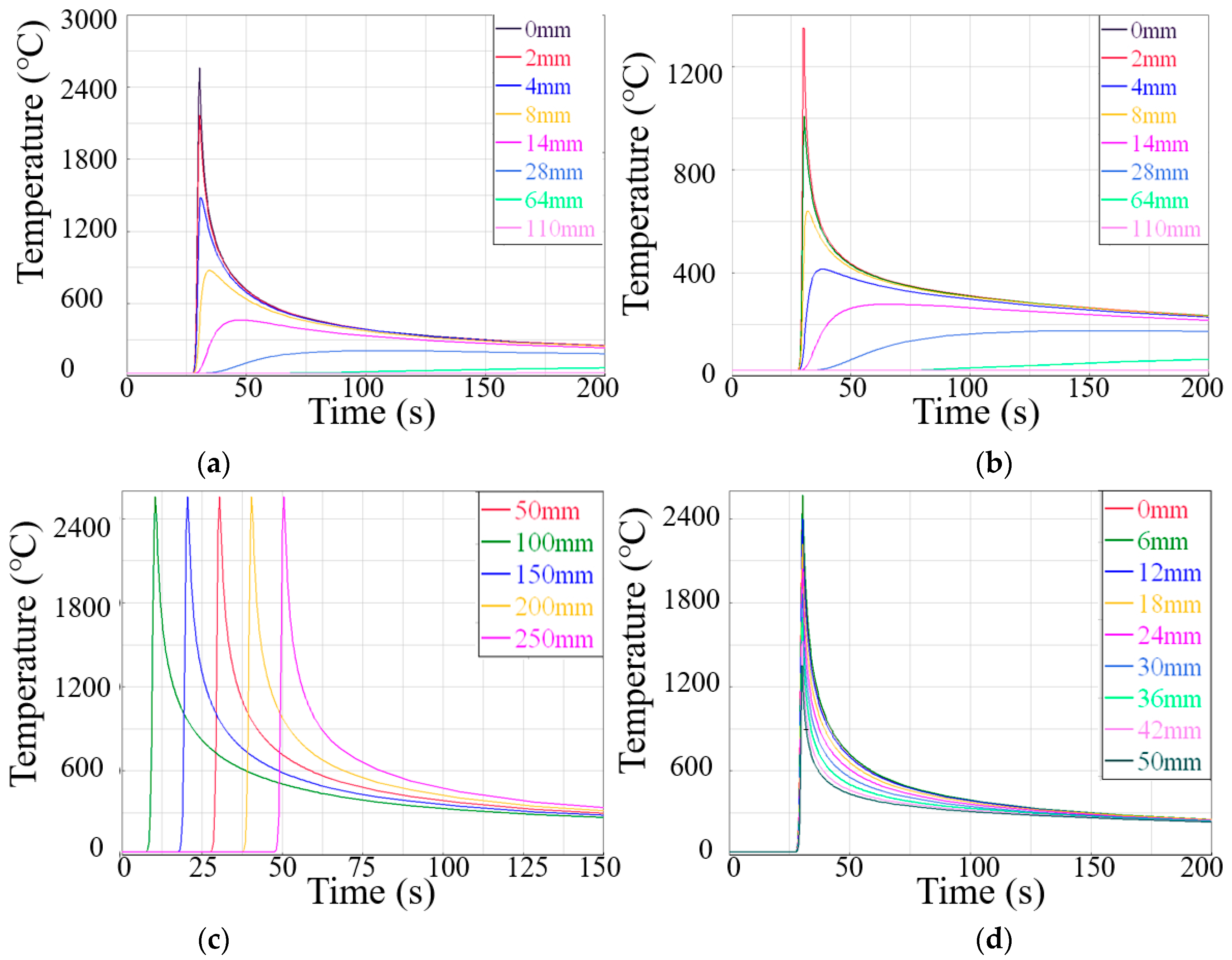
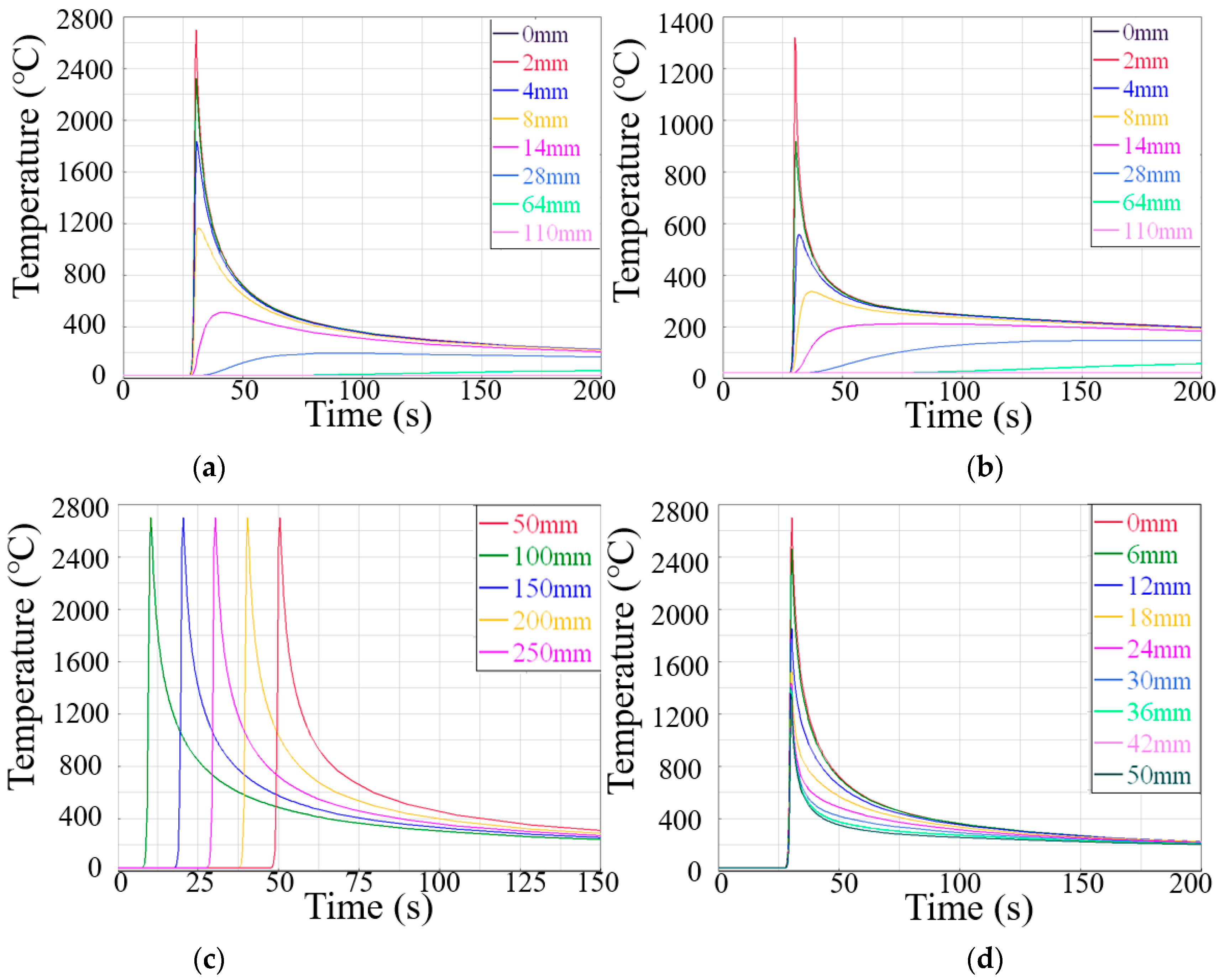
According to the different paths indicated in Figure 12, the welding thermal cycle curves of different positions near the weld are obtained by simulation, as shown in Figure 13a–d and Figure 14a–d.

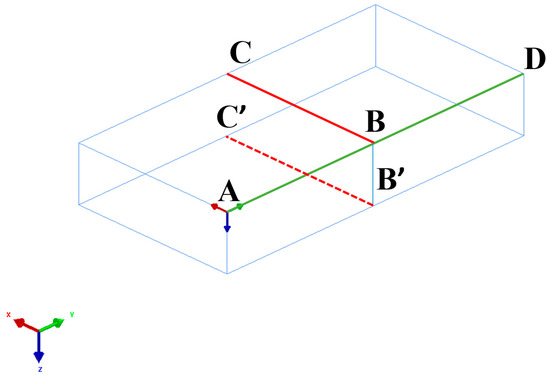
Figure 12. Schematic diagram of path BC, B′C′, AD, BB′.

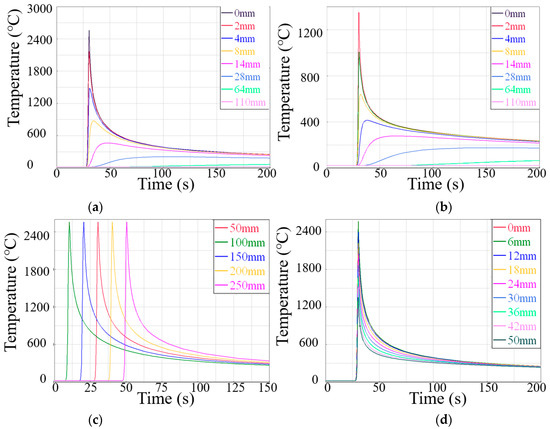
Figure 13. The simulated thermal cycle curve (°C) using the 3D Gaussian heat source in different paths: (a) BC, (b) B′C′, (c) AD, (d) BB′.

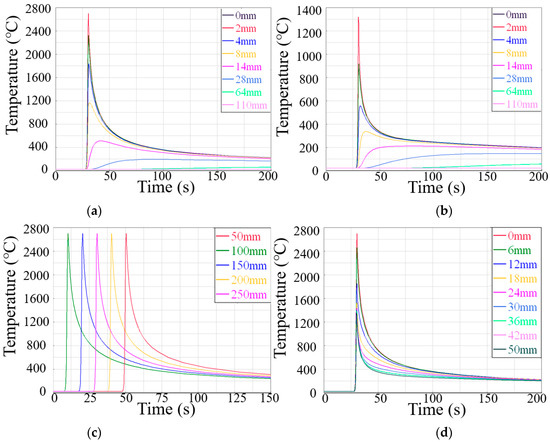
Figure 14. The simulated thermal cycle curve (°C) using the composite heat source in different paths: (a) BC, (b) B′C′, (c) AD, (d) BB′.

Figure 13a,b and Figure 14a,b are the welding thermal cycle curves simulation results of two heat source models on the upper and lower surfaces of the sample from the weld center to heat-affected zone. The several variation trends of the two simulation results were nearly the same. The welding thermal cycle curve of the weld and its vicinity showed a sudden upward trend in a short time with the approaching of the EBW heat source. The temperature near the weld decreased rapidly, and the temperature reduction rate tended to be slow with distance from the heat source. The temperature of the point far away from the weld varied steadily, and the peak temperature was low. It was found that the peak temperature of the thermal cycle curve of the lower surface was much lower than that of the upper surface. All the conclusions above proved that EBW had the characteristics of concentrated energy density and narrow weld, with the maximum heating/cooling rates of 690 °C·s⁻¹/557 °C·s⁻¹ during welding.

Figure 13c and Figure 14c are the simulation results in the welding direction. It can be seen from the figure that the results of the two heat sources were alike. Each node’s temperature and heat cycle curve were similar in a quasi-steady state—the temperature rose sharply first and then decreased rapidly. It is worth noting that the cooling rate was significantly lower than the heating rate due to the continuous effect of the welding heat source on the plate and the low thermal conductivity of austenitic stainless steel, which could lead to slow heat dissipation.

Figure 13d and Figure 14d are the simulation results in the penetration direction. The peak temperature of the node from top to bottom gradually decreased, but all higher than the melting temperature of 1400 °C, the primary cause was the distance from the heat source. The different shapes of the two welding heat sources had a slight impact on welding heat cycle curves. The main difference was that the combined heat source cooling speed after the heat source left was high. This phenomenon was probably due to a more narrow range of the composite heat source than the 3D Gaussian heat source. Moreover, the temperature change rate and temperature gradient of the welding heat cycle curve at different welding positions determined the inhomogeneity of microstructure and mechanical properties.

3.5.3. The Stress–Strain Field Results

The above analysis indicated that the simulation results of the composite heat source model were more approached the actual EBW process. Therefore, only the stress–strain field results of the composite heat source and comparing it with the plate butt welding residual stresses test will be discussed in this section. The findings could provide a reliable theoretical basis and experimental parameters for the numerical simulation of the tailor welding process for the port stub.

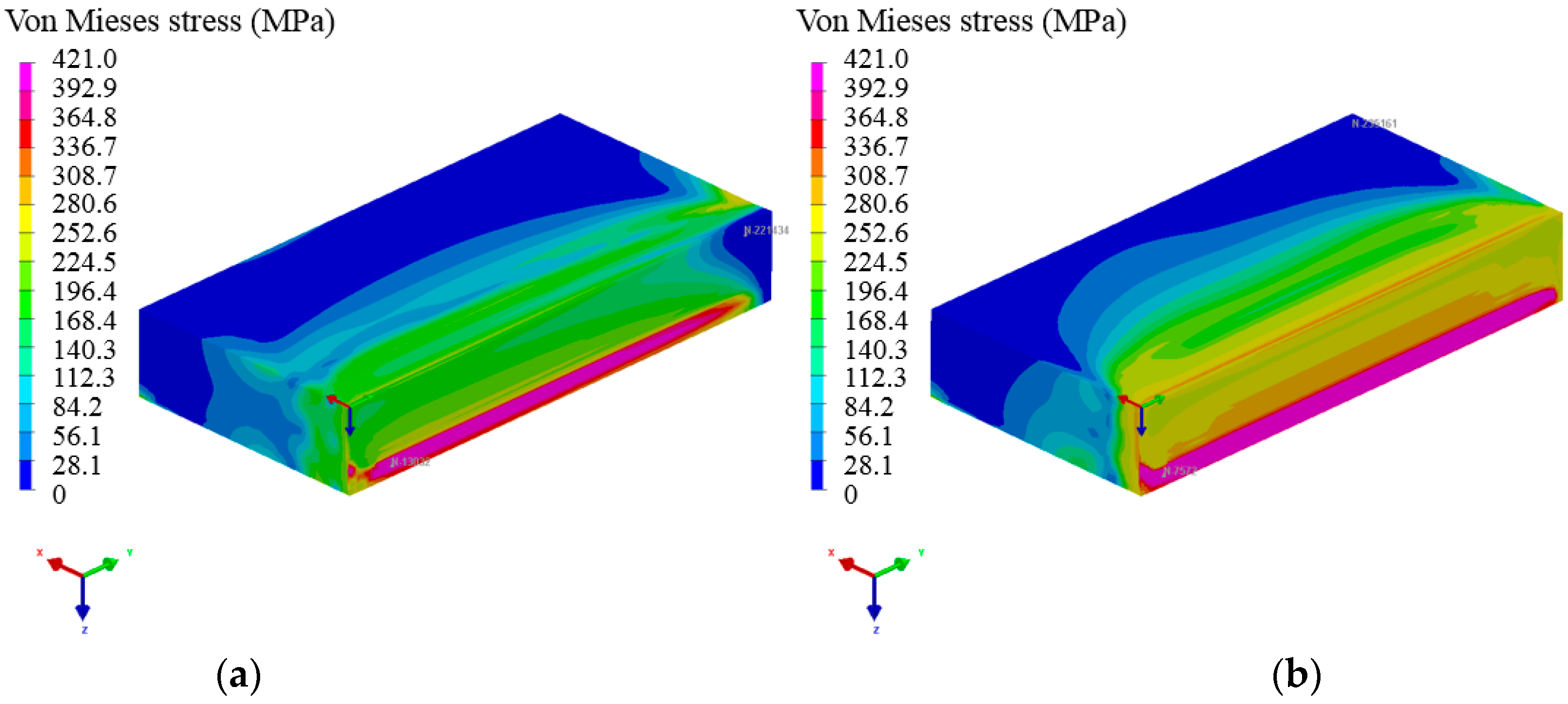
In SYSWELD, the results of stress–strain were obtained by sequential coupling method using the results of the temperature field. Figure 15a,b presents the distribution of nodes’ stresses at 60 s and 600 s after welding. During welding, the temperature around the weld was high, leading to the expansion of metals. The temperature dropped after welding, resulting in the tensile stresses with the metal cooling shrinkage. With the metal cooled to room temperature, the residual stresses increased gradually. The weld and its nearby residual stresses were higher, but the residual stresses far away from the weld were low, and the maximum residual stresses existed at the bottom of the weld.

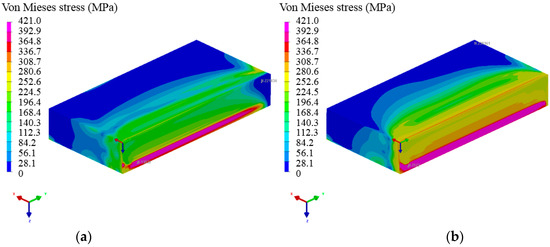
Figure 15. The simulated stresses contour maps at a time of: (a) 60 s, (b) 600 s.

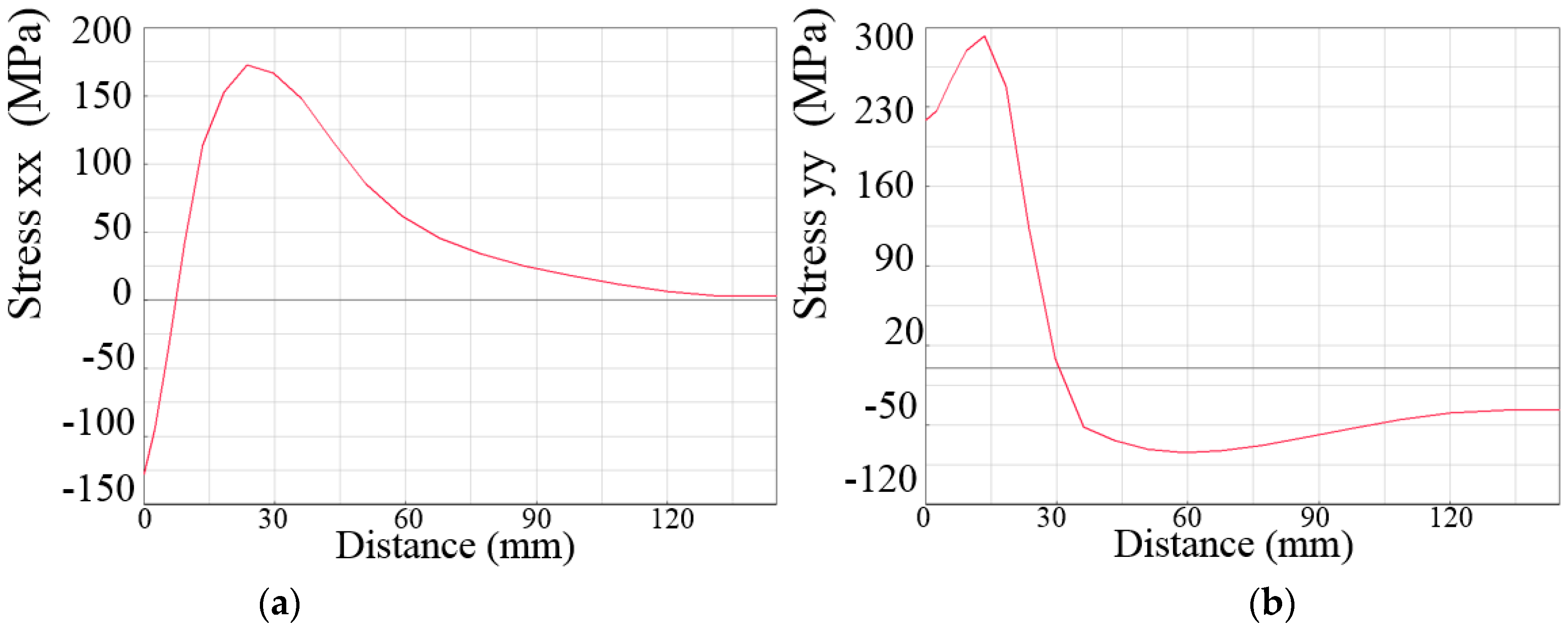
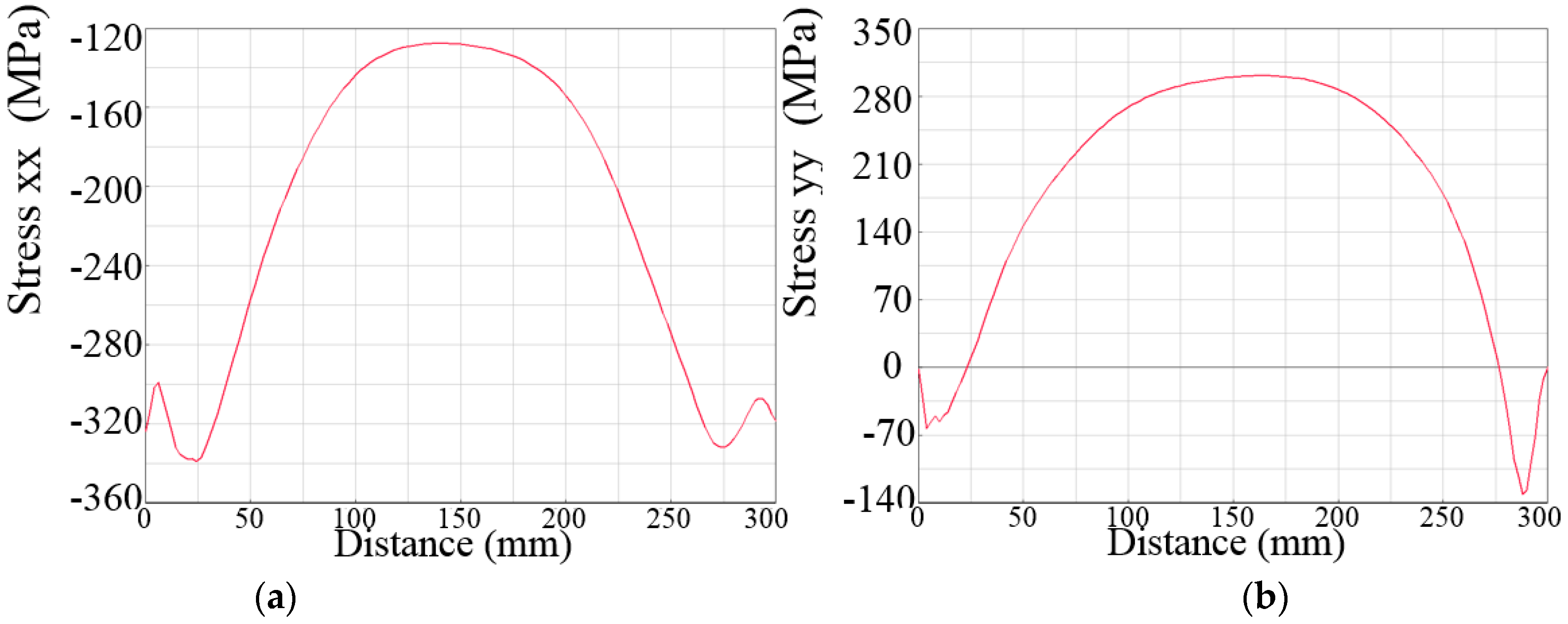
Figure 16 and Figure 17 illustrate the residual stresses distribution in BC and AD directions after welding. It can be seen from Figure 16a that the transverse residual stresses in the weld area (within 7 mm from the weld centerline) were compressive stresses, and excess of the weld area were tensile stresses. The tensile stresses reached a maximum stress of 175 MPa at about 24 mm away from the weld centerline and then decreased to 0 MPa. The rigidly fixed samples caused the transverse restraint to be enormous, so most residual stresses in the BC direction were tensile stresses. In Figure 16b, the longitudinal residual stresses gradually transited from tensile stresses to compressive stresses in the BC direction and gradually decreased to 0.

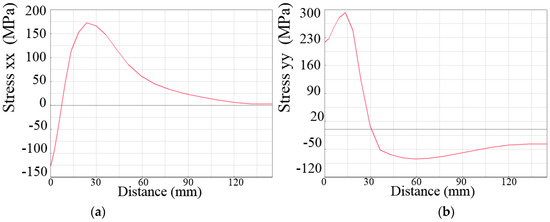
Figure 16. The simulated distribution of residual stresses in BC direction: (a) transverse, (b) longitudinal.

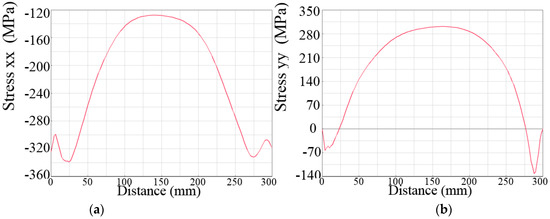
Figure 17. The simulated distribution of residual stresses in AD direction: (a) transverse, (b) longitudinal.

The transverse and longitudinal residual stresses resulted from the cooling shrinkage. As shown in Figure 17a, the transverse residual stresses along the welding direction were mainly compressive stresses. Furthermore, the compressive stresses increased at both ends of the weld and then decreased. Figure 17b shows that the longitudinal residual stresses changed from tensile stresses to compressive stresses. In the middle of the weld, the longitudinal residual stresses were positive with the maximum value of 302 MPa, while at both ends of the weld, it was compressive stresses. That change was owing to the constraints at both ends.

3.5.4. Welding Residual Stresses Test

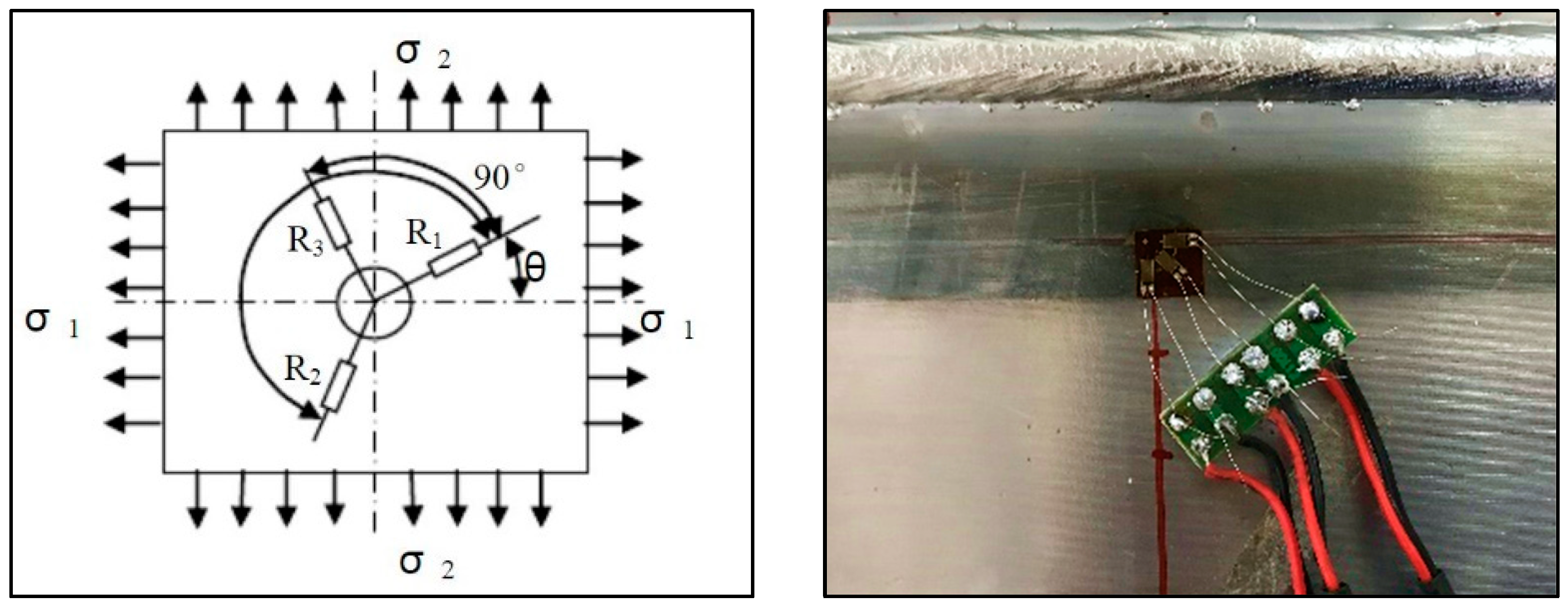
Two 316L austenitic stainless steel thick plates with dimensions of 300 mm × 150 mm × 50 mm were welded under the same constraint conditions and experimental parameters and then cooled to room temperature. The residual surface stresses of the EBW plate were measured by the blind hole method (Figure 18). The test uses the haokeneng stress detector HK21B (Huayun Electromechanical Technology Co., Ltd., Shandong, China). Drill a small hole in the position to be measured. Because the residual stress near the small hole is released, the residual stress field near the hole area changes. As long as the strain change in the local area is measured, the residual stress value at the borehole before release can be calculated.

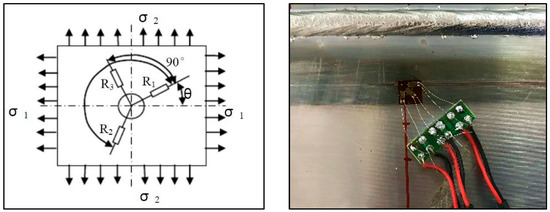
Figure 18. Residual stresses measurement by blind hole method (σ is stress, R is the resistor).

The measured strain in three directions are ε₁, ε₂, ε₃, then the residual stress σ_max, σ_min can be calculated by the following formulas [19]:

$${\sigma }_{\max }=\frac{{\epsilon }_1+{\epsilon }_3}{4A}+\frac{\sqrt{2}}{4B}\sqrt{{({\epsilon }_1-{\epsilon }_3)}^2+{\left[2{\epsilon }_2-{({\epsilon }_1+{\epsilon }_3)}^2\right]}^2}$$

(22)

$${\sigma }_{\min }=\frac{{\epsilon }_1+{\epsilon }_3}{4A}-\frac{\sqrt{2}}{4B}\sqrt{{({\epsilon }_1-{\epsilon }_3)}^2+{\left[2{\epsilon }_2-{({\epsilon }_1+{\epsilon }_3)}^2\right]}^2}$$

(23)

where A, B are the strain release coefficient, which can be obtained by Kirsch theory [19].

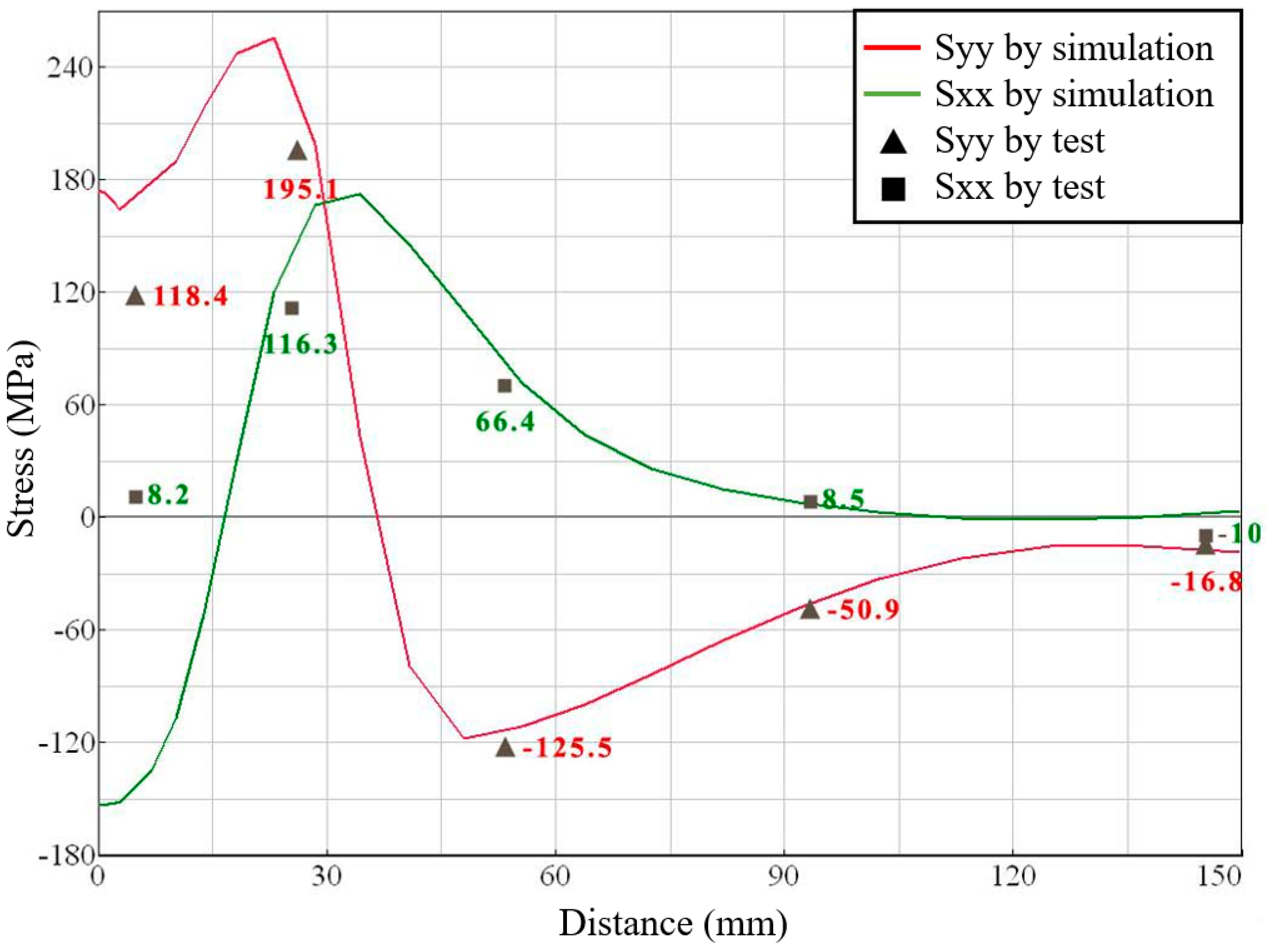
The residual stresses of BC and AD paths were collected and compared with the simulation data above, as presented in Figure 19.

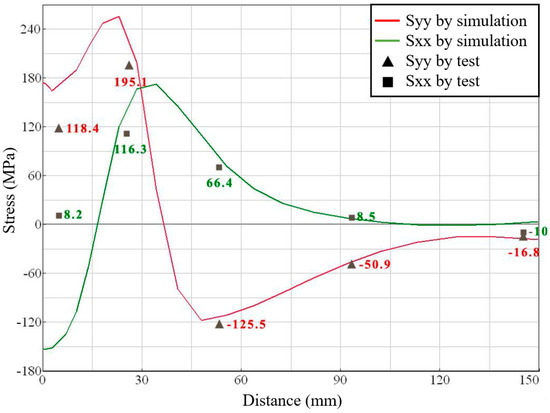
Figure 19. Comparison of test and simulation residual stresses results in BC path.

From the graph above, we can see that the simulation results of the BC path on the upper surface of the test plate were close to the test results, showing the same change trend, which could verify the reliability and validity of the simulation method. The maximum difference of stress was 15 MPa, except for the weld center. The residual stresses measurement in the weld center needs to remove the weld reinforcement, which released the residual stresses in the weld. Above all, the test results were consistent with the variation of simulated residual stresses that verified the model’s reliability.

4. Mechanism Analysis of Microstructure Heterogeneity

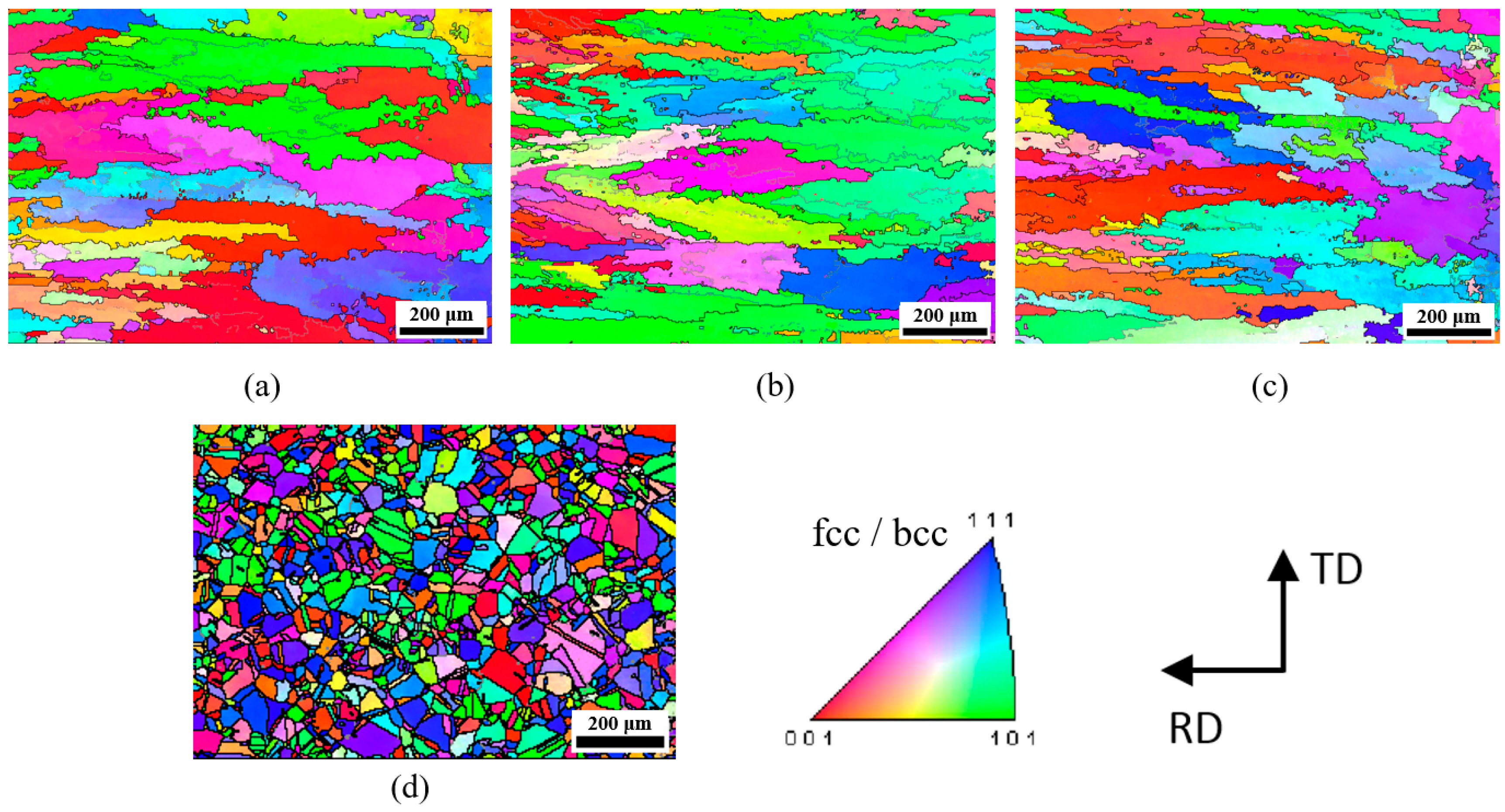
In order to further examine the microstructure in different positions of the EBW welded joint, the grain size and crystallographic orientation were analyzed using EBSD, the sampling location as shown in Figure 3. The inverse pole figure (IPF) maps are presented in Figure 20, indicating the orientation distribution of grains. It can be clearly observed that the microstructure of the weld metal (WM) was composed of coarse columnar grains; this was obviously different from the base metal (BM), which was composed of fine equiaxed grains. Meanwhile, there are a certain number of twins in base metal. The WM was concentrated toward the <001> and <101>, while the grain orientation of the base metal is not obvious.

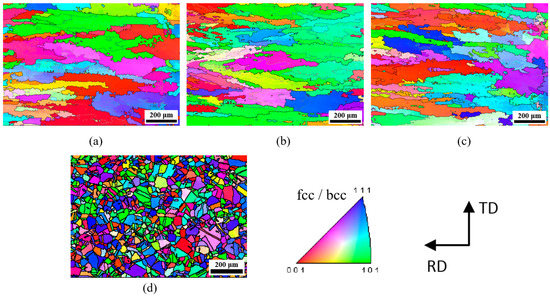
Figure 20. IPF maps of: (a) “a” sample, (b) “b” sample, (c) “c” sample, (d) base metal. See the sampling location of the EBSD samples in Figure 3.

The kernel average misorientation (KAM) of the welded joint is shown in Figure 21. The KAM result can be used to characterize the degree of plastic deformation of the material [20]. The brighter the color in the figure, the greater the residual stress. It can be found that low angle grain boundaries (2–10°, gray line in Figure 20a–c) had higher residual stress compared with high angle grain boundaries (>10°, black line in Figure 20a–c). The sample “a” at the top of the welded joint was easier to form stress concentration than the bottom sample “c”, possibly due to the greater heat input at the top. Compared with the simulation results, it can be seen from Figure 14d that the weld at the top is closer to the heat source, the temperature peak is higher, and the temperature change is more intense.

Figure 21. KAM maps of: (a) “a” sample, (b) “b” sample, (c) “c” sample.

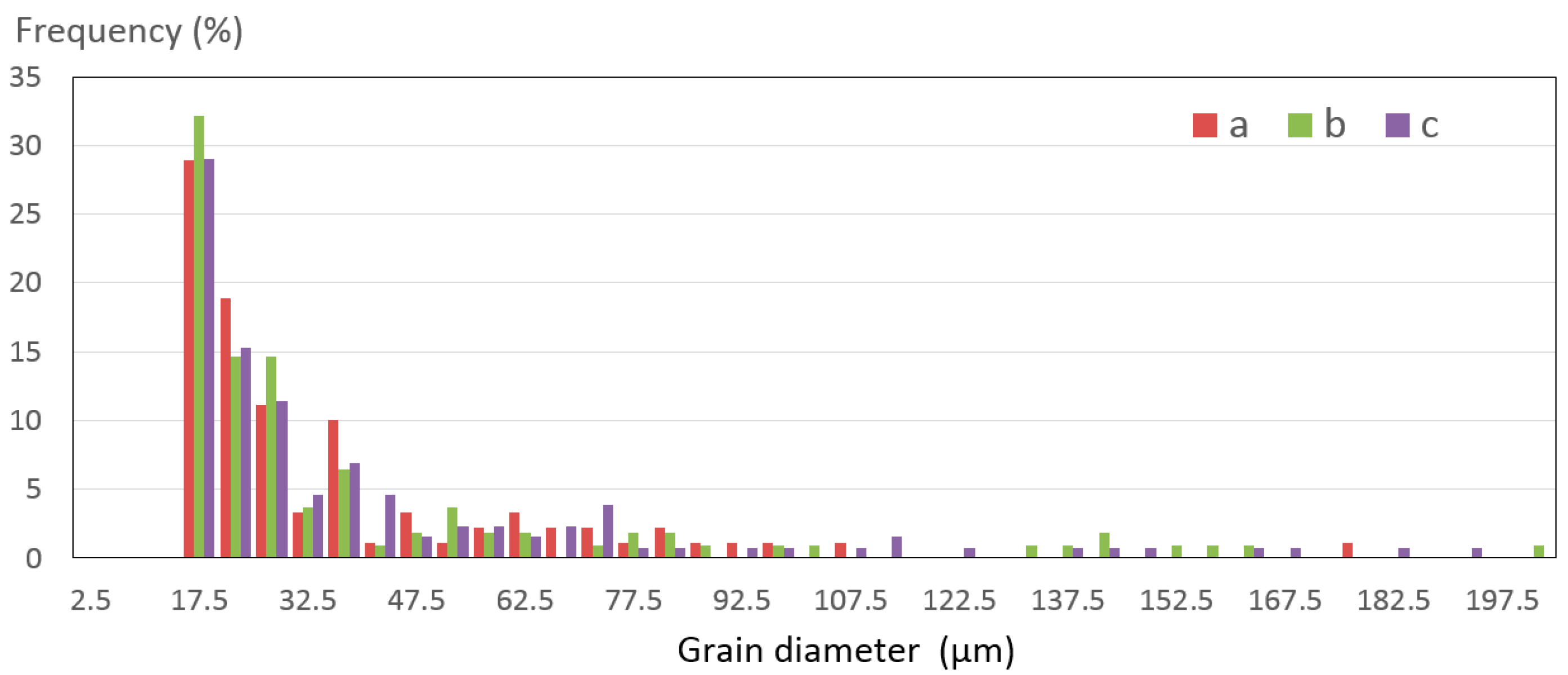
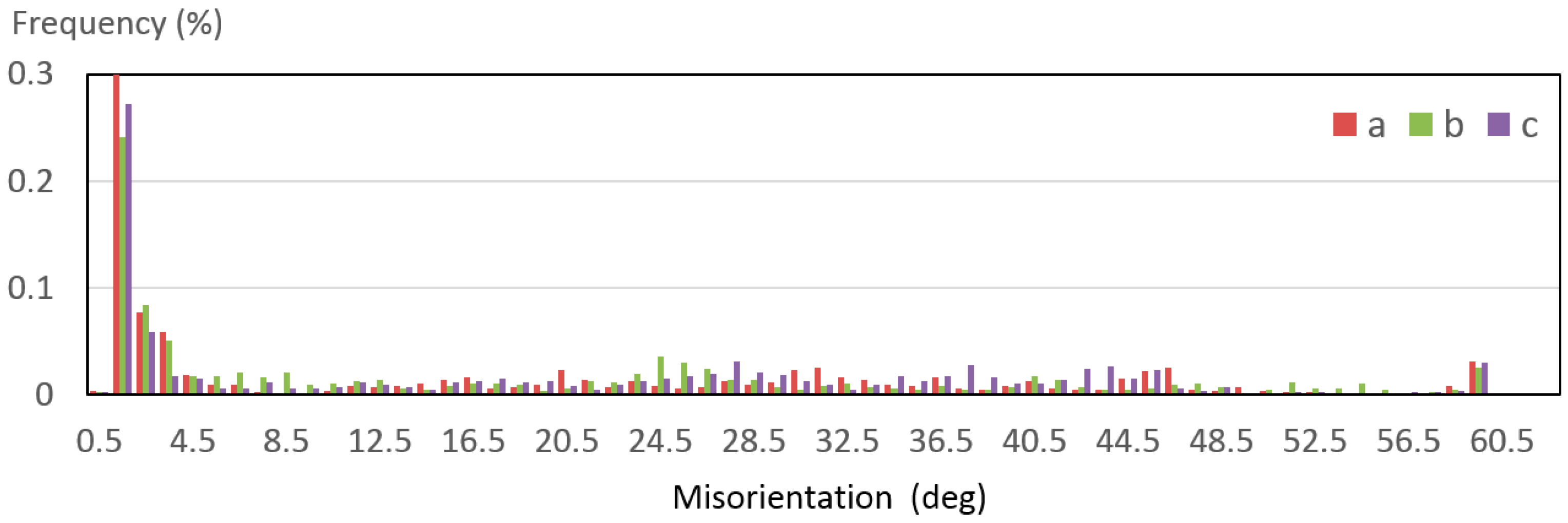
To obtain more microstructural information on the EBW weld joint, the distribution of the grain diameter and the misorientation angle were obtained by EBSD data, as shown in Figure 22 and Figure 23. Figure 22 shows the equivalent grain size. The grain size of EBW welded joint WM is mainly distributed in the range of 15–80 μm and no obvious change in grain size can be seen from the statistical chart. Combined with the PIF map, the grain morphology at the bottom (sample c) is more slender than others without considering low-angle grain boundaries. This may be related to the higher cooling rate at the bottom, and is also confirmed by simulation results, Figure 14d. The distribution of misorientation angle in Figure 23 indicated that the grain boundary misorientation of WM is mainly distributed within 0.5–5°. The formation of the low angle grain boundary was due to the influence of thermal driving force on the grains by welding and the release of deformation stored energy in the grains [21].

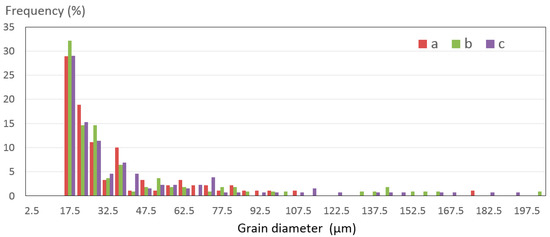
Figure 22. The grain diameter of the welded joint.

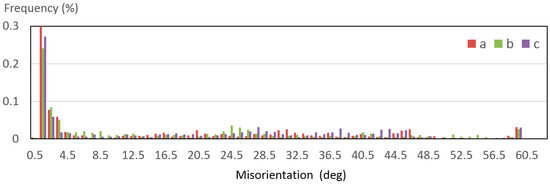
Figure 23. Misorientation angle in the welded joint.

5. Conclusions

• Compared with the 3D Gaussian heat source, the combined heat sources simulation was closer to the weld cross-section of the EBW 50 mm 316L butt welding.
• The results showed that the welding thermal cycle curves of different positions in the penetration direction are different, and EBW was a rapid heating and cooling process with the maximum heating/cooling rates of 690 °C·s⁻¹/557 °C·s⁻¹ during welding.
• The numerical and measurement results of the residual stresses showed a similar trend (the maximum difference of stress was 15 MPa, except for the weld center), confirming the reliability of the simulation results.
• The differences in heating and cooling rates were the main reason for the inhomogeneity of microstructure and mechanical properties. The grains of the weld turned into a group of large columnar crystals. The inhomogeneities in microstructure mainly showed that the sample at the top of the WM was easier to form stress concentration than the bottom sample.