Machine Learning Assisted Prediction of Microstructures and Young’s Modulus of Biomedical Multi-Component β-Ti Alloys
Abstract
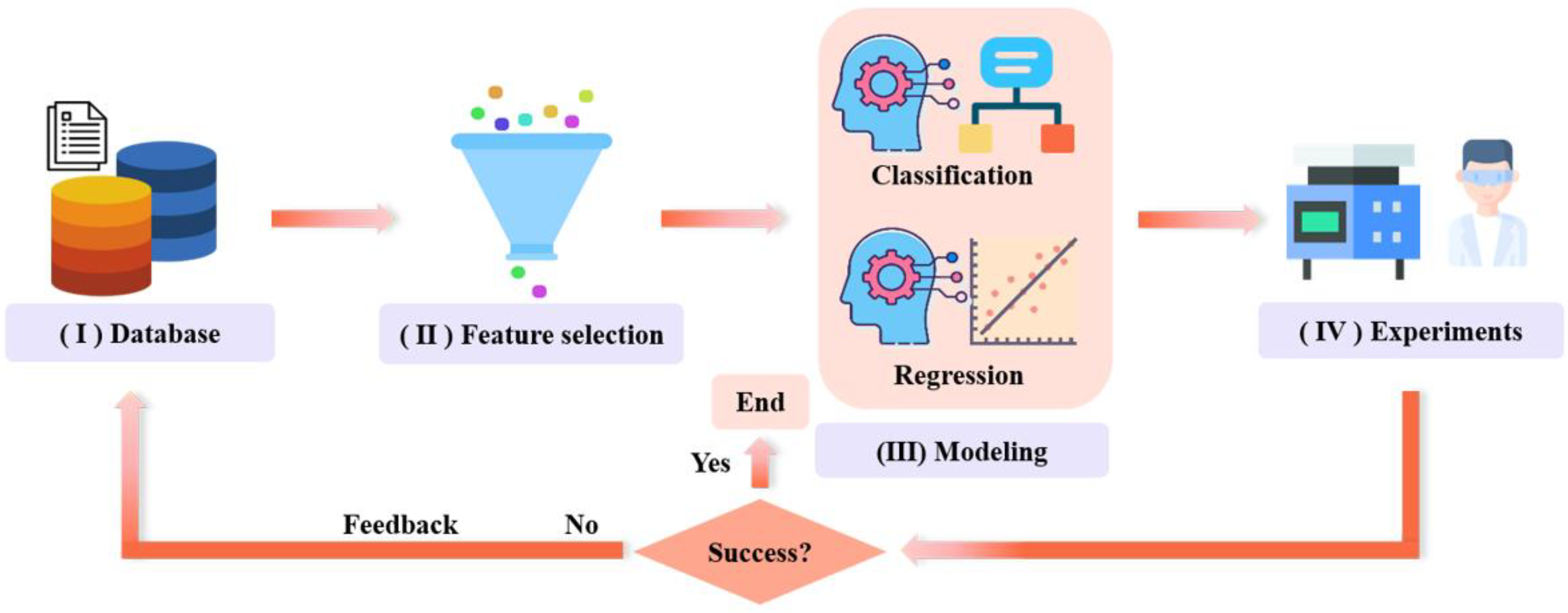
:1. Introduction
2. Materials and Methods
2.1. Approach
- (1)
- Collecting biomedical Ti alloys data reported in the relevant literature as machine learning databases were used for the training and testing of models.
- (2)
- It is difficult to interpret the prediction results only considering the chemical compositions as features for machine learning. The interpretability and robustness of the model could be improved by embedding the material domain knowledge into the machine learning. Some features were suggested, including heat-treatment process parameters, and macroscopic as well as microscopic properties. Following the feature selection method, the most relevant features were retained.
- (3)
- A classification model and a regression model were built. The classification model was utilized to predict the microstructures, and the regression model was utilized to predict Young’s modulus. It is worth noting that there were many hyperparameters to optimize the modeling process. The Bayesian optimization algorithm was used to automatically find the hyperparameters. The optimized hyperparameters were then subjected to machine learning training.
- (4)
- Once the models were built, the microstructures and Young’s modulus of the β-Ti alloys could be predicted in the virtual space of the compositions and heat-treatment process. To validate the performances of the models, the multi-component Ti alloys were prepared. Subsequently, the observation of the microstructures and mechanical property test were performed. Finally, the experimental results were fed back into the machine learning databases for the next iteration and design.
2.2. Datasets
| Features | Formula | Range | Description |
|---|---|---|---|
| Ti | - | 30~92 | mass% |
| Nb | - | 0~45 | mass% |
| Sn | - | 0~14 | mass% |
| Mo | - | 0~20 | mass% |
| Zr | - | 0~41 | mass% |
| Ta | - | 0~16 | mass% |
| Cr | - | 0~14 | mass% |
| Mn | - | 0~18 | mass% |
| Temp | - | Solution temperature | |
| Time | - | Solution time | |
| Atomic weight [37] | |||
| Density [37] | |||
| Metallic radius [37] | |||
| Heat of fusion [38] | |||
| Heat of vaporization [38] | |||
| Specific heat [38] | |||
| Melting point [37] | |||
| Bulk modulus [38] | |||
| Shear modulus [38] | |||
| Young’s modulus [38] | |||
| Thermal conductivity [37] | |||
| Lattice volume [37] | |||
| Valence electrons [39] | |||
| Difference of atomic radii [37] | |||
| Pauling electronegativity [37] | |||
| Mixing enthalpy [37] | |||
| Mixing entropy [37] | |||
| Free energy of mixing [37] | |||
| Ω parameter [37] | |||
| Molybdenum equivalence [40] | |||
| Effective nuclei charges [41] | |||
| Bond order [41] | |||
| d-orbital energy level [41] | |||
| Bonding | Approximate interatomic bonding force [41] |
2.3. Feature Selection
- (1)
- Create an empty subset of features.
- (2)
- Randomly insert a new feature into the previous subset of features. The newly inserted feature can be kept as part of the subset of features, if it improves the performance of the model.
- (3)
- Repeat (2) until no more features are available to be inserted into the subset of features.
- (4)
- Keep repeating processes (1)–(3) until no more optimal subsets of the features are found.
2.4. Model Building
2.4.1. Classification Models
2.4.2. Regression Models
2.4.3. K-Fold Cross Validation
2.4.4. Hyperparameter Optimization
2.4.5. Modeling Method
2.5. Experiment Method
3. Results and Discuss
3.1. Feature Selection
3.1.1. Features Correlation Analysis
3.1.2. Forward Sequential Feature Selection
3.2. The Establishment of the Predicting Models
3.2.1. The Predicting Model of the Microstructures
3.2.2. The Predicting Model of Young’s Modulus
3.3. Feature Importance
3.4. Model Validation
3.4.1. Experimental Validation
3.4.2. Latest Reference Validation
| Index | Composition (wt.%) | Experiment E/GPa | Prediction E/GPa | Error E/GPa | Reference |
|---|---|---|---|---|---|
| #1 | Ti–12Nb–12Zr–12Sn | 42 | 47.68 | 5.68 | [53] |
| #2 | Ti–14Nb–12Zr–12Sn | 51 | 48.98 | −2.02 | [53] |
| #3 | Ti–6Nb–3Mo–12Zr–12Sn | 52 | 50.18 | −1.82 | [53] |
| #4 | Ti–6Nb–6Mo–12Zr–12Sn | 69 | 65.15 | −3.85 | [53] |
| #5 | Ti–26Nb–2Fe | 83 | 78.39 | −4.61 | [54] |
| #6 | Ti–26Nb–2Fe–2Sn | 65 | 66.25 | 1.25 | [54] |
| #7 | Ti–26Nb–2Fe–4Sn | 58 | 59.37 | 1.37 | [54] |
| #8 | Ti–26Nb–2Fe–6Sn | 60 | 59.51 | −0.49 | [54] |
| #9 | Ti–26Nb–2Fe–8Sn | 63 | 62.49 | −0.51 | [54] |
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Niinomi, M.; Liu, Y.; Nakai, M.; Liu, H.; Li, H. Biomedical titanium alloys with Young’s moduli close to that of cortical bone. Regen. Biomater. 2016, 3, 173–185. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Q.; Dong, C.; Liaw, P.K. Structural Stabilities of β-Ti Alloys Studied Using a New Mo Equivalent Derived from [β/(α + β)] Phase-Boundary Slopes. Metall. Mater. Trans. A 2015, 46, 3440–3447. [Google Scholar] [CrossRef]
- Sumitomo, N.; Noritake, K.; Hattori, T.; Morikawa, K.; Niwa, S.; Sato, K.; Niinomi, M. Experiment study on fracture fixation with low rigidity titanium alloy. J. Mater. Sci. Mater. Med. 2008, 19, 1581–1586. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Hady Gepreel, M.; Niinomi, M. Biocompatibility of Ti-alloys for long-term implantation. J. Mech. Behav. Biomed. Mater. 2013, 20, 407–415. [Google Scholar] [CrossRef] [PubMed]
- Eisenbarth, E.; Velten, D.; Müller, M.; Thull, R.; Breme, J. Biocompatibility of β-stabilizing elements of titanium alloys. Biomaterials 2004, 25, 5705–5713. [Google Scholar] [CrossRef] [PubMed]
- Long, M.; Rack, H.J. Titanium alloys in total joint replacement—A materials science perspective. Biomaterials 1998, 19, 1621–1639. [Google Scholar] [CrossRef]
- Niinomi, M. Mechanical properties of biomedical titanium alloys. Mater. Sci. Eng. A 1998, 243, 231–236. [Google Scholar] [CrossRef]
- Sidhu, S.S.; Singh, H.; Gepreel, M.A.-H. A review on alloy design, biological response, and strengthening of β-titanium alloys as biomaterials. Mater. Sci. Eng. C 2021, 121, 111661. [Google Scholar] [CrossRef]
- Li, P.; Ma, X.; Tong, T.; Wang, Y. Microstructural and mechanical properties of β-type Ti–Mo–Nb biomedical alloys with low elastic modulus. J. Alloys Compd. 2020, 815, 152412. [Google Scholar] [CrossRef]
- Wang, P.; Wu, L.; Feng, Y.; Bai, J.; Zhang, B.; Song, J.; Guan, S. Microstructure and mechanical properties of a newly developed low Young’s modulus Ti–15Zr–5Cr–2Al biomedical alloy. Mater. Sci. Eng. C 2017, 72, 536–542. [Google Scholar] [CrossRef]
- Zhao, Z.; Lee, K. Effect of Alloying Elements on Plastic Workability and Corrosion Behavior of Ti-X (X = 6 Co, 8 Cr, 4 Fe, 6 Mn, 10 Mo, and 36 Nb) Binary Alloys. Arch. Met. Mater. 2017, 62, 1185–1190. [Google Scholar] [CrossRef] [Green Version]
- Mehjabeen, A.; Xu, W.; Qiu, D.; Qian, M. Redefining the β-Phase Stability in Ti-Nb-Zr Alloys for Alloy Design and Microstructural Prediction. JOM 2018, 70, 2254–2259. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Niinomi, M.; Nakai, M.; Miyamoto, G.; Furuhara, T. Microstructures and mechanical properties of metastable Ti–30Zr–(Cr, Mo) alloys with changeable Young’s modulus for spinal fixation applications. Acta Biomater. 2011, 7, 3230–3236. [Google Scholar] [CrossRef] [PubMed]
- Liang, S.; Feng, X.; Yin, L.; Liu, X.; Ma, M.; Liu, R. Development of a new β Ti alloy with low modulus and favorable plasticity for implant material. Mater. Sci. Eng. C 2016, 61, 338–343. [Google Scholar] [CrossRef]
- Li, Y.; Yang, C.; Wang, F.; Zhao, H.; Qu, S.; Li, X.; Zhang, W. Biomedical TiNbZrTaSi alloys designed by d-electron alloy design theory. Mater. Des. 2015, 85, 7–13. [Google Scholar] [CrossRef]
- Chen, W.; Li, W.; Du, Y. Investigations on diffusion behaviors in Ti–rich Ti–Nb–Zr–Cr system: Experimental measurement and CALPHAD modeling. Calphad 2018, 62, 223–231. [Google Scholar] [CrossRef]
- Tan, J.; Xu, G.; Tao, X.; Chen, F.; Cui, Y.; Zhou, L. CALPHAD assessment of bio-oriented Ti–Zr–Sn system and experimental validation in Ti/Zr-rich alloys. Calphad 2019, 67, 101686. [Google Scholar] [CrossRef]
- Song, Y.; Xu, D.; Yang, R.; Li, D.; Wu, W.; Guo, Z.X. Theoretical study of the effects of alloying elements on the strength and modulus of β-type bio-titanium alloys. Mater. Sci. Eng. A 1999, 260, 269–274. [Google Scholar] [CrossRef]
- Raabe, D.; Sander, B.; Friák, M.; Ma, D.; Neugebauer, J. Theory-guided bottom-up design of β-titanium alloys as biomaterials based on first principles calculations: Theory and experiments. Acta Mater. 2007, 55, 4475–4487. [Google Scholar] [CrossRef]
- Luo, M.; Liang, L.; Lang, L.; Xiao, S.; Hu, W.; Deng, H. Molecular dynamics simulations of the characteristics of Mo/Ti interfaces. Comput. Mater. Sci. 2018, 141, 293–301. [Google Scholar] [CrossRef]
- Song, J.; Wang, L.; Zhang, L.; Wu, W.; Gao, Z. First-principles molecular dynamics studying the solidification of Ti-6Al-4V alloy. J. Mol. Liq. 2020, 315, 113606. [Google Scholar] [CrossRef]
- Vivanco-Benavides, L.E.; Martínez-González, C.L.; Mercado-Zúñiga, C.; Torres-Torres, C. Machine learning and materials informatics approaches in the analysis of physical properties of carbon nanotubes: A review. Comput. Mater. Sci. 2022, 201, 110939. [Google Scholar] [CrossRef]
- Juan, Y.; Dai, Y.; Yang, Y.; Zhang, J. Accelerating materials discovery using machine learning. J. Mater. Sci. Technol. 2021, 79, 78–190. [Google Scholar] [CrossRef]
- Liu, Y.; Esan, O.C.; Pan, Z.; An, L. Machine learning for advanced energy materials. Energy AI 2021, 3, 100049. [Google Scholar] [CrossRef]
- Yu, J.; Xi, S.; Pan, S.; Wang, Y.; Peng, Q.; Shi, R.; Wang, C.; Liu, X. Machine learning-guided design and development of metallic structural materials. J. Mater. Inform. 2021, 1, 9. [Google Scholar] [CrossRef]
- Pan, S.; Wang, Y.; Yu, J.; Yang, M.; Zhang, Y.; Wei, H.; Chen, Y.; Wu, J.; Han, J.; Wang, C.; et al. Accelerated discovery of high-performance Cu-Ni-Co-Si alloys through machine learning. Mater. Des. 2021, 209, 109929. [Google Scholar] [CrossRef]
- Yu, J.; Guo, S.; Chen, Y.; Han, J.; Lu, Y.; Jiang, Q.; Wang, C.; Liu, X. A two-stage predicting model for γ′ solvus temperature of L12-strengthened Co-base superalloys based on machine learning. Intermetallics 2019, 110, 106466. [Google Scholar] [CrossRef]
- Yu, J.; Wang, C.; Chen, Y.; Wang, C.; Liu, X. Accelerated design of L12-strengthened Co-base superalloys based on machine learning of experimental data. Mater. Des. 2020, 195, 108996. [Google Scholar] [CrossRef]
- Honysz, R. Modeling the Chemical Composition of Ferritic Stainless Steels with the Use of Artificial Neural Networks. Metals 2021, 11, 724. [Google Scholar] [CrossRef]
- Churyumov, A.; Kazakova, A.; Churyumova, T. Modelling of the Steel High-Temperature Deformation Behaviour Using Artificial Neural Network. Metals 2022, 12, 447. [Google Scholar] [CrossRef]
- Yang, F.; Li, Z.; Wang, Q.; Jiang, B.; Yan, B.; Zhang, P.; Xu, W.; Dong, C.; Liaw, P.K. Cluster-formula-embedded machine learning for design of multicomponent β-Ti alloys with low Young’s modulus. npj Comput. Mater. 2020, 6, 101. [Google Scholar] [CrossRef]
- Wu, C.-T.; Chang, H.-T.; Wu, C.-Y.; Chen, S.-W.; Huang, S.-Y.; Huang, M.; Pan, Y.-T.; Bradbury, P.; Chou, J.; Yen, H.-W. Machine learning recommends affordable new Ti alloy with bone-like modulus. Mater. Today 2019, 34, 41–50. [Google Scholar] [CrossRef]
- Xiong, S.; Li, X.; Wu, X.; Yu, J.; Gorbatov, O.I.; Di Marco, I.; Kent, P.R.; Sun, W. A combined machine learning and density functional theory study of binary Ti-Nb and Ti-Zr alloys: Stability and Young’s modulus. Comput. Mater. Sci. 2020, 184, 109830. [Google Scholar] [CrossRef]
- Zhang, H.; Fu, H.; Zhu, S.; Yong, W.; Xie, J. Machine learning assisted composition effective design for precipitation strengthened copper alloys. Acta Mater. 2021, 215, 117118. [Google Scholar] [CrossRef]
- Yuan, R.; Xue, D.; Xue, D.; Li, J.; Ding, X.; Sun, J.; Lookman, T. Knowledge-Based Descriptor for the Compositional Dependence of the Phase Transition in BaTiO3-Based Ferroelectrics. ACS Appl. Mater. Interfaces 2020, 12, 44970–44980. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, C.; Wang, C.; Antonov, S.; Xue, D.; Bai, Y.; Su, Y. Phase prediction in high entropy alloys with a rational selection of materials descriptors and machine learning models. Acta Mater. 2019, 185, 528–539. [Google Scholar] [CrossRef]
- Xiong, J.; Shi, S.-Q.; Zhang, T.-Y. A machine-learning approach to predicting and understanding the properties of amorphous metallic alloys. Mater. Des. 2020, 187, 108378. [Google Scholar] [CrossRef]
- W.R. Inc. Properties of the Elements. 2021. Available online: https://periodictable.com/Properties/ (accessed on 1 August 2020).
- Guo, S.; Ng, C.; Lu, J.; Liu, C.T. Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys. J. Appl. Phys. 2011, 109, 103505. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B.; Wang, Q.; Wen, D.; Xu, F.; Chen, G.; Dong, C.; Sun, L.; Liaw, P.K. Effects of Nb and Zr on structural stabilities of Ti-Mo-Sn-based alloys with low modulus. Mater. Sci. Eng. A 2017, 687, 1–7. [Google Scholar] [CrossRef]
- You, L.; Song, X. A study of low Young′s modulus Ti–Nb–Zr alloys using d electrons alloy theory. Scr. Mater 2012, 67, 57–60. [Google Scholar] [CrossRef]
- Khaire, U.M.; Dhanalakshmi, R. Stability of feature selection algorithm: A review. J. King Saud Univ. Comput. Inf. Sci. 2019, 34, 1060–1073. [Google Scholar] [CrossRef]
- Bengio, Y.; Grandvalet, Y. Bias in Estimating the Variance of K-Fold Cross-Validation. In Statistical Modeling and Analysis for Complex Data Problems; Duchesne, P., RÉMillard, B., Eds.; Springer: Boston, MA, USA, 2005; pp. 75–95. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3146–3154. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D.D. Hyperopt: A Python Library for Optimizing the Hyperparameters of Machine Learning Algorithms. In Proceedings of the 12th Python in Science Conference, Austin, TX, USA, 24–29 June 2013; p. 20. [Google Scholar]
- Puth, M.-T.; Neuhäuser, M.; Ruxton, G.D. Effective use of Pearson’s product–moment correlation coefficient. Anim. Behav. 2014, 93, 183–189. [Google Scholar] [CrossRef]
- Guo, S.; Liu, C.T. Phase stability in high entropy alloys: Formation of solid-solution phase or amorphous phase. Prog. Nat. Sci. Mater. Int. 2011, 21, 433–446. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Guo, S.; Nieh, T.; Liu, C.; Hirata, A.; Chen, M. Effects of mixing enthalpy and cooling rate on phase formation of AlxCoCrCuFeNi high-entropy alloys. Materialia 2019, 6, 100292. [Google Scholar] [CrossRef]
- Roy, A.; Babuska, T.; Krick, B.; Balasubramanian, G. Machine learned feature identification for predicting phase and Young’s modulus of low-, medium- and high-entropy alloys. Scr. Mater 2020, 185, 152–158. [Google Scholar] [CrossRef]
- Niinomi, M.; Nakai, M.; Hieda, J. Development of new metallic alloys for biomedical applications. Acta Biomater. 2012, 8, 3888–3903. [Google Scholar] [CrossRef]
- Wu, C.-T.; Lin, P.-H.; Huang, S.-Y.; Tseng, Y.-J.; Chang, H.-T.; Li, S.-Y.; Yen, H.-W. Revisiting alloy design of low-modulus biomedical β-Ti alloys using an artificial neural network. Materialia 2022, 21, 101313. [Google Scholar] [CrossRef]
- Li, Q.; Liu, T.; Li, J.; Cheng, C.; Niinomi, M.; Yamanaka, K.; Chiba, A.; Nakano, T. Microstructure, mechanical properties, and cytotoxicity of low Young’s modulus Ti–Nb–Fe–Sn alloys. J. Mater. Sci. 2022, 57, 5634–5644. [Google Scholar] [CrossRef]
- Sakaguchi, N.; Mitsuo, N.; Akahori, T.; Saito, T.; Furuta, T. Effects of Alloying Elements on Elastic Modulus of Ti-Nb-Ta-Zr System Alloy for Biomedical Applications. Mater. Sci. Forum 2004, 449-452, 1269–1272. [Google Scholar] [CrossRef]
- Dai, S.-J.; Wang, Y.; Chen, F.; Yu, X.-Q.; Zhang, Y.-F. Design of new biomedical titanium alloy based on d-electron alloy design theory and JMatPro software. Trans. Nonferrous Met. Soc. China 2013, 23, 3027–3032. [Google Scholar] [CrossRef]









| Model | Features | |||
|---|---|---|---|---|
| Microstructures | Ti | Ta | Temp | Time |
| Young’s modulus | Ti | Ta | Sn | Temp |
| Time | ||||
| Bonding | ||||
| Iteration | Nominal Alloy | Ti | Nb | Ta | Zr | Sn | Mo | |
|---|---|---|---|---|---|---|---|---|
| I-1 | Ti–19Nb–16Ta–7Zr–4Mo | Bal | 22.28 | 15.43 | 4.81 | 0 | 4.77 | 17.5 |
| I-2 | Ti–19Nb–5Ta–1Zr–9Sn | Bal | 21.19 | 6.64 | 0.45 | 9.47 | 0 | 11.6 |
| II-1 | Ti–18Nb–9Ta–11Zr–6Mo | Bal | 19.65 | 10.36 | 8.92 | 0 | 6.52 | 18.4 |
| II-2 | Ti–13Nb–12Ta–10Zr–4Sn | Bal | 10.67 | 12.83 | 11.66 | 4.41 | 0 | 11.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Peng, Q.; Pan, S.; Du, J.; Yang, S.; Han, J.; Lu, Y.; Yu, J.; Wang, C. Machine Learning Assisted Prediction of Microstructures and Young’s Modulus of Biomedical Multi-Component β-Ti Alloys. Metals 2022, 12, 796. https://doi.org/10.3390/met12050796
Liu X, Peng Q, Pan S, Du J, Yang S, Han J, Lu Y, Yu J, Wang C. Machine Learning Assisted Prediction of Microstructures and Young’s Modulus of Biomedical Multi-Component β-Ti Alloys. Metals. 2022; 12(5):796. https://doi.org/10.3390/met12050796
Chicago/Turabian StyleLiu, Xingjun, Qinghua Peng, Shaobin Pan, Jingtao Du, Shuiyuan Yang, Jiajia Han, Yong Lu, Jinxin Yu, and Cuiping Wang. 2022. "Machine Learning Assisted Prediction of Microstructures and Young’s Modulus of Biomedical Multi-Component β-Ti Alloys" Metals 12, no. 5: 796. https://doi.org/10.3390/met12050796
APA StyleLiu, X., Peng, Q., Pan, S., Du, J., Yang, S., Han, J., Lu, Y., Yu, J., & Wang, C. (2022). Machine Learning Assisted Prediction of Microstructures and Young’s Modulus of Biomedical Multi-Component β-Ti Alloys. Metals, 12(5), 796. https://doi.org/10.3390/met12050796






