Recrystallization Mechanism and Processing Map of 18CrNiMo7-6 Alloy Steel during Hot Deformation
Abstract
:1. Introduction
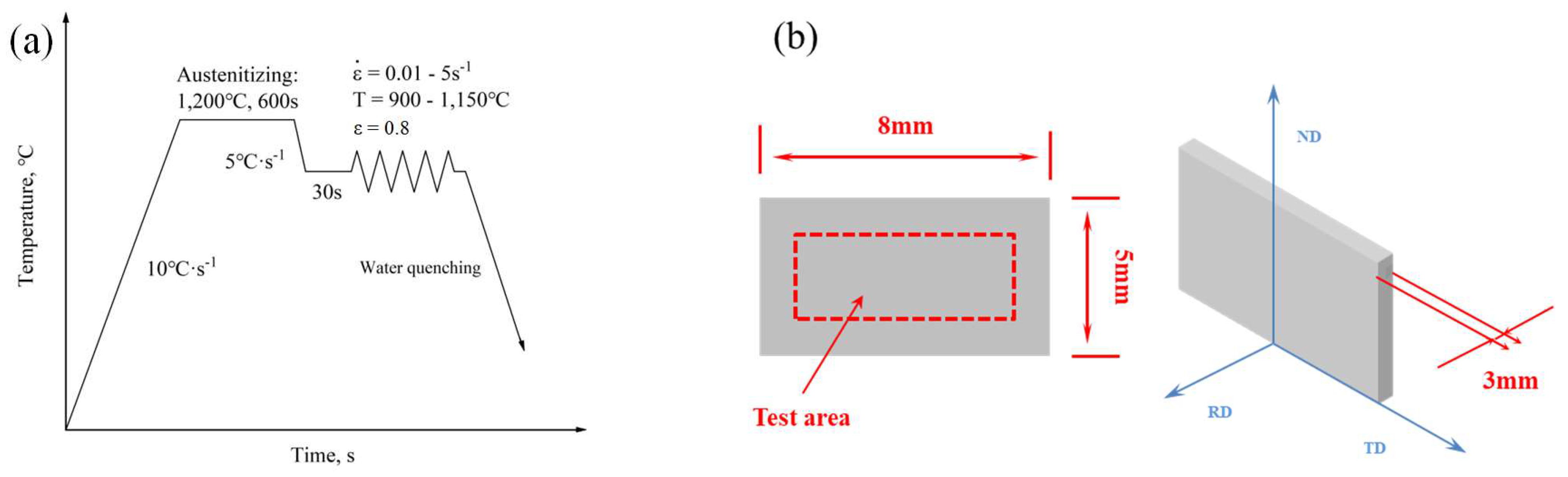
2. Experimental
3. Results and Discussion
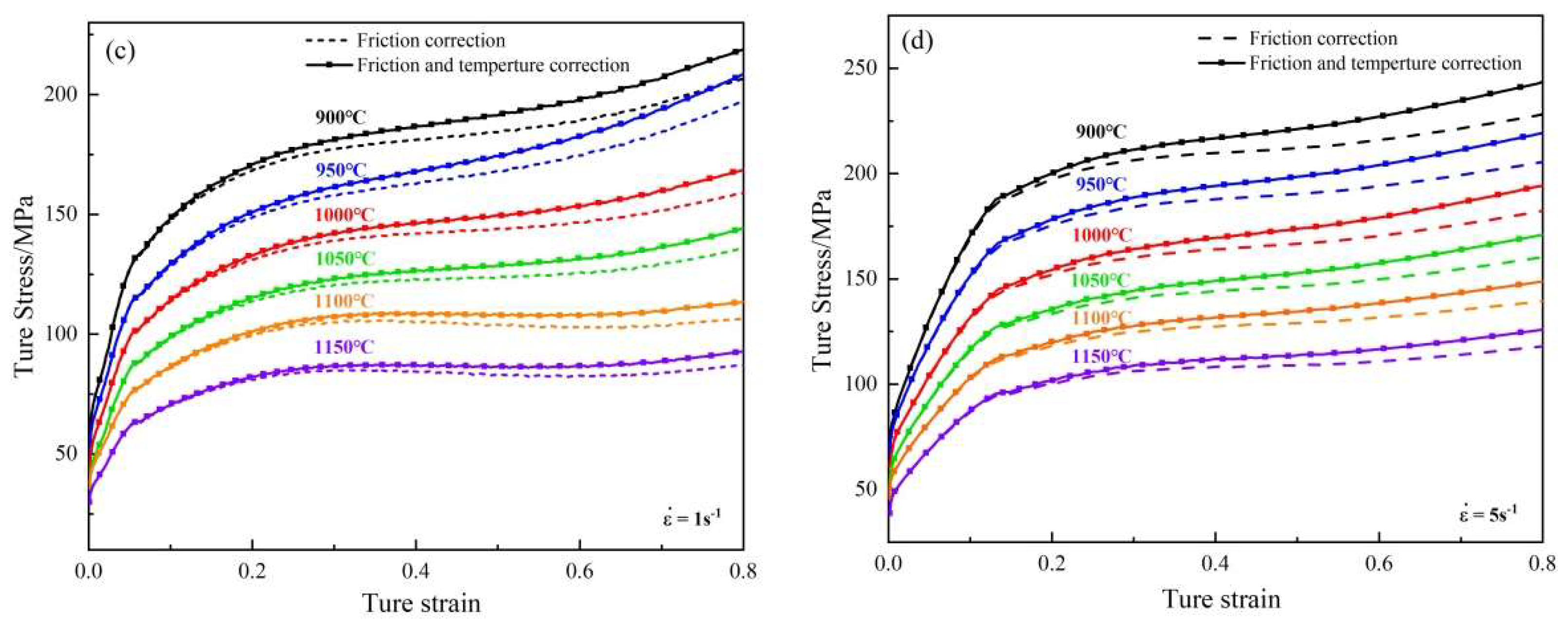
3.1. Correction of Friction and Temperature
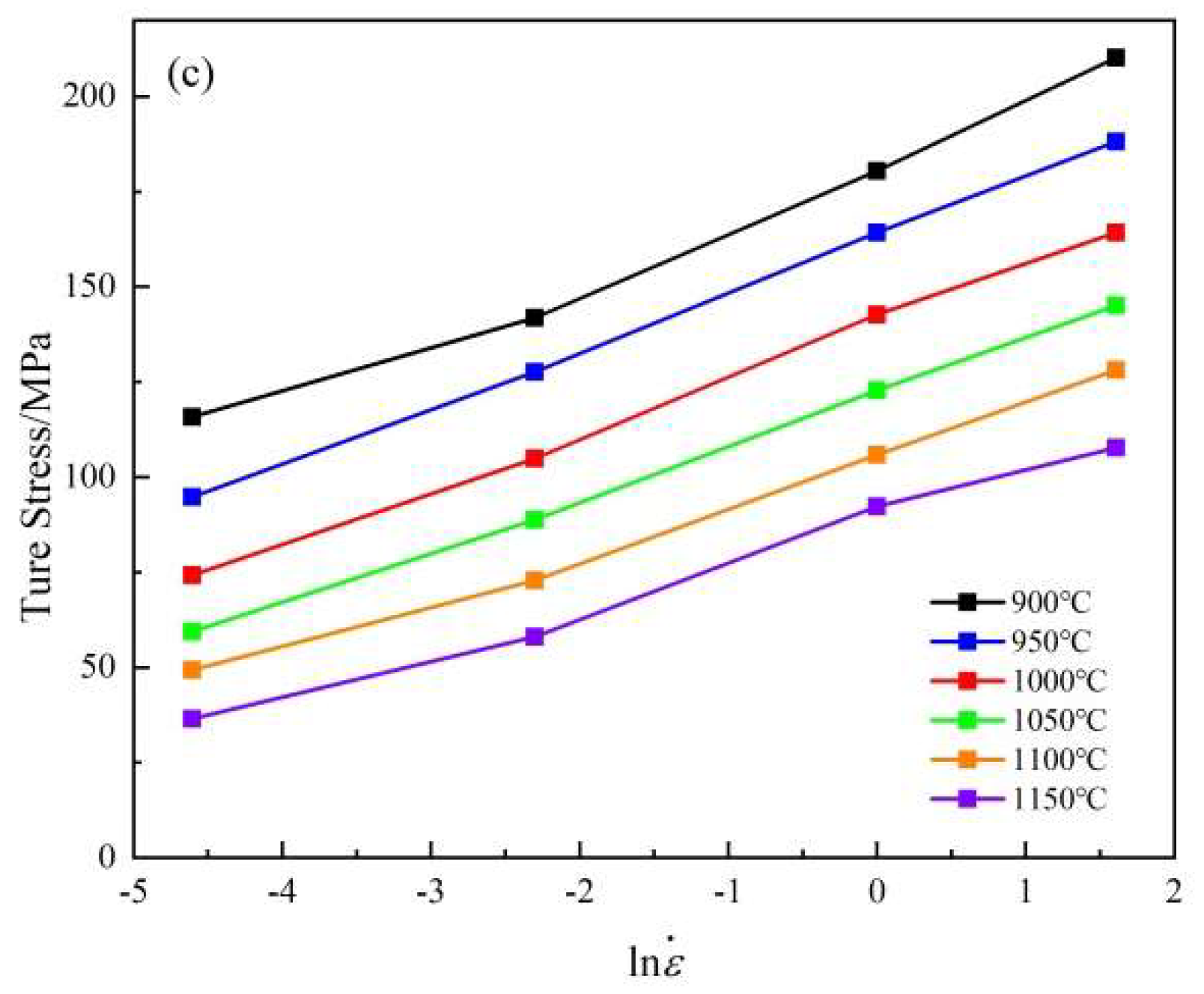
3.2. Flow Behavior
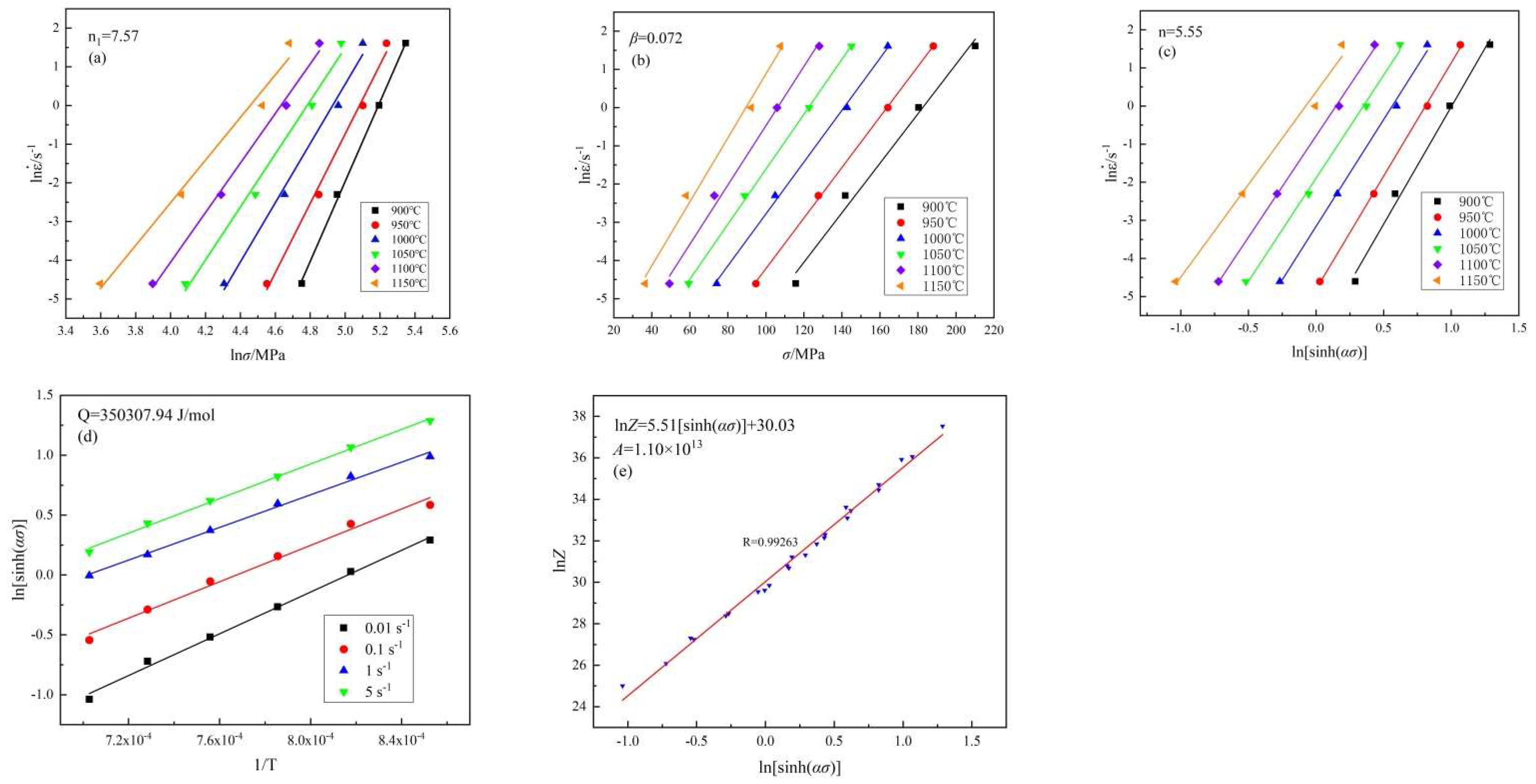
3.3. Constitutive Equation of Hot Deformation
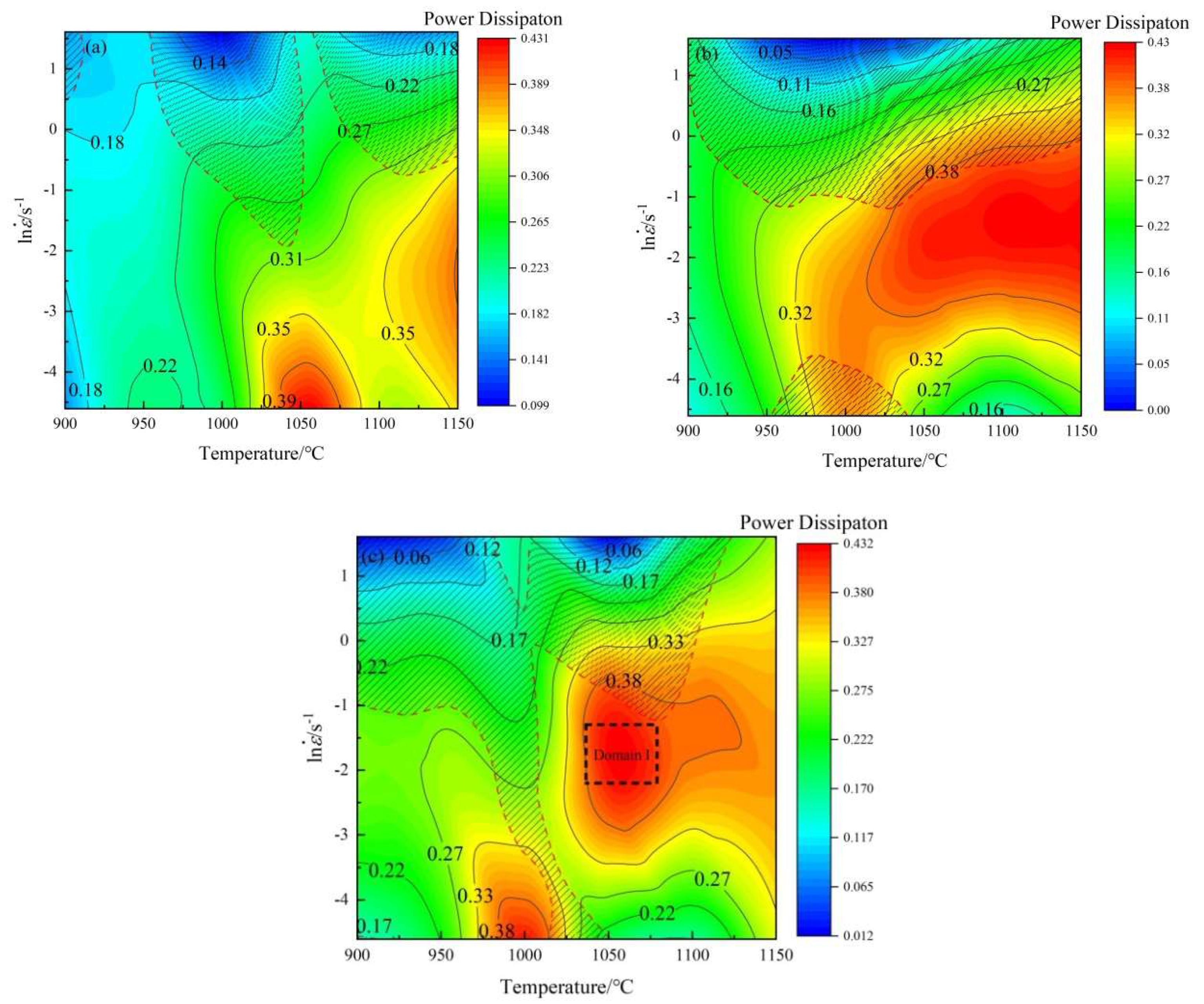
3.4. Analysis of Processing Map
3.5. EBSD Analysis of the Microstructure Evolution
4. Conclusions
- The constitutive equation of 18CrNiMo7-6 alloy steel is .
- According to the processing maps and microstructure evolution law, the optimum hot process parameters are temperature 1025–1075 °C and strain rate 0.1 s−1. And the peak value of power dissipation efficiency is 0.432.
- There are three evolution mechanisms CDRX, DDRX and grain growth during hot deformation. The rotation of sub-grains under CDRX mechanism is the main factor for the formation of new grains. In addition, the DDRX mechanism is formed by the bulging of HAGBs at the grain boundary triple junction of the original grains.
- The temperature and strain rate have an influence on the DRX process. When the strain temperature is low, DDRX mechanism plays a leading role. With the increase of deformation temperature, CDRX begins to play a leading role and forms finer grains. When the deformation temperature rises to 1150 °C, the grain will continue to grow at higher temperature.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mandal, P.; Olasolo, M.; Da Silva, L.; Lalvani, H. Impact of a Multi-step Heat Treatment on Different Manufacturing Routes of 18CrNiMo7-6 Steel. Met. Mater. Trans. A 2020, 51, 3009–3029. [Google Scholar] [CrossRef] [Green Version]
- An, X.; Tian, Y.; Wang, B.; Jia, T.; Wang, H.; Wang, Z. Prediction of the formation of carbide network on grain boundaries in carburizing of 18CrNiMo7-6 steel alloys. Surf. Coat. Technol. 2021, 421, 127348. [Google Scholar] [CrossRef]
- Bambach, M.D.; Stieben, A.; Bleck, W. 18CrNiMo7-6 with TRIP-Effect for Increasing the Damage Tolerance of Gear Components—Part I: Alloy Design. In Materials Science Forum; Trans Tech Publications: Kapellweg, Switzerland, 2014; Volume 783–786, pp. 633–638. [Google Scholar] [CrossRef]
- Papaefthymiou, S.; Bleck, W.; Kruijver, S.; Sietsma, J.; Zhao, L.; Van der Zwaag, S. Influence of intercritical deformation on microstructure of TRIP steels containing Al. Mater. Sci. Technol. Lond. 2004, 20, 201–206. [Google Scholar]
- Speer, J.G.; Assunção, F.C.R.; Matlock, D.K.; Edmonds, D.V. The “quenching and partitioning” process: Background and recent progress. Mater. Res. 2005, 8, 417–423. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Zhang, L.; Shen, W.; Xu, Q.; Cui, Y. The processing map and microstructure evolution of Ni-Cr-Mo-based C276 superalloy during hot compression. J. Alloy. Compd. 2017, 728, 1269–1278. [Google Scholar] [CrossRef]
- Lin, Y.; Wen, D.-X.; Huang, Y.-C.; Chen, X.-M.; Chen, X.-W. A unified physically based constitutive model for describing strain hardening effect and dynamic recovery behavior of a Ni-based superalloy. J. Mater. Res. 2015, 30, 3784–3794. [Google Scholar] [CrossRef]
- Al-Saadi, M.; Hulme-Smith, C.; Sandberg, F.; Jönsson, P.G. Hot Deformation Behaviour and Processing Map of Cast Alloy 825. J. Mater. Eng. Perform. 2021, 30, 7770–7782. [Google Scholar] [CrossRef]
- Adam, B.M.; Tucker, J.D.; Tewksbury, G. Comparative study of the hot processing behavior in advanced Ni-based superalloys for use in A-USC applications. J. Alloy. Compd. 2020, 818, 152907. [Google Scholar] [CrossRef]
- Sui, F.-L.; Xu, L.-X.; Chen, L.-Q.; Liu, X.-H. Processing map for hot working of Inconel 718 alloy. J. Mater. Process. Technol. 2011, 211, 433–440. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Rao, K.P.; Sasidhar, S. (Eds.) Hot Working Guide: A Compendium of Processing Maps; ASM International: Almere, The Netherlands, 2015. [Google Scholar]
- Prasad, Y.; Seshacharyulu, T. Processing maps for hot working of titanium alloys. Mater. Sci. Eng. A 1998, 243, 82–88. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Gegel, H.L.; Doraivelu, S.M.; Malas, J.C.; Morgan, J.T.; Lark, K.A.; Barker, D.R. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Metall. Trans. A 1984, 15, 1883–1892. [Google Scholar] [CrossRef]
- Jiang, M.; Xu, C.; Yan, H.; Fan, G.; Nakata, T.; Lao, C.; Chen, R.; Kamado, S.; Han, E.; Lu, B. Unveiling the formation of basal texture variations based on twinning and dynamic recrystallization in AZ31 magnesium alloy during extrusion. Acta Mater. 2018, 157, 53–71. [Google Scholar] [CrossRef]
- Wan, Z.; Hu, L.; Sun, Y.; Wang, T.; Li, Z. Hot deformation behavior and processing workability of a Ni-based alloy. J. Alloy. Compd. 2018, 769, 367–375. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Najafizadeh, A. A new method for evaluation of friction in bulk metal forming. J. Mater. Process. Technol. 2004, 152, 136–143. [Google Scholar] [CrossRef]
- Goetz, R.L.; Semiatin, S.L. The Adiabatic Correction Factor for Deformation Heating During the Uniaxial Compression Test. J. Mater. Eng. Perform. 2001, 10, 710–717. [Google Scholar] [CrossRef]
- Luo, R.; Zheng, Q.; Zhu, J.J.; Guo, S.; Li, D.S.; Xu, G.F.; Cheng, X.N. Dynamic recrystallization behavior of Fe–20Cr–30Ni–0.6 Nb–2Al–Mo alloy. Rare Met. 2019, 38, 181–188. [Google Scholar] [CrossRef]
- Geng, P.; Qin, G.; Zhou, J.; Zou, Z. Hot deformation behavior and constitutive model of GH4169 superalloy for linear friction welding process. J. Manuf. Process. 2018, 32, 469–481. [Google Scholar] [CrossRef]
- Sandström, R.; Lagneborg, R. A model for hot working occurring by recrystallization. Acta Met. 1975, 23, 387–398. [Google Scholar] [CrossRef]
- Poliak, E.I.; Jonas, J.J. Initiation of Dynamic Recrystallization in Constant Strain Rate Hot Deformation. ISIJ Int. 2003, 43, 684–691. [Google Scholar] [CrossRef] [Green Version]
- Sellars, C.; McTegart, W. On the mechanism of hot deformation. Acta Met. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Liu, G.; Mao, C.; Ding, R.; Yu, L.; Liu, C.; Liu, Y. The kinetics of dynamic recrystallization and construction of constitutive modeling of RAFM steel in the hot deformation process. J. Nucl. Mater. 2021, 557, 153285. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Q.; Chen, X.; Bao, J.; Chen, Z. Effect of Sn addition on the deformation behavior and microstructural evolution of Mg-Gd-Y-Zr alloy during hot compression. Mater. Sci. Eng. A 2021, 826, 142026. [Google Scholar] [CrossRef]
- Lin, H.-B. Dynamic recrystallization behavior of 6082 aluminum alloy during hot deformation. Adv. Mech. Eng. 2021, 13, 16878140211046107. [Google Scholar] [CrossRef]
- Zhu, H.; Ou, H. Constitutive modelling of hot deformation behaviour of metallic materials. Mater. Sci. Eng. A 2022, 832, 142473. [Google Scholar] [CrossRef]
- An, J.; Zhou, M.; Tian, B.; Geng, Y.; Ban, Y.; Liang, S. Hot deformation behavior of nano-Al2O3-dispersion-strengthened Cu20W composite. Sci. Eng. Compos. Mater. 2021, 28, 500–509. [Google Scholar] [CrossRef]
- Medina, S.; Hernandez, C. General expression of the Zener-Hollomon parameter as a function of the chemical composition of low alloy and microalloyed steels. Acta Mater. 1996, 44, 137–148. [Google Scholar] [CrossRef]
- ZenerC, H. Effect of strain-rate upon the plastic flow of steel. J. Appl. Phys. 1944, 15, 22–27. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K. Author’s reply: Dynamic materials model: Basis and principles. Met. Mater. Trans. A 1996, 27, 235–236. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Seshacharyulu, T. Modelling of hot deformation for microstructural control. Int. Mater. Rev. 1998, 43, 243–258. [Google Scholar] [CrossRef]
- Guan, Y.; Liu, Y.; Ma, Z.; Li, H.; Yu, H. Hot Deformation Behavior and Recrystallization Mechanism in an As-Cast CoNi-Based Superalloy. Met. Mater. Int. 2021, 11, 1–11. [Google Scholar] [CrossRef]
- Mokdad, F.; Chen, D.L.; Liu, Z.Y.; Ni, D.R.; Xiao, B.L.; Ma, Z.Y. Three-dimensional processing maps and microstructural evolution of a CNT-reinforced Al-Cu-Mg nanocomposite. Mater. Sci. Eng. A 2017, 702, 425–437. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, X.; Yue, H.; Liu, S.; Ren, L.; Xin, Y.; Lyu, L.; Zhao, Y.; Quan, G.; Gupta, M. Hot deformation behavior and processing maps of hybrid SiC and CNTs reinforced AZ61 alloy composite. J. Alloy. Compd. 2021, 868, 159098. [Google Scholar] [CrossRef]
- Xi, S.-P.; Gao, X.-L.; Liu, W.; Lu, Y.-L.; Fu, G.-Q.; Tao, H.-C.; Zang, Y.-C. Hot deformation behavior and processing map of low-alloy offshore steel. J. Iron Steel Res. Int. 2021, 29, 474–483. [Google Scholar] [CrossRef]
- Geng, Y.; Zhang, Y.; Song, K.; Jia, Y.; Li, X.; Stock, H.-R.; Zhou, H.; Tian, B.; Liu, Y.; Volinsky, A.A.; et al. Effect of Ce addition on microstructure evolution and precipitation in Cu-Co-Si-Ti alloy during hot deformation. J. Alloy. Compd. 2020, 842, 155666. [Google Scholar] [CrossRef]
- He, G.; Zhao, Y.; Gan, B.; Sheng, X.; Liu, Y.; Tan, L. Mechanism of grain refinement in an equiatomic medium-entropy alloy CrCoNi during hot deformation. J. Alloy. Compd. 2020, 815, 152382. [Google Scholar] [CrossRef]
- Huang, K.; Marthinsen, K.; Zhao, Q.; Logé, R.E. The double-edge effect of second-phase particles on the recrystallization behaviour and associated mechanical properties of metallic materials. Prog. Mater. Sci. 2018, 92, 284–359. [Google Scholar] [CrossRef]
- Wang, X.; Brünger, E.; Gottstein, G. Microstructure characterization and dynamic recrystallization in an Alloy 800H. Mater. Sci. Eng. A 2000, 290, 180–185. [Google Scholar] [CrossRef]
- Chen, W.; Hu, B.; Jia, C.; Zheng, C.; Li, D. Continuous dynamic recrystallization during the transient deformation in a Ni-30%Fe austenitic model alloy. Mater. Sci. Eng. A 2019, 751, 10–14. [Google Scholar] [CrossRef]
- Kumar, N.R.; Blandin, J.; Desrayaud, C.; Montheillet, F.; Suéry, M. Grain refinement in AZ91 magnesium alloy during thermomechanical processing. Mater. Sci. Eng. A 2003, 359, 150–157. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, C.; Feng, H.; Zhang, S.; Han, J.; Zhang, W.; Zhao, E.; Wang, H. Dynamic recrystallization mechanism and improved mechanical properties of a near α high temperature titanium alloy processed by severe plastic deformation. Mater. Charact. 2020, 163, 110281. [Google Scholar] [CrossRef]
- Wusatowska-Sarnek, A.; Miura, H.; Sakai, T. Nucleation and microtexture development under dynamic recrystallization of copper. Mater. Sci. Eng. A 2002, 323, 177–186. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Wang, Q.; Chen, Z.; Wu, X.; Liu, H.; Wang, Z. Recrystallization Mechanism and Processing Map of 18CrNiMo7-6 Alloy Steel during Hot Deformation. Metals 2022, 12, 838. https://doi.org/10.3390/met12050838
Xie Y, Wang Q, Chen Z, Wu X, Liu H, Wang Z. Recrystallization Mechanism and Processing Map of 18CrNiMo7-6 Alloy Steel during Hot Deformation. Metals. 2022; 12(5):838. https://doi.org/10.3390/met12050838
Chicago/Turabian StyleXie, Yikui, Qicheng Wang, Zikun Chen, Xiaodong Wu, Hui Liu, and Zhongying Wang. 2022. "Recrystallization Mechanism and Processing Map of 18CrNiMo7-6 Alloy Steel during Hot Deformation" Metals 12, no. 5: 838. https://doi.org/10.3390/met12050838
APA StyleXie, Y., Wang, Q., Chen, Z., Wu, X., Liu, H., & Wang, Z. (2022). Recrystallization Mechanism and Processing Map of 18CrNiMo7-6 Alloy Steel during Hot Deformation. Metals, 12(5), 838. https://doi.org/10.3390/met12050838





