Bending Behaviour Analysis of Aluminium Profiles in Differential Velocity Sideways Extrusion Using a General Flow Field Model
Abstract
:1. Introduction
2. Materials and Methods
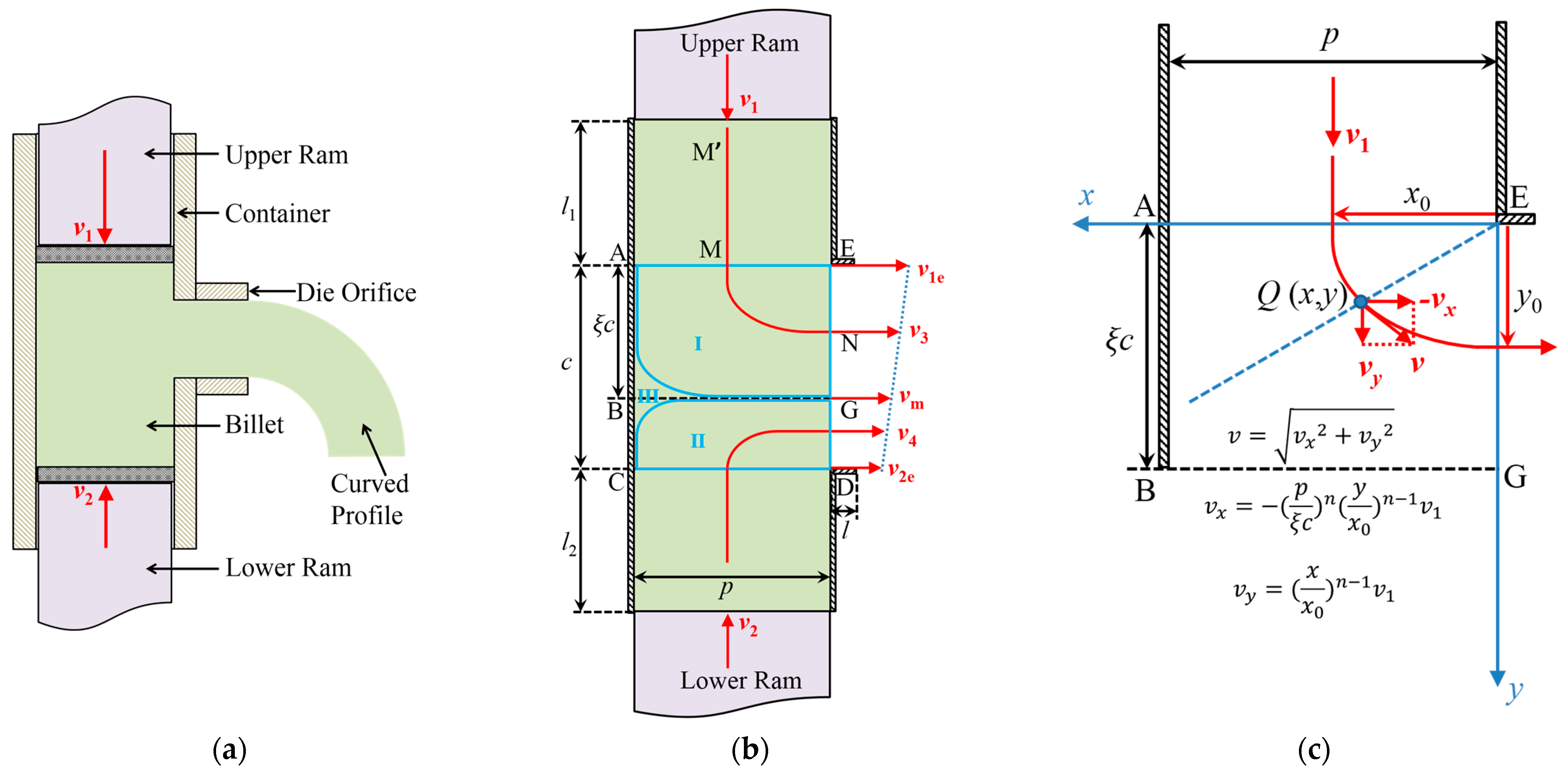
2.1. Theoretical Model
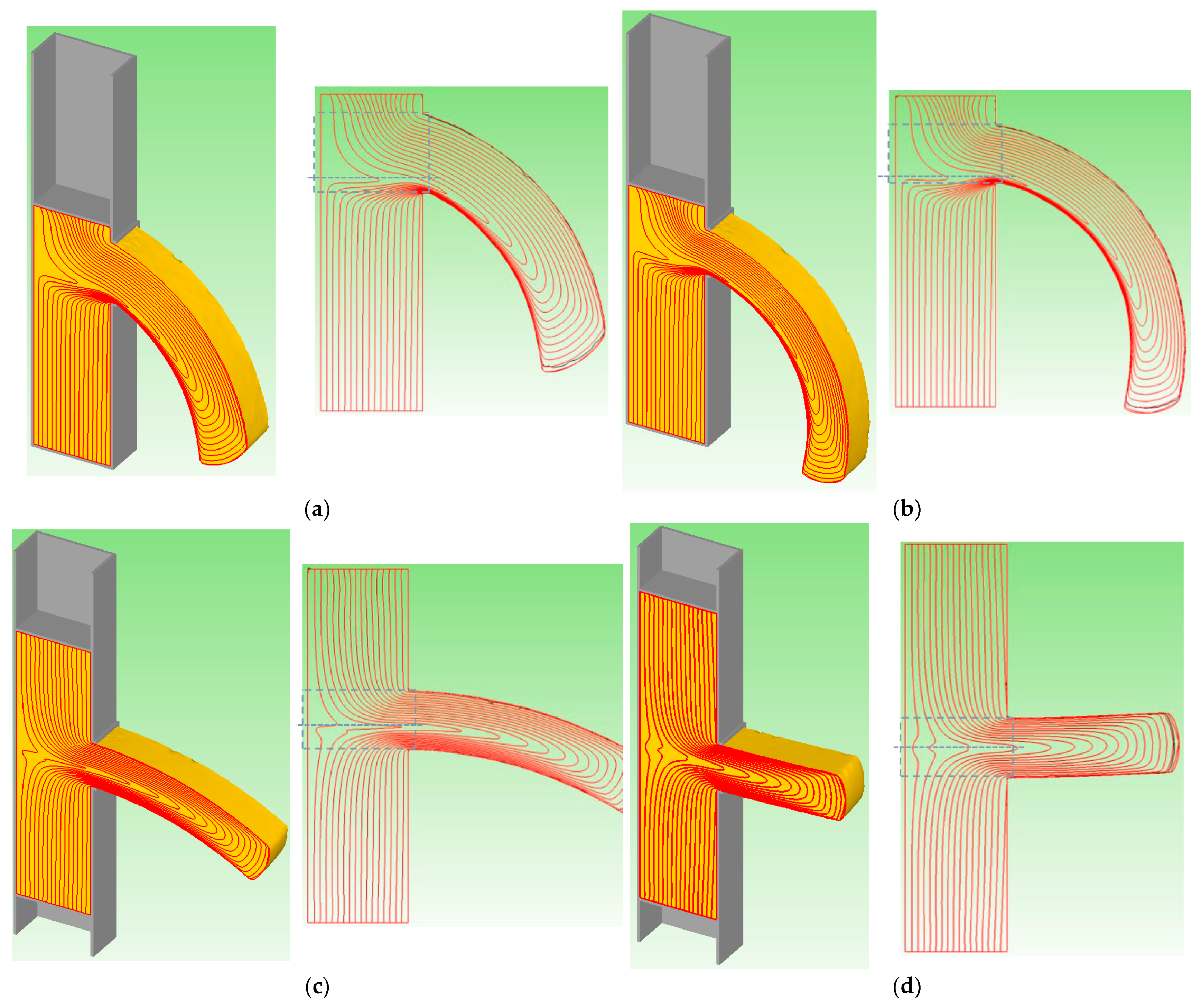
2.2. Experimental and Numerical Methods
3. Results and Discussion
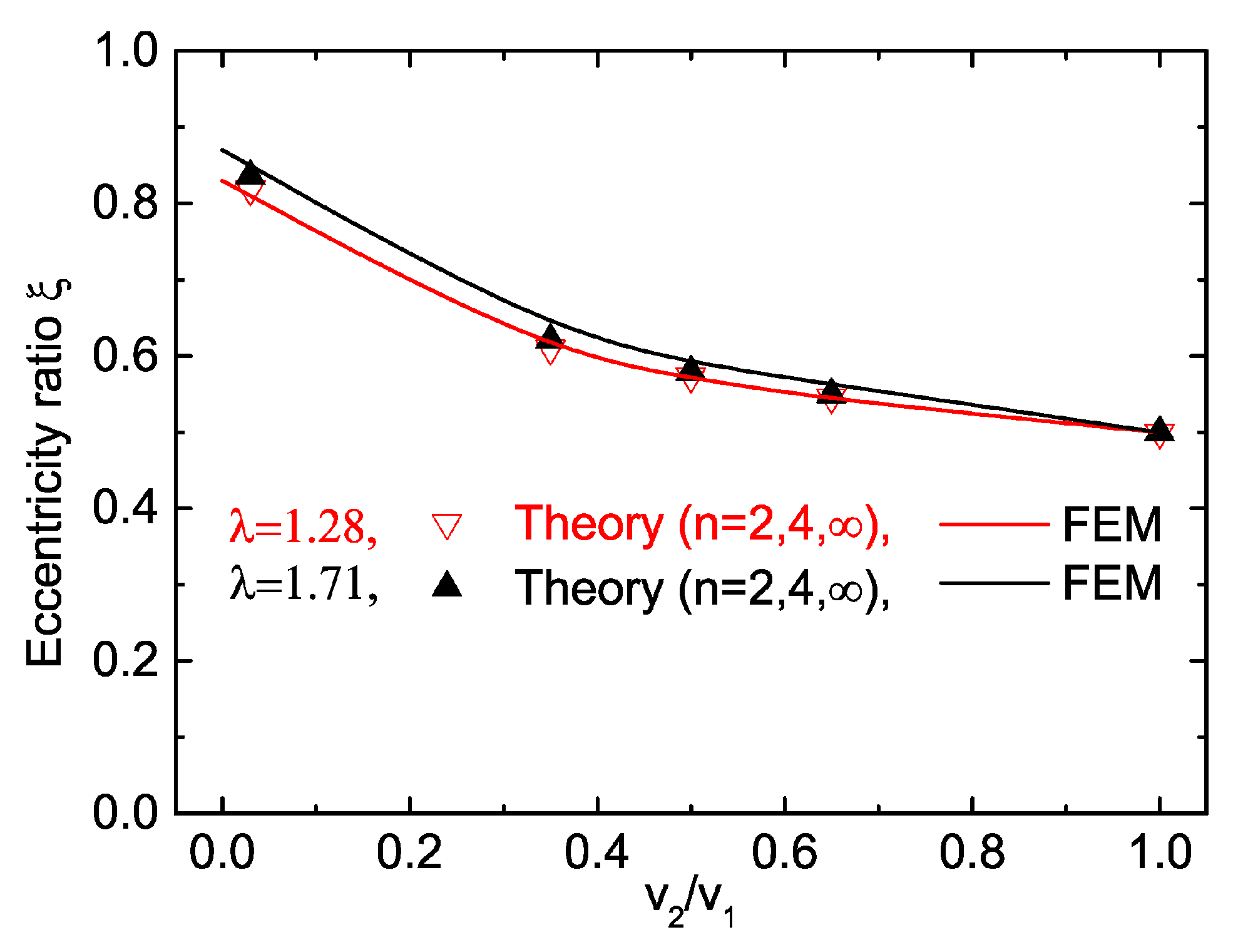
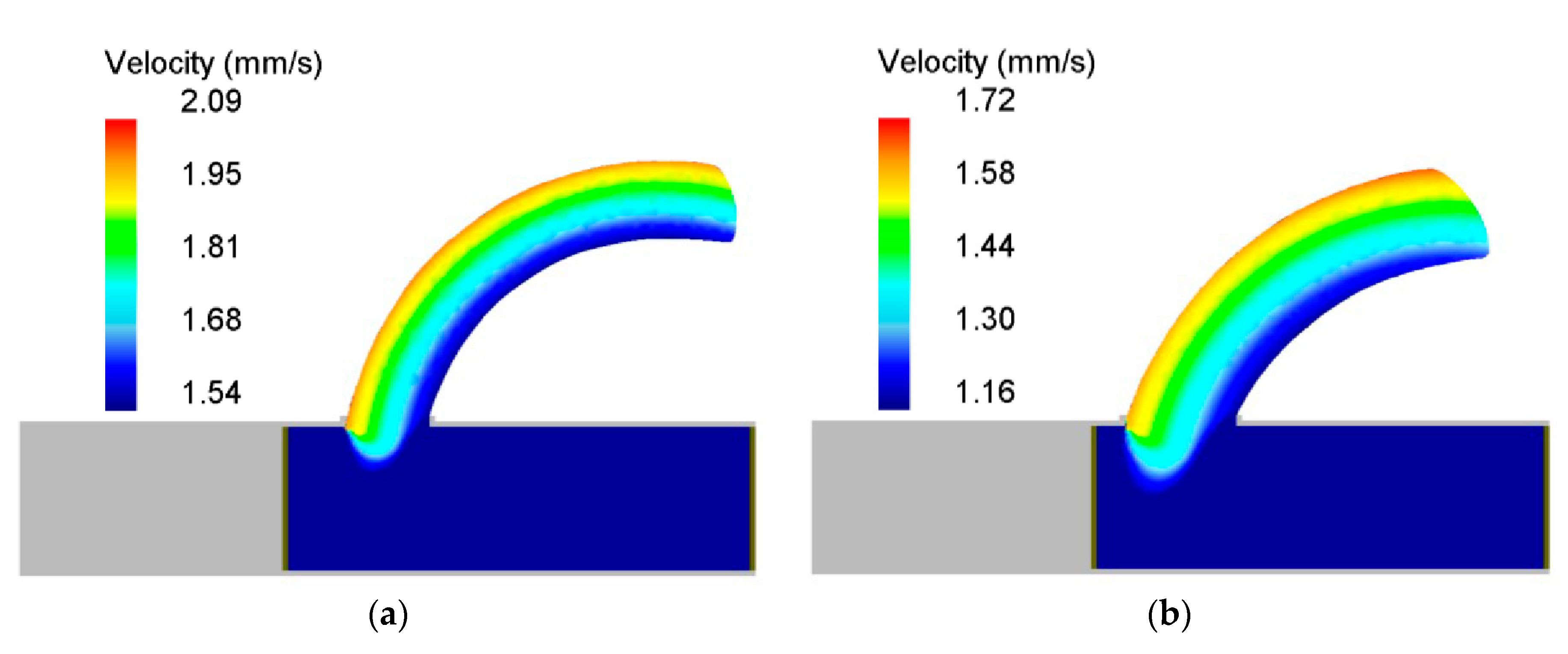
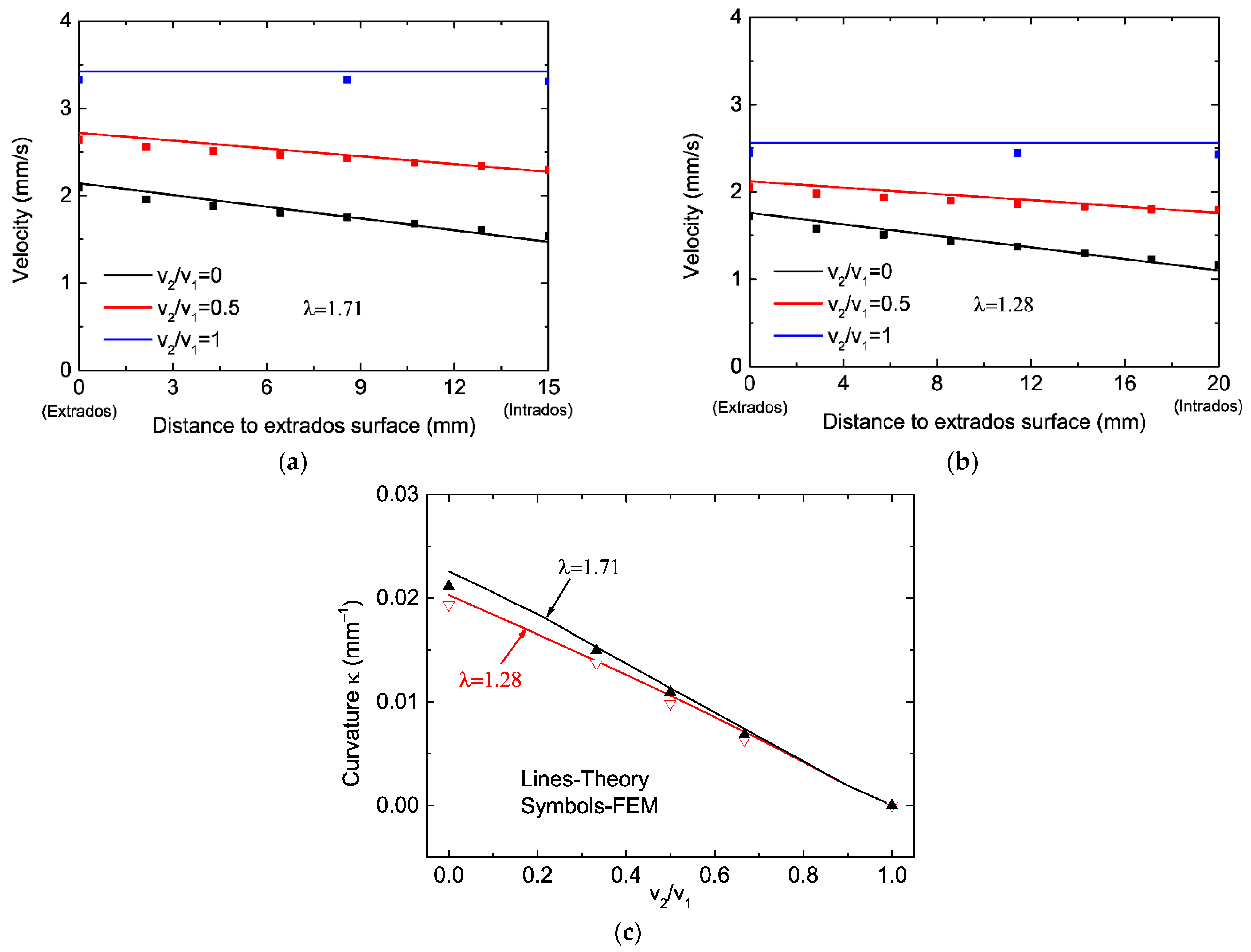
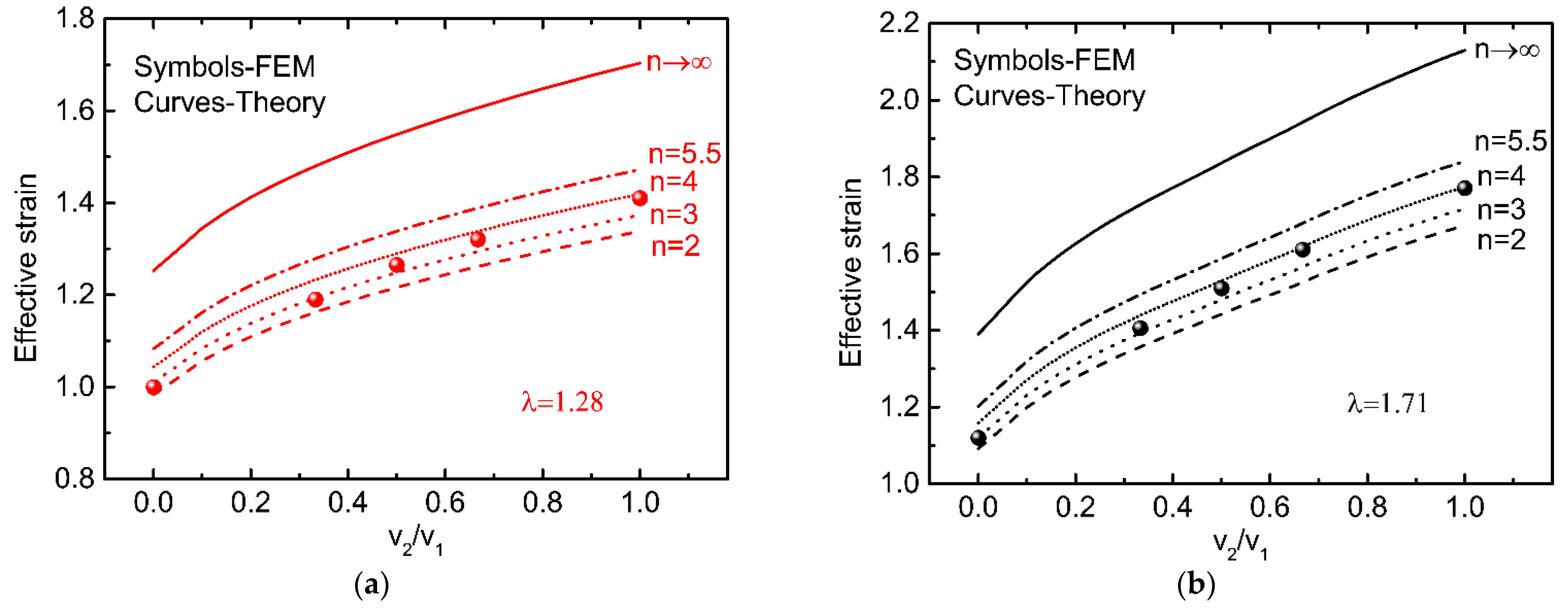
3.1. Prediction of the Extrudate Curvature
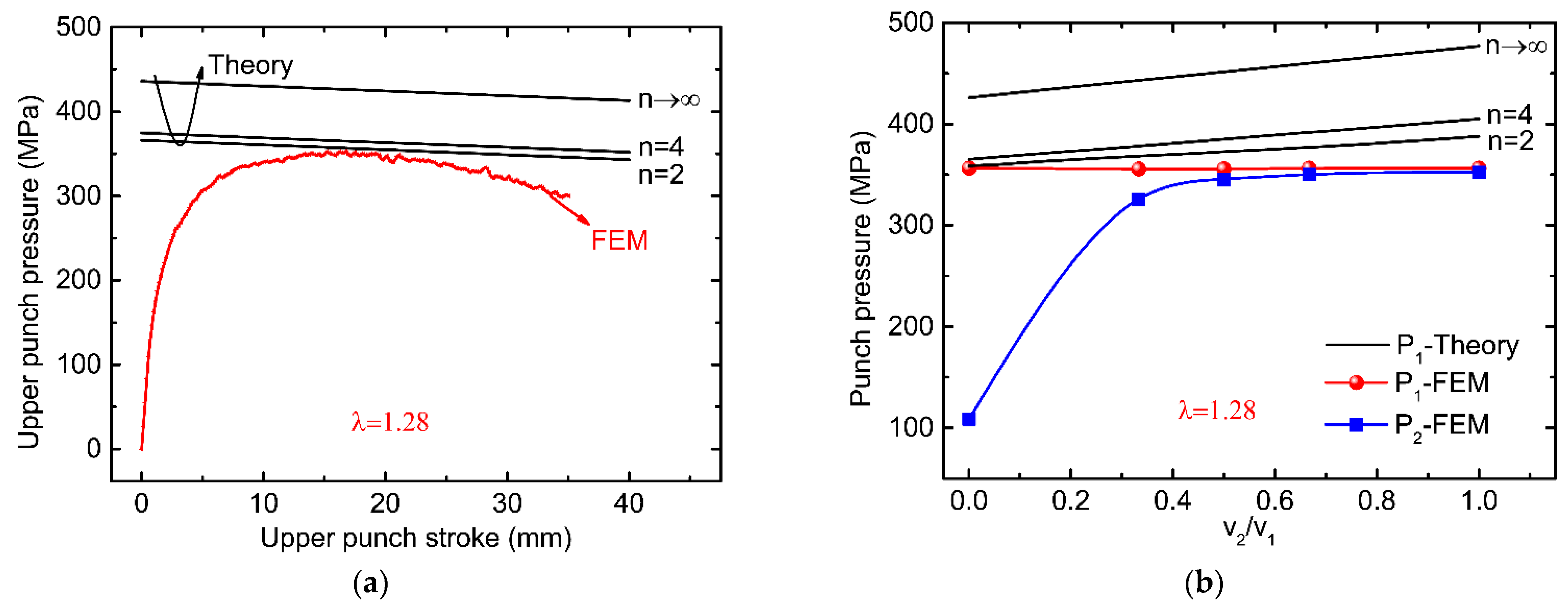
3.2. Prediction of the Extrusion Pressure
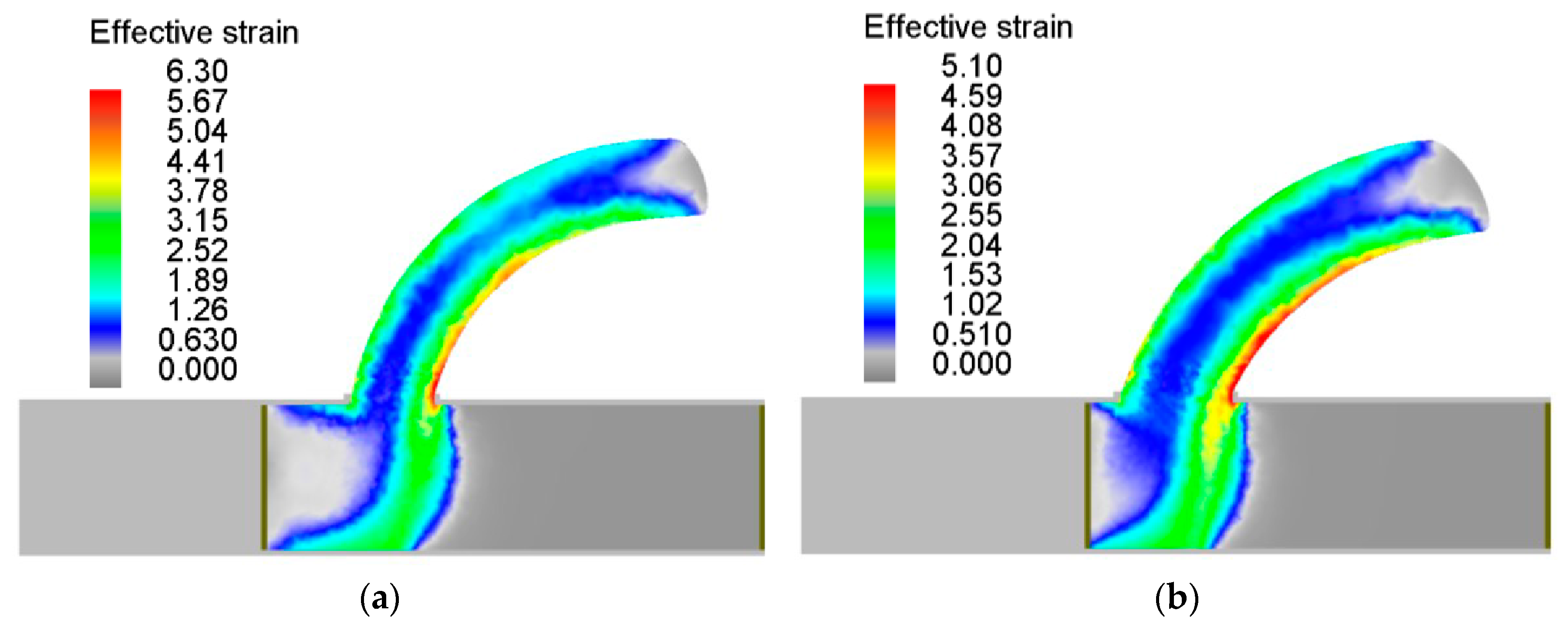
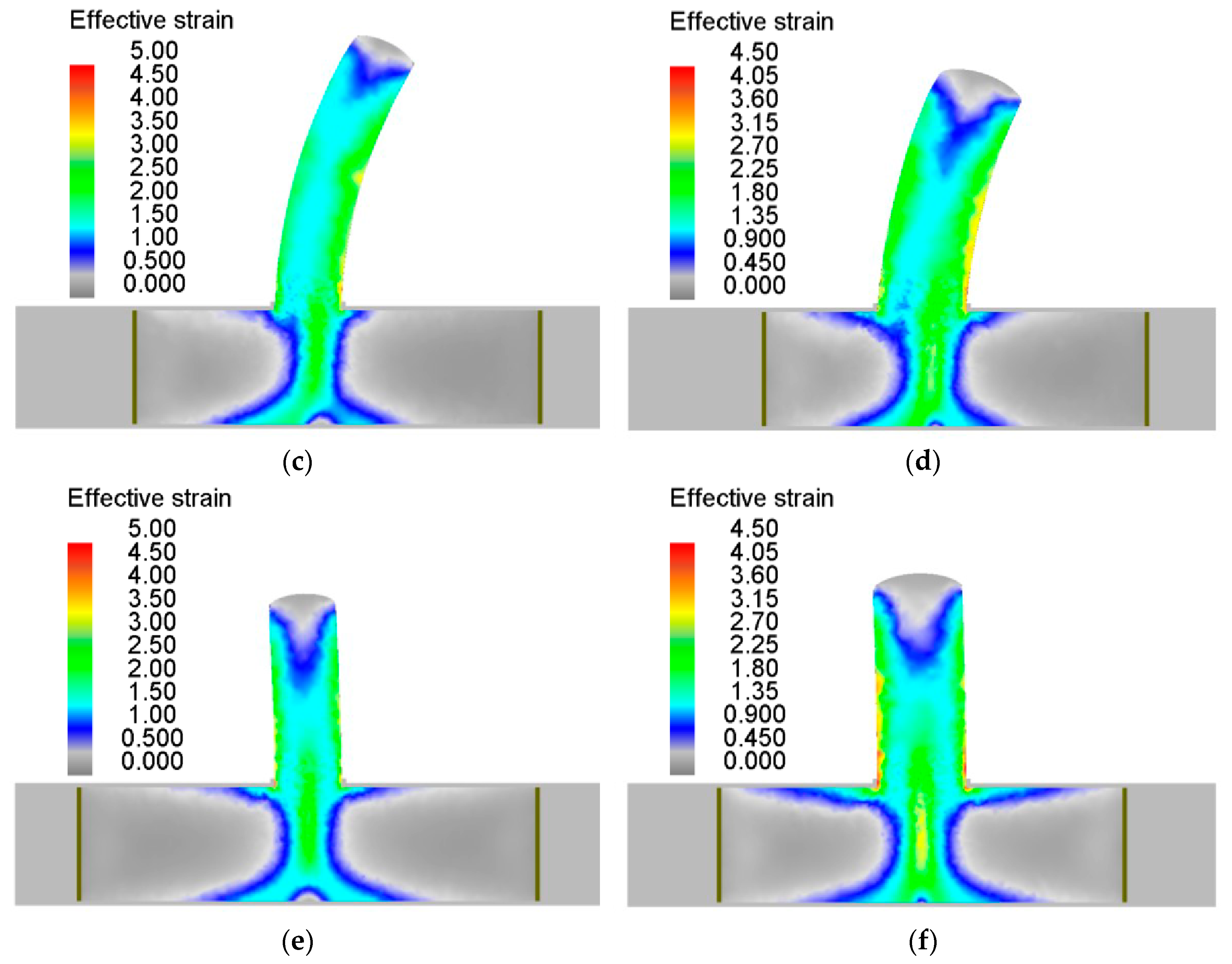
3.3. Prediction of the Effective Strain
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
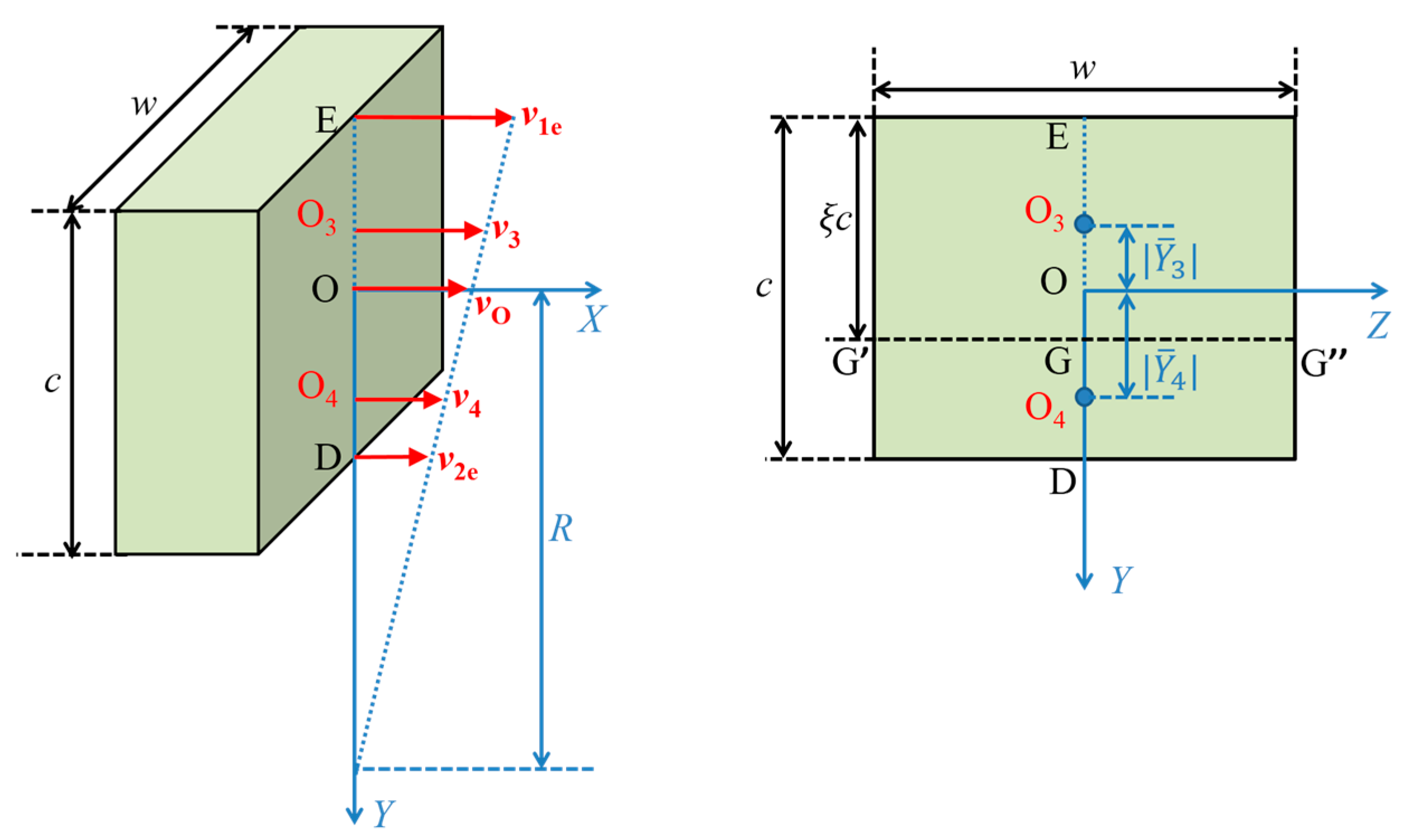
Appendix A. Determination of the Velocity Field, Strain Rate and Effective Strain
Appendix B. Determination of the Internal Power Dissipation
Appendix C. Determination of the Extrudate Curvature
References
- Allwood, J.M.; Dunant, C.F.; Lupton, R.C.; Cleaver, C.J.; Serrenho, A.C.H.; Azevedo, J.M.C.; Horton, P.M.; Clare, A.; Low, H.; Horrocks, I.; et al. Absolute zero: Delivering the UK’s climate change commitment with incremental changes to today’s technologies. UK FIRES 2019. [Google Scholar] [CrossRef]
- Joost, W.J. Reducing vehicle weight and improving U.S. energy efficiency using integrated computational materials engineering. JOM 2012, 64, 1032–1038. [Google Scholar] [CrossRef] [Green Version]
- Hirsch, J. Recent development in aluminium for automotive applications. Trans. Nonferr. Met. Soc. China 2014, 24, 1995–2002. [Google Scholar] [CrossRef]
- Kohar, C.P.; Zhumagulov, A.; Brahme, A.; Worswick, M.J.; Mishra, R.K.; Inal, K. Development of high crush efficient, extrudable aluminium front rails for vehicle lightweighting. Int. J. Impact Eng. 2016, 95, 17–34. [Google Scholar] [CrossRef]
- Zhou, W.; Shao, Z.; Yu, J.; Lin, J. Advances and trends in forming curved extrusion profiles. Materials 2021, 14, 1603. [Google Scholar] [CrossRef]
- Chatti, S.; Dirksen, U.; Schikorra, M.; Kleiner, M. System for design and computation of lightweight structures made of bent profiles. Adv. Mater. Res. 2005, 6, 279–286. [Google Scholar] [CrossRef]
- Chatti, S. Production of Profiles for Lightweight Structures; Books on Demand GmbH: Norderstedt, Germany, 2005. [Google Scholar]
- Stevenson, K. Aluminum Extrusion Manual, 4th ed.; Aluminum Extruders Council: Chicago, IL, USA, 2014. [Google Scholar]
- Tekkaya, A.E.; Chatti, S. Bending (Tubes, Profiles); Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Merklein, M.; Geiger, M. New materials and production technologies for innovative lightweight constructions. J. Mater. Process. Technol. 2002, 125, 532–536. [Google Scholar] [CrossRef]
- Kleiner, M.; Chatti, S.; Klaus, A. Metal forming techniques for lightweight construction. J. Mater. Process. Technol. 2006, 177, 2–7. [Google Scholar] [CrossRef]
- Tekkaya, A.E.; Khalifa, N.B.; Grzancic, G.; Hölker, R. Forming of lightweight metal components: Need for new technologies. Procedia Eng. 2014, 81, 28–37. [Google Scholar] [CrossRef] [Green Version]
- Vollertsen, F.; Sprenger, A.; Kraus, J.; Arnet, H. Extrusion, channel, and profile bending: A review. J. Mater. Process. Technol. 1999, 87, 1–27. [Google Scholar] [CrossRef]
- Yang, H.; Li, H.; Zhang, Z.; Zhan, M.; Liu, J.; Li, G. Advances and trends on tube bending forming technologies. Chin. J. Aeronaut. 2012, 25, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Chatti, S.; Hermes, M.; Kleiner, M. Three-Dimensional Bending of Profiles by Stress Superposition; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Hermes, M.; Staupendahl, D.; Kleiner, M. Torque Superposed Spatial Bending; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Hermes, M.; Kleiner, M. Method and Device for Profile Bending. U.S. Patent 9,227,236, 5 January 2016. [Google Scholar]
- Hermes, M.; Kurze, S.; Tekkaya, A.E. Method and Device for Forming a Bar Stock. European Patent EP2203264B1, 27 April 2011. [Google Scholar]
- Chatti, S.; Hermes, M.; Weinrich, A.; Ben-Khalifa, N.; Tekkaya, A.E. New incremental methods for springback compensation by stress superposition. Int. J. Mater. Form. 2009, 2, 817–820. [Google Scholar] [CrossRef]
- Kleiner, M.; Tekkaya, A.E.; Chatti, S.; Hermes, M.; Weinrich, A.; Ben-Khalifa, N.; Dirksen, U. New incremental methods for springback compensation by stress superposition. Prod. Eng. 2009, 3, 137–144. [Google Scholar] [CrossRef]
- Becker, C.; Hermes, M.; Tekkaya, A.E. Incremental Tube Forming; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Chatti, S.; Hermes, M.; Tekkaya, A.E.; Kleiner, M. The new TSS bending process: 3D bending of profiles with arbitrary cross-sections. CIRP Ann. 2010, 59, 315–318. [Google Scholar] [CrossRef] [Green Version]
- Kleiner, M.; Arendes, D. The manufacture of non-linear aluminium sections applying a combination of extrusion and curving. In Proceedings of the Fifth International Conference on Technology of Plasticity, Columbus, OH, USA, 7–10 October 1996; pp. 971–974. [Google Scholar]
- Selvaggio, A.; Becker, D.; Klaus, A.; Arendes, D.; Kleiner, M. Curved Profile Extrusion; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Müller, K.B. Bending of extruded profiles during extrusion process. Mater. Forum 2004, 28, 264–269. [Google Scholar] [CrossRef]
- Müller, K.B. Bending of extruded profiles during extrusion process. Int. J. Mach. Tools Manuf. Mater. 2006, 46, 1238–1242. [Google Scholar] [CrossRef]
- Brosius, A.; Hermes, M.; Ben Khalifa, N.; Trompeter, M.; Tekkaya, A.E. Innovation by forming technology: Motivation for research. Int. J. Mater. Form. 2009, 2, 29–38. [Google Scholar] [CrossRef]
- Ben Khalifa, N.; Selvaggio, A.; Pietzka, D.; Haase, M.; Tekkaya, A.E. Advanced extrusion processes. Mater. Res. Innov. 2011, 15, 487–490. [Google Scholar] [CrossRef]
- Nikawa, M.; Shiraishi, M.; Miyajima, Y.; Horibe, H.; Goto, Y. Production of shaped tubes with various curvatures using extrusion process through inclined die aperture. J. Jpn. Soc. Technol. Plast. 2002, 43, 654–656. [Google Scholar]
- Shiraishi, M.; Nikawa, M.; Goto, Y. An investigation of the curvature of bars and tubes extruded through inclined dies. Int. J. Mach. Tools Manuf. 2003, 43, 1571–1578. [Google Scholar] [CrossRef]
- Takahashi, Y.; Kihara, S.; Yamaji, K.; Shiraishi, M. Effects of die dimensions for curvature extrusion of curved rectangular bars. Mater. Trans. 2015, 56, 844–849. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Lin, J.; Dean, T.A.; Wang, L. Feasibility studies of a novel extrusion process for curved profiles: Experimentation and modelling. Int. J. Mach. Tools Manuf. 2018, 126, 27–43. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Yu, J.; Lin, J.; Dean, T.A. Manufacturing a curved profile with fine grains and high strength by differential velocity sideways extrusion. Int. J. Mach. Tools Manuf. 2019, 140, 77–88. [Google Scholar] [CrossRef]
- Zhou, W.; Yu, J.; Lu, X.; Lin, J.; Dean, T.A. A comparative study on deformation mechanisms, microstructures and mechanical properties of wide thin-ribbed sections formed by sideways and forward extrusion. Int. J. Mach. Tools Manuf. 2021, 168, 103771. [Google Scholar] [CrossRef]
- Ghassemali, E.; Tan, M.-J.; Jarfors, A.E.W.; Lim, S.C.V. Optimization of axisymmetric open-die micro-forging/extrusion processes: An upper bound approach. Int. J. Mech. Sci. 2013, 71, 58–67. [Google Scholar] [CrossRef]
- Parvizi, A.; Abrinia, K. A two dimensional upper bound analysis of the ring rolling process with experimental and FEM verifications. Int. J. Mech. Sci. 2014, 79, 176–181. [Google Scholar] [CrossRef]
- Wu, Y.; Dong, X.; Yu, Q. Upper bound analysis of axial metal flow inhomogeneity in radial forging process. Int. J. Mech. Sci. 2015, 93, 102–110. [Google Scholar] [CrossRef]
- Zhang, X.J.; Li, F.; Wang, Y.; Chen, Z.Y. An analysis for magnesium alloy curvature products formed by staggered extrusion (SE) based on the upper bound method. Int. J. Adv. Manuf. Technol. 2021, 119, 303–313. [Google Scholar] [CrossRef]
- Farahmand, H.R.; Abrinia, K. An upper bound analysis for reshaping thick tubes to polygonal cross-section tubes through multistage roll forming process. Int. J. Mech. Sci. 2015, 100, 90–98. [Google Scholar] [CrossRef]
- Wu, Y.; Dong, X. An upper bound model with continuous velocity field for strain inhomogeneity analysis in radial forging process. Int. J. Mech. Sci. 2016, 115, 385–391. [Google Scholar] [CrossRef]
- Cai, S.-p.; Wang, Z.-j. An analysis for three-dimensional upset forging of elliptical disks and rings based on the upper-bound method. Int. J. Mech. Sci. 2020, 183, 105835. [Google Scholar] [CrossRef]
- Lee, D.N. An upper-bound solution of channel angular deformation. Scr. Mater. 2000, 43, 115–118. [Google Scholar] [CrossRef]
- Segal, V.M. Equal channel angular extrusion: From micromechanics to structure formation. Mater. Sci. Eng. A 1999, 271, 322–333. [Google Scholar] [CrossRef]
- Altan, B.S.; Purcek, G.; Miskioglu, I. An upper-bound analysis for equal-channel angular extrusion. J. Mater. Process. Technol. 2005, 168, 137–146. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Reihanian, M.; Kanaani, M.; Moshksar, M.M. An upper-bound analysis of the tube extrusion process. J. Mater. Process. Technol. 2008, 199, 214–220. [Google Scholar] [CrossRef]
- Laptev, A.M.; Perig, A.V.; Vyal, O.Y. Analysis of equal channel angular extrusion by upper bound method and rigid blocks model. Mater. Res. 2013, 17, 359–366. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Lin, J.; Dean, T.A.; Wang, L. Analysis and modelling of a novel process for extruding curved metal alloy profiles. Int. J. Mech. Sci. 2018, 138, 524–536. [Google Scholar] [CrossRef]
- Kwan, C.-T.; Hsu, Y.-C. An analysis of pseudo equal-cross-section lateral extrusion through a curved channel. J. Mater. Process. Technol. 2002, 122, 260–265. [Google Scholar] [CrossRef]
- Zhou, W.; Yu, J.; Lin, J.; Dean, T.A. Effects of die land length and geometry on curvature and effective strain of profiles produced by a novel sideways extrusion process. J. Mater. Process. Technol. 2020, 282, 116682. [Google Scholar] [CrossRef]
- Zhou, W.; Shi, Z.; Lin, J. Upper bound analysis of differential velocity sideways extrusion process for curved profiles using a fan-shaped flow line model. Int. J. Lightweight Mater. Manuf. 2018, 1, 21–32. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Xi, Z. Bending Behaviour Analysis of Aluminium Profiles in Differential Velocity Sideways Extrusion Using a General Flow Field Model. Metals 2022, 12, 877. https://doi.org/10.3390/met12050877
Zhou W, Xi Z. Bending Behaviour Analysis of Aluminium Profiles in Differential Velocity Sideways Extrusion Using a General Flow Field Model. Metals. 2022; 12(5):877. https://doi.org/10.3390/met12050877
Chicago/Turabian StyleZhou, Wenbin, and Ziqi Xi. 2022. "Bending Behaviour Analysis of Aluminium Profiles in Differential Velocity Sideways Extrusion Using a General Flow Field Model" Metals 12, no. 5: 877. https://doi.org/10.3390/met12050877
APA StyleZhou, W., & Xi, Z. (2022). Bending Behaviour Analysis of Aluminium Profiles in Differential Velocity Sideways Extrusion Using a General Flow Field Model. Metals, 12(5), 877. https://doi.org/10.3390/met12050877





