Assessing Microstructure Tensile Properties Relationships in Al-7Si-Mg Alloys via Multiple Regression
Abstract
:1. Introduction
- Proposal of experimental equations to represent the coarsening of dendrite arms of Al-7wt.%Si-xMg (x = 0.5 and 1 wt.%) alloys during solidification under transient heat flow conditions.
- A better understanding of the microstructure evolution, with a special focus on the inherent features of the Mg2Si and AlSiFeMg IMCs.
- Implementation of MLR analysis to determine the quantitative correlations for the prediction of tensile properties and hardness from microstructural parameters.
2. Materials and Methods
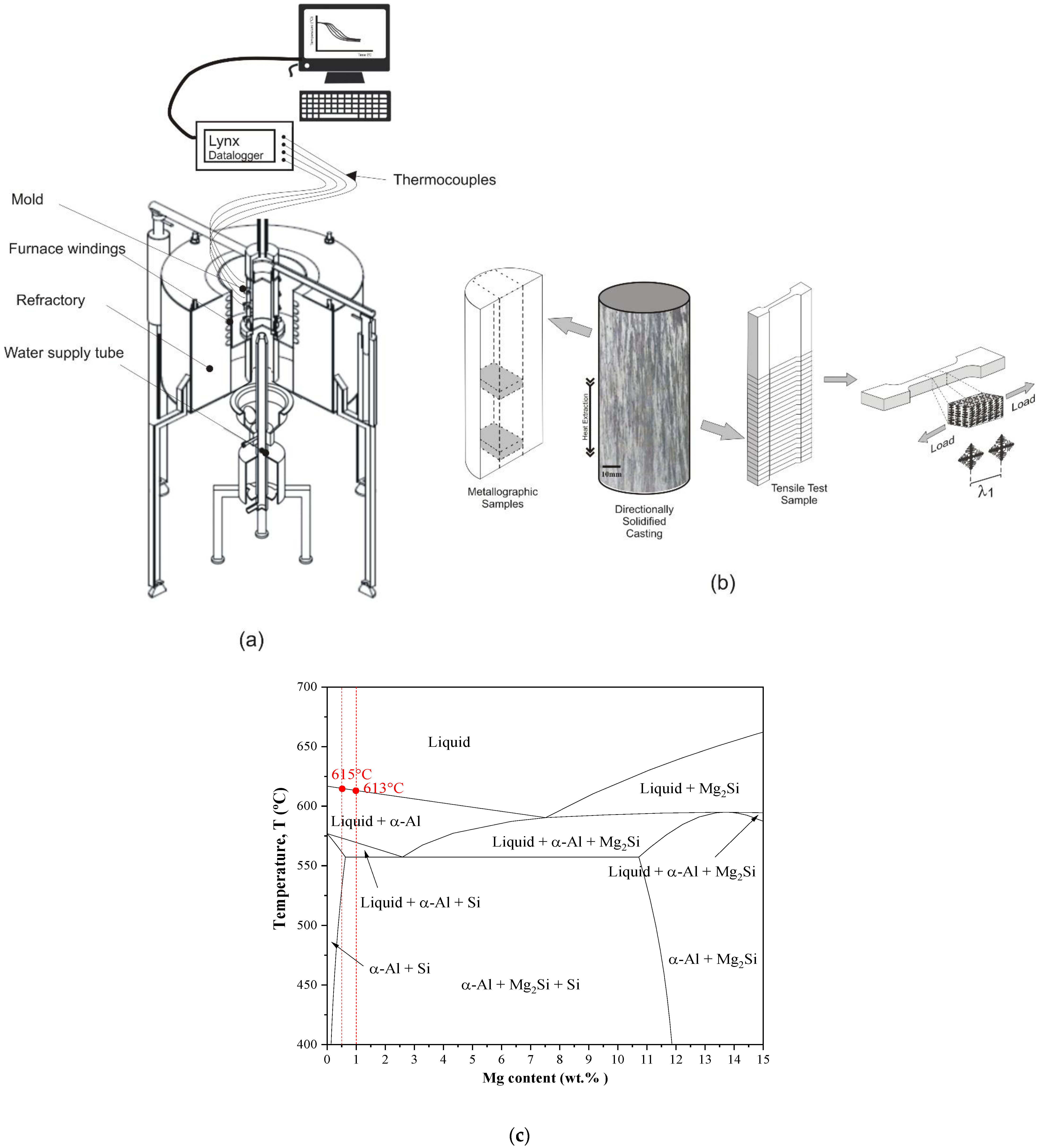
2.1. Al-Si-Mg Alloys
2.2. Metallography
2.3. Mechanical Tests
2.4. Multiple Linear Regression (MLR) Analysis
3. Results and Discussion
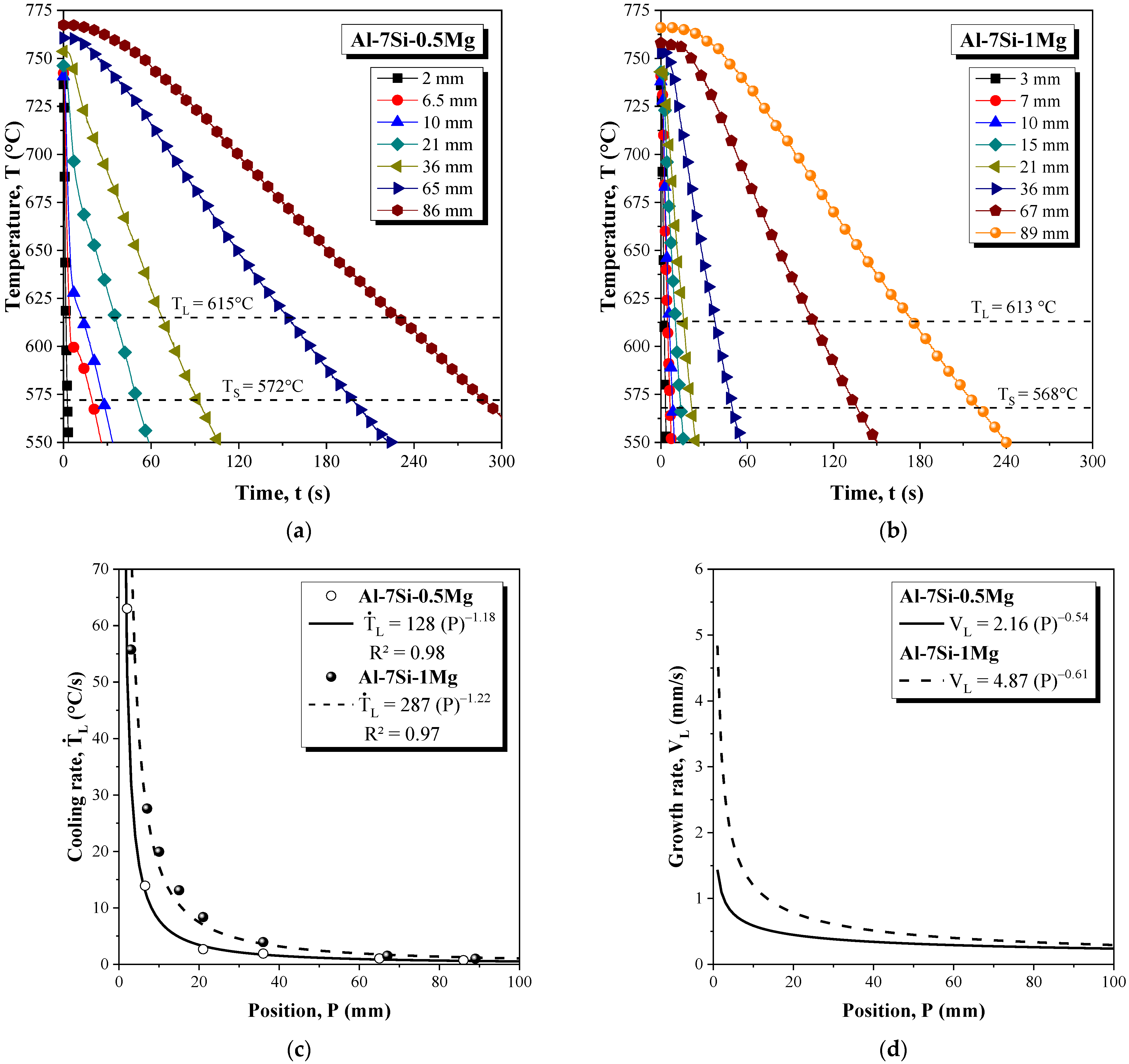
3.1. Cooling Rate, Growth Rate and Macrosegregation
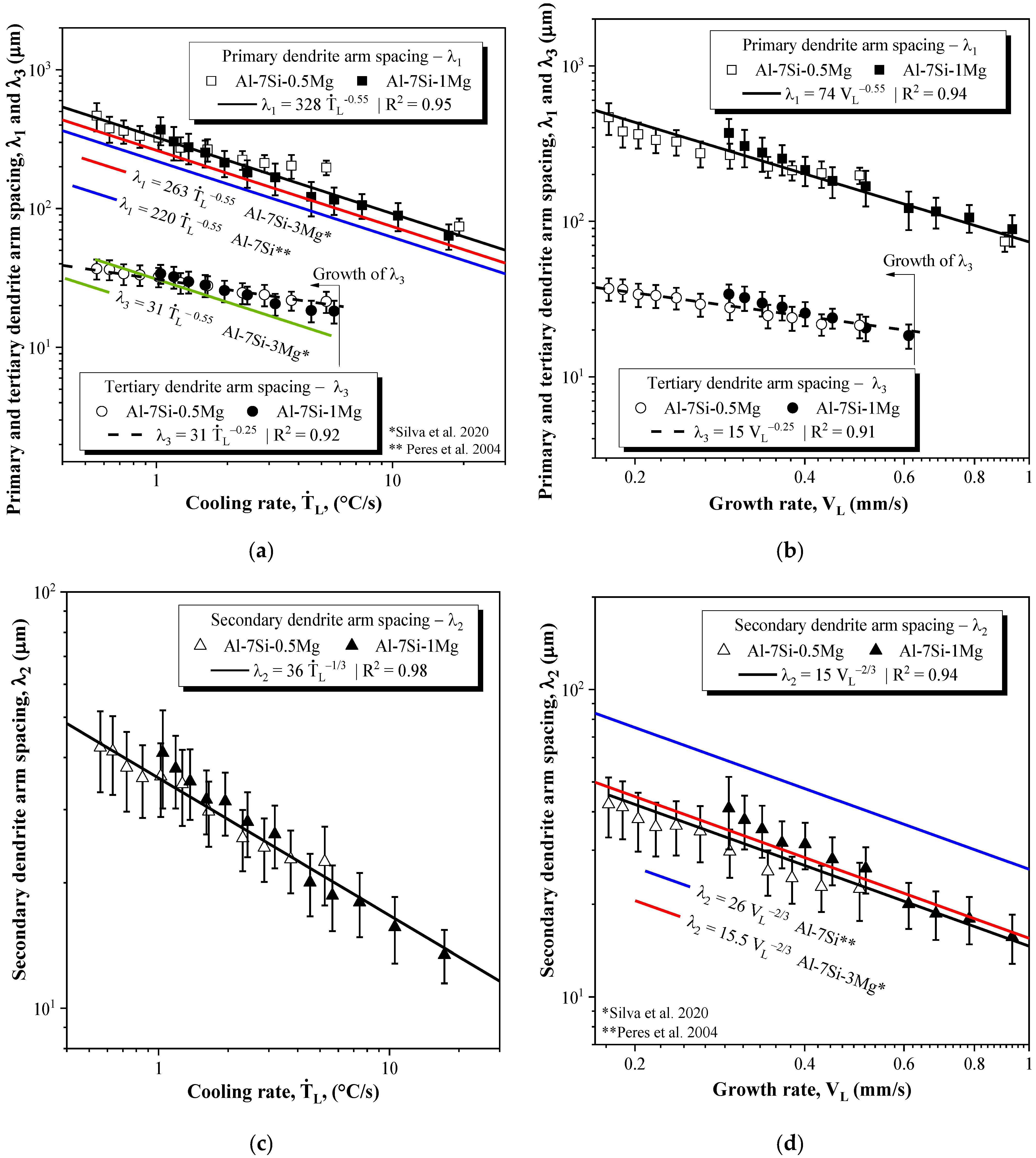
3.2. Macrostructure, Microstructure and Microstructural Spacing
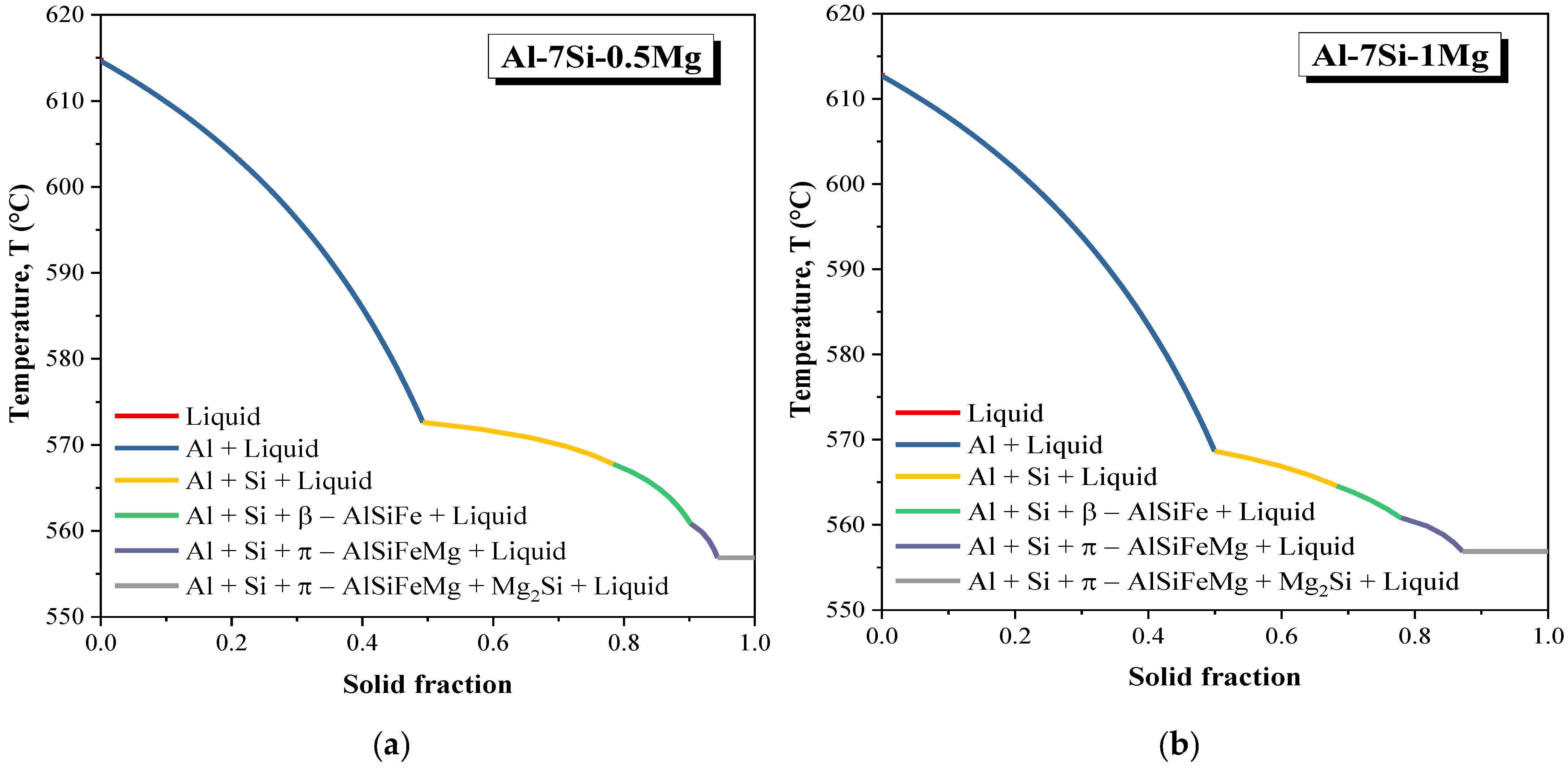
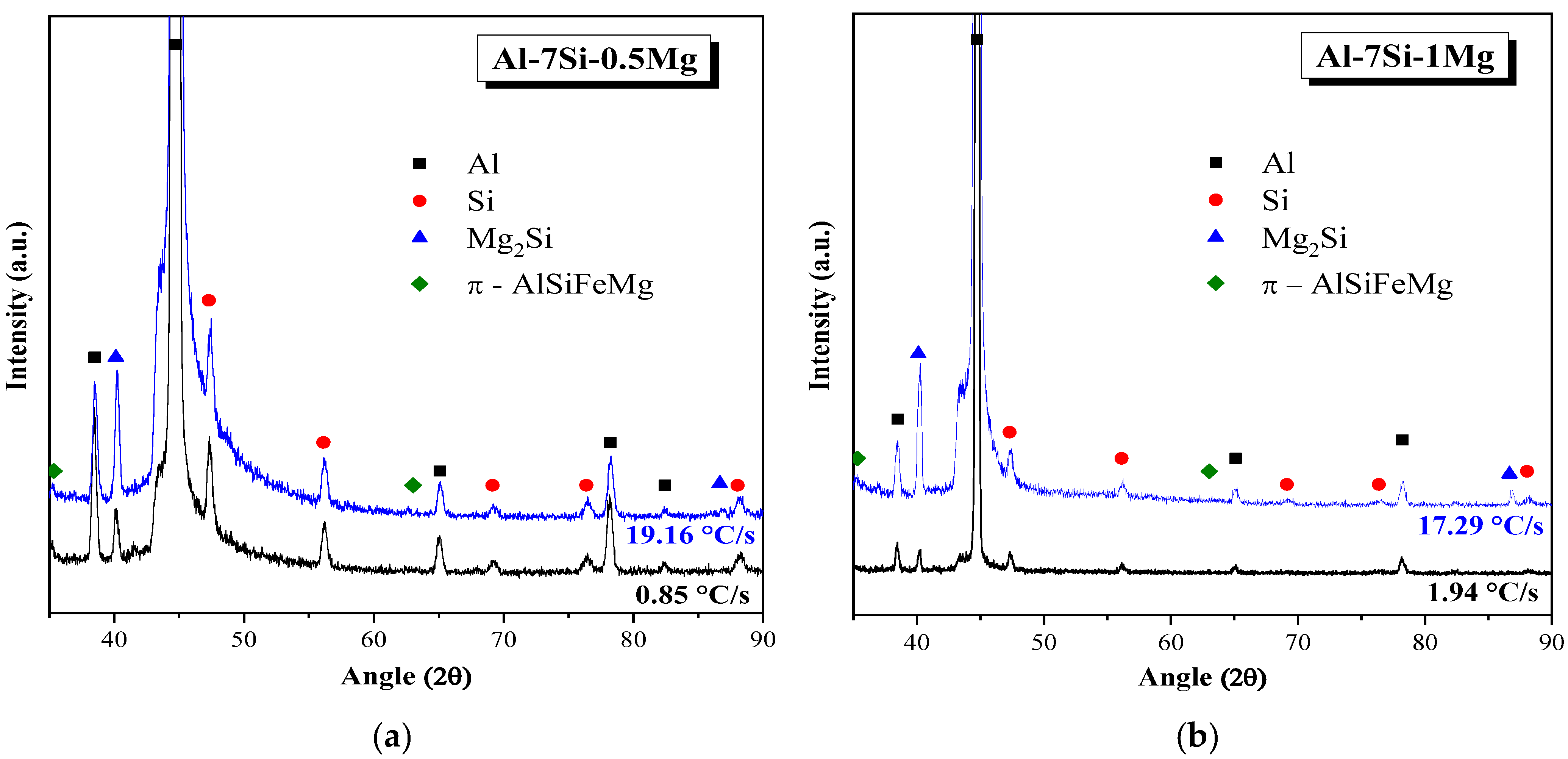
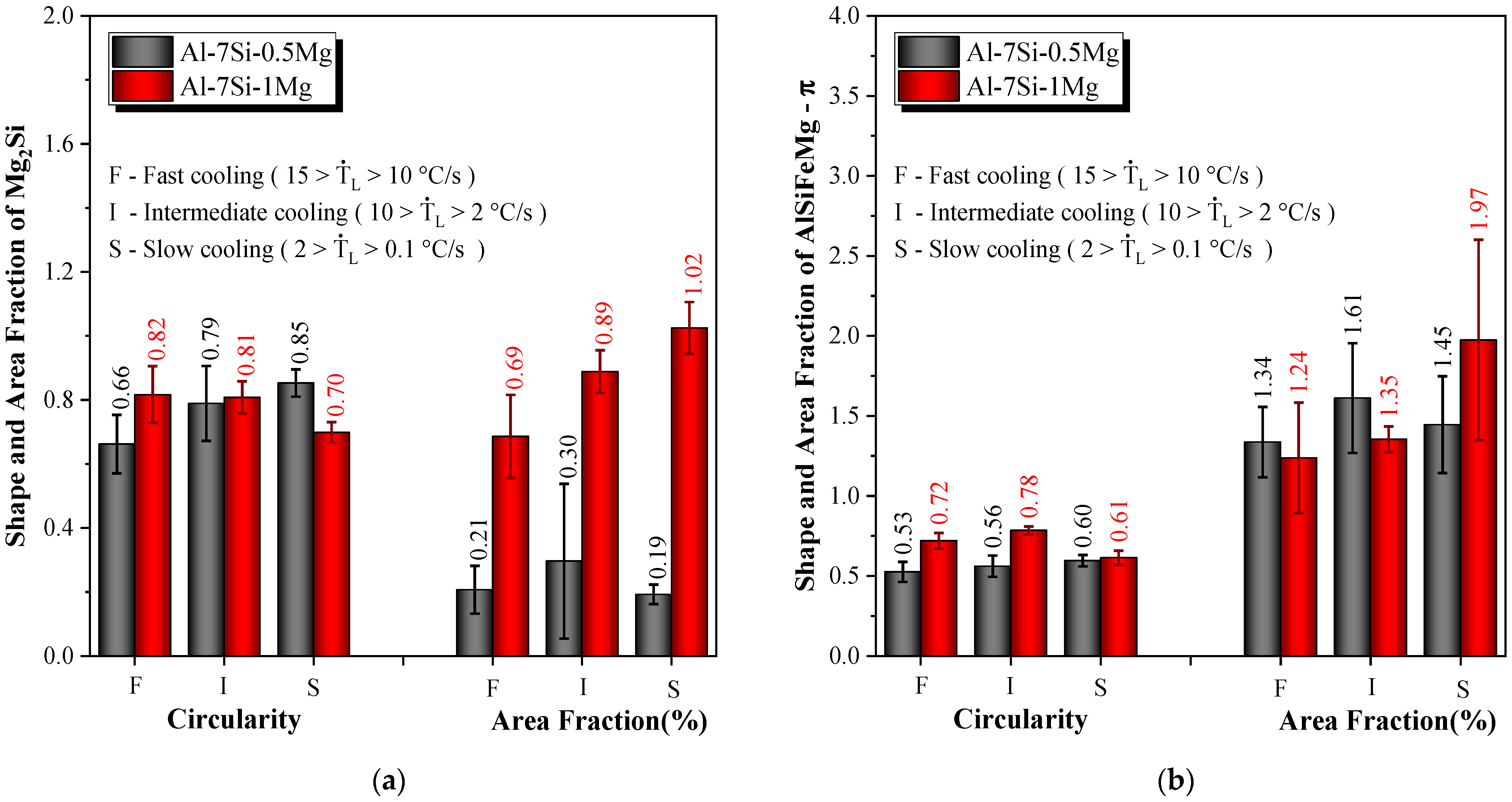
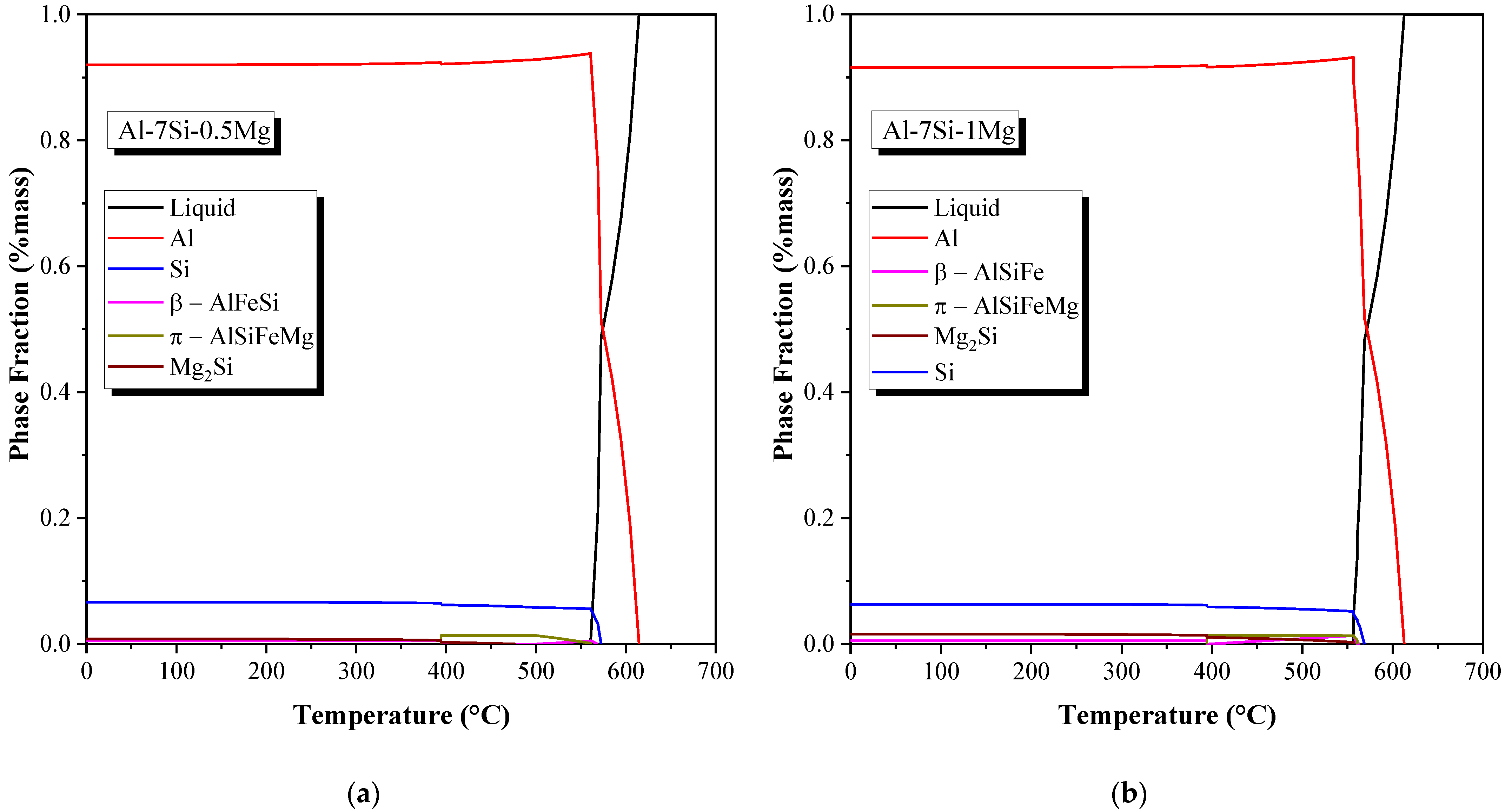
3.3. Intermetallic Compound (IMC) Analysis
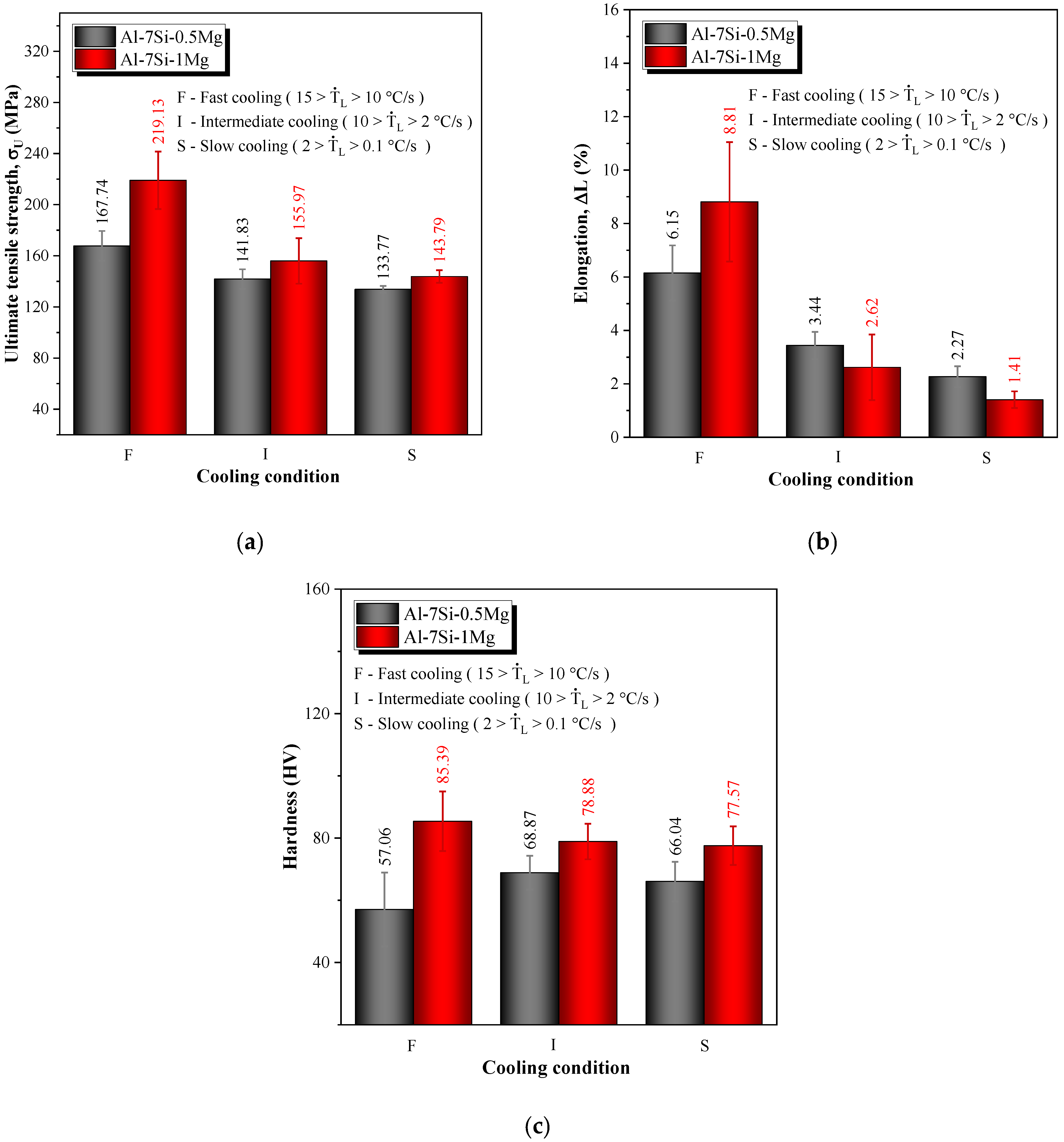
3.4. Mechanical Behavior and MLR Analysis
4. Conclusions
- The macrostructures of both the Al-7Si-0.5Mg and Al-7Si-1.0Mg DS castings were shown to be characterized by columnar grains with no trace of equiaxed grains, thereby confirming the directionality of the solidification process. The microstructures were shown to be formed by Al-rich dendrites with a Maltese-cross morphology, with a complex eutectic mixture of Si particles and π-AlSiFeMg/Mg2Si intermetallics distributed in the interdendritic regions.
- Experimental power-type functions have been derived relating the interdendritic spacings λ1, λ2 and λ3 to VL:
- These expressions were shown to be valid for both the Al-7Si-0.5Mg and Al-7Si-1.0Mg alloys, i.e., the increase in Mg content from 0.5wt% to 1.0wt.% has not affected the coarsening of the dendrite arms.
- The highest values of the ultimate tensile strength, the elongation to fracture and the hardness are shown to be associated with high solidification cooling rates and consequently related to the refinement of the microstructure. The only exception is the hardness of the Al-7Si-0.5Mg alloy, which seems to be unaffected. Overall, it was shown that the Al-7Si-1Mg alloy presents a better mechanical response as compared with that of the Al-7Si-0.5Mg alloy.
- MLR plots relating the tensile properties (ultimate tensile strength and elongation to fracture) and hardness of the Al-7Si-(0.5 and 1) Mg alloys to the inverse of the square root of λ1, λ2 and λ3 (in terms of Hall–Petch-type equations) were developed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mishra, R.S.; Thapliyal, S. Design approaches for printability-performance synergy in Al alloys for laser-powder bed additive manufacturing. Mater. Des. 2021, 204, 109640. [Google Scholar] [CrossRef]
- Shehadeh, L.M.; Jalham, I.S. The Effect of Adding Different Percentages of Manganese (Mn) and Copper (Cu) on the Mechanical Behavior of Aluminum. Jordan J. Mech. Ind. Eng. 2016, 10, 19–26. [Google Scholar]
- Lee, B.H.; Kim, S.H.; Park, J.H.; Kim, H.W.; Lee, J.C. Role of Mg in simultaneously improving the strength and ductility of Al–Mg alloys. Mater. Sci. Eng. A 2016, 657, 115–122. [Google Scholar] [CrossRef]
- Rana, R.S.; Purohit, R.; Das, S. Reviews on the influences of alloying elements on the microstructure and mechanical properties of aluminum alloys and aluminum alloy composites. Int. J. Sci. Res. Publ. 2012, 2, 1–7. [Google Scholar]
- Lima, J.O.; Barbosa, C.R.; Magno, I.A.B.; Nascimento, J.M.; Barros, A.S.; Oliveira, M.C.; Rocha, O. L Microstructural evolution during unsteady-state horizontal solidification of Al-Si-Mg (356) alloy. Trans. Nonferrous Met. Soc. China 2018, 28, 1073–1083. [Google Scholar] [CrossRef]
- Chen, R.; Shi, Y.F.; Xu, Q.Y.; Liu, B.C. Effect of cooling rate on solidification parameters and microstructure of Al-7Si-0.3 Mg-0.15 Fe alloy. Trans. Nonferrous Met. Soc. China 2014, 24, 1645–1652. [Google Scholar] [CrossRef]
- Septimio, R.S.; Costa, T.A.; Silva, C.A.; Vida, T.A.; de Damborenea, J.; Garcia, A.; Cheung, N. Correlation between unsteady-state solidification thermal parameters and microstructural growth of Zn–8 mass% Al and Zn–8 mass% Al–XBi tribological alloys. J. Therm. Anal. Calorim. 2020, 139, 1741–1761. [Google Scholar] [CrossRef]
- Rajkumar, B.; Du, Y.; Zeng, Y.; Tang, S. Phase-field simulation of solidification microstructure in Ni and Cu–Ni alloy using the Wheeler, Boettinger and McFadden model coupled with the CALPHAD data. Calphad 2020, 68, 101691. [Google Scholar] [CrossRef]
- Barros, A.; Cruz, C.; Silva, A.P.; Cheung, N.; Garcia, A.; Rocha, O.; Moreira, A. Length scale of solidification microstructure tailoring corrosion resistance and microhardness in T6 heat treatment of an Al–Cu–Mg alloy. Corros. Eng. Sci. Technol. 2020, 55, 471–479. [Google Scholar] [CrossRef]
- Chen, R.; Xu, Q.; Guo, H.; Xia, Z.; Wu, Q.; Liu, B. Correlation of solidification microstructure refining scale, Mg composition and heat treatment conditions with mechanical properties in Al-7Si-Mg cast aluminum alloys. Mater. Sci. Eng. A 2017, 685, 391–402. [Google Scholar] [CrossRef]
- Apelian, D. Aluminum Cast Alloys: Enabling Tools for Improved Performance; North American Die Casting Association: New York, NY, USA, 2009. [Google Scholar]
- Zolotorevsky, V.S.; Belov, N.A.; Glazoff, M.V. Casting Aluminum Alloys; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Liu, Y.L.; Kang, S.B.; Kim, H.W. The complex microstructures in an as-cast Al–Mg–Si alloy. Mater. Lett. 1999, 41, 267–272. [Google Scholar] [CrossRef]
- Wang, Q.G. Microstructural effects on the tensile and fracture behavior of aluminum casting alloys A356/357. Metall. Mater. Trans. A 2003, 34, 2887–2899. [Google Scholar] [CrossRef]
- Grugel, R.N. Secondary and tertiary dendrite arm spacing relationships in directionally solidified Al-Si alloys. J. Mater. Sci. 1993, 28, 677–683. [Google Scholar] [CrossRef]
- Brito, C.; Costa, T.A.; Vida, T.A.; Bertelli, F.; Cheung, N.; Spinelli, J.E.; Garcia, A. Characterization of dendritic microstructure, intermetallic phases, and hardness of directionally solidified Al-Mg and Al-Mg-Si alloys. Metall. Mater. Trans. A 2015, 46, 3342–3355. [Google Scholar] [CrossRef]
- Silva, B.L.; Reyes, R.V.; Garcia, A.; Spinelli, J.E. Dendritic Growth, Eutectic Features and Their Effects on Hardness of a Ternary Sn–Zn–Cu Solder Alloy. Acta Metall. Sin. 2017, 30, 528–540. [Google Scholar] [CrossRef] [Green Version]
- Kakitani, R.; Reyes, R.V.; Garcia, A.; Spinelli, J.E.; Cheung, N. Relationship between spacing of eutectic colonies and tensile properties of transient directionally solidified Al-Ni eutectic alloy. J. Alloy. Compd. 2018, 733, 59–68. [Google Scholar] [CrossRef]
- Schon, A.F.; Castro, N.A.; Barros, A.B.; Spinelli, J.E.; Garcia, A.; Cheung, N.; Silva, B.L. Multiple linear regression approach to predict tensile properties of Sn-Ag-Cu (SAC) alloys. Mater. Lett. 2021, 304, 130587. [Google Scholar] [CrossRef]
- Kwak, S.; Kim, J.; Ding, H.; Xu, X.; Chen, R.; Guo, J.; Fu, H. Using multiple regression analysis to predict directionally solidified TiAl mechanical property. J. Mater. Sci. Technol. 2022, 104, 285–291. [Google Scholar] [CrossRef]
- Suh, J.S.; Suh, B.C.; Bae, J.H.; Lee, S.E.; Moon, B.G.; Kim, Y.M. Quantitative relationship analysis of mechanical properties with microstructure and texture evolution in AZ series alloys. In Magnesium Technology; Springer: Cham, Switzerland, 2020; pp. 347–353. [Google Scholar]
- Li, Q.; Li, B.; Li, J.; Xia, T.; Lan, Y.; Guo, T. Effects of the addition of Mg on the microstructure and mechanical properties of hypoeutectic Al–7% Si alloy. Int. J. Met. 2017, 11, 823–830. [Google Scholar] [CrossRef]
- Kashyap, K.T.; Murali, S.; Raman, K.S.; Murthy, K.S.S. Casting and heat treatment variables of Al–7Si–Mg alloy. Mater. Sci. Technol. 1993, 9, 189–204. [Google Scholar] [CrossRef]
- Edwards, G.A.; Stiller, K.; Dunlop, G.L.; Couper, M.J. The precipitation sequence in Al–Mg–Si alloys. Acta Mater. 1998, 46, 3893–3904. [Google Scholar] [CrossRef]
- Hearn, W.; Bogno, A.A.; Spinelli, J.; Valloton, J.; Henein, H. Microstructure Solidification Maps for Al-10 Wt Pct Si Alloys. Metall. Mater. Trans. A 2019, 50, 1333–1345. [Google Scholar] [CrossRef]
- Canté, M.V.; Lima, T.S.; Brito, C.; Garcia, A.; Cheung, N.; Spinelli, J.E. An alternative to the recycling of Fe-contaminated Al. J. Sustain. Metall. 2018, 4, 412–426. [Google Scholar] [CrossRef]
- Silva, C.; Soares, T.; Cheung, N.; Garcia, A.; Reis, D.A.; Brito, C. Dendritic Spacing and Macrosegregation Affecting Microhardness of an Al-Si-Mg Alloy Solidified Under Unsteady State Conditions. Mater. Res. 2020, 22. [Google Scholar] [CrossRef]
- Oliveira, R.; Cruz, C.; Barros, A.; Bertelli, F.; Spinelli, J.E.; Garcia, A.; Cheung, N. Thermal conductance at Sn-0.5 mass% Al solder alloy/substrate interface as a factor for tailoring cellular/dendritic growth. J. Therm. Anal. Calorim. 2021, 147, 4945–4958. [Google Scholar] [CrossRef]
- Konno, C.; Cruz, C.; Costa, T.; Barros, A.; Goulart, P.; Garcia, A.; Cheung, N. Solidification microstructure-dependent hydrogen generation behavior of Al–Sn and Al–Fe alloys in alkaline medium. Int. J. Hydrog. Energy 2021, 46, 12654–12671. [Google Scholar] [CrossRef]
- ASTM E562-11; Standard Test Method for Determining Volume Fraction by Systematic Manual Point Count. ASTM International: West Conshohocken, PA, USA, 2011.
- ASTM E1382-97; Standard Test Methods for Determining Average Grain Size Using Semiautomatic and Automatic Image Analysis. ASTM International: West Conshohocken, PA, USA, 2010.
- ASTM E384-17; Standard Test Method for Microindentation Hardness of Materials. ASTM International: West Conshohocken, PA, USA, 2017; pp. 1–40. [CrossRef]
- ASTM E8/E8M-21; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2021; pp. 1–27. [CrossRef]
- Kakitani, R.; Oliveira, R.; Reyes, R.V.; Rodrigues, A.V.; Bertelli, F.; Garcia, A.; Spinelli, J.E.; Cheung, N. Metal/mold thermal conductance affecting ultrafine scale microstructures in aluminum eutectic alloys. Case Stud. Therm. Eng. 2021, 26, 101144. [Google Scholar] [CrossRef]
- Gomes, L.F.; Silva, B.L.; Garcia, A.; Spinelli, J.E. Dendritic growth, solidification thermal parameters, and Mg content affecting the tensile properties of Al-Mg-1.5 wt pct Fe alloys. Metall. Mater. Trans. A 2017, 48, 1841–1855. [Google Scholar] [CrossRef]
- Osório, W.R.; Moutinho, D.J.; Peixoto, L.C.; Ferreira, I.L.; Garcia, A. Macrosegregation and microstructure dendritic array affecting the electrochemical behaviour of ternary Al–Cu–Si alloys. Electrochim. Acta 2011, 56, 8412–8421. [Google Scholar] [CrossRef]
- Bertelli, F.; Brito, C.; Ferreira, I.L.; Reinhart, G.; Nguyen-Thi, H.; Mangelinck-Noel, N.; Cheung, N.; Garcia, A. Cooling thermal parameters, microstructure, segregation and hardness in directionally solidified Al–Sn-(Si; Cu) alloys. Mater. Des. 2015, 72, 31–42. [Google Scholar] [CrossRef]
- Kakitani, R.; Reyes, R.V.; Garcia, A.; Cheung, N.; Spinelli, J.E. Effects of melt superheating on the microstructure and tensile properties of a ternary Al-15 Wt Pct Si-1.5 wt pct Mg alloy. Metall. Mater. Trans. A 2019, 50, 1308–1322. [Google Scholar] [CrossRef]
- Samoilovich, Y.A.; Timoshpol`ski, V.I.; Kabishov, S.M. Calculation of Dendritic Liquation (Microsegregation) in a Solidified Steel Ingot with Allowance for Ionic Migration. J. Eng. Phys. Thermophys. 2009, 82, 98–105. [Google Scholar] [CrossRef]
- Eskinm, D.G. Structural Factors of Dendritic Segregation in Aluminum Alloys. Russ. J. Non-Ferr. Metals 2008, 49, 373–378. [Google Scholar] [CrossRef]
- Meza, E.S.; Bertelli, F.; Goulart, P.R.; Cheung, N.; Garcia, A. The Effect of Growth Rate on Microsegregation: Experimental Investigation in Hypoeutectic Al-Fe and Al-Cu alloys Directionally Solidified. J. Alloy. Compd. 2013, 561, 193–200. [Google Scholar] [CrossRef]
- Barros, A.; Cruz, C.; Silva, A.P.; Cheung, N.; Garcia, A.; Rocha, O.; Moreira, A. Horizontally Solidified Al–3wt%Cu–(0.5wt% Mg) Alloys: Tailoring Thermal Parameters, Microstructure, Microhardness, and Corrosion Behavior. Acta Metall. Sin. 2019, 32, 695–709. [Google Scholar] [CrossRef] [Green Version]
- Rosa, D.M.; Spinelli, J.E.; Garcia, A. Tertiary dendrite arm spacing during downward transient solidification of Al–Cu and Al–Si alloys. Mater. Lett. 2006, 60, 1871–1874. [Google Scholar] [CrossRef]
- Peres, M.D.; Siqueira, C.A.; Garcia, A. Macrostructural and microstructural development in Al–Si alloys directionally solidified under unsteady-state conditions. J. Alloy. Compd. 2004, 381, 168–181. [Google Scholar] [CrossRef]
- Bouchard, D.; Kirkaldy, J.S. Prediction of dendrite arm spacings in unsteady-and steady-state heat flow of unidirectionally solidified binary alloys. Metall. Mater. Trans. B 1997, 28, 651–663. [Google Scholar] [CrossRef]
- Silva, B.L.; Garcia, A.; Spinelli, J.E. Cooling thermal parameters and microstructure features of directionally solidified ternary Sn–Bi–(Cu, Ag) solder alloys. Mater. Charact. 2016, 114, 30–42. [Google Scholar] [CrossRef]
- Jackson, K.A.; Hunt, J.D. Lamellar and rod eutectic growth. In Dynamics of Curved Fronts; Academic Press: Cambridge, MA, USA, 1988; pp. 363–376. [Google Scholar]
- Arrabal, R.; Mingo, B.; Pardo, A.; Mohedano, M.; Matykina, E.; Rodríguez, I. Pitting corrosion of rheocast A356 aluminium alloy in 3.5 wt.% NaCl solution. Corros. Sci. 2013, 73, 342–355. [Google Scholar] [CrossRef]
- Mingo, B.; Arrabal, R.; Pardo, A.; Matykina, E.; Skeldon, P. 3D study of intermetallics and their effect on the corrosion morphology of rheocast aluminium alloy. Mater. Charact. 2016, 112, 122–128. [Google Scholar] [CrossRef]
- Jian, X.; Meek, T.T.; Han, Q. Refinement of eutectic silicon phase of aluminum A356 alloy using high-intensity ultrasonic vibration. Scr. Mater. 2006, 54, 893–896. [Google Scholar] [CrossRef]
- Didier, C.; Pang, W.K.; Guo, Z.; Schmid, S.; Peterson, V.K. Phase evolution and intermittent disorder in electrochemically lithiated graphite determined using in operando neutron diffraction. Chem. Mater. 2020, 32, 2518–2531. [Google Scholar] [CrossRef]
- Ross, K.C.; Petrus, J.A.; Mcdonald, A.M. An empirical assessment of two-dimensional (2D) Debye–Scherrer-type image-plate X-ray diffraction data collapsed into a 1D diffractogram. Powder Diffr. 2014, 29, 337–345. [Google Scholar] [CrossRef]
- Kubouchi, M.; Hayashi, K.; MiyazakI, Y. Quantitative analysis of interstitial Mg in Mg2Si studied by single crystal X-ray diffraction. J. Alloy. Compd. 2014, 617, 389–392. [Google Scholar] [CrossRef]
- Perlitz, H.; Westgren, A. The Crystal Structure of Al8Si6Mg3Fe; Almqvist & Wiksell: Stockholm, Sweden, 1942. [Google Scholar]




| Metals | Al | Si | Mg | Cu | Fe | Pb | Zn |
|---|---|---|---|---|---|---|---|
| Al | Balance | 0.006 | 0.0011 | 0.01 | 0.073 | 0.006 | 0.005 |
| Si | 0.109 | Balance | - | - | 0.316 | - | - |
| Mg-Al | 6.981 | 0.246 | Balance | 0.115 | 0.001 | - | 0.631 |
| Element | Alloy (wt.%) | 5 mm | 25 mm | 50 mm | 70 mm | 90 mm |
|---|---|---|---|---|---|---|
| Si | Al-7Si-0.5Mg | 6.67 | 6.30 | 7.48 | 7.41 | 7.67 |
| Al-7Si-1Mg | 6.48 | 6.56 | 7.18 | 7.55 | 8.33 | |
| Mg | Al-7Si-0.5Mg | 0.58 | 0.55 | 0.57 | 0.54 | 0.55 |
| Al-7Si-1Mg | 1.09 | 0.98 | 0.95 | 0.97 | 0.96 | |
| Fe | Al-7Si-0.5Mg | 0.15 | 0.14 | 0.15 | 0.14 | 0.14 |
| Al-7Si-1Mg | 0.13 | 0.11 | 0.12 | 0.11 | 0.10 |
| Alloy | Phase | Experimental | Calculated from Thermo-Calc | |
|---|---|---|---|---|
| Cooling Regime | Mass Fraction (wt.%) | Equilibrium Mass Fraction (wt.%) | ||
| Al-7Si-0.5Mg | Mg2Si | Fast | 0.002 | 0.01 |
| Intermediate | 0.002 | |||
| Slow | 0.002 | |||
| π-AlFeSiMg | Fast | 0.015 | 0.01 | |
| Intermediate | 0.018 | |||
| Slow | 0.016 | |||
| Al-7Si-1Mg | Mg2Si | Fast | 0.005 | 0.02 |
| Intermediate | 0.007 | |||
| Slow | 0.008 | |||
| π-AlFeSiMg | Fast | 0.014 | 0.01 | |
| Intermediate | 0.015 | |||
| Slow | 0.022 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, C.; Barros, A.; Vida, T.; Garcia, A.; Cheung, N.; Reis, D.A.P.; Brito, C. Assessing Microstructure Tensile Properties Relationships in Al-7Si-Mg Alloys via Multiple Regression. Metals 2022, 12, 1040. https://doi.org/10.3390/met12061040
Silva C, Barros A, Vida T, Garcia A, Cheung N, Reis DAP, Brito C. Assessing Microstructure Tensile Properties Relationships in Al-7Si-Mg Alloys via Multiple Regression. Metals. 2022; 12(6):1040. https://doi.org/10.3390/met12061040
Chicago/Turabian StyleSilva, Cássio, André Barros, Talita Vida, Amauri Garcia, Noé Cheung, Danieli A. P. Reis, and Crystopher Brito. 2022. "Assessing Microstructure Tensile Properties Relationships in Al-7Si-Mg Alloys via Multiple Regression" Metals 12, no. 6: 1040. https://doi.org/10.3390/met12061040
APA StyleSilva, C., Barros, A., Vida, T., Garcia, A., Cheung, N., Reis, D. A. P., & Brito, C. (2022). Assessing Microstructure Tensile Properties Relationships in Al-7Si-Mg Alloys via Multiple Regression. Metals, 12(6), 1040. https://doi.org/10.3390/met12061040









