Numerical Simulation of Flow Field, Bubble Distribution and Solidified Shell in Slab Mold under Different EMBr Conditions Assisted with High-Temperature Quantitative Velocity Measurement
Abstract
:1. Introduction
2. Mathematical Model
2.1. Assumptions
- (1)
- Liquid steel and mold flux are incompressible Newtonian fluids;
- (2)
- Liquid steel and mold flux in the mold are in the homogeneous phase, and parameters such as density and viscosity are set to be constants;
- (3)
- The influence of mold oscillation and taper is not considered;
- (4)
- The shape of argon bubbles is spherical, ignoring the breakage and coalescence of argon bubbles;
- (5)
- The influence of Joule heat generated by electric currents is ignored;
- (6)
- The molten steel in the paste zone obeys Darcy’s law;
- (7)
- The influence of liquid steel flow on the electromagnetic field is ignored.
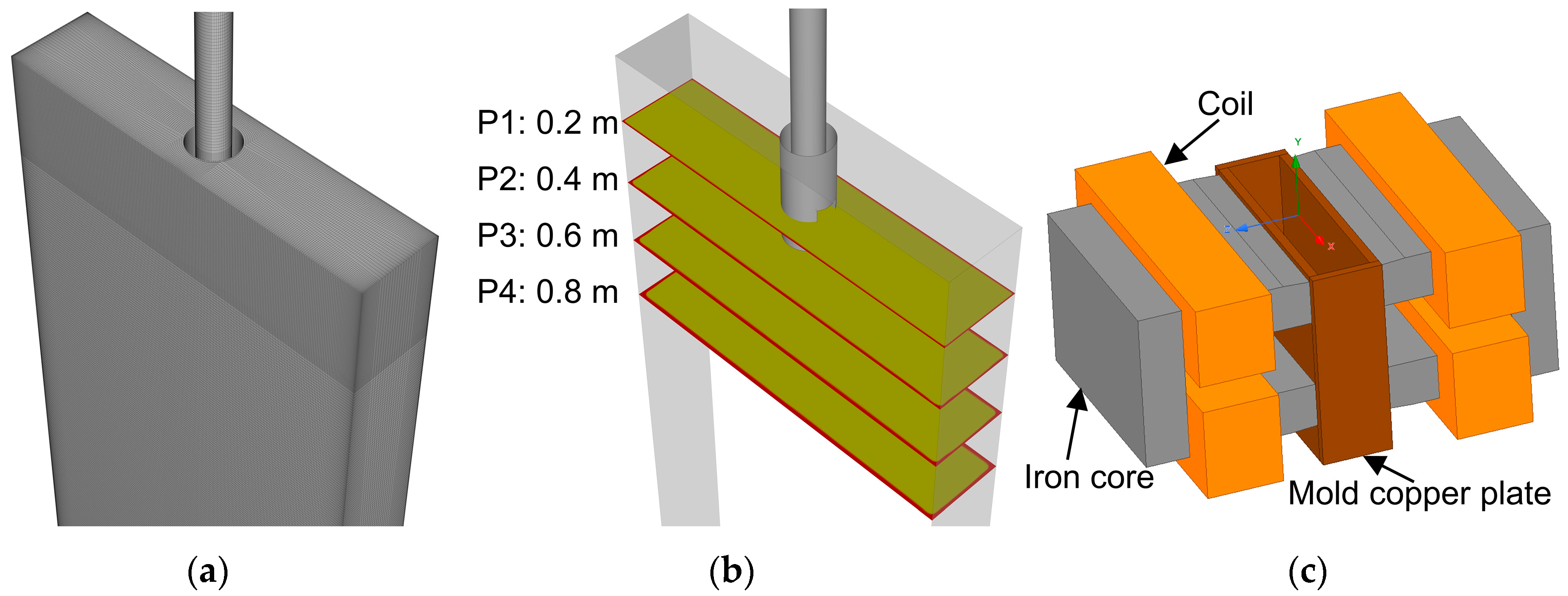
2.2. Electromagnetic Force Model
2.3. Discrete Phase Model
2.4. Multiphase Flow Model
2.5. Large Eddy Simulation and Solidification
2.6. Numerical-Simulation-Related Calculation Parameters
3. Results and Discussion
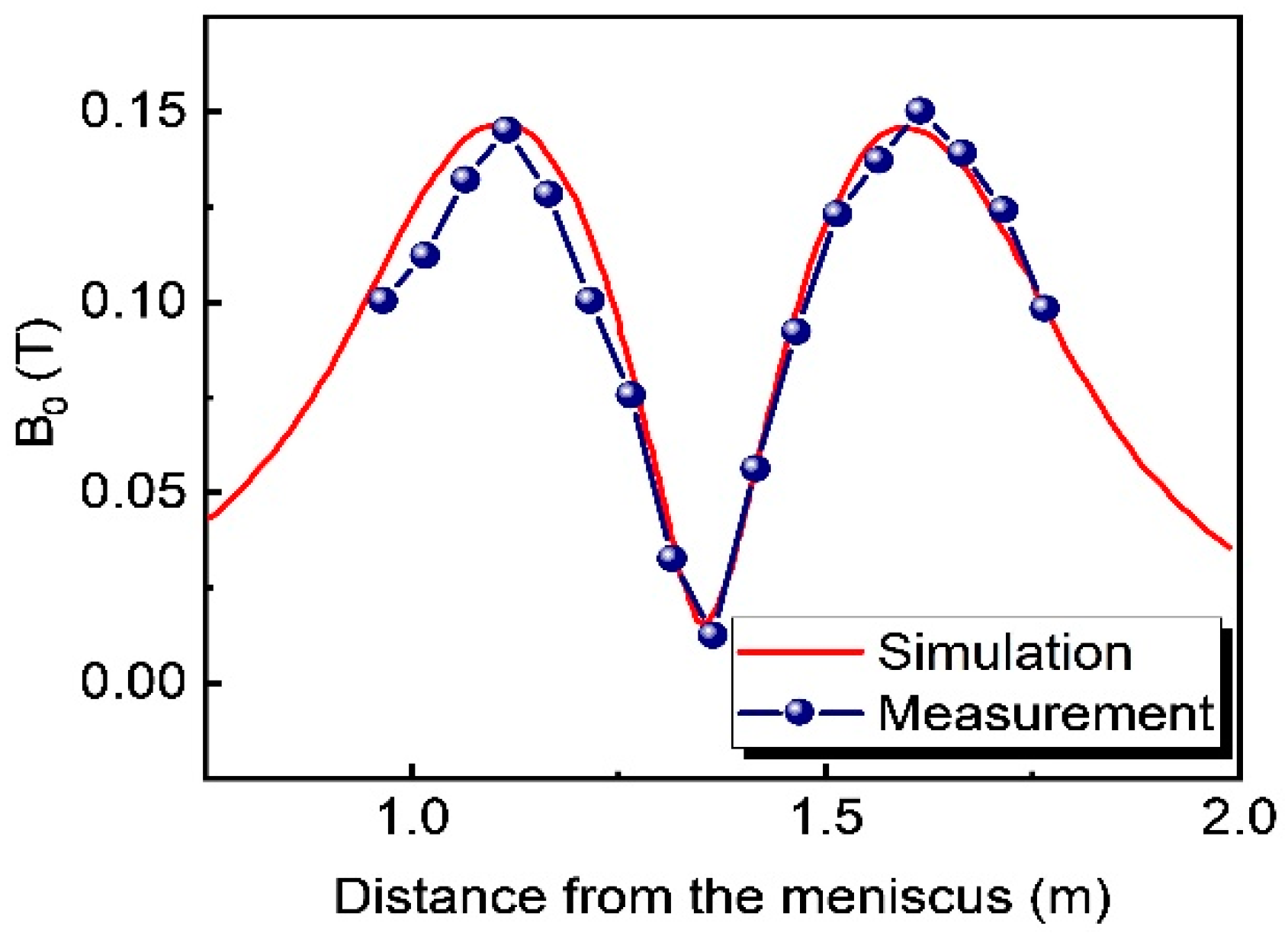
3.1. Magnetic Flux Density Distribution and Model Verification
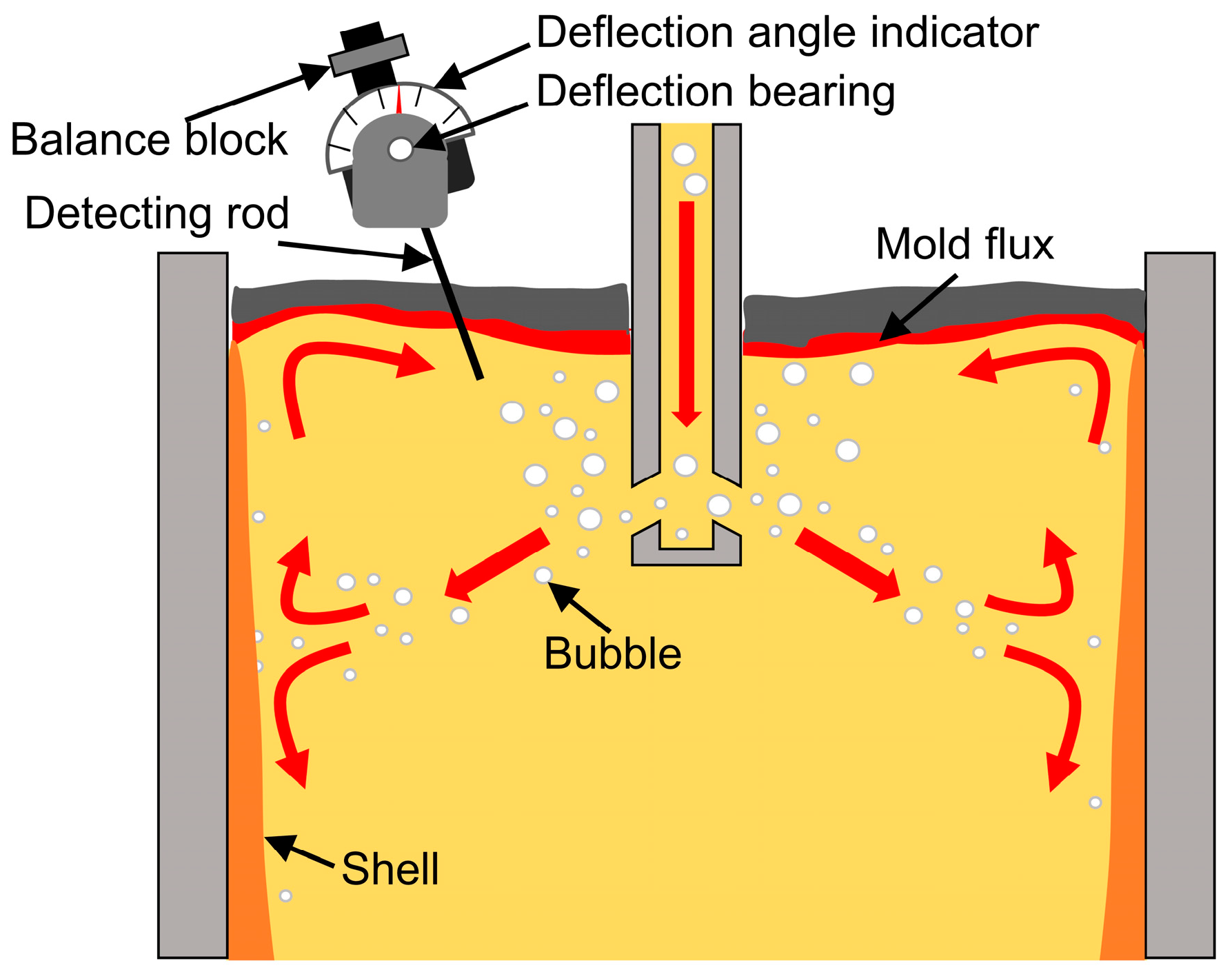
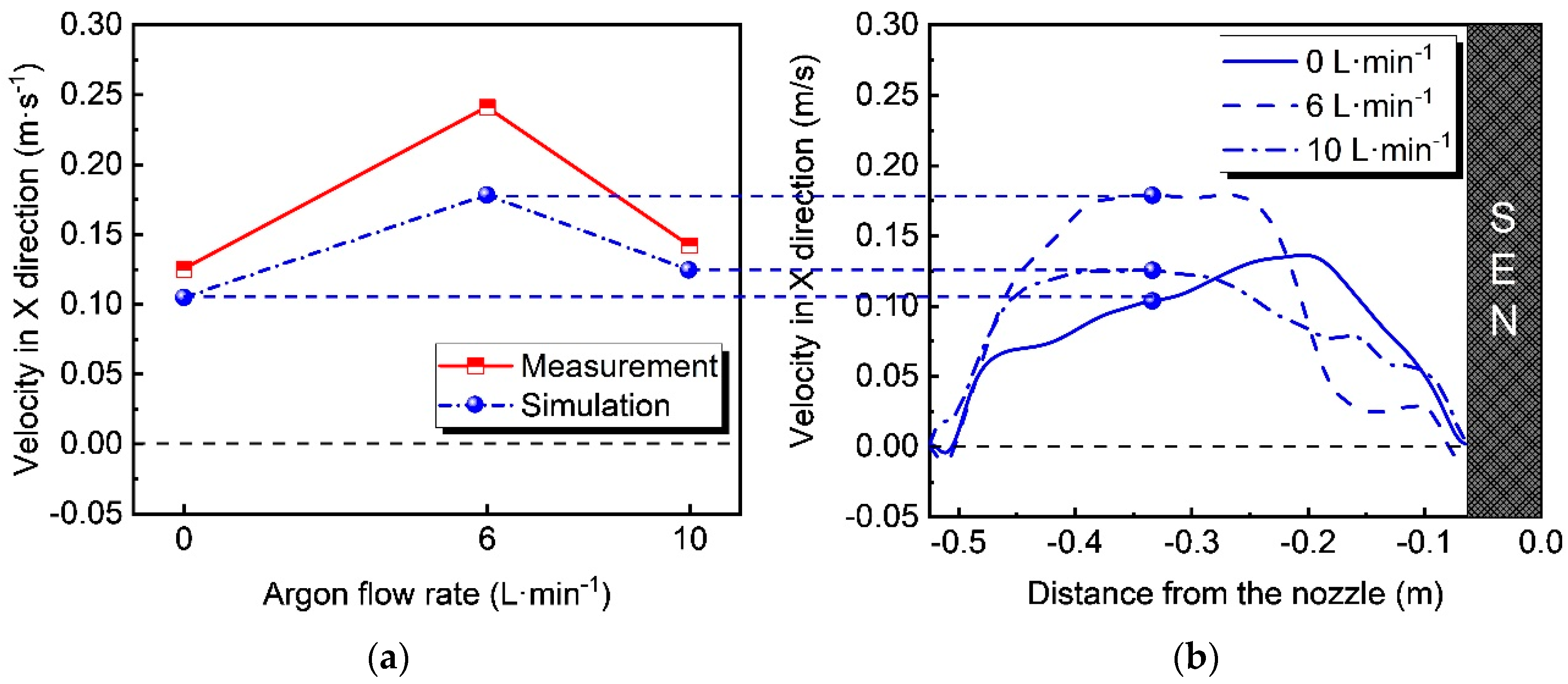
3.2. Comparison between the Calculated and Measured Velocities near the Mold Surface
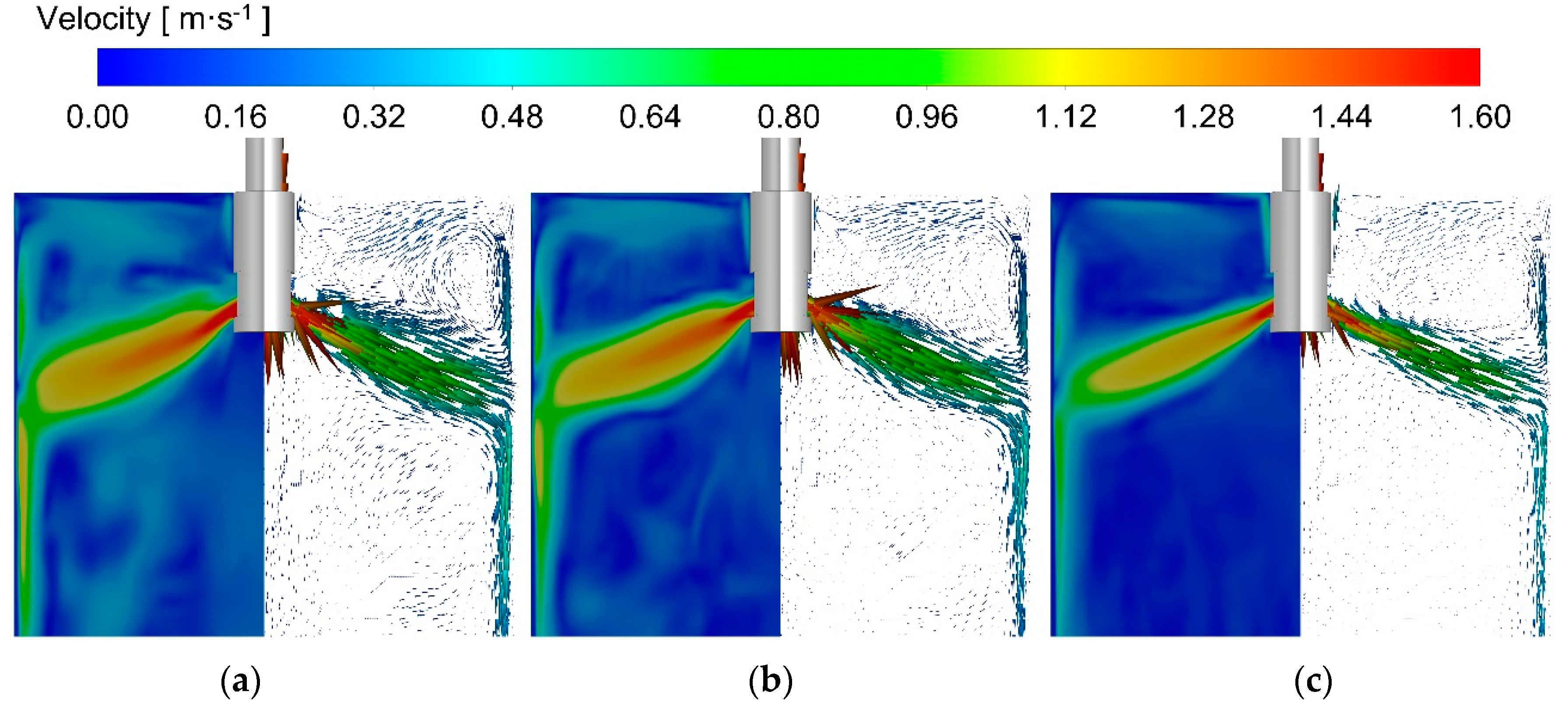
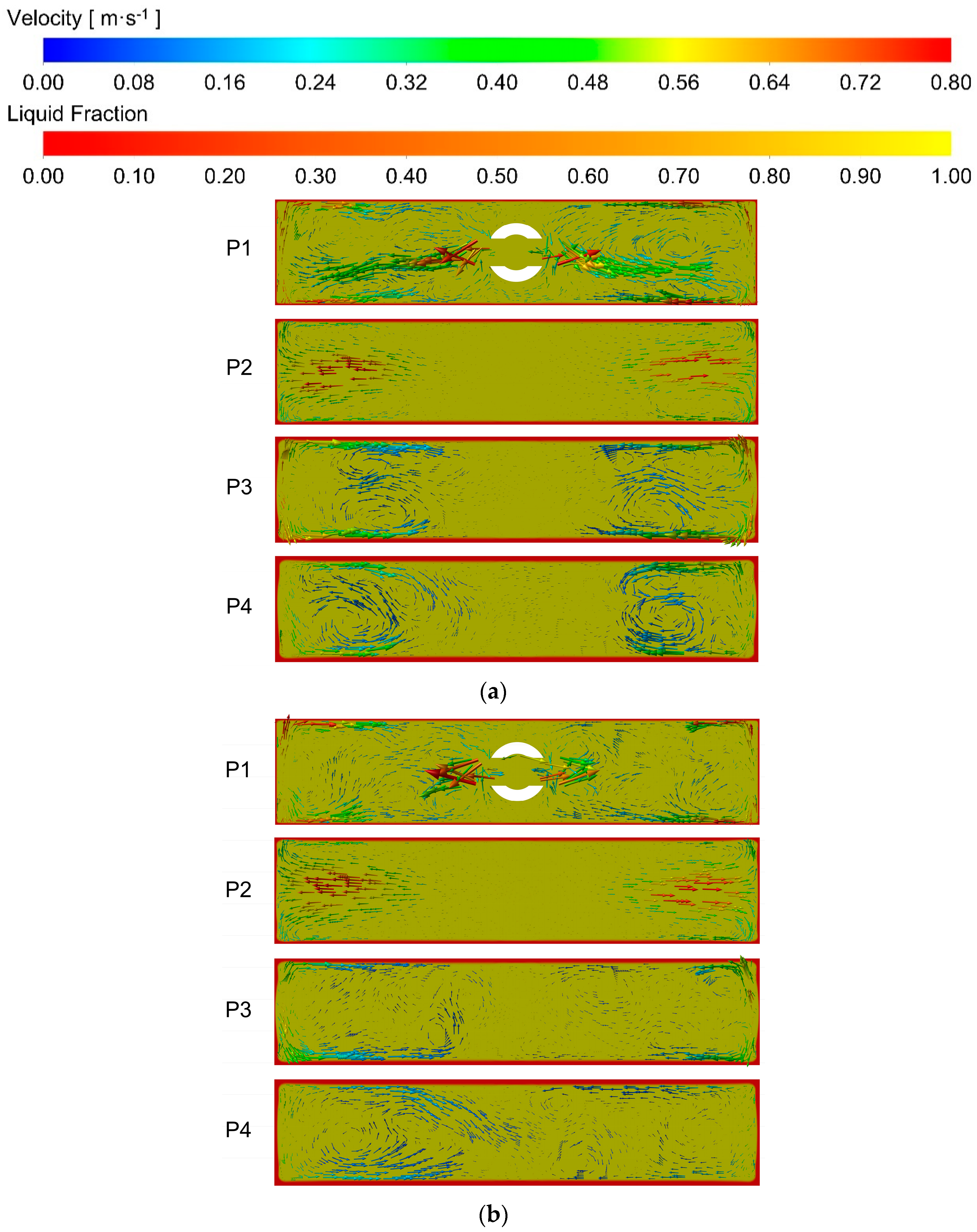
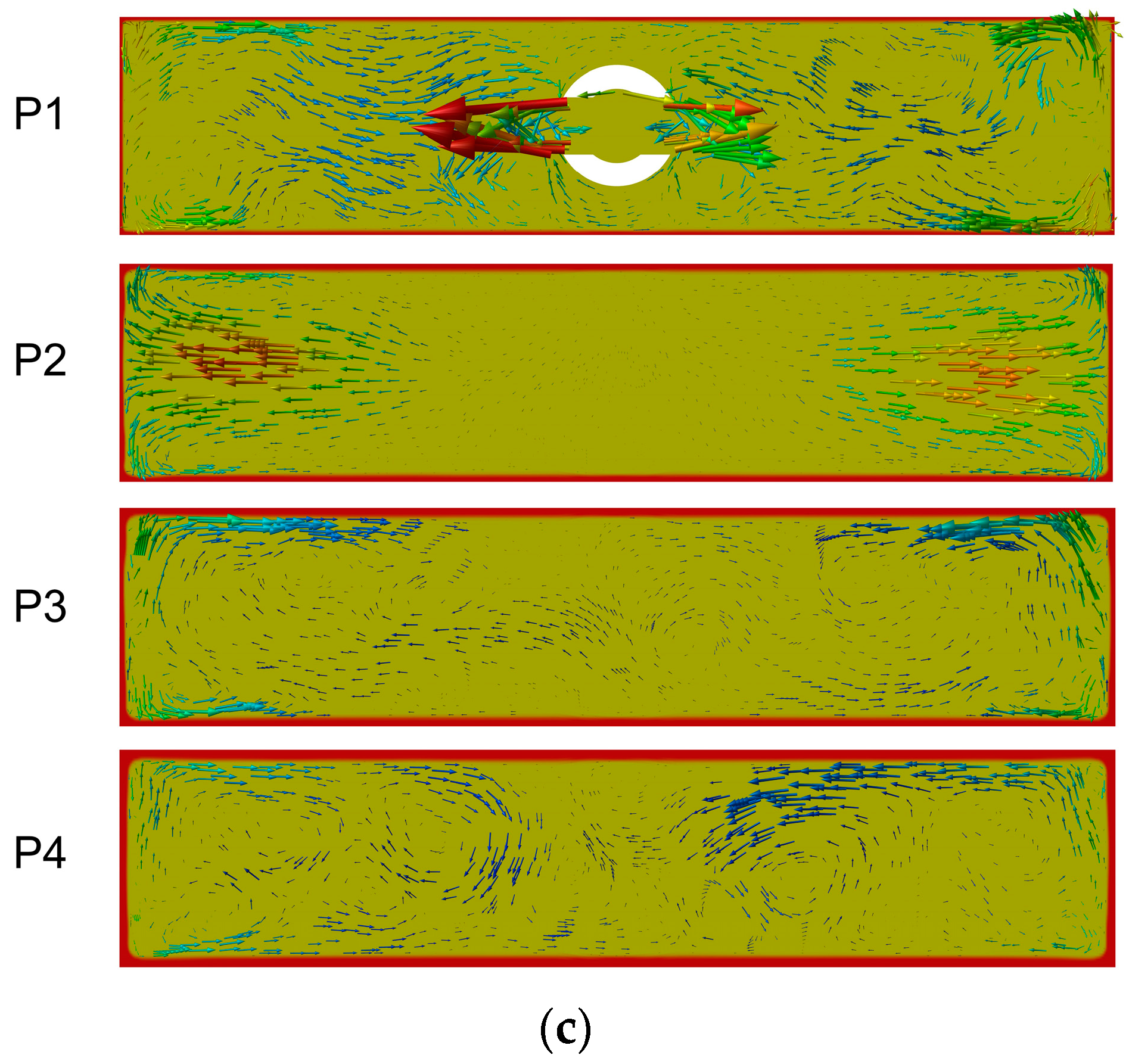
3.3. Effects of Argon Flow Rate and EMBr on Mold Flow Field
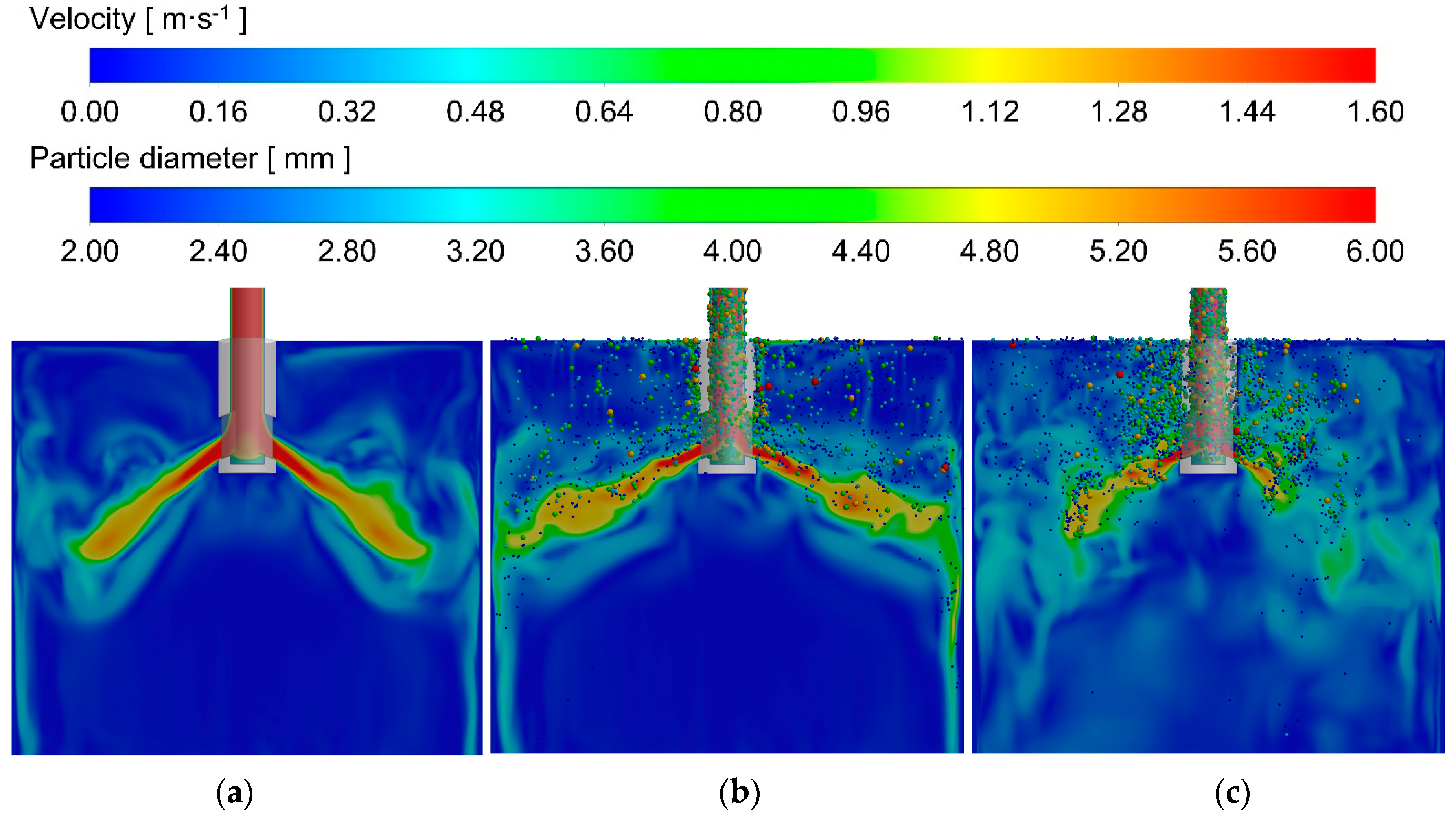
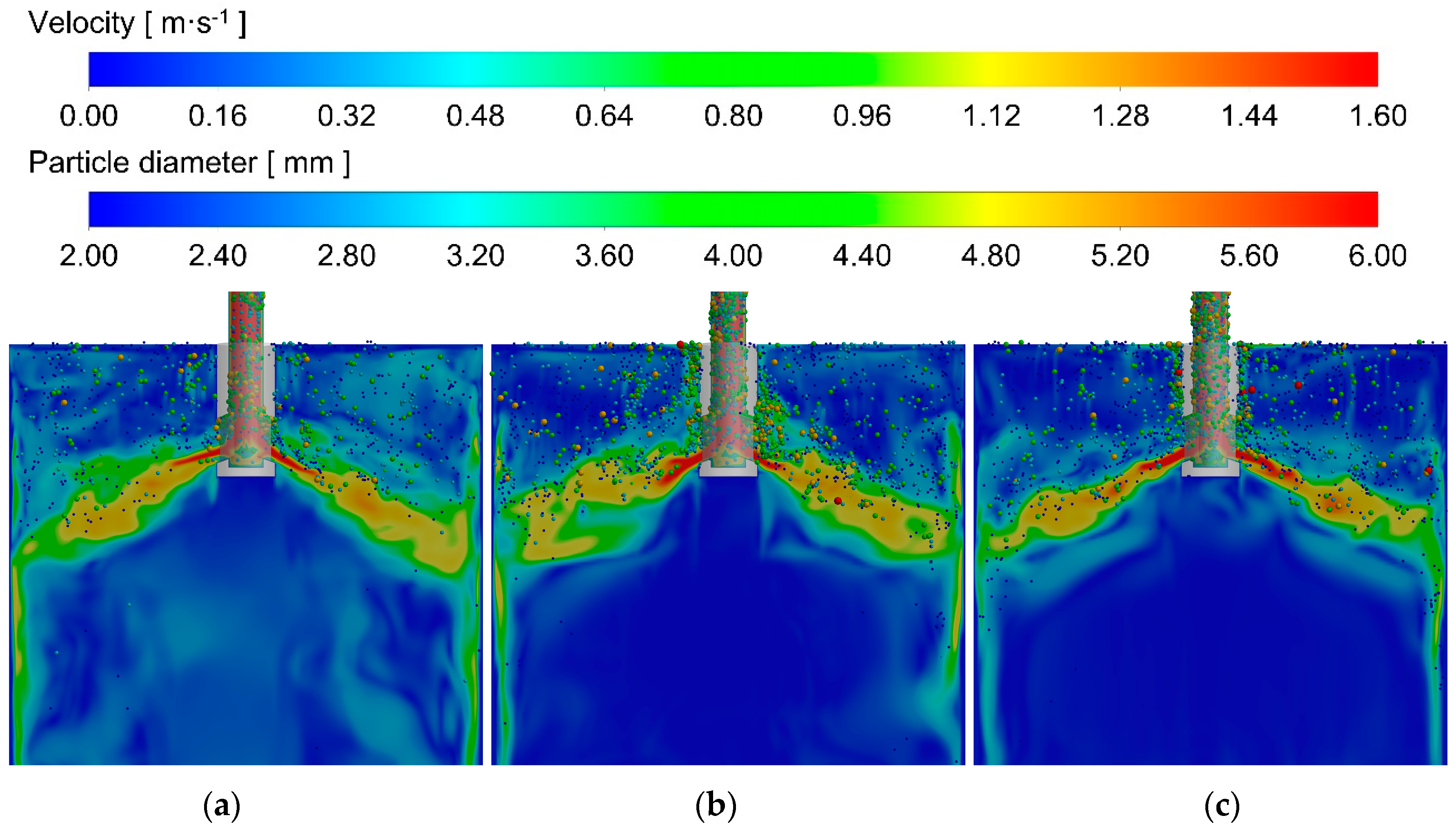
3.4. Effects of Argon Flow and EMBr on Argon Bubble Distribution
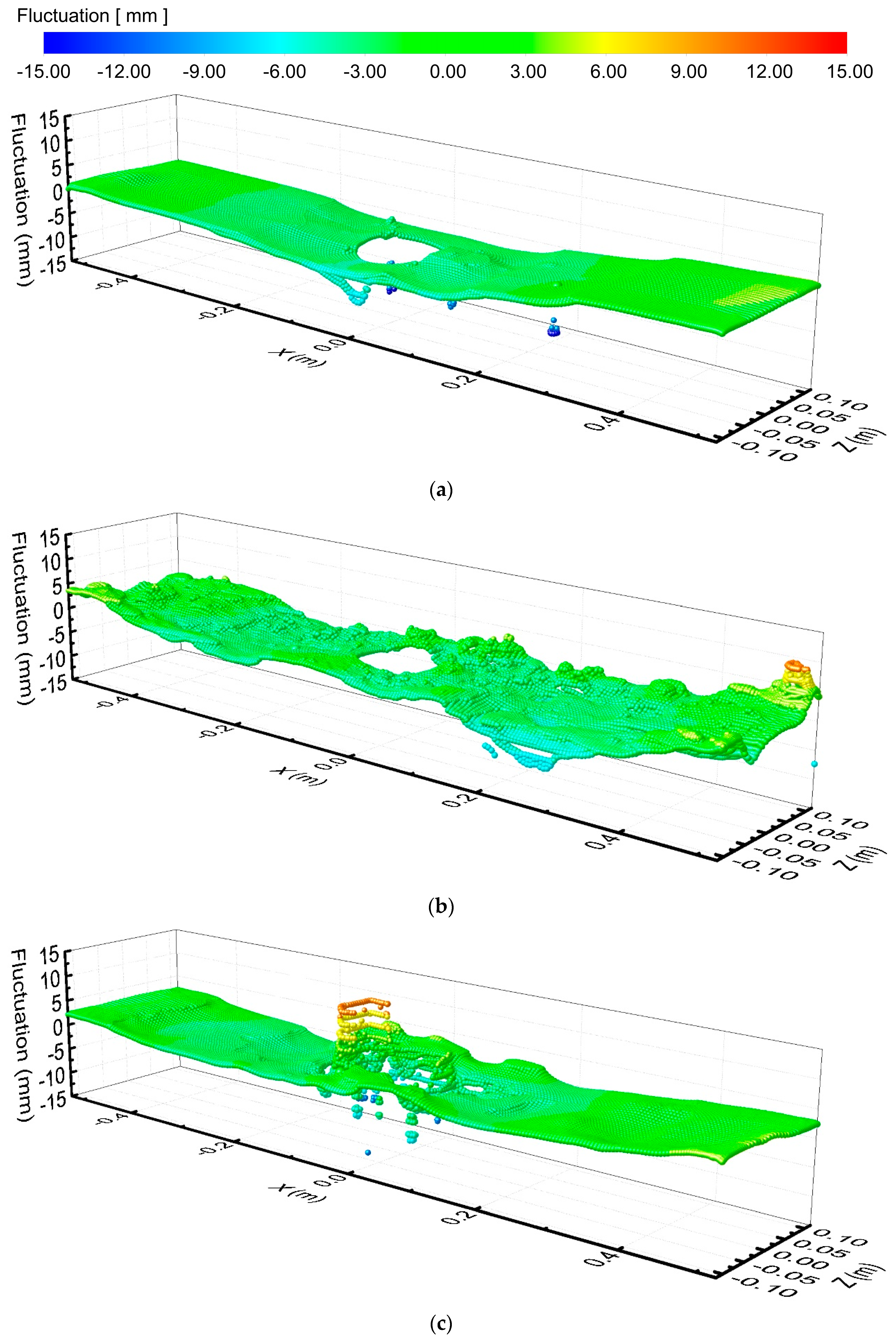
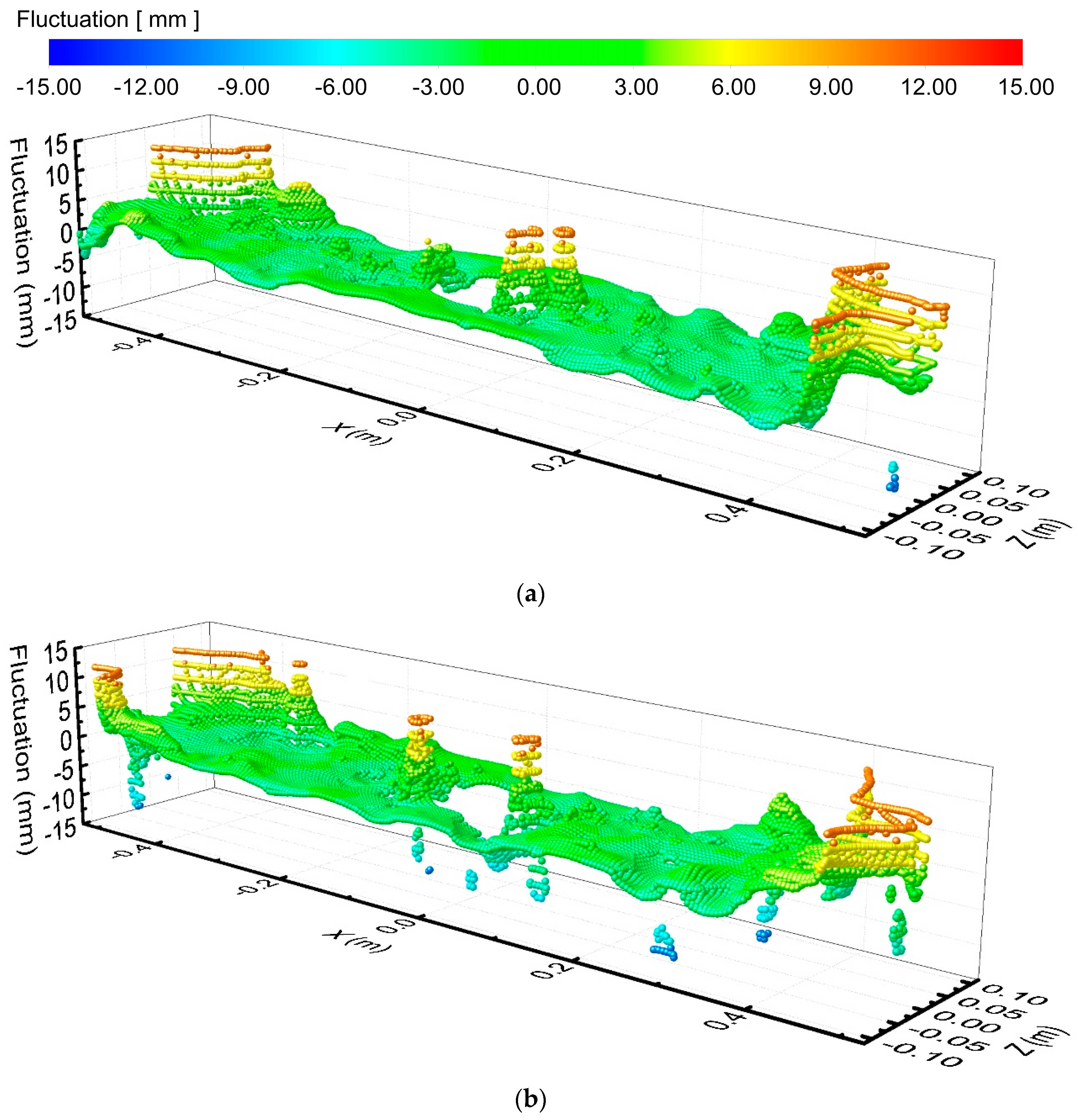
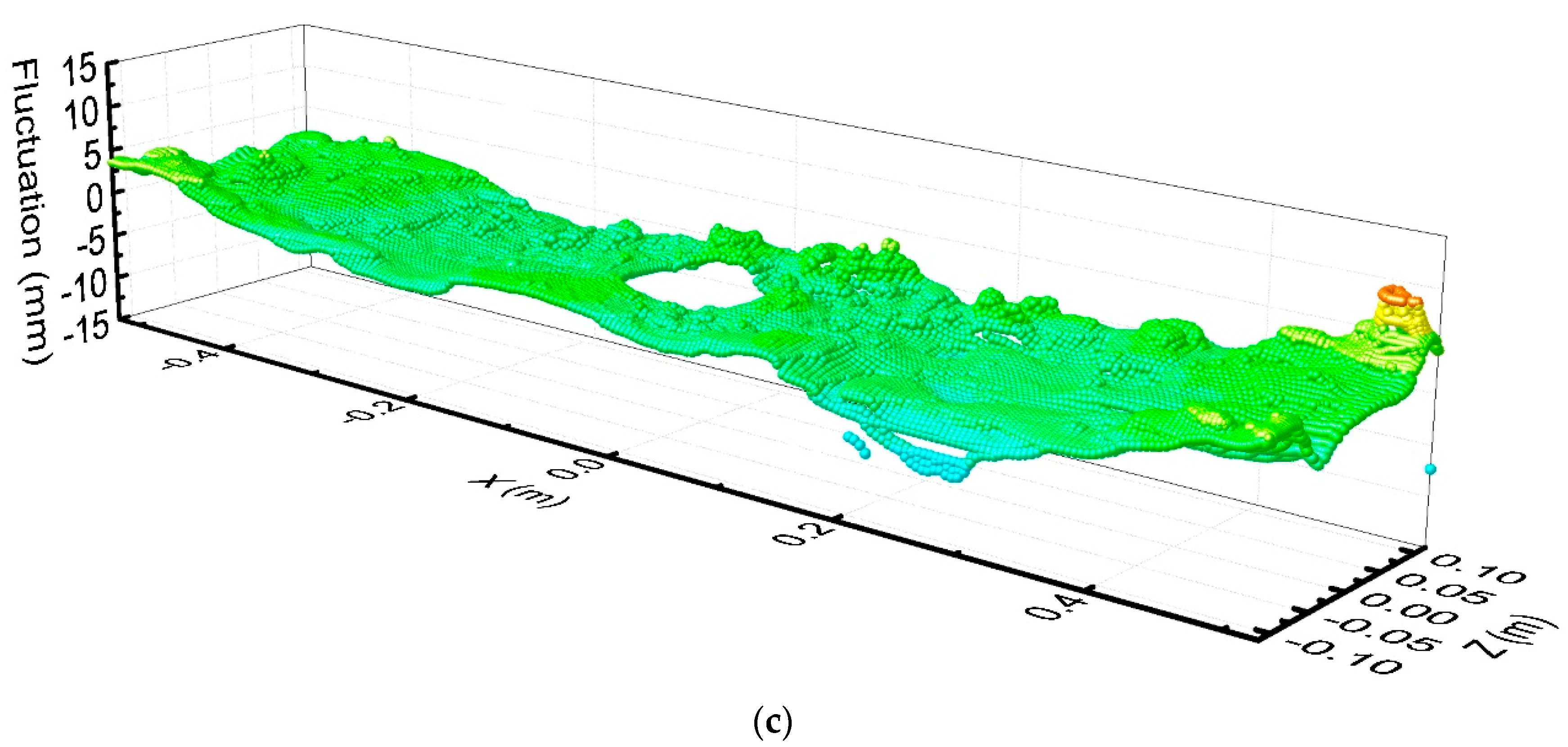
3.5. Fluctuation on Mold Surface
3.6. Effect of EMBr on Solidified Shell
4. Conclusions
- (1)
- The calculated velocities on the mold surface are in good agreement with the measured values of the industrial experiment at high temperature with the rod deflection method. As the argon flow rate is increased from 0 to 6 L·min−1 and 10 L·min−1, both of the calculated and measured velocities on the mold surface first increase and then decrease. As the EMBr mode changes from Mode 1 without EMBr to Mode 2 with upper coil current 0 A and lower coil current 700 A, and then to Mode3 with upper coil current 300 A and lower coil current 700 A, both of the calculated and measured velocities on the mold surface gradually decrease.
- (2)
- With EMBr Mode 3 and at the argon flow rate of 0 L·min−1, the velocity on the mold surface is too low, which is not conducive to the melting of the mold flux. When the argon flow rate is 6 L·min−1, the jet angle increases, and the velocity on the mold surface increases, which is conducive to heat and mass transfer near the meniscus. When the argon flow rate is further increased to 10 L·min−1, the upper circulating flow is affected by floating up of more argon bubbles; the surface velocity of the mold decreases, and the liquid level fluctuation near the SEN increases.
- (3)
- When the argon flow rate is 6 L·min−1 and the casting speed is 1.9 m·min−1, with EMBr Mode 1, the liquid level fluctuation is too large, which may lead to slag entrainment in the mold. With Mode 2, as the lower circulation stream is restrained by the lower magnitude field, the velocity on the mold surface decreases, but the liquid level fluctuation is still large. With Mode 3, both of the lower and upper circulation streams are restrained by the magnetic field, the velocity on the mold surface is reduced, and the fluctuation is at a relatively reasonable level.
- (4)
- With EMBr Mode 3, when the argon flow rate is 10 L·min−1, due to the strong upward floating of argon bubbles, the jet at the port becomes disordered, and the liquid level fluctuation near the SEN wall intensifies, which increases the risk of slag entrainment and slag layer breaking, as well as the risk of argon bubbles being captured. When the argon flow rate is 6 L·min−1, the liquid level fluctuation of the mold is in a reasonable range under the conditions of Mode 3. Therefore, it is reasonable to control the argon flow rate to be 6 L·min−1.
- (5)
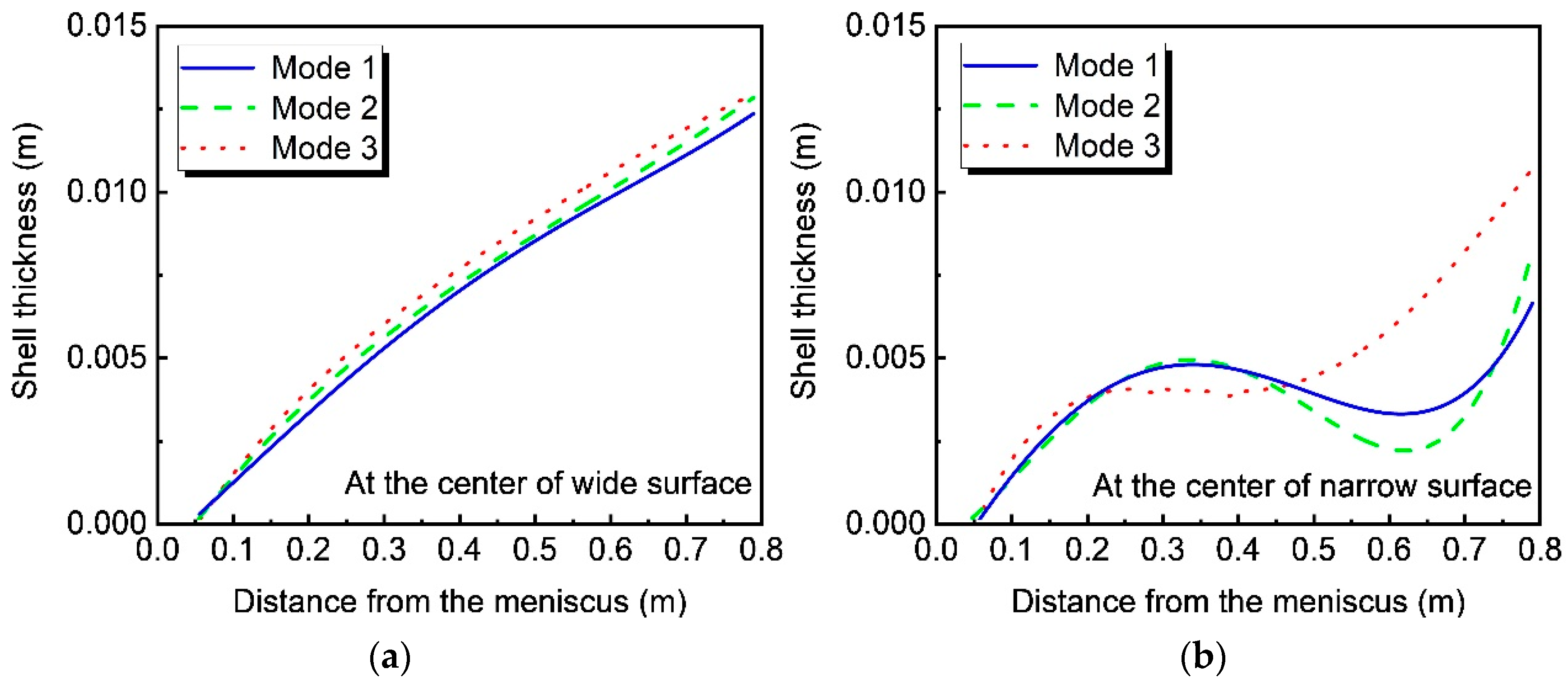
- With Mode 1 and Mode 2, due to no braking or insufficient braking capacity, the jet scours the narrow face violently, resulting in the decrease in thickness of the solidified shell in the range above 0.45 m from the mold surface. With Mode 3, as the impact of the jet on the narrow face is well restrained, the solidified shell thickness of the narrow surface is significantly greater than those in Modes 1 and 2 in the range above 0.45 m from the mold surface.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.F.; Yang, S.B.; Cai, K.K.; Li, J.Y.; Wan, X.G.; Thomas, B.G. Investigation of fluid flow and steel cleanliness in the continuous casting strand. Metall. Mater. Trans. B 2007, 38, 63–83. [Google Scholar] [CrossRef]
- Yuan, Q.; Thomas, B.G.; Vanka, S.P. Study of transient flow and particle transport in continuous steel caster molds: Part I. Fluid flow. Metall. Mater. Trans. B 2004, 35, 685–702. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Q.; Thomas, B.G.; Vanka, S.P. Study of transient flow and particle transport in continuous steel caster molds: Part II. Particle transport. Metall. Mater. Trans. B 2004, 35, 703–714. [Google Scholar] [CrossRef]
- Thomas, B.G.; Yuan, Q.; Mahmood, S.; Liu, R.; Chaudhary, R. Transport and Entrapment of Particles in Steel Continuous Casting. Metall. Mater. Trans. B 2014, 45, 22–35. [Google Scholar] [CrossRef]
- Jin, K.; Vanka, S.P.; Thomas, B.G. Large Eddy Simulations of Electromagnetic Braking Effects on Argon Bubble Transport and Capture in a Steel Continuous Casting Mold. Metall. Mater. Trans. B 2018, 49, 1360–1377. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y.; Wang, Q.; Yan, C. Prediction model for steel/slag interfacial instability in continuous casting process. Ironmak. Steelmak. 2015, 42, 705–713. [Google Scholar] [CrossRef]
- Hagemann, R.; Schwarze, R.; Heller, H.P.; Scheller, P.R. Model Investigations on the Stability of the Steel-Slag Interface in Continuous-Casting Process. Metall. Mater. Trans. B 2013, 44, 80–90. [Google Scholar] [CrossRef]
- Fei, P.; Min, Y.; Liu, C.J.; Jiang, M.F. Effect of continuous casting speed on mold surface flow and the related near-surface distribution of non-metallic inclusions. Int. J. Miner. Metall. Mater 2019, 26, 186–193. [Google Scholar] [CrossRef]
- Chen, W.; Ren, Y.; Zhang, L.; Scheller, P.R. Numerical Simulation of Steel and Argon Gas Two-Phase Flow in Continuous Casting Using LES plus VOF plus DPM Model. JOM 2019, 71, 1158–1168. [Google Scholar] [CrossRef]
- Takatani, K. Effects of electromagnetic brake and meniscus electromagnetic stirrer on transient molten steel flow at meniscus in a continuous casting mold. ISIJ Int. 2003, 43, 915–922. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L. Fluid Flow-Related Transport Phenomena in Steel Slab Continuous Casting Strands under Electromagnetic Brake. Metall. Mater. Trans. B 2011, 42, 1319–1351. [Google Scholar] [CrossRef]
- Garcia-Hernandez, S.; Morales, R.D.; Torres-Alonso, E. Effects of EMBr position, mould curvature and slide gate on fluid flow of steel in slab mould. Ironmak. Steelmak. 2010, 37, 360–368. [Google Scholar] [CrossRef]
- Xu, L.; Wang, E.; Karcher, C.; Deng, A.; Xu, X. Numerical Simulation of the Effects of Horizontal and Vertical EMBr on Jet Flow and Mold Level Fluctuation in Continuous Casting. Metall. Mater. Trans. B 2018, 49, 2779–2793. [Google Scholar] [CrossRef]
- Singh, R.; Thomas, B.G.; Vanka, S.P. Large Eddy Simulations of Double-Ruler Electromagnetic Field Effect on Transient Flow During Continuous Casting. Metall. Mater. Trans. B 2014, 45, 1098–1115. [Google Scholar] [CrossRef] [Green Version]
- Cho, S.M.; Thomas, B.G.; Kim, S.H. Transient Two-Phase Flow in Slide-Gate Nozzle and Mold of Continuous Steel Slab Casting with and without Double-Ruler Electro-Magnetic Braking. Metall. Mater. Trans. B 2016, 47, 3080–3098. [Google Scholar] [CrossRef]
- Liu, Z.; Li, L.; Li, B. Large Eddy Simulation of Transient Flow and Inclusions Transport in Continuous Casting Mold under Different Electromagnetic Brakes. JOM 2016, 68, 2180–2190. [Google Scholar] [CrossRef]
- Sarkar, S.; Singh, V.; Ajmani, S.K.; Singh, R.K.; Chacko, E.Z. Effect of Argon Injection in Meniscus Flow and Turbulence Intensity Distribution in Continuous Slab Casting Mold Under the Influence of Double Ruler Magnetic Field. ISIJ Int. 2018, 58, 68–77. [Google Scholar] [CrossRef] [Green Version]
- Yin, Y.; Zhang, J.; Ma, H.; Zhou, Q. Large Eddy Simulation of Transient Flow, Particle Transport, and Entrapment in Slab Mold with Double-Ruler Electromagnetic Braking. Steel Res. Int. 2021, 92, 2000582. [Google Scholar] [CrossRef]
- Sarkar, S.; Singh, V.; Ajmani, S.K.; Ranjan, R.; Rajasekar, K. Effect of Double Ruler Magnetic Field in Controlling Meniscus Flow and Turbulence Intensity Distribution in Continuous Slab Casting Mold. ISIJ Int. 2016, 56, 2181–2190. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Zhu, M. Numerical simulation of the effects of electromagnetic brake and argon gas injection on the three-dimensional multiphase flow and heat transfer in slab continuous casting mold. ISIJ Int. 2008, 48, 584–591. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Zhang, L.; Ma, D.; Wang, E. Numerical Simulation on Flow Characteristic of Molten Steel in the Mold with Freestanding Adjustable Combination Electromagnetic Brake. Metall. Mater. Trans. B 2020, 51, 2609–2627. [Google Scholar] [CrossRef]
- Jin, K.; Vanka, S.P.; Thomas, B.G. Large Eddy Simulations of the Effects of EMBr and SEN Submergence Depth on Turbulent Flow in the Mold Region of a Steel Caster. Metall. Mater. Trans. B 2017, 48, 162–178. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, J. Mathematical Modeling on Transient Multiphase Flow and Slag Entrainment in Continuously Casting Mold with Double-ruler EMBr through LES plus VOF plus DPM Method. ISIJ Int. 2021, 61, 853–864. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, J.; Jiang, P. Measurement of Molten Steel Velocity near the Surface and Modeling for Transient Fluid Flow in the Continuous Casting Mold. Metals 2019, 9, 36. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Yang, J.; Xu, G.J.; Liu, H.J.; Zhou, J.J.; Qin, W. Effects of operating parameters on the flow field in slab continuous casting molds with narrow widths. Int. J. Miner. Metall. Mater 2021, 28, 238–248. [Google Scholar] [CrossRef]
- Ma, C.; He, W.Y.; Qiao, H.S.; Zhao, C.L.; Liu, Y.B.; Yang, J. Flow Field in Slab Continuous Casting Mold with Large Width Optimized with High Temperature Quantitative Measurement and Numerical Calculation. Metals 2021, 11, 261. [Google Scholar] [CrossRef]
- Jiang, P.; Yang, J.; Zhang, T.; Xu, G.; Liu, H.; Zhou, J.; Qin, W. Optimization of Flow Field in Slab Continuous Casting Mold with Medium Width Using High Temperature Measurement and Numerical Simulation for Automobile Exposed Panel Production. Metals 2020, 10, 9. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Yang, J.; Huang, F.; Zhu, K.; Liu, F.; Gong, J. Comparison of the Flow Field in a Slab Continuous Casting Mold between the Thicknesses of 180 mm and 250 mm by High Temperature Quantitative Measurement and Numerical Simulation. Metals 2021, 11, 1886. [Google Scholar] [CrossRef]
- Chaudhary, R.; Thomas, B.G.; Vanka, S.P. Effect of Electromagnetic Ruler Braking (EMBr) on Transient Turbulent Flow in Continuous Slab Casting using Large Eddy Simulations. Metall. Mater. Trans. B 2012, 43, 532–553. [Google Scholar] [CrossRef]
- Liu, Y.B.; Yang, J.; Lin, Z.Q. Mathematical Modeling of Mold Flow Field and Mold Flux Entrainment Assisted With High-Temperature Quantitative Velocity Measurement and Water Modeling. Metall. Mater. Trans. B 2022, 53B. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Liu, Y.B.; Yang, J.; Ma, C.; Zhang, T.; Gao, F.B.; Li, T.Q.; Chen, J.L. Mathematical modeling of flow field in slab continuous casting mold considering mold powder and solidified shell with high temperature quantitative measurement. J. Iron Steel Res. Int. 2022, 29, 445–461. [Google Scholar] [CrossRef]



| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Mold width (mm) | 1050 | Slag thickness (mm) | 15 |
| Mold thickness (mm) | 230 | Slag density (kg·m−3) | 2800 |
| Mold length (mm) | 800 | Slag viscosity (kg·m−1·s−1) | 0.18 |
| SEN submergence depth (mm) | 170 | Liquidus temperature (K) | 1807 |
| SEN port angle (°) | 20 | Solidus temperature (K) | 1796 |
| SEN port size (mm × mm) | 70 × 90 | Thermal conductivity (W·m−1·K−1) | 34 |
| SEN inner diameter (mm) | 78 | Steel latent heat (J·kg−1) | 270,000 |
| SEN outer diameter (mm) | 140 | Steel electric conductivity (S·m−1) | 580,000 |
| Argon flow rate (L·min−1) | 0\6\10 | Steel magnetic conductivity (H·m−1) | 1.257 × 10−6 |
| Argon density (kg·m−3) | 0.4 | Steel viscosity (kg·m−1·s−1) | 0.0062 |
| Steel density (kg·m−3) | 7020 | Casting speed (m·min−1) | 1.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Yang, J.; Liu, Y.; He, W.; Zhao, C.; Liu, Y. Numerical Simulation of Flow Field, Bubble Distribution and Solidified Shell in Slab Mold under Different EMBr Conditions Assisted with High-Temperature Quantitative Velocity Measurement. Metals 2022, 12, 1050. https://doi.org/10.3390/met12061050
Guo Y, Yang J, Liu Y, He W, Zhao C, Liu Y. Numerical Simulation of Flow Field, Bubble Distribution and Solidified Shell in Slab Mold under Different EMBr Conditions Assisted with High-Temperature Quantitative Velocity Measurement. Metals. 2022; 12(6):1050. https://doi.org/10.3390/met12061050
Chicago/Turabian StyleGuo, Yi, Jian Yang, Yibo Liu, Wenyuan He, Changliang Zhao, and Yanqiang Liu. 2022. "Numerical Simulation of Flow Field, Bubble Distribution and Solidified Shell in Slab Mold under Different EMBr Conditions Assisted with High-Temperature Quantitative Velocity Measurement" Metals 12, no. 6: 1050. https://doi.org/10.3390/met12061050
APA StyleGuo, Y., Yang, J., Liu, Y., He, W., Zhao, C., & Liu, Y. (2022). Numerical Simulation of Flow Field, Bubble Distribution and Solidified Shell in Slab Mold under Different EMBr Conditions Assisted with High-Temperature Quantitative Velocity Measurement. Metals, 12(6), 1050. https://doi.org/10.3390/met12061050





