Faceting and Twin–Twin Interactions in {1121} and {1122} Twins in Titanium
Abstract
:1. Introduction
2. Methods
2.1. Atomistic Simulations
2.2. Interfacial Defect Theory of Twin–Twin Interactions
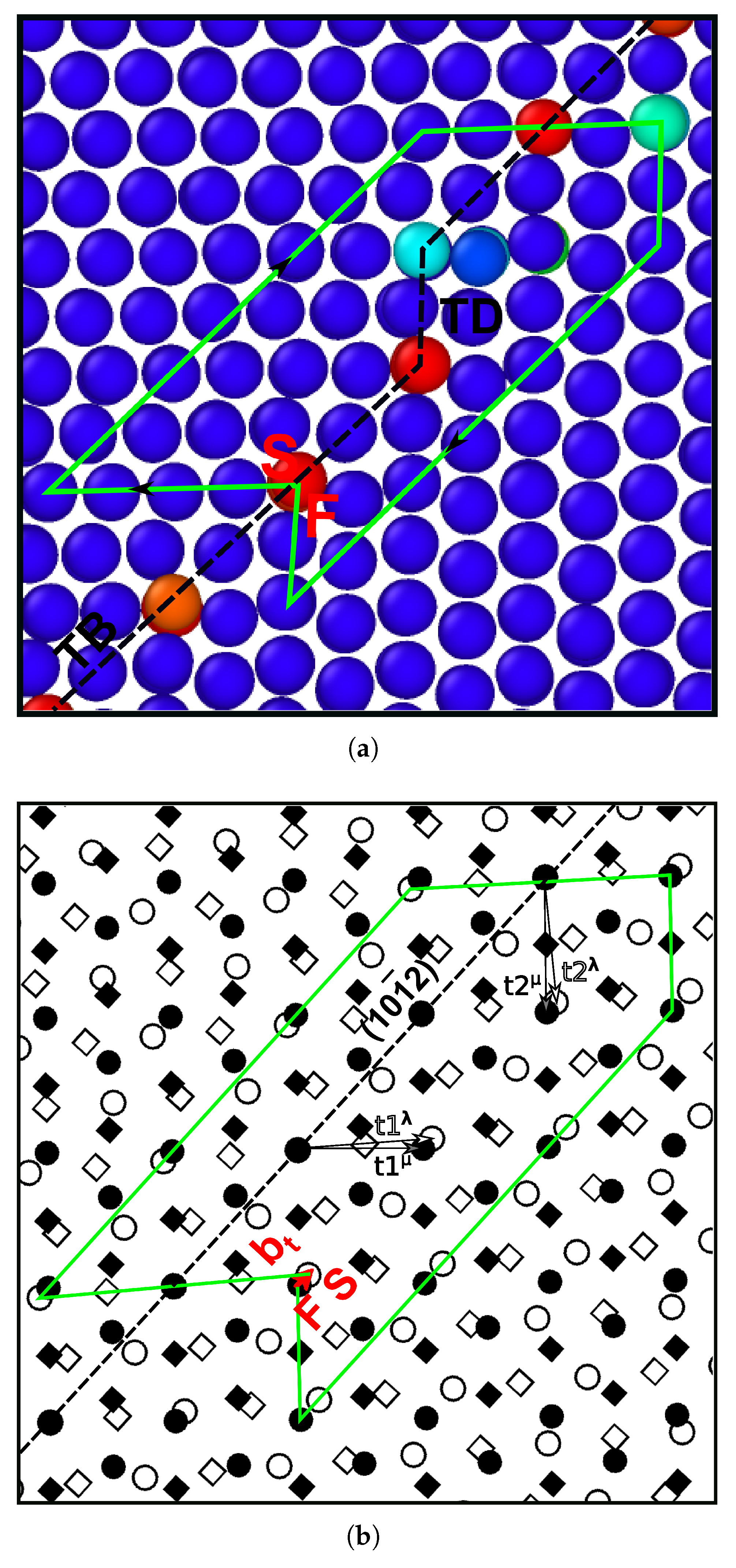
2.2.1. Disconnections and Dichromatic Patterns
2.2.2. Lattice Correspondence
2.2.3. Twin Faceting
2.2.4. Twin–Twin Interactions
2.2.5. Double Twinning
2.2.6. Compound Reactions
3. Results and Discussion
3.1. Synopsis of Results
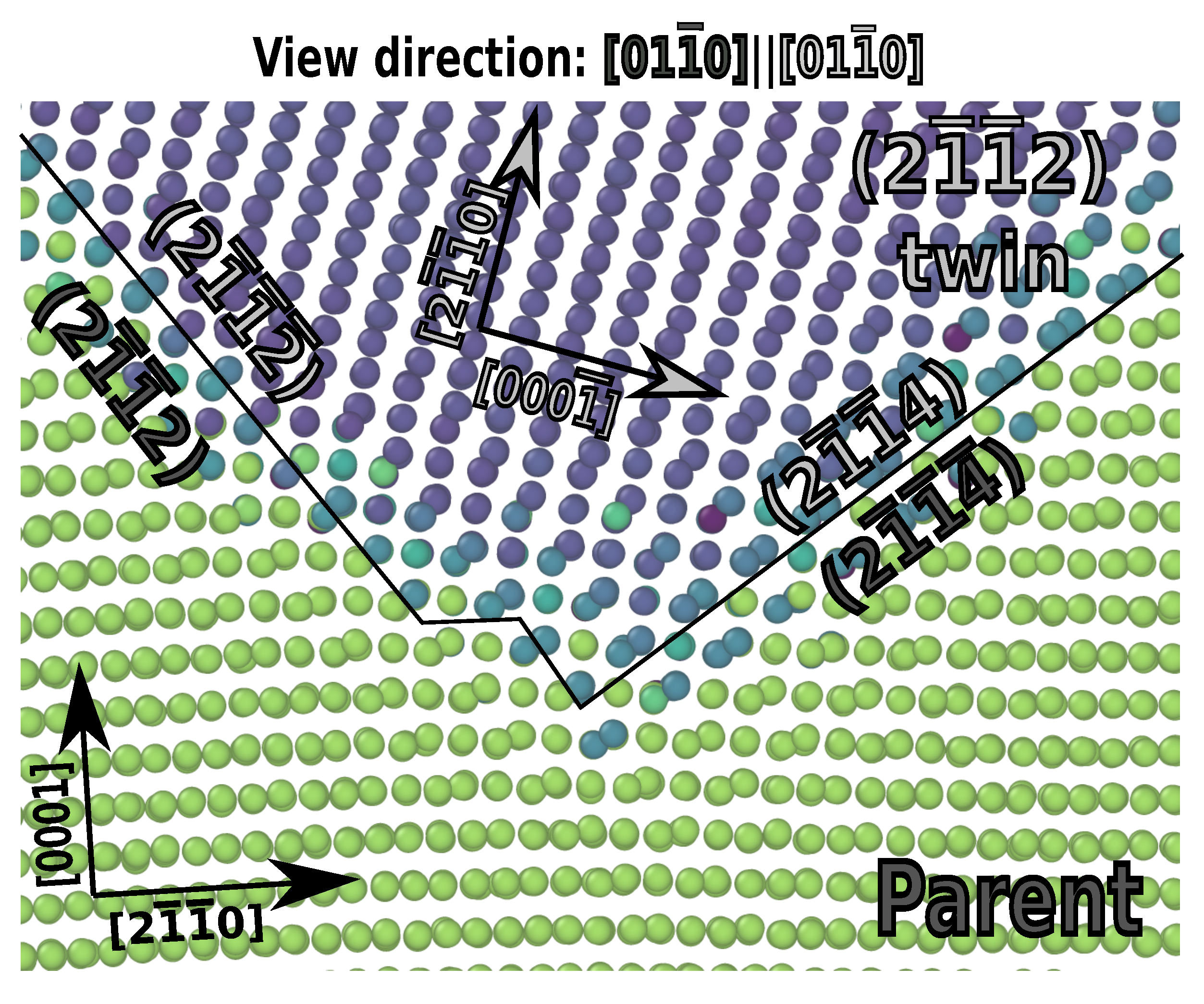
3.2. Tilt Faceting onto the {1122} Boundaries
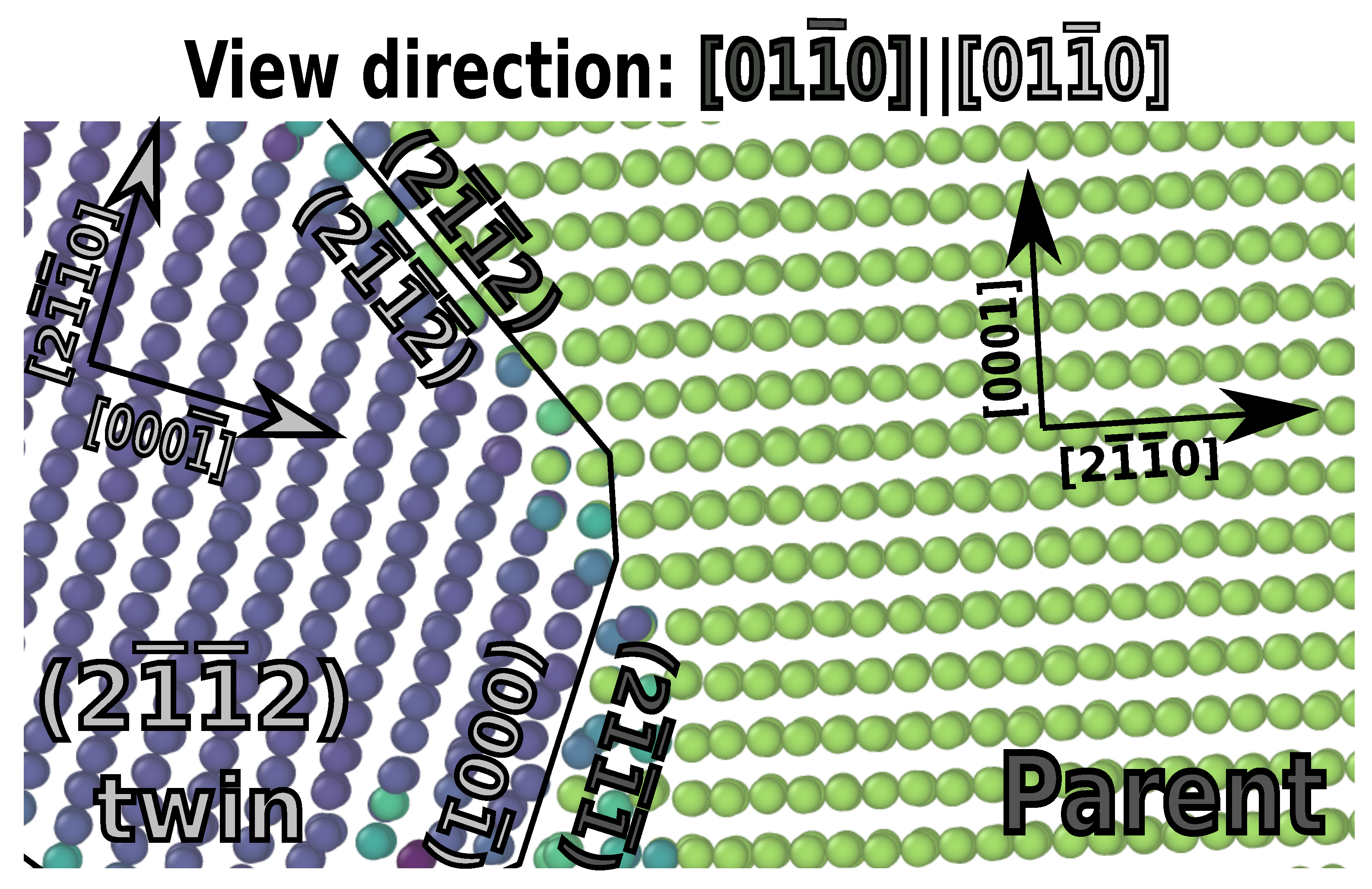
3.2.1. The {2111}{0001} Facet
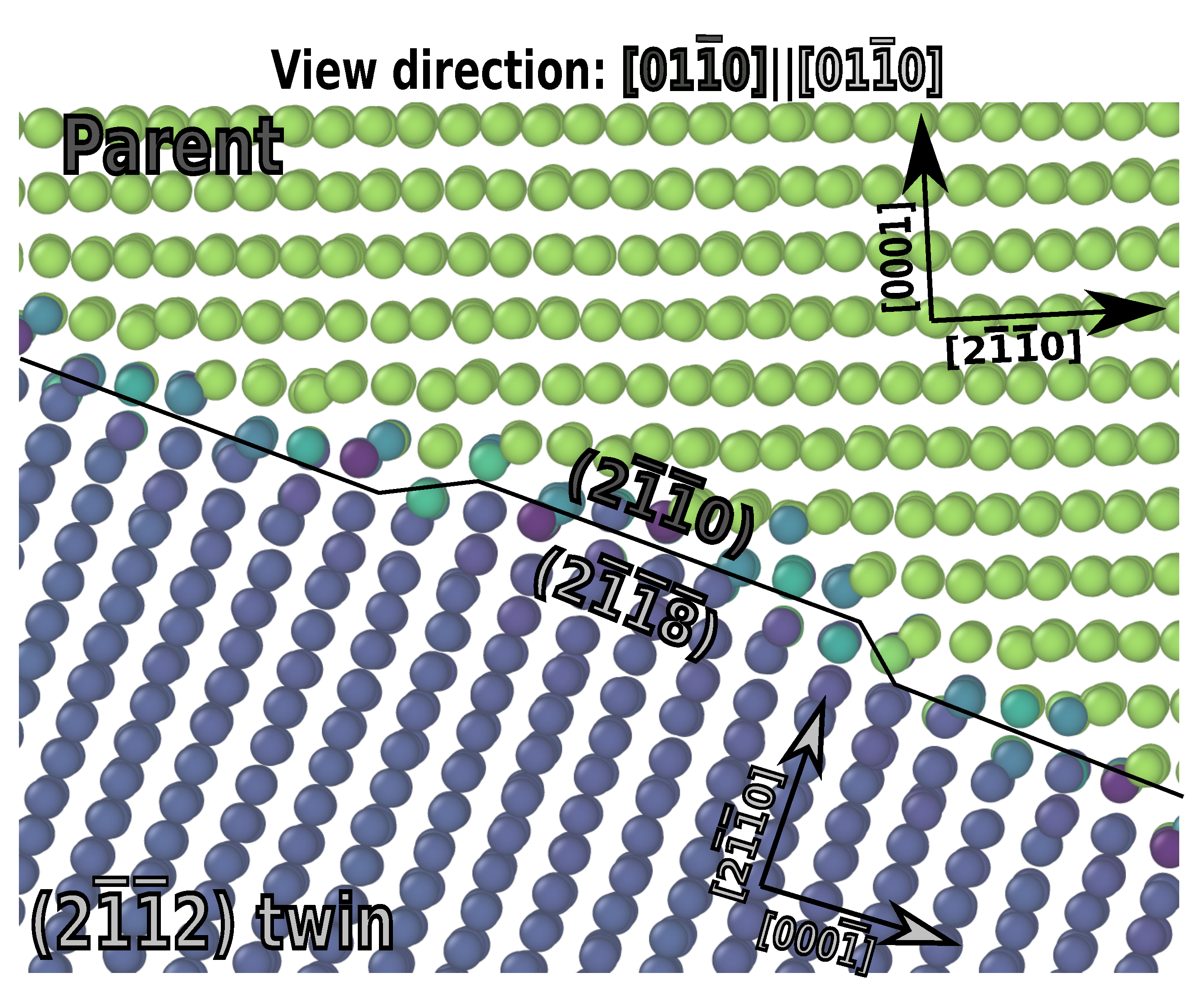
3.2.2. The {2118}{2110} Facet Interface
3.2.3. The 2114 Twin Facet
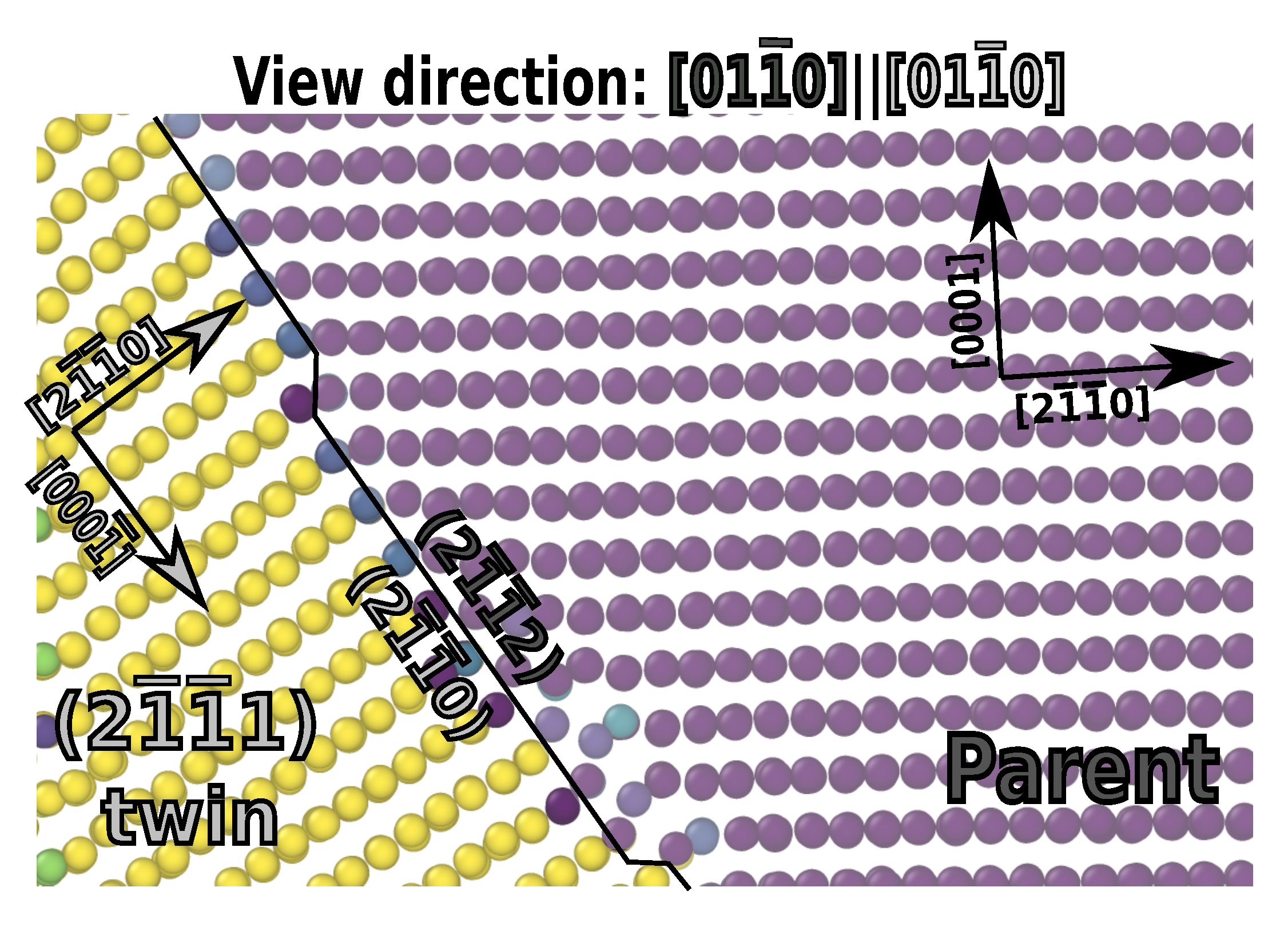
3.3. Faceting on the {1121} Boundaries
The {1122}{1120} Facet Interface
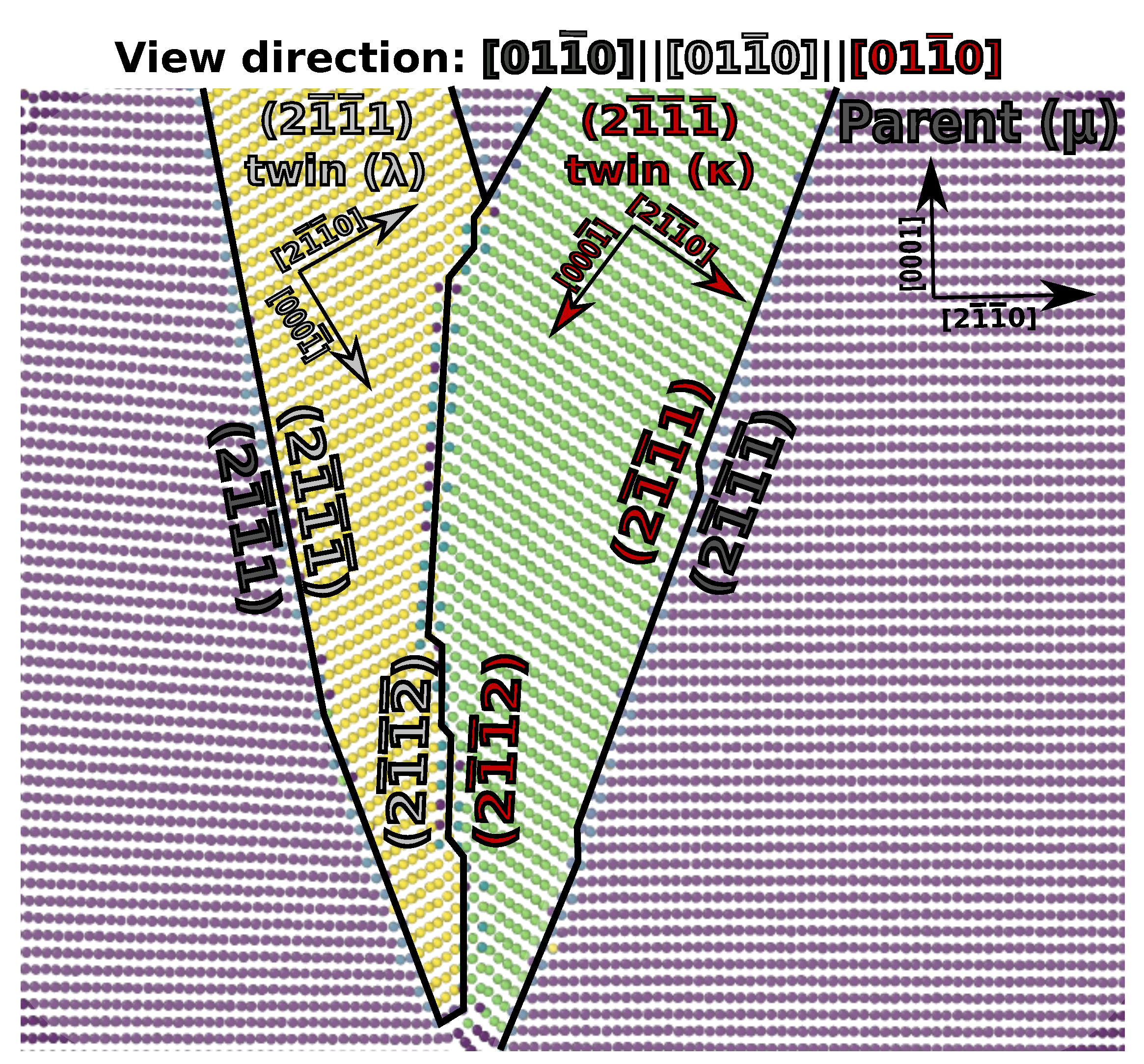
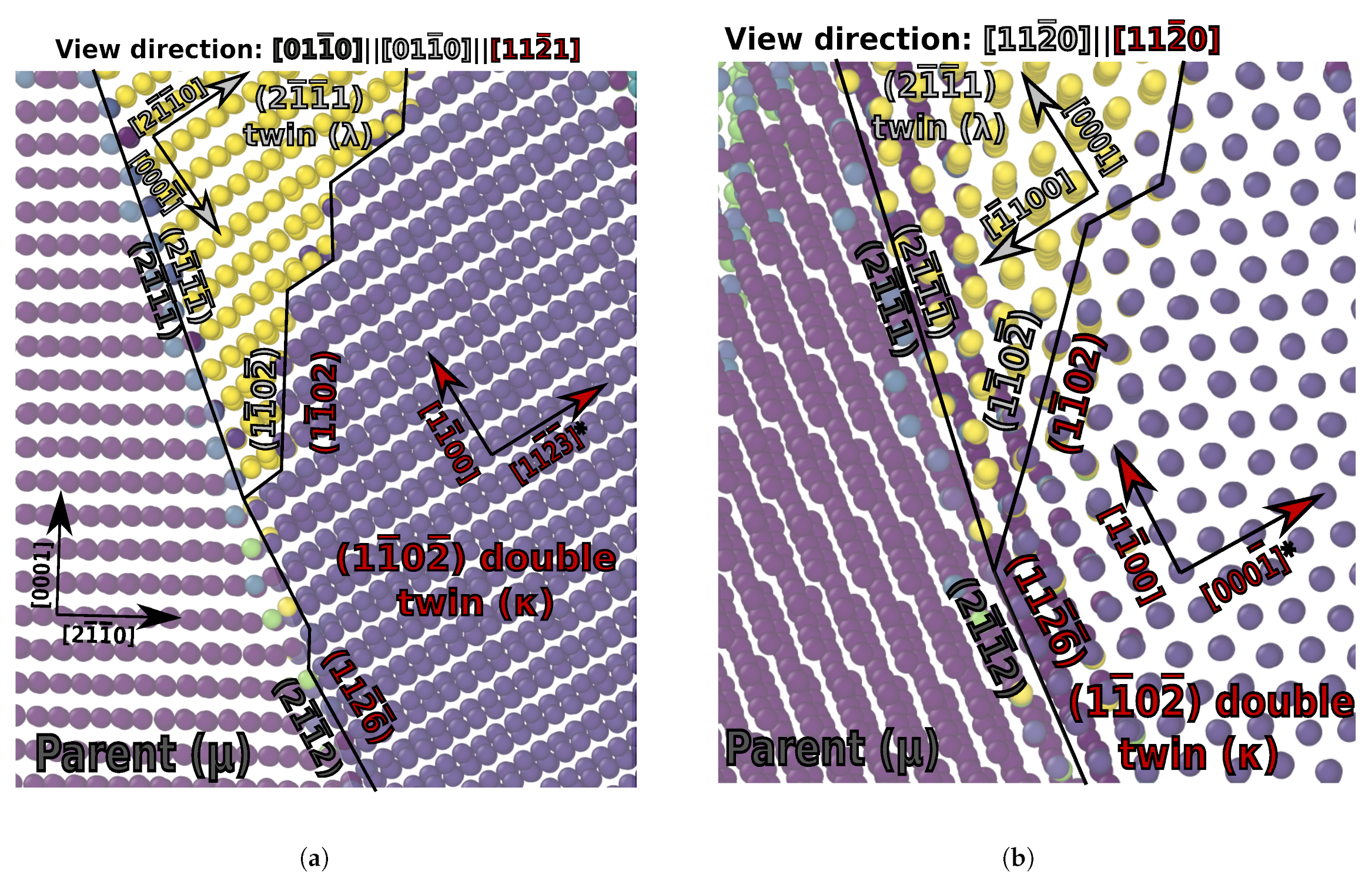
3.4. {1121} Twin–Twin Interactions
3.5. {1121}-{1012} Twin Interactions
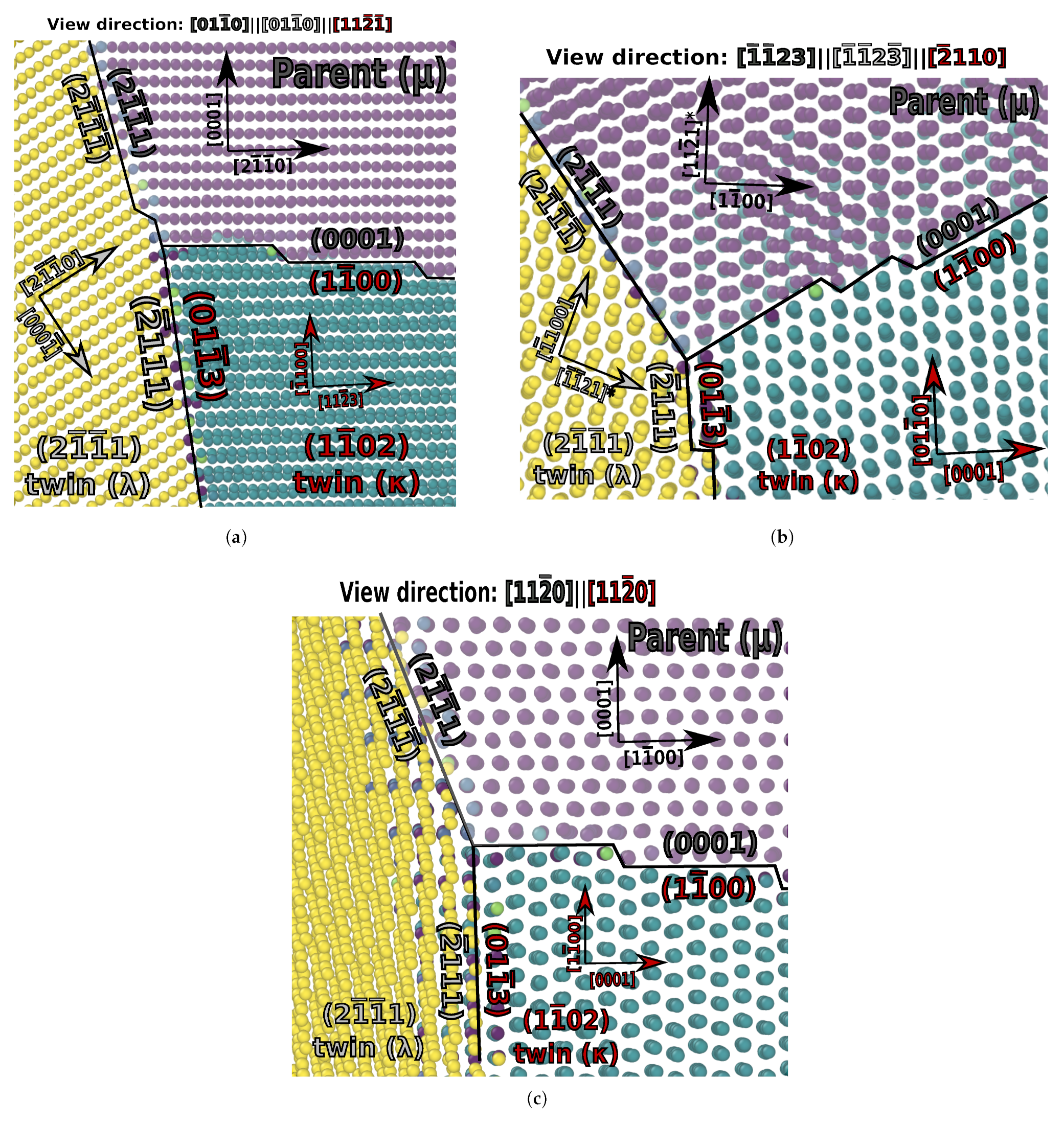
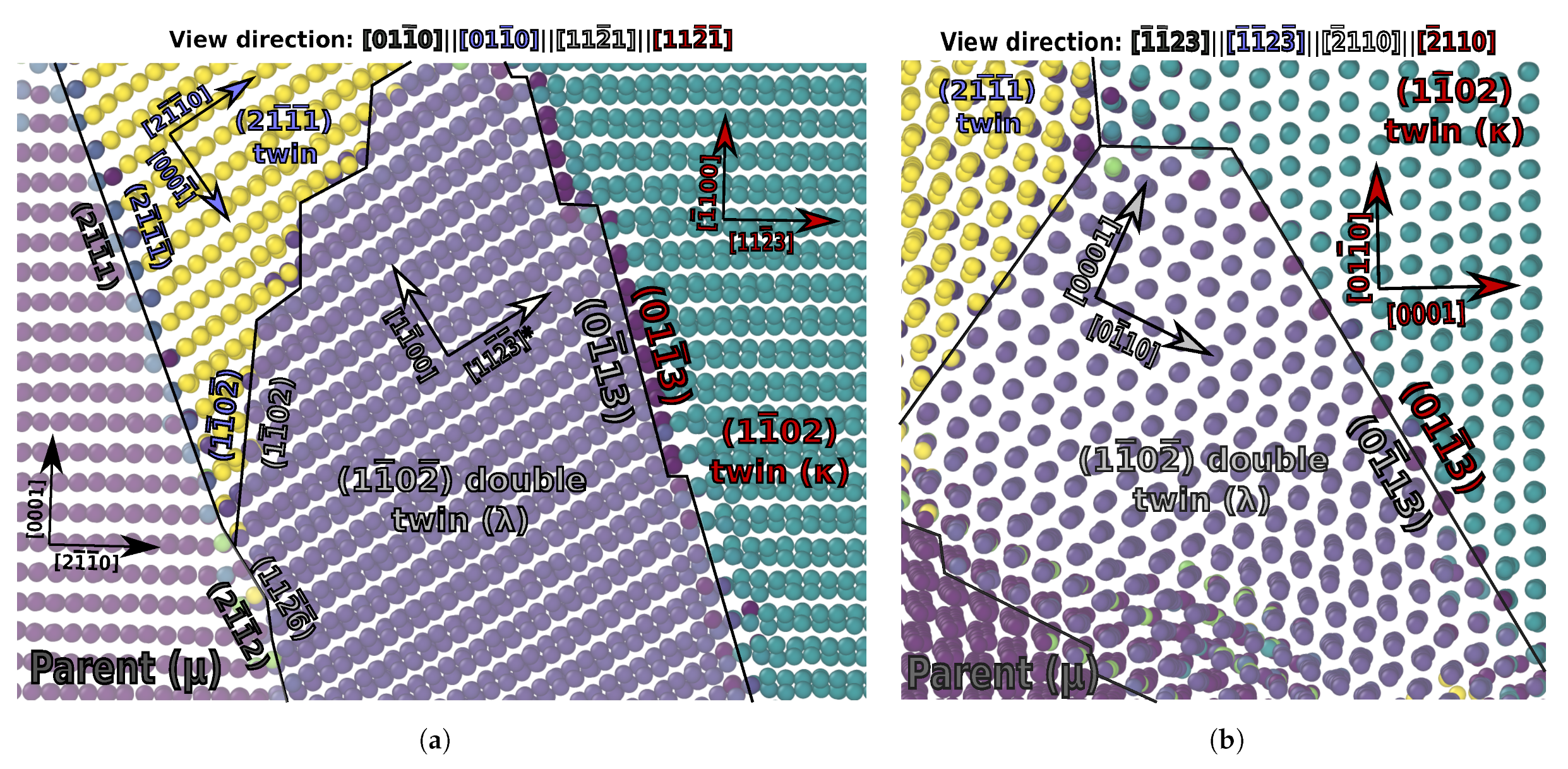
3.6. {1121}-{1012} Double Twinning
3.7. Interaction between {1121}-{1012} Double Twin and {1012} Twin
4. Conclusions
- {1121} co-zonal twins readily react to form a {1122} twin boundary. However, the boundary formed in this manner has limited mobility because the triple points cannot conservatively move normal to the initial interface plane without the emission of 〈c+a〉 dislocations.
- {1121} twins faceted onto the {1120}{1122} interface in agreement with the experimental findings.
- {1122} twins faceted onto the {0001}{1121} facet. This disagreed with experimental reports of the {0001}{1122} facet; however, according to interfacial defect theory, the lattice correspondence requires that the former be the facet produced.
- {1122} twins also faceted onto the {1120}{1128} facet and the {1124} twin boundary. The latter of these agrees with previous observations that all twins appear to be able to facet onto their conjugate, which shares the same axis and shear.
- Compound twin–twin interactions were observed, including one case where a double twin (1121}-{1102) interacted with a single twin, (1012), to form a new mobile twin boundary: {1013}. Cases where twins within twins lead to a highly mobile ordered boundary like this were not anticipated, however, may have significant implications for plasticity under highly strained conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dang, K.; Tomé, C.N.; Capolungo, L. The 1012 non-cozone twin–twin interactions in Mg: A stability and mobility study using 3-D atomistic simulations. Scr. Mater. 2021, 200, 113913. [Google Scholar] [CrossRef]
- Suh, B.C.; Kim, J.H.; Hwang, J.H.; Shim, M.S.; Kim, N.J. Twinning-mediated formability in Mg alloys. Sci. Rep. 2016, 6, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, B.; Guo, N.; Liu, T.; Yang, Q. Improvement of formability and mechanical properties of magnesium alloys via pre-twinning: A review. Mater. Des. 2014, 62, 352–360. [Google Scholar] [CrossRef]
- Morrow, B.; McCabe, R.; Cerreta, E.; Tomé, C. Observations of the Atomic Structure of Tensile and Compressive Twin Boundaries and Twin–Twin Interactions in Zirconium. Metall. Mater. Trans. A 2014, 45, 5891–5897. [Google Scholar] [CrossRef]
- Hirth, J.P. Dislocations, steps and disconnections at interfaces. J. Phys. Chem. Solids 1994, 55, 985–989. [Google Scholar] [CrossRef]
- Won, J.W.; Park, C.H.; Hong, J.; Lee, C.S.; Hong, S.G. Simultaneous Improvement in the Strength and Formability of Commercially Pure Titanium via Twinning-induced Crystallographic Texture Control. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef]
- Won, J.W.; Lee, J.H.; Jeong, J.S.; Choi, S.W.; Lee, D.J.; Hong, J.K.; Hyun, Y.T. High strength and ductility of pure titanium via twin-structure control using cryogenic deformation. Scr. Mater. 2020, 178, 94–98. [Google Scholar] [CrossRef]
- Wang, J.T.; Yin, D.L.; Liu, J.Q.; Tao, J.; Su, Y.L.; Zhao, X. Effect of grain size on mechanical property of Mg–3Al–1Zn alloy. Scr. Mater. 2008, 59, 63–66. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, J.; Jiang, Y.; McCabe, R.J.; Li, N.; Tomé, C.N. Twin–twin interactions in magnesium. Acta Mater. 2014, 77, 28–42. [Google Scholar] [CrossRef]
- Wang, S.; Dang, K.; McCabe, R.J.; Capolungo, L.; Tomé, C.N. Three-dimensional atomic scale characterization of {112 2} twin boundaries in titanium. Acta Mater. 2021, 208, 116707. [Google Scholar] [CrossRef]
- Xu, B.; Capolungo, L.; Rodney, D. On the importance of prismatic/basal interfaces in the growth of 1012 twins in hexagonal close packed crystals. Scr. Mater. 2013, 68, 901–904. [Google Scholar] [CrossRef] [Green Version]
- Barrett, C.D.; El Kadiri, H. The roles of grain boundary dislocations and disclinations in the nucleation of {1012} twinning. Acta Materialia 2014, 63, 1–15. [Google Scholar] [CrossRef]
- Barrett, C.D.; El Kadiri, H. Fundamentals of mobile tilt grain boundary faceting. Scr. Mater. 2014, 84, 15–18. [Google Scholar] [CrossRef]
- Barrett, C.; Kadiri, H.E. The Deformation Gradient of Interfacial Defects on Twin-like Interfaces. In Magnesium Technology 2015; Springer: Cham, Switzerland, 2015; pp. 121–125. [Google Scholar] [CrossRef]
- Pond, R.C.; Hirth, J.P.; Serra, A.; Bacon, D.J. Atomic displacements accompanying deformation twinning: Shears and shuffles. Mater. Res. Lett. 2016, 4, 185–190. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Liu, L.; Tomé, C.; Mao, S.; Gong, S. Twinning and de-twinning via glide and climb of twinning dislocations along serrated coherent twin boundaries in hexagonal-close-packed metals. Mater. Res. Lett. 2013, 1, 81–88. [Google Scholar] [CrossRef]
- Pond, R.; Nabarro, F. Dislocations in solids. VOL 1989, 8, 1–66. [Google Scholar]
- Pond, R. Dislocations and Properties of Real Materials. In Dislocations and Properties of Real Materials; Institute of Metals: London, UK, 1985; chapter Interfaces and dislocations; pp. 71–93. [Google Scholar]
- Pond, R.C.; Casey, S.M. Topological Theory of Line-Defects. In Equilibrium Structure and Properties of Surfaces and Interfaces; Springer: Boston, MA, USA, 1992; pp. 139–174. [Google Scholar] [CrossRef]
- Serra, A.; Pond, R.C.; Bacon, D.J. Computer simulation of the structure and mobility of twinning disclocations in HCP Metals. Acta Metall. Mater. 1991, 39, 1469–1480. [Google Scholar] [CrossRef]
- Serra, A.; Bacon, D.J. Computer simulation of twin boundaries in the h. c. p. metals. Philos. Mag. A 1986, 54, 793–804. [Google Scholar] [CrossRef]
- Serra, A.; Bacon, D.J. Computer simulation of screw dislocation interactions with twin boundaries in hcp metals. Acta Metall. Mater. 1995, 43, 4465–4481. [Google Scholar] [CrossRef]
- Serra, A.; Bacon, D.J.; Pond, R.C. Twins as barriers to basal slip in hexagonal-close-packed metals. Metall. Mater. Trans. A 2002, 33, 809–812. [Google Scholar] [CrossRef]
- Barrett, C.D.; El Kadiri, H. Impact of deformation faceting on and embryonic twin nucleation in hexagonal close-packed metals. Acta Mater. 2014, 70, 137–161. [Google Scholar] [CrossRef]
- Hirth, J.; Pond, R. Steps, dislocations and disconnections as interface defects relating to structure and phase transformations. Acta Mater. 1996, 44, 4749–4763. [Google Scholar] [CrossRef]
- Christian, J.W.; Mahajan, S. Deformation twinning. Prog. Mater. Sci. 1995, 39, 1–157. [Google Scholar] [CrossRef]
- Ostapovets, A.; Molnár, P. On the Relationship between the “Shuffling Dominated” and “Shear Dominated” Mechanisms for Twinning in Magnesium. Scr. Mater. 2013, 69, 287–290. [Google Scholar] [CrossRef]
- Ostapovets, A.; Gröger, R. Twinning disconnections and basal–prismatic twin boundary in magnesium. Model. Simul. Mater. Sci. Eng. 2014, 22, 025015. [Google Scholar] [CrossRef]
- Yu, S.; Liu, C.; Gao, Y.; Jiang, S.; Chen, Z. A rotation-shear model on the atomic motion during {1012} twinning in magnesium alloys. Mater. Lett. 2016, 165, 185–188. [Google Scholar] [CrossRef]
- El Kadiri, H.; Barrett, C.D.; Wang, J.; Tomé, C.N. Why are twins profuse in magnesium? Acta Mater. 2015, 85, 354–361. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Barrett, C.D.; McCabe, R.J.; Kadiri, H.E.; Capolungo, L.; Agnew, S.R. Dislocation induced twin growth and formation of basal stacking faults in {1012} twins in pure Mg. Acta Mater. 2019, 165, 471–485. [Google Scholar] [CrossRef]
- Gong, M.; Liu, G.; Wang, J.; Capolungo, L.; Tomé, C.N. Atomistic simulations of interaction between basal〈 a〉 dislocations and three-dimensional twins in magnesium. Acta Mater. 2018, 155, 187–198. [Google Scholar]
- Wang, J.; Beyerlein, I.; Hirth, J. Nucleation of elementary and twinning dislocations at a twin boundary in hexagonal close-packed crystals. Model. Simul. Mater. Sci. Eng. 2012, 20, 024001. [Google Scholar] [CrossRef]
- Reed-Hill, R.; Buchanan, E. Zig-zag twins in zirconium. Acta Met. 1963, 11. [Google Scholar] [CrossRef]
- Oppedal, A.L.; El Kadiri, H.; Tomé, C.N.; Kaschner, G.C.; Vogel, S.C.; Baird, J.C.; Horstemeyer, M.F. Effect of dislocation transmutation on modeling hardening mechanisms by twinning in magnesium. Int. J. Plast. 2012, 30–31, 41–61. [Google Scholar] [CrossRef]
- El Kadiri, H.; Kapil, J.; Oppedal, A.; Hector Jr, L.; Agnew, S.R.; Cherkaoui, M.; Vogel, S. The effect of twin–twin interactions on the nucleation and propagation of {1012} twinning in magnesium. Acta Mater. 2013, 61, 3549–3563. [Google Scholar] [CrossRef]
- Jiang, L.; Jonas, J.J.; Luo, A.A.; Sachdev, A.K.; Godet, S. Influence of {1012} extension twinning on the flow behavior of AZ31 Mg alloy. Mater. Sci. Eng. A 2007, 445, 302–309. [Google Scholar] [CrossRef]
- Cahn, R.W. Soviet work on mechanical twinning. Il Nuovo Cimento (1943–1954) 1953, 10, 350–386. [Google Scholar] [CrossRef]
- Barrett, C.; El Kadiri, H.; Tschopp, M. Breakdown of the Schmid law in homogeneous and heterogeneous nucleation events of slip and twinning in Magnesium. J. Mech. Phys. Solids 2012, 60, 2084–2099. [Google Scholar] [CrossRef]
- Hennig, R.G.; Lenosky, T.J.; Trinkle, D.R.; Rudin, S.P.; Wilkins, J.W. Classical potential describes martensitic phase transformations between the α, β, and ω titanium phases. Phys. Rev. B 2008, 78, 054121. [Google Scholar] [CrossRef] [Green Version]
- El Kadiri, H.; Barrett, C.; Tschopp, M. The candidacy of shuffle and shear during compound twinning in hexagonal close-packed structures. Acta Mater. 2013, 61, 7646–7659. [Google Scholar] [CrossRef] [Green Version]
- Dickel, D.; Barrett, C.D.; Carino, R.L.; Baskes, M.I.; Horstemeyer, M.F. Mechanical instabilities in the modeling of phase transitions of titanium. Model. Simul. Mater. Sci. Eng. 2018, 26, 065002. [Google Scholar] [CrossRef]
- Nitol, M.S.; Dickel, D.E.; Barrett, C.D. Machine learning models for predictive materials science from fundamental physics: An application to titanium and zirconium. Acta Mater. 2021, 224, 117347. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Dickel, D.; Nitol, M.; Barrett, C.D. LAMMPS implementation of rapid artificial neural network derived interatomic potentials. Comput. Mater. Sci. 2021, 196, 110481. [Google Scholar] [CrossRef]
- Baskes, M.I.; Johnson, R.A. Modified embedded atom potentials for HCP metals. Modell. Simul. Mater. Sci. Eng. 1994, 2, 147–163. [Google Scholar] [CrossRef]
- Nitol, M.S.; Mun, S.; Dickel, D.E.; Barrett, C.D. Unraveling Mg 〈c + a〉 slip using neural network potential. Philos. Mag. 2022, 102, 651–673. [Google Scholar] [CrossRef]
- Nitol, M.S.; Dickel, D.E.; Barrett, C.D. Artificial neural network potential for pure zinc. Comput. Mater. Sci. 2021, 188, 110207. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations; John Wiley & Sons: Hoboken, NJ, USA, 1982. [Google Scholar]
- Balluffi, R.W. Introduction to Elasticity Theory for Crystal Defects; World Scientific Publishing Company: Singapore, 2016. [Google Scholar]
- Ostapovets, A.; Serra, A.; Pond, R.C. Non-diffusional growth mechanism of I1 basal stacking-faults inside twins in hcp metals. Scr. Mater. 2019, 172, 149–153. [Google Scholar] [CrossRef]
- Christian, J.W. The Theory of Transformations in Metals and Alloys: Part I + II; Elsevier: Amsterdam, The Netherlands, 2002; p. 933. [Google Scholar]
- Niewczas, M. Lattice correspondence during twinning in hexagonal close-packed crystals. Acta Mater. 2010, 58, 5848–5857. [Google Scholar] [CrossRef]
- Serra, A.; Bacon, D.J. Computer simulation of twinning dislocation in magnesium using a many-body potential. Philos. Mag. A 1991, 63, 1001–1012. [Google Scholar] [CrossRef]
- Serra, A.; Bacon, D.; Pond, R. A comment on B. Li, H. El Kadiri and MF Horstemeyer ‘Extended zonal dislocations mediating twinning in titanium’. Philos. Mag. 2013, 93, 3495–3503. [Google Scholar] [CrossRef]
- El Kadiri, H.; Barrett, C.D. Comments on “extended zonal dislocations mediating twinning in titanium”. Philos. Mag. 2013, 93, 3491–3494. [Google Scholar] [CrossRef]
- Romanov, A.; Kolesnikova, A. Application of disclination concept to solid structures. Prog. Mater. Sci. 2009, 54, 740–769. [Google Scholar] [CrossRef]
- Wang, J.; Beyerlein, I.; Hirth, J.; Tomé, C. Twinning dislocations on {1 011} and {1 013} planes in hexagonal close-packed crystals. Acta Mater. 2011, 59, 3990–4001. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrett, C.; Martinez, J.; Nitol, M. Faceting and Twin–Twin Interactions in {1121} and {1122} Twins in Titanium. Metals 2022, 12, 895. https://doi.org/10.3390/met12060895
Barrett C, Martinez J, Nitol M. Faceting and Twin–Twin Interactions in {1121} and {1122} Twins in Titanium. Metals. 2022; 12(6):895. https://doi.org/10.3390/met12060895
Chicago/Turabian StyleBarrett, Christopher, Jose Martinez, and Mashroor Nitol. 2022. "Faceting and Twin–Twin Interactions in {1121} and {1122} Twins in Titanium" Metals 12, no. 6: 895. https://doi.org/10.3390/met12060895
APA StyleBarrett, C., Martinez, J., & Nitol, M. (2022). Faceting and Twin–Twin Interactions in {1121} and {1122} Twins in Titanium. Metals, 12(6), 895. https://doi.org/10.3390/met12060895





