Cross-Scale Simulation Research on the Macro/Microstructure of TC4 Alloy Wire Laser Additive Manufacturing
Abstract
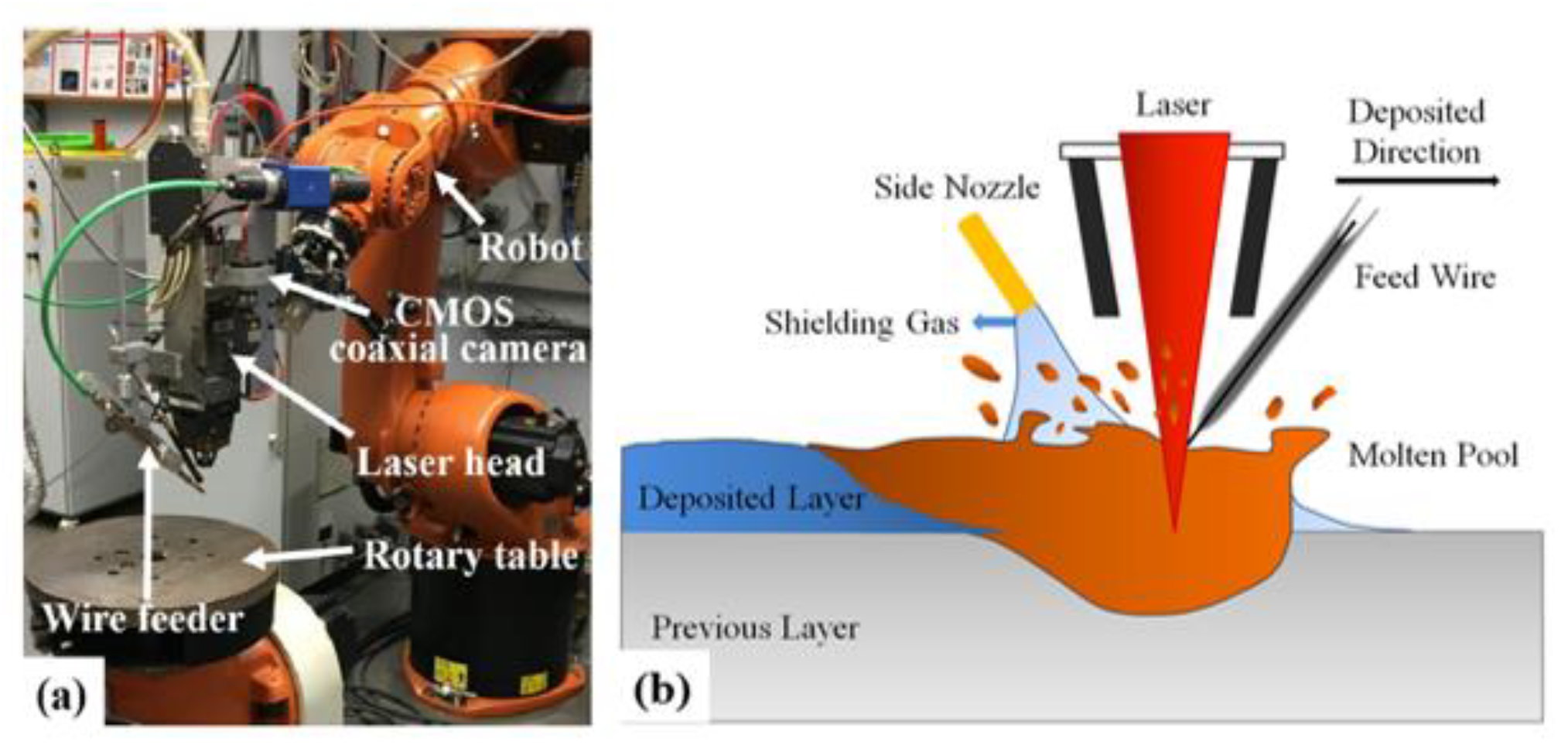
:1. Introduction
2. Physical Model
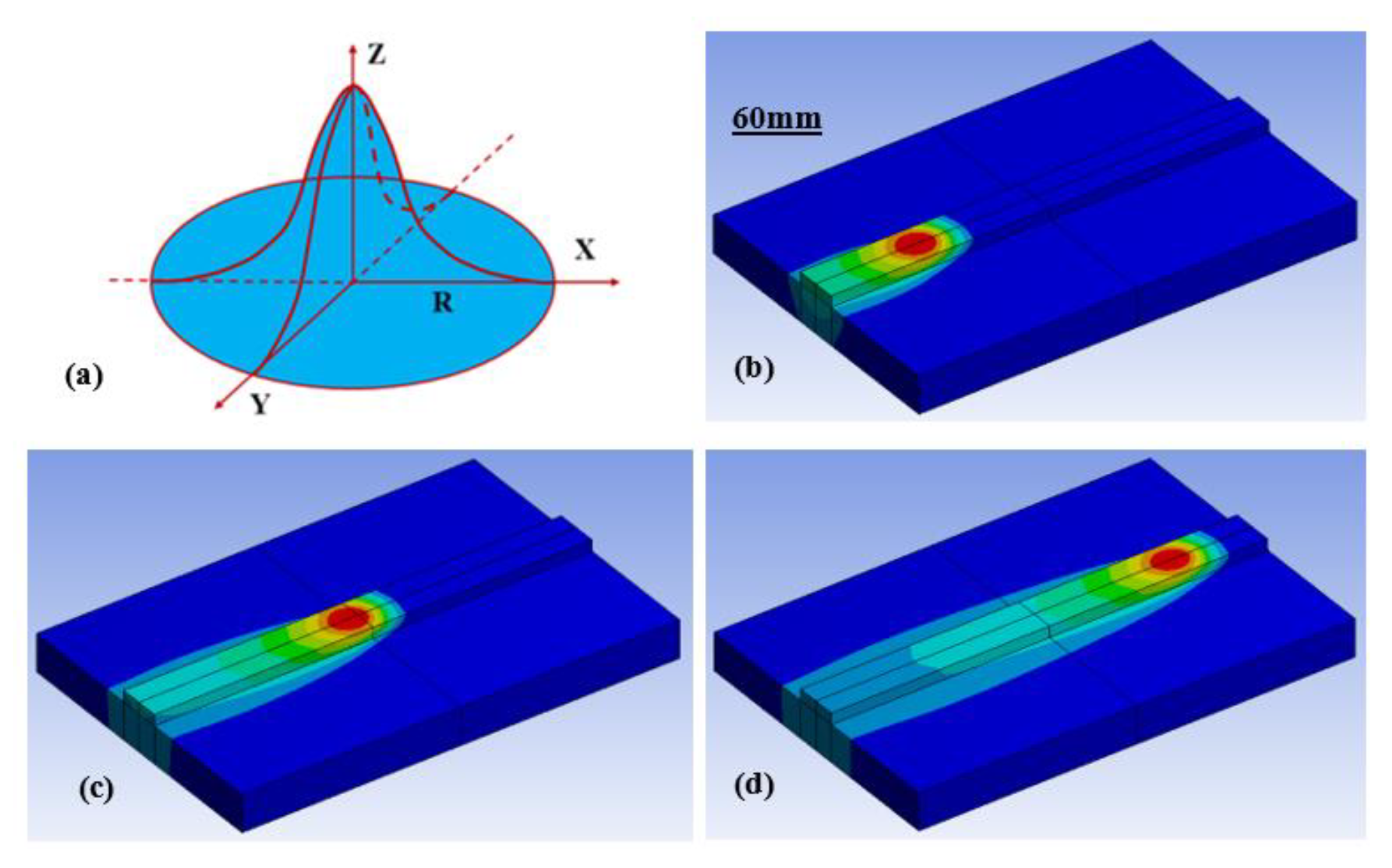
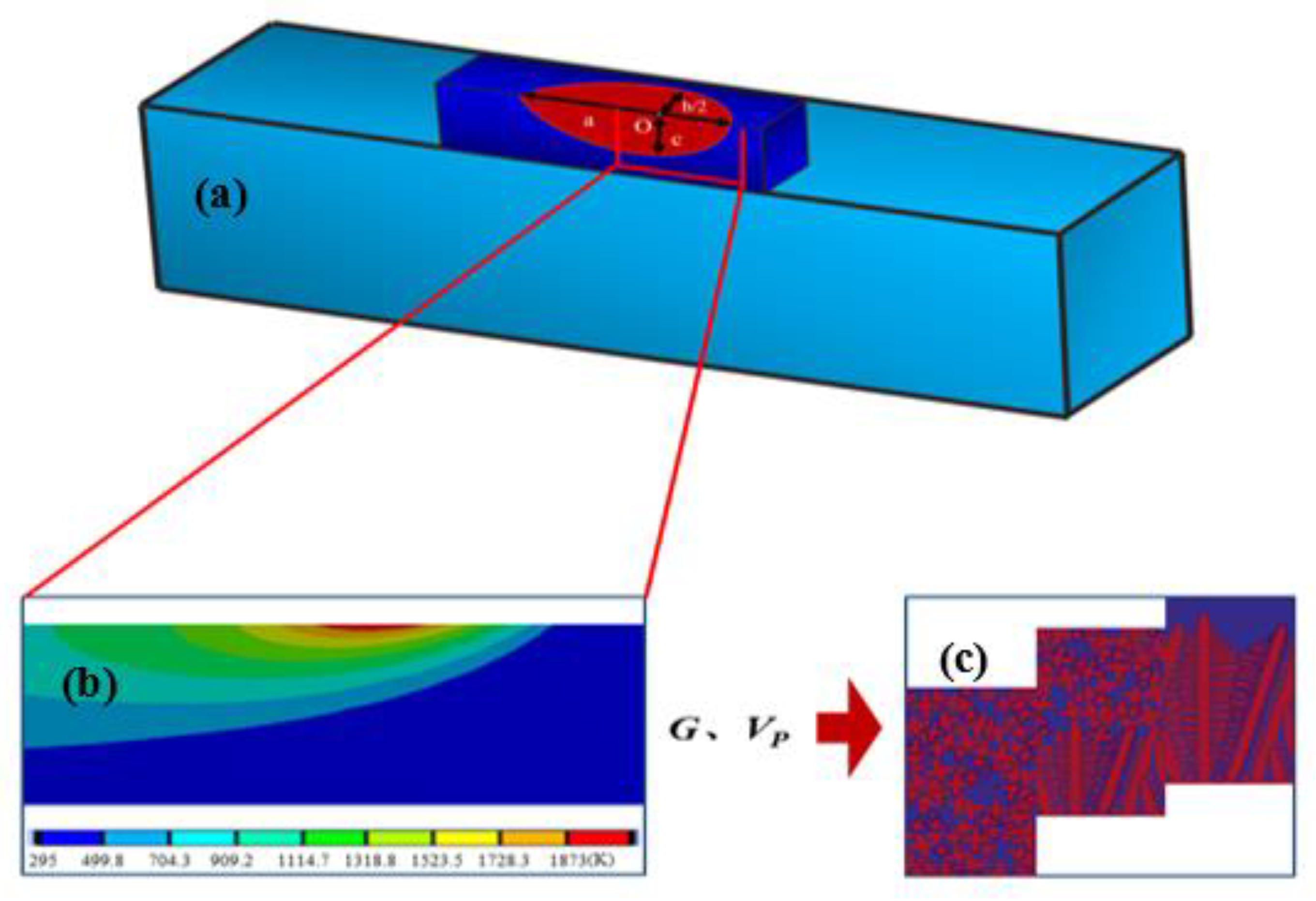
2.1. Molten Pool Model
2.2. Phase Field Model
3. Results and Discussion
3.1. Influence of Process Parameters on Macro/Microstructure of Molten Pool
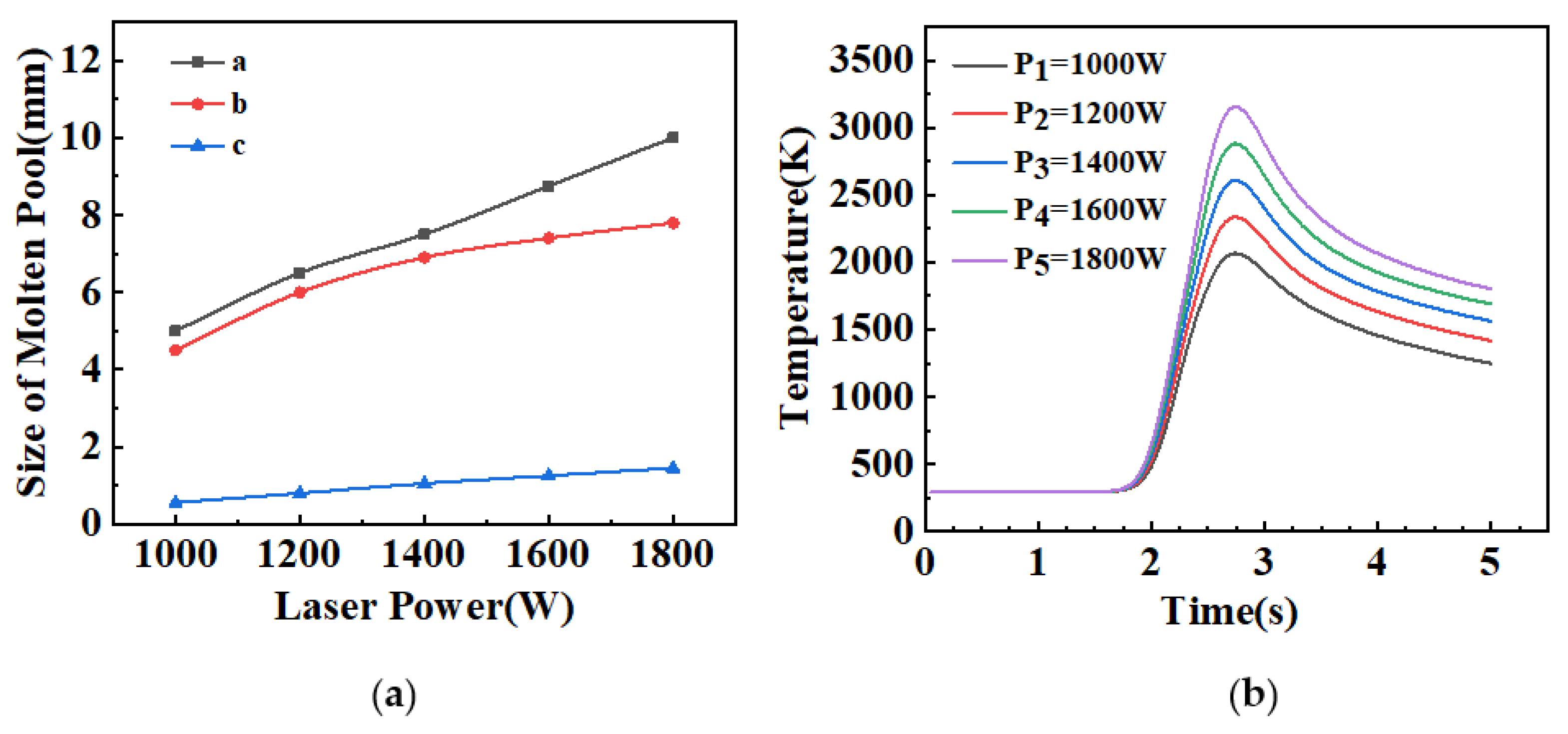
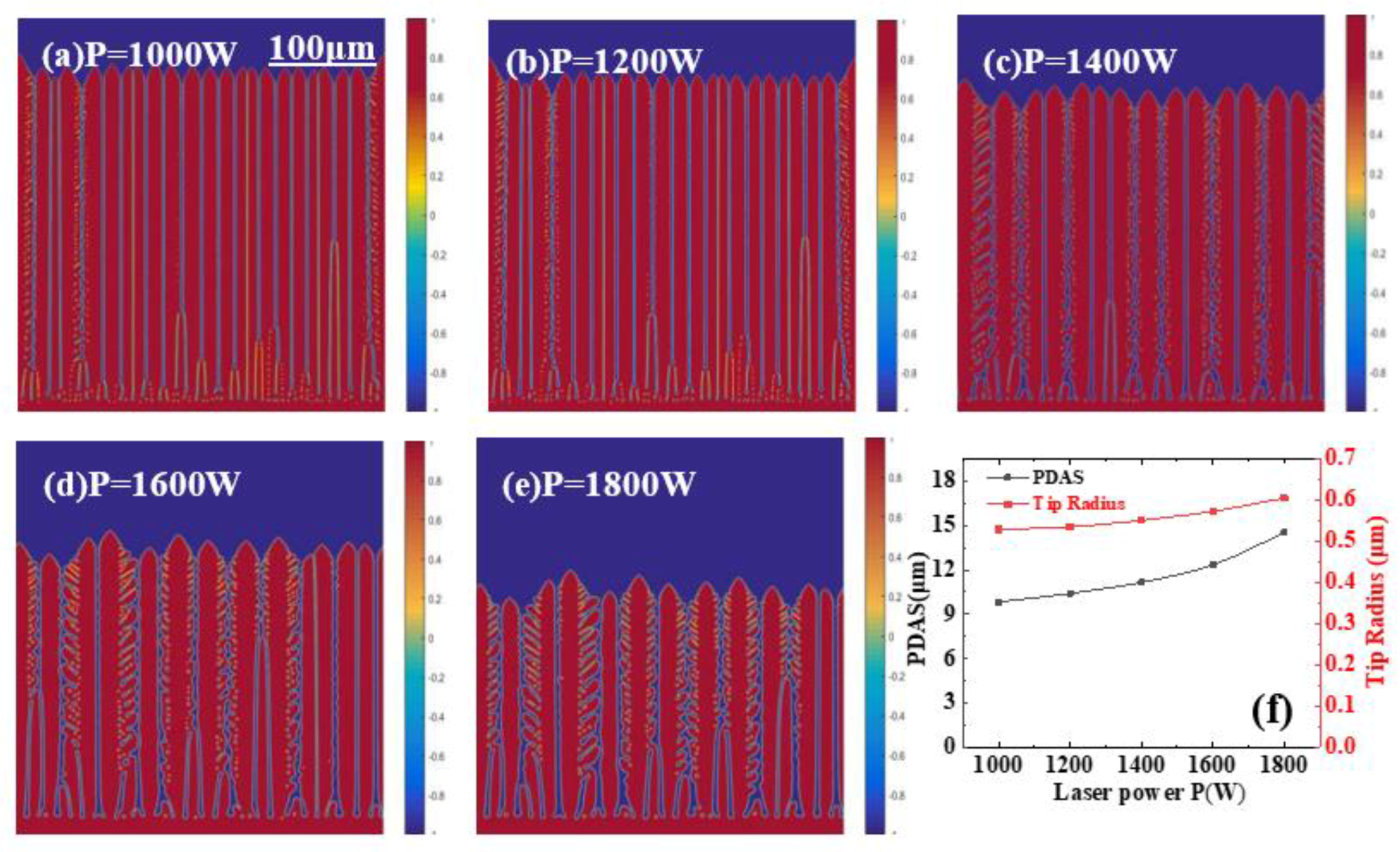
3.1.1. Effect of Laser Power on Macro/Microstructure of Molten Pool
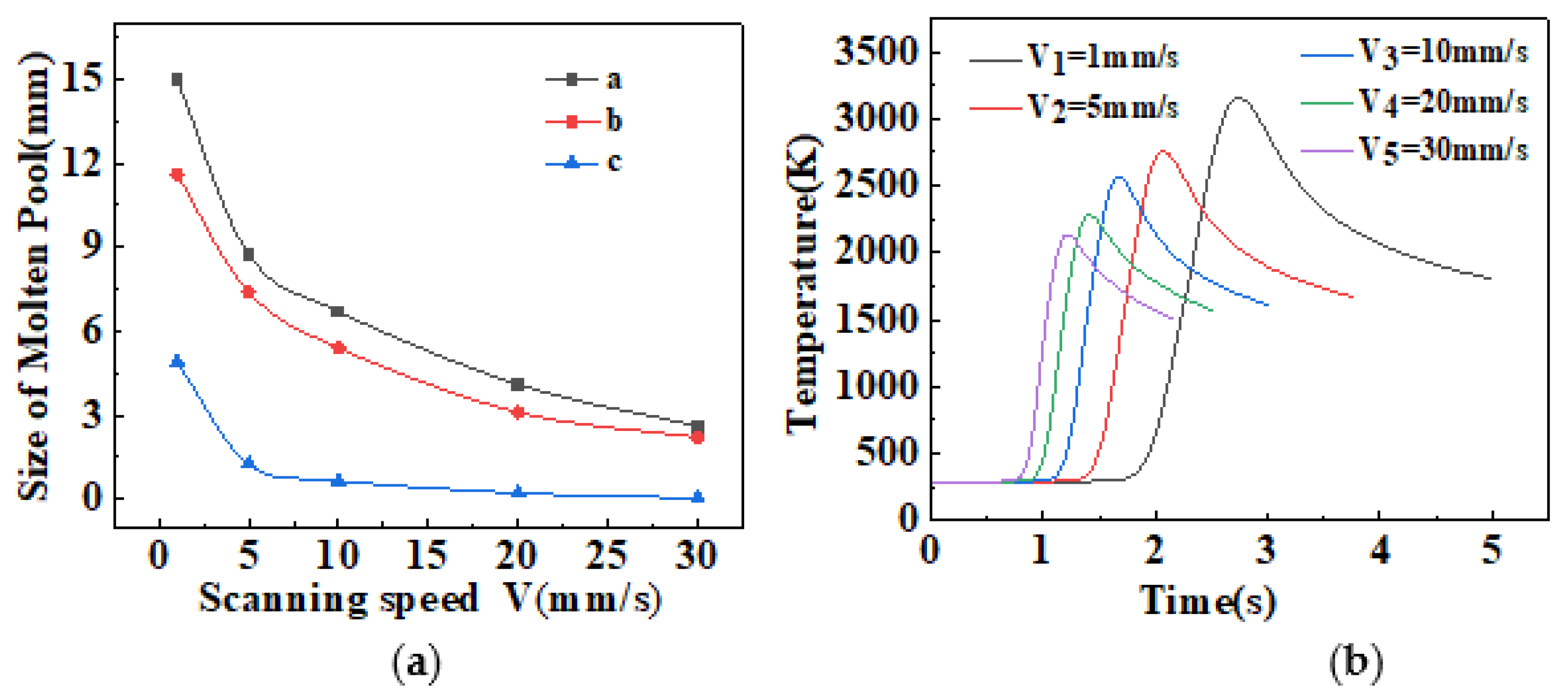
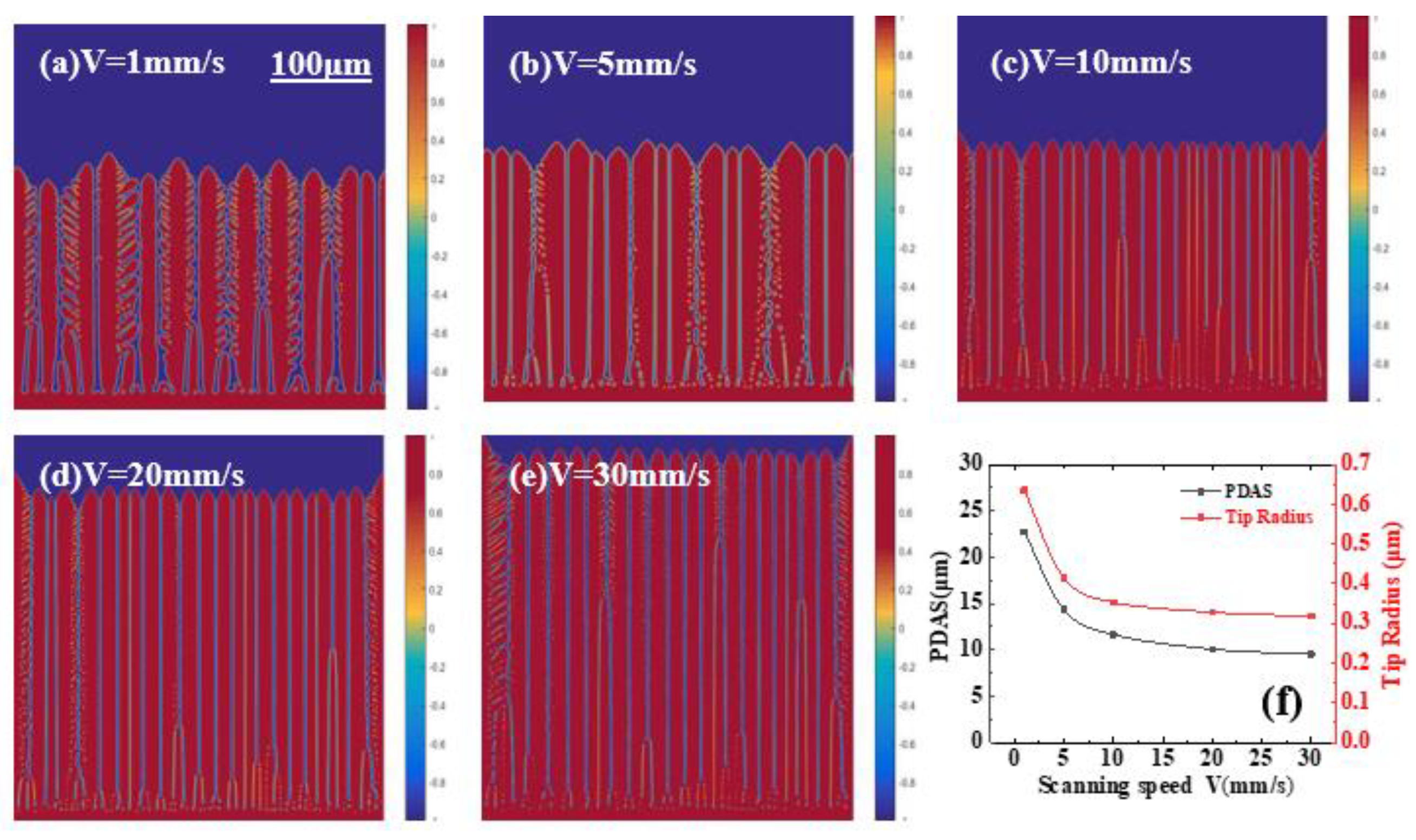
3.1.2. Influence of Laser Scanning Speed on Macro/Microstructure of Molten Pool
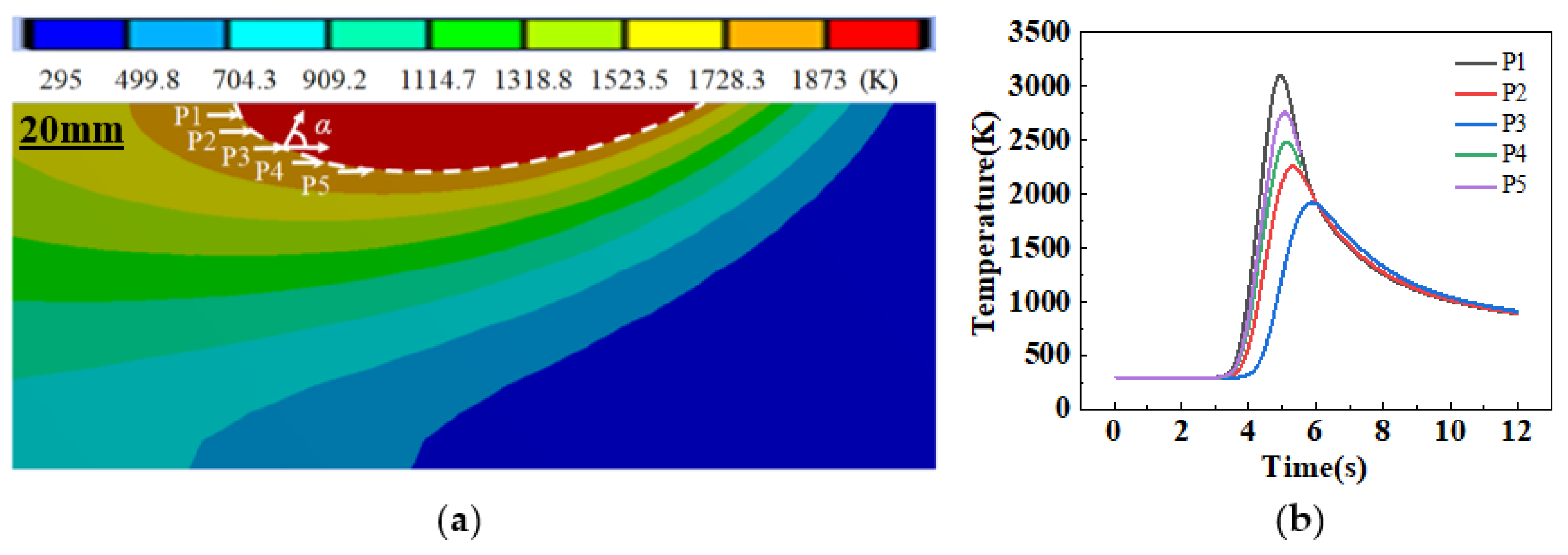
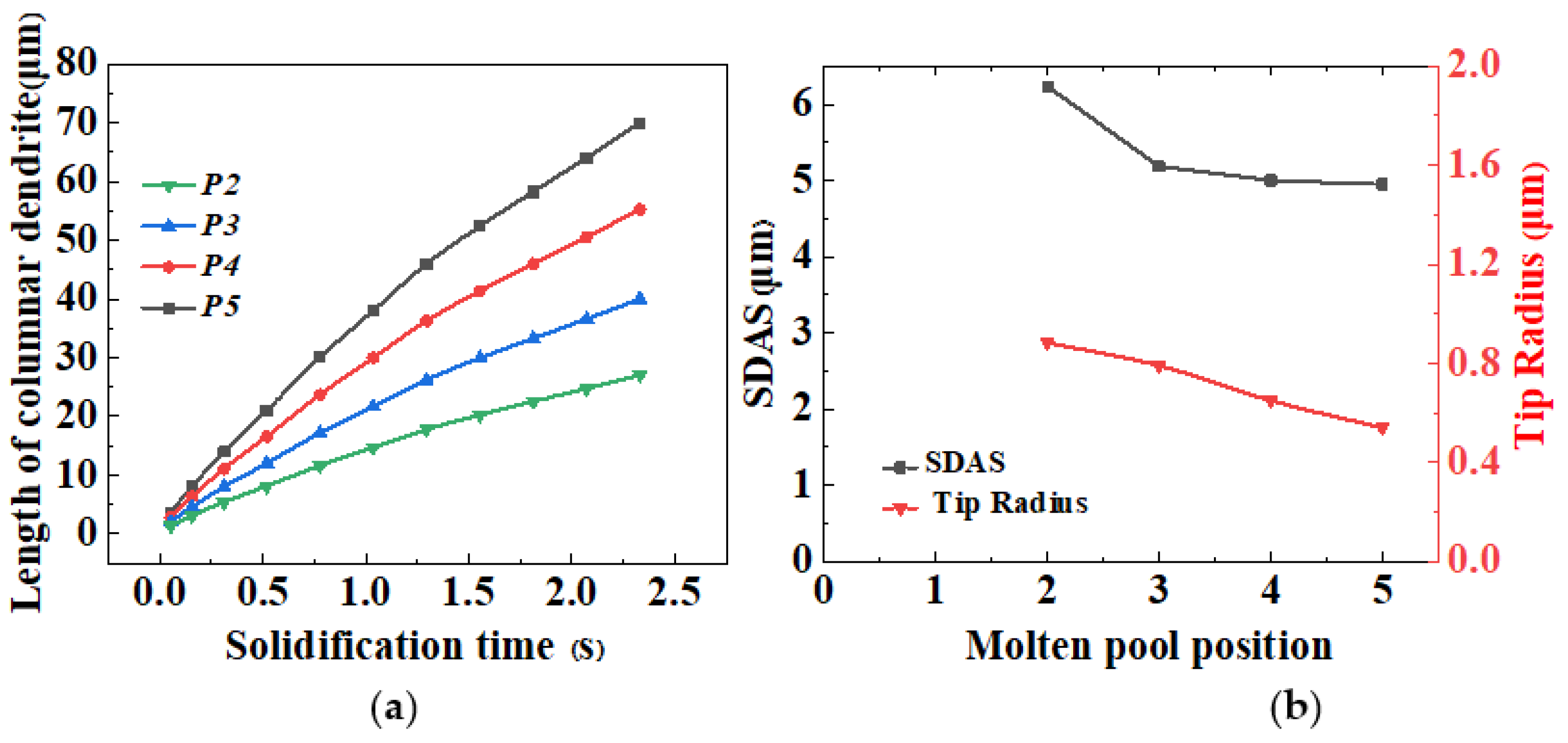
3.2. Microstructure Analysis of Different Positions of Molten Pool
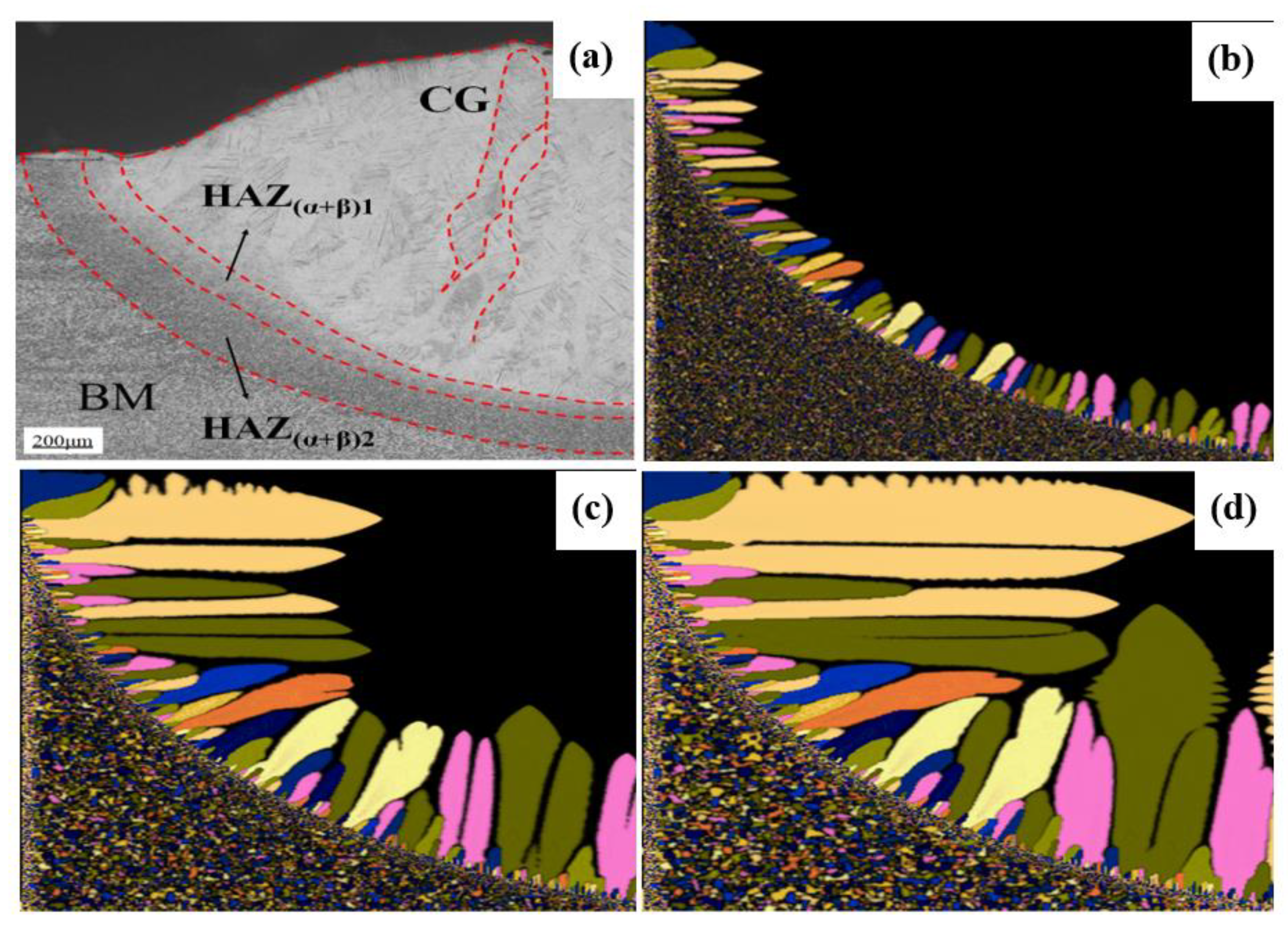
3.3. Comparative Analysis of Experiments
4. Conclusions
- (1)
- With the increase in laser power, the molten pool temperature rises rapidly and the molten pool size expands gradually. When the laser scanning speed increases, the peak temperature and size of the molten pool decrease, and when the laser scanning speed is greater than 5 mm/s, the molten pool length decreases significantly.
- (2)
- Under the fixed process parameters, the cooling rate at the upper part of the molten pool is smaller, and fine equiaxed crystal structure is formed after solidification. The columnar to equiaxed transition occurs in the middle of the molten pool, and the bottom of the molten pool is elongated as a columnar crystal. In addition, the cooling rate at the bottom of the molten pool is relatively high, the dendrite growth rate is relatively fast, and the solute is mostly concentrated between the primary and secondary dendrite arms due to the delay of solute diffusion, resulting in a more serious solute segregation phenomenon.
- (3)
- When the laser scanning speed V = 1 mm/s, the position of the solid–liquid interface of columnar dendrites decreases with an increase in laser power, the dendrite arm spacing ranges from 9.83 μm to 14.51 μm, the tip radius ranges from 0.529 μm to 0.650 μm, and the development of secondary dendrites becomes more perfect. At the same time, the dendrites obtained gradually change from long and thin to short, and the average level of columnar crystal spacing increases gradually.
- (4)
- When the laser power P = 1800 W, the dendrite growth rate increases with an increase in the laser scanning speed. When the liquid–solid interface position is higher, the solid phase volume fraction of columnar dendrites is larger, the tip radius of dendrites is smaller, the dendrite size is finer, the dendrite arrangement becomes more dense, and the development of secondary dendrites is inhibited. When the scan rate is 10 mm/s, the dendrite spacing is almost half of that at 1 mm/s.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, T.; Song, Q.H.; Du, Y.C.; Liu, Z. Development of Tool Wear Standards and Wear Mechanism for Micro Milling Ti-6Al-4V Alloy. Metals 2021, 12, 726. [Google Scholar] [CrossRef]
- Surmeneva, M.; Grubova, I.; Glukhova, N.; Khrapov, D.; Koptyug, A.; Volkova, A.; Ivanov, Y.; Cotrut, C.M.; Vladescu, A.; Teresov, A.; et al. New Ti–35Nb–7Zr–5Ta Alloy Manufacturing by Electron Beam Melting for Medical Application Followed by High Current Pulsed Electron Beam Treatment. Metals 2021, 11, 1066. [Google Scholar] [CrossRef]
- Wu, S.Q.; Lu, Y.J.; Gan, Y.L.; Huang, T.T.; Zhao, C.Q.; Lin, J.J.; Guo, S.; Lin, J.X. Microstructural evolution and microhardness of a selective-laser-melted Ti–6Al–4V alloy after post heat treatments. J. Alloys Compd. 2016, 672, 643–652. [Google Scholar] [CrossRef]
- Zhuang, Z.; Jing, C.; Hua, T.; Xiaolin, Z.; Weidong, H. Microstructure and mechanical properties of laser repaired TC4 titanium alloy. Trans. Nonferrous Met. Soc. China 2017, 27, 2613–2621. [Google Scholar] [CrossRef] [Green Version]
- Ren, Y.M.; Lin, X.; Fu, X.; Tan, H.; Chen, J.; Huang, W.D. Microstructure and deformation behavior of Ti-6Al-4V alloy by high-power laser solid forming. Acta Mater. 2017, 132, 82–95. [Google Scholar] [CrossRef]
- Lu, S.L.; Qian, M.; Tang, H.P.; Yan, M.; Wang, J.; StJohn, D.H. Massive transformation in Ti-6Al-4V additively manufactured by selective electron beam melting. Acta Mater. 2016, 104, 303–315. [Google Scholar] [CrossRef]
- Xu, W.; Brandt, M.; Sun, S.; Elambasseril, J.; Liu, Q.; Latham, K.; Xia, K.; Qian, M. Additive manufacturing of strong and ductile Ti-6Al-4V by selective laser melting via in situ martensite decomposition. Acta Mater. 2015, 85, 74–84. [Google Scholar] [CrossRef]
- Shi, X.Z.; Ma, S.Y.; Liu, C.M.; Wu, Q.; Lu, J.; Liu, Y.; Shi, W. Selective laser melting-wire arc additive manufacturing hybrid fabrication of Ti-6Al-4V alloy: Microstructure and mechanical properties. Mater. Sci. Eng. 2017, 684A, 196–204. [Google Scholar] [CrossRef]
- Lin, J.J.; Lv, Y.H.; Liu, Y.X.; Xu, B.S.; Sun, Z.; Li, Z.G.; Wu, Y.X. Microstructural evolution and mechanical properties of Ti-6Al-4V wall deposited by pulsed plasma arc additive manufacturing. Mater. Des. 2016, 102, 30–39. [Google Scholar] [CrossRef]
- Donoghue, J.; Antonysamy, A.A.; Martina, F.; Colegrove, P.; Williams, S.; Prangnell, P. The effectiveness of combining rolling deformation with Wire–Arc Additive Manufacture on β-grain refinement and texture modification in Ti-6Al-4V. Mater. Charact. 2016, 114, 103–114. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Mahyar, K.; Ghasemi, A.; Rolfe, B.; Gibson, I. Additive manufacturing a powerful tool for the aerospace industry. Rapid Prototyp. J. 2022, 28, 87–100. [Google Scholar]
- Oliveira, J.P.; Santos, T.G.; Miranda, R.M. Revisiting fundamental welding concepts to improve additive manufacturing: From theory to practice. Prog. Mater. Sci. 2020, 107, 100590. [Google Scholar] [CrossRef]
- Akbari, M.; Kovacevic, R. An investigation on mechanical and microstructural properties of 316LSi parts fabricated by a robotized laser/wire direct metal deposition system. Addit. Manuf. 2018, 23, 487–497. [Google Scholar] [CrossRef]
- Günther, J.; Krewerth, D.; Lippmann, T.; Leuders, S.; Tröster, T.; Weidner, A.; Biermann, H.; Niendorf, T. Fatigue life of additively manufactured Ti-6Al-4V in the very high cycle fatigue regime. Int. J. Fatigue 2017, 94, 236–245. [Google Scholar] [CrossRef]
- Fatemi, A.; Molaei, R.; Simsiriwong, J.; Sanaei, N.; Pegues, J.; Torries, B.; Phan, N.; Shamsaei, N. Fatigue behaviour of additive manufactured materials: An overview of some recent experimental studies onTi-6Al-4V considering various processing and loading direction effects. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 991–1009. [Google Scholar] [CrossRef]
- Zhang, D.; Qiu, D.; Gibson, M.A.; Zheng, Y.; Fraser, H.L.; StJohn, D.H.; Easton, M.A. Additive manufacturing of ultrafine-grained high-strength titanium alloys. Nature 2019, 576, 91–95. [Google Scholar] [CrossRef]
- Xu, W.; Lui, E.W.; Pateras, A.; Qian, M.; Brandt, M. In situ tailoring microstructure in additively manufactured Ti-6Al-4V for superior mechanical performance. Acta Mater. 2017, 125, 390–400. [Google Scholar] [CrossRef]
- Zhao, C.; Fezzaa, K.; Cunningham, R.W.; Wen, H.; De Carlo, F.; Chen, L.; Rollett, A.D.; Sun, T. Real-time monitoring of laser powder bed fusion process using high-speed X-ray imaging and diffraction. Sci. Rep. 2017, 7, 3602–3614. [Google Scholar] [CrossRef]
- Leung, C.L.A.; Marussi, S.; Atwood, R.C.; Towrie, M.; Withers, P.J.; Lee, P.D. In situ X-ray imaging of defect and molten pool dynamics in laser additive manufacturing. Nat. Commun. 2018, 9, 1355–1364. [Google Scholar] [CrossRef] [Green Version]
- Enneti, R.; Morgan, R.; Atre, S. Effect of process parameters on the selective laser melting (SLM) of tungsten. Int. J. Refract. Met. Hard Mater. 2018, 71, 315–319. [Google Scholar] [CrossRef]
- Peyre, P.; Rouchausse, Y.; Defauchy, D.; Régnier, G. Expermental and numerical analysis of the selective laser sintering (SLS) of PA12 and PEKK semi-crystalline polymers. J. Mater. Process. Technol. 2015, 225, 326–336. [Google Scholar] [CrossRef]
- Singh, S.; Sharma, V.S.; Sachdeva, A. Optimization and analysis of shrinkage in selective laser sintered polyamide parts. Mater. Manuf. Process. 2012, 27, 707–714. [Google Scholar] [CrossRef]
- Almangour, B.; Grzesiak, D.; Borkar, T.; Yang, J.-M. Densification behavior, microstructural evolution, and mechanical properties of TiC/316L stainless steel nanocomposites fabricated by selective laser melting. Mater. Des. 2018, 138, 119–128. [Google Scholar] [CrossRef]
- Kolleck, R.; Vollmer, R.; Veit, R. Investigation of a combined micro-forming and punching process for the realization of tight geometrical tolerances of conically formed hole patterns. CIRP Ann. Manuf. Technol. 2011, 60, 331–334. [Google Scholar] [CrossRef]
- Zhu, Z.; Dhokia, V.G.; Nassehi, A.; Newman, S.T. A review of hybrid manufacturing processes—State of the art and future perspectives. Int. J. Comput. Integr. Manuf. 2013, 26, 596–615. [Google Scholar] [CrossRef] [Green Version]
- Francois, M.M.; Sun, A.; King, W.E.; Henson, N.; Tourret, D.; Bronkhorst, C.; Carlson, N.; Newman, C.; Haut, T.; Bakosi, J.; et al. Modeling of additive manufacturing processes for metals: Challenges and opportunities. Curr. Opin. Solid State Mater. Sci. 2017, 21, 198–206. [Google Scholar] [CrossRef]
- Harrison, N.J.; Todd, I.; Mumtaz, K. Reduction of micro-cracking in nickel super alloys processed by selective laser melting: A fundamental alloy design approach. Acta Mater. 2015, 94, 59–68. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.B.; Wei, M.M.; Chen, C.; Wu, Y.; Peng, L.; Chen, L.-Q. Phase-field study of the effects of the multi-controlling parameters on columnar dendrite during directional solidification in hexagonal materials. Eur. Phys. J. E 2020, 43, 41. [Google Scholar] [CrossRef]
- Wang, Y.B.; Jia, S.S.; Wei, M.G.; Peng, L.; Wu, Y.; Ji, Y.; Chen, L.-Q.; Liu, X. Coupling in situ synchrotron X-ray radiography and phase-field simulation to study the effect of low cooling rates on dendrite morphology during directional solidification in Mg-Gd alloys. J. Alloys Compd. 2020, 815, 152385. [Google Scholar] [CrossRef]
- Tourret, D.; Clarke, A.; Imhoff, S.; Gibbs, P.J.; Gibbs, J.W.; Karma, A. Three-dimensional multiscale modeling of dendritic spacing selection during Al-Si directional solidification. JOM 2015, 67, 1776–1785. [Google Scholar] [CrossRef]
- Steinbach, I.; Beckermann, C.; Kauerauf, B.; Li, Q.; Guo, J. Three-dimensional modeling of equiaxed dendritic growth on a mesoscopic scale. Acta Mater. 1999, 47, 971–982. [Google Scholar] [CrossRef]
- Shang, S.; Han, Z.; Sun, W.; Luo, A.A. A phase field model coupled with pressure-effect-embedded thermodynamic modeling for describing microstructure and microsegregation in pressurized solidification of a ternary magnesium alloy. Comput. Mater. Sci. 2017, 136, 264–270. [Google Scholar] [CrossRef]
- Pan, H.; Han, Z.; Liu, B. Study on Dendritic Growth in Pressurized Solidification of Mg–Al Alloy Using Phase Field Simulation. J. Mater. Sci. Technol. 2016, 32, 68–75. [Google Scholar] [CrossRef]
- Yang, M.; Xiong, S.; Guo, Z. Effect of different solute additions on dendrite morphology and orientation selection in cast binary magnesium alloys. Acta Mater. 2016, 112, 261–272. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Shanmugan, S.; Muthuramalingam, T.; Kumar, R.; Essa, F.A.; Ibrahim, A.M.M. Modeling of the Transient Temperature Field during Laser Heating. Lasers Manuf. Mater. Process. 2021, 8, 97–112. [Google Scholar] [CrossRef]
- Khoshaim, A.B.; Elsheikh, A.H.; Moustafa, E.B.; Basha, M.; Showaib, E.A. Experimental investigation on laser cutting of PMMA sheets: Effects of process factors on kerf characteristics. J. Mater. Res. Technol. 2021, 11, 235–246. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Shehabeldeen, T.A.; Zhou, J.; Showaib, E.; Elaziz, M.A. Prediction of laser cutting parameters for polymethylmethacrylate sheets using random vector functional link network integrated with equilibrium optimizer. J. Intell. Manuf. 2021, 32, 1377–1388. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Deng, W.; Showaib, E.A. Improving laser cutting quality of polymethylmethacrylate sheet: Experimental investigation and optimization. J. Mater. Res. Technol. 2020, 9, 1325–1339. [Google Scholar] [CrossRef]
- Muthuramalin, T.; Akash, R.; Krishnan, S.; Phan, N.H.; Pi, V.N.; Elsheikh, A.H. Surface quality measures analysis and optimization on machining titanium alloy using CO 2 based laser beam drilling process. J. Manuf. Process. 2021, 62, 1–6. [Google Scholar] [CrossRef]
- Zhou, H.Y.; Wu, C.H.; Tang, D.Y.; Shi, X.L.; Xue, Y.; Huang, Q.; Zhang, J.; Elsheikh, A.H.; Ibrahim, A.M.M. Tribological performance of gradient Ag-multilayer graphene/TC4 alloy self-lubricating composites prepared by laser additive manufacturing. Tribol. Trans. 2021, 64, 819–829. [Google Scholar] [CrossRef]
- Giganto, S.; Martínez-Pellitero, S.; Cuesta, E.; Zapico, P.; Barreiro, J. Proposal of design rules for improving the accuracy of selective laser melting (SLM) manufacturing using benchmarks parts. Rapid Prototyp. J. 2021, 28, 1129–1143. [Google Scholar] [CrossRef]
- Zhou, Y.; Abbara, E.M.; Jiang, D.; Azizi, A.; Poliks, M.D.; Ning, F. High-cycle fatigue properties of curved-surface AlSi10Mg parts fabricated by powder bed fusion additive manufacturing. Rapid Prototyp. J. 2021, 1–15. [Google Scholar] [CrossRef]
- Linares, J.M.; Chaves-Jacob, J.; Lopez, Q. Fatigue life optimization for 17-4Ph steel produced by selective laser melting. Rapid Prototyp. J. 2022, 28, 1182–1192. [Google Scholar] [CrossRef]
- Sahoo, S.; Chou, K. Phase-field simulation of microstructure evolution of Ti–6Al–4V in electron beam additive manufacturing process. Addit. Manuf. 2016, 9, 14–24. [Google Scholar] [CrossRef]
- Xiao, W.; Li, S.; Wang, C.; Shi, Y.; Mazumder, J.; Xing, H.; Song, L. Multi-scale simulation of dendrite growth for direct energy deposition of nickel-based super alloys. Mater. Des. 2018, 164, 107553. [Google Scholar] [CrossRef]
- Yao, X.X.; Ge, P.; Li, J.Y.; Wang, Y.; Li, T.; Liu, W.; Zhang, Z. Controlling the solidification process parameters of direct energy deposition additive manufacturing considering laser and powder properties. Comput. Mater. Sci. 2020, 182, 109788. [Google Scholar] [CrossRef]
- Sammons, P.M.; Bristow, D.A.; Landers, R.G. Height Dependent Laser Metal Deposition Process Modeling. ASME/ISCIE 2013, 135, 054501. [Google Scholar] [CrossRef]
- Wang, Q.; Li, J.; Gouge, M.; Nassar, A.R.; Michaleris, P.; Reutzel, E. Physics-Based Multivariable Modeling and Feedback Linearization Control of Melt-Pool Geometry and Temperature in Directed Energy Deposition. J. Eng. Ind. 2017, 139, 021013. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, N.G.X.; Wang, X.; Guo, X. Simulation Research on Temperature Field of IN 625 Alloy by Micro-arc Plasma Additive Manufacturing Using Gaussian Heat Source. IOP Conf. Ser. Earth Environ. Sci. 2021, 692, 022060. [Google Scholar] [CrossRef]
- Zhou, Q.Y. Study on Calculation Methods of Transient Temperature Field during Selective Laser Melting. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2017. [Google Scholar]
- Echebarria, B.; Folch, R.; Karma, A.; Plapp, M. Quantitative phase-field model of alloy solidification. Phys. Rev. E 2004, 70, 061604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, D.; Wang, Y. Mesoscale multi-physics simulation of rapid solidification of Ti-6Al-4V alloy. Addit. Manuf. 2019, 25, 551–562. [Google Scholar] [CrossRef]


| Alloy Element | Impurities not Greater Than | |||||||
|---|---|---|---|---|---|---|---|---|
| Al | V | Ti | Fe | C | N | H | O | Others |
| 5.5–6.8 | 3.5–4.5 | margin | 0.30 | 0.10 | 0.05 | 0.015 | 0.20 | 0.40 |
| Temperature /°C | Specific Heat /(J/(kg·°C)) | Thermal Conductivity /(W/(m·°C)) | Density /(g/cm3) |
|---|---|---|---|
| 20 | 611 | 6.8 | 4.51 |
| 100 | 624 | 7.4 | 4.42 |
| 200 | 653 | 8.7 | 4.38 |
| 300 | 674 | 9.8 | 4.32 |
| 500 | 703 | 11.8 | 4.28 |
| 1000 | 1030 | 15.2 | 4.24 |
| 1500 | 1850 | 22.1 | 4.19 |
| 2500 | 1852 | 22.2 | 3.92 |
| Symbol | Value | Unit |
|---|---|---|
| Tl | 1928 | K |
| Ts | 1878 | K |
| c0 | 10 | wt.% |
| k | 0.5 | - |
| DL | 9.5 × 10−9 | m2 s−1 |
| Γ | 1.88 × 10−7 | K·m |
| mL | 0.5 | K·wt.%−1 |
| ε | 0.05 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, C.; Liu, X.; Wang, J.; Zhang, Y.; Long, W.; Guan, S.; Peng, L. Cross-Scale Simulation Research on the Macro/Microstructure of TC4 Alloy Wire Laser Additive Manufacturing. Metals 2022, 12, 934. https://doi.org/10.3390/met12060934
Wang Y, Chen C, Liu X, Wang J, Zhang Y, Long W, Guan S, Peng L. Cross-Scale Simulation Research on the Macro/Microstructure of TC4 Alloy Wire Laser Additive Manufacturing. Metals. 2022; 12(6):934. https://doi.org/10.3390/met12060934
Chicago/Turabian StyleWang, Yongbiao, Cong Chen, Xintian Liu, Jiaxin Wang, Yang Zhang, Weimin Long, Shaokang Guan, and Liming Peng. 2022. "Cross-Scale Simulation Research on the Macro/Microstructure of TC4 Alloy Wire Laser Additive Manufacturing" Metals 12, no. 6: 934. https://doi.org/10.3390/met12060934
APA StyleWang, Y., Chen, C., Liu, X., Wang, J., Zhang, Y., Long, W., Guan, S., & Peng, L. (2022). Cross-Scale Simulation Research on the Macro/Microstructure of TC4 Alloy Wire Laser Additive Manufacturing. Metals, 12(6), 934. https://doi.org/10.3390/met12060934





