Numerical Investigation of Impact Behavior of Strut-Based Cellular Structures Designed by Spatial Voronoi Tessellation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Design of Cellular Structures
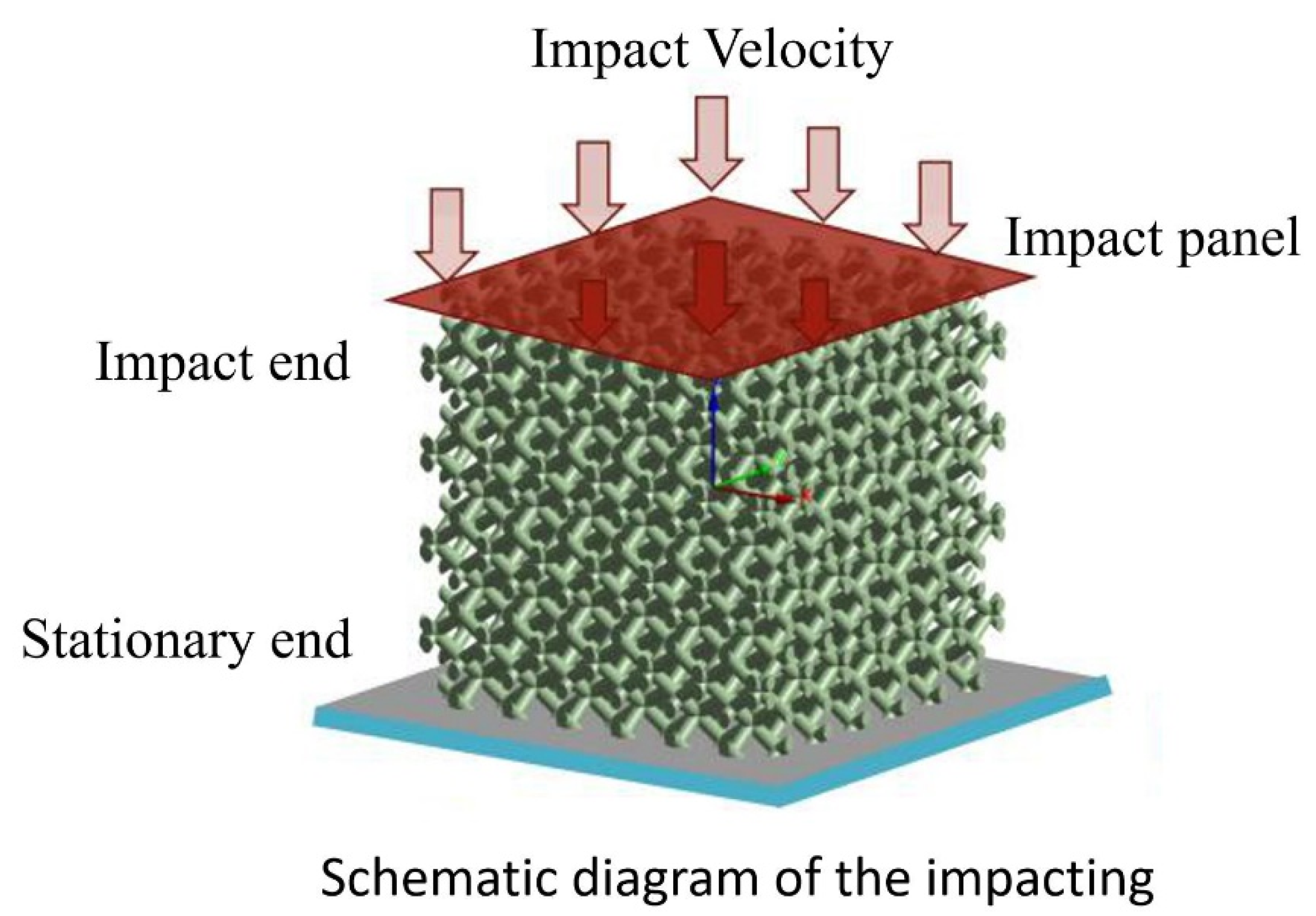
2.2. Impact Finite-Element Modeling
2.3. Mesh Sensitivity Tests
3. Results and Discussion
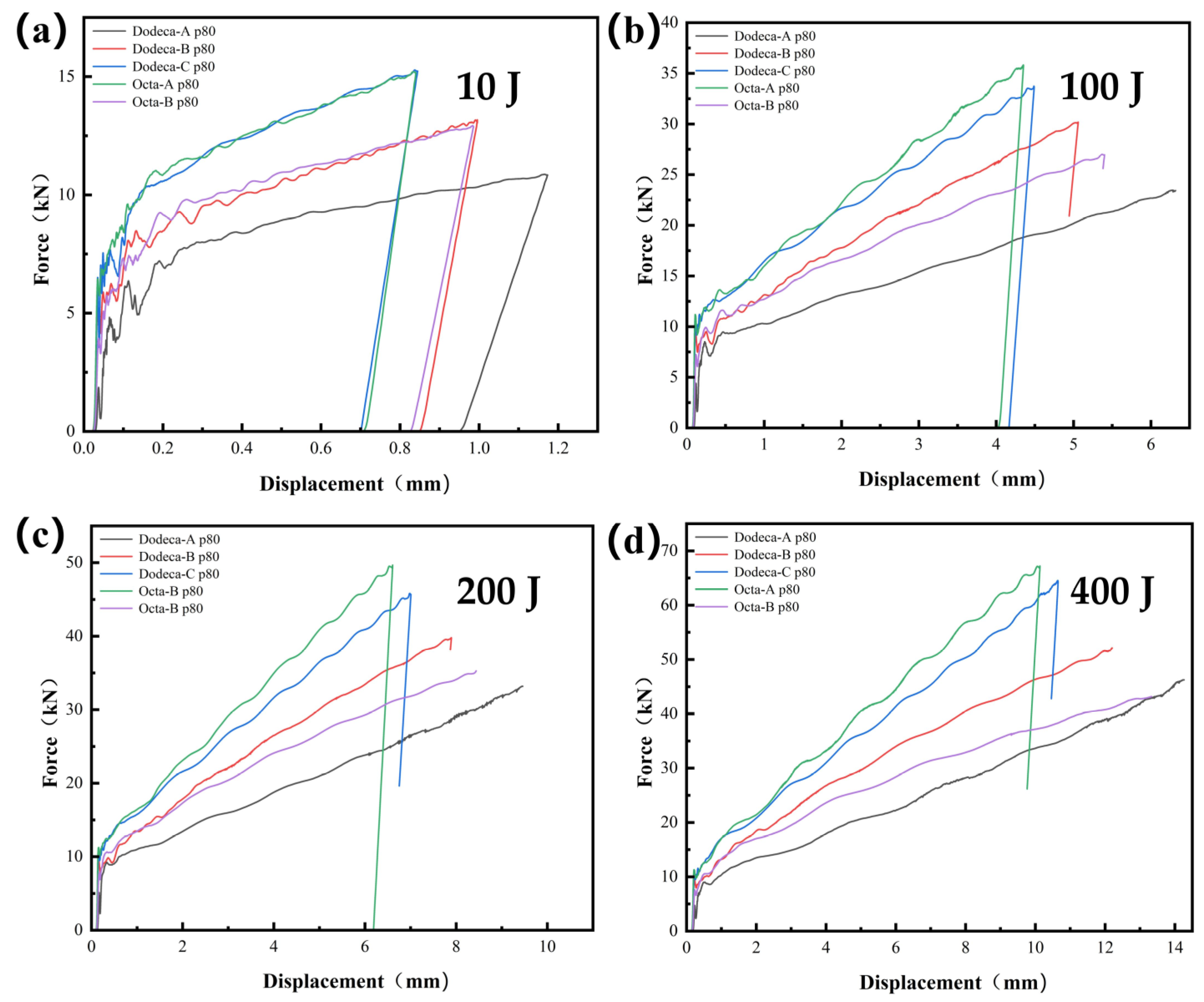
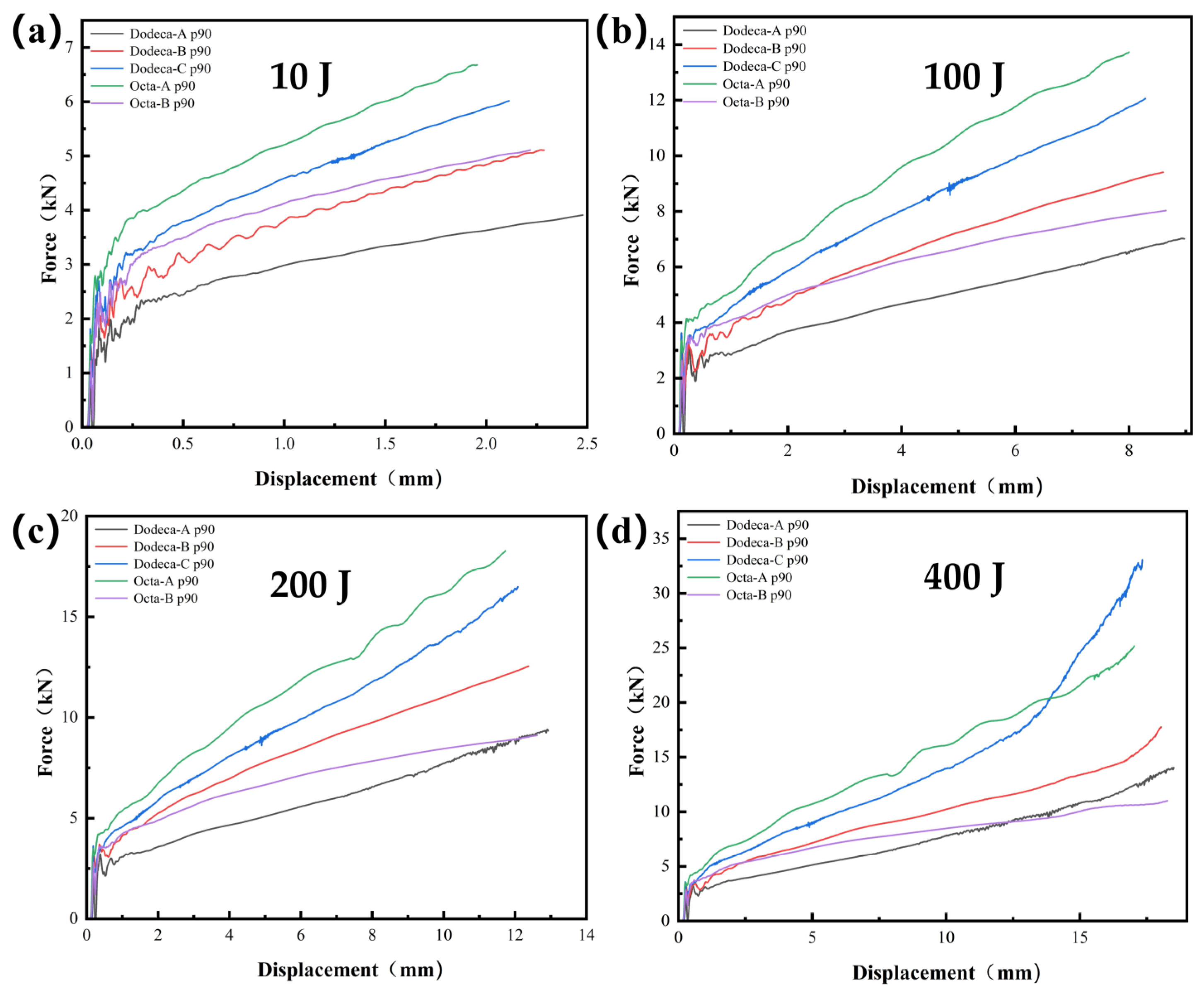
3.1. Load-Displacement Curves
3.2. Energy Absorption Performance
3.2.1. Influence of Porosity
3.2.2. Influence of Unit-Cell Shape and Rotating Unit Cell
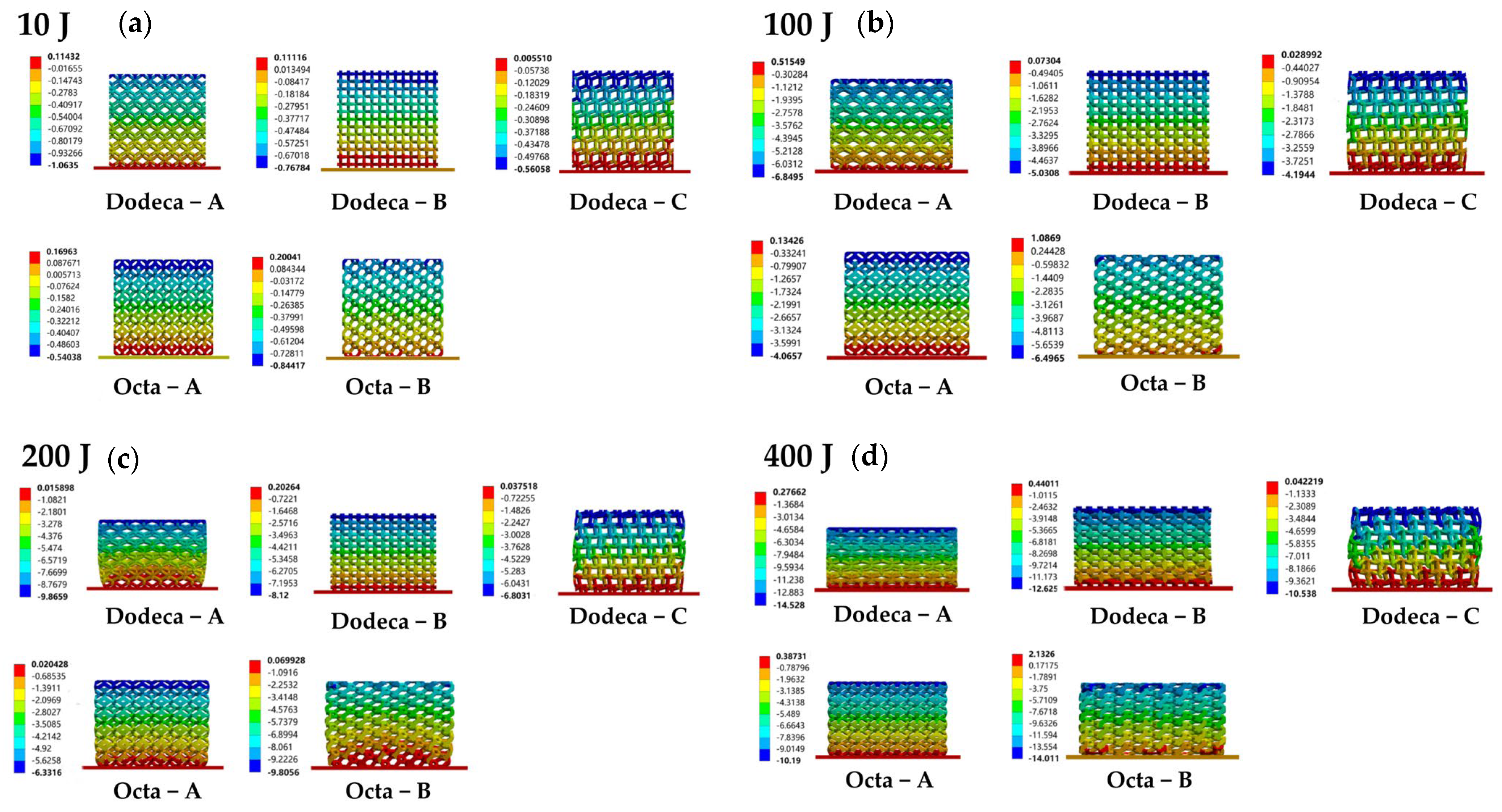
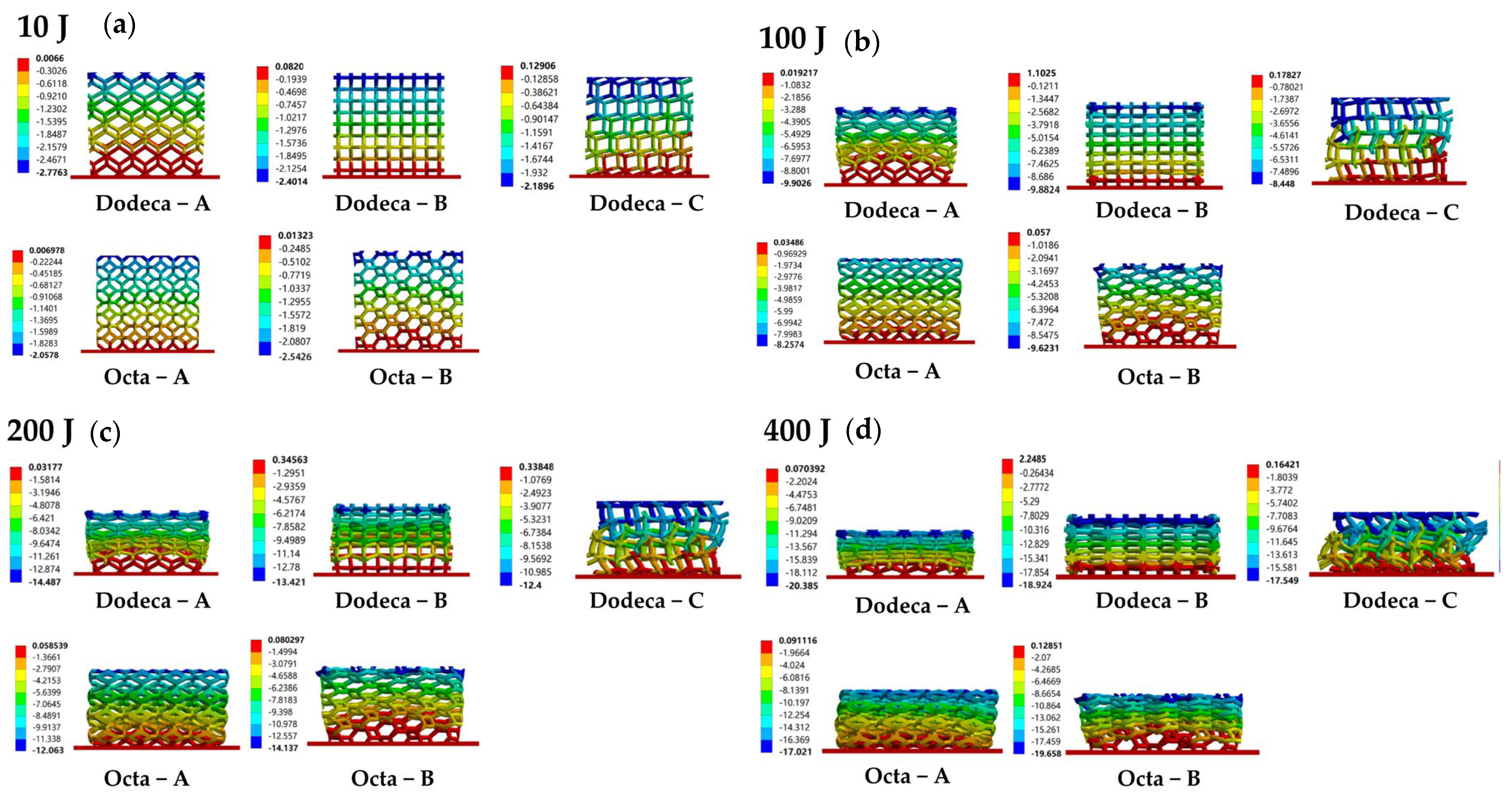
3.3. Deformation Modes
3.3.1. Influence of Porosity
3.3.2. Influence of Unit-Cell Shape and Rotating Unit Cell
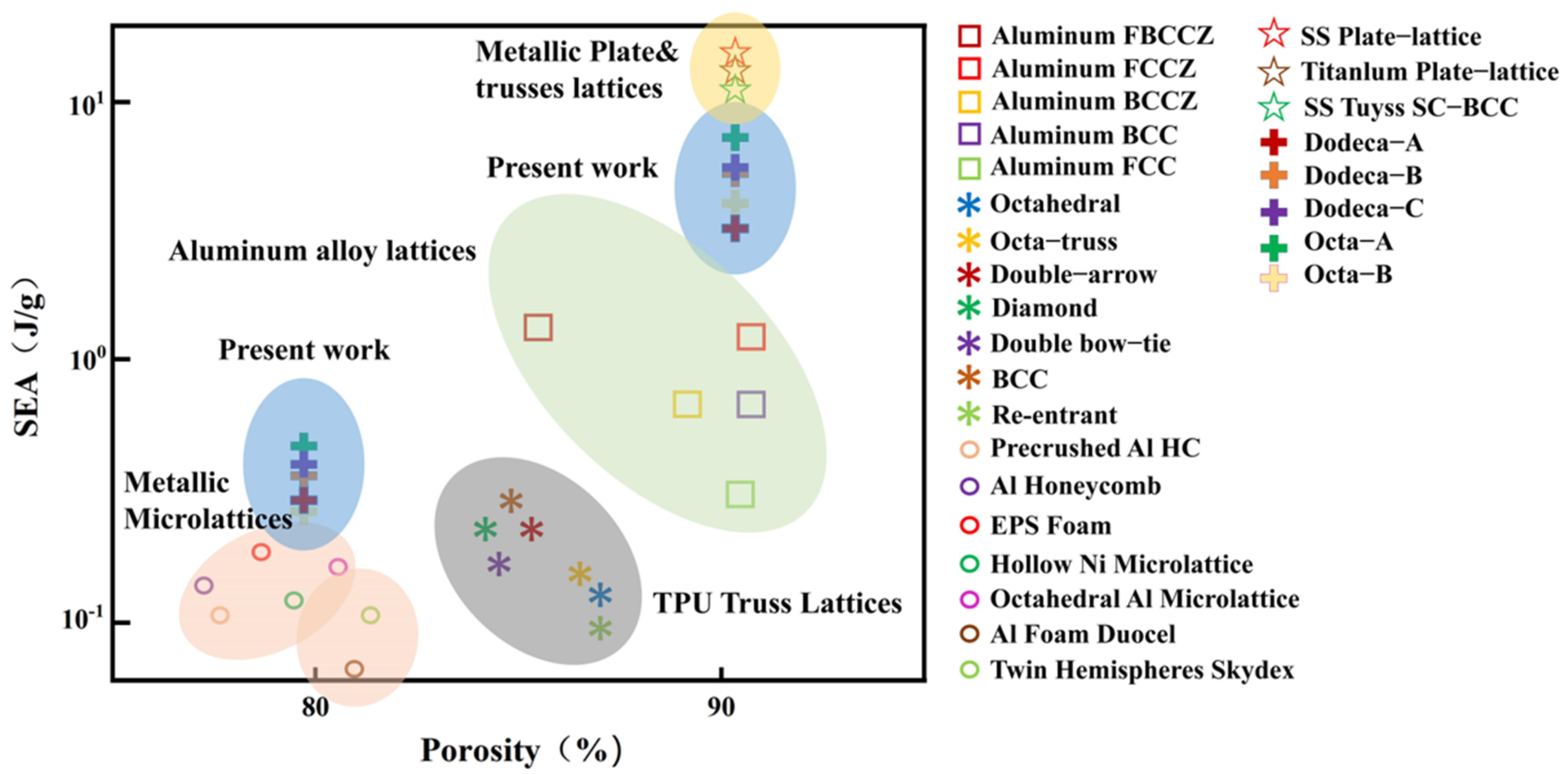
3.4. Comparative Specific Energy-Absorption Characteristics of Porous Structures Studied in This Paper
4. Conclusions
- For the porous structures subjected to various impact energies, the force-displacement curve showed three modes: one was a single peak that then sharply descended, almost back to the origin; the next was a single peak, followed by a slight decrease, but without approaching the origin; and the third increased sharply and then experienced oscillations, before beginning to rise slowly. In the first, the impact energy was not sufficient to cause damage to the sample; in the second, the impactor rebounded within the impact time; and in the third, the impactor did not.
- When subjected to impact, the shape of the unit cell has a significant effect on the impact resistance of the porous structure. By rotating the unit cell, its number of oblique edges can be changed; a porous structure with more oblique edges has better stiffness and can resist higher impact loads. The results show that the Dodeca structure rotated 54.7 degrees around the y-axis to absorb energy the best, while the energy-absorption behavior of the Octa structure decreased after rotation.
- At the same impact energy, the stiffness of porous structures increases as their porosity decreases. When the impact energy is not sufficient to destroy a porous structure, its porosity has no significant effect on the energy absorption, but for economic reasons, it is recommended to use a higher porosity (90%), through which about 89% or more of the impact energy can be absorbed. When the impact energy is large, porous structures with low porosity (80%) may show stronger energy-absorption characteristics.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Paolini, A.; Kollmannsberger, S.; Rank, E. Additive manufacturing in construction: A review on processes, applications, and digital planning methods. Addit. Manuf. 2019, 30, 100894. [Google Scholar] [CrossRef]
- Schaedler, T.A.; Carter, W.B. Architected Cellular Materials. Annu. Rev. Mater. Sci. 2016, 46, 187–210. [Google Scholar] [CrossRef]
- Ngoc, S.H.; Lu, G. A review of recent research on bio-inspired structures and materials for energy absorption applications. Compos B Eng. 2020, 181, 107406. [Google Scholar]
- Fang, J.; Sun, G.; Qiu, N.; Kim, N.H.; Li, Q. On design optimization for structural crashworthiness and its state of the art. Struct. Multidiscip. Optim. 2016, 55, 1091–1119. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, X.; Zhang, H. A review on functionally graded structures and materials for energy absorption. Eng. Struct. 2018, 171, 309–325. [Google Scholar] [CrossRef]
- Lu, L.; Sharf, A.; Zhao, H. Build-to-Last: Strength to Weight 3D Printed Objects. ACM Trans Graph. 2014, 33, 97. [Google Scholar] [CrossRef]
- Quey, R.; Dawson, P.R.; Barbe, F. Large-scale 3D random polycrystals for the finite element method: Generation, meshing and remeshing. Comput. Methods Appl. Mech. Eng. 2011, 200, 1729–1745. [Google Scholar] [CrossRef] [Green Version]
- Calka, P. An explicit expression for the distribution of the number of sides of the typical Poisson-Voronoi cell. Adv. Appl. Probab. 2003, 35, 863–870. [Google Scholar] [CrossRef]
- Hug, D.; Reitzner, M.; Schneider, R. Large Poisson-Voronoi cells and Crofton cells. Adv. Appl. Probab. 2004, 36, 667–690. [Google Scholar] [CrossRef] [Green Version]
- Falco, S.; Jiang, J.; De Cola, F.; Petrinic, N. Generation of 3D polycrystalline microstructures with a conditioned Laguerre-Voronoi tessellation technique. Comput. Mater. Sci. 2017, 136, 20–28. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, W.; Shen, A.; Mellado, N.; Cai, S.; Luo, L.; Wang, N.; Yan, G.; Zhou, G. Seed point set-based building roof extraction from airborne LiDAR point clouds using a top-down strategy. Autom. Constr. 2021, 126, 103660. [Google Scholar] [CrossRef]
- Zheng, N.; Yu, L. Numerical investigation of pressure drop and heat transfer through open cell foams with 3D La-guerre-Voronoi model—ScienceDirect. Int. J. Heat Mass Transf. 2017, 113, 819–839. [Google Scholar]
- Ćwieka, K.; Wejrzanowski, T.; Kurzydłowski, K.J. Incorporation of the Pore Size Variation to Modeling of the Elastic Behavior of Metallic Open-Cell Foams. Arch. Met. Mater. 2017, 62, 259–262. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Cao, W.; Zhang, L.; Jiang, K.; Lu, P. A design method of Voronoi porous structures with graded relative elasticity distri-bution for functionally gradient porous materials. Int. J. Mech. Mater. Des. 2021, 17, 863–883. [Google Scholar] [CrossRef]
- Chen, D.; Kitipornchai, S.; Yang, J. Dynamic response and energy absorption of functionally graded porous structures. Mater. Des. 2018, 140, 473–487. [Google Scholar] [CrossRef] [Green Version]
- Peixinho, N.; Carvalho, O.; Areias, C.; Pinto, P.; Silva, F. Compressive properties and energy absorption of metal-polymer hybrid cellular structures. Mater. Sci. Eng. A 2020, 794, 139921. [Google Scholar] [CrossRef]
- Tan, J.H.K.; Sing, S.L.; Yeong, W.Y. Microstructure modelling for metallic additive manufacturing: A review. Virtual Phys. Prototyp. 2019, 15, 87–105. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Diamantopoulou, M.; Gorji, M.B.; Bonatti, C.; Mohr, D. 3D Plate-Lattices: An Emerging Class of Low-Density Metamaterial Exhibiting Optimal Isotropic Stiffness. Adv. Mater. 2018, 30, e1803334. [Google Scholar] [CrossRef]
- Berger, J.B.; Wadley, H.N.G.; McMeeking, R.M. Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness. Nature 2017, 543, 533–537. [Google Scholar] [CrossRef] [Green Version]
- Şerban, D.A.; Linul, E.; Voiconi, T.; Marşavina, L.; Modler, N. Numerical evaluation of two-dimensional micromechanical structures of anisotropic cellular materials: Case study for polyurethane rigid foams. Iran. Polym. J. 2015, 24, 515–529. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A.; Wildman, R.D.; Hague, R.J.M. A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting. Mater. Sci. Eng. A 2016, 670, 264–274. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.; Ren, X.; Zhao, T.; Li, Y.; Xiao, D.; Fang, D. Numerical and theoretical analysis of the dynamic mechanical behaviour of a modified rhombic dodecahedron lattice structure. Int. J. Mech. Mater. Des. 2020, 17, 271–283. [Google Scholar] [CrossRef]
- Yue, X.-Z.; Matsuo, K.; Kitazono, K. Compressive Behavior of Open-Cell Titanium Foams with Different Unit Cell Geometries. Mater. Trans. 2017, 58, 1587–1592. [Google Scholar] [CrossRef] [Green Version]
- Gibson, L.J. Mechanical Behavior of Metallic Foams. Annu. Rev. Mater. Sci. 2000, 30, 191–227. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Spierings, A.B.; Mohr, D. Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading. Acta Mater. 2016, 116, 14–28. [Google Scholar] [CrossRef]
- Erban, D.A.; Negru, R.; Srndan, S.; Belgiu, G.; Maravina, L. Numerical and experimental investigations on the mechanical prop-erties of cellular structures with open Kelvin cells. Mech. Adv. Mater. Struct. 2019, 28, 1367–1376. [Google Scholar] [CrossRef]
- Kraynik, A.M.; Reinelt, D.A.; Van Swol, F. Structure of Random Foam. Phys. Rev. Lett. 2004, 93, 208301. [Google Scholar] [CrossRef]
- Babaee, S.; Jahromi, B.H.; Ajdari, A.; Nayeb-Hashemi, H.; Vaziri, A. Mechanical properties of open-cell rhombic dodecahedron cellular structures. Acta Mater. 2012, 60, 2873–2885. [Google Scholar] [CrossRef]
- Hedayati, R.; Sadighi, M.; Mohammadi-Aghdam, M.; Zadpoor, A. Mechanical behavior of additively manufactured porous biomaterials made from truncated cuboctahedron unit cells. Int. J. Mech. Sci. 2016, 106, 19–38. [Google Scholar] [CrossRef]
- Yue, D.; Liang, H.; Xie, D.; Mao, N.; Zhao, J.; Tian, Z.; Wang, C.; Shen, L. Design and statistical analysis of irregular porous scaffolds for orthopedic reconstruction based on voronoi tessellation and fabricated via selective laser melting (SLM). Mater. Chem. Phys. 2020, 239, 121968. [Google Scholar]
- Zhang, J.; Wang, Z.; Zhao, L. Dynamic response of functionally graded cellular materials based on the Voronoi model. Compos. Part B Eng. 2016, 85, 176–187. [Google Scholar] [CrossRef]
- Ma, G.; Ye, Z.; Shao, Z. Modeling loading rate effect on crushing stress of metallic cellular materials. Int. J. Impact Eng. 2009, 36, 775–782. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Tran, P.; Harris, J.; Liu, Q.; Lu, G.; Ruan, D.; Faruque, O.; Brandt, M. The effect of topology on the quasi-static and dynamic behaviour of SLM AlSi10Mg lattice structures. Int. J. Adv. Manuf. Technol. 2021, 118, 4085–4104. [Google Scholar] [CrossRef]
- Kumar, S.; Wardle, B.L.; Arif, M.F.; Ubaid, J. Stress Reduction of 3D Printed Compliance-Tailored Multilayers. Adv. Eng. Mater. 2017, 20, 1700883. [Google Scholar] [CrossRef]
- Andrew, J.J.; Schneider, J.; Ubaid, J.; Velmurugan, R.; Gupta, N.K.; Kumar, S. Energy absorption characteristics of additively manufactured plate-lattices under low- velocity impact loading. Int. J. Impact Eng. 2020, 149, 103768. [Google Scholar] [CrossRef]
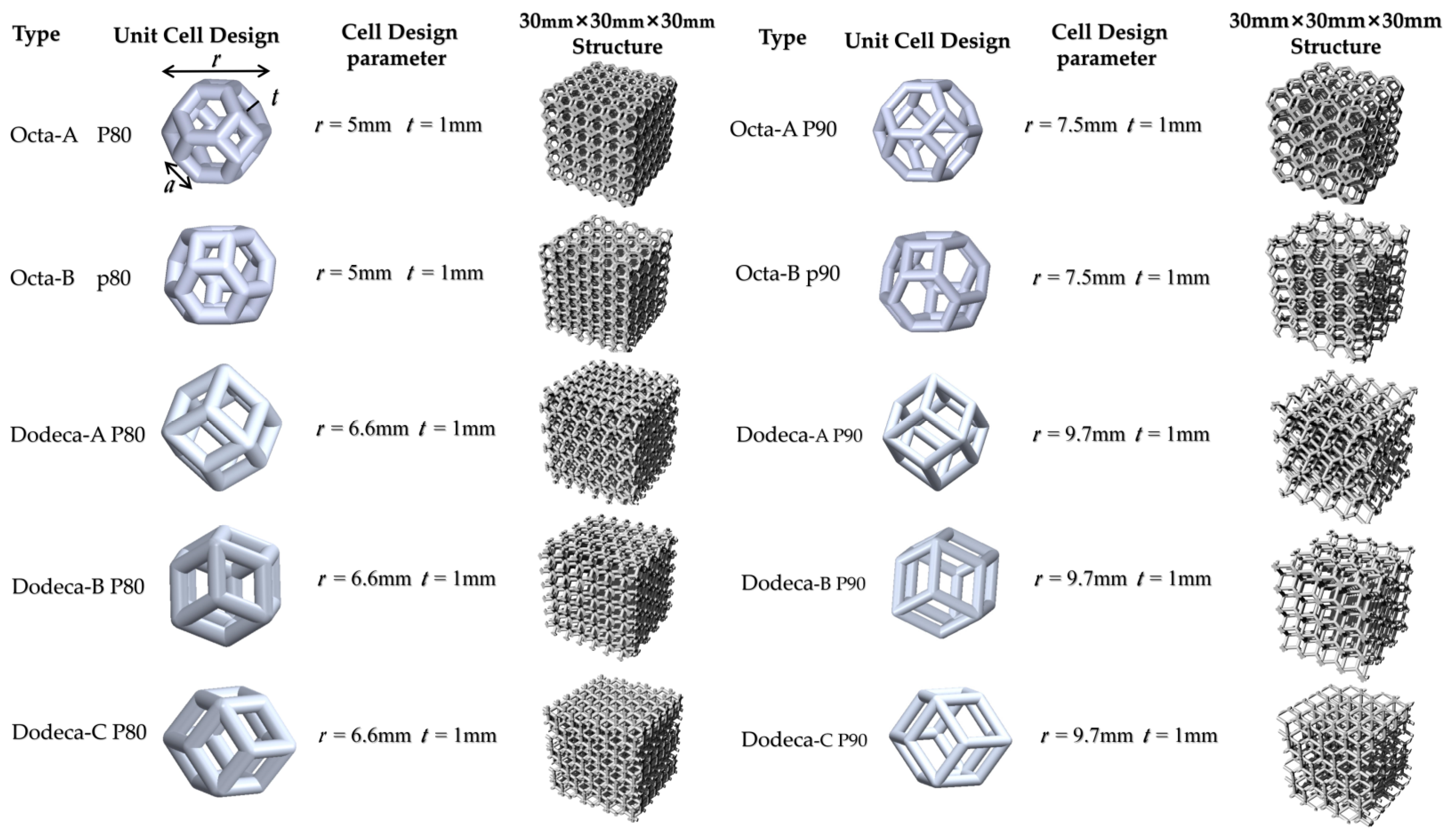



| Structure | Nominal Porosity (%) | True Porosity (%) | Unit Cell Size (mm) | Volume of Cellular Structures (mm3) | Number of Oblique Edges |
|---|---|---|---|---|---|
| Dodeca-A | 80 | 80.16 | 6.6 | 5356.726 | 12 |
| Dodeca-A | 90 | 89.87 | 9.7 | 2734.927 | 12 |
| Dodeca-B | 80 | 80.16 | 6.6 | 5356.729 | 18 |
| Dodeca-B | 90 | 89.87 | 9.7 | 2735.293 | 18 |
| Dodeca-C | 80 | 79.82 | 6.6 | 5449.094 | 24 |
| Dodeca-C | 90 | 89.56 | 9.7 | 2818.537 | 24 |
| Octa-A | 80 | 79.38 | 5 | 5568.376 | 24 |
| Octa-A | 90 | 89.95 | 7.5 | 2712.67 | 24 |
| Octa-B | 80 | 79.78 | 5 | 5458.301 | 18 |
| Octa-B | 90 | 89.53 | 7.5 | 2827.830 | 18 |
| Items | Values |
|---|---|
| Density | 2770 kg/m3 |
| Young’s modulus | 71,000 MPa |
| Poisson’s ratio | 0.33 |
| Tensile ultimate strength Tensile yield strength | 246.1 MPa 164.8 MPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, S.; Zhang, M.; Guo, S.; Hur, B.; Yue, X. Numerical Investigation of Impact Behavior of Strut-Based Cellular Structures Designed by Spatial Voronoi Tessellation. Metals 2022, 12, 1189. https://doi.org/10.3390/met12071189
Lu S, Zhang M, Guo S, Hur B, Yue X. Numerical Investigation of Impact Behavior of Strut-Based Cellular Structures Designed by Spatial Voronoi Tessellation. Metals. 2022; 12(7):1189. https://doi.org/10.3390/met12071189
Chicago/Turabian StyleLu, Songhao, Minghao Zhang, Shiyue Guo, Boyoung Hur, and Xuezheng Yue. 2022. "Numerical Investigation of Impact Behavior of Strut-Based Cellular Structures Designed by Spatial Voronoi Tessellation" Metals 12, no. 7: 1189. https://doi.org/10.3390/met12071189






