In Situ X-ray Radiography and Computational Modeling to Predict Grain Morphology in β-Titanium during Simulated Additive Manufacturing
Abstract
:1. Introduction
2. Experimental Setup
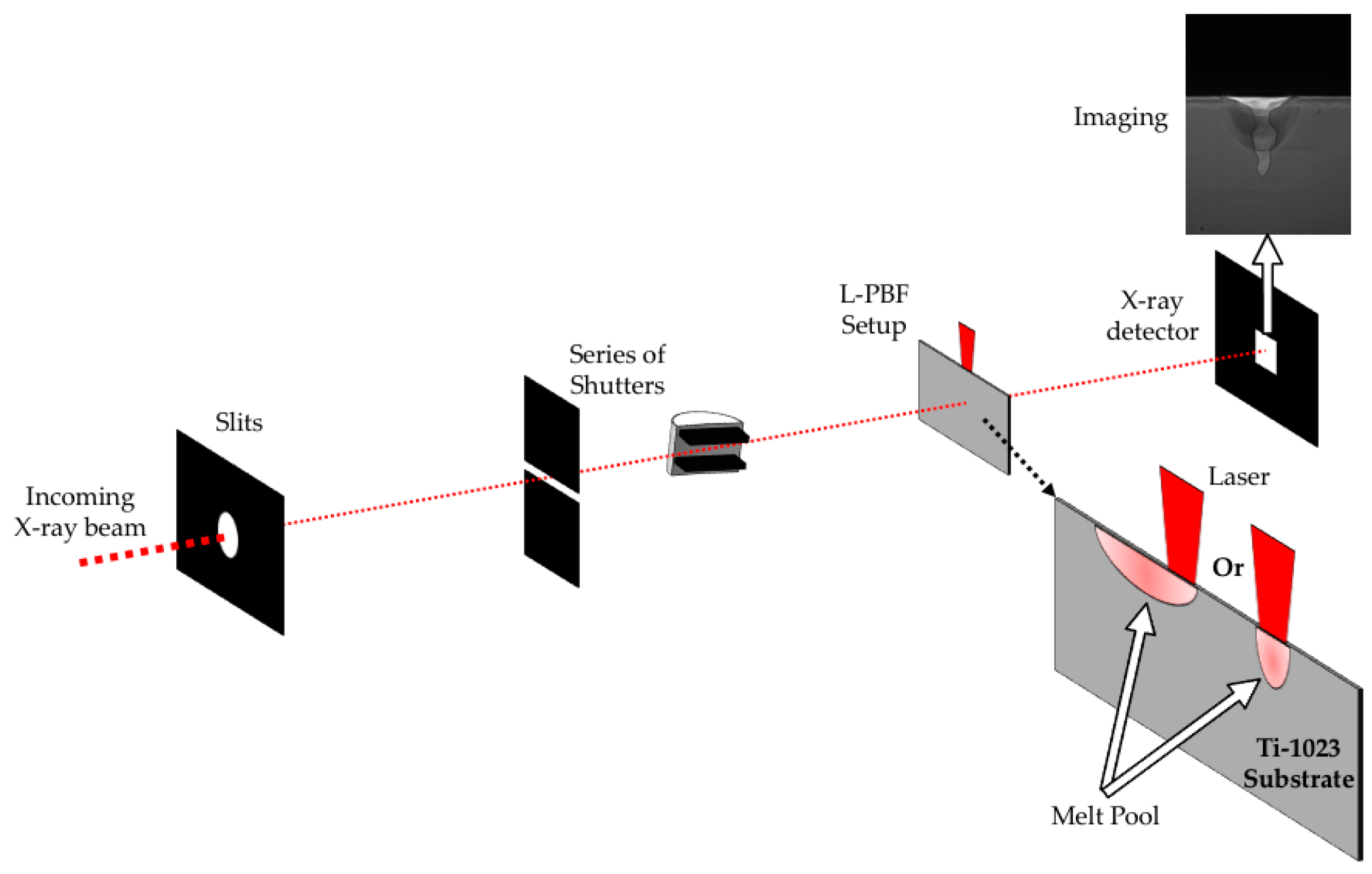
2.1. APS L-PBF Simulator and In Situ X-ray Radiography
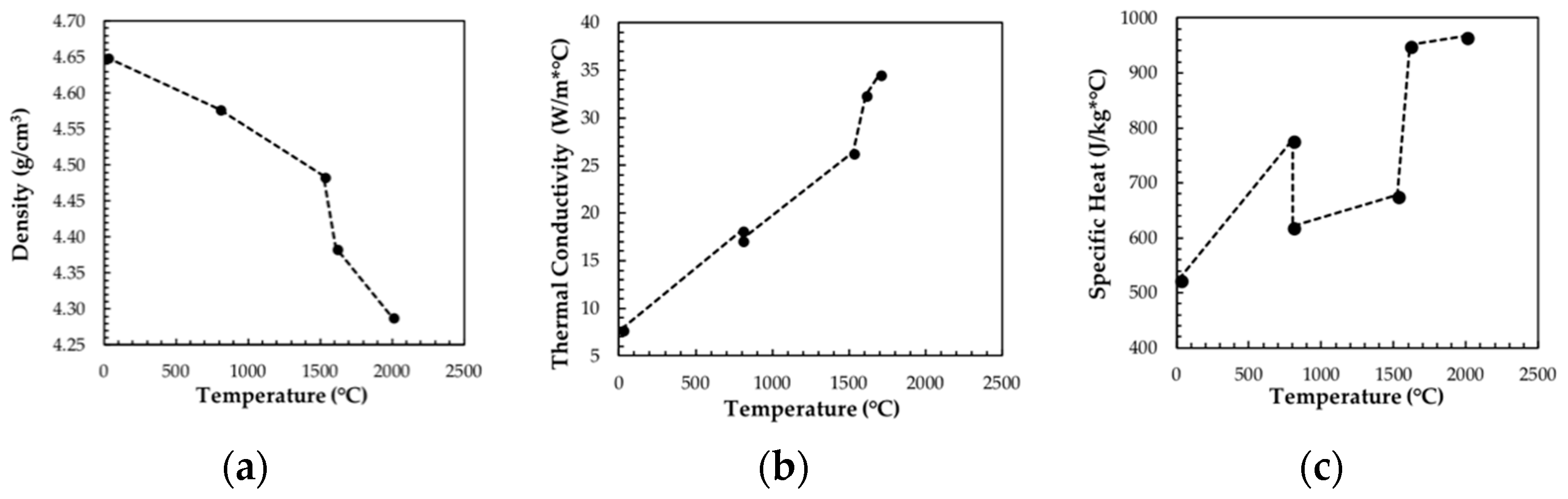
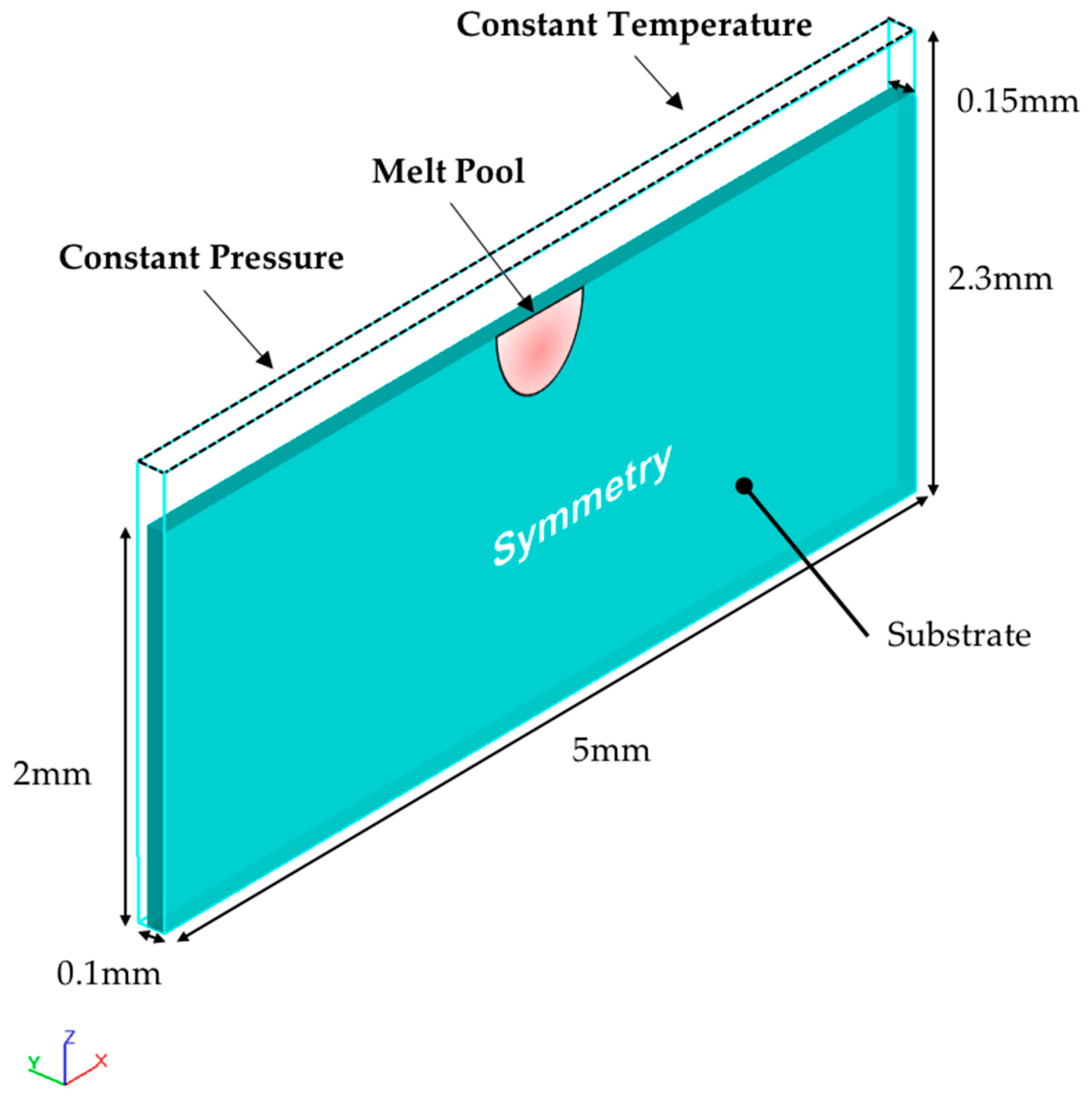
2.2. Model Setup and Inputs
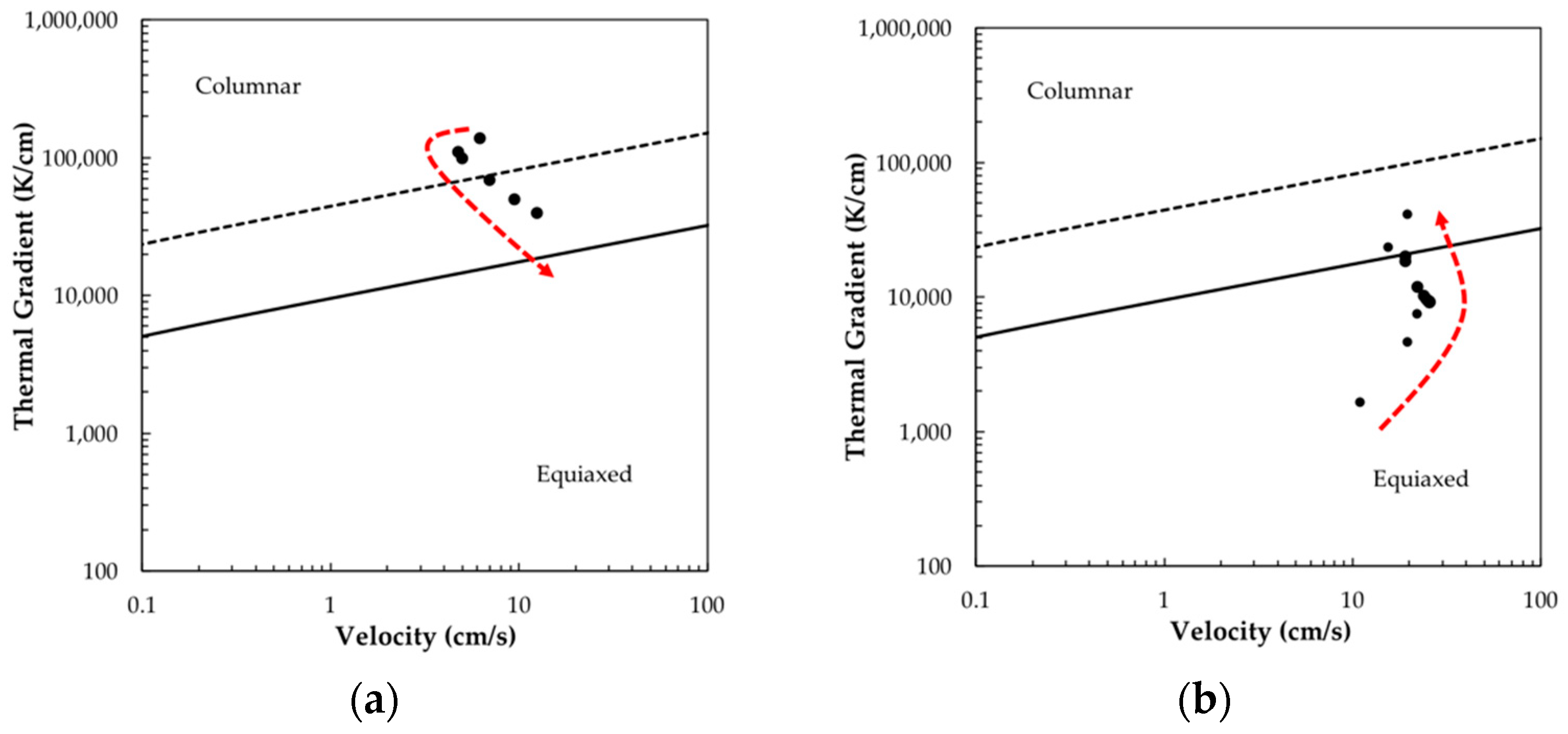
2.3. Columnar-to-Equiaxed Transition Model
3. Results and Discussion
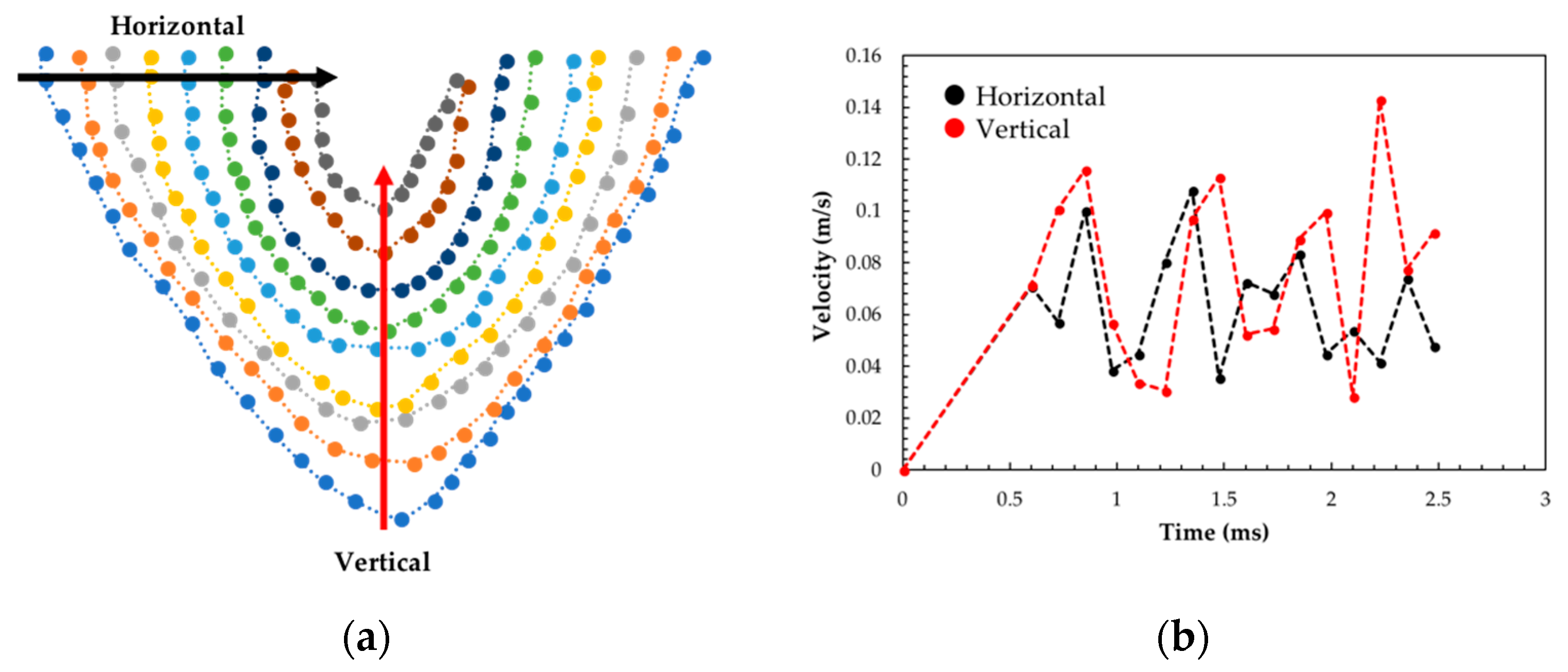
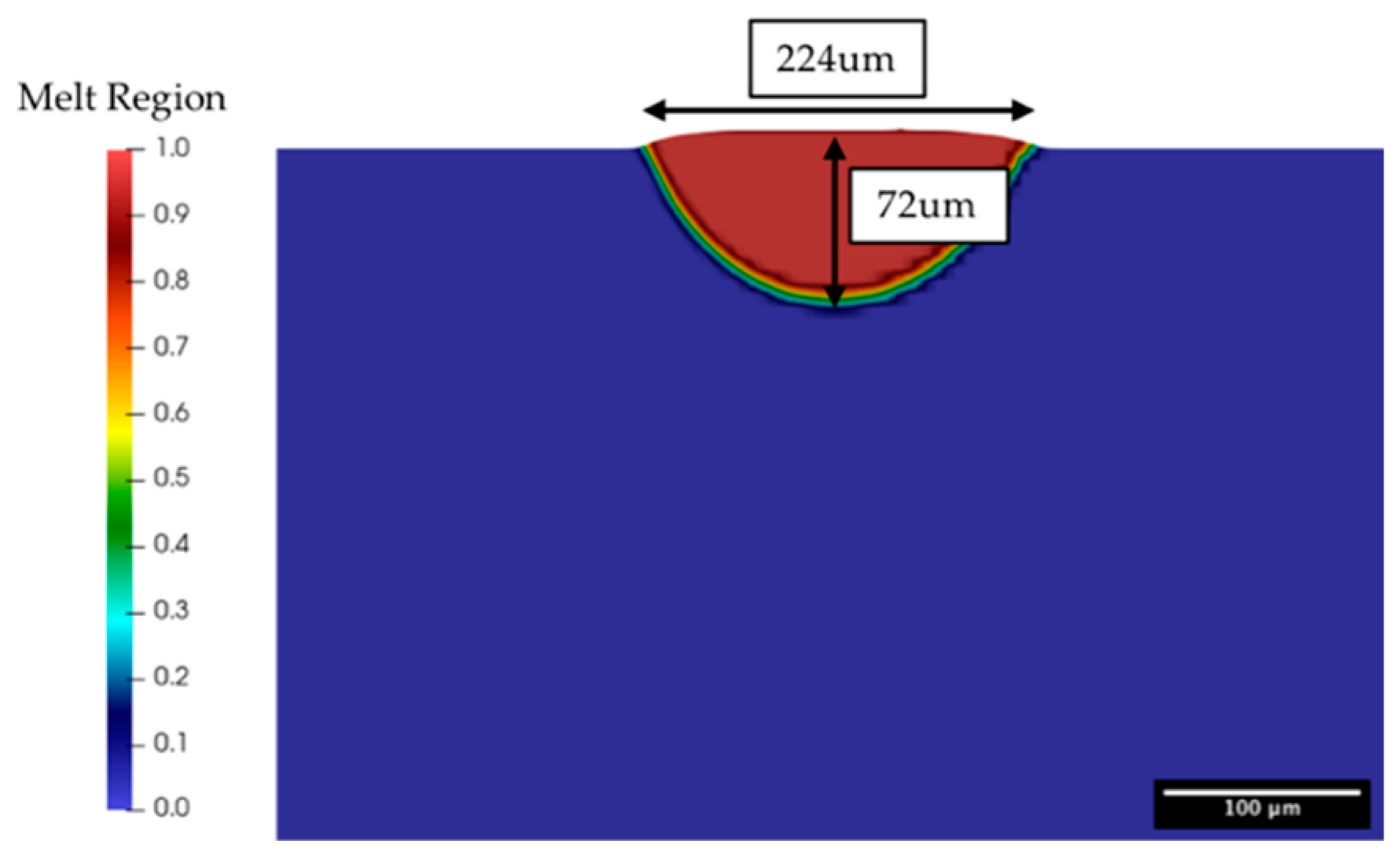
3.1. APS Experiment Melt Pool Tracking
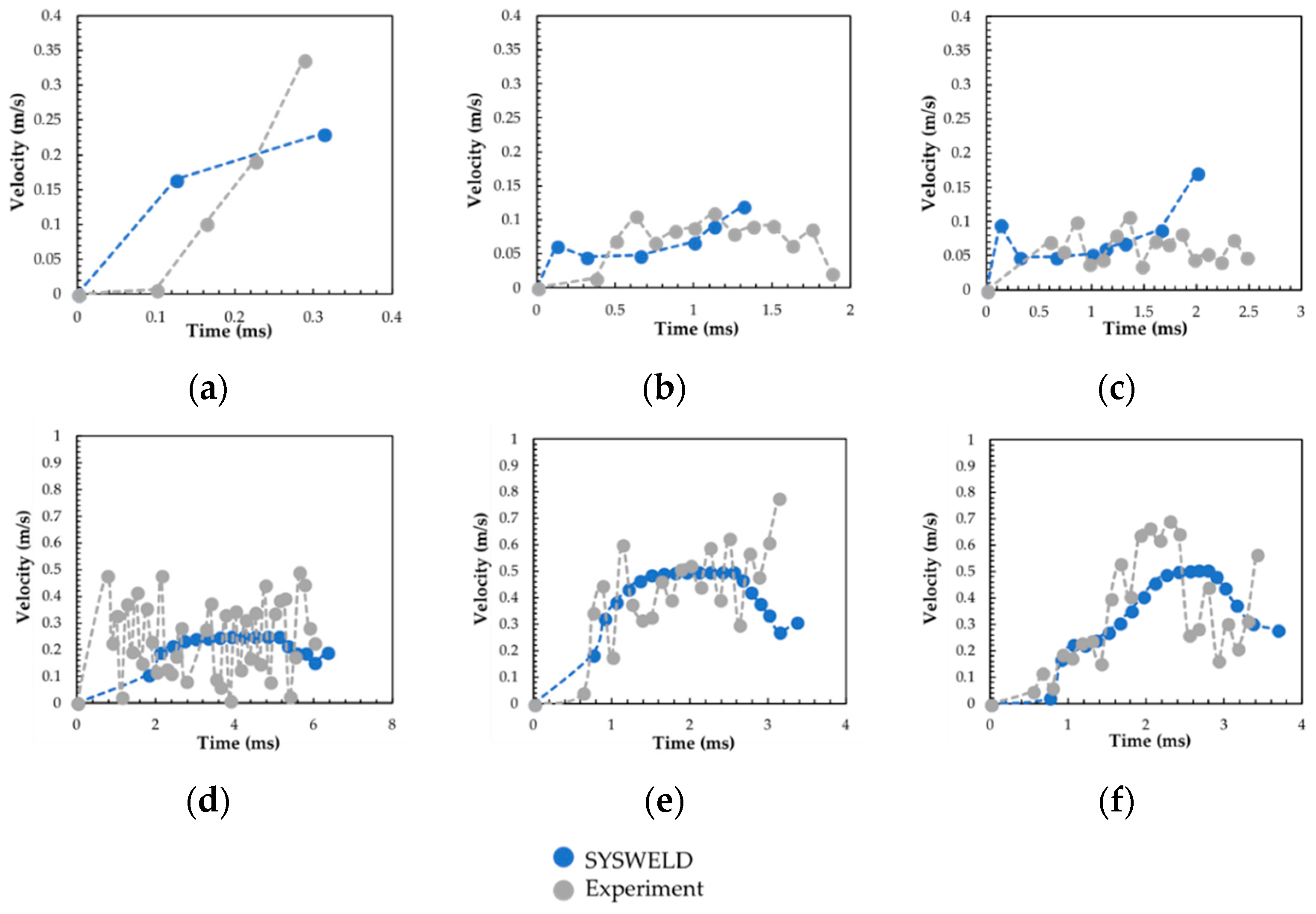
3.2. Melt-Pool Modeling
4. Conclusions
- (1)
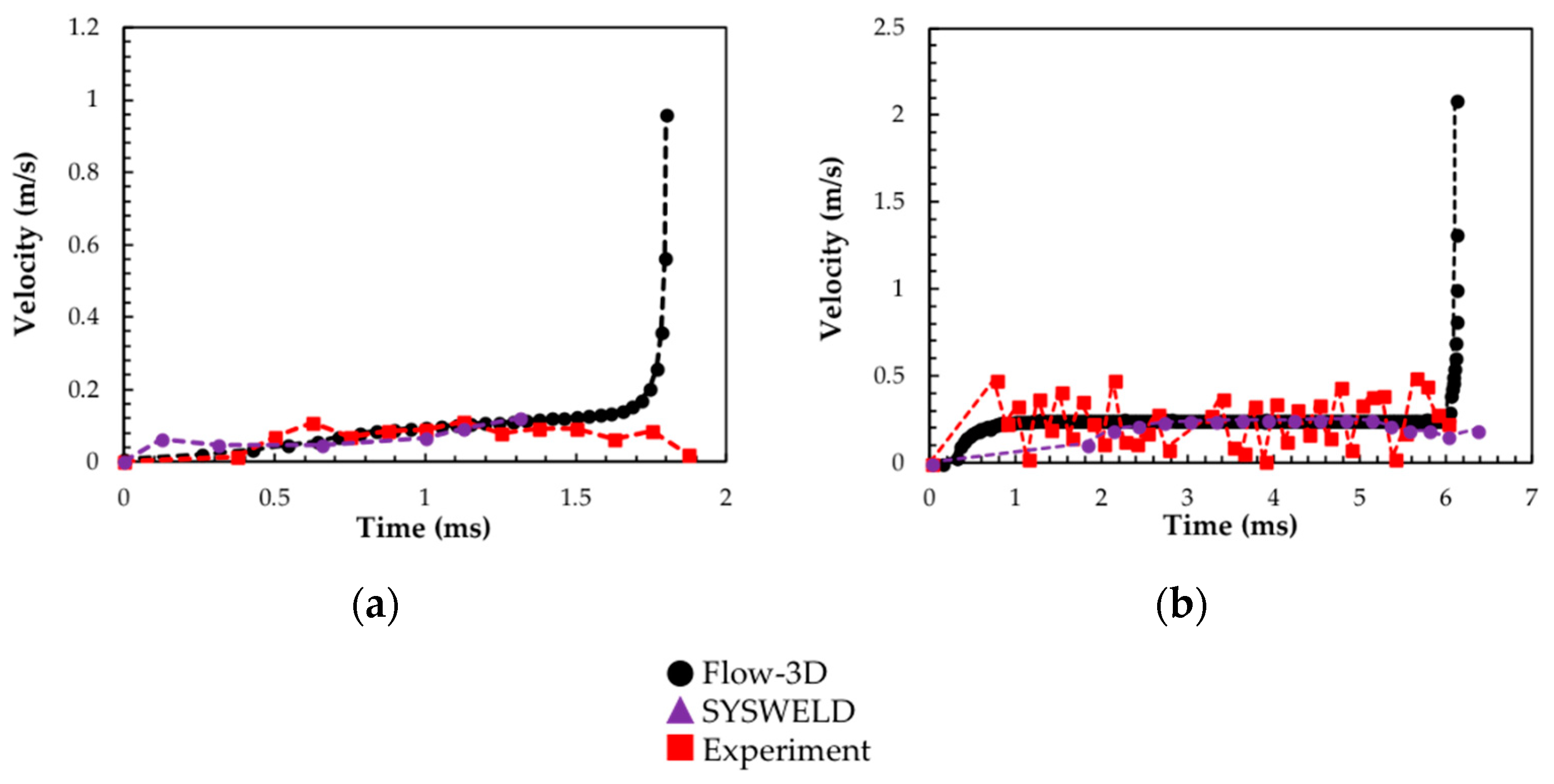
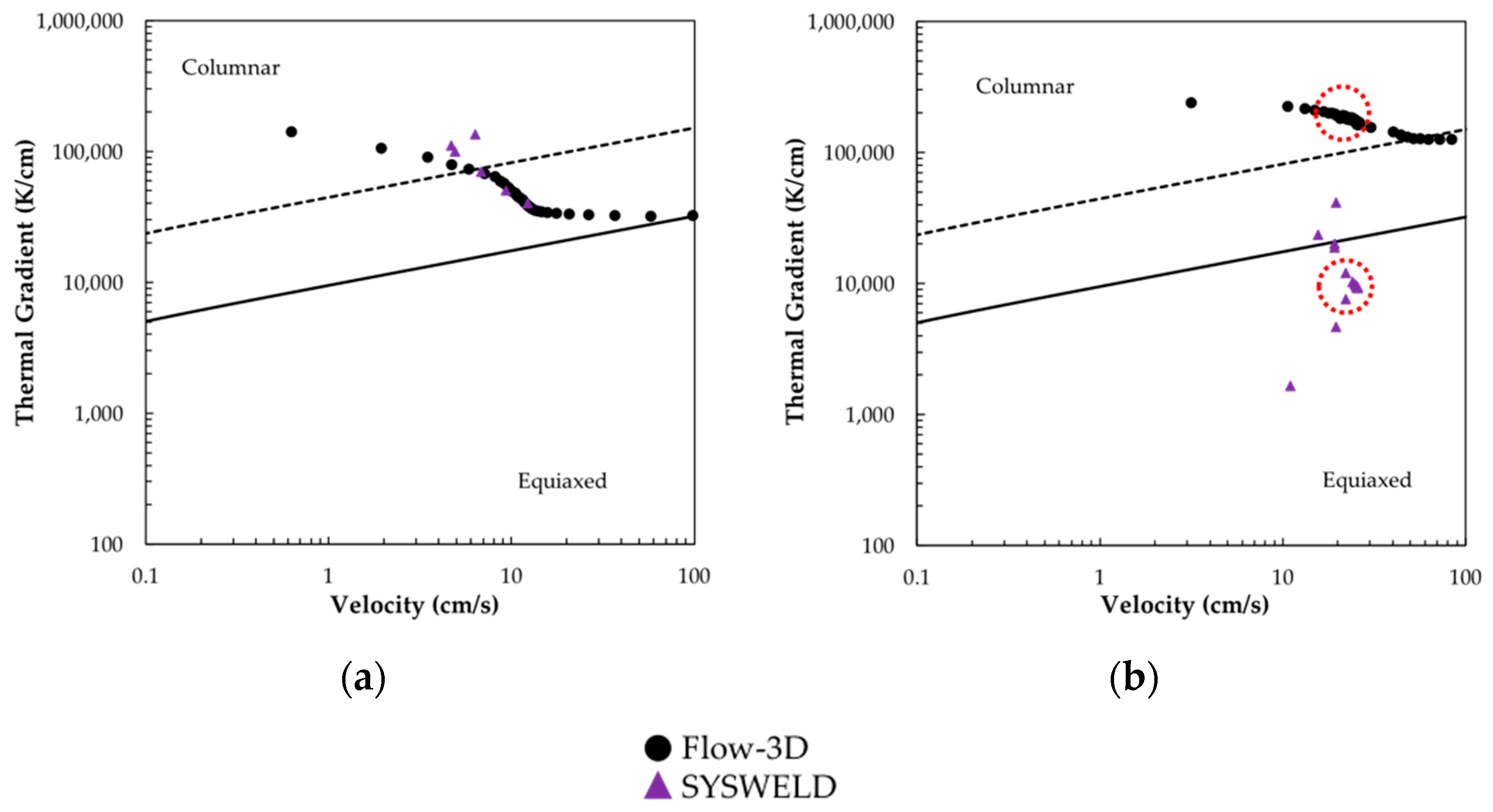
- For spot-melts, model predictions from more simplistic tools such as SYSWELD are able to match velocity profiles obtained from specialized AM-simulated experiments. However, the relatively coarse time-steps make it difficult to fully capture the initial, intermediate, and final stages of melt-pool solidification.
- (2)
- Final solidification phenomena known to occur in rapid solidification experiments, such as rapid acceleration of the solid–liquid interface, were undetectable with the utilized in situ synchrtoron x-ray imaging, but were predicted by FLOW-3D. This capability shows that high-fidelity models are able to provide insights into melt-pool solidification conditions that may not be detectable with some experimental setups.
- (3)
- G-V predictions of spot-melts from SYSWELD and FLOW-3D align with each other and experimental observations from other work. This is not true of raster simulations, where SYSWELD predicts G-V trends different from those of FLOW-3D and basic knowledge of melt-pool solidification. This presents a limitation of SYSWELD for predicting as-built grain morphologies using solidification maps.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duerig, T.W.; Terlinde, G.T.; Williams, J.C. Phase transformations and tensile properties of Ti-10V-2Fe-3AI. Met. Mater. Trans. A 1980, 11, 1987–1998. [Google Scholar] [CrossRef]
- Duerig, T.W.; Williams, J.C. Beta Titanium Alloys in the 80s: Proceedings of the Symposium; Metallurgical Society of AIME: Englewood, CO, USA, 1984; pp. 19–67. [Google Scholar]
- Lütjering, G.; Williams, J.C. Titanium, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007. [Google Scholar]
- Bermingham, M.; StJohn, D.; Krynen, J.; Tedman-Jones, S.; Dargusch, M. Promoting the columnar to equiaxed transition and grain refinement of titanium alloys during additive manufacturing. Acta Mater. 2019, 168, 261–274. [Google Scholar] [CrossRef]
- Roehling, T.T.; Shi, R.; Khairallah, S.A.; Roehling, J.D.; Guss, G.M.; McKeown, J.T.; Matthews, M.J. Controlling grain nucleation and morphology by laser beam shaping in metal additive manufacturing. Mater. Des. 2020, 195, 109071. [Google Scholar] [CrossRef]
- Qiu, C.; Ravi, G.; Attallah, M.M. Microstructural control during direct laser deposition of a β-titanium alloy. Mater. Des. 2015, 81, 21–30. [Google Scholar] [CrossRef]
- Zhu, Y.-Y.; Tang, H.-B.; Li, Z.; Xu, C.; He, B. Solidification behavior and grain morphology of laser additive manufacturing titanium alloys. J. Alloy. Compd. 2018, 777, 712–716. [Google Scholar] [CrossRef]
- Balla, V.K.; Das, M.; Mohammad, A.; Al-Ahmari, A.M. Additive Manufacturing of γ-TiAl: Processing, Microstructure, and Properties: Additive Manufacturing of γ-TiAl: Processing. Adv. Eng. Mater. 2016, 18, 1208–1215. [Google Scholar] [CrossRef]
- Kurzynowski, T.; Gruber, K.; Stopyra, W.; Kuźnicka, B.; Chlebus, E. Correlation between process parameters, microstructure and properties of 316 L stainless steel processed by selective laser melting. Mater. Sci. Eng. A 2018, 718, 64–73. [Google Scholar] [CrossRef]
- Liang, Y.-J.; Cheng, X.; Li, J.; Wang, H.-M. Microstructural control during laser additive manufacturing of single-crystal nickel-base superalloys: New processing–microstructure maps involving powder feeding. Mater. Des. 2017, 130, 197–207. [Google Scholar] [CrossRef]
- Yang, J.; Yu, H.; Yin, J.; Gao, M.; Wang, Z.; Zeng, X. Formation and control of martensite in Ti-6Al-4V alloy produced by selective laser melting. Mater. Des. 2016, 108, 308–318. [Google Scholar] [CrossRef]
- Zhai, Y.; Galarraga, H.; Lados, D.A. Microstructure, static properties, and fatigue crack growth mechanisms in Ti-6Al-4V fabricated by additive manufacturing: LENS and EBM. Eng. Fail. Anal. 2016, 69, 3–14. [Google Scholar] [CrossRef]
- Thijs, L.; Verhaeghe, F.; Craeghs, T.; Van Humbeeck, J.; Kruth, J.-P. A study of the microstructural evolution during selective laser melting of Ti–6Al–4V. Acta Mater. 2010, 58, 3303–3312. [Google Scholar] [CrossRef]
- Levkulich, N.; Semiatin, S.; Gockel, J.; Middendorf, J.; DeWald, A.; Klingbeil, N. The effect of process parameters on residual stress evolution and distortion in the laser powder bed fusion of Ti-6Al-4V. Addit. Manuf. 2019, 28, 475–484. [Google Scholar] [CrossRef]
- Saville, A.I.; Vogel, S.C.; Creuziger, A.; Benzing, J.T.; Pilchak, A.L.; Nandwana, P.; Klemm-Toole, J.; Clarke, K.D.; Semiatin, S.L.; Clarke, A.J. Texture evolution as a function of scan strategy and build height in electron beam melted Ti-6Al-4V. Addit. Manuf. 2021, 46, 102118. [Google Scholar] [CrossRef]
- Norsk Titanium Delivers First FAA-Certified, Additive Manufactured Ti64 Structural Aviation Components. Available online: http://www.norsktitanium.com/media/press/norsk-titanium-delivers-first-faacertified-additive-manufactured-ti64-structural-aviation-components (accessed on 20 October 2021).
- Zopp, C.; Blümer, S.; Schubert, F.; Kroll, L. Processing of a metastable titanium alloy (Ti-5553) by selective laser melting. Ain Shams Eng. J. 2017, 8, 475–479. [Google Scholar] [CrossRef] [Green Version]
- Schwab, H.; Palm, F.; Kühn, U.; Eckert, J. Microstructure and mechanical properties of the near-beta titanium alloy Ti-5553 processed by selective laser melting. Mater. Des. 2016, 105, 75–80. [Google Scholar] [CrossRef]
- Dehoff, R.; Kirka, M.M.; Sames, W.J.; Bilheux, H.; Tremsin, A.; Lowe, L.E.; Babu, S. Site specific control of crystallographic grain orientation through electron beam additive manufacturing. Mater. Sci. Technol. 2014, 31, 931–938. [Google Scholar] [CrossRef]
- Plotkowski, A.; Ferguson, J.; Stump, B.; Halsey, W.; Paquit, V.; Joslin, C.; Babu, S.; Rossy, A.M.; Kirka, M.; Dehoff, R. A stochastic scan strategy for grain structure control in complex geometries using electron beam powder bed fusion. Addit. Manuf. 2021, 46, 102092. [Google Scholar] [CrossRef]
- Kobryn, P.; Semiatin, S. Microstructure and texture evolution during solidification processing of Ti–6Al–4V. J. Mater. Process. Technol. 2003, 135, 330–339. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components–Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Al-Bermani, S.S.; Blackmore, M.L.; Zhang, W.; Todd, I. The Origin of Microstructural Diversity, Texture, and Mechanical Properties in Electron Beam Melted Ti-6Al-4V. Met. Mater. Trans. A 2010, 41, 3422–3434. [Google Scholar] [CrossRef]
- Zhao, C.; Fezzaa, K.; Cunningham, R.W.; Wen, H.; De Carlo, F.; Chen, L.; Rollett, A.D.; Sun, T. Real-time monitoring of laser powder bed fusion process using high-speed X-ray imaging and diffraction. Sci. Rep. 2017, 7, 3602. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, N.; Dehoff, R.; Pannala, S.; Simunovic, S.; Kirka, M.; Turner, J.; Carlson, N.; Babu, S.S. Numerical modeling of heat-transfer and the influence of process parameters on tailoring the grain morphology of IN718 in electron beam additive manufacturing. Acta Mater. 2016, 112, 303–314. [Google Scholar] [CrossRef] [Green Version]
- Mills, K.C. Recommended Values of Thermophysical Properties for Selected Commercial Alloys; Woodhead: Cambridge, UK, 2002. [Google Scholar] [CrossRef]
- Thermo-Calc Software TCTI/Ti-Alloys Database Version 3.
- Bayat, M.; Thanki, A.; Mohanty, S.; Witvrouw, A.; Yang, S.; Thorborg, J.; Tiedje, N.S.; Hattel, J. Keyhole-induced porosities in Laser-based Powder Bed Fusion (L-PBF) of Ti6Al4V: High-fidelity modelling and experimental validation. Addit. Manuf. 2019, 30, 100835. [Google Scholar] [CrossRef]
- Kurz, W.; Giovanola, B.; Trivedi, R. Theory of microstructural development during rapid solidification. Acta Met. 1986, 34, 823–830. [Google Scholar] [CrossRef]
- Gäumann, M.; Bezençon, C.; Canalis, P.; Kurz, W. Single-crystal laser deposition of superalloys: Processing–microstructure maps. Acta Mater. 2001, 49, 1051–1062. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y. Mesoscale multi-physics simulation of rapid solidification of Ti-6Al-4V alloy. Addit. Manuf. 2018, 25, 551–562. [Google Scholar] [CrossRef]
- Rolchigo, M.; LeSar, R. Modeling of binary alloy solidification under conditions representative of Additive Manufacturing. Comput. Mater. Sci. 2018, 150, 535–545. [Google Scholar] [CrossRef]
- Hunt, J. Steady state columnar and equiaxed growth of dendrites and eutectic. Mater. Sci. Eng. 1984, 65, 75–83. [Google Scholar] [CrossRef]
- McKeown, J.T.; Zweiacker, K.; Liu, C.; Coughlin, D.R.; Clarke, A.J.; Baldwin, J.K.; Gibbs, J.; Roehling, J.D.; Imhoff, S.D.; Gibbs, P.J.; et al. Time-Resolved In Situ Measurements During Rapid Alloy Solidification: Experimental Insight for Additive Manufacturing. JOM 2016, 68, 985–999. [Google Scholar] [CrossRef]
- McKeown, J.T.; Kulovits, A.K.; Liu, C.; Zweiacker, K.; Reed, B.W.; LaGrange, T.; Wiezorek, J.M.; Campbell, G.H. In situ transmission electron microscopy of crystal growth-mode transitions during rapid solidification of a hypoeutectic Al–Cu alloy. Acta Mater. 2014, 65, 56–68. [Google Scholar] [CrossRef]
- He, X.; Fuerschbach, P.W.; DebRoy, T. Heat transfer and fluid flow during laser spot welding of 304 stainless steel. J. Phys. D Appl. Phys. 2003, 36, 1388–1398. [Google Scholar] [CrossRef]
- He, X.; Elmer, J.W.; DebRoy, T. Heat transfer and fluid flow in laser microwelding. J. Appl. Phys. 2005, 97, 084909. [Google Scholar] [CrossRef]
- Lienert, T.; Siewert, T.; Babu, S.; Acoff, V. (Eds.) Fundamentals of Weld Solidification. In Welding Fundamentals and Processes; ASM International: Almere, The Netherlands, 2011; pp. 96–114. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A.T.; Rubenchik, A.; King, W.E. Laser powder-bed fusion additive manufacturing: Physics of complex melt flow and formation mechanisms of pores, spatter, and denudation zones. Acta Mater. 2016, 108, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Polonsky, A.T.; Raghavan, N.; Echlin, M.P.; Kirka, M.M.; Dehoff, R.R.; Pollock, T.M. 3D Characterization of the Columnar-to-Equiaxed Transition in Additively Manufactured Inconel 718. In Superalloys 2020; Tin, S., Hardy, M., Clews, J., Cormier, J., Feng, Q., Marcin, J., O’Brien, C., Suzuki, A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 990–1002. [Google Scholar] [CrossRef]



| Experiment | Power (W) | Travel Speed (m/s) or Dwell Time (ms) | Energy Input (J/m) |
|---|---|---|---|
| Spot-melt | 82 | 1 | - |
| Spot-melt | 139 | 1 | - |
| Spot-melt | 197 | 1 | - |
| Raster | 53.5 | 0.25 | 214 |
| Raster | 82 | 0.50 | 164 |
| Raster | 139 | 0.50 | 278 |
| Property | Value | Reference |
|---|---|---|
| Surface Tension Coefficient | 1.5 N/m | [28] |
| Surface Tension Temperature Dependence | −2.6 × 10−4 N/m/K | |
| Solidus Temperature | 1798 K | [27] |
| Liquidus Temperature | 1883 K | |
| Vaporization Temperature | 3315 K | [28] |
| Latent Heat of Melting | 0.286 MJ/kg | |
| Latent Heat of Vaporization | 9.7 MJ/kg |
| Model Input | Value | Reference | |
|---|---|---|---|
| Solute Diffusivity | 7.9 × 10−9 m/s2 | [31] | |
| Gibbs–Thomson Coefficient | 5 × 10−7 m·K | [32] | |
| Nucleation Undercooling | 5 K | ||
| Nucleation Density | 1× 1015 nuclei/m3 | ||
| m | Vanadium | −4.744 K/wt.% | [27] |
| Iron | −12.841 K/wt.% | ||
| Aluminum | −5.932 K/wt.% | ||
| k | Vanadium | 0.756 | [27] |
| Iron | 0.317 | ||
| Aluminum | 0.894 | ||
| 0.0066 | [33] | ||
| 0.66 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasien, C.; Saville, A.; Becker, C.G.; Klemm-Toole, J.; Fezzaa, K.; Sun, T.; Pollock, T.; Clarke, A.J. In Situ X-ray Radiography and Computational Modeling to Predict Grain Morphology in β-Titanium during Simulated Additive Manufacturing. Metals 2022, 12, 1217. https://doi.org/10.3390/met12071217
Jasien C, Saville A, Becker CG, Klemm-Toole J, Fezzaa K, Sun T, Pollock T, Clarke AJ. In Situ X-ray Radiography and Computational Modeling to Predict Grain Morphology in β-Titanium during Simulated Additive Manufacturing. Metals. 2022; 12(7):1217. https://doi.org/10.3390/met12071217
Chicago/Turabian StyleJasien, Chris, Alec Saville, Chandler Gus Becker, Jonah Klemm-Toole, Kamel Fezzaa, Tao Sun, Tresa Pollock, and Amy J. Clarke. 2022. "In Situ X-ray Radiography and Computational Modeling to Predict Grain Morphology in β-Titanium during Simulated Additive Manufacturing" Metals 12, no. 7: 1217. https://doi.org/10.3390/met12071217
APA StyleJasien, C., Saville, A., Becker, C. G., Klemm-Toole, J., Fezzaa, K., Sun, T., Pollock, T., & Clarke, A. J. (2022). In Situ X-ray Radiography and Computational Modeling to Predict Grain Morphology in β-Titanium during Simulated Additive Manufacturing. Metals, 12(7), 1217. https://doi.org/10.3390/met12071217






