Delamination of Fibre Metal Laminates Due to Drilling: Experimental Study and Fracture Mechanics-Based Modelling

Abstract

Fibre metal laminates (FML) are significantly adopted in the aviation industry due to their convenient combination of specific strength, impact resistance and ductility. Drilling of such materials is a regular pre-requisite which enables assembly operations, typically through rivet joining. However, the hole-making operation is of increased complexity due to the dissimilarity of the involved materials, often resulting in defects (i.e., material interface delamination), which can significantly compromise the otherwise excellent fatigue strength. This work explores the potential of three different drill geometries, operating under variable cutting speeds and feeds on CFRP-AA laminates. In addition, the usage of sacrificial back support is investigated and cutting load, surface roughness and delamination extension are examined. In order to predict delamination occurrence, ADCB tests are performed, enabling the calculation of fracture energy threshold. Drill geometry presents a very significant influence on delamination occurrence. The usage of specific step-tools with secondary cutting edge showed superior performance. Despite its simplicity, the applied critical force threshold model was able to successfully predict interface delamination with good accuracy.

1. Introduction

Fibre metal laminates (FML) are hybrid materials comprised of alternating metal sheet and fibre composite layers, that can be bonded in distinct sequences. Unlike hybrid multi-material stacks, in which thicker composite and metal layers are simply stacked and fastened by means of rivets, adhesive joints or bolted connections, the FML layers’ thickness is typically less than 1 mm and consolidated through hot-curing cycles [1,2]. The superior performance of the laminate combination when compared to the isolated composite and metallic materials is highly relevant in structural applications, such as the transportation sector, where high specific strength is required, while also maintaining good impact and bending resistance [3,4]. Moreover, when such materials are adopted in the aviation industry, energy savings of approximately 30% are achieved [5,6]. Effectively illustrating the FML expression in aircraft applications and its increasing adoption [7] is the excellent fatigue strength, damage tolerance and overall durability of these materials, due to fibres acting as a barriers, thus delaying metal crack propagation [8]. Furthermore, worth mentioning is the good thermal insulation, corrosion and flame resistance properties of such materials [7,9].

FML can be currently manufactured in near-net shape geometries, such as large fuselage panels and stringers in aeronautics and also complex-shaped floor assemblies in the automotive industry [10]. Nonetheless, the fastening of multiple components relies mostly on mechanical joints, such as rivets or bolts, which can amount up to 3 million in a commercial aircraft [11]. Hole-making is, therefore, intensively performed for parts assembly, enabling riveting of aircraft panels such as the fuselage, wings and stabilizers [12,13] and despite the existent non-conventional feasible alternatives, such as laser machining and water-jet cutting, drilling remains the most employed technique [14]. The heterogeneity of FML allied to the highly abrasive properties of fibre reinforcement make drilling operations a challenging task. Their success may be compromised by simultaneous occurrence of (i) the well-known entry (peel-up) and exit (push-out) delamination, matrix thermal damage, fibre pull out and formation of abrasive fibre particles in composite layers as well as (ii) strain-hardening, continuous chip formation and thermal softening in the metal layers [15,16,17].

The lack of research regarding drilling operations on FML is evidenced by Bonhin et al. [16], especially in what concerns aluminium alloy (AA) and carbon-fibre-reinforced polymers (CFRP) configurations with thermoset matrices. To the authors’ knowledge, no studies have been performed in AA-CFRP laminates with thermoplastic matrices. The enhanced sustainability of the thermoplastic polymers (promoted by their improved recyclability) has encouraged the increasing usage of thermoplastic-based FML in relevant sectors, such as the aeronautical industry. Ekici et al. [18] experimentally analysed hole quality and delamination on AA-CFRP material samples, using Physical Vapour Deposition (PVD)-coated and uncoated drills. Despite the little number of holes each drill performed, the authors found that the uncoated condition (carbide) outperforms (PVD) coated drills in terms of entry delamination and hole nominal size. Sridhar et al. [19] systematically analysed the influence of operative conditions on drilling performance indicators such as thrust force and roughness, being able to identify ideal cutting parameters for AA-CFRP laminates using a conventional drill geometry. Despite the more intricate process kinematics of helical milling when compared to drilling, Bolar et al. [20] report advantages of the former, concerning cutting load, thermal impact, chip evacuation and hole nominal size. The implementation of analytic/numerical models capable of delamination prediction is of key relevance for both FML processing/assembly and drill tool manufacturers. Although some work can be found for CFRP materials, no data are available regarding these novel AA-CFRP material configurations. Feito et al. [21] compare the predictability of both complete simulation of a drilling operation with a simplistic model, in which the drill acts as a punch that pierces the laminate. The latter yields very reasonable cost-effective results with slight overestimation of delamination factor, setting upper limits that are highly valuable as support decision techniques.

2. Materials and Methods

This work focuses on the assessment of three distinct drill geometries with regard to their cutting performance of AA-CFRP hybrid laminates, through conventional single-step drilling operations. Roughness measurement and load monitoring were carried out for distinct sets of cutting parameters on each geometry. Delamination, which may account for 60% of the rejected parts [22] is thoroughly analysed and a critical load threshold was estimated for its occurrence, based on delamination modelling of AA-CFRP interface through asymmetric double cantilever beam experimental testing procedure. Previous knowledge of the critical loads associated with the drilling operation is highly convenient in the design and selection of appropriate tooling solutions for hole quality compliance.

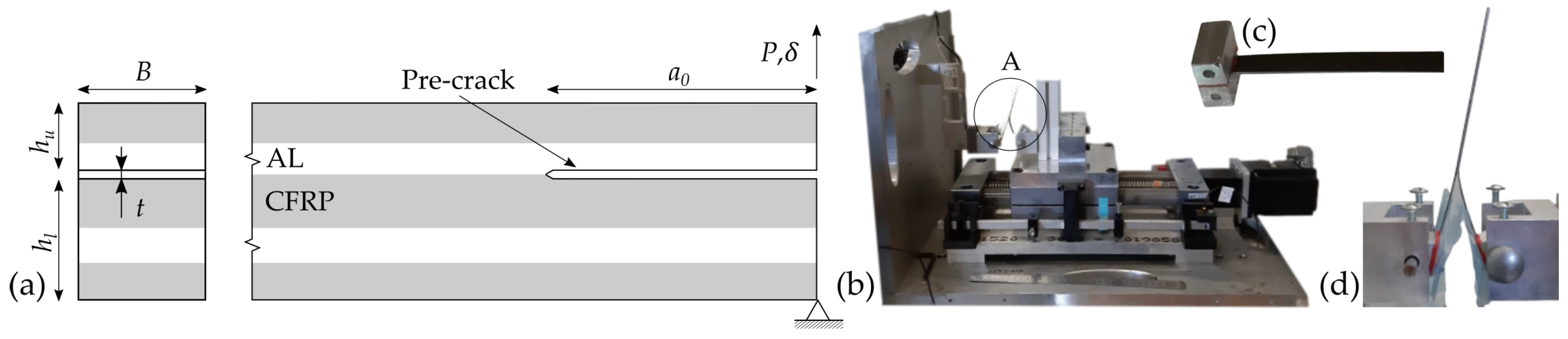
Specimens were built from CFRP and AA, with a stacking configuration of three CFRP layers (two external, one internal) and two internal aluminium layers, as illustrated in Figure 1a. The CFRP layers consisted of four 0.13 mm thick prepreg plies for the internal CFRP layer and three of the same plies for the external CFRP layers. Each aluminium layer was composed of 0.2 mm thick AA 5754 sheet. The composite material was constituted by polyamide 6 (PA 6) thermoplastic matrix reinforced by uni-directional carbon fibre with a volume fraction of 48.5%. Layer adhesion was promoted using conventional pre-treatment techniques such as degreasing and laser texturing of the metallic sheets. The laminate was submitted to a hot plate press curing process at a temperature interval between 240 and 280 °C and a pressure of 2 to 6 bar. Fibre direction was kept the same in all composite layers (uni-directional). Rectangular-shaped plates (240 × 250 mm${}^2$) were manufactured, with a resulting thickness (post-curing) of 1.2mm, which were posteriorly cut into 40 × 225 mm${}^2$ strips.

Table 1. Mechanical properties of the AA and CFRP separate materials.

Materials	AA 5754	CFRP (PA 6)
Density [g/cm${}^3$]	2.67	1.45
Young’s modulus [GPa]	65-75	100
Tensile strength [MPa]	200-350	1910
Strain at fracture [%]	<25	1.76

exhibits the mechanical properties of each material, according to the respective datasheets [23,24]. The experimental tests were conducted in a DMG Mori DMU60eVo series machining centre (25 kW), equipped with a piezoeletric dynamometer (Kistler 9272) and a signal amplifier (Kistler 5070A), connected to a data aquisition system (Advantech USB4711). A clamping system was developed for fixation of the material strips to the load cell, enabling drilling operations with and without sacrificial back support. The laminate strip is secured in-between two circular plates (top and bottom, refer to Figure 1b,c) which have a centre hole ($\varphi$ 36 mm), enabling the drilling operation and placement of a PTFE cylinder under the laminates for sacrificial back support (when used). A constant torque was applied on the bolts which hold the top plate against the material and lower plate. With regard to the cutting tools, diamond-coated (through Chemical Vapour Deposition, CVD) tungsten carbide drills with a diameter of 6 mm were employed. This drill material and coating configuration has been increasingly used in the hole-making of hybrid materials [25,26]. Moreover, three different drill geometries were tested: (i) a conventional drill geometry (herein referred to as CNV) with a 120° point angle, 30° helix angle, 20° rake angle and 10° clearance angle, refer to Figure 1d; (ii) a chip-breaking drill geometry (herein referred to as CBR) identical to CNV, with v-shaped grooves on the principal cutting edge periphery, refer to Figure 1e; (iii) a double-point angle tool (herein referred to as 2PA) also identical to the CNV with a 60° secondary point angle (2:1 ratio) and the same geometry as the previous tools, refer to Figure 1f.

Despite the constant search for novel drill geometries capable of generating fewer defects, the conventional drill geometry (such as the CNV in the current study) still constitutes a widely employed solution, which in this work has been used for reference/control and comparison with other geometries. It is also relevant to note that their performance can sometimes match or exceed newer, more intricate geometries regarding drilled hole quality [27]. Diamond-coated double-point angle drills, such as the considered 2PA, can be effectively employed in hole drilling of CFRP materials given the consequent action of lower cutting forces on the drill step (secondary cutting edge), that is mainly responsible for the final surface condition of the drilled hole [28]. Their overall good performance has motivated its study in fibre metal laminated hole drilling. With regard to chip-breaking features on drills (such as the considered CBR drill) the goal is to promote more efficient chip evacuation by creating grooves on the drill geometry (typically on principal cutting edge) capable of chip segmentation and width dividing, thus minimizing load and torque. Such concern is particularly relevant when drilling materials with thermoplastic resin (such as PA 6) which unlike the often employed thermoset resins (i.e., epoxy) promotes long chip morphology rather than fragmented chips. By dividing the chip width, a more convenient scenario of chip removal could be attained (i.e., more fragile resultant split chips, clogging minimization at flute). Moreover, in order to avoid excessive friction of the chip with the newly generated hole surface, the groove has been positioned at the cutting edge margin in order to act as a chip relief that tentatively minimizes delamination due to smaller chip-hole contact. Cutting parameters testing range was selected based on the literature and tool manufacturer indications for laminate materials.

Table 2. Variables and respective levels used for cutting parameter assessment in experimental drilling operation tests, considering a full factorial testing plan.

Variables	Levels
Cutting speed [m/min]	80	100	120
Feed [mm/rev]	0.03	0.05	0.07
Drill geometry	CNV	CBR	2PA
Back support	with	without	-

illustrates the tested levels of each considered variable. The full combination of parameters was tested using a random order generated by the Response Surface Methodology (RSM) Design Expert 13 software. Moreover, the operative conditions’ influence on cutting load, roughness and delamination was investigated through analysis of variance (ANOVA). In order to mitigate the occurrence of wear mechanisms, each drill performed a maximum of 20 holes.

Delamination defects were observed through radiographic image analysis, using Satelec X-Mind X-Ray generator and a Kodak RVG 5100 digital sensor. For this, the samples were submitted to a diidomethane bath for a period of 30 min, which enables contrast creation between delaminated and non-delaminated zones. A fixed exposure time of 0.16 s and a radiographic contrast of 70 kVp were selected. The obtained X-ray images were post-processed (converted into binary maps) allowing for delamination assessment and quantification, using the the criteria shown in Equations (1)–(3), where: $D_{max}$ and $A_{max}$ correspond to the maximum diameter of the delamination area and its area, respectively; $A_d$ to the actual delamination area; $D_{nom}$ and $A_{nom}$ to the nominal hole diameter and area, respectively. For the calculation of the delamination factors, a Matlab script capable of measuring $A_{max}$ and $D_{max}$ from the previously generated binary maps was used. This method ensures control process repeatability and minimization of data analysis effort.

$$F_d=D_{max}/D_{nom}$$

(1)

$$F_a=A_d/A_{nom}$$

(2)

Although the diameter-based ($F_d$) and area-based ($F_a$) delamination factors are the most employed criteria, they do not fully portray the drilled hole quality [11]. The diameter-based delamination factor ($F_d$) may account for the same delamination values (same maximum diameter around hole), for instance, in two very different scenarios: (i) whole delamination of a full annular section area or (ii) crack delamination of a crack (very small area). Similar interpretation errors can occur when considering an area-based delamination factor, given that (i) uniform damage and (ii) uniform damage with small cracks may result in the same area. In sum, whereas $F_d$ accounts only for the delamination maximum extent in the radial direction, $F_a$ cannot account for crack delamination, prone to occur in CFRP, as only the area is used for its calculation. For this reason, an adjusted delamination factor $F_{da}$, proposed by Davim et al. [29] has been used. It tends to $F_d^2$ values with uniformly distributed delamination and to $F_d$ values when it is strongly directional, allowing for a more accurate estimate of delamination shape and its extension.

$$F_{da}=F_d+\frac{A_d}{(A_{max}-A_{nom})}(F_d^2-F_d)$$

(3)

With regard to roughness analysis, it was optically estimated using the 3D measurement system (Alicona Infinite Focus SL). A three-measurement average was calculated for each drilled hole.

Delamination Modelling

Delamination has long been viewed from a fracture mechanics perspective as a crack propagation phenomenon and the critical force at its onset ($C_F$) can be calculated according to Equation (4), proposed by Cheng et al. [15], assuming a point load applied on an isotropic-circular-clamped plate, where $G_{IC}$ corresponds to the mode I fracture energy associated to the material interface delamination, E is the Young’s modulus, $\nu$ is the Poisson coefficient and h is the depth of uncut material under the drill tool.

$$C_F=\pi {\left[\frac{8G_{IC}E{h}^3}{3(1-{\nu }^2)}\right]}^{1/2}$$

(4)

In order to estimate the fracture energy of the CFRP-AA interface, asymmetric double cantilever beam (ADCB) tests were performed. In this type of test, a traction load is applied to the specimen arms, inducing the propagation of an existent pre-crack at a specified specimen plane, with a length and thickness of $a_0$ and t (refer to Figure 2a). A specially built testing machine coupled with a 50N capacity load cell (Tedea-Huntleigh Model 1042), intended for fracture characterization, was employed (refer to Figure 2b). The specimens arms were bonded (Araldite 2052-1 structural adhesive) to aluminium blocks with a 6 mm hole to allow for ADCB specimen gripping in the testing machine. The challenging real-time monitoring of crack propagation can be avoided using an equivalent crack length ($a_e$) procedure [30,31]. A relationship between $a_e$ and specimen compliance (defined as the ratio between the applied displacement, $\delta$, and load, P), can be obtained considering the strain energy (U) of the specimen due to bending and shear effects (Timoshenko beam theory) and applying the Castigliano theorem ($\delta$ = $dU$/$dP$). In this context, specimen current compliance can be defined as shown in Equation (5), where B, $h_u$ and $h_l$ correspond to specimen dimensions, $D_u$ and $D_l$ are the bending stiffness of upper and lower arms. Although critical load estimation relies exclusively on mode I fracture, in this work the ADCB specimens were selected given the relative difficulty in inducing a pre-crack in middle layer when compared to layer interfaces. Moreover, the fracture mechanism in drilling is consistent with the representation of mixed mode fracture with predominant mode I [32].

$$C=\frac{a_e^3}{3}\left(\frac{1}{D_u}+\frac{1}{D_l}\right)+\frac{6a_e}{5B{G}_{13}}\left(\frac{1}{h_u}+\frac{1}{h_l}\right)$$

(5)

Combining Equation (5) with the Irwin–Kies relation, Equation (6) can be derived, providing the total strain energy release under mixed mode I + II (with predominant mode I) as a function of $a_e$. Other approaches could be applied, namely within the scope of the linear-elastic fracture mechanics, such as that described in [33,34].

$$G_T=\frac{P^2}{2B}\left[a_e^2\left(\frac{1}{D_u}+\frac{1}{D_l}\right)+\frac{6}{5B{G}_{13}}\left(\frac{1}{h_u}+\frac{1}{h_l}\right)\right]$$

(6)

3. Results and Discussion

The thrust force ($F_t$) evolution of each tested tool geometry and its association with current drill point position is exhibited in Figure 3. A specific load signature can be identified and significant correspondence can be made with each layer of the laminate material. Common to all drill geometries, a rise in $F_t$ is observed due to the contact increase (between the drill’s primary cutting edge and the laminate material), from the start of the drilling operation up to instant B. A steeper increase of the force is noticed from instants B to C, corresponding to the CFRP material layer, evidencing the higher cutting resistance of this material as compared to the AA. This effect is further highlighted by the subsequent $F_t$ decrease in the C to D path. Load curve tends to another maximum as the drill exits the laminate material (E). Up to this instant, $F_t$ signature is rather indistinct of drill geometry, which is coherent with the identical point and helix angles of the three tested drills.

Instant X, in Figure 3a, indicates the moment the CNV drill’s secondary cutting edge engages the first layer of the laminate material. A slight transition (increase) in the curve’s slope is noticed. Similarly, and referring to Figure 3c, the instant Z corresponds to the moment the second point angle of the 2PA drill engages the laminate material. It is interesting to note that with the addition of a second (smaller) point angle, $F_t$ conveniently decreases more rapidly. In contrast, as the chip-breaking groove of CBR drill engages the laminate material (instant Y of Figure 3b) a very significant load increase is noticed, peaking at approximate double $F_t$ values of the A-Y drill tip path. Given the assumption that higher loads may contribute to higher delamination, the CBR drill might be inadequate. The load signature differences between drilling operations with and without back support are illustrated in Figure 3. It is possible to note that the overall thrust force signature does not significantly change. Still, the maximum values (peak of the $F_t$ curves) are consistently higher for all drill geometries, promoted by the stiffness increase of the clamping system. Moreover, at the end of the drilling operation, a load plateau is maintained, corresponding to the cutting of the PTFE disk (back support provider).

The analysis of variance (ANOVA) conducted for the maximum thrust force revealed significant impact of drill geometry, feed as well as the usage of back support. Such is illustrated by the <0.05 p-values respective of those variables, in

Table 3. ANOVA results on maximum axial force of the conducted experimental campaign.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	0.0192	5	0.0038	89.98	<0.0001
Cut. speed	0.0000	1	0.0000	0.851	0.3539
Feed	0.0018	1	0.0018	41.72	<0.0001
Drill geom.	0.0126	2	0.0063	147.7	<0.0001
Back support	0.0038	1	0.0038	88.96	<0.0001
Residual	0.0030	70	-	-	-

. Moreover, despite the slight increase of maximum $F_t$ with cutting speed, it did not present a relevant influence, especially when compared with the other considered variables, as shown in Figure 4. Drill geometry CBR seems to develop much higher thrust forces (approximately two-times higher), when compared with the other two drill configurations, which show identical results (slightly lower axial force with the CNV), as illustrated in Figure 4c. Therefore, as thrust force magnitude may be an indicator of delamination severity, the CBR drill may not perform adequately.

Figure 5a–c illustrate some representative examples of delamination occurrence on the machined holes using each drill geometry. The X-ray analysis has enabled the observation of the otherwise indiscernible defects. Figure 5a shows the delamination type mostly associated with the usage of CNV drill. The high directionality of damage occurrence (aligned with fibre orientation) is coherent with the push-out delamination mechanism resultant from AA-CFRP material de-bonding caused by the drill thrust. Since this interface de-bonding is predominantly mode I fracture, the developed modelling towards delamination prediction using ADCB is in accordance with the obtained results.

Alternatively, uniformly distributed delamination (as illustrated in Figure 5b) was more prone to occur with the CBR drill. The damage around the hole contour may be associated with the chip-breaking v-grooves on the principal cutting edge of the drill. These structures have seemingly failed to control chip morphology, which was identical regardless of the employed tool as well as operative conditions: continuous (ribbon) chips constituted of an aluminium core and with discontinuous bonded CFRP, as illustrated in Figure 5d. Unable to improve chip segmentation or breakage (comparatively to CNV and 2PA drills), the v-shaped grooves on the CBR drill seem to have caused internal delamination due to chip imprisonment. Repositioning of the groove towards a more central position of the drill’s cutting edge or increasing the number of grooves along the cutting edge may promote better chip splitting. Further research on the identification of suitable drill morphologies towards effective chip partition in fibre metal laminates is required, which may be supported using more advanced numerical methods. Constitutive and damage modelling may be convenient towards accurate portrayal of chip flow. Apart from the delamination effects, an example of a delamination-free drilled hole (using 2PA drill) is shown in Figure 5c.

The influence of the tested variables on the considered delamination factors results is shown in Figure 6. In addition,

Table 4. ANOVA results on $F_a$ delamination factor of the conducted experimental campaign.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	30,963	5	6192	17.74	<0.0001
Cut. speed	46	1	46	0.133	0.715
Feed	241	1	241	0.691	0.408
Drill geom.	28,572	2	14286	40.92	<0.0001
Back support	1675	1	1675	4.80	0.0318
Residual	24,438	70	349	-	-

,

Table 5. ANOVA results on $F_d$ delamination factor of the conducted experimental campaign.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	1.61	5	0.3220	5.68	0.0002
Cut. speed	0.0064	1	0.0064	0.1126	0.7382
Feed	0.0112	1	0.0112	0.1973	0.6583
Drill geom.	1.59	2	0.7947	14.02	<0.0001
Back support	0.0048	1	0.0048	0.0850	0.7715
Residual	3.97	70	0.0567	-	-

and

Table 6. ANOVA results on $F_{da}$ delamination factor of the conducted experimental campaign.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	1.74	5	0.3479	7.56	<0.0001
Cut. speed	0.0045	1	0.0045	0.0970	0.7564
Feed	0.0041	1	0.0041	0.0883	0.7672
Drill geom.	1.73	2	0.8645	18.79	<0.0001
Back support	0.0030	1	0.0030	0.0659	0.7982
Residual	3.22	70	0.0460	-	-

present the analysis of variance details. Despite having a negative impact on maximum thrust force (refer to Figure 4d), back support is commonly employed with the goal of increasing the fixture stiffness and minimizing delamination (preventing displacement of FML layers up to fracture initiation and propagation). Figure 6 shows the influence of the tested variables on the calculated delamination factors ($F_a$, $F_d$, $F_{ad}$) for each used drill tool. Although it is not expressive for the $F_d$ and $F_{da}$ delamination factors, a significant correlation between back support employment and delamination factor minimization ($F_a$) is observed in Figure 6d, illustrating its decreasing tendency with back support usage. Cutting speed and feed did not show accountable statistical impact (p-value higher than 0.05), as illustrated in Figure 6a,b. Drill geometry is the most influential variable on delamination results. The CBR drill yields the worst case scenario regarding delamination values for all calculated factors (up to three-times higher than CNV). In addition, 2PA seems to slightly outperform the CNV drill geometry. It is important to note the consistency of delamination results with the previous maximum load measurements, illustrating the importance of load prediction in metal cutting operations.

The arithmetical mean height roughness (Ra) has been estimated on a 5 mm length profile of the generated hole surface. Three measurement repetitions were performed for each hole and the average values were taken into consideration for ANOVA. The ANOVA statistical results show that drill geometry is the only relevant variable with regard to roughness (Ra) values (refer to Figure 7). Still, both cutting speed and feed p-values range relatively close to the 0.05 limit, from which significant impact can be inferred, thus showing slight tendencies for smaller roughness values when higher cutting speed and smaller feed operative conditions are applied. With regard to drill geometry, an identical trend to the tested variables has been identified, meaning that lower surface quality holes have resulted from hole making with the CBR drill. Moreover, from all machined holes, only 20% were above the 3.2 $\mathsf{\mu }$m surface roughness limit (Ra). The majority of those were performed using the CBR drill (87%) with the remainder using the CNV drill. Only the 2PA drill was capable of attaining Ra < 3.2 $\mathsf{\mu }$m in all machined holes. This criterion has been a useful indicator of the Ra quality in industrial conditions, with special relevance to the aeronautics sector [35].

The arithmetical mean height roughness (Ra) has been estimated on a 5 mm length profile of the generated hole surface. Three measurement repetitions were performed for each hole and the average values were taken into consideration for ANOVA. The ANOVA statistical results show that drill geometry is the only relevant variable with regard to roughness (Ra) values (refer to Figure 7). Still, as can be seen from

Table 7. ANOVA results on Ra surface roughness conducted during the experimental campaign.

Source	Sum of Squares	df	Mean Square	F-Value	p-Value
Model	0.8707	5	0.1741	15.23	<0.0001
Cut. speed	0.0249	1	0.0249	2.18	0.1447
Feed	0.0126	1	0.0126	1.10	0.2979
Drill geom.	0.8245	2	0.4122	36.06	<0.0001
Back support	0.0016	1	0.0016	0.1408	0.7086
Residual	0.8002	70	0.0114	-	-

, both cutting speed and feed p-values range relatively close to the 0.05 limit, from which significant impact can be inferred, thus showing slight tendencies for smaller roughness values when higher cutting speed and smaller feed operative conditions are applied. With regard to drill geometry, an identical trend to the tested variables has been identified, meaning that lower surface quality holes have resulted from hole making with the CBR drill. Moreover, from all machined holes, only 20% were above the 3.2 $\mathsf{\mu }$m surface roughness limit (Ra). The majority of those were performed using the CBR drill (87%) with the remainder using the CNV drill. Only the 2PA drill was capable of attaining Ra < 3.2 $\mathsf{\mu }$m in all machined holes. This criterion has been a useful indicator of the Ra quality in industrial conditions, with special relevance to the aeronautics sector [35].

The load–displacement results of the ADCB fracture tests are shown in Figure 8a. The resistance curves (refer to Figure 8b) were obtained to determine the energy release rate, needed to estimate a delamination critical force ($C_F$) through Equation (5). From the analysis of Figure 8b, an energy value plateau of approximately 0.249 N/mm with upper and lower boundaries of 0.29 and 0.20, respectively, is identified. Although delamination is more likely to occur as the drill approaches material exit (commonly known as exit delamination and promoted by the lack of subsequent material layers), the critical force, $C_F$ (or delamination onset load) has been calculated for three distinct interfaces as the tool advances on the laminate. These are labelled and highlighted in Figure 8c. Since the ADCB fracture tests were conducted at an AA-CFRP interface, delamination prediction is limited to those interfaces within the considered laminate. It is important to note that the critical force value obtained by Equation (5) refers to a single point at the drill tool path. This point is defined by the distance between the drill point and the bottom surface of the laminate (also called depth of uncut material, h).

Table 8. Estimation of critical force range for each respective interface, based on ADCB fracture tests critical energies.

Interface Number	Drill Point Distance [mm]	MVF	Elastic Modulus [MPa]	${\mathit{C}}_{\mathit{F}}$ Range [N]
1	0.76	0.26	92,200	503.6–585.1
2	0.44	0.45	86,500	214.9–249.7
3	0.24	0	100,000	93.1–108.1

presents the range of critical forces for each identified interface of Figure 8c, based on the upper and lower boundaries energy values. Elastic modulus has been calculated based on weighted average of metal volume fraction (MVF) of the uncut material, which in the case of interface 3 corresponds exclusively to CFRP material. A Poisson ratio of 0.4 was considered for the $C_F$ estimation.

The estimated critical force $C_F$ range can be seen as a threshold of values from which delamination is likely to occur. This range has been compared with several drilling operation thrust force signatures and the X-ray images of drilled holes showing delamination occurrence (or the absence thereof). It is important to note that the usage of back support hinders delamination by bending prevention (and thus interface de-bonding) of the laminate layers. For this reason, the tests conducted with sacrificial back support were not considered in this part of the study. In adition, the model proposed by Cheng et al. [15], is not valid for such support conditions.

Figure 9a shows the critical force range thresholds comparison with the thrust force loading signature of the CNV drill using a cutting speed of 120 m/min and 0.03 mm/rev feed. Since maximum thrust force was consistently below the drill point path corresponding threshold, delamination is not predicted, which is coherent with its absence in the X-ray image of the corresponding hole. Figure 9b shows a similar example for a CNV drill with a cutting speed of 100 m/min and 0.07 mm/rev of feed, where maximum thrust force surpasses the minimum delamination threshold at “interface 3” (refer to Figure 8c for interface relative position) resulting in delamination occurrence, as verified in the corresponding X-ray image of the drilled hole.

One of the shortcomings of the presented methodology is illustrated by Figure 9c. Although the critical force limit is not attained within the considered tool path, it may have been surpassed by the action of the drill’s chip grooves. Such a possibility is consistent with the delamination morphology and its occurrence at an internal interface (contrary to the exit delamination of the previous examples in Figure 9a,b). The estimated critical force of Equation (4) relies on the assumption of a point load (associated with the cutting phenomenon) and thus, in the current case, its applicability is compromised since it is only valid to drill features that are effectively cutting (principal cutting edge). Still, when considering a critical load value that is independent of drill position, the developed model would correctly predict delamination occurrence.

Given that the load has not surpassed the critical force threshold, Figure 9d shows an example of unexpected defects. It is, however, noticeable that the pattern of damage occurrence (indicated by red arrows) is compatible with the delamination type of chip formation in fibre-reinforced polymers [32,36], suggesting fibre-matrix interface failure (and crack propagation) within the composite material. In drilling, the relative position constantly changes with each rotation and when the cutting direction and fibre direction are the same (occurring in two distinct instants) mixed mode fracture occurs. Thus, predominant type I or II, depending on rake angle, develops within fibre-composite material, promoting crack initiation and its propagation along the fibre-reinforcement interface. This observation explains the non-compliance of the developed criterion (only valid for AA-CFRP interfaces).

4. Conclusions

In this study, the impact of tool geometry and operative conditions on the hole drilling of thermoplastic-based fibre metal laminates was investigated. Cutting load, delamination and internal roughness were assessed. Drill geometry shows very significant influence on all measured machinability indicators. The inclusion of grooves on the primary cutting edges of the drill revealed neither an appropriate technique toward efficient chip control nor delamination mitigation. In contrast, the usage of a double-point angle drill stands out as an effective method toward improved hole-making in fibre metal laminates, with minimal delamination. Back support was shown to be an adequate alternative method for minimizing delamination, especially when in conjunction with smaller feed rates. Fracture energy was successfully estimated using asymmetric double cantilever beam tests, enabling the calculation of critical force thresholds for delamination occurrence, which adequately predicts the delamination with some exceptions duly justified from known model limitations.