Time-Domain Inversion Method of Impact Loads Based on Strain Monitoring Data
Abstract
:1. Introduction
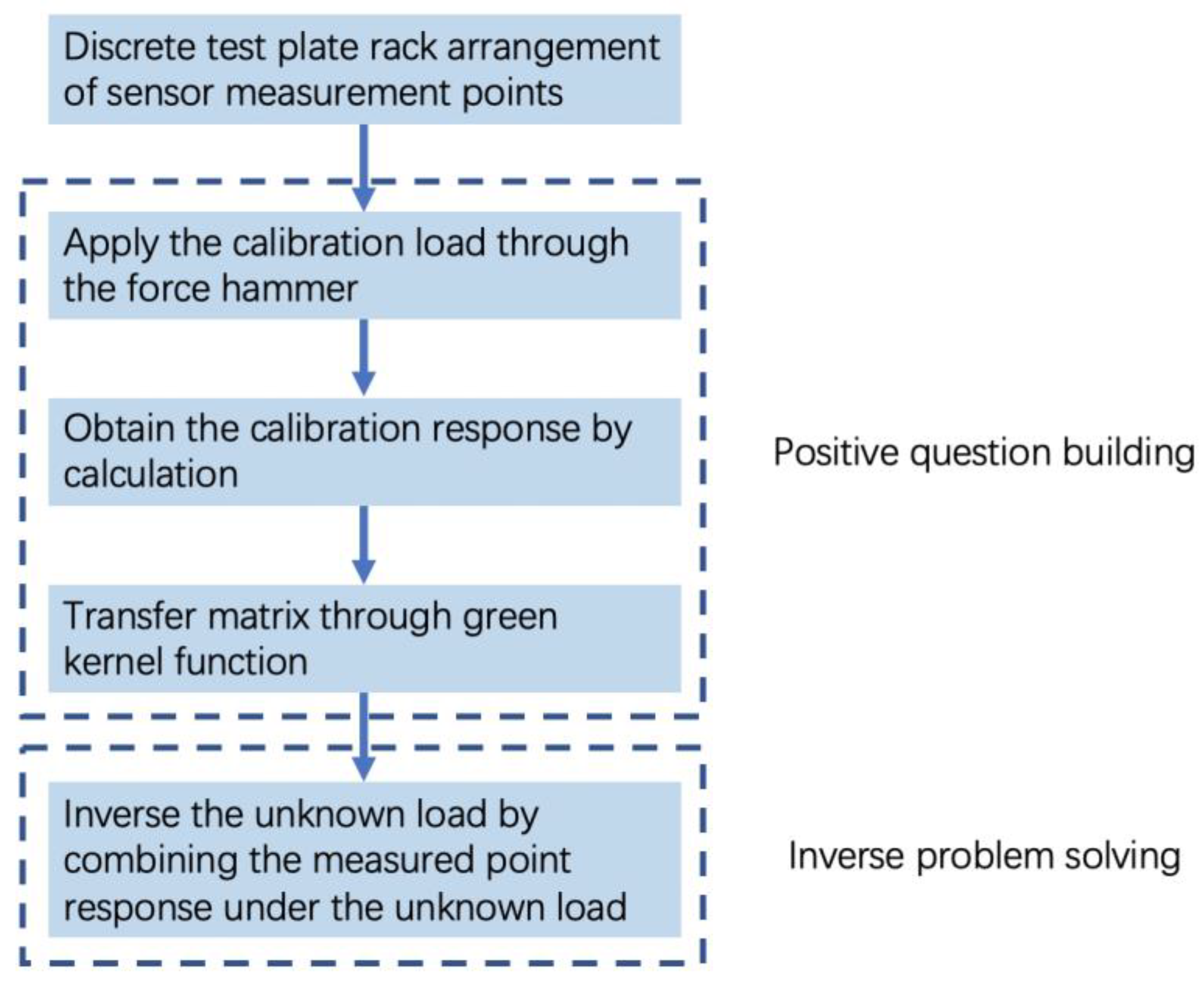
2. Inversion Method
2.1. Basic Theory
2.2. Regularization Method
2.2.1. Truncated Singular Value Decomposition
2.2.2. Tikhonov Regularization
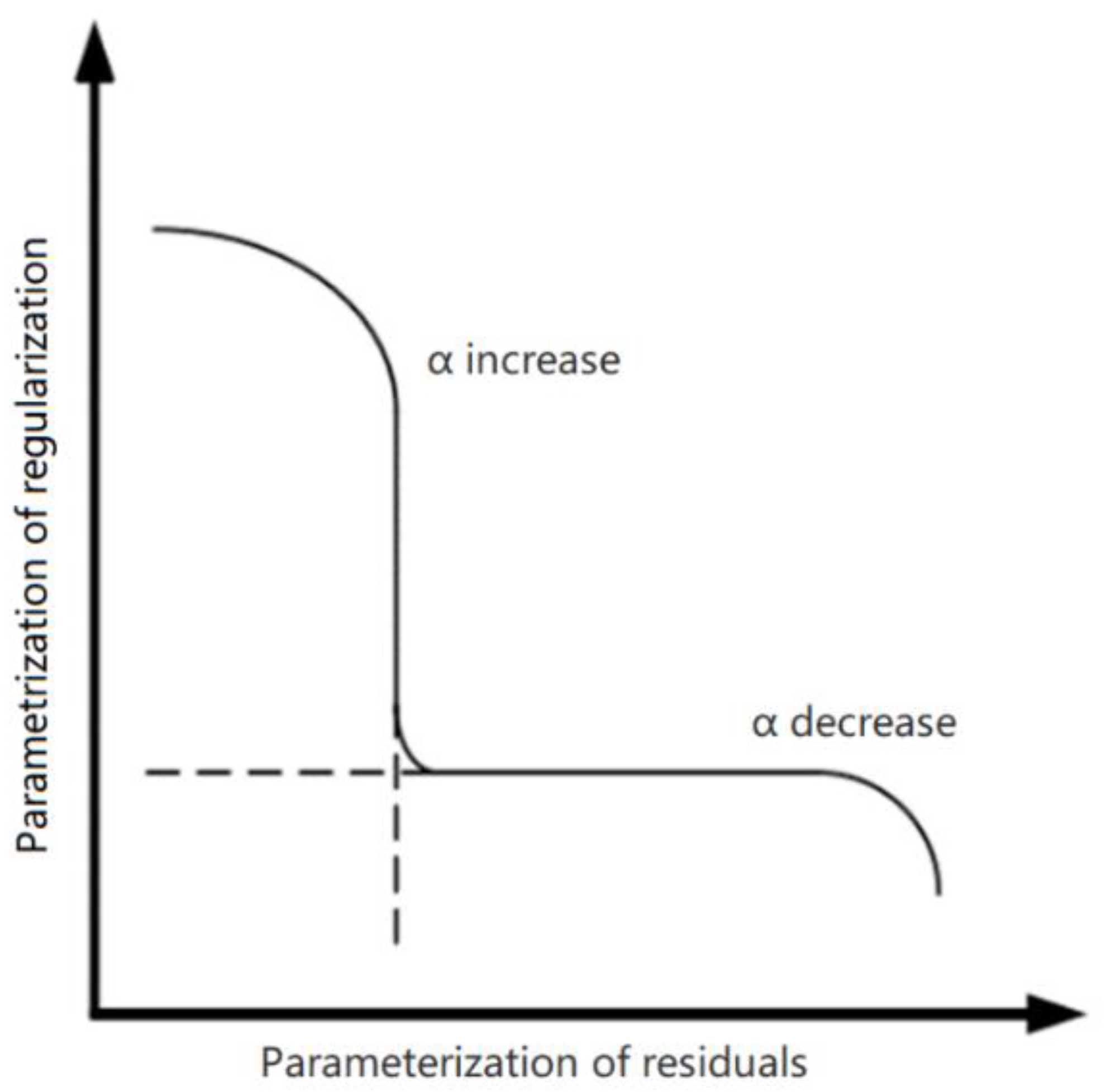
2.3. Selection Method of Regularization Parameters
2.3.1. L-Curve Criterion
2.3.2. Generalized Cross Validation Criterion (GCV)
3. Impact Load Model Test
3.1. Test Scheme
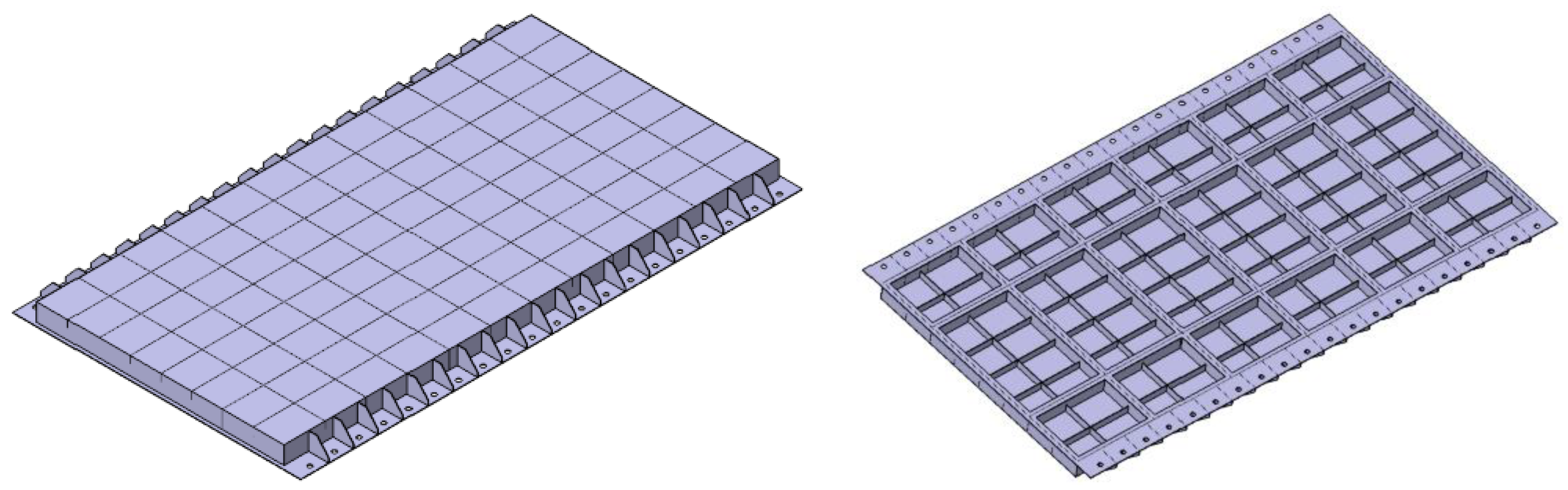
3.1.1. Test Model
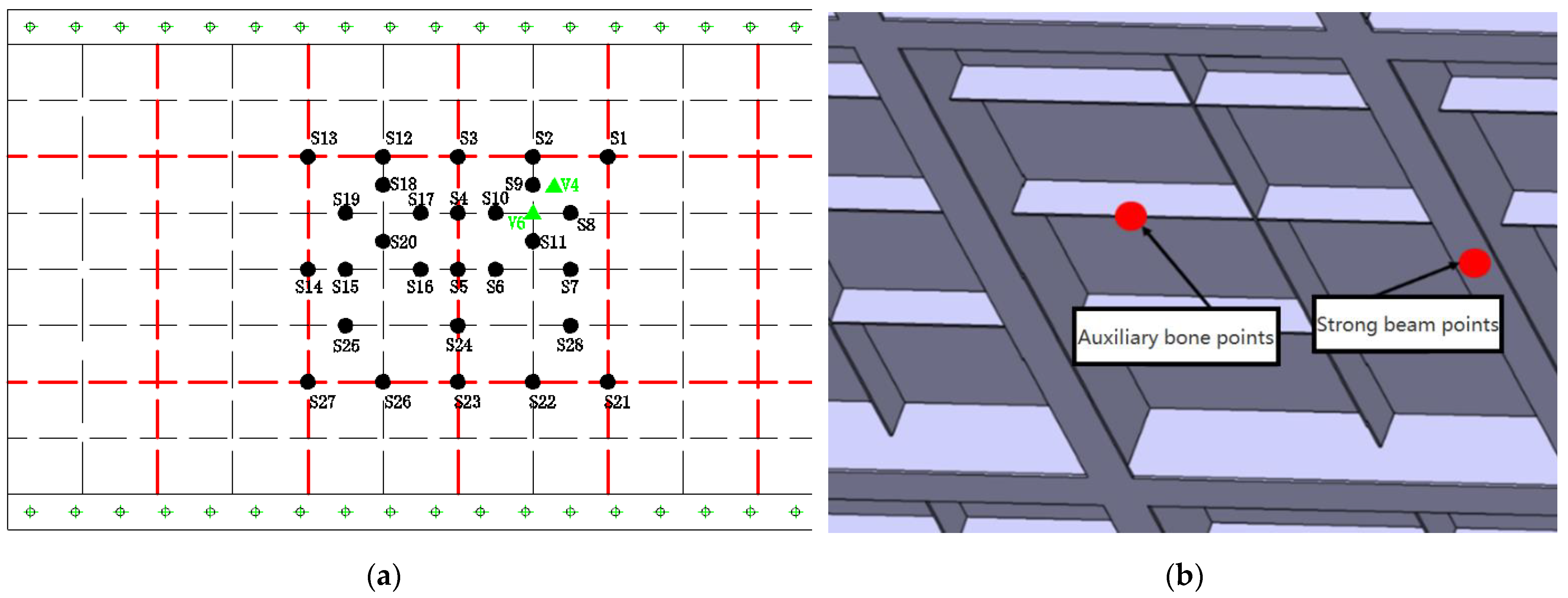
3.1.2. Sensors
3.1.3. Test Conditions
- A test bench for a falling wheel was set up on the test grillage, as shown in Figure 7, and the force mapping sensor and photoelectric speed sensor were positioned at the expected impact area.
- According to the test conditions (Table 1), the weight, tire pressure, and other parameters of the falling wheel were adjusted.
- First, a pretest was conducted in the other positions of the test grillage, ensuring the safety of the test equipment and test personnel.
- By lifting the falling wheel to a certain height, the wheel was released to complete the impact load model test.
- We collected the data recorded by the sensors.
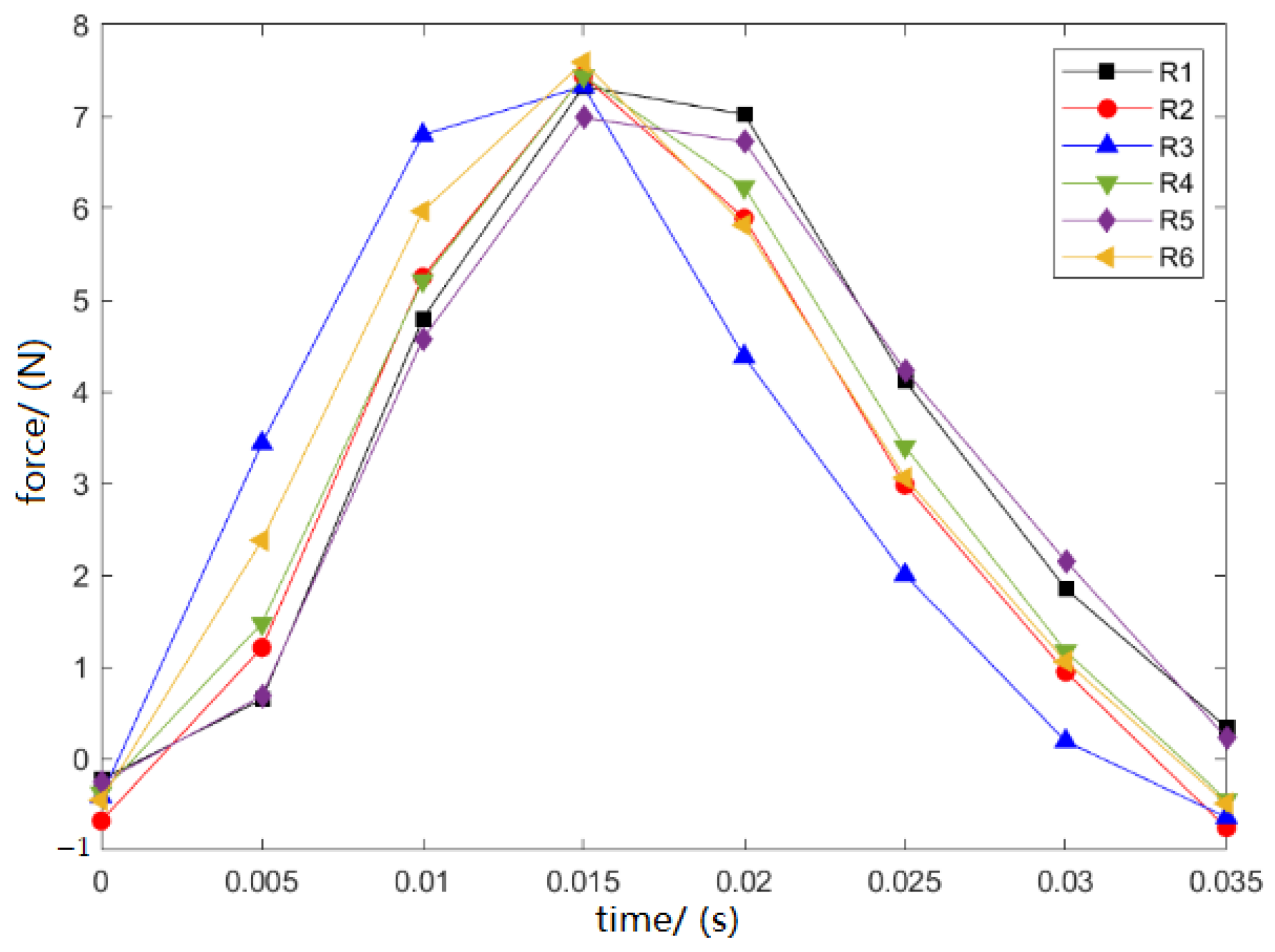
3.2. Reproducibility Validation
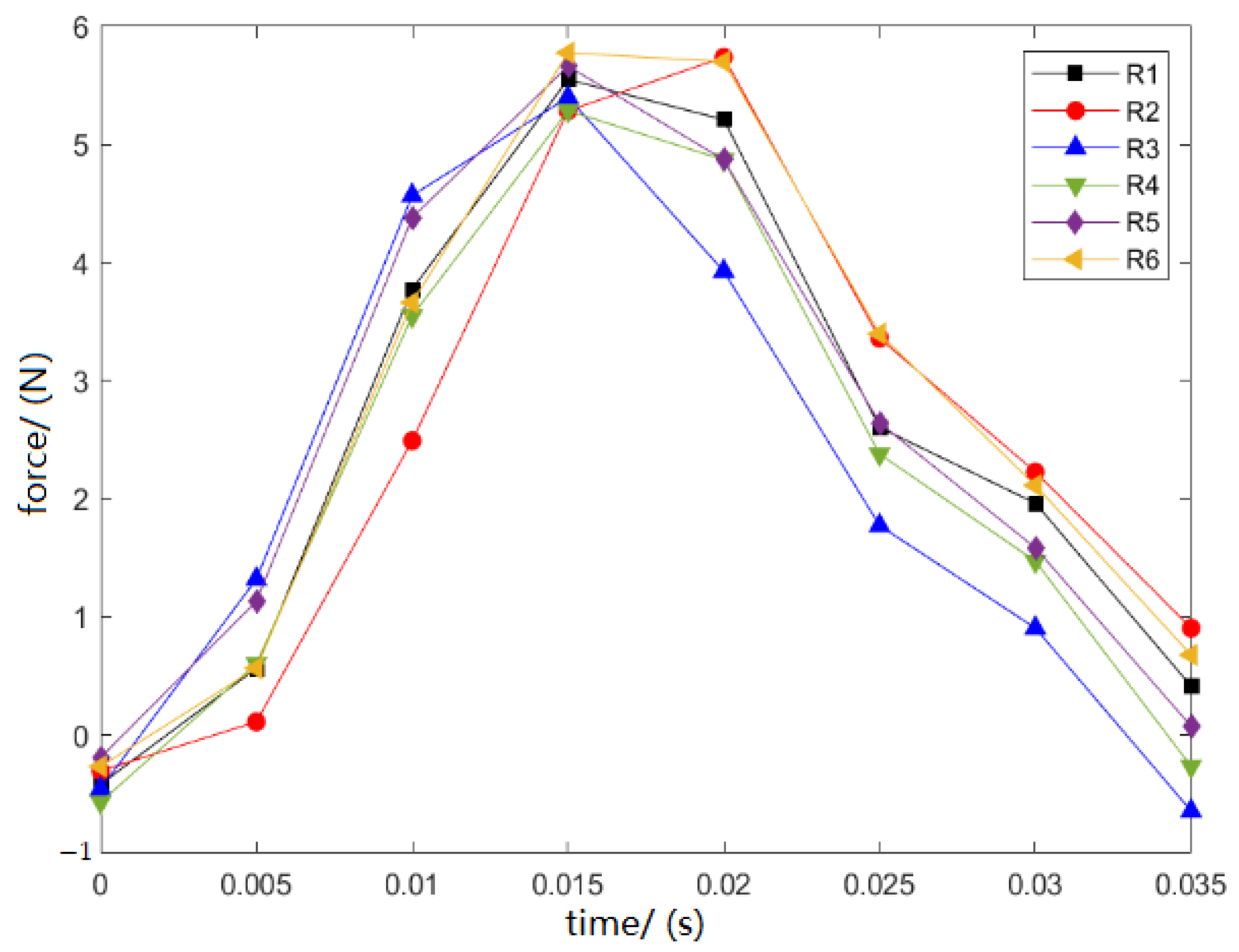
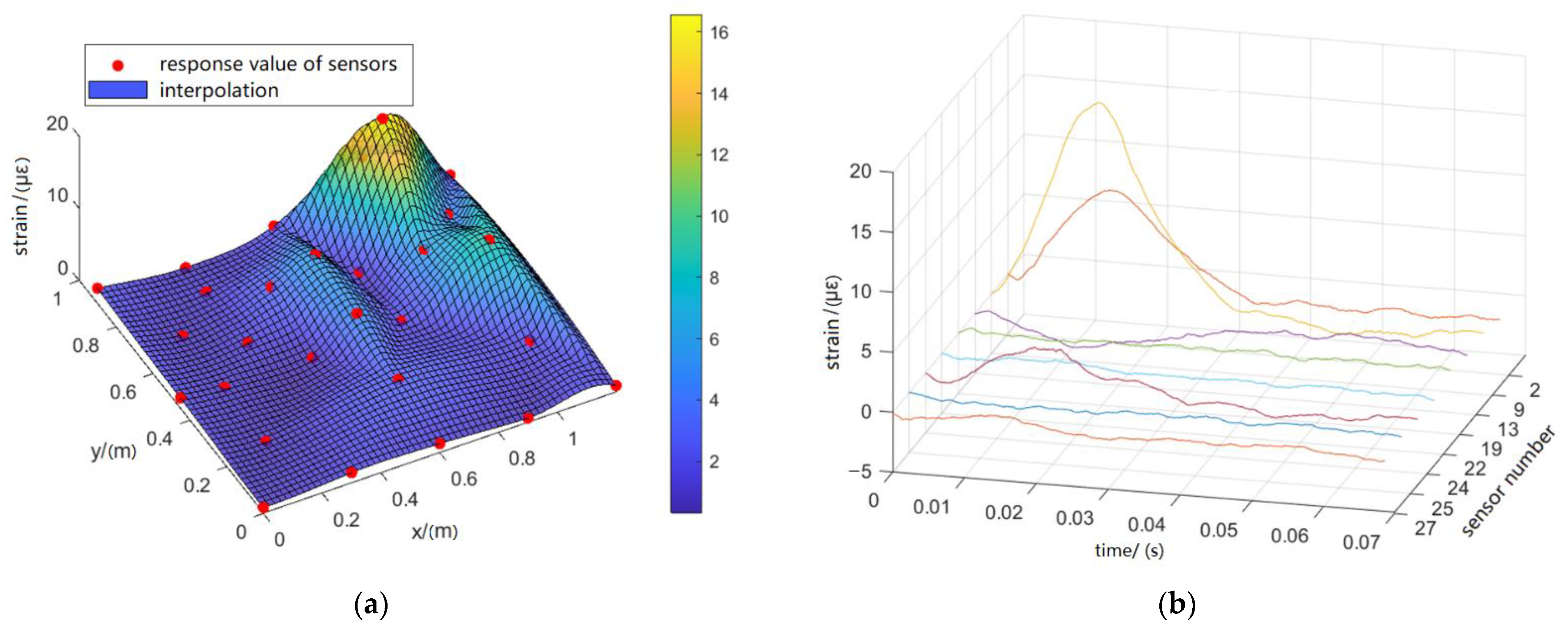
3.3. Characterization of Impact Load and Structure Responses
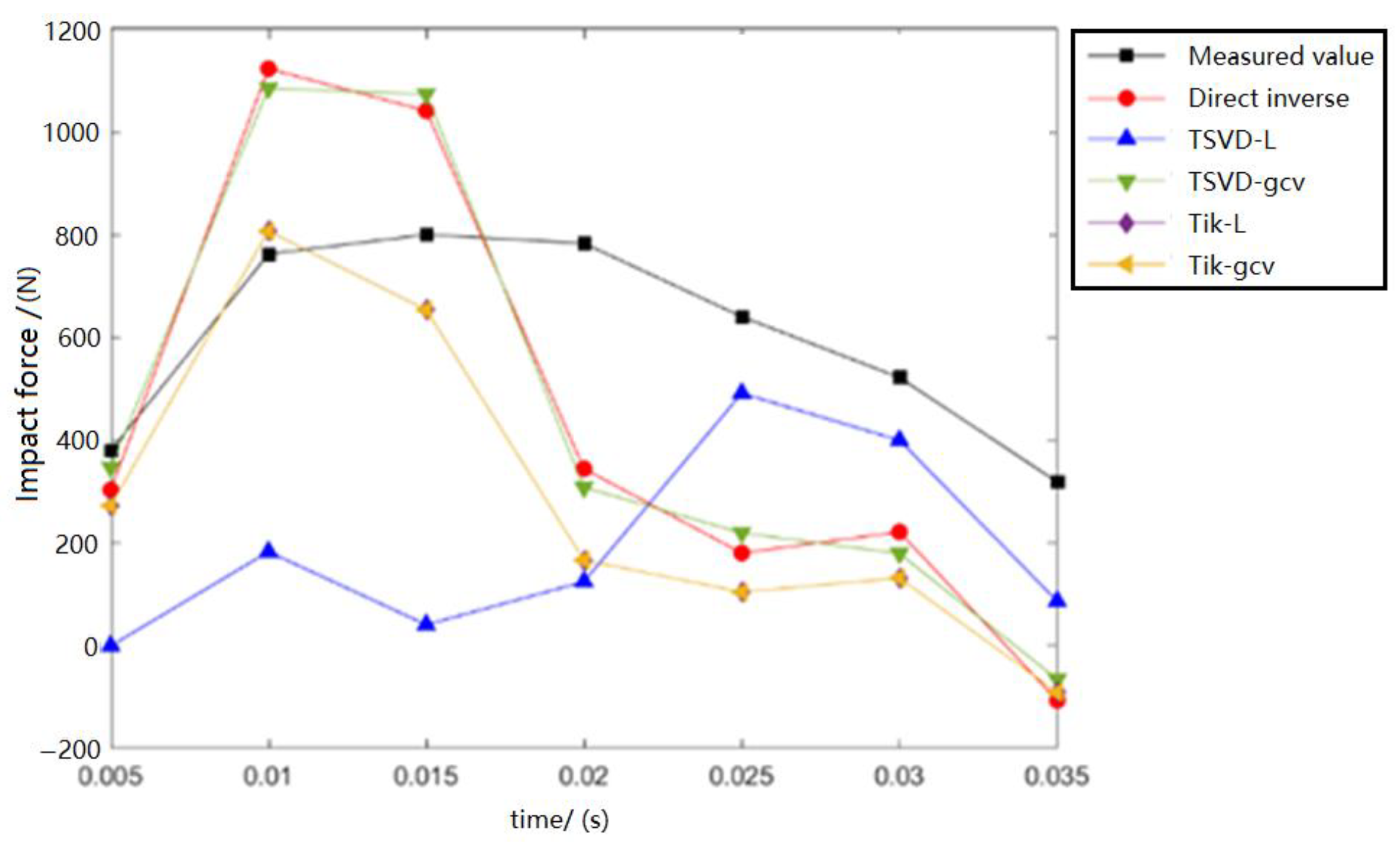
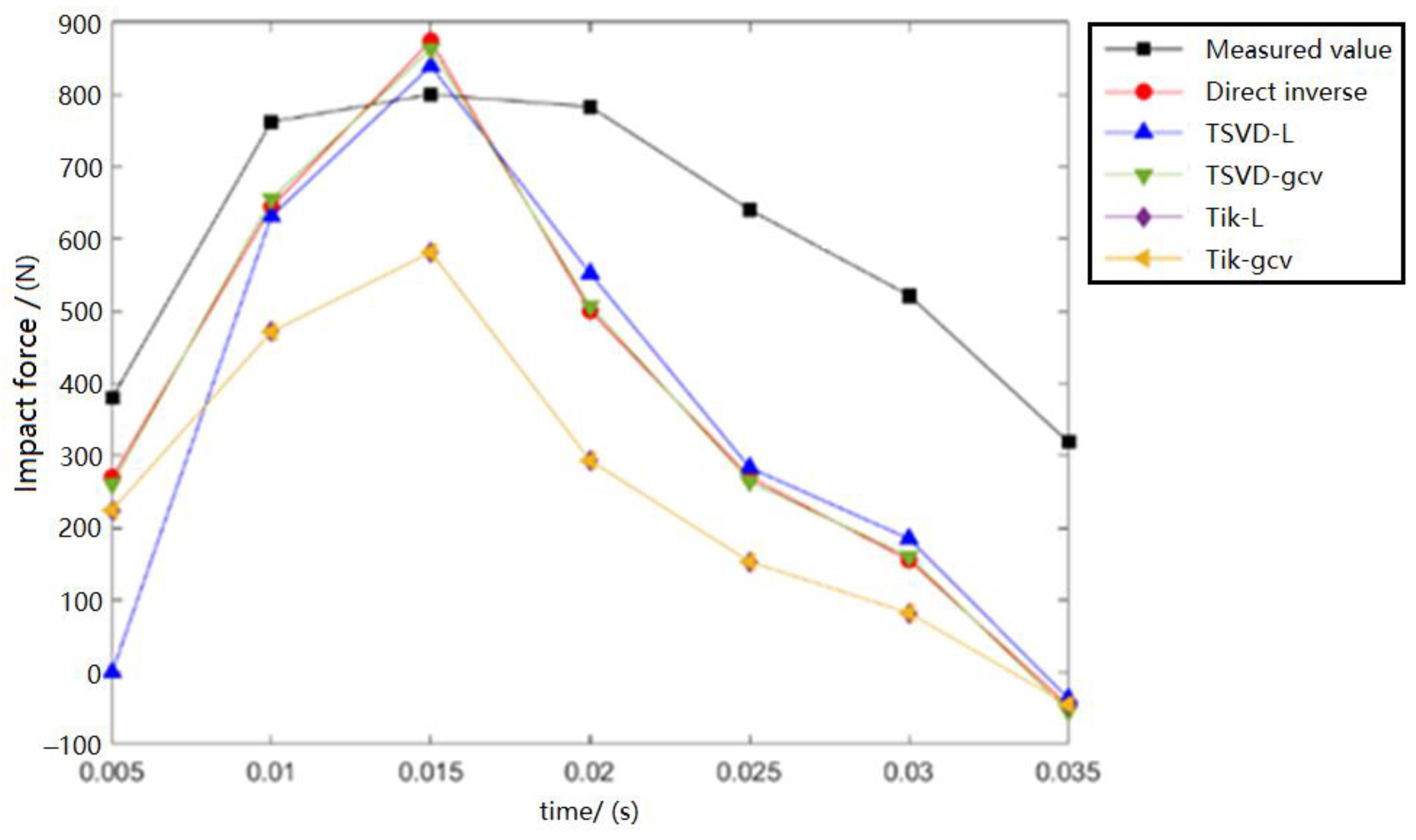
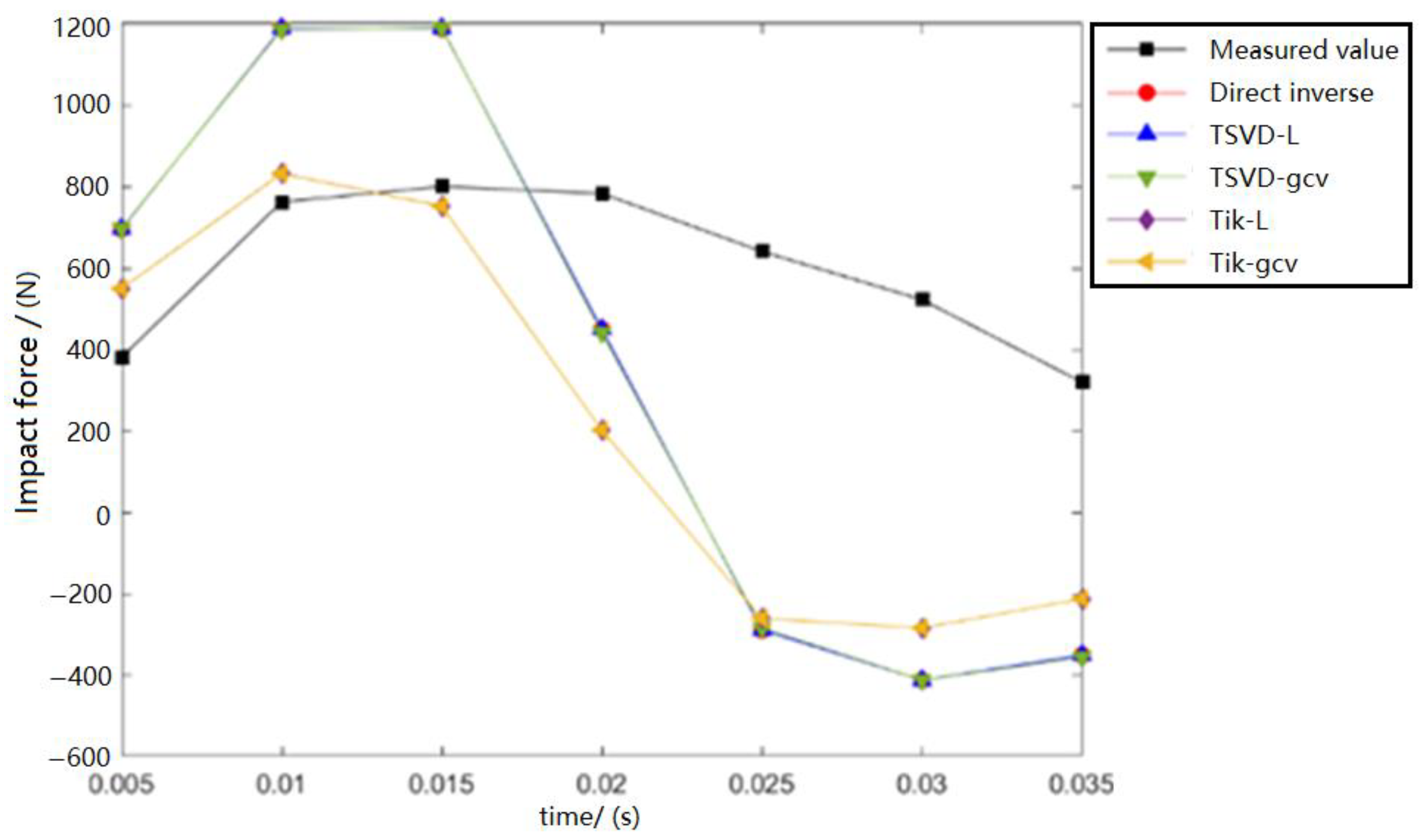
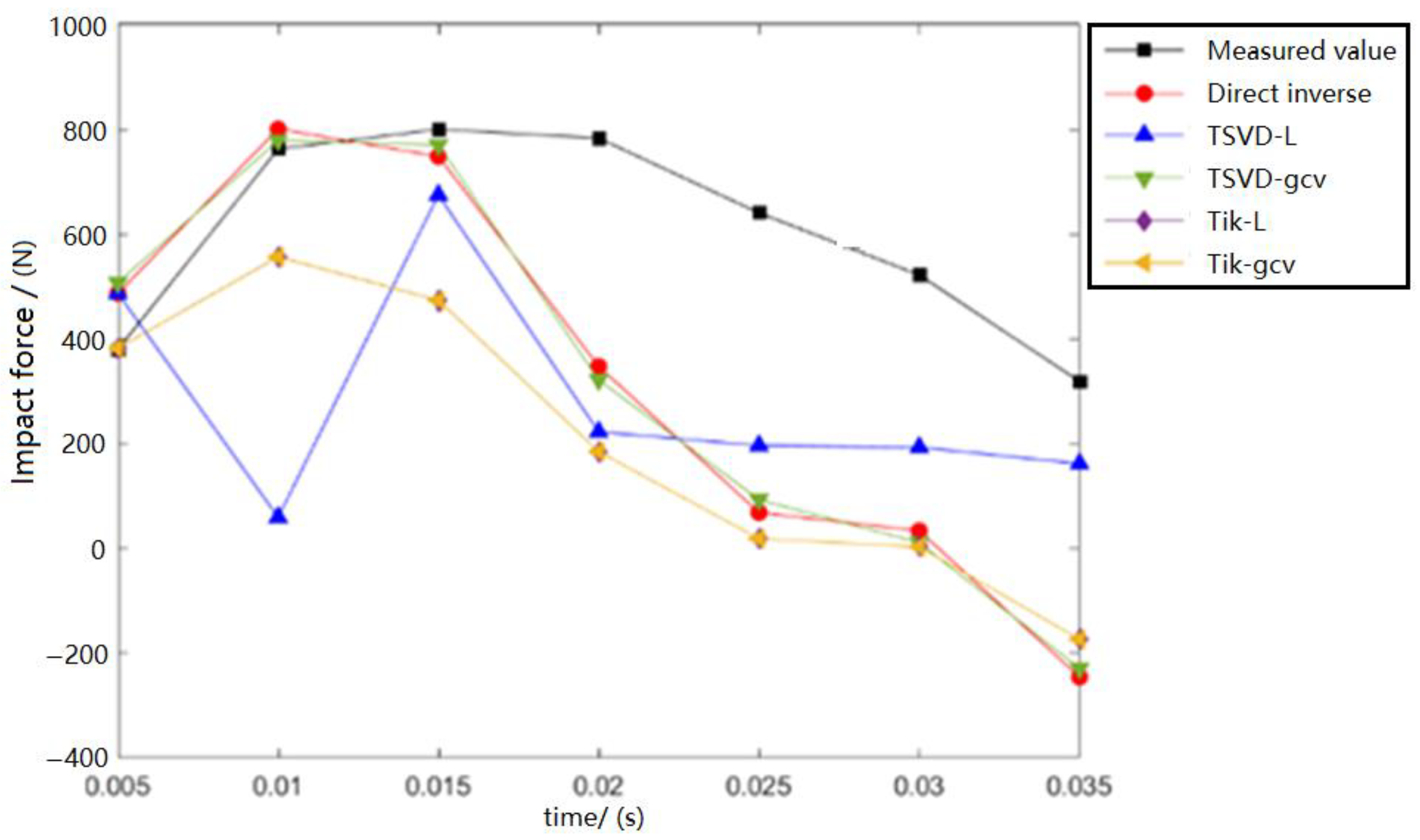
4. Impact Load Inversion Calculation
- Direct inverse method: direct matrix inversion in inverse matrix operations.
- TSVD-L method: The TSVD regularization technique is applied in the inverse matrix operation, and the regularization parameters are selected by the L-curve criterion method.
- TSVD-GCV method: The TSVD regularization technique is applied in the inverse matrix operation, and the regularization parameters are selected by the GCV determination criterion method.
- Tik-L method: The Tikhonov regularization technique is applied in the inverse matrix operation, and the regularization parameters are selected by the L-curve criterion method.
- Tik-GCV method: The Tikhonov regularization technique is applied in the inverse matrix operation, and the regularization parameters are selected using the GCV determination criterion method.
5. Conclusions
- The impact load value is related to the impact speed and weight of the impact wheel, and the impact load is positively correlated to the weight and vertical impact speed of the wheel.
- The structural strain response shows an obvious triangular distribution in the time history. In space, the structural dynamic response quickly extends around the impact position, and the strain wave strength steadily decreases as the spreading distance increases. When the strain wave spreads to a certain range (approximately one strong frame spacing), the strain response decays to the structural vibration response.
- Compared with the other inversion methods used in this study, the Tik-L method shows the highest accuracy, and the accuracy of the results is proportional to the number of strain sensors. When the number of strain sensors reaches four or more, the Tik-L method can reach a high accuracy within 10%, which meets the requirements of engineering applications.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Z.C.; Jia, Y. Dynamic load identification method. Adv. Mech. 2015, 45, 29–54. [Google Scholar]
- Sanchez, J.; Benaroya, H. Review of force reconstruction techniques. J. Sound Vib. 2014, 333, 2999–3018. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Rubust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef] [Green Version]
- Tikhonov, A.N.; Arsenin, V.Y. Solutions of Ill-Posed Problems; Winston & Sons: Washington, DC, USA, 1977. [Google Scholar]
- Hansen, P.C. Truncated SVD solutions to discrete ill-posed problems with ill-determined numerical rank. SIAM J. Sci. Comput. 1990, 11, 503–518. [Google Scholar] [CrossRef]
- Jacquelin, E.; Bennani, A.; Hamelin, P. Force reconstruction: Analysis and regularization of a deconvolution problem. J. Sound Vib. 2003, 265, 81–107. [Google Scholar] [CrossRef]
- Morozov, V.A. Methods for Solving Incorrectly Posed Problems; Springer: New York, NY, USA, 1984. [Google Scholar]
- Bonesky, T. Morozov’s discrepancy principle and Tikhonov type functionals. Inverse Probl. 2009, 25, 015015. [Google Scholar] [CrossRef]
- Hansen, P.C. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 1992, 34, 561–580. [Google Scholar] [CrossRef]
- Kindermann, S.; Neubauer, A. On the convergence of the quasi-optimality criterion for (iterated) Tikhonov regularization. Inverse Probl. Imaging 2008, 2, 291–299. [Google Scholar] [CrossRef]
- Golub, G.H.; Heath, M.; Wahba, G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Wahba, G. Spline models for observational data. In Proceedings of the Cbms-Nsf Regional Conference Series in Applied Mathematics, Based on A Series of 10 Lectures at Ohio State University at Columbus, Columbus, OH, USA, 23–27 March 1987; pp. 113–114. [Google Scholar]
- Lawson, C.L.; Hanson, R.J. Solving Least Squares Problems; Prentice-Hall: Hoboken, NJ, USA, 1974. [Google Scholar]
- Hansen, P.C.; O’Leary, D.P. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput. 2006, 14, 1487–1503. [Google Scholar] [CrossRef]
- Lourens, E.; Reynders, E.; Roeck, G.D.; Degrande, G.; Lombaert, G. An augmented Kalman filter for force identification in structural dynamics. Mech. Syst. Signal Process. 2012, 27, 446–460. [Google Scholar] [CrossRef]
- Hansen, P.C.; Jensen, T.K.; Rodriguez, G. An adaptive pruning algorithm for the discrete L-curve criterion. J. Comput. Appl. Math. 2007, 198, 483–492. [Google Scholar] [CrossRef]
- Liu, J. Research on Computational Inverse Technique for Dynamic Load Identification. Ph.D. Thesis, Hunan University, Changsha, China, 2011. [Google Scholar]
- Liu, C.-K.; Ding, X.-H.; Ni, W.-Y.; Li, G.-Y. Inversion technique of external load of mechanical structure with multi-information fusion of simulation and real measurement. China Mech. Eng. 2022, 33, 639–646. [Google Scholar]
- Nan, M.-Y.; Hu, J.-J.; Wang, X.-L.; Yakimov, V. A study of ice load inversion based on long and short-term memory networks. J. Ship Mech. 2021, 25, 1675–1684. [Google Scholar]
- Kong, S.; Cui, H.-Y.; Ji, S.-Y. Study on real ship measurement and inversion method of sea ice load on ship structure. Vib. Shock. 2020, 39, 8–16. [Google Scholar]
- De Waal, R.; Bekker, A.; Heyns, P. Indirect load case estimation for propeller-ice moments from shaft line torque measurements. Cold Reg. Sci. Technol. 2018, 151, 237–248. [Google Scholar] [CrossRef] [Green Version]
- De Koker, N.; Bekker, A. Assessment of ice impact load threshold exceedance in the propulsion shaft of an ice-faring vessel via Bayesian inversion. Struct. Health Monit. 2022, 21, 757–769. [Google Scholar] [CrossRef]
- Ikonen, T.; Peltokorpi, O.; Karhunen, J. Inverse ice-induced moment determination on the propeller of an ice-going vessel. Cold Reg. Sci. Technol. 2015, 112, 1–13. [Google Scholar] [CrossRef]
- Jin, X.; Yin, J.-Z.; Wang, J.-Z. Research on flight load testing and inversion method based on deep learning. Adv. Aeronaut. Eng. 2020, 11, 887–893. [Google Scholar]





| Work Condition Number | Landing Position | Weight | Vertical Speed |
|---|---|---|---|
| Condition 1 | V4 | 6.27 kg | 3.30 m/s |
| Condition 2 | V6 | 9.19 kg | 3.30 m/s |
| Condition 3 | V6 | 12.11 kg | 1.87 m/s |
| Condition 4 | V6 | 12.11 kg | 2.68 m/s |
| Condition 5 | V6 | 12.11 kg | 3.30 m/s |
| Inversion Method | Direct Inverse | TSVD-L | TSVD-GCV | Tik-L | Tik-gcv |
|---|---|---|---|---|---|
| Total number of times | 20 times | 20 times | 20 times | 20 times | 20 times |
| Average error | 26.60% | 29.77% | 35.86% | 20.99% | 21.82% |
| Error < 10% | 6 times | 5 times | 5 times | 5 times | 5 times |
| 10% < Error < 30% | 6 times | 7 times | 4 times | 9 times | 9 times |
| 30% < Error < 50% | 5 times | 5 times | 7 times | 5 times | 5 times |
| Error < 50% | 3 times | 3 times | 4 times | 1 time | 1 time |
| Inversion Method | Single Sensor | Two Sensors | Three Sensors | Four Sensors |
|---|---|---|---|---|
| Average error of extreme value | 20.99% | 18.06% | 14.93% | 9.41% |
| Maximum error of extreme value | 51.27% | 42.65% | 37.64% | 26.24% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Zheng, K.; Chen, B.; Peng, Y.; Liu, K.; Tang, D. Time-Domain Inversion Method of Impact Loads Based on Strain Monitoring Data. Metals 2022, 12, 1279. https://doi.org/10.3390/met12081279
Wang F, Zheng K, Chen B, Peng Y, Liu K, Tang D. Time-Domain Inversion Method of Impact Loads Based on Strain Monitoring Data. Metals. 2022; 12(8):1279. https://doi.org/10.3390/met12081279
Chicago/Turabian StyleWang, Fanchao, Kai Zheng, Bihao Chen, Yinghao Peng, Kun Liu, and Dewen Tang. 2022. "Time-Domain Inversion Method of Impact Loads Based on Strain Monitoring Data" Metals 12, no. 8: 1279. https://doi.org/10.3390/met12081279
APA StyleWang, F., Zheng, K., Chen, B., Peng, Y., Liu, K., & Tang, D. (2022). Time-Domain Inversion Method of Impact Loads Based on Strain Monitoring Data. Metals, 12(8), 1279. https://doi.org/10.3390/met12081279






