Real and Imaginary Impedance Prediction of Ni-P Composite Coating for Additive Manufacturing Steel via Multilayer Perceptron
Abstract
:1. Introduction
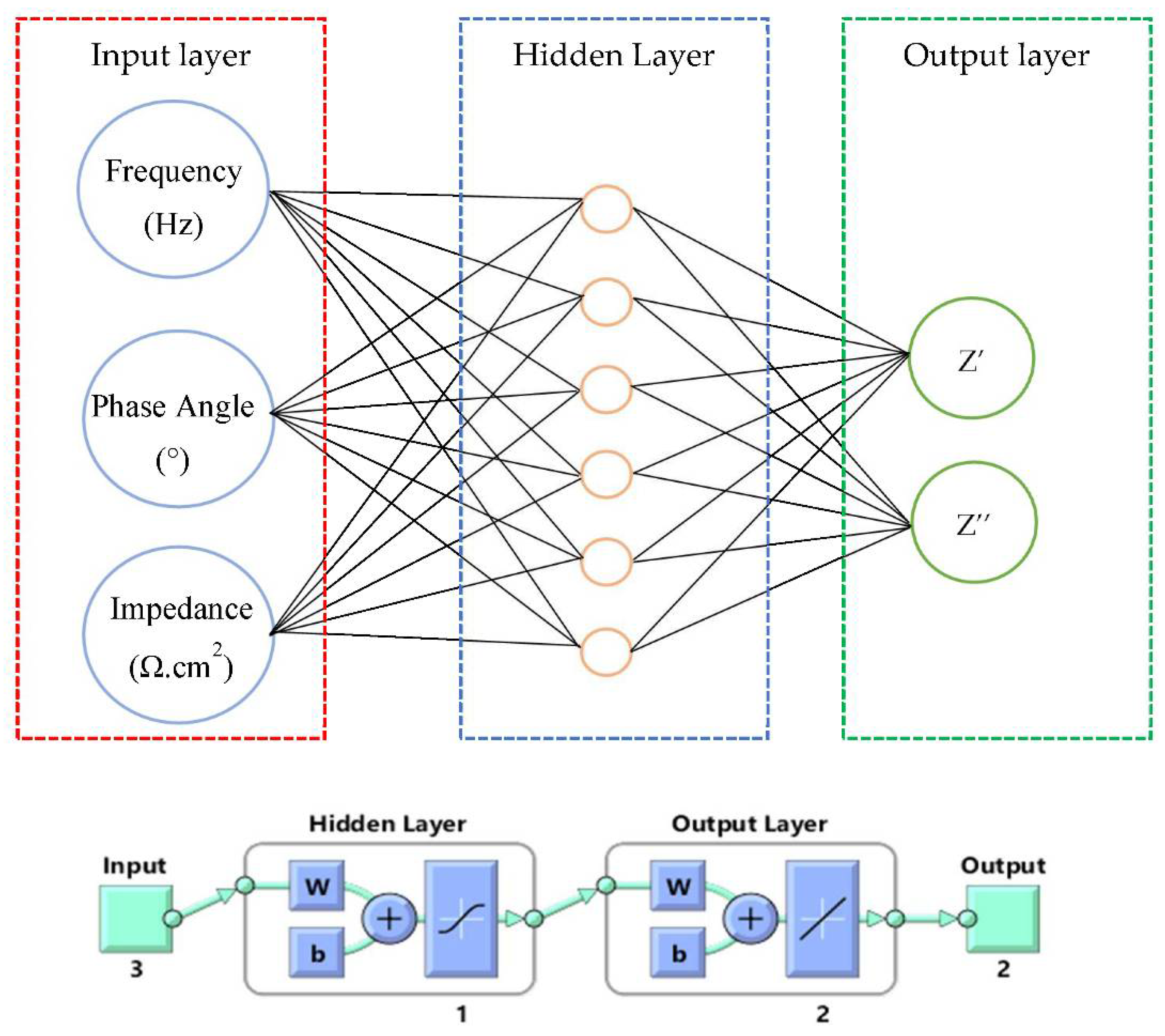
2. Methodology
2.1. Levenberg–Marquardt (LM) Algorithm
- x = Weight of neural networks
- J = Jacobian matrix of the performance criteria to be minimised
- μ = Scalar that controls the learning process
- e = The residual error factor
2.2. Secondary Data Retrieved for Electrochemical Investigation
2.3. The Prediction Model
3. Results
4. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bajaj, P.; Hariharan, A.; Kini, A.; Kürnsteiner, P.; Raabe, D.; Jägle, E.A. Steels in Additive Manufacturing: A Review of Their Microstructure and Properties. Mater. Sci. Eng. A 2020, 772, 138633. [Google Scholar] [CrossRef]
- Agredo Diaz, D.G.; Barba Pingarrón, A.; Olaya Florez, J.J.; González Parra, J.R.; Cervantes Cabello, J.; Angarita Moncaleano, I.; Covelo Villar, A.; Hernández Gallegos, M.Á. Effect of a Ni-P Coating on the Corrosion Resistance of an Additive Manufacturing Carbon Steel Immersed in a 0.1 M NaCl Solution. Mater. Lett. 2020, 275, 128159. [Google Scholar] [CrossRef]
- Ron, T.; Levy, G.K.; Dolev, O.; Leon, A.; Shirizly, A.; Aghion, E. Environmental Behavior of Low Carbon Steel Produced by a Wire Arc Additive Manufacturing Process. Metals 2019, 9, 888. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Wu, Y.; Cheng, X.; Zhang, S.; Wang, H. Study of Microstructure Evolution and Preference Growth Direction in a Fully Laminated Directional Micro-Columnar TiAl Fabricated Using Laser Additive Manufacturing Technique. Mater. Lett. 2019, 243, 62–65. [Google Scholar] [CrossRef]
- Berkh, O.; Zahavi, J. Electrodeposition and Properties of NiP Alloys and Their Composites—A Literature Survey. Corros. Rev. 1996, 14, 323–341. [Google Scholar] [CrossRef]
- Daly, B.P.; Barry, F.J. Electrochemical Nickel–Phosphorus Alloy Formation. Int. Mater. Rev. 2013, 48, 326–338. [Google Scholar] [CrossRef]
- Lelevic, A.; Walsh, F.C. Electrodeposition of NiP Alloy Coatings: A Review. Surf. Coat. Technol. 2019, 369, 198–220. [Google Scholar] [CrossRef]
- Narayanan, T.S.N.S.; Krishnaveni, K.; Seshadri, S.K. Electroless Ni–P/Ni–B Duplex Coatings: Preparation and Evaluation of Microhardness, Wear and Corrosion Resistance. Mater. Chem. Phys. 2003, 82, 771–779. [Google Scholar] [CrossRef]
- Ilangovan, S. Investigation of The Mechanical, Corrosion Properties and Wear Behaviour of Electroless Ni-P Plated Mild Steel. IJRET Int. J. Res. Eng. Technol. 2014, 3, 151–155. [Google Scholar]
- Xia, D.H.; Deng, C.M.; Macdonald, D.; Jamali, S.; Mills, D.; Luo, J.L.; Strebl, M.G.; Amiri, M.; Jin, W.; Song, S.; et al. Electrochemical Measurements Used for Assessment of Corrosion and Protection of Metallic Materials in the Field: A Critical Review. J. Mater. Sci. Technol. 2022, 112, 151–183. [Google Scholar] [CrossRef]
- Xia, D.H.; Song, S.; Tao, L.; Qin, Z.; Wu, Z.; Gao, Z.; Wang, J.; Hu, W.; Behnamian, Y.; Luo, J.L. Review-Material Degradation Assessed by Digital Image Processing: Fundamentals, Progresses, and Challenges. J. Mater. Sci. Technol. 2020, 53, 146–162. [Google Scholar] [CrossRef]
- Chou, J.S.; Ngo, N.T.; Chong, W.K. The Use of Artificial Intelligence Combiners for Modeling Steel Pitting Risk and Corrosion Rate. Eng. Appl. Artif. Intell. 2017, 65, 471–483. [Google Scholar] [CrossRef]
- Bhandari, J.; Khan, F.; Abbassi, R.; Garaniya, V.; Ojeda, R. Modelling of Pitting Corrosion in Marine and Offshore Steel Structures—A Technical Review. J. Loss Prev. Process Ind. 2015, 37, 39–62. [Google Scholar] [CrossRef]
- Millán-Ocampo, D.E.; Parrales-Bahena, A.; González-Rodríguez, J.G.; Silva-Martínez, S.; Porcayo-Calderón, J.; Hernández-Pérez, J.A. Modelling of Behavior for Inhibition Corrosion of Bronze Using Artificial Neural Network (ANN). Entropy 2018, 20, 409. [Google Scholar] [CrossRef] [Green Version]
- Wu, D.; Olson, D.L.; Dolgui, A. Decision Making in Enterprise Risk Management: A Review and Introduction to Special Issue. Omega 2015, 57, 1–4. [Google Scholar] [CrossRef]
- Chou, J.S.; Ngo, N.T. Smart Grid Data Analytics Framework for Increasing Energy Savings in Residential Buildings. Autom. Constr. 2016, 72, 247–257. [Google Scholar] [CrossRef]
- Yao, X. Evolving Artificial Neural Networks. Proc. IEEE 1999, 87, 1423–1447. [Google Scholar] [CrossRef] [Green Version]
- Møller, M.F. A Scaled Conjugate Gradient Algorithm for Fast Supervised Learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Shrestha, A.; Fang, H.; Wu, Q.; Qiu, Q. Approximating Back-Propagation for a Biologically Plausible Local Learning Rule in Spiking Neural Networks. In Proceedings of the ICONS ’19 International Conference on Neuromorphic Systems, Knoxville, TN, USA, 23–25 July 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Battiti, R.; Tecchiolli, G. Training Neural Nets with the Reactive Tabu Search. IEEE Trans. Neural Netw. 1995, 6, 1185–1200. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, I.; Routroy, S. Comparing the Performance of Neural Networks Developed by Using Levenberg–Marquardt and Quasi-Newton with the Gradient Descent Algorithm for Modelling a Multiple Response Grinding Process. Expert Syst. Appl. 2012, 39, 2397–2407. [Google Scholar] [CrossRef]
- Ranganathan, V.; Natarajan, S. A New Backpropagation Algorithm without Gradient Descent. arXiv 2018, arXiv:1802.00027. [Google Scholar] [CrossRef]
- Agredo Diaz, D.G.; Barba Pingarrón, A.; Olaya Florez, J.J.; González Parra, J.R.; Cervantes Cabello, J.; Angarita Moncaleano, I.; Covelo Villar, A.; Hernández Gallegos, M.Á. Evaluation of the Corrosion Resistance of a Ni-P Coating Deposited on Additive Manufacturing Steel: A Dataset. Data Brief 2020, 32, 106159. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Neural Network Toolbox for Use with MATLAB. Available online: https://www.researchgate.net/publication/2801351_Neural_Network_Toolbox_for_use_with_MATLAB (accessed on 9 June 2022).
- Kumari, S.; Tiyyagura, H.R.; Douglas, T.E.L.; Mohammed, E.A.A.; Adriaens, A.; Fuchs-Godec, R.; Mohan, M.K.; Skirtach, A.G. ANN Prediction of Corrosion Behaviour of Uncoated and Biopolymers Coated Cp-Titanium Substrates. Mater. Des. 2018, 157, 35–51. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Q.; Li, H.L.; Wu, Q.; Ma, L.; Ngan, K.N. Parametric Deformable Exponential Linear Units for Deep Neural Networks. Neural Netw. 2020, 125, 281–289. [Google Scholar] [CrossRef]
- Normalizing Your Data (Specifically, Input and Batch Normalization). Available online: https://www.jeremyjordan.me/batch-normalization/ (accessed on 9 June 2022).
- Liu, H. On the Levenberg-Marquardt Training Method for Feed-Forward Neural Networks. In Proceedings of the 6th International Conference on Natural Computation, ICNC, Yantai, China, 10–12 August 2010; Volume 1, pp. 456–460. [Google Scholar] [CrossRef]
- Al Bataineh, A.; Kaur, D. A Comparative Study of Different Curve Fitting Algorithms in Artificial Neural Network Using Housing Dataset. In Proceedings of the IEEE National Aerospace Electronics Conference, NAECON, Dayton, OH, USA, 23–26 July 2018; pp. 174–178. [Google Scholar] [CrossRef]
- Al-Shehri, D.A. Oil and Gas Wells: Enhanced Wellbore Casing Integrity Management through Corrosion Rate Prediction Using an Augmented Intelligent Approach. Sustainability 2019, 11, 818. [Google Scholar] [CrossRef] [Green Version]
- Shaik, N.B.; Pedapati, S.R.; Ammar Taqvi, S.A.; Othman, A.R.; Abd Dzubir, F.A. A Feed-Forward Back Propagation Neural Network Approach to Predict the Life Condition of Crude Oil Pipeline. Processes 2020, 8, 661. [Google Scholar] [CrossRef]
- Rocabruno-Valdés, C.I.; González-Rodriguez, J.G.; Díaz-Blanco, Y.; Juantorena, A.U.; Muñoz-Ledo, J.A.; El-Hamzaoui, Y.; Hernández, J.A. Corrosion Rate Prediction for Metals in Biodiesel Using Artificial Neural Networks. Renew. Energy 2019, 140, 592–601. [Google Scholar] [CrossRef]
- Zulkifli, F.; Abdullah, S.; Suriani, M.J.; Kamaludin, M.I.A.; Wan Nik, W.B. Multilayer Perceptron Model for the Prediction of Corrosion Rate of Aluminium Alloy 5083 in Seawater via Different Training Algorithms. IOP Conf. Ser. Earth Environ. Sci. 2021, 646, 012058. [Google Scholar] [CrossRef]
- Tuntas, R.; Dikici, B. An Investigation on the Aging Responses and Corrosion Behaviour of A356/SiC Composites by Neural Network: The Effect of Cold Working Ratio. J. Compos. Mater. 2015, 50, 2323–2335. [Google Scholar] [CrossRef]
- Colorado-Garrido, D.; Ortega-Toledo, D.M.; Hernández, J.A.; González-Rodríguez, J.G.; Uruchurtu, J. Neural Networks for Nyquist Plots Prediction during Corrosion Inhibition of a Pipeline Steel. J. Solid State Electrochem. 2009, 13, 1715–1722. [Google Scholar] [CrossRef]

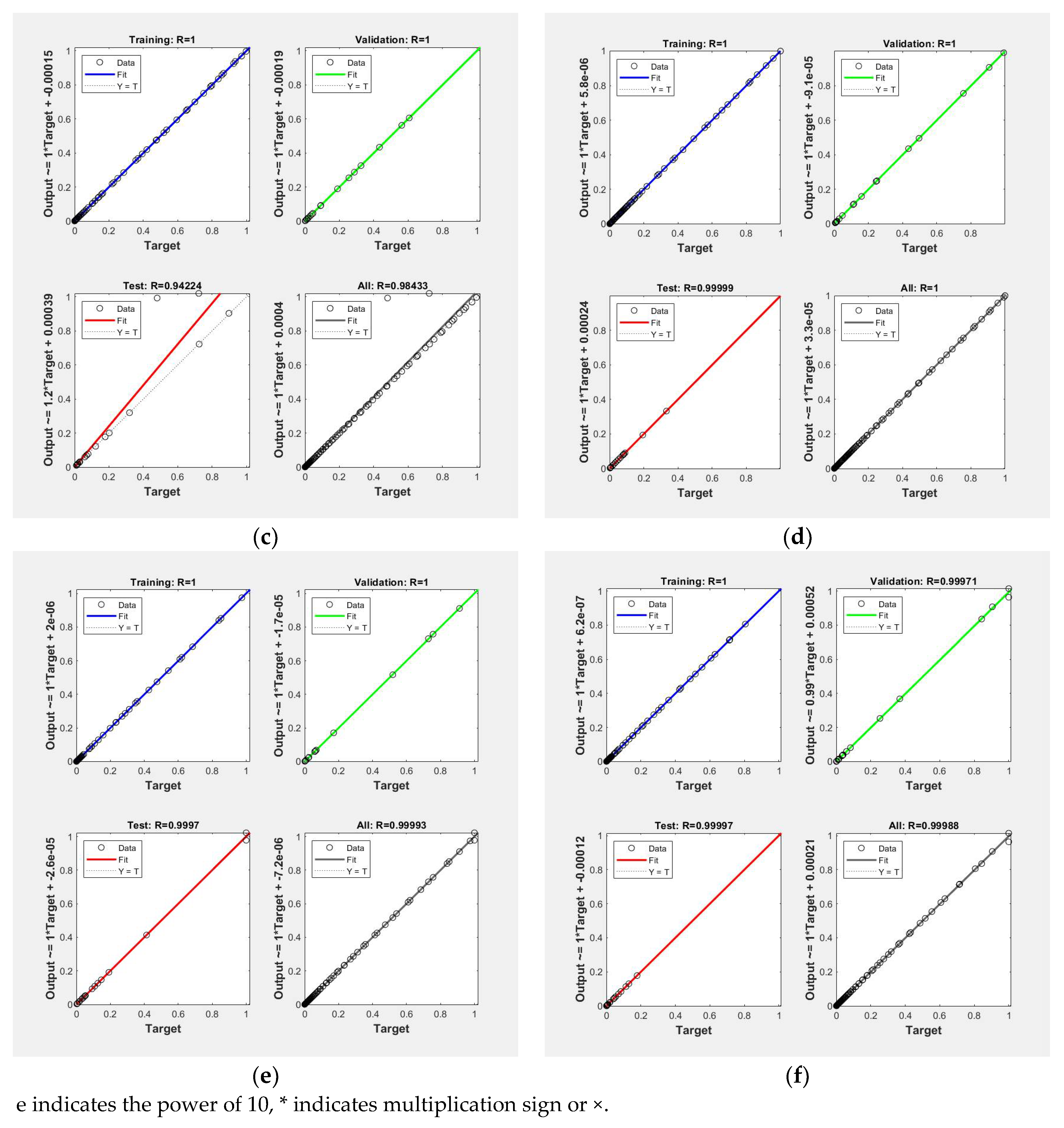
| Non-coated additive manufacturing steel | 0 h | ||||||
| Neuron | 1 | 2 | 3 | 4 * | 5 | 6 | |
| R | 0.99177 | 0.99981 | 0.99987 | 0.99999 | 0.99999 | 0.99996 | |
| MSE | 1.69 × 10−3 | 3.76 × 10−5 | 2.63 × 10−5 | 1.14 × 10−6 | 1.48 × 10−6 | 9.11 × 10−6 | |
| 288 h | |||||||
| Neuron | 1 | 2 | 3 | 4 * | 5 | 6 | |
| R | 0.99578 | 0.99478 | 1 | 1 | 0.99998 | 0.99999 | |
| MSE | 5.34 × 10−4 | 9.75 × 10−4 | 5.03 × 10−7 | 2.99 × 10−7 | 3.06 × 10−6 | 2.61 × 10−6 | |
| 576 h | |||||||
| Neuron | 1 | 2 | 3 | 4 * | 5 | 6 | |
| R | 0.99264 | 0.98665 | 0.98673 | 1 | 0.99894 | 0.99264 | |
| MSE | 1.08 × 10−3 | 2.08 × 10−3 | 1.69 × 10−3 | 5.10 × 10−7 | 1.94 × 10−4 | 1.09 × 10−3 | |
| Coated additive manufacturing steel | 0 h | ||||||
| Neuron | 1 | 2 | 3 | 4 | 5 | 6 * | |
| R | 0.99544 | 0.99999 | 0.99963 | 1 | 1 | 1 | |
| MSE | 6.90 × 10−4 | 1.60 × 10−6 | 6.45 × 10−5 | 8.10 × 10−7 | 3.84 × 10−7 | 1.06 × 10−7 | |
| 288 h | |||||||
| Neuron | 1 | 2 | 3 * | 4 | 5 | 6 | |
| R | 0.99327 | 0.99994 | 1 | 0.99999 | 1 | 1 | |
| MSE | 6.54 × 10−4 | 8.31 × 10−6 | 1.15 × 10−8 | 8.24 × 10−7 | 7.13 × 10−7 | 1.32 × 10−8 | |
| 576 h | |||||||
| Neuron | 1 | 2 | 3 | 4 * | 5 | 6 | |
| R | 0.99708 | 1 | 0.99943 | 1 | 1 | 1 | |
| MSE | 3.37 × 10−4 | 7.71 × 10−8 | 7.67 × 10−5 | 6.59 × 10−8 | 7.62 × 10−8 | 6.44 × 10−7 | |
| Steel Type | Testing Period (h) | Prediction Model |
|---|---|---|
| Non-coated additive manufacturing steel | 0 | y = x + 0.00017 |
| 288 | y = x + 2.4 × 10−6 | |
| 576 | y = x + 0.00015 | |
| Coated additive manufacturing steel | 0 | y = x + 5.8 × 10−6 |
| 288 | y = x + 2 × 10−6 | |
| 576 | y = x + 6.2 × 10−7 |
| Scope | Value of R | Authors |
|---|---|---|
| Life condition prediction of a crude oil pipeline | 0.9998 | [33] |
| Corrosion rate prediction for metals in biodiesel | 0.93237 | [34] |
| Prediction of corrosion rate of Aluminium Alloy 5083 in seawater | 0.99272 | [35] |
| The effect of a cold working ration on the ageing responses and corrosion behaviour | 0.99986 | [36] |
| Nyquist plots prediction of corrosion inhibition in pipeline steel | 0.9840 | [37] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zulkifli, M.F.R.; Roslan, N.F.; Mat Jusoh, S.; Mohd Ghazali, M.S.; Abdullah, S.; Wan Nik, W.M.N. Real and Imaginary Impedance Prediction of Ni-P Composite Coating for Additive Manufacturing Steel via Multilayer Perceptron. Metals 2022, 12, 1306. https://doi.org/10.3390/met12081306
Zulkifli MFR, Roslan NF, Mat Jusoh S, Mohd Ghazali MS, Abdullah S, Wan Nik WMN. Real and Imaginary Impedance Prediction of Ni-P Composite Coating for Additive Manufacturing Steel via Multilayer Perceptron. Metals. 2022; 12(8):1306. https://doi.org/10.3390/met12081306
Chicago/Turabian StyleZulkifli, Mohammad Fakhratul Ridwan, Nur Faraadiena Roslan, Suriani Mat Jusoh, Mohd Sabri Mohd Ghazali, Samsuri Abdullah, and Wan Mohd Norsani Wan Nik. 2022. "Real and Imaginary Impedance Prediction of Ni-P Composite Coating for Additive Manufacturing Steel via Multilayer Perceptron" Metals 12, no. 8: 1306. https://doi.org/10.3390/met12081306
APA StyleZulkifli, M. F. R., Roslan, N. F., Mat Jusoh, S., Mohd Ghazali, M. S., Abdullah, S., & Wan Nik, W. M. N. (2022). Real and Imaginary Impedance Prediction of Ni-P Composite Coating for Additive Manufacturing Steel via Multilayer Perceptron. Metals, 12(8), 1306. https://doi.org/10.3390/met12081306






