A New Computational Method for Predicting Ductile Failure of 304L Stainless Steel
Abstract
:1. Introduction
2. Phenomenological Ductile Fracture Criteria
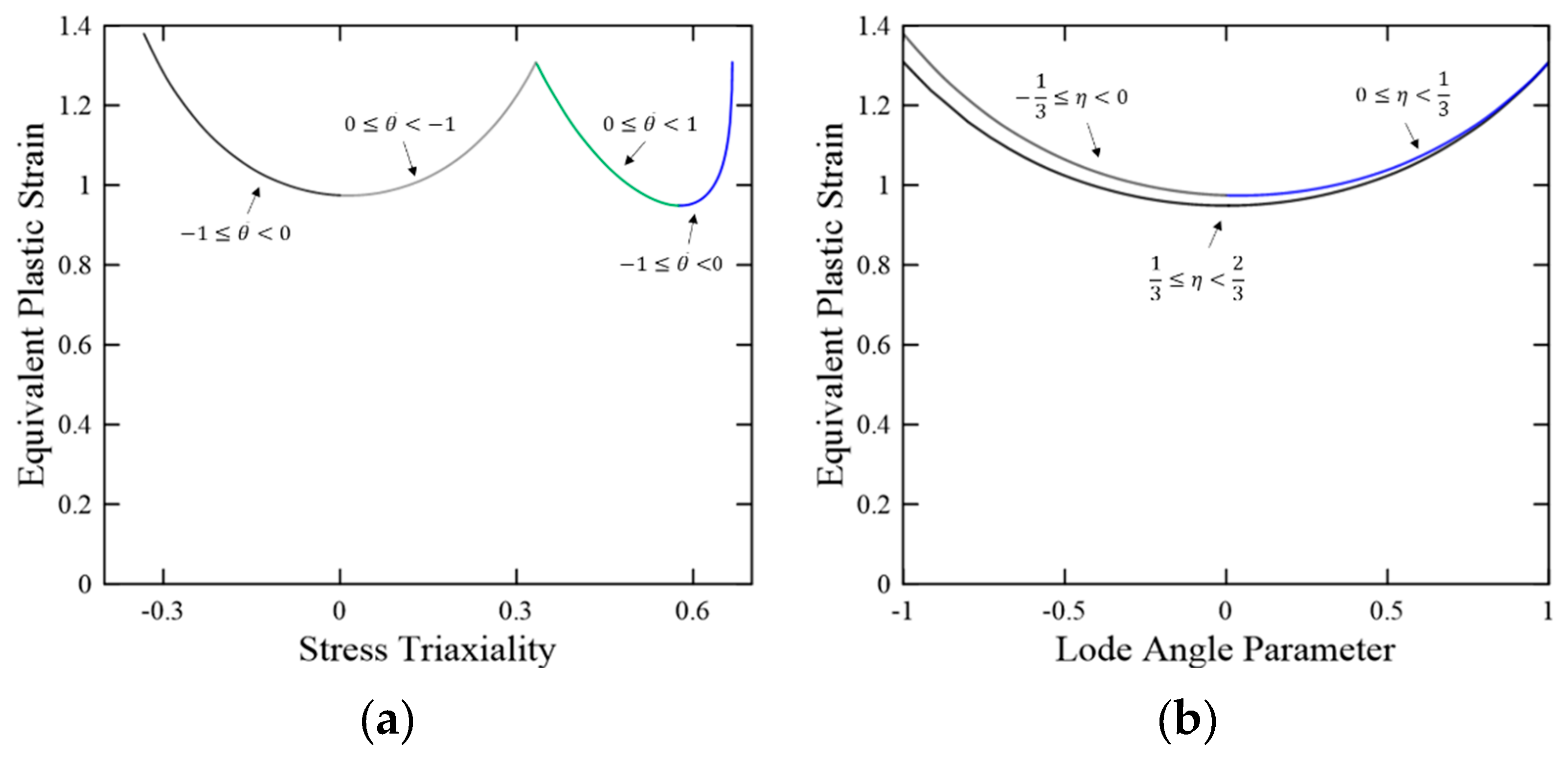
2.1. Characterization of Stress State
2.2. Modified Mohr–Coulomb Model
3. Elastoplastic-Damage Coupled Constitutive Model
3.1. Hardening Function
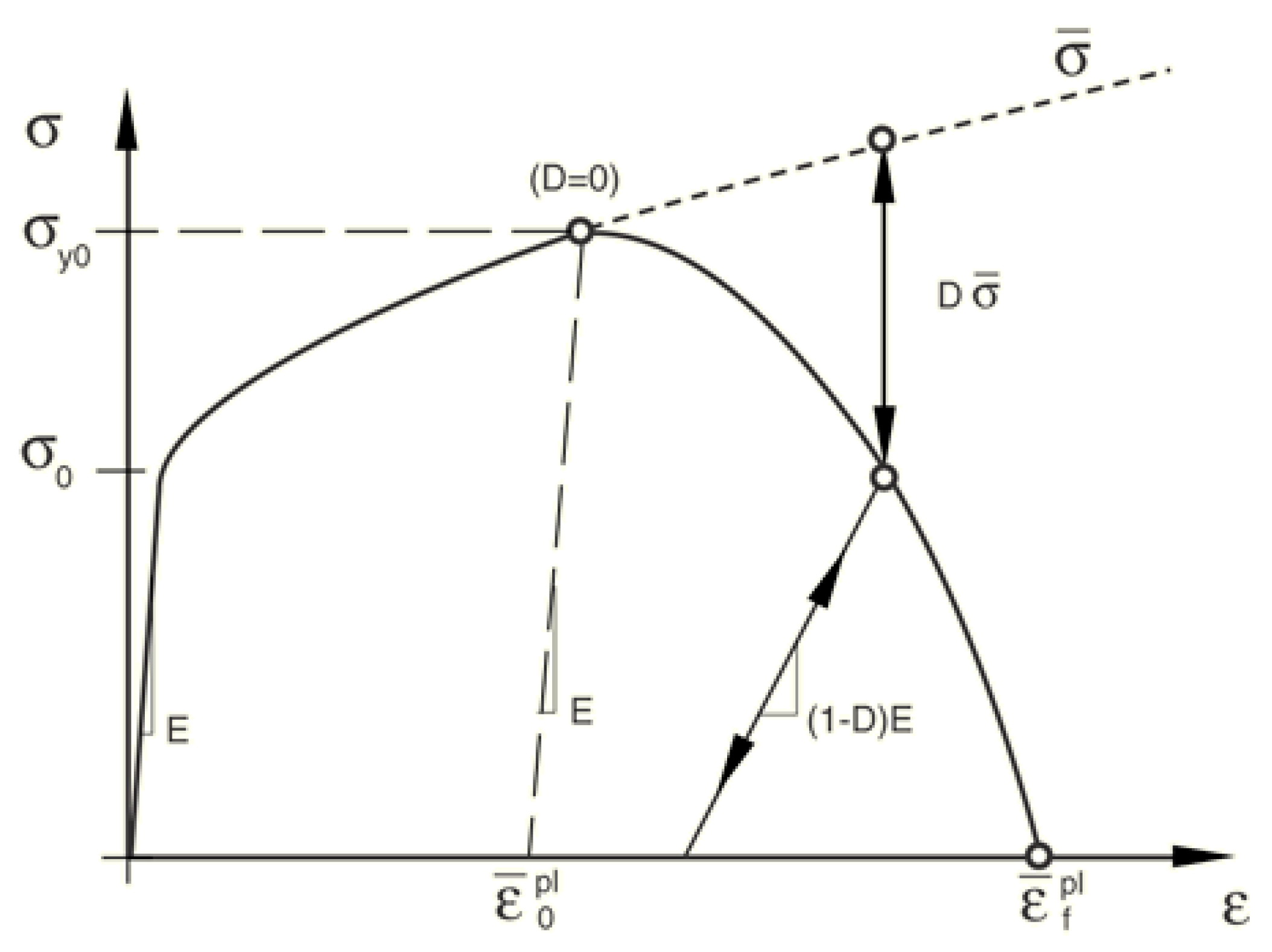
3.2. Damage Evolution Rules
3.3. Constitutive Model
3.4. Numerical Implementation Algorithm
4. Comparison with Experimental Results
4.1. Specimen
4.2. Experimental Set-Up
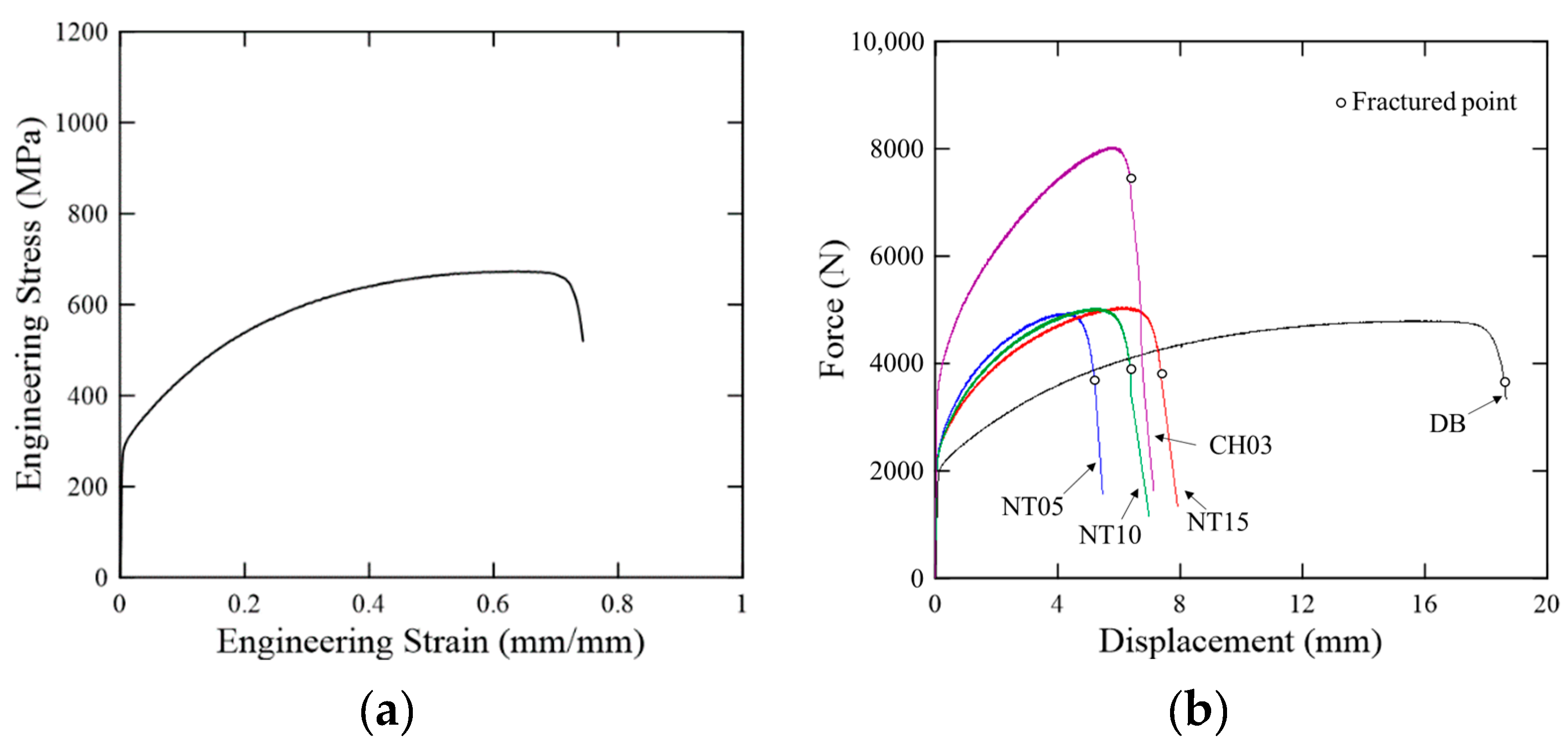
4.3. Experimental Results
5. Calibration of Ductile Fracture Model
5.1. FE Model
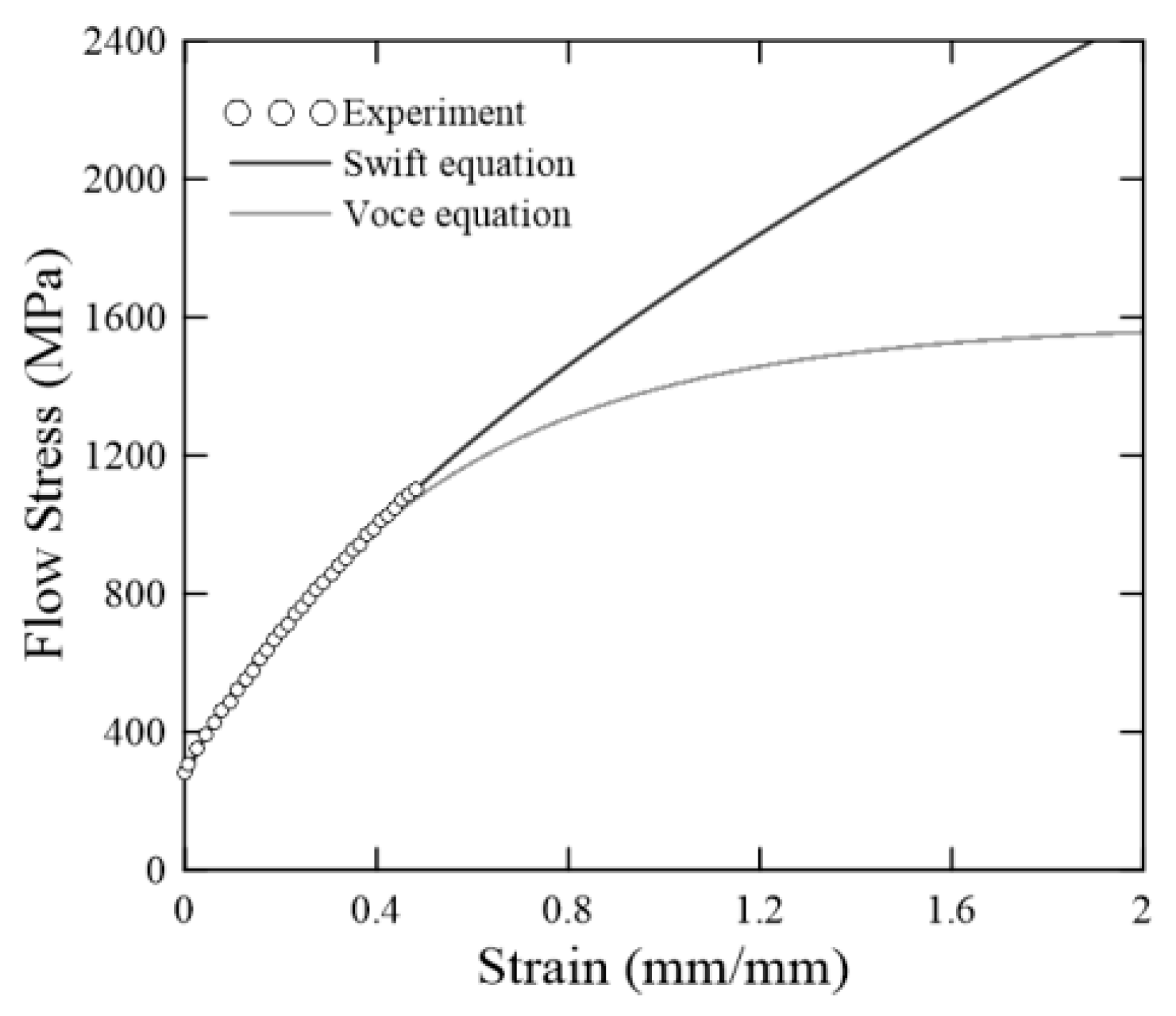
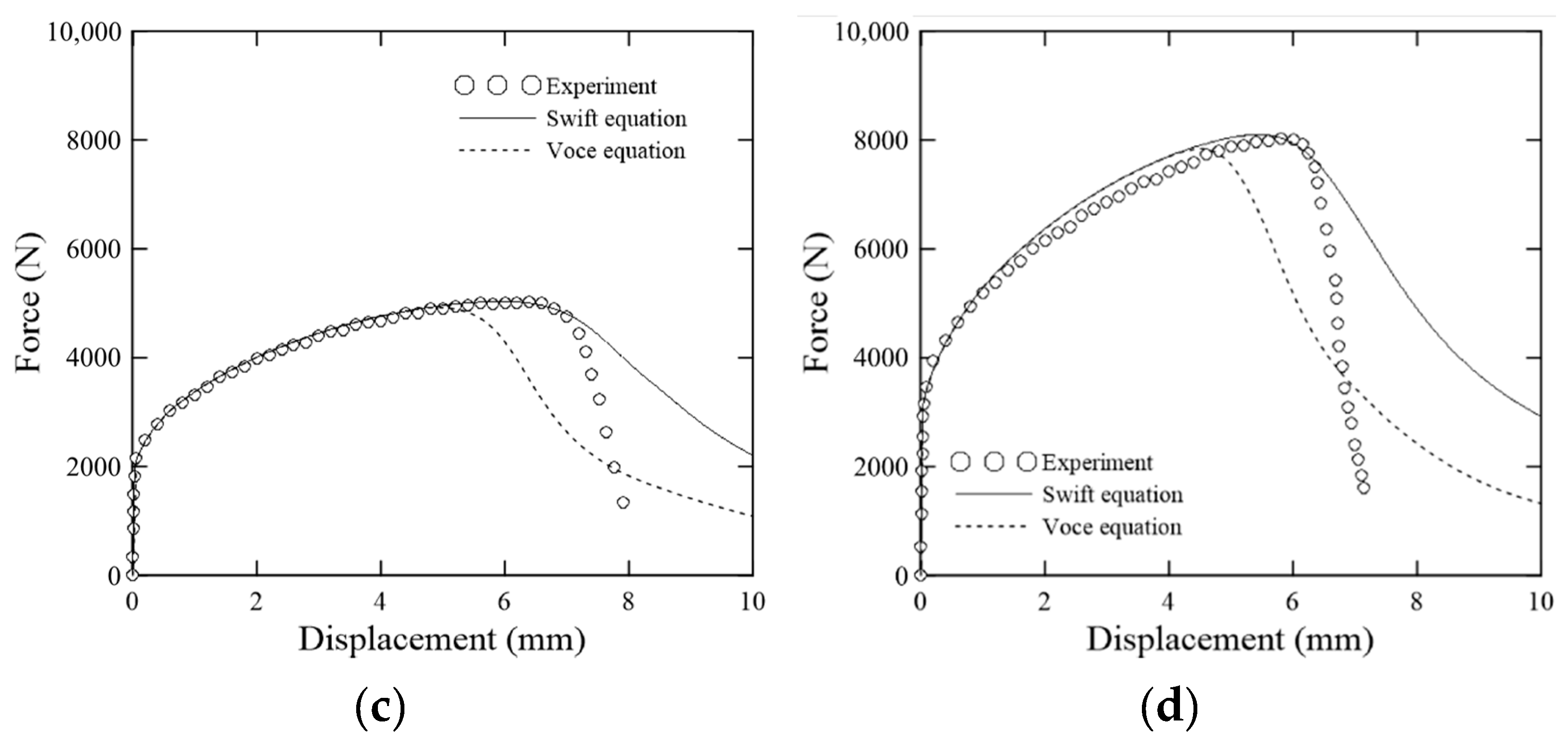
5.2. Calculation of Flow Stress
5.3. Loading Path to Failure
5.4. Determination of Fracture Parameters
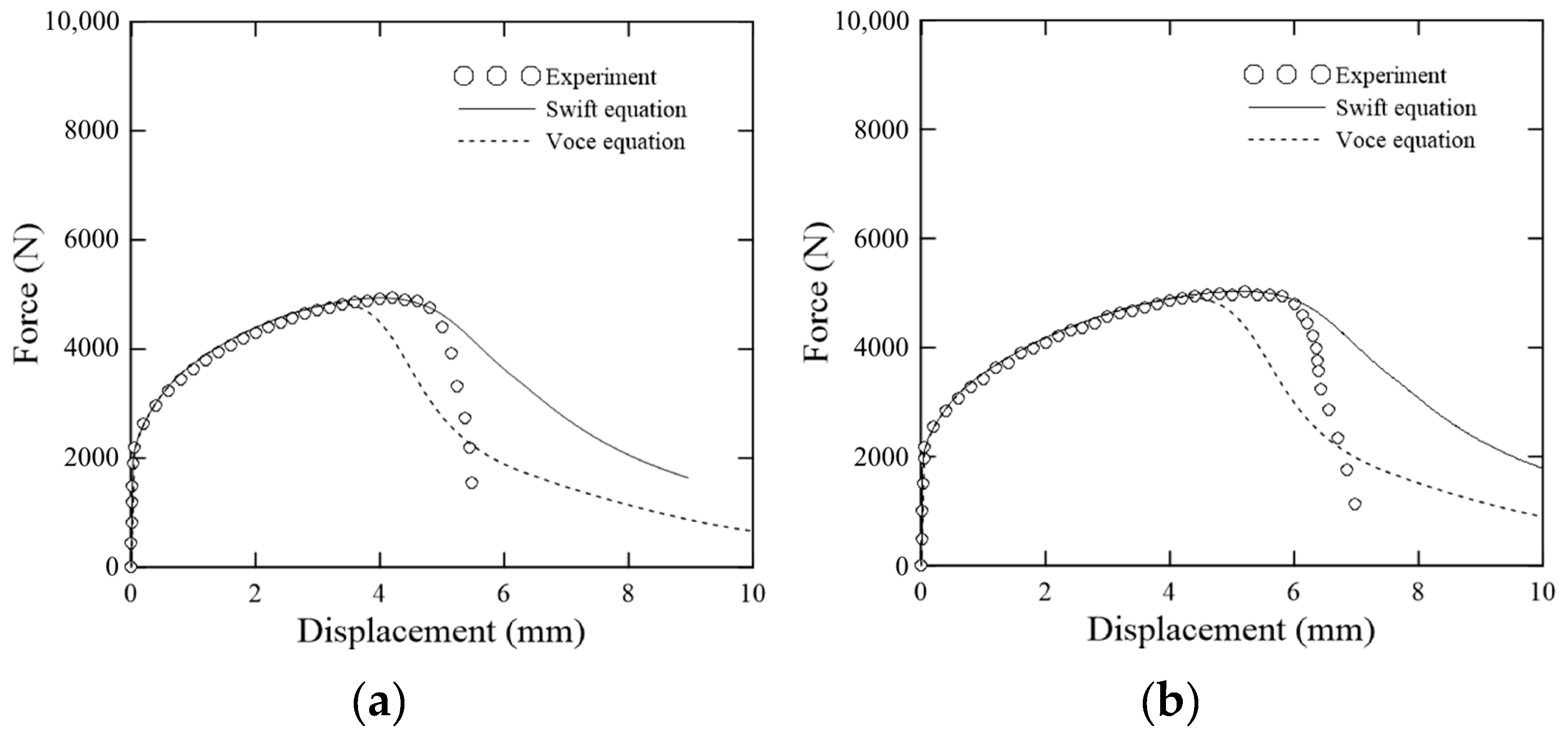
6. Prediction of Ductile Fracture
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jia, S.; Tan, Q.; Ye, J.; Zhu, Z.; Jiang, Z. Experiments on dynamic mechanical properties of austenitic stainless steel S30408 and S31608. J. Constr. Steel Res. 2021, 179, 106556. [Google Scholar] [CrossRef]
- Kim, J.-H.; Park, W.-S.; Chun, M.-S.; Kim, J.-J.; Bae, J.-H.; Kim, M.-H.; Lee, J.-M. Effect of pre-straining on low-temperature mechanical behavior of AISI 304L. Mater. Sci. Eng. A 2012, 543, 50–57. [Google Scholar] [CrossRef]
- Kim, S.-K.; Lee, C.-S.; Kim, J.-H.; Kim, M.-H.; Lee, J.-M. Computational evaluation of resistance of fracture capacity for SUS304L of liquefied natural gas insulation system under cryogenic temperatures using ABAQUS user-defined material subroutine. Mater. Des. 2013, 50, 522–532. [Google Scholar] [CrossRef]
- Zheng, C.; Liu, C.; Ren, M.; Jiang, H.; Li, L. Microstructure and mechanical behavior of an AISI 304 austenitic stainless steel prepared by cold- or cryogenic-rolling and annealing. Mater. Sci. Eng. A 2018, 724, 260–268. [Google Scholar] [CrossRef]
- Mallick, P.; Tewary, N.; Ghosh, S.; Chattopadhyay, P. Effect of cryogenic deformation on microstructure and mechanical properties of 304 austenitic stainless steel. Mater. Charact. 2017, 133, 77–86. [Google Scholar] [CrossRef]
- Singh, R.; Sachan, D.; Verma, R.; Goel, S.; Jayaganthan, R.; Kumar, A. Mechanical behavior of 304 austenitic stainless steel processed by cryogenic rolling. Mater. Today Proc. 2018, 5, 16880–16886. [Google Scholar] [CrossRef]
- Oh, D.-J.; Kim, N.-K.; Song, S.-W.; Kim, Y.-D.; Kim, M.-H. Investigation of fatigue performance for new membrane-type LNG CCS at cryogenic temperature. Mar. Struct. 2018, 62, 90–105. [Google Scholar] [CrossRef]
- Park, S.Y.; Kim, W.T.; Choi, J.H.; On, S.Y.; Kim, S.S. Effects of process-induced residual stress and geometric characteristics on pressure-resisting capability of corrugation in primary barriers of liquefied natural gas carriers. Ocean Eng. 2021, 237, 109613. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, S.-K.; Kim, M.-H.; Lee, J.-M. Numerical model to predict deformation of corrugated austenitic stainless steel sheet under cryogenic temperatures for design of liquefied natural gas insulation system. Mater. Des. 2014, 57, 26–39. [Google Scholar] [CrossRef]
- Kim, M.-S.; Kwon, S.-B.; Kim, S.-K.; Kim, J.-H.; Lee, J.-S.M. Impact failure analysis of corrugated steel plate in LNG containment cargo system. J. Constr. Steel Res. 2019, 156, 287–301. [Google Scholar] [CrossRef]
- Kim, M.-S.; Kim, J.-H.; Kim, S.-K.; Lee, J.-M. Experimental Investigation of Structural Response of Corrugated Steel Sheet Subjected to Repeated Impact Loading: Performance of LNG Cargo Containment System. Appl. Sci. 2019, 9, 1558. [Google Scholar] [CrossRef] [Green Version]
- Kim, B.C.; Yoon, S.H.; Gil Lee, D. Pressure resistance of the corrugated stainless steel membranes of LNG carriers. Ocean Eng. 2011, 38, 592–608. [Google Scholar] [CrossRef]
- Lee, D.; Kim, K.H.; Choi, I.; Gil Lee, D. Pressure-resisting capability of the knot area of the primary barrier for a LNG containment system. Ocean Eng. 2015, 95, 128–133. [Google Scholar] [CrossRef]
- Jeong, Y.-J.; Kim, H.-T.; Kim, S.-K.; Kim, J.-H.; Kim, Y.-T.; Heo, W.-S.; Lee, J.-M. Evaluation of the pressure-resisting capability of membrane-type corrugated sheet under hydrodynamic load. Thin-Walled Struct. 2021, 162, 107388. [Google Scholar] [CrossRef]
- Deng, X.; Wang, B. Peridynamic modeling of dynamic damage of polymer bonded explosive. Comput. Mater. Sci. 2020, 173, 109405. [Google Scholar] [CrossRef]
- Depraetere, R.; De Waele, W.; Hertelé, S. Fully-coupled continuum damage model for simulation of plasticity dominated hydrogen embrittlement mechanisms. Comput. Mater. Sci. 2021, 200, 110857. [Google Scholar] [CrossRef]
- Varandas, L.F.; Catalanotti, G.; Melro, A.R.; Falzon, B.G. On the importance of nesting considerations for accurate computational damage modelling in 2D woven composite materials. Comput. Mater. Sci. 2020, 172, 109323. [Google Scholar] [CrossRef]
- Paredes, M.; Wierzbicki, T.; Zelenak, P. Prediction of crack initiation and propagation in X70 pipeline steels. Eng. Fract. Mech. 2016, 168, 92–111. [Google Scholar] [CrossRef]
- Björklund, O.; Larsson, R.; Nilsson, L. Failure of high strength steel sheets: Experiments and modelling. J. Mater. Process. Technol. 2013, 213, 1103–1117. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.-K.; Kim, J.-H.; Kim, J.-H.; Lee, J.-M. Numerical Model for Mechanical Nonlinearities of High Manganese Steel Based on the Elastoplastic Damage Model. Metals 2018, 8, 680. [Google Scholar] [CrossRef] [Green Version]
- Baltic, S.; Magnien, J.; Gänser, H.-P.; Antretter, T.; Hammer, R. Coupled damage variable based on fracture locus: Modelling and calibration. Int. J. Plast. 2019, 126, 102623. [Google Scholar] [CrossRef]
- Charoensuk, K.; Panich, S.; Uthaisangsuk, V. Damage initiation and fracture loci for advanced high strength steel sheets taking into account anisotropic behaviour. J. Mater. Process. Technol. 2017, 248, 218–235. [Google Scholar] [CrossRef]
- Hancock, J.W.; Mackenzie, A.C. On the mechanisms of ductile failure in high-strength steels subjected to multi-axial stress-states. J. Mech. Phys. Solids 1976, 24, 147–160. [Google Scholar] [CrossRef]
- Theocaris, P.S. Failure criteria for isotropic bodies revisited. Eng. Fract. Mech. 1995, 51, 239–255, 257–264. [Google Scholar] [CrossRef]
- Schiffmann, R.; Bleck, W.; Dahl, W. The influence of strain history on ductile failure of steel. Comput. Mater. Sci. 1998, 13, 142–147. [Google Scholar] [CrossRef]
- Schliiter, N.; Grimpe, F.; Bleck, W.; Dahl, W. Modelling of the damage in ductile steels. Comput. Mater. Sci. 1996, 7, 27–33. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. A new model of metal plasticity and fracture with pressure and Lode dependence. Int. J. Plast. 2008, 24, 1071–1096. [Google Scholar] [CrossRef]
- Bai, Y.; Wierzbicki, T. Application of extended Mohr–Coulomb criterion to ductile fracture. Int. J. Fract. 2010, 161, 1–20. [Google Scholar] [CrossRef]
- Kim, S.-K.; Lee, C.-S.; Kim, J.-H.; Kim, M.-H.; Noh, B.-J.; Matsumoto, T.; Lee, J.-M. Estimation of Fatigue Crack Growth Rate for 7% Nickel Steel under Room and Cryogenic Temperatures Using Damage-Coupled Finite Element Analysis. Metals 2015, 5, 603–627. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.-K.; Kang, K.-Y.; Kim, M.-S.; Lee, J.-M. Low-Temperature Mechanical Behavior of Super Duplex Stainless Steel with Sigma Precipitation. Metals 2015, 5, 1732–1745. [Google Scholar] [CrossRef] [Green Version]
- Paredes, M.; Grolleau, V.; Wierzbicki, T. On ductile fracture of 316L stainless steels at room and cryogenic temperature level: An engineering approach to determine material parameters. Materialia 2020, 10, 100624. [Google Scholar] [CrossRef]
- Dunand, M.; Mohr, D. On the predictive capabilities of the shear modified Gurson and the modified Mohr–Coulomb fracture models over a wide range of stress triaxialities and Lode angles. J. Mech. Phys. Solids 2011, 59, 1374–1394. [Google Scholar] [CrossRef]
- Luo, M.; Dunand, M.; Mohr, D. Experiments and modeling of anisotropic aluminum extrusions under multi-axial loading—Part II: Ductile fracture. Int. J. Plast. 2012, 32–33, 36–58. [Google Scholar] [CrossRef]
- Chen, X.; Shi, M.F.; Shih, H.-C.; Luo, M.; Wierzbicki, T. AHSS Shear Fracture Predictions Based on a Recently Developed Fracture Criterion. SAE Int. J. Mater. Manuf. 2010, 3, 723–731. [Google Scholar] [CrossRef]
- Granum, H.; Morin, D.; Børvik, T.; Hopperstad, O.S. Calibration of the modified Mohr-Coulomb fracture model by use of localization analyses for three tempers of an AA6016 aluminium alloy. Int. J. Mech. Sci. 2021, 192, 106122. [Google Scholar] [CrossRef]
- Quach, H.; Kim, J.-J.; Nguyen, D.-T.; Kim, Y.-S. Uncoupled ductile fracture criterion considering secondary void band behaviors for failure prediction in sheet metal forming. Int. J. Mech. Sci. 2020, 169, 105297. [Google Scholar] [CrossRef]
- Qian, L.-Y.; Fang, G.; Zeng, P. Modeling of the ductile fracture during the sheet forming of aluminum alloy considering non-associated constitutive characteristic. Int. J. Mech. Sci. 2017, 126, 55–66. [Google Scholar] [CrossRef]
- Ben Othmen, K.; Haddar, N.; Jegat, A.; Manach, P.-Y.; Elleuch, K. Ductile fracture of AISI 304L stainless steel sheet in stretching. Int. J. Mech. Sci. 2020, 172, 105404. [Google Scholar] [CrossRef]
- Pham, H.; Iwamoto, T. An evaluation of fracture properties of type-304 austenitic stainless steel at high deformation rate using the small punch test. Int. J. Mech. Sci. 2018, 144, 249–261. [Google Scholar] [CrossRef]
- Kim, J.-H.; Lee, C.-S.; Kim, M.-H.; Lee, J.-M. Prestrain-dependent viscoplastic damage model for austenitic stainless steel and implementation to ABAQUS user-defined material subroutine. Comput. Mater. Sci. 2013, 67, 273–281. [Google Scholar] [CrossRef]
- Mohr, D.; Marcadet, S.J. Micromechanically-motivated phenomenological Hosford–Coulomb model for predicting ductile fracture initiation at low stress triaxialities. Int. J. Solids Struct. 2015, 67–68, 40–55. [Google Scholar] [CrossRef]
- Palchik, V. Application of Mohr–Coulomb failure theory to very porous sandy shales. Int. J. Rock Mech. Min. Sci. 2006, 43, 1153–1162. [Google Scholar] [CrossRef]
- Zhao, J. Applicability of Mohr–Coulomb and Hoek–Brown strength criteria to the dynamic strength of brittle rock. Int. J. Rock Mech. Min. Sci. 2000, 37, 1115–1121. [Google Scholar] [CrossRef]
- Kofiani, K.; Nonn, A.; Wierzbicki, T. New calibration method for high and low triaxiality and validation on SENT specimens of API X70. Int. J. Press. Vessel. Pip. 2013, 111–112, 187–201. [Google Scholar] [CrossRef]
- Swift, H.W. Plastic Instability under Plane Stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Voce, E. The relationship between stress and strain for homogeneous deformation. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]
- Lemaitre, J. A continuous damage mechanics model for ductile fracture. J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Neto, E.A.; de Eduardo, S.; Perić, D.; Owen, D.R.J. Computational Methods for Plasticity: Theory and Applications; Wiley: Chichester, UK, 2008; ISBN 9780470694527. [Google Scholar]
- Lian, J.; Wu, J.; Münstermann, S. Evaluation of the cold formability of high-strength low-alloy steel plates with the modified Bai–Wierzbicki damage model. Int. J. Damage Mech. 2015, 24, 383–417. [Google Scholar] [CrossRef]
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Sancho, A.; Cox, M.; Cartwright, T.; Davies, C.; Hooper, P.; Dear, J. An experimental methodology to characterise post-necking behaviour and quantify ductile damage accumulation in isotropic materials. Int. J. Solids Struct. 2019, 176–177, 191–206. [Google Scholar] [CrossRef]
- Lou, Y.; Huh, H. Extension of a shear-controlled ductile fracture model considering the stress triaxiality and the Lode parameter. Int. J. Solids Struct. 2013, 50, 447–455. [Google Scholar] [CrossRef] [Green Version]
- Xue, Z.; Pontin, M.; Zok, F.; Hutchinson, J. Calibration procedures for a computational model of ductile fracture. Eng. Fract. Mech. 2010, 77, 492–509. [Google Scholar] [CrossRef] [Green Version]
- Erice, B.; Gálvez, F. A coupled elastoplastic-damage constitutive model with Lode angle dependent failure criterion. Int. J. Solids Struct. 2014, 51, 93–110. [Google Scholar] [CrossRef] [Green Version]
- Kubík, P.; Šebek, F.; Hůlka, J.; Petruška, J. Calibration of ductile fracture criteria at negative stress triaxiality. Int. J. Mech. Sci. 2016, 108–109, 90–103. [Google Scholar] [CrossRef]






| C | Si | Mn | P | S | Cr | Ni |
|---|---|---|---|---|---|---|
| 0.0152 | 0.379 | 1.130 | 0.0227 | 0.0017 | 18.653 | 10.178 |
| Swift equation part | ||||
| 1610.0 | 0.0496 | 0.6 | 0.0 | |
| Voce equation part | ||||
| 1.0 | 282.0 | 1300.0 | 1.95 |
| Specimen | Average Stress Triaxiality, | Average Normalized Lode Angle, | Equivalent Plastic Strain at Damage Initiation, |
|---|---|---|---|
| NT05 | 0.442 | 0.665 | 0.987 |
| NT10 | 0.399 | 0.799 | 0.900 |
| NT15 | 0.395 | 0.817 | 1.053 |
| CH03 | 0.343 | 0.936 | 1.262 |
| Fracture parameter | |||
| 0.016 | 961 | 1.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.-S.; Kim, H.-T.; Choi, Y.-H.; Kim, J.-H.; Kim, S.-K.; Lee, J.-M. A New Computational Method for Predicting Ductile Failure of 304L Stainless Steel. Metals 2022, 12, 1309. https://doi.org/10.3390/met12081309
Kim M-S, Kim H-T, Choi Y-H, Kim J-H, Kim S-K, Lee J-M. A New Computational Method for Predicting Ductile Failure of 304L Stainless Steel. Metals. 2022; 12(8):1309. https://doi.org/10.3390/met12081309
Chicago/Turabian StyleKim, Myung-Sung, Hee-Tae Kim, Young-Hwan Choi, Jeong-Hyeon Kim, Seul-Kee Kim, and Jae-Myung Lee. 2022. "A New Computational Method for Predicting Ductile Failure of 304L Stainless Steel" Metals 12, no. 8: 1309. https://doi.org/10.3390/met12081309
APA StyleKim, M.-S., Kim, H.-T., Choi, Y.-H., Kim, J.-H., Kim, S.-K., & Lee, J.-M. (2022). A New Computational Method for Predicting Ductile Failure of 304L Stainless Steel. Metals, 12(8), 1309. https://doi.org/10.3390/met12081309







