Incremental Capacity Curve Health-Indicator Extraction Based on Gaussian Filter and Improved Relevance Vector Machine for Lithium–Ion Battery Remaining Useful Life Estimation

Abstract

Accurate prediction of the remaining useful life (RUL) of lithium–ion batteries is the focus of lithium–ion battery health management. To achieve high–precision RUL estimation of lithium–ion batteries, a novel RUL prediction model is proposed by combining the extraction of health indicators based on incremental capacity curve (IC) and the method of improved adaptive relevance vector machine (RVM). First, the IC curve is extracted based on the charging current and voltage data. To attenuate the noise effects on the IC curve, Gaussian filtering is used and the optimal filtering window is determined to remove the noise interference. Based on this, the peak characteristics of the IC curve are analyzed and four groups of health indicators are extracted, and the strong correlation between health indicators and capacity degradation is determined using Pearson correlation analysis. Then, to optimize the traditional fixed kernel parameter RVM model, an RVM regression model whose kernel parameters are optimized by the Bayesian algorithm is established. Finally, four sets of datasets under CS2 battery in the public dataset of the University of Maryland are carried out for experimental validation. The validation results show that the improved RVM model has better short–term prediction performance and long–term prediction stability, the RUL prediction error is less than 20 cycles, and the mean absolute error is less than 0.02. The performance of the improved RVM model is better than that of the traditional RVM model.

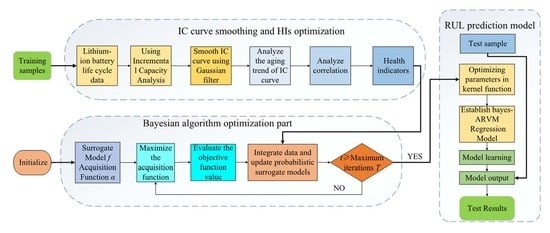
1. Introduction

As the reserves of traditional energy sources are decreasing, the development of new energy sources such as renewable energy and green energy has become the future direction of energy development [1]. With the advantages of high specific energy, small size, and recyclability, lithium–ion batteries have become one of the main research objects and application directions in the field of new energy. Therefore, how to effectively manage the lithium–ion battery state is the premise and key to the safe and stable operation of the lithium battery system [2]. Among them, remaining useful life is a key point in the process of battery management, and is also one of the indicators to evaluate the aging degree of the battery [3]. A highly accurate prediction of RUL can ensure the safe operation of lithium–ion batteries and avoid the occurrence of safety hazards.

RUL is the number of remaining charge/discharge cycles before the battery reaches the failure threshold under certain charge/discharge conditions [4]. Usually, the battery reaches the end of life (EOL) when the capacity degrades to 70% or 80% of the rated capacity, and the RUL can obtain the remaining number of cycles to reach the EOL of the lithium–ion battery in advance to give an early warning of the aging battery and effectively reduce the possibility of failure. At the same time, the complex electrochemical mechanism involved in battery aging makes the RUL estimation method more challenging. In recent years, model–based methods have been gradually replaced by data–driven methods in battery–aging diagnosis and evaluation, and the study of how to use externally measurable voltage and current data, etc., in the battery–aging process to replace the complex internal battery–aging mechanism is the focus of scholars’ research [5]. In this regard, data–driven methods have been widely studied and applied. The data–driven approach can be applied to various types of batteries and can achieve more accurate estimation, which is not possible with model–based approaches [6]. The essence of the data–driven approach is to extract health indicators that characterize the historical and current data of the battery system to predict the next stage of battery aging state.

How to extract health indicators (HIs) to qualitatively characterize the aging characteristics of batteries is an important prerequisite for using data–driven methods. Many studies have used direct health characteristics such as capacity degradation trend and internal resistance as objects of study, but it is difficult to obtain capacity degradation data and internal resistance changes of lithium–ion batteries during actual use, so it is not appropriate to use direct health characteristics as the object of study. Therefore, many scholars have extracted numerous features as HIs for their research by using external measurable battery data such as voltage, current, temperature, and time variation scales [7,8]. Guo et al. [9] extracted 14 health features by studying the regular changes of voltage and current curves during the charging phase, and used gray correlation analysis (GRA) to investigate the correlation between HIs and capacity degradation using NASA data for validation, and good results were achieved. However, such a method can only be extracted at some high sampling frequency with intact information, and if the sampling interval is large, such a method to study with the help of curve transformation law does not apply to data with incomplete information. Compared with the traditional methods, the use of incremental capacity analysis (ICA) [10] and differential voltage analysis (DVA) [11] has good performance in estimating RUL and can reflect the aging mechanism of the battery. ICA and DVA start with IC and differential voltage (DV) curves by deriving the capacity–voltage curve and studying the peak size, location, and area variation law [12]. DVA has limited application for RUL, which is a capacity–based study, because it is mainly for voltage variation. Therefore, the IC curve is more widely used in predicting battery capacity and RUL. In addition, ICA–based RUL estimation has shown good adaptability to the uniform chemical evolution process of different batteries. Dubarry et al. [13] conducted a large number of experiments to verify the correlation between the peak change of IC curve and the phase change of cathode material using different batteries, and related the IC curve change pattern to the battery–aging mechanism and attributed it to three degradation modes, namely loss of lithium inventory (LLI) and loss of active material on the positive and negative electrodes (LAM_NE, LAM_PE, respectively). In addition, a large number of studies have verified the feasibility of IC curves for capacity estimation. Based on IC curves, more scholars use data–driven methods to go for RUL estimation. For example, Lin et al. [14] used the ICA method with the backpropagation neural network (BPNN) to convert constant–current and constant–voltage charging data into IC curves, and then built corresponding BPNN for multiple voltage segments to supplement the information, and finally experimentally verified that the maximum average absolute error of the estimated capacity did not exceed 2%. Zhou et al. [15] proposed a new RUL estimation method based on incremental capacity analysis and Gaussian process regression (GPR). The estimation method was constructed by analyzing the characteristics of battery aging under high rate charging, and finally the proposed method was validated on two rechargeable battery datasets, and the model estimation accuracy was greatly improved.

The IC curve is defined as dQ/dV and the discretization can be approximated as ΔQ/ΔV. Among them, Q represents the current capacity of the battery and V refers to the current terminal voltage value of the battery. The step size Δ depends on the sampling interval of the experimental data, i.e., the sampling frequency. Li et al. [16] studied in depth the effect of different sampling frequencies on the peak of the IC curve. They compared six different sampling frequencies and found that too high a sampling frequency makes the peak appear large and noisy due to the appearance of a voltage plateau, which makes the derivative curve spike. Therefore, it is concluded that the peak of the IC curve is highly sensitive to noise. Thus, how to obtain a smooth IC curve is a prerequisite for extracting a reliable HI. Nowadays, some scholars smooth the volume–voltage curve by mathematical models [17], such as the peak–fitting function and least–squares method, and then obtain the smooth IC curve, but this method tends to cover the original characteristic information of IC and artificially create the characteristics of the IC curve. On the other hand, many scholars have proposed a series of curve–noise–reduction methods starting from IC curves, such as moving average filtering [18], least–squares [19], Gaussian filter [7], support vector regression [20], Savitzky–Golay (S–G) filtering [21], etc. The Gaussian filter is widely used due to its simplicity, fast operation speed, and ease at finding the suitable window length. Combining the above, the curve–denoising method studied in this paper carries out research with Gaussian filtering as the core.

The selection of a suitable prediction model is the key to accurate RUL prediction. RVM is a machine learning method well–suited for lithium–ion battery RUL prediction because it has the advantages of low computational effort, no need to satisfy Mercer’s condition for the kernel function, and strong generalization ability [22]. Chen et al. [23] proposed a fusion algorithm of RVM and the generalized learning system (BLS), firstly, the training data are input into the BLS network, different prediction starting points are set, and the corresponding prediction data are output. The experimental results show that the BLS–RVM has higher prediction accuracy and stronger long–term prediction and generalization ability, and its root–mean–square error is about 0.01. Wei et al. [24] introduce the phase–space reconstruction method as the input of RVM in order to enhance the long–term prediction ability of the RVM model, with the aim of enhancing the long–term prediction performance of the capacity data. The results show that the long–term prediction ability of the RVM model is greatly enhanced. Although these papers achieved good prediction results, they are all centered on the RVM model with fixed kernel parameters, due to the role of the kernel function to map nonlinear data into a high–dimensional space and make it linearly differentiable in the high–dimensional space [25]. Therefore, using the RVM model with fixed kernel parameters does not give full play to the advantages and predictive power of the RVM model. Therefore, it is necessary to optimize the parameters of the kernel function on the premise of choosing a suitable kernel function, and constructing an adaptive RVM model is one of the focuses of this research. At the same time, how to obtain the optimal kernel parameters of the kernel function is the key to construct adaptive relevance vector machine (ARVM). Currently, the commonly used parameter–finding algorithms are the genetic algorithm (GA) [26], particle swarm algorithm (PSO) [27], fruit fly optimization algorithm (FOA) [28], Bayesian optimization algorithm (BOA) [29,30], etc. Since BOA has the advantages of being a simple algorithm, easy to understand, and having fewer parameters compared with other optimization algorithms, it is widely used in science and engineering fields. Therefore, the BOA algorithm was chosen in this study to carry out the research in order to obtain the optimal ARVM model.

In summary, in this paper, three aspects of IC curve extraction and smoothing, ARVM model, and Bayesian algorithm are investigated to develop a reliable and accurate RUL prognostic model. The three main contributions are as follows:

(1) Using the charging data of a battery to extract the IC curve, using the moving average window, S–G filtering method, and Gaussian filtering to smooth the IC curve, to find the most suitable filtering window, this paper compares the smoothing effect of four windows (10, 25, 50, 100) to finally determine the best filtering method and filtering window.

(2) Based on the degradation trend and peak characteristics of the IC curve, four groups of features are extracted, and the correlation between the features and capacity degradation is analyzed by using the Pearson correlation analysis method, and finally a collection of lithium–ion battery health indicators is formed.

(3) The adaptive RVM model is proposed, and the polynomial kernel is selected to construct the RVM model according to the capacity degradation characteristics of lithium batteries. To optimize the parameters of the polynomial kernel function, the BOA algorithm is used to optimize the kernel parameters, so as to construct the BOA–based ARVM model.

The structure of this paper is as follows: Section 2 is IC curve smoothing and health indicator extraction. Section 3 is the construction of the ARVM model, including the construction of the RVM regression model, the selection of kernel function, the optimization of kernel parameters by Bayes algorithm, and the overall flow chart. In Section 4, experimental validation with two different prediction starting points is performed. Section 5 is the conclusion and outlook.

2. IC Curve Smoothing and HI Extraction

2.1. Experimental Dataset Analysis

This study uses the battery–aging dataset from the CALCE Engineering Center at the University of Maryland and chooses to use experimental data from the cyclic charging and discharging of CS2 with batteries. The battery–aging experiment is divided into a constant–current and constant–voltage charging part and a constant–current discharging part. The charging process can be divided into two stages of constant current (CC) and constant voltage (CV), i.e., the CC–CV charging mode is used. During the charging process, the lithium–ion battery is first charged with 0.5 C constant current, and the battery voltage reaches 4.2 V before switching to constant–voltage charging until the charging current drops to 0.05 A and charging ends. In the discharge stage, the discharge process is completed by using 1C current to the end voltage of 2.7 V. The dataset records the battery voltage, battery current, battery temperature, time parameters and capacity parameters during the charging phase. The lithium–ion battery is cyclically charged and discharged until the battery reaches the EOL standard and the aging experiment is terminated. In this paper, the charge/discharge cycle data of four groups of batteries were selected, and their battery and experimental parameters are shown in

Table 1. Use of battery data parameters.

Battery Number	Ambient Temperature	Rated Capacity	Discharge Current	Cut off Voltage	EOL
CS2–35	24 °C	1.1 Ah	1.1 A	2.7 V	0.9 Ah
CS2–36					0.85 Ah
CS2–37					0.9 Ah
CS2–38					0.9 Ah

.

This study will use these four sets of data to carry out the next step. The capacity degradation curve of the used battery is shown in Figure 1.

Figure 1 shows the capacity degradation curves of the four sets of data selected, and this paper will use the data as the basis to explore the IC curve smoothing and feature extraction and the construction of an RUL estimation model with high accuracy.

2.2. IC Curve Extraction and Smoothing

ICA is a common tool for studying the remaining cycle life of lithium–ion batteries. IC curve is defined as the derivative of the capacity–voltage curve of the CC–CV charging process of the battery. That is, it is defined as the derivative of the charging capacity with respect to the voltage. The definition is shown in Equation (1).

$$\mathrm{IC}=\frac{dQ}{dV}=\frac{\Delta Q}{\Delta V}=\frac{Q_{t+1}-Q_t}{V_{t+1}-V_t}$$

(1)

where Q_t and V_t denote the battery capacity and voltage at moment t during the charging process, and the step size Δ depends on the sampling frequency of the aging experiment. According to the defined equation, the raw IC curves of CS2–35 and CS2–36 at the 50th cycle are plotted, as shown in Figure 2.

From Figure 2a,b, it can be seen that the peak of the IC curve is not obvious due to the large amount of noise in the measurement process, and it is difficult to extract the effective HIs for capacity estimation. Therefore, to further obtain an identifiable IC curve, this study synthesizes the filter–smoothing methods from the reference literature and selects the commonly used moving window average filter, S–G filter, and Gaussian filter to smooth the IC curve for the study. A more suitable filtering method is selected for smoothing. The following are the smoothed curves using the above three filtering methods at different window values, as shown in Figure 3.

As shown in Figure 3, from the original IC curve, there are two obvious peaks: the first peak area in (3.75, 3.85) and the second peak area in (3.85, 3.95) two voltage intervals; to extract the characteristic change pattern on the IC peaks, the IC curve was smoothed using moving window averaging filter (IC–Movmean), S–G filter (IC–Sgolay) and Gaussian filter (IC–Guass) to smooth the IC curve, and four different windows (10, 25, 50, 100, respectively) were selected to compare the smoothing effect. From Figure 3a, we can see that the three filtering methods in the case of window = 10; although the first peak area is smoothed better, the second peak area is poorly smoothed, and the peak also has multiple fluctuation points, which may lead to errors in HI extraction in the subsequent second peak interval, and this situation is often referred to as undersmoothing. As can be seen from Figure 3b, the smoothing effect of the IC–Movmean curve in the first peak interval appears to deviate substantially from the peak contour of the original IC curve, specifically by presenting a straight line through the peak interval, making the peak interval seriously deformed and unable to propose HIs, a situation usually referred to as oversmoothing. In contrast, Gaussian filtering and S–G filtering have a better smoothing effect in the first peak interval, and no phenomenon occurs. In the second peak interval, both moving window average filtering and S–G filtering showed an undersmoothing phenomenon, while Gaussian filtering had a better smoothing effect. From Figure 3c, it can be seen that in the first peak interval, all three filter curves show an oversmoothing phenomenon, which indicates that this window value is not suitable for the current data. In Figure 3d, it can be seen that oversmoothing occurs in both the first peak interval and the second peak interval. In summary, the selected window value of 25 is the best length that can guarantee the smoothness of the curve and the integrity of the feature information.

2.3. Health Indicators Extraction and Correlation Analysis

The IC curves of batteries are extracted and smoothed using the experimental data during the charging and discharging cycles of batteries. Here, CS2–35 is used as an example to plot the IC curves of multiple groups after smoothing with a 25–window value Gaussian filter, as shown in Figure 4.

As shown in the aging trend in Figure 4, it can be seen from Figure 4a that two peak intervals (named Peak I and Peak II, respectively) appear clearly in the IC curve as the number of cycles increases, and the IC curve as a whole shifts downward to the right. At the same time, peak I and peak II also changed downward to the right with the shift of IC, and the information of obvious changes could be extracted from the two peaks for the next step of the study. In this study, a total of four groups of features, peak height and peak position, were extracted from the two peaks, respectively, for analysis, as shown in Figure 4b. In order to represent the trend of the four groups of features more visually with the aging degree, the feature change curve of CS2–35 was plotted, as shown in Figure 5.

As shown in Figure 5, to explore the correlation between the four groups of His and capacity degradation, Pearson correlation analysis was used to investigate the correlation between His and capacity degradation. In general, the higher the correlation between the input features and the output of the data–driven model, the better the accuracy of the model. Pearson correlation coefficient [31] is widely used to study the degree of linear correlation between two variables, and the calculation formula is shown in Equation (2).

$${\rho }_{xi}=\frac{\mathsf{\Sigma }\left(x_j-{\overline{x}}_j\right)\left(y-\overline{y}\right)}{\sqrt{\mathsf{\Sigma }{\left(x_j-{\overline{x}}_j\right)}^2\mathsf{\Sigma }{\left(y-\overline{y}\right)}^2}}$$

(2)

where x_j is the characteristic sequence, y is the reference sequence of battery capacity degradation, and ${\overline{x}}_j$ and $\overline{y}$ are their mean values, respectively. The correlation degree between CS2–35 capacity degradation and the four groups of HIs is calculated according to Equation (2). To see more intuitively whether there is a linear relationship between them, the following four sets of curves are plotted with HI as the horizontal axis and capacity as the vertical axis, and the calculated Pearson correlation coefficients are given together in the figure, as shown in Figure 6.

The Pearson correlation coefficient is between −1 and 1. The closer its absolute value is to 1, the stronger the correlation between the two variables. It is clear from Figure 6a,c that the correlation coefficient is close to 1, indicating a strong positive correlation between the CS2–35 battery capacity and the two peak heights. In addition, it can be seen from Figure 6b,d that the position is negatively correlated with the capacity, but the correlation degree of peak I is low, while the correlation of peak II is more significant whether the peak position is chosen, as HIs are needed to further analyze the correlation degree of other batteries. The Pearson correlation coefficients of the four selected batteries were further calculated by using Pearson correlation analysis to screen reliable HIs as the input to the prediction model, and the calculation results are shown in

Table 2. Results of Pearson correlation coefficient calculation for 4 groups of cells.

HIs	I Peak Value	I Peak Position	II Peak Value	II Peak Position
CS2–35	0.8019	−0.4759	0.9555	−0.9147
CS2–36	0.8759	−0.8370	0.9579	−0.9196
CS2–37	0.7751	−0.5186	0.9608	−0.8718
CS2–38	0.7494	−0.7507	0.9567	−0.2942

.

From Table 2 above, it can be seen that the I peak value and II peak value have a higher correlation in all four groups of cells, among which the lowest correlation of the II peak value is 0.9555, showing a strong correlation, and the lowest of the I peak value is 0.7494, while the others are around 0.8, indicating that this HI has a strong correlation with capacity. It makes sense to select two sets of HI, the I peak–peak value and the II peak–peak value. From the size of the correlation of the I peak position, the correlation of the CS2–36 battery and CS2–38 battery is higher, while the correlation of the CS2–35 battery and CS2–37 battery is lower. From the size of the correlation of the II peak position, the correlation of the other three groups of batteries is higher except for the CS2–38 battery, which has a lower correlation, and in combination with the above, the correlation of the four groups of batteries in the peak position cannot be kept consistent. If only the peak is used as HI without considering the peak position, the feature dimension is too small and the problem of underfitting may occur, so this study selected the highest three groups of HI for each battery as the set of HIs on the basis of Table 2, and the HI table was selected as shown in

Table 3. Collection of selected HIs.

	HIs1	HIs2	HIs3
CS2–35	I peak value	II peak value	II peak position
CS2–36	I peak value	II peak value	II peak position
CS2–37	I peak value	II peak value	II peak position
CS2–38	I peak value	I peak position	II peak position

.

The accuracy of battery capacity estimation and the accuracy of RUL prediction are directly related to the selection of HIs. Selecting three HIs with high correlation as feature inputs can avoid the occurrence of underfitting, as well as eliminating HIs with lower correlation to ensure the effectiveness of data preprocessing and the accuracy of model prediction.

3. Improved Adaptive RVM Model Based on Bayesian Optimization

After having the health indicators with high correlation as the model input, the RVM model is selected as the prediction model. In this paper, the traditional RVM with fixed kernel parameters is improved, and an ARVM model with adaptive kernel function is proposed to improve the accuracy and robustness of the model.

3.1. Relevance Vector Machine Regression Model

The RUL forecasting problem can be categorized as a multistep forecasting problem for time series, which is essentially a relevance vector regression problem. Given a data set {x_i, t_i${\}}_{i=1}^N$, N is the number of samples. A nonlinear model can be built, t = y(x) + ε, where y (·) is a nonlinear function and ε~N(0, σ²) is an independent Gaussian noise, which can be written in model form as shown in Equation (3).

$$y\left(x\right)={\displaystyle \sum _{n=1}^N{w}_{n}k\left(x,x_n\right)}+b$$

(3)

where w = [w₁, ⋯, w_N] denotes the relevance vector regression weight, k(x,x_n) is the kernel function, and the key to RVM regression is the introduction of a separate hyperparameter α_i for the weight parameter w_i, as shown in Equation (4).

$$p\left(w\left|\alpha \right.\right)={\displaystyle \prod _{i=1}^M{\rm N}\left(w_i\left|0,{\alpha }_i^{-1}\right.\right)}$$

(4)

wherein α_i denotes the precision of the corresponding parameter w_i, $\alpha =\left({\alpha }_1,\dots ,{\alpha }_M\right)$. The posterior probability distribution of the weights using literature [22] is given in Equation (5).

$$p\left(w\left|t,X,\alpha ,\beta \right.\right)={\rm N}\left(w\left|m,\mathsf{\Sigma }\right.\right)$$

(5)

where the mean $m=\beta \cdot \mathsf{\Sigma }\cdot {\mathsf{\Phi }}^{T}t$ and the covariance $\mathsf{\Sigma }={\left(A+\beta {\mathsf{\Phi }}^T\mathsf{\Phi }\right)}^{-1}$, Φ is the design matrix of N × M. The values of α and β can be approximated by maximizing the marginal likelihood function. Referring to the literature [22], the re–estimation equations of α, β are obtained as shown in Equation (6).

$$\left\{\begin{array}{l}{a}_i^{new}=\frac{{\gamma }_i}{m_i^2}\\ {\left({\beta }^{new}\right)}^{-1}=\frac{{‖t-\mathsf{\Phi }m‖}^2}{N-{\mathsf{\Sigma }}_i{\gamma }_i}\end{array}\right.$$

(6)

wherein m_i is the i–th component of the posterior mean m, γ_i measures the corresponding parameter w_i, ${\gamma }_i=1-{\alpha }_i{\mathsf{\Sigma }}_{ii}$. ${\mathsf{\Sigma }}_{ii}$ is the i–th diagonal element of the posterior covariance Σ. For a new set of data x_* (health indicator series), the corresponding predicted capacity and predicted variance are shown in Equation (7).

$$\left\{\begin{array}{l}{t}_{*}=m^T\mathsf{\Phi }\left(x_{*}\right)\\ {\sigma }_{*}^2={\left({\beta }^{\max }\right)}^{-1}+\mathsf{\Phi }{\left(x_{*}\right)}^T\sum \mathsf{\Phi }\left(x_{*}\right)\end{array}\right.$$

(7)

t_* is the predicted capacity at of the RVM model at the health indicator x_*.

3.2. Adaptive Kernel Function Based on Bayesian Optimization Algorithm

3.2.1. Analysis and Selection of Kernel Functions

In RVM, kernel functions play the role of mapping nonlinear data into a high–dimensional space, making them linearly differentiable in the high–dimensional space. However, there are inevitably hyperparameters in each kernel function, and usually, the process of model construction is to determine the size of hyperparameters by virtue of previous experience, but this has great limitations. Therefore, this paper proposes an adaptive kernel function construction method for RVM. Firstly, a suitable kernel function needs to be selected, and the commonly used kernel functions are linear kernel function, Gaussian kernel function, and polynomial kernel function. Among then, the polynomial kernel function has a wide range of application, good global generalization performance, and strong long–term prediction performance, and the expression is shown in Equation (8).

$$K_{poly}\left(x,x_i\right)={\left(\gamma \cdot x\cdot x_i^T+c\right)}^d$$

(8)

where γ is the width of the kernel function, c is the bias, and d denotes the highest count term. The lithium–ion battery degradation process is a highly nonlinear process, and it can be seen from Figure 1 that the capacity degradation process shows a monotonically decreasing trend, with more localized capacity rebound, but the rebound is not large. Therefore, the polynomial kernel function is chosen for this study to construct the adaptive kernel function model.

3.2.2. Bayesian Optimization Algorithm

The Bayesian optimization algorithm finds the optimal value of a function by constructing the posterior probability of the output of a black box function with a known finite number of sample points [32]. Let f(x) be the mapping function from the hyperparameter vector x to the model. The goal of hyperparameter optimization is to find the hyperparameter x^* in the hyperparameter space that makes the model generalization performance optimal. In this paper, we take finding the minimum value as an example, and the objective function is shown in Equation (9).

$$x^{*}=\arg \min f\left(x\right)$$

(9)

f is a black–box objective function with high evaluation cost. Therefore, the probabilistic agent model is used to approximate the current objective function. The probabilistic agent model starts from an initial hypothetical prior and refines the model by continuously adding information to the data. The Gaussian process (GP) has become the most commonly used model in agent models due to the recursive modeling process. Assume that the function f satisfies the GP function $f\sim GP\left(\mu ,C\right)$ with mean μ and covariance C. Therefore, the prediction points also obey a normal distribution, and then we have Equation (10).

$$\left\{\begin{array}{l}p\left(y\left|x,D\right.\right)=N\left(y\left|\widehat{\mu },{\widehat{\sigma }}^2\right.\right)\\ y={\left(y_1,y_2,\cdots ,y_i\right)}^T\\ \widehat{\mu }=c{\left(x\right)}^T{\left(C+{\sigma }_n^{2}I\right)}^{-1}y\\ {\widehat{\sigma }}^2=C\left(x,x\right)-c{\left(x\right)}^T{\left(C+{\sigma }_n^{2}I\right)}^{-1}c\left(x\right)\end{array}\right.$$

(10)

where I is the unit matrix and D is the initialized data set, $D=\left(x_1,y_1\right),\cdots ,\left(x_n,y_n\right)$, $y_i=f\left(x_i\right)$. Covariance function $c\left(x\right)={\left(C\left(x,x_1\right),\cdots ,C\left(x,x_i\right)\right)}^T$, $C_{j,k}=C\left(x_j,x_k\right)$. To avoid the emergence of local optimal solutions, many studies have used the acquisition function [33] as a solution. In this paper, the probability improvement function [34] is used as the sampling function, as shown in Equation (11).

$$POI\left(x\right)=P\left(f\left(x\right)\ge f\left(x^{*}\right)+r\right)=\mathsf{\Phi }\left(\frac{\mu \left(x\right)-f\left(x^{*}\right)-r}{\sigma \left(x\right)}\right)$$

(11)

where r serves to equalize the proportion of exploitation and exploration, Φ is the normal cumulative distribution function, f(x^*) is the current maximum, μ is the mean, and σ is the standard deviation.

3.3. Adaptive RVM Prediction Model Based on Bayesian Algorithm Optimization

The flow block diagram of the adaptive RVM model optimized based on Bayesian Algorithm Optimization (BOA) is shown in Figure 7.

The RUL prediction steps based on BOA and ARVM are as follows:

(1) IC curve smoothing. In order to reduce the noise effect of ICs, the IC curve is smoothed using a Gaussian filter with a window length of 25 to obtain a more discriminative IC curve.

(2) HI extraction and analysis. According to the IC degradation trend after smoothing, four different groups of HIs were extracted for study, and the correlation between the four groups of HIs and the capacity degradation was analyzed using Pearson correlation analysis, and finally three groups of HIs with high correlation were selected as the feature vectors, as shown in Table 3. These health indicators constitute the model input sequence x for model training and testing.

(3) Kernel function hyperparameter optimization and adaptive RVM model construction. The polynomial kernel function is selected to construct the RVM regression model, and the hyperparameters in the polynomial kernel are adaptively optimized using a Bayesian optimization algorithm. The objective function is shown in Equation (12).

$$\begin{array}{l}\min f\left(x\right)=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(x\left(i\right)-\widehat{x}\left(x\right)\right)}^2}}\\ s.t.1<d<7;2e-6<g<2e+6;\\ \hfill 2e-6<c<2e+6;\hfill \end{array}$$

(12)

where the objective function is to find the minimum root–mean–square value between the predicted capacity $\widehat{y}$ and the reference capacity y under the sequence of HIs. After obtaining the optimal combination of parameters for the current kernel function according to the objective function, the polynomial kernel function is used to construct the ARVM prediction model to output the optimal prediction capacity $\widehat{y}(x)$.

(4) Model prediction. The constructed adaptive RVM model is predicted using the test set, and the RUL prediction results are output.

4. Experimental Results and Discussion

The validation experiments are divided into two separate types: one is validation using more training data to verify the short–term predictive ability of the algorithm; the other one is validation using less training data to verify the long–term expected performance of the algorithm. The training–set and test–set data groupings for the validation experiments are shown in

Table 4. Experimental classification and the basis of classification.

	Short–Term Prediction Experiments		Long–Term Prediction Experiments
	Training Data Length	Test Data Length	Training Data Length	Test Data Length
CS2–35	60% (360 cycle)	40% (140 cycle)	30% (180 cycle)	70% (420 cycle)
CS2–36
CS2–37
CS2–38

.

Three evaluation criteria are used to evaluate the performance of the algorithm, namely RE (RUL Error), MAE (Mean Absolute Error) and R² coefficient of determination as the evaluation index of the model.RE denotes the absolute error of the remaining life prediction value, MAE denotes the mean absolute error of the battery capacity prediction, and R² to quantify the performance of the model and is a measure of the predictive ability of the model. good or bad, and the value ranges from 0 to 1, which indicates the percentage of the squared correlation between the predicted and actual values of the target variable. The three evaluation criteria are shown in Equation (13).

$$\left\{\begin{array}{l}\mathrm{RE}=\left|RT-RP\right|\\ \mathrm{MAE}=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|y\left(i\right)-\widehat{y}\left(i\right)\right|}\\ {\mathrm{R}}^2=1-\frac{{\displaystyle \sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}}{{\displaystyle \sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}\end{array}\right.$$

(13)

In Equation (13), RT represents the actual RUL value of the battery, RP represents the RUL value predicted by the proposed algorithm, y(i) represents the capacity value of the i–th cycle, $\widehat{y}\left(i\right)$ represents the capacity predicted value of the i–th cycle, and $\overline{y}$ represents the average predicted values.

4.1. Short–Term Prediction Experiments

The proposed algorithm is first verified for its ability to predict battery RUL with more training data, or in another way, to verify the short–term prediction ability of the model. The experiments are compared using two prediction algorithms. The first one is a single–kernel–construction RVM model and the second one is a Bayesian optimized adaptive kernel RVM model, with the aim of exploring whether the predictive ability of the adaptive kernel model is improved compared to the conventional model. The multicore construction process is the same as the improved algorithm, and the health indicators and model parameters used in both algorithms are all the same. The results are shown in Figure 8.

In Figure 8, SP is the prediction starting point, the data before SP are used as the training sample, EOL is the lithium battery failure threshold, and the capacity degradation curve and the prediction curve drop to EOL, which is considered as the current RUL value of the battery. Among them, 80% of the initial capacity of CS2–35, CS2–37 and CS2–38 is taken as EOL, rounded to 0.9Ah. For CS2–36, if 0.9Ah is taken as EOL, the RUL is around 500 cycles. In order to make full use of the data, EOL is set to 0.85Ah. The prediction results of four datasets with 60% of the total number of cycles as the training sample for both methods are shown in the figure, respectively. Among them, C1 is the battery capacity degradation curve, C2 is the proposed algorithm BOA–ARVM, and C3 is the traditional single–kernel RVM algorithm using the polynomial kernel function to construct the model with the same kernel parameter settings. The prediction results and error analysis of C2 and C3 are shown in

Table 5. Short–term prediction experimental error analysis.

Battery Number	EOL	RT	SP	Algorithm	RP	RE	MAE	R2
CS2–35	0.9 Ah	531	360	C2	523	8	0.0081	0.9204
				C3	593	62	0.0146	0.6781
CS2–36	0.85 Ah	525	360	C2	516	9	0.0118	0.9312
				C3	486	39	0.0371	0.7123
CS2–37	0.9 Ah	550	360	C2	554	4	0.0074	0.8196
				C3	496	54	0.0325	0.5716
CS2–38	0.9 Ah	578	360	C2	577	1	0.006	0.8474
				C3	404	174	0.0444	0.3776

.

As can be seen from Table 5, the RE of the improved algorithm C2 is the smallest in all four groups of experiments, and the maximum RE is 9, which proves that the improved algorithm has good RUL estimation. The maximum RE of algorithm C3 reaches 174, and the RUL prediction of the four groups is poor, which proves the poor prediction ability of the RVM algorithm under fixed kernel parameters. In terms of the accuracy of capacity prediction, the maximum MAE of the improved algorithm C2 is 0.0081, which proves the high accuracy of capacity prediction of the improved algorithm. It can also be seen from the four sets of C2 curves in Figure 8 that the improved algorithm has good tracking ability and high accuracy of short–term prediction of capacity. From the four sets of C3 curves in Figure 8, the curves all deviate from the true capacity curve, and although the MAE is small, there are some oscillation points, which make the RUL prediction unreliable. From the reliability R² of the regression model, the closer the R² is to 1, the better the prediction of the regression model is, and the lowest value of R² of the improved algorithm is 0.81, which proves that the regression model constructed by the C2 algorithm is more reliable and the prediction results are more credible., while the lowest R² value of C3 is 0.57, which indicates that the single–kernel RVM model prediction model is not reliable. From the MAE of the four groups of experiments, the MAE are all small, with the maximum being only 0.444. Although the RUL values are poorly predicted, there is a smaller MAE, indicating that the overall capacity prediction of the prediction model deviates less from the reference value, which proves that the input training data are more accurate, i.e., the HIs obtained by smoothing the IC curve in Section 2 play a key role in model training. In summary, the short–term prediction performance of the RUL prediction model constructed by IC curve feature extraction through Gaussian filtering and BOA–ARVM algorithm is better, the RUL prediction accuracy is higher, and the prediction model is more reliable.

4.2. Long–Term Prediction Experiments

To verify the long–term predictive capability of the proposed algorithm, 30% of the data were used for training and the obtained regression model was used to validate the remaining 70% of the capacity data. The algorithm setup is the same as in Section 4.1, and the results are shown in Figure 9.

The same as described in Section 4.1, the prediction results and evaluation criteria of the two algorithms C2 and C3 are shown in

Table 6. Long–term prediction experimental error analysis.

Battery Number	EOL	RT	SP	Algorithm	RP	RE	MAE	R2
CS2–35	0.9 Ah	531	180	C2	543	13	0.0089	0.9145
				C3	461	70	0.0334	0.7077
CS2–36	0.85 Ah	525	180	C2	520	5	0.0128	0.9516
				C3	406	119	0.1044	0.4705
CS2–37	0.9 Ah	550	180	C2	543	7	0.0105	0.9153
				C3	361	189	0.0529	0.5676
CS2–38	0.9 Ah	578	180	C2	549	29	0.0114	0.8916
				C3	309	269	0.0421	0.6034

.

As can be seen from Table 6, the RE of the improved algorithm C2 is the smallest in all four groups of tests, and the maximum RE is 29, which proves that the improved algorithm has better long–term prediction ability and higher accuracy of RUL estimation. From the accuracy of capacity prediction, the maximum MAE of the improved algorithm C2 is 0.0128, which is not much different from the error of the short–term prediction experiment, proving that the improved algorithm has higher accuracy of capacity prediction with less training data. It can also be seen from the four groups of C2 curves in Figure 9 that the improved algorithm has good tracking performance, while the prediction curve of C3 in the figure deviates from the real capacity curve. From the reliability R² of the regression model, the lowest value of R² of the improved algorithm is 0.89, which proves that the long–term prediction model constructed by the C2 algorithm is more reliable. In contrast, the R² values of C3 are all concentrated at 0.5, indicating that the RVM model with fixed kernel parameters has a lower reliability of the prediction model. From the MAE of the four sets of experiments, the MAE is 0.1044 at maximum, mostly concentrated within 0.05, such as the same as described for the short–term prediction experiments, which verifies the necessity of accurate input training data. In summary, the long–term prediction performance of the RUL prediction model constructed by IC curve feature extraction with Gaussian filtering and BOA–ARVM algorithm is good.

5. Conclusions

Accurate prediction of lithium–ion battery RUL can guarantee the safe and stable operation of the battery and avoid accidents. In this paper, we propose an RUL prediction model based on health indicators and BOA–ARVM algorithm after an in–depth analysis of the current status of RUL research in recent years. It improves the problems such as imprecise and unreliable prediction of the traditional RVM model. The experimental degradation data set of the battery provided by the University of Maryland is used, and four sets of degradation data of the CS2 battery are selected for validation. Four sets of HIs were extracted from the smoothed IC curves using a Gaussian filter of 25 window length. These HIs were proved to be highly correlated with capacity by Pearson analysis. Finally, the BOA–ARVM model was established, and the RUL estimation errors in the experimental validation were all less than 20 cycles, and the MAE was less than 0.02, which proved the accuracy of the method prediction. Meanwhile, two different experiments were set up to verify the short–term prediction performance and long–term prediction accuracy of the improved model. At the same time, we realize that the model building method proposed in this paper has some shortcomings. One is that the Gaussian filter window selected for IC curve smoothing needs to be adjusted one by one, and in future work, we seek an adaptive method to adjust the window for validation. Second, the model was not validated at other temperatures, focusing on research work to explore the estimation effects of the improved model at various temperatures.