Analysis of the Effect of Magnetic Field on Solidification of Stainless Steel in Laser Surface Processing and Additive Manufacturing
Abstract
:1. Introduction
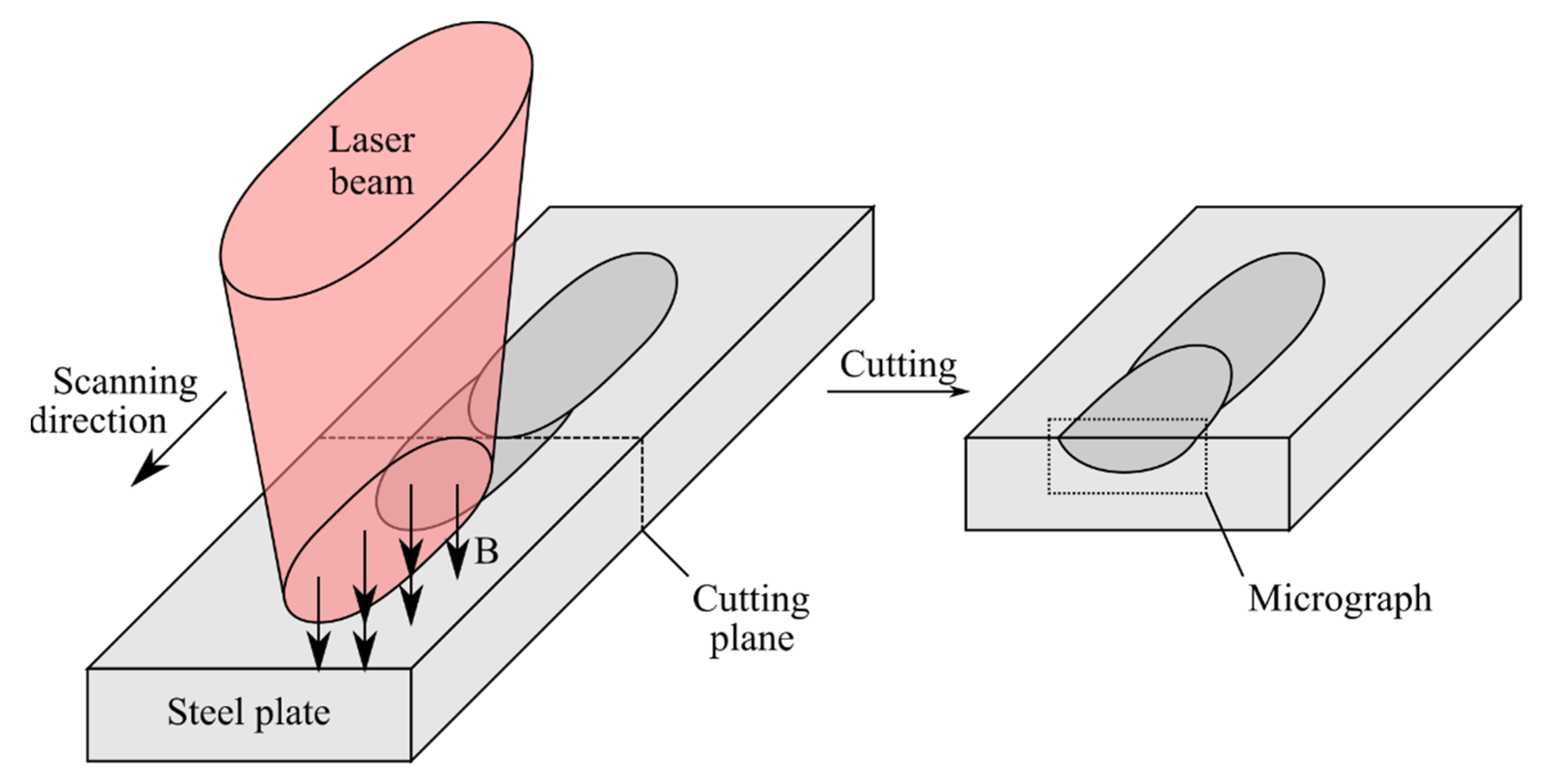
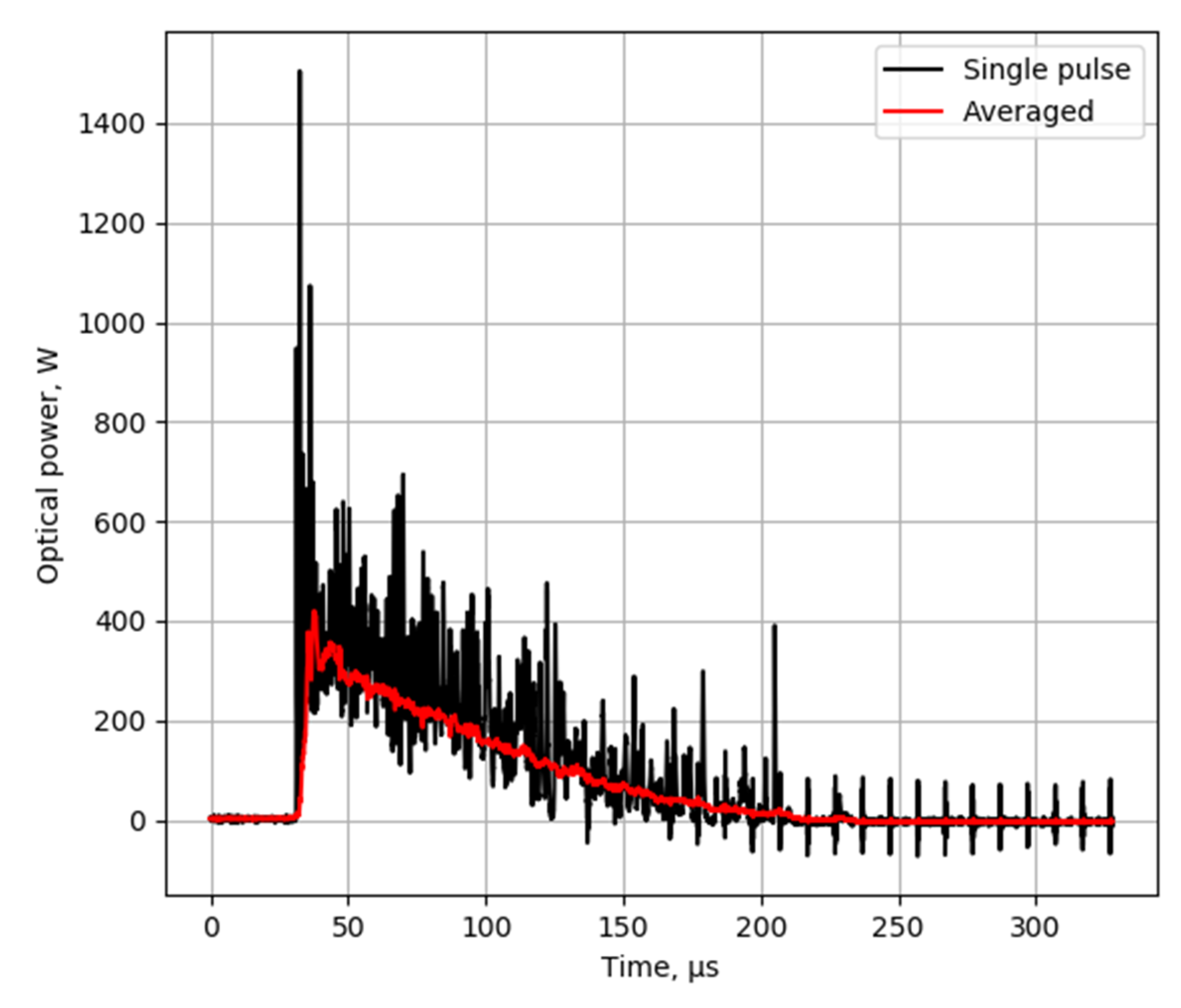
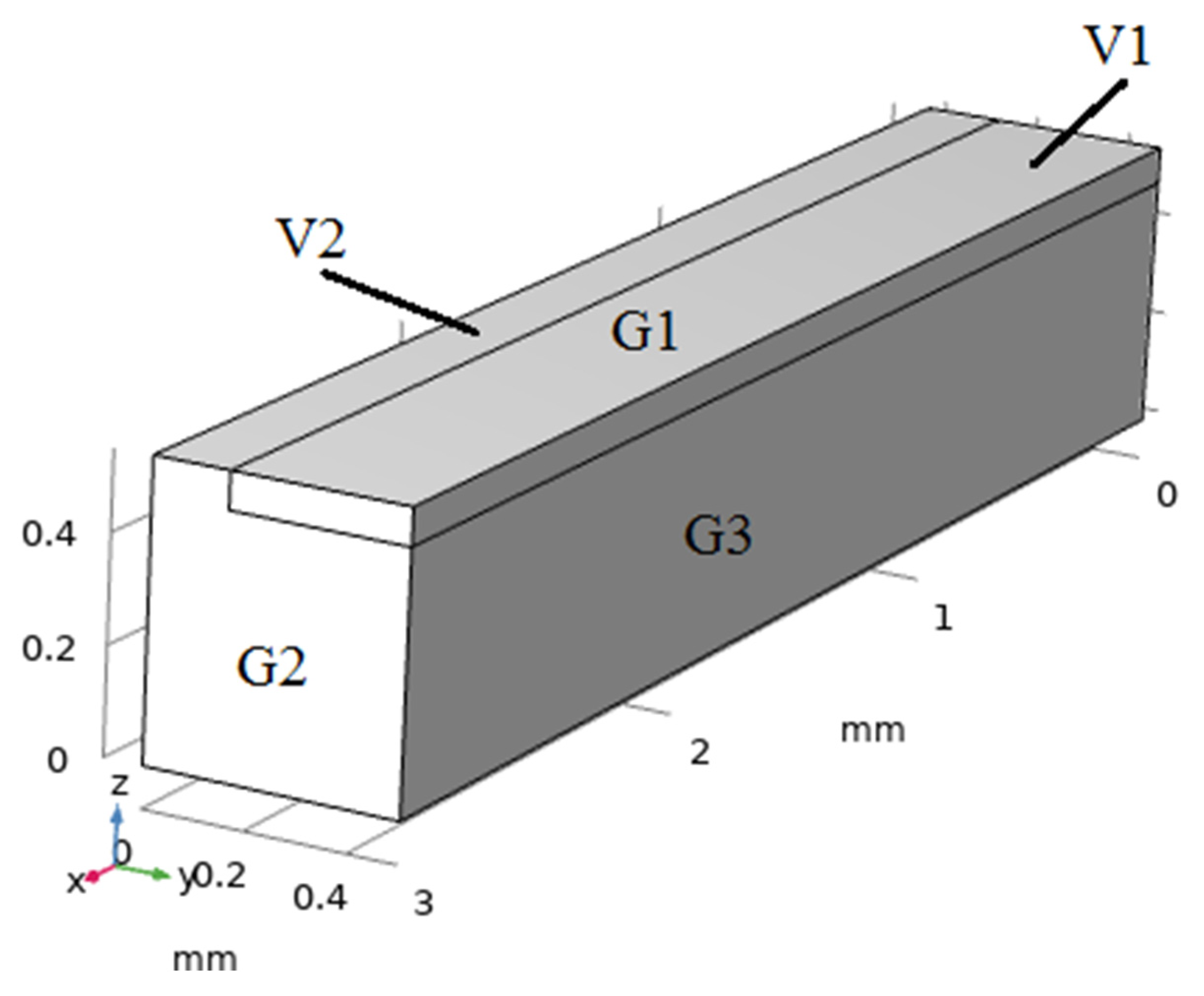
2. Experimental Methodology and Microstructure Assessment
- (1)
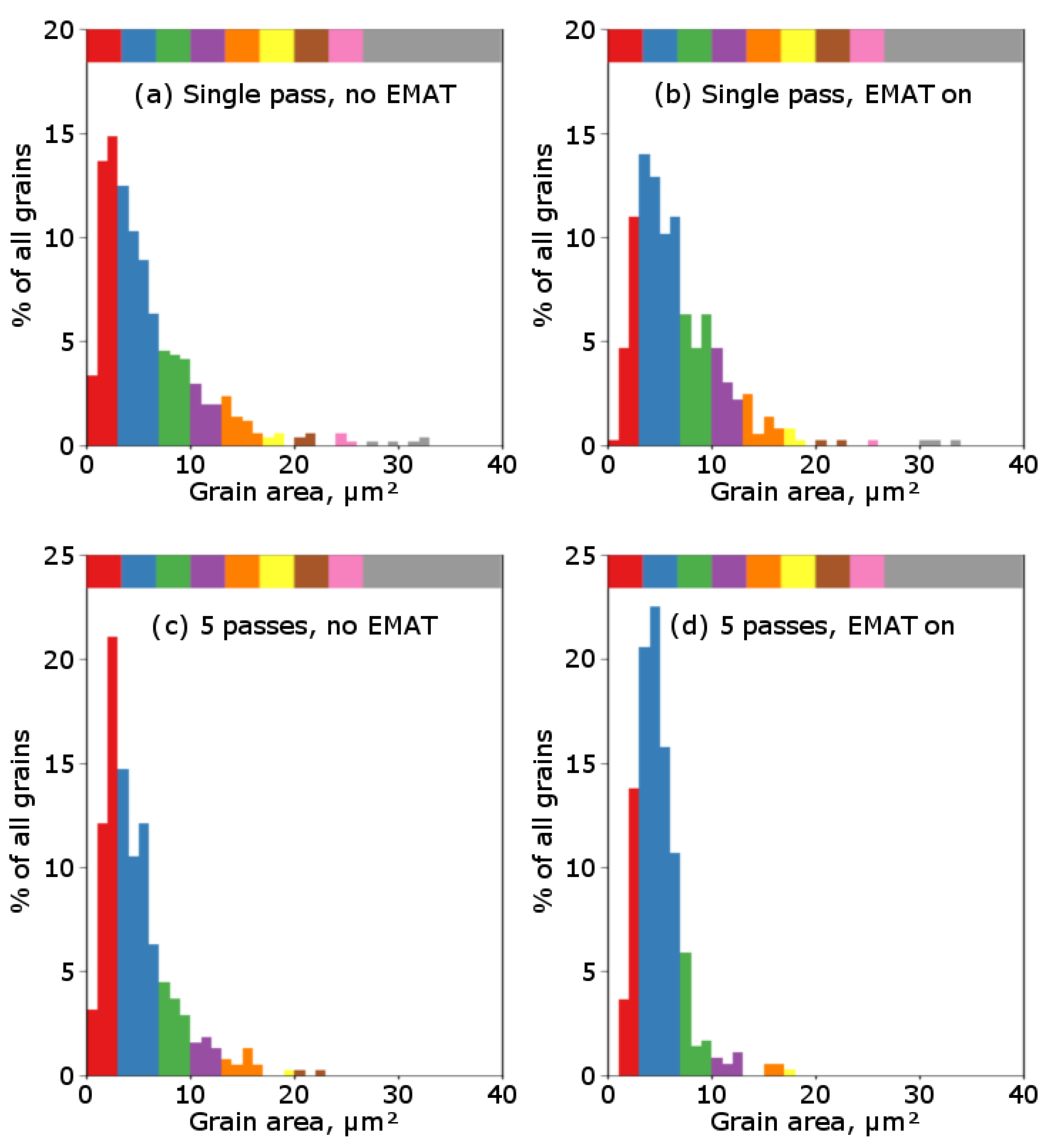
- Comparison of the histograms in Figure 5a–d, respectively, shows that the microstructure under the effect of magnetic fields is more homogeneous, and the spread in grain sizes is smaller with EMAT turned on than with EMAT turned off. The fraction of grains with an area of less than 2 µm2 or more than 15 µm2 become smaller. Presumably, the reason for this is alignment of the flow conditions near the solidification front under the influence of an electromagnetic field. Random oscillations of the convective currents from uneven laser exposure are excluded that impacts on the spatial distribution of chemical components and microsegregation.
- (2)
- The initial microstructure was characterized by an average grain area of ~30 µm2 and a median grain area of ~20 µm2. With a single laser pass, no statistically significant differences between the modes with EMAT turned off/on were detected: the average areas were 6.5 and 7.4 µm2, respectively, while the median areas were 4.5 and 5.6 µm2, respectively.
- (3)
- With five laser passes, the effect of magnetic fields leads to reduction of the number of large grains. A shift to the left (toward smaller grain areas) is clearly visible in the histograms in Figure 5c,d, respectively, when exposed to an EM field.
3. Relevant Physical Phenomena and Quantitative Estimation of the EM Field Effect
4. Effect of the Alternating EM Field on the Molten Pool
5. Effect of the Permanent Magnetic Field
6. Conclusions
- (1)
- It is confirmed experimentally that the EM field with the frequency of 100 kHz has a minor effect on the microstructure of stainless AISI 321H samples in comparison with ultrasound treatment induced by modulated laser processing.
- (2)
- The industrial parts produced by additive manufacturing techniques typically have lower plasticity in contrast to casted parts. We have received that additional EM treatment performed simultaneously with laser treatment yields a decrease of the grain’s area S (where an estimate of the grain size is related to S as d~√S) between 10% and 15%. At the same time, the histogram exhibits that the distribution becomes more narrow, i.e., the range of grain areas is smaller. The revealed effect is similar to microstructure homogenization known in heat treatment processing. The revealed new effect can facilitate the improvement of material performance owing to improvement of its plasticity.
- (3)
- The alternating magnetic field with the frequency up to 100 kHz is characterized by a skin penetration thickness in the range between 1 and 5 mm. Consequently, application of this additional exposure is more effective in laser annealing where the molten pool is sufficiently large and has the size of L ≥ 1 mm. This explains the physical background in the positive effect of applied electromagnetic fields during welding, which is noted in numerous studies available in the literature.
- (4)
- The alternating magnetic field results in the formation of the inhomogeneous Lorence force field that has a minor impact on convection in the molten pool in comparison with other physical factors of laser annealing. In the performed laboratory experiments, this effect is registered at the susceptibility threshold. The registered small modification of grain sizes can only be explained by the magnetic field effect, which is substantially mitigated by other physical phenomena in the molten pool.
- (5)
- According to the literature, the thermoelectrical Seebeck effect provides a meaningful impact on solidification of aluminum alloys owing to the intensification of convection in the zone of dendritic growth. For the case of stainless steel, it has been shown that this effect is small. It happens due to the following factors. First, the sensitivity Seebeck coefficient, which defines generation of thermoelectromotive force, is small for stainless steels. Second, the relaxation time of electromotive force is few orders of magnitude smaller than the time interval required for temperature stabilization in the molten pool.
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Moghaddam, A.O.; Shaburova, N.A.; Samodurova, M.N.; Abdollahzadeh, A.; Trofimov, E.A. Additive manufacturing of high entropy alloys: A practical review. J. Mater. Sci. Technol. 2021, 77, 131–162. [Google Scholar] [CrossRef]
- Le, K.Q.; Wong, C.H.; Chua, K.H.G.; Tang, C.; Du, H. Discontinuity of overhanging melt track in selective laser melting process. Int. J. Heat Mass Transf. 2020, 162, 120284. [Google Scholar] [CrossRef]
- Gokuldoss, P.K.; Kolla, S.K.; Eckert, J. Additive Manufacturing Processes: Selective Laser Melting, Electron Beam Melting and Binder Jetting—Selection Guidelines. Materials 2017, 10, 672. [Google Scholar] [CrossRef] [PubMed]
- Peverini, O.A.; Lumia, M.; Calignano, F.; Addamo, G.; Lorusso, M.; Ambrosio, E.P.; Manfredi, D.; Virone, G. Selective Laser Melting Manufacturing of Microwave Waveguide Devices. Proceeding IEEE 2017, 105, 620–631. [Google Scholar] [CrossRef]
- Ivanov, I.A.; Dub, V.S.; Karabutov, A.A.; Cherepetskaya, E.B.; Bychkov, A.S.; Kudinov, I.A.; Gapeev, A.A.; Krivilyov, M.D.; Simakov, N.N.; Gruzd, S.A.; et al. Effect of laser-induced ultrasound treatment on material structure in laser surface treatment for selective laser melting applications. Sci. Rep. 2021, 11, 23501. [Google Scholar] [CrossRef] [PubMed]
- Lomaev, S.; Krivilyov, M.; Fransaer, J. Exact analytical solution based on the vector potential technique for a conjugated hydrodynamic and joule heating problem in an electromagnetically levitated drop. Magnetohydrodynamics 2016, 52, 105–116. [Google Scholar] [CrossRef]
- Lomaev, S.; Krivilyov, M.; Fransaer, J.; Lee, J.; Volkmann, T.; Matson, D.M. Simulation of fluid flow in levitated Fe-Co droplets electromagnetically processed onboard the ISS. Magnetohydrodynamics 2019, 55, 251–260. [Google Scholar] [CrossRef]
- Khlybov, O.A.; Lyubimova, T.P. Effect of rotating magnetic field on mass transfer during directional solidification of semiconductors. Magnetohydrodynamics 2016, 52, 61–70. [Google Scholar] [CrossRef]
- Nick, A.S.; Vynnycky, M.; Fredriksson, H. Pores and clustering of inclusions in the continuous casting of steel. Metall. Mater. Trans. A 47 2016, 6, 2985–2999. [Google Scholar] [CrossRef]
- Goda, J.R.V.; Dhayamraji, J. Effect of Electromagnetic Stirring on continuous casting of a steel billet using 2D magnetohydrodynamic analysis. Authorea 2020. [Google Scholar] [CrossRef]
- Luo, L.; Luo, L.; Su, Y.; Su, L.; Wang, L.; Chen, R. Reducing porosity and optimizing performance for Al-Cu-based alloys with large solidification intervals by coupling travelling magnetic fields with sequential solidification. J. Mater. Sci. Technol. 2021, 79, 1–14. [Google Scholar] [CrossRef]
- Wang, P.; Shuai, S.; Huang, C.; Liu, X.; Fu, Y.; Wang, J.; Ren, Z. Revealing the influence of high magnetic field on the solute distribution during directional solidification of Al-Cu alloy. J. Mater. Sci. Technol. 2021, 88, 226–232. [Google Scholar] [CrossRef]
- Bachmann, M.; Avilov, V.; Gumenyuk, A.; Rethmeier, M. Experimental and numerical investigation of an electromagnetic weld pool support system for high power laser beam welding of austenitic stainless steel. J. Mater. Processing Technol. 2014, 214, 578–591. [Google Scholar] [CrossRef]
- Lan, Q.; Cheng, C.; Zang, J.; Guo, R.; Le, Q. The relationship between the thermoelectric power and resultant solidification microstructures of Al-Si melt under electromagnetic field. Mater. Chem. Phys 2019, 231, 203–215. [Google Scholar] [CrossRef]
- Li, X.; Fautrelle, Y.; Gagnoud, A.; Du, D.; Wang, J.; Ren, Z.; Nguyen-Thi, H.; Mangelinck-Noel, N. Effect of a weak transverse magnetic field on solidification structure during directional solidification. Acta Mater. 2014, 64, 367–381. [Google Scholar] [CrossRef]
- Meng, X.; Artinov, A.; Bachmann, M.; Rethmeier, M. Numerical and experimental investigation of thermo-fluid flow and element transport in electromagnetic stirring enhanced wire feed laser beam welding. Int. J. Heat Mass Transf. 2019, 144, 118663. [Google Scholar] [CrossRef]
- Cao, L.; Zhou, Q.; Liu, H.; Li, J.; Wang, S. Mechanism investigation of the influence of the magnetic field on the molten pool behavior during laser welding of aluminum alloy. Int. J. Heat Mass Transf. 2020, 162, 120390. [Google Scholar] [CrossRef]
- Gatzen, M. Influence of low-frequency magnetic fields during laser beam welding of aluminium with filler wire. Phys. Procedia 2012, 39, 59–66. [Google Scholar] [CrossRef]
- Zhang, R.; Tang, X.; Xu, L.; Lu, F.; Cui, H. Mechanism study of thermal fluid flow and weld root hump suppression in full penetration laser welding of Al alloy with alternating magnetic field support. Int. J. Heat Mass Transf. 2021, 166, 120759. [Google Scholar] [CrossRef]
- Kao, A.; Gan, T.; Tonry, C.; Krastins, I.; Pericleous, K. Thermoelectric magnetohydrodynamic control of melt pool dynamics and microstructure evolution in additive manufacturing. Philos. Trans. R. Soc. A 2019, 378, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Du, D.; Haley, J.C.; Dong, A.; Fautrelle, Y.; Shu, D.; Zhu, G.; Li, X.; Sun, B.; Lavernia, E.J. Influence of static magnetic field on microstructure and mechanical behavior of selective laser melted AlSi10Mg alloy. Mater. Des. 2019, 181, 107923. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, C.; Ling, X. Effects of laser shock processing on corrosion resistance of AISI 304 stainless steel in acid chloride solution. J. Alloys Compd. 2017, 723, 237–242. [Google Scholar] [CrossRef]
- Zhang, Z.; Chu, B.; Wang, L.; Lu, Z. Comprehensive effects of placement orientation and scanning angle on mechanical properties and behavior of 316L stainless steel based on the selective laser melting process. J. Alloys Compd. 2019, 791, 166–175. [Google Scholar] [CrossRef]
- ЭMAΠ. 2021. Available online: https://ultrakraft.ru/ru/technology/emat (accessed on 19 December 2021).
- Gawad, J.; van Bael, A.; Eyckens, P.; Samaey, G.; van Houtte, P.; Roose, D. Hierarchical multi-scale modeling of texture induced plastic anisotropy in sheet forming. Comp. Mater. Sci. 2013, 66, 65–83. [Google Scholar] [CrossRef]
- Trusov, P.V.; Shveykin, A.I. Multilevel crystal plasticity models of single-and polycrystals. Direct models. Phys. Mesomech. 2013, 16, 99–124. [Google Scholar] [CrossRef]
- Trusov, P.V.; Shveykin, A.I. Multilevel crystal plasticity models of single-and polycrystals. Statistical models. Phys. Mesomech. 2013, 16, 23–33. [Google Scholar] [CrossRef]
- Kern, M.; Berger, P.; Hügel, H. Magneto-Fluid Dynamic Control of Seam Quality in CO2 Laser Beam Welding. Weld. J. 2000, 3, 72–78. [Google Scholar]
- Hu, S.; Hou, L.; Wang, K.; Liao, Z.; Zhu, W.; Yi, A.; Li, W.; Fautrelle, Y.; Li, X. Effect of transverse static magnetic field on radial microstructure of hypereutectic aluminum alloy during directional solidification. J. Mater. Sci. Technol. 2021, 76, 207–214. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Galenko, P.K.; Toropova, L.V. Thermo-solutal and kinetic modes of stable dendritic growth with different symmetries of crystalline anisotropy in the presence of convection. Philos. Trans. R. Soc. A 2018, 376, 20170215. [Google Scholar] [CrossRef]
- COMSOL Multiphysics; Version 5.6.; Licence No. 9602304; COMSOLAB: Stockholm, Sweden, 2021.
- Blatt, F.J.; Flood, D.J.; Rowe, V.; Schroeder, P.A.; Magnon, J.E.C. Drag Thermopower in Iron. Phys. Rev. Lett. 1967, 18, 395. [Google Scholar] [CrossRef]
- Shercliff, J.A. Thermoelectric magnetohydrodynamics. J. Fluid Mech. 1979, 91, 231–251. [Google Scholar] [CrossRef]
- Shevchenko, N.; Boden, S.; Eckert, S.; Borin, D.; Heinze, M.; Odenbach, S. Application of X-ray radioscopic methods for characterization of two-phase phenomena and solidification processes in metallic melts. Eur. Phys. J. Spec. Top. 2013, 220, 63–77. [Google Scholar] [CrossRef]
- Kao, A.; Shevchenko, N.; He, S.; Lee, P.D.; Eckert, S.; Pericleous, K. Magnetic Effects on Microstructure and Solute Plume Dynamics of Directionally Solidifying Ga-In Alloy. JOM 2020, 72, 3645–3651. [Google Scholar] [CrossRef]
- Samokhin, A.A. First-order phase transitions induced by laser radiation in absorbing condensed matter. In Effect of Laser Radiation on Absorbing Condensed Matter; Fedorov, V.B., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 1990. [Google Scholar]
- CRC Handbook of Chemistry and Physics, 89th ed.; Lide, D.R. (Ed.) Taylor & Francis Group: London, UK, 2008. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2007. [Google Scholar]
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification, 3rd ed.; Trans Tech Publication Ltd.: Wollerau, Switzerland, 1989. [Google Scholar]


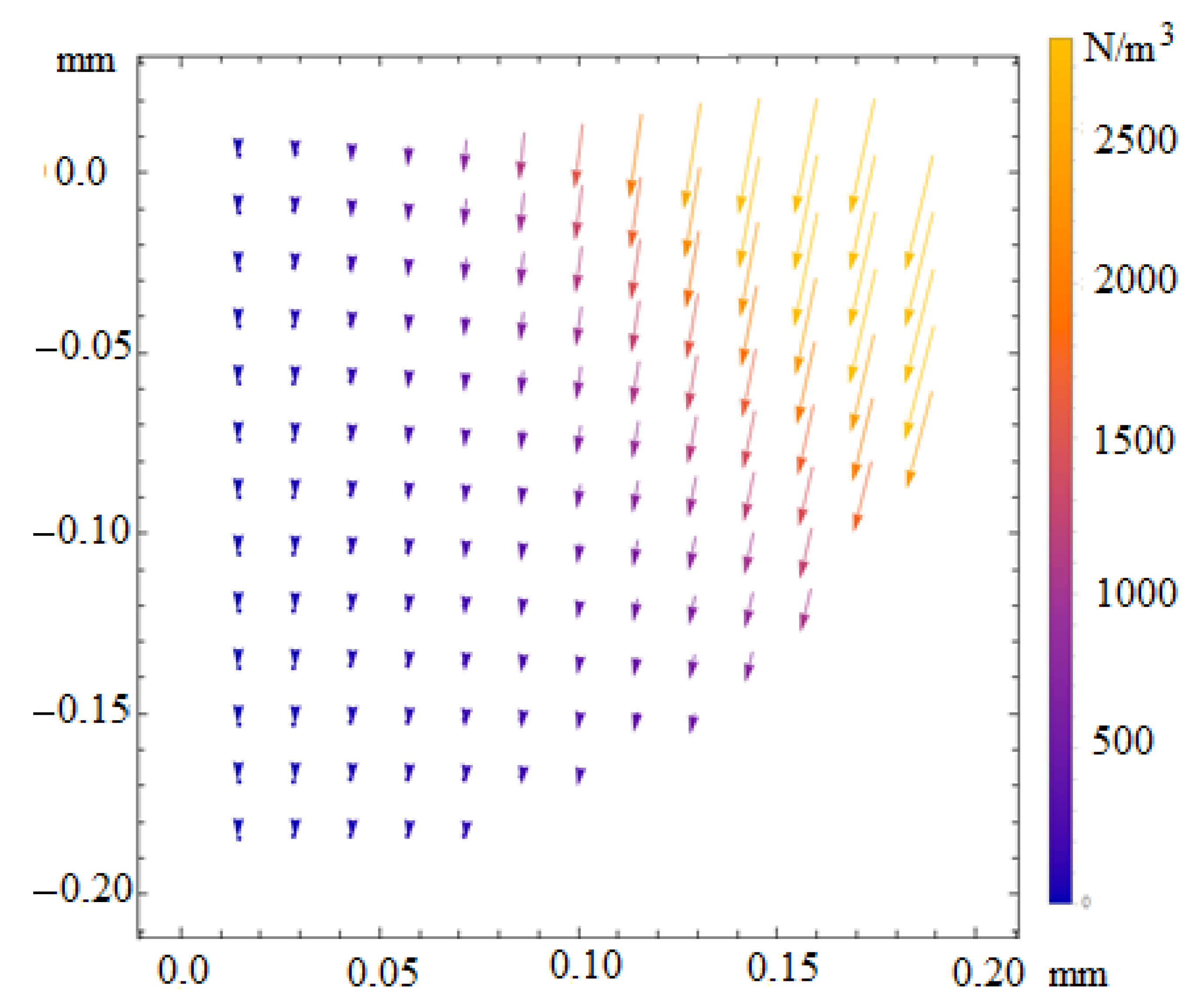

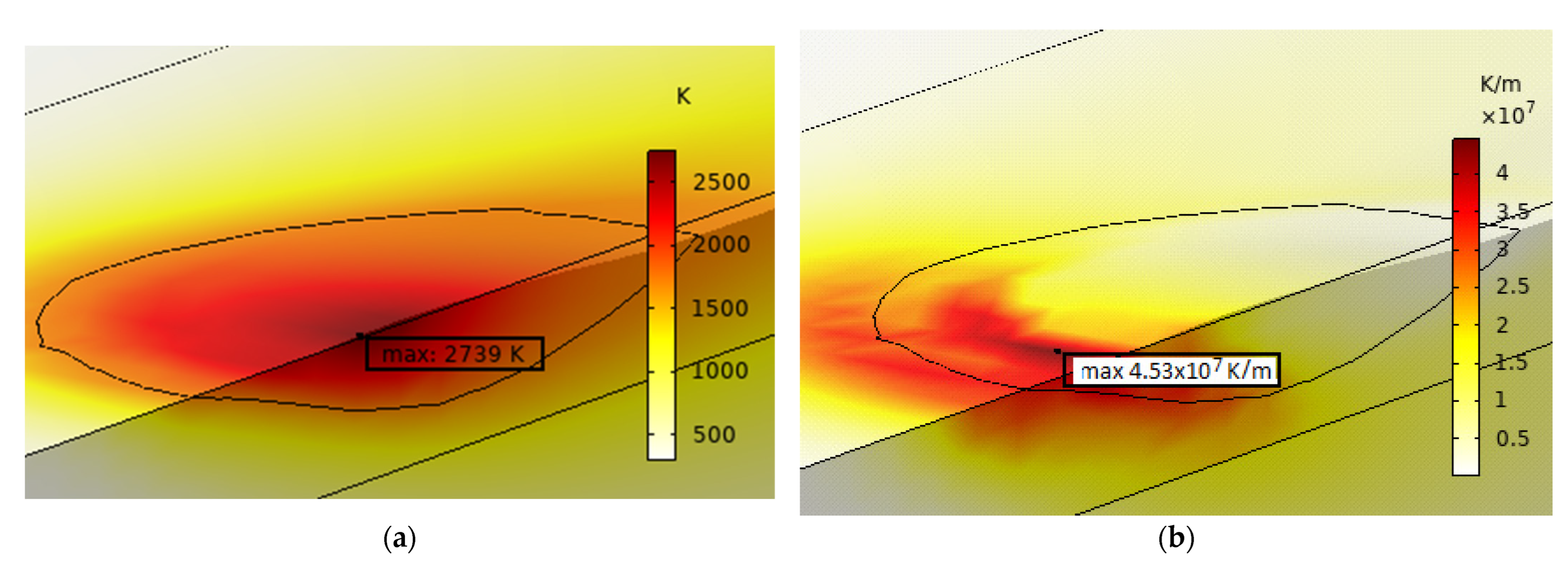
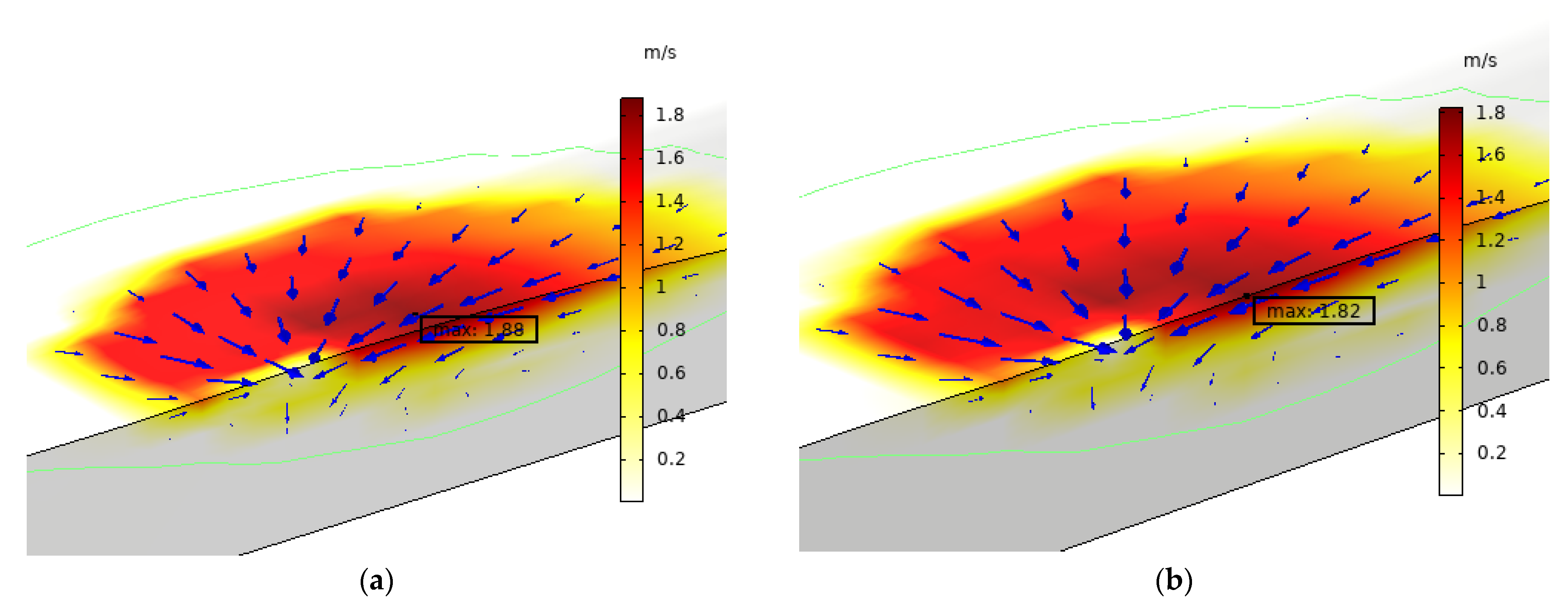
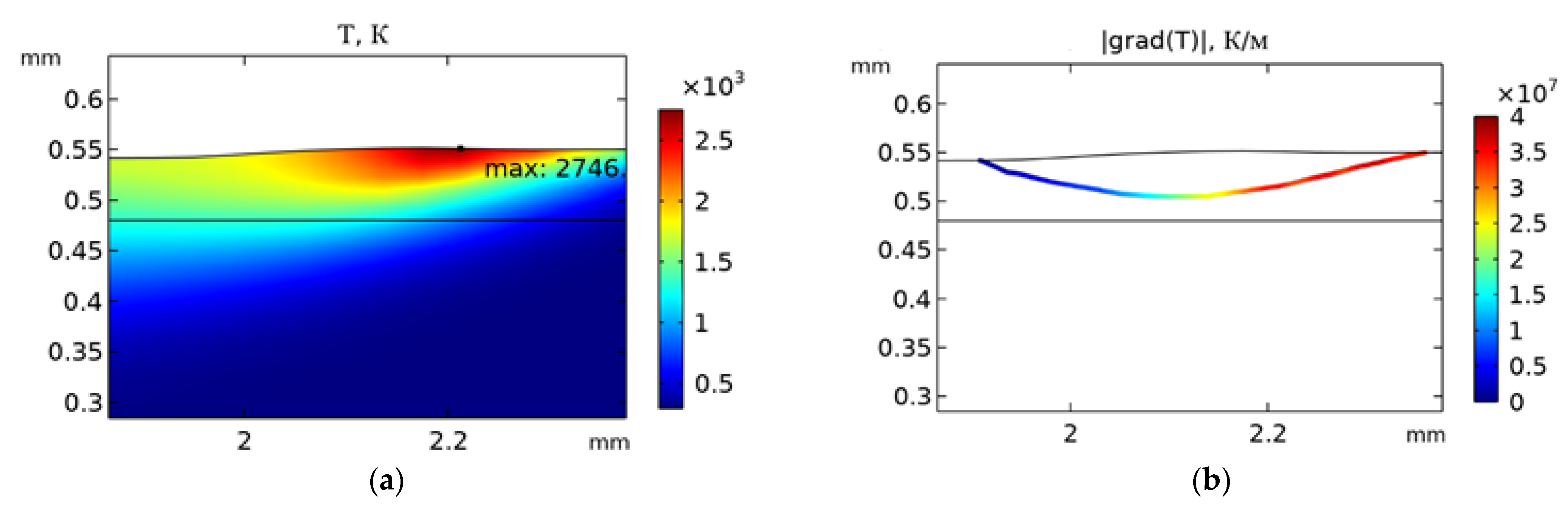
| Parameter | Symbol | Value | Units |
|---|---|---|---|
| Density of the solid phase | |||
| Density of the melt | |||
| Specific heat of the solid phase | J/kg | ||
| Specific heat of the melt | J/kg | ||
| Thermal conductivity of the solid phase | W/(K m) | ||
| Thermal conductivity of the melt | W/(K m) | ||
| Melting temperature | K | ||
| Viscosity of the melt | Pa s | ||
| Viscosity of the solid phase | Pa s | ||
| Thermocapillary coefficient | |||
| Velocity of the laser beam | m/s |
| Magnetic Flux Density, T | Mean Temperature in the Molten Pool, K | Time-Averaged Maximum Flow Velocity in the Molten Pool, m/s | Spatially Averaged Flow Velocity in the Molten Pool, m/s |
|---|---|---|---|
| 0 | 1949 | 1.879 | 0.378 |
| 0.1 | 1949 | 1.878 | 0.378 |
| 1 | 1949 | 1.879 | 0.377 |
| 10 | 1994 | 1.818 | 0.354 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gruzd, S.A.; Lomaev, S.L.; Simakov, N.N.; Gordeev, G.A.; Bychkov, A.S.; Gapeev, A.A.; Cherepetskaya, E.B.; Krivilyov, M.D.; Ivanov, I.A. Analysis of the Effect of Magnetic Field on Solidification of Stainless Steel in Laser Surface Processing and Additive Manufacturing. Metals 2022, 12, 1540. https://doi.org/10.3390/met12091540
Gruzd SA, Lomaev SL, Simakov NN, Gordeev GA, Bychkov AS, Gapeev AA, Cherepetskaya EB, Krivilyov MD, Ivanov IA. Analysis of the Effect of Magnetic Field on Solidification of Stainless Steel in Laser Surface Processing and Additive Manufacturing. Metals. 2022; 12(9):1540. https://doi.org/10.3390/met12091540
Chicago/Turabian StyleGruzd, Svetlana A., Stepan L. Lomaev, Nikolay N. Simakov, Georgii A. Gordeev, Anton S. Bychkov, Artem A. Gapeev, Elena B. Cherepetskaya, Mikhail D. Krivilyov, and Ivan A. Ivanov. 2022. "Analysis of the Effect of Magnetic Field on Solidification of Stainless Steel in Laser Surface Processing and Additive Manufacturing" Metals 12, no. 9: 1540. https://doi.org/10.3390/met12091540
APA StyleGruzd, S. A., Lomaev, S. L., Simakov, N. N., Gordeev, G. A., Bychkov, A. S., Gapeev, A. A., Cherepetskaya, E. B., Krivilyov, M. D., & Ivanov, I. A. (2022). Analysis of the Effect of Magnetic Field on Solidification of Stainless Steel in Laser Surface Processing and Additive Manufacturing. Metals, 12(9), 1540. https://doi.org/10.3390/met12091540






