Research on the Curvature Prediction Method of Profile Roll Bending Based on Machine Learning
Abstract
1. Introduction
2. Prediction Model for Springback of Fixed Curvature Based on XGBoost
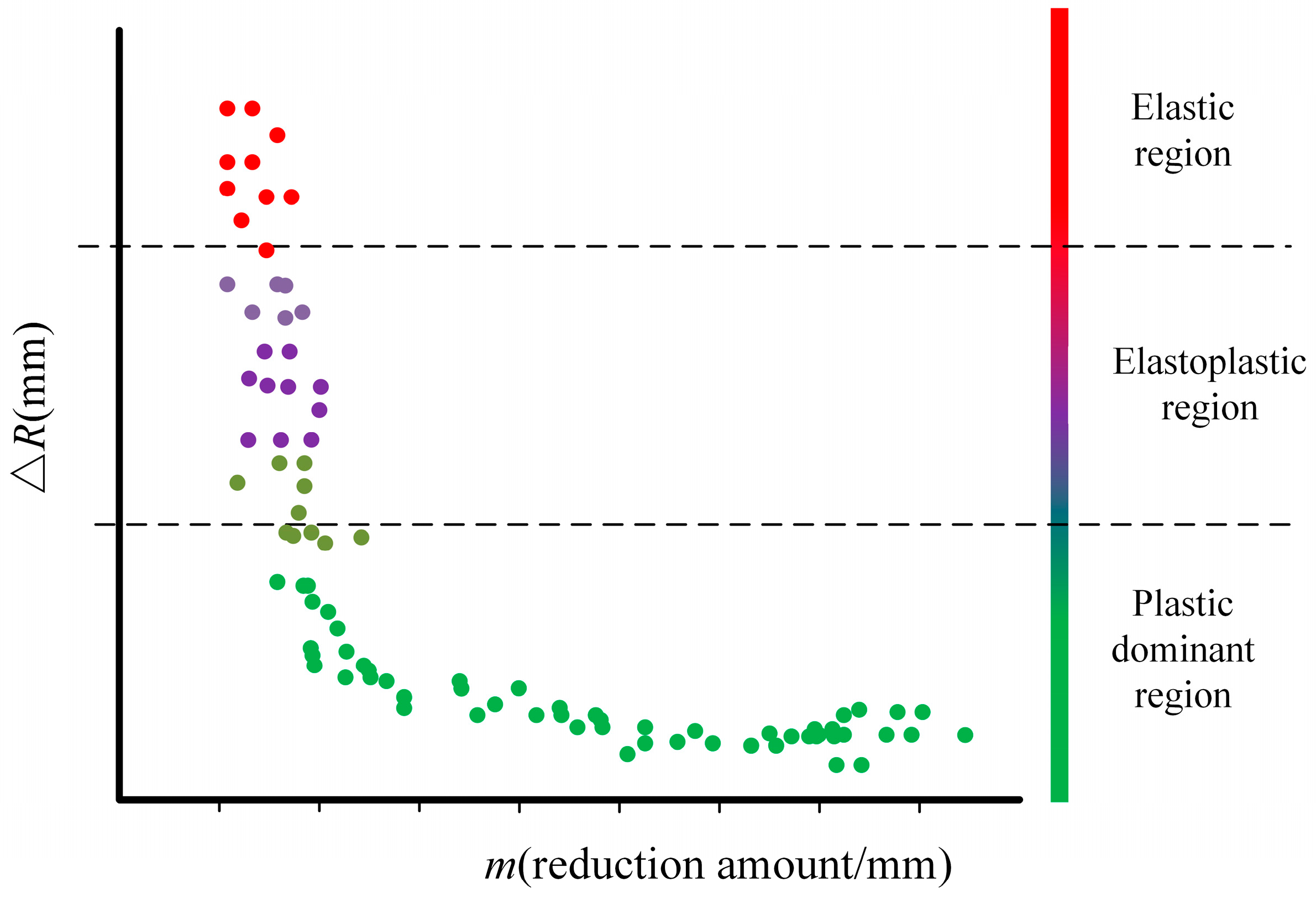
2.1. Analysis of Influencing Factors of Springback and Data Preprocessing
Construction of Density Clustering Features
2.2. Comparison and Analysis of Machine-Learning Methods
2.3. Construction of Springback Prediction Model with Fixed Curvature Based on XGBoost
2.4. Realization of Springback Prediction Model with Fixed Curvature Based on XGBoost
| Algorithm 1: Fixed-curvature springback prediction algorithm based on XGBoost |
| Input: training set dataset_train and test set dataset_test |
| Output: Springback prediction model f |
| Step 1: Initialize the parametric model . |
| Step 2: Iteratively generate M weak learners and update the strong learner as follows: |
|
| Step 3: If the prediction result of the model reaches the set standard or the update times reaches the set upper limit, go to Step 4; otherwise, go to Step 2. |
| Step 4: Use the test set to evaluate the model and store the current hyperparameter combination and model evaluation score. |
| Step 5: If the set upper limit of Bayesian optimization times is reached or the result meets the expected standard, go to Step 6; otherwise, go to Step 1. |
| Step 6: Select the optimal hyperparameter combination from the searched hyperparameter combinations. |
| Step 7: Use the optimal hyperparameter combination selected in Step 6 to construct a prediction model f, f(P,V,E,RS) = RE. |
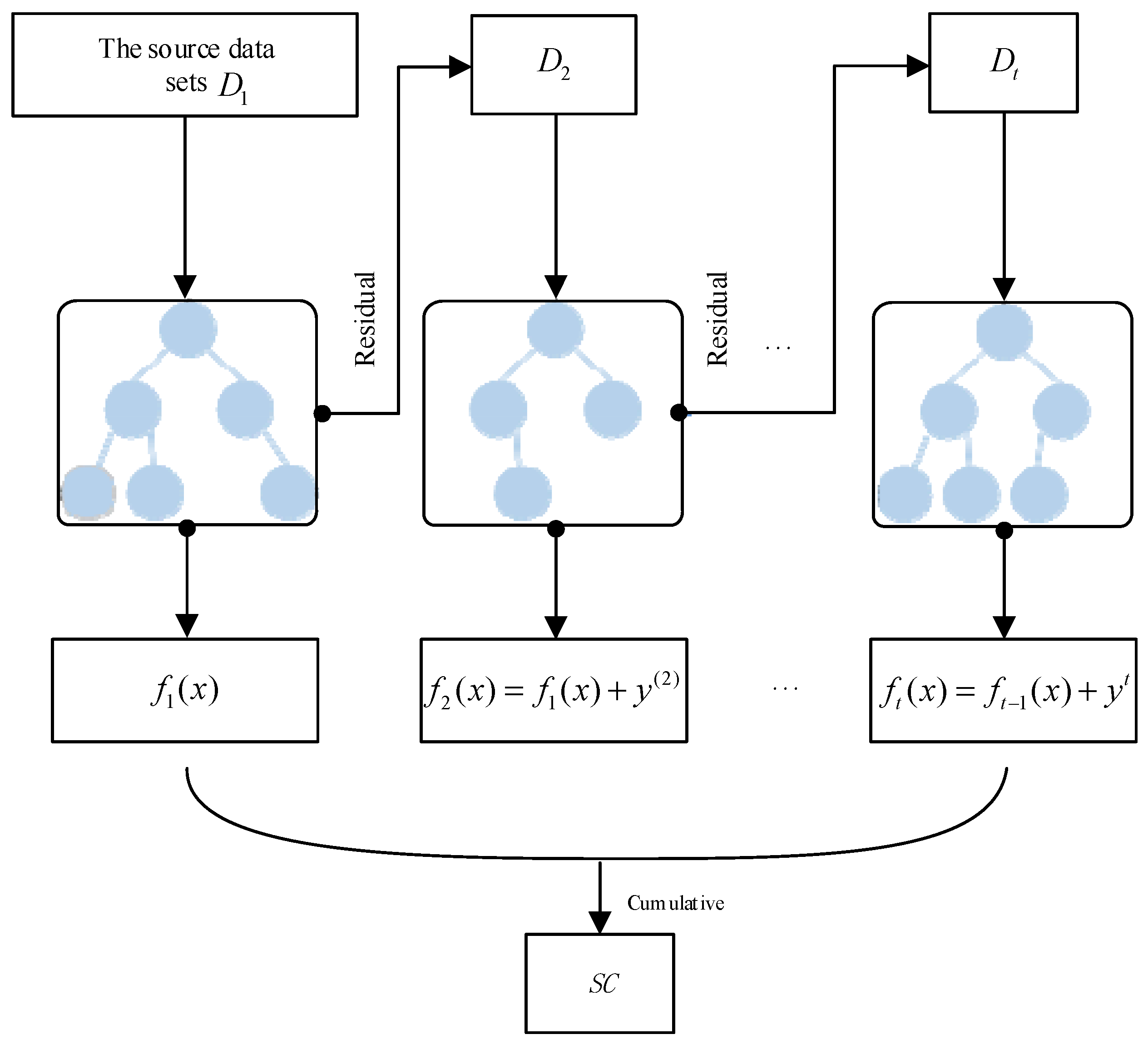
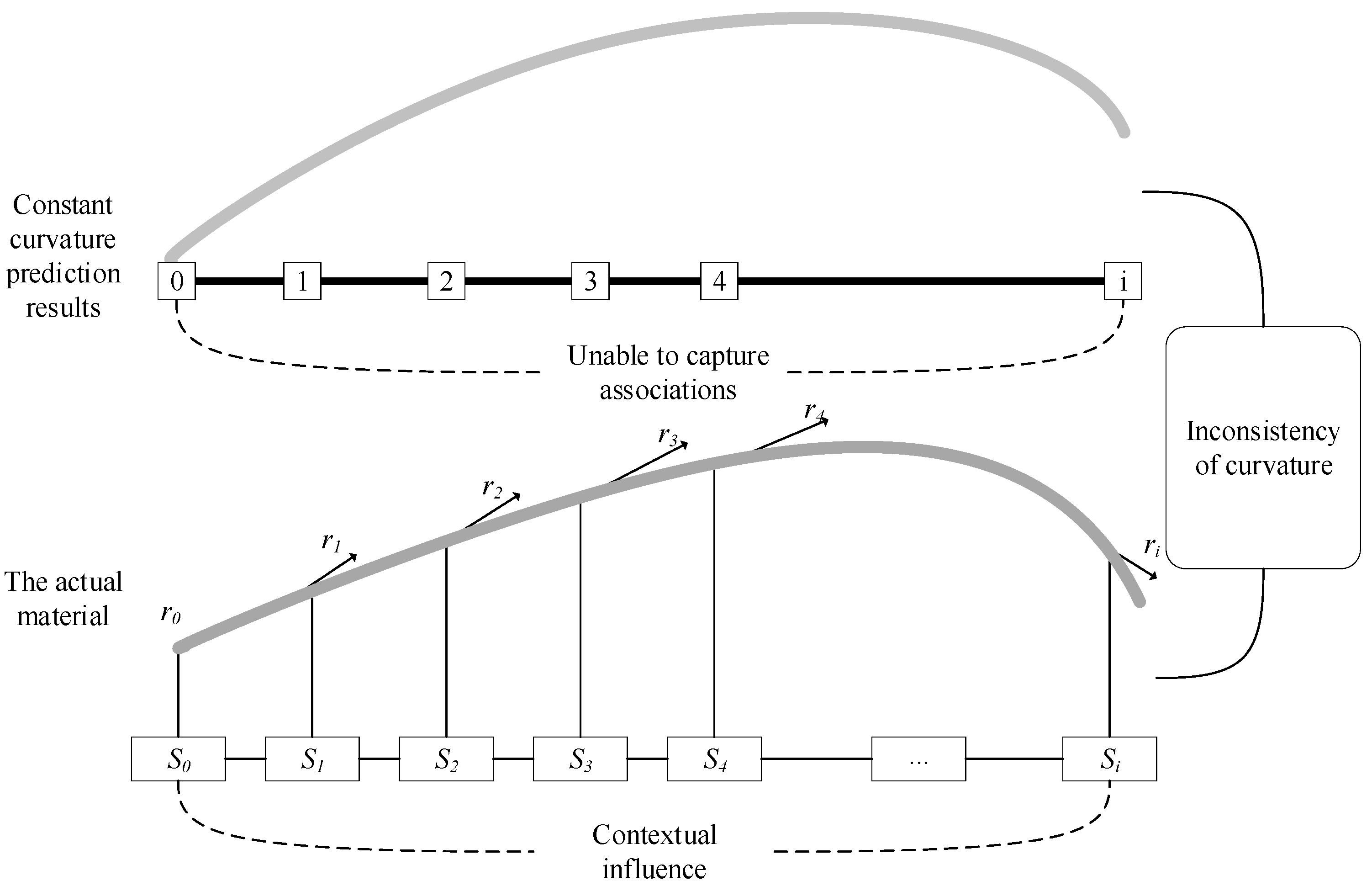
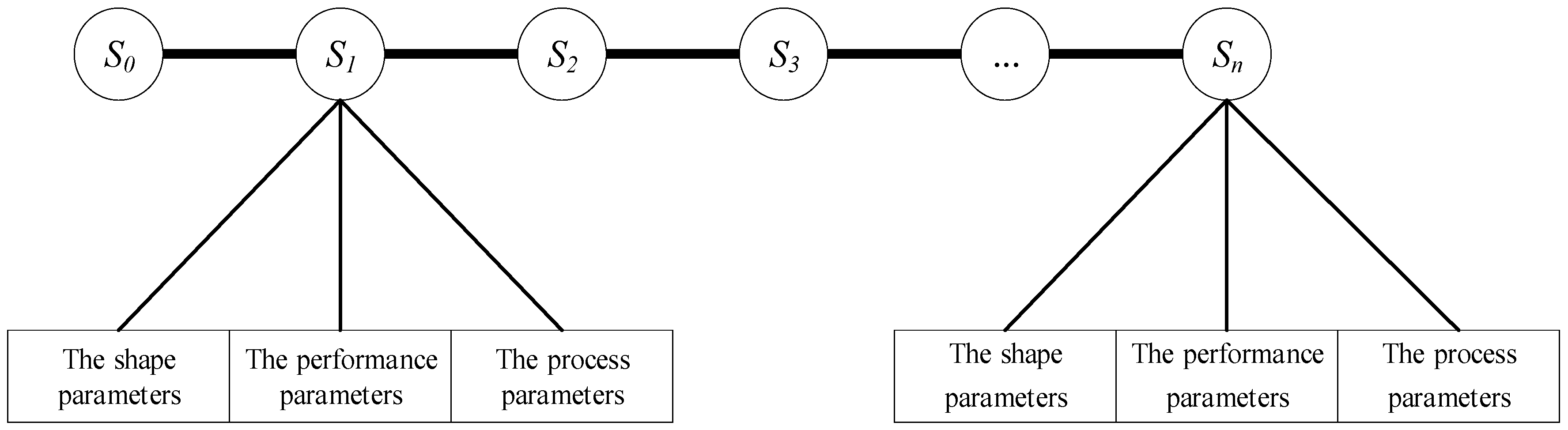
3. Variable-Curvature Springback Prediction Model Based on Conditional Random Field
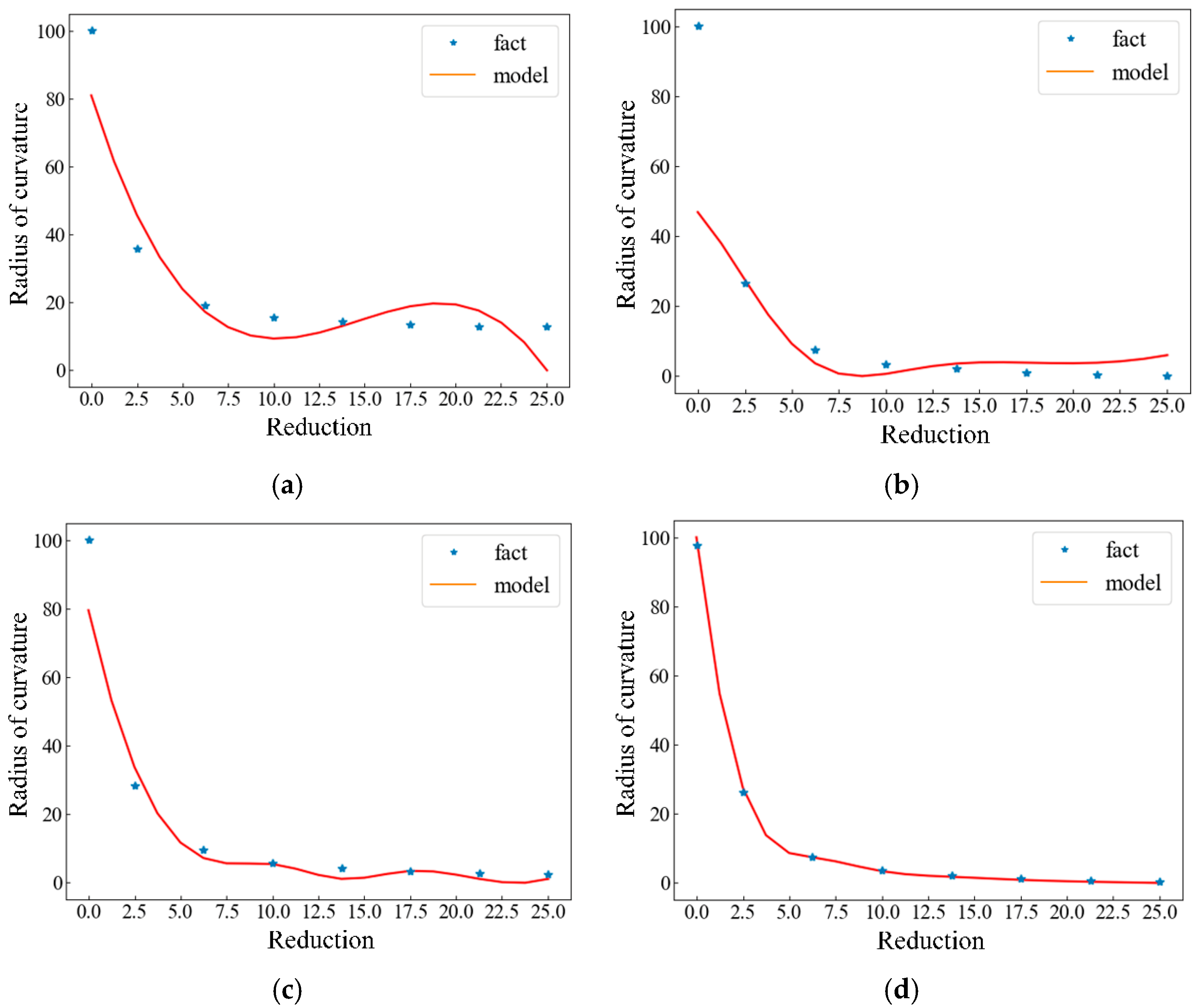
3.1. Comparison and Analysis of Machine-Learning Methods
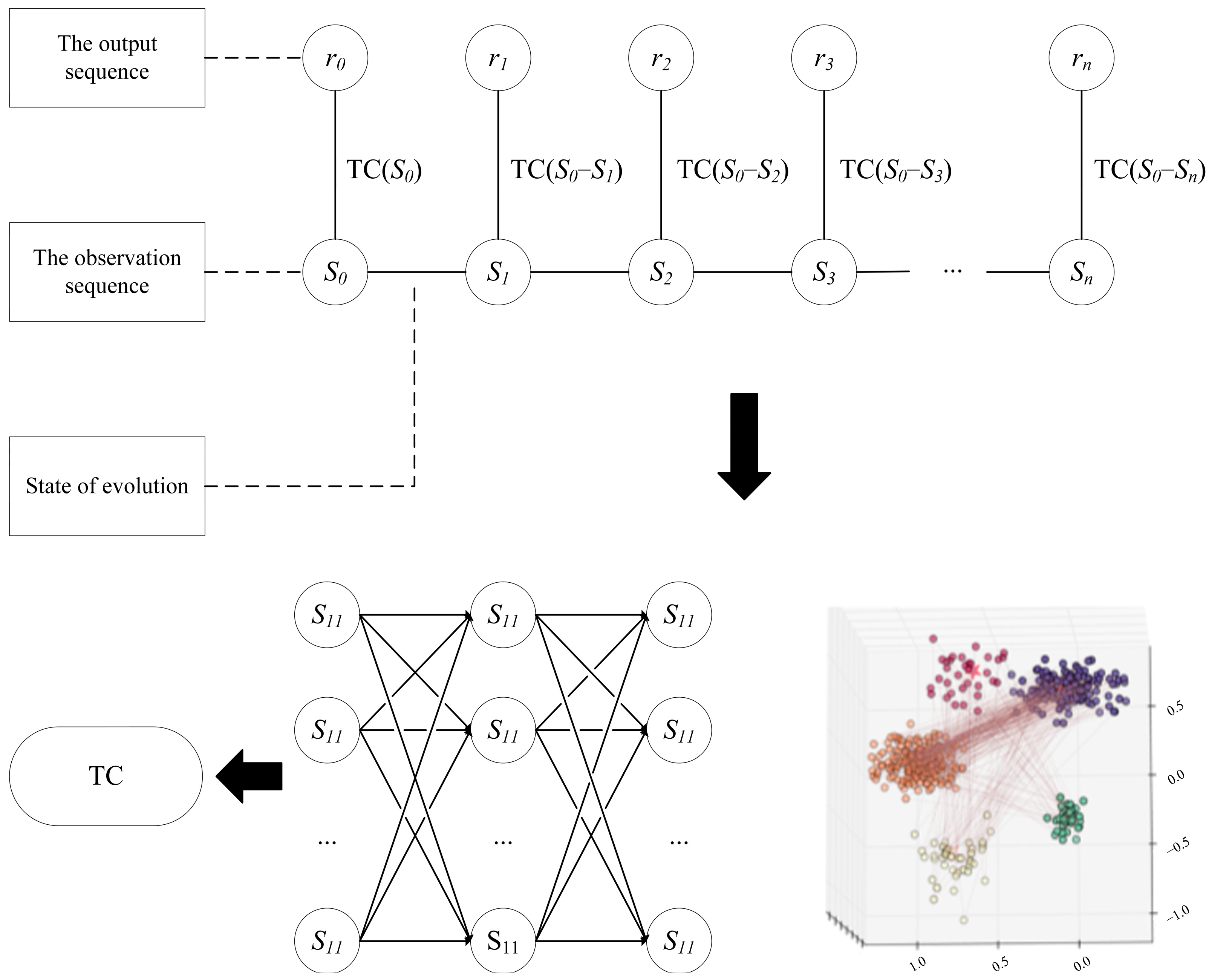
3.2. Construction of Variable-Curvature Springback Prediction Model Based on Conditional Random Field
3.3. Realization of Springback Prediction Model with Variable-Curvature Based on Conditional Random Field
| Algorithm 2: Curvature prediction after springback for variable-curvature roll bending based on conditional random fields |
| Input: training set dataset_train and test set dataset_test |
| Output: Actual curvature radius sequence R after variable-curvature forming springback |
| Step 1: Define and determine the model hyperparameters. |
| Step 2: Calculate the empirical distribution . |
| Step 3: Use the quasi-Newton method to learn the optimal parameter value and obtain the optimal model . The steps are as follows: |
|
| Step 4: Use the Viterbi algorithm to predict the observation sequence to obtain the optimal path sequence . |
| Step 5: Use an error network for error compensation on the optimal path in discrete form, and map to continuous values. |
4. Experimental Results and Analysis
4.1. Experimental Conditions
4.2. Experimental Profile Specifications
4.3. Experimental Evaluation Method
4.4. Fixed-Curvature Experiment
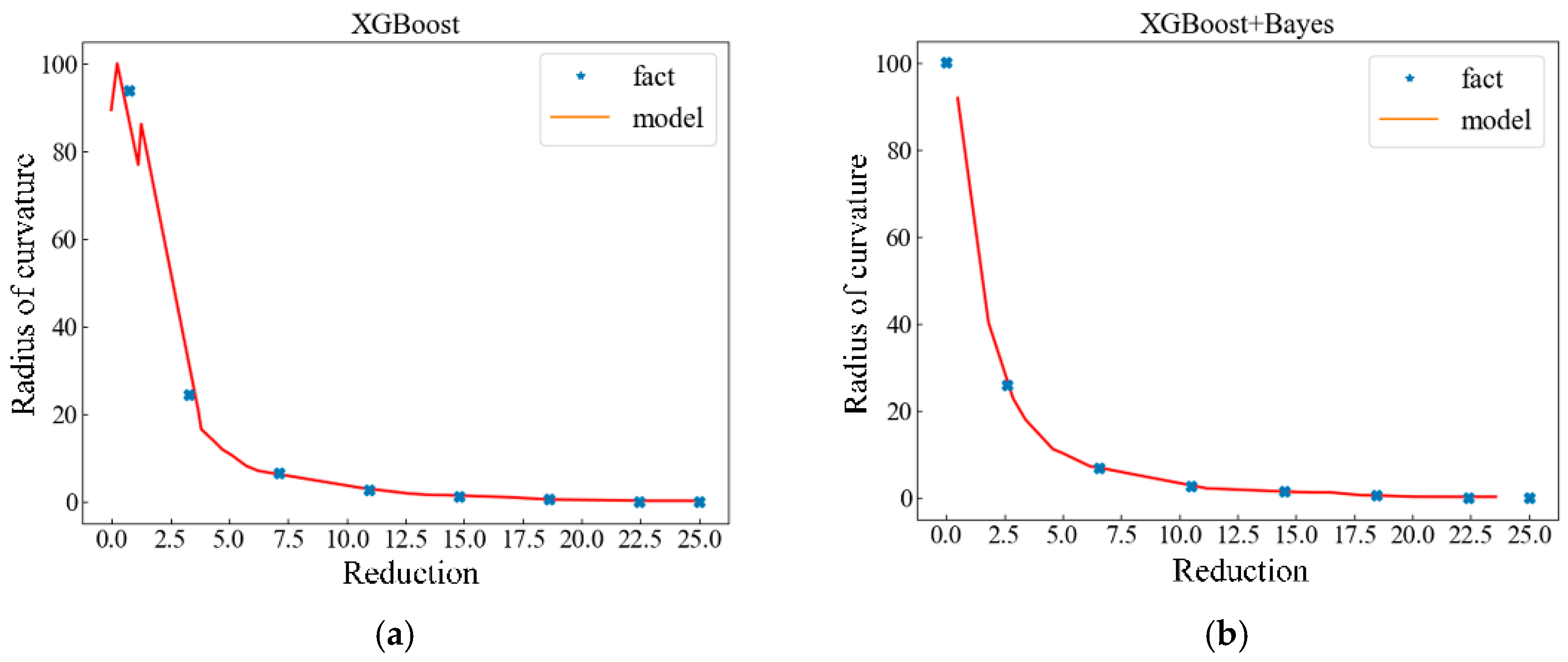
4.4.1. Analysis of Bayesian Optimization Effect
4.4.2. Comparative Analysis of the Results of XGBoost Algorithm and Other Algorithms
4.5. Variable-Curvature Experiment
4.5.1. Analysis of the Impact of Related Effect on the Results
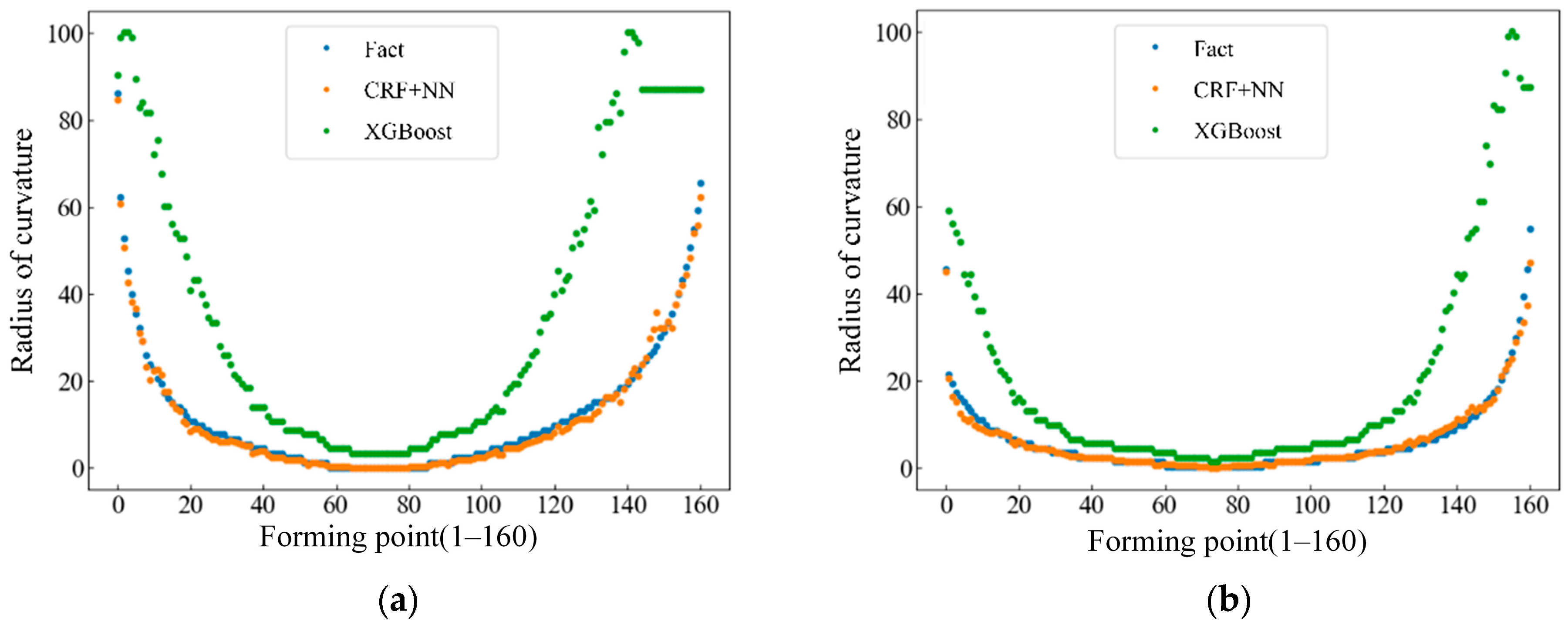
4.5.2. Comparative Analysis of Artificial Neural Network Error Compensation Results and Experimental Results
5. Conclusions
- (1)
- Based on XGBoost, a curvature prediction model of fixed-curvature roll bending after springback was proposed, which could achieve an accurate prediction of the curvature of formed profiles, and the coupling effect of process parameters and material performance parameters on the roll-bending process was explored. Combined with the Bayesian optimization algorithm, the hyperparameters of the fixed-curvature prediction model were optimized. Table 6 shows the comparison between MSE, MAE, and MAPE for the predictions from Bayesian-optimized hyperparameters and unoptimized hyperparameters. The MSE, MAE and MAPE corresponding to the prediction results of the best hyperparameter combination were 28.7, 2.28 and 12.69, respectively. The MSE, MAE, and MAPE corresponding to the prediction results of the worst hyperparameter combination were 256.23, 7.94, and 35.53, respectively. It was proved that Bayesian optimization improves the prediction accuracy. Table 7 shows the comparison between the MSE, MAE and MAPE of the XGBoost model and other models for the fixed-curvature springback prediction results, and the MSE, MAE and MAPE prediction results of the XGBoost model were 28.7, 2.28 and 12.69, respectively. The best performance of the other models was exhibited by the neural network model, which had an MSE, MAE, and MAPE of 49.01, 3.99, and 41.42, respectively. The superiority of the proposed model was proved.
- (2)
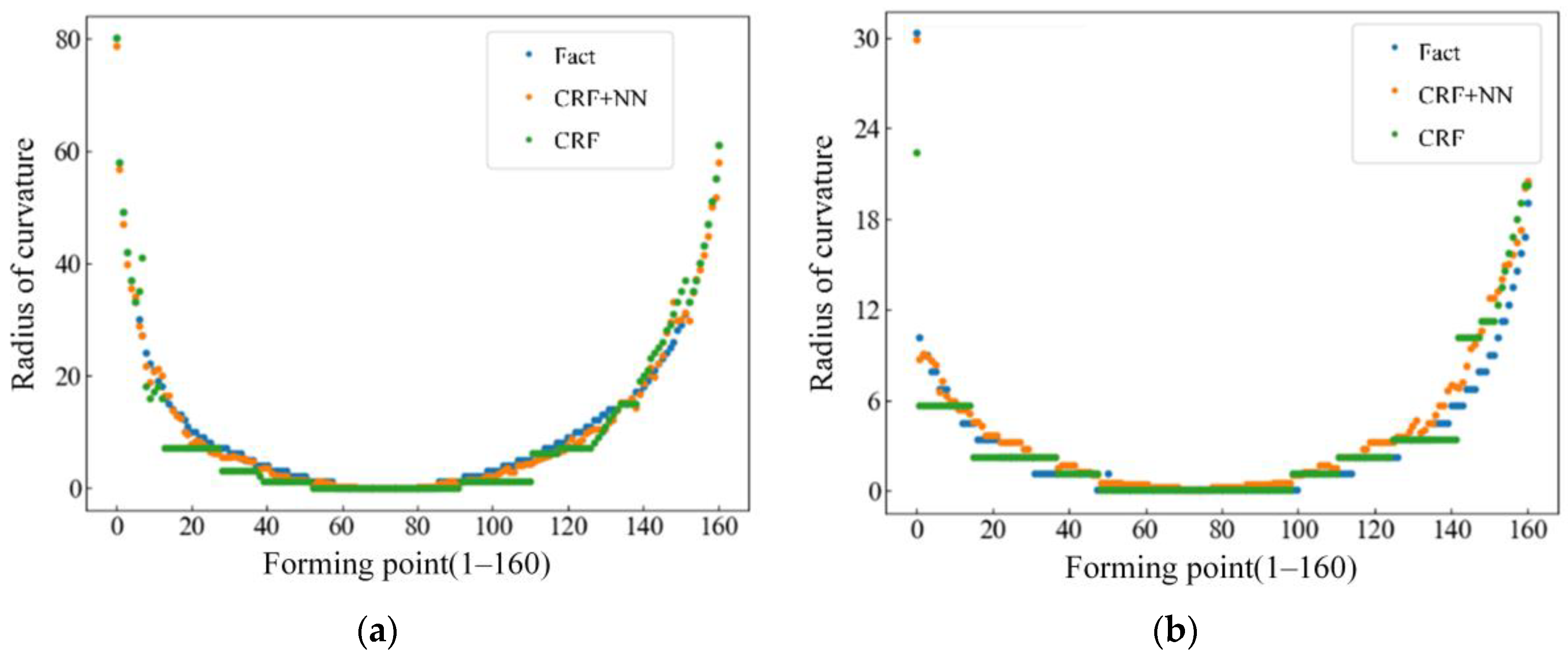
- Based on the prediction results of a fixed curvature, a variable-curvature prediction model based on the conditional random field was established, the state transition law of variable-curvature forming was explored, and the accurate prediction of the curvature of the variable-curvature rolling profile was realized. By adding an error compensation network after the result of the conditional random field, the discrete sequence was mapped to the continuous sequence. Table 8 shows the comparison between the MSE, MAE, and MAPE of the prediction results of the two variable-curvature springback prediction models. The MSE, MAE, and MAPE prediction results of the model without an error compensation network are 3.42, 2.12, and 24.30, respectively. The MAE, MSE, and MAPE prediction results of the model with an error compensation network are 1.40, 0.66, and 13.72, respectively. The improvement of model accuracy by adding the error compensation network was shown. A variable-curvature prediction model that can accurately predict the curvature after forming was obtained.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tao, J.; Xiong, H.; Wan, B.F.; Wei, W.B.; Cheng, X.; Wang, L.T.; Yu, Y.H.; Wang, C.; Guo, X.Z. 3D Free-bending forming equipment and key technology. J. Netshape Form. Eng. 2018, 10, 1–13. [Google Scholar] [CrossRef]
- Desinghege, S.G.; Hodgson, P.; Weiss, M. Microstructure effects on the material behaviour of magnesium sheet in bending dominated forming. J. Mater. Process. Technol. 2021, 289, 116951. [Google Scholar] [CrossRef]
- Su, C.; Liu, J.; Zhao, Z.; Lou, S.; Wang, R.; Yang, L. Research on roll forming process and springback based on five-boundary condition forming angle distribution function. J. Mech. Sci. Technol. 2020, 34, 5193–5204. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, Y.; Qiu, L.; Zhang, S.; Fang, D.; He, C.; Wang, L. Spatial variable curvature metallic tube bending springback numerical approximation prediction and compensation method considering cross-section distortion defect. Int. J. Adv. Manuf. Technol. 2021, 118, 1811–1827. [Google Scholar] [CrossRef]
- Fan, L.-F.; Gou, J.; Wang, G.; Gao, Y. Springback Characteristics of Cylindrical Bending of Tailor Rolled Blanks. Adv. Mater. Sci. Eng. 2020, 2020, 9371808. [Google Scholar] [CrossRef]
- Chang, Y.; Wang, N.; Wang, B.; Li, X.; Wang, C.; Zhao, K.; Dong, H. Prediction of bending springback of the medium-Mn steel considering elastic modulus attenuation. J. Manuf. Process. 2021, 67, 345–355. [Google Scholar] [CrossRef]
- Sharma, P.K.; Gautam, V.; Agrawal, A.K. Analytical and Numerical Prediction of Springback of SS/Al-Alloy Cladded Sheet in V-Bending. J. Manuf. Sci. Eng. 2021, 143, 031011. [Google Scholar] [CrossRef]
- Liu, X.-L.; Cao, J.-G.; Huang, S.-X.; Yan, B.; Li, Y.-L.; Zhao, R.-G. Experimental and numerical prediction and comprehensive compensation of springback in cold roll forming of UHSS. Int. J. Adv. Manuf. Technol. 2020, 111, 657–671. [Google Scholar] [CrossRef]
- Julsri, W.; Sanrutsadakorn, A.; Uthaisangsuk, V. Experimental and numerical study of springback effect of advanced high strength steel in a V-shape bending. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1157, 012042. [Google Scholar] [CrossRef]
- Wu, J.J.; Zhang, H.G.; Wang, J.B.; Wang, Y.J. Mechanical and spring-back analysis for the stretch-bending process of extruded profile. Mater. Sci. Technol. 2004, 12, 357–359. [Google Scholar] [CrossRef]
- Choi, H.; Fazily, P.; Park, J.; Kim, Y.; Cho, J.H.; Kim, J.; Yoon, J.W. Artificial intelligence for springback compensation with electric vehicle motor component. Int. J. Mater. Form. 2022, 15, 22. [Google Scholar] [CrossRef]
- Sun, C.; Wang, Z.; Zhang, S.; Liu, X.; Wang, L.; Tan, J. Toward axial accuracy prediction and optimization of metal tube bending forming: A novel GRU-integrated Pb-NSGA-III optimization framework. Eng. Appl. Artif. Intell. 2022, 114, 105193. [Google Scholar] [CrossRef]
- Lu, K.; Zou, T.; Luo, J.; Li, D.; Peng, Y. Stretch bending process design by machine learning. Int. J. Adv. Manuf. Technol. 2022, 120, 781–799. [Google Scholar] [CrossRef]
- Cruz, D.J.; Barbosa, M.R.; Santos, A.D.; Miranda, S.S.; Amaral, R.L. Application of Machine Learning to Bending Processes and Material Identification. Metals 2021, 11, 1418. [Google Scholar] [CrossRef]
- Liu, S.; Xia, Y.; Shi, Z.; Yu, H.; Li, Z.; Lin, J. Deep Learning in Sheet Metal Bending with a Novel Theory-Guided Deep Neural Network. IEEE/CAA J. Autom. Sin. 2021, 8, 565–581. [Google Scholar] [CrossRef]
- Xu, B.; Li, L.; Wang, Z.; Zhou, H.; Liu, D. Prediction of springback in local bending of hull plates using an optimized backpropagation neural network. Mech. Sci. 2021, 12, 777–789. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Z.; Xu, B. Prediction of Spherical Sheet Springback Based on a Sparrow-Search-Algorithm-Optimized BP Neural Network. Metals 2022, 12, 1377. [Google Scholar] [CrossRef]
- Wasif, M.; Fatima, A.; Ahmed, A.; Iqbal, S.A. Investigation and Optimization of Parameters for the Reduced Springback in JSC-590 Sheet Metals Occurred During the V-Bending Process. Trans. Indian Inst. Met. 2021, 74, 2751–2760. [Google Scholar] [CrossRef]
- Serban, F.M.; Grozav, S.; Ceclan, V.; Turcu, A. Artificial Neural Networks Model for Springback Prediction in the Bending Operations. Teh. Vjesn.-Tech. Gaz. 2020, 27, 868–873. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Lemu, H.G. Improving Prediction of Springback in Sheet Metal Forming Using Multilayer Perceptron-Based Genetic Algorithm. Materials 2020, 13, 3129. [Google Scholar] [CrossRef]
- Liang, Z.; Zou, T.; Dai, W.; Zhang, Z.; Liu, Y.; Lu, K.; Li, D.; Ding, S.; Peng, Y. Compensate for longitudinally discrepant springback and bow in chain-die forming processes by multiple sections optimization. Int. J. Adv. Manuf. Technol. 2022, 121, 6407–6430. [Google Scholar] [CrossRef]
- El Mrabti, I.; Touache, A.; El Hakimi, A.; Chamat, A. Springback optimization of deep drawing process based on FEM-ANN-PSO strategy. Struct. Multidiscip. Optim. 2021, 64, 321–333. [Google Scholar] [CrossRef]
- Jia, X.; Gong, H.; Shi, W.; Yang, C.; Yuan, K. Multi-objective Optimization of Forming Quality on High-Strength Steel Rocker Arm Parts. Trans. Indian Inst. Met. 2022, 75, 2661–2671. [Google Scholar] [CrossRef]
- Akrichi, S.; Abid, S.; Bouzaien, H.; Ben Yahia, N. SPIF Quality Prediction Based on Experimental Study Using Neural Networks Approaches. Mech. Solids 2020, 55, 138–151. [Google Scholar] [CrossRef]
- Ciubotariu, V.A.; Radu, M.C.; Herghelegiu, E.; Zichil, V.; Grigoras, C.C.; Nechita, E. Structural and Behaviour Optimization of Tubular Structures Made of Tailor Welded Blanks by Applying Taguchi and Genetic Algorithms Methods. Appl. Sci. 2022, 12, 6794. [Google Scholar] [CrossRef]
- Kong, Q.; Yu, Z. Dynamic Evaluation Method of Straightness Considering Time-Dependent Springback in Bending-Straightening Based on GA-BP Neural Network. Machines 2022, 10, 345. [Google Scholar] [CrossRef]
- Ji, C.; Lei, Y. Parallel clustering by fast search and find of density peaks. In Proceedings of the 2016 International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, China, 11–12 July 2016; pp. 563–567. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD’16: The 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Banerjee, I.; Ling, Y.; Chen, M.C.; Hasan, S.A.; Langlotz, C.P.; Moradzadeh, N.; Chapman, B.; Amrhein, T.; Mong, D.; Rubin, D.L.; et al. Comparative effectiveness of convolutional neural network (CNN) and recurrent neural network (RNN) architectures for radiology text report classification. Artif. Intell. Med. 2019, 97, 79–88. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Song, R.; Liu, Y.; Zhao, Y.; Martin, R.R.; Rosin, P.L. Conditional random field-based mesh saliency. In Proceedings of the 2012 IEEE International Conference on Image Processing (ICIP 2012), Orland, FL, USA, 30 September–3 October 2012; pp. 637–640. [Google Scholar] [CrossRef]





| Roll Spacing (mm) | Feed Rate (mm/s) | Reduction (mm) | Radius of Curvature before Springback (mm) |
|---|---|---|---|
| 465 | 14.65 | 3 | 166,111 |
| 6 | 24,901 | ||
| 9 | 8098 | ||
| 12 | 4426 | ||
| 15 | 3207 | ||
| 18 | 2385 | ||
| 21 | 1837 | ||
| 24 | 1591 |
| Roller Spacing (mm) | Feed Rate (mm/s) | Reduction (mm) | Degree of Springback | Radius of Curvature (mm) |
|---|---|---|---|---|
| 465 | 14.65 | 3 | 3 | 166,111 |
| 6 | 3 | 24,901 | ||
| 9 | 2 | 8098 | ||
| 12 | 2 | 4426 | ||
| 15 | 2 | 3207 | ||
| 18 | 1 | 2385 | ||
| 21 | 1 | 1837 | ||
| 24 | 1 | 1591 |
| Device Parameters | Value (mm) |
|---|---|
| Lower roller spacing | 465 |
| Lower roller diameter | 120 |
| Upper roller diameter | 120 |
| Attributes | Unit | Value |
|---|---|---|
| Tensile strength | MPa | ≥205 |
| Conditional yield strength | MPa | ≥170 |
| Elongation | % | ≥7 |
| Maximum shear stress | MPa | 115 |
| Roll Spacing (mm) | Feed Rate (mm/s) | Reduction (mm) | Radius of Curvature (mm) |
|---|---|---|---|
| 465 | 14.65 | 3 | 166,111 |
| 465 | 14.65 | 6 | 24,901 |
| 465 | 14.65 | 9 | 8098 |
| 665 | 14.65 | 12 | 7688 |
| 665 | 14.65 | 15 | 5431 |
| 665 | 14.65 | 18 | 3241 |
| 465 | 10.65 | 12 | 7022 |
| 465 | 10.65 | 15 | 4899 |
| 465 | 10.65 | 18 | 2514 |
| MSE | MAE | MAPE | |
|---|---|---|---|
| Initial hyperparameter combination | 44.5 | 2.85 | 13.19 |
| Optimal hyperparameter combination | 28.7 | 2.28 | 12.69 |
| Worst hyperparameter combination | 256.23 | 7.94 | 35.53 |
| MSE | MAE | MAPE | |
|---|---|---|---|
| Polynomial regression | 93.44 | 7.79 | 191.37 |
| SVR | 80.45 | 7.07 | 88.29 |
| Neural Networks | 49.01 | 3.99 | 41.42 |
| XGBoost | 28.7 | 2.28 | 12.69 |
| MSE | MAE | MAPE | |
|---|---|---|---|
| CRF | 3.42 | 2.12 | 24.30 |
| CRF + NN | 1.40 | 0.66 | 13.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, H.; Yu, G.; Liu, T.; Fu, P.; Huang, G.; Zhao, J. Research on the Curvature Prediction Method of Profile Roll Bending Based on Machine Learning. Metals 2023, 13, 143. https://doi.org/10.3390/met13010143
Cao H, Yu G, Liu T, Fu P, Huang G, Zhao J. Research on the Curvature Prediction Method of Profile Roll Bending Based on Machine Learning. Metals. 2023; 13(1):143. https://doi.org/10.3390/met13010143
Chicago/Turabian StyleCao, Hongqiang, Gaochao Yu, Tong Liu, Pengcheng Fu, Guoyan Huang, and Jun Zhao. 2023. "Research on the Curvature Prediction Method of Profile Roll Bending Based on Machine Learning" Metals 13, no. 1: 143. https://doi.org/10.3390/met13010143
APA StyleCao, H., Yu, G., Liu, T., Fu, P., Huang, G., & Zhao, J. (2023). Research on the Curvature Prediction Method of Profile Roll Bending Based on Machine Learning. Metals, 13(1), 143. https://doi.org/10.3390/met13010143








