An Improved Optimization Model to Predict the Deposition Rate and Smoothness of Ni Pulse-Reverse Electroplating Based on ANN and Experimental Results
Abstract
:1. Introduction
2. Experimental Setup
2.1. Microfabrication Process
- One-sided oxide silicon wafers are selected as the substrate.
- RCA1 cleaning for 3 min to remove contaminants.
- RCA2 cleaning for 3 min.
- Deeping in deionized water for 3 min.
- Washing wafer with water and drying with nitrogen.
- SiO2 passivation layer etching.
- Cr adhesive layer deposition by sputtering (50 nm).
- Au conductive layer deposition by sputtering (150 nm).
- Cleaning with acetone and IPA.
- KMPR photolithography by UV- exposure.
- Ni structural layer deposition by pulse-reverse electroplating.
- Photoresist stripping.
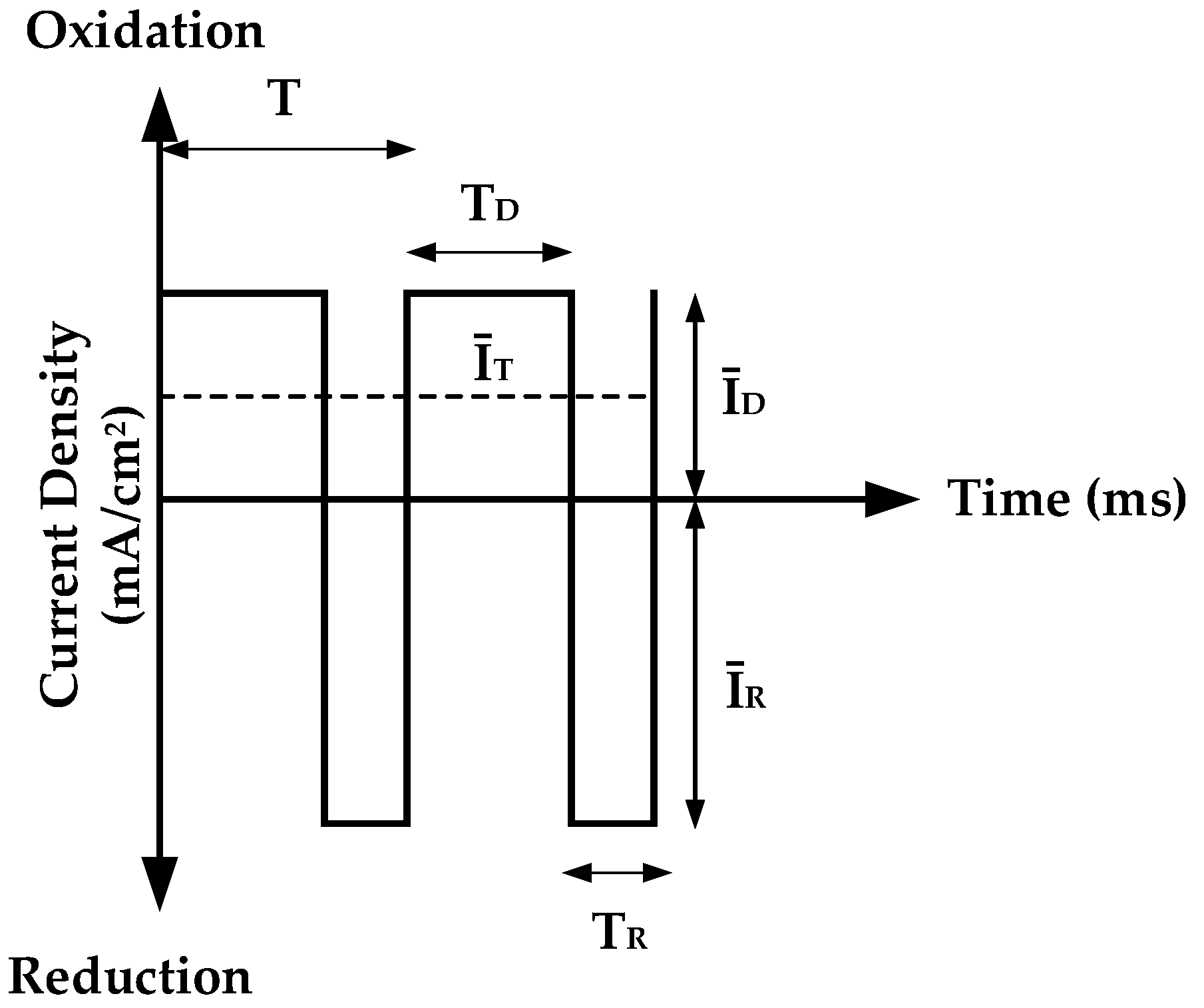
2.2. Design of Experiments
2.3. Surface Roughness and Layer Thickness Measurement Method
3. Neural Network Modeling
Layer’s Thickness and Surface Roughness Prediction Using NN
4. Results and Discussion
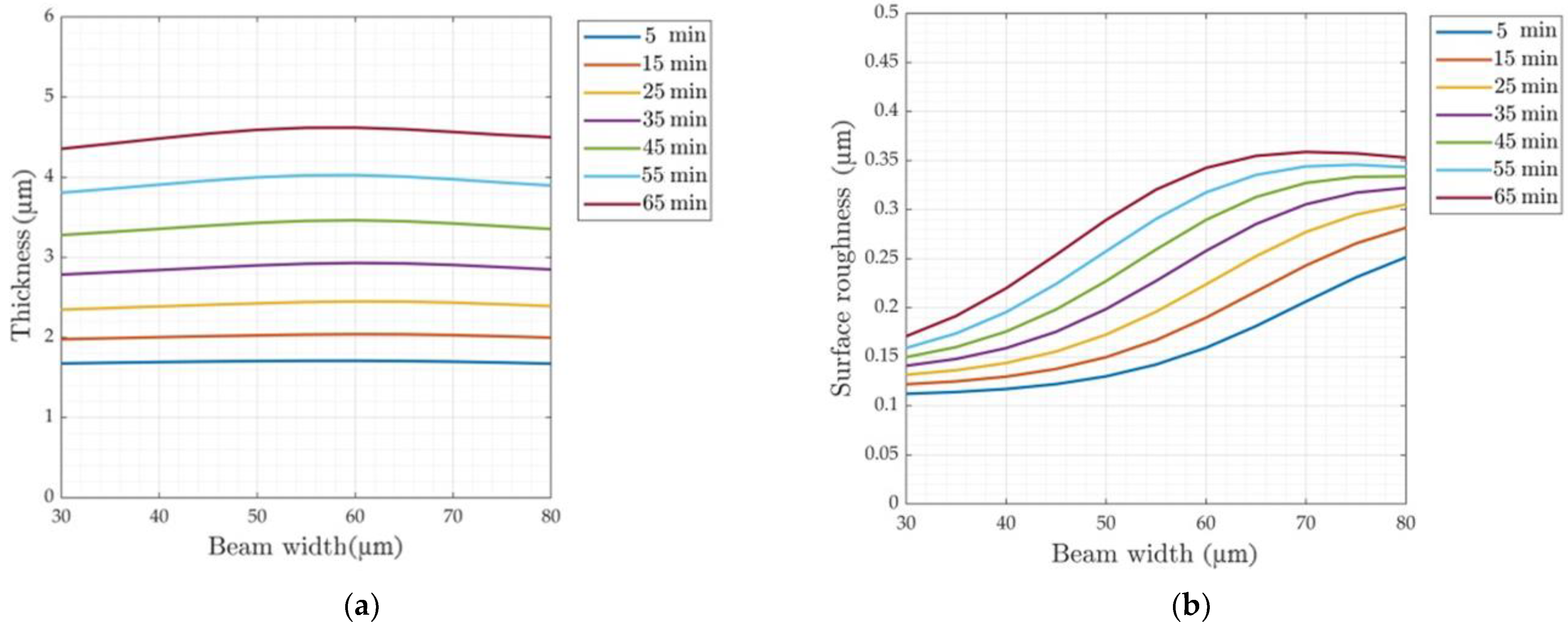
4.1. The Effect of the Beam Width on the Layer Thickness and Surface Roughness
4.2. The Effect of Stirring Speed on the Layer’s Thickness and Surface Roughness
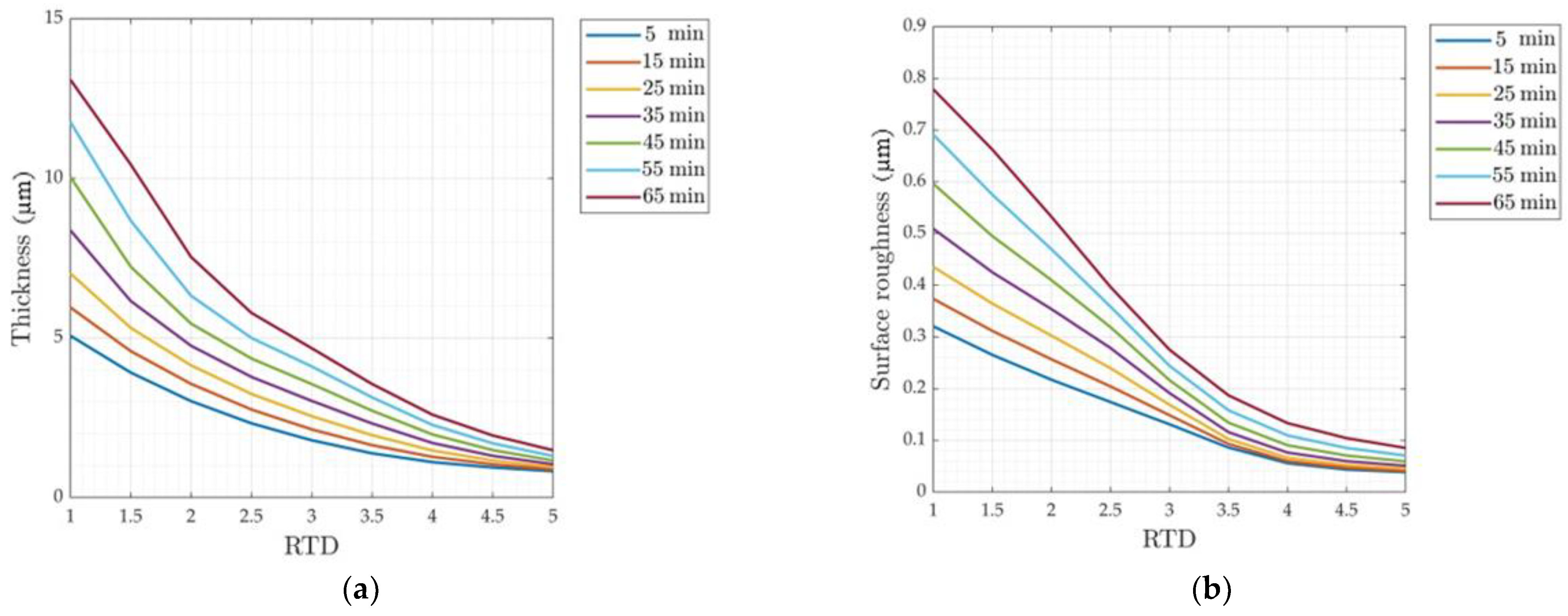
4.3. The Effect of RTD on the Layer Thickness and Surface Roughness
4.4. The Effect of Current Density on the Layer Thickness and Surface Roughness
4.5. Optimization and Adjustment of Parameters for Nickel Pulse-Reverse Electroplating
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hartzell, A.L.; Da Silva, M.G.; Shea, H.R. MEMS Reliab; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- Algamili, A.S.; Algamili, A.S.; Khir, M.H.M.; Dennis, J.O.; Ahmed, A.Y.; Alabsi, S.S.; Hashwan, S.S.B.; Junaid, M.M. A review of actuation and sensing mechanisms in mems-based sensor devices. Nanoscale Res. Lett. 2021, 16, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Ghazali, F.A.M.; Hasan, M.N.; Rehman, T.; Nafea, M.; Ali, M.S.M.; Takahata, K. MEMS actuators for biomedical applications: A review. J. Micromech. Microeng. 2020, 30, 073001. [Google Scholar] [CrossRef]
- Qu, H. CMOS MEMS fabrication technologies and devices. Micromachines 2016, 7, 14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, Y.; Vasan, A.S.S.; Doraiswami, R.; Osterman, M.; Pecht, M. MEMS reliability review. IEEE Trans. Device Mater. Reliab. 2012, 12, 482–493. [Google Scholar] [CrossRef] [Green Version]
- Malek, C.K.; Saile, V. Applications of LIGA technology to precision manufacturing of high-aspect-ratio micro-components and-systems: A review. Microelectron. J. 2004, 35, 131–143. [Google Scholar] [CrossRef]
- Park, J.; Fujita, H.; Kim, B. Fabrication of metallic microstructure on curved substrate by optical soft lithography and copper electroplating. Sens. Actuators A Phys. 2011, 168, 105–111. [Google Scholar] [CrossRef]
- Basrour, S.; Robert, L. X-ray characterization of residual stresses in electroplated nickel used in LIGA technique. Mater. Sci. Eng. A 2000, 288, 270–274. [Google Scholar] [CrossRef]
- Yamamoto, T.; Jiang, Y.; Chen, C.-Y.; Kurioka, T.; Luo, X.; Yamane, D.; Mizoguchi, M.; Kudo, O.; Maeda, R.; Sone, M.; et al. Effects of current density on mechanical properties of electroplated nickel with high speed sulfamate bath. Microelectron. Eng. 2019, 213, 18–23. [Google Scholar] [CrossRef]
- Luo, J.; Flewitt, A.; Spearing, S.; Fleck, N.; Milne, W. Comparison of microtweezers based on three lateral thermal actuator configurations. J. Micromech. Microeng. 2005, 15, 1294. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Jabbireddy, S.; Zhang, Y.; Peckerar, M.; Dagenais, M.; Varshney, A. A low cost micro-heater for aerosol generation applications. Microelectron. Eng. 2014, 129, 46–52. [Google Scholar] [CrossRef]
- Sun, S.; Dai, X.; Sun, Y.; Xiang, X.; Ding, G.; Zhao, X. MEMS-based wide-bandwidth electromagnetic energy harvester with electroplated nickel structure. J. Micromech. Microeng. 2017, 27, 115007. [Google Scholar] [CrossRef]
- Hamid, H.A.; Çelik-Butler, Z. A novel MEMS triboelectric energy harvester and sensor with a high vibrational operating frequency and wide bandwidth fabricated using UV-LIGA technique. Sens. Actuators A Phys. 2020, 313, 112175. [Google Scholar] [CrossRef]
- Chandrasekar, M.; Pushpavanam, M. Pulse and pulse reverse plating—Conceptual, advantages and applications. Electrochim. Acta 2008, 53, 3313–3322. [Google Scholar] [CrossRef]
- Dai, W.; Oropeza, C.; Lian, K.; Wang, W. Experiment design and UV-LIGA microfabrication technology to study the fracture toughness of Ni microstructures. Microsyst. Technol. 2006, 12, 306–314. [Google Scholar] [CrossRef]
- Nawaz, H.; Masood, M.U.; Saleem, M.M.; Iqbal, J.; Zubair, M. Surface roughness effects on electromechanical performance of RF-MEMS capacitive switches. Microelectron. Reliab. 2020, 104, 113544. [Google Scholar] [CrossRef]
- Bora, C.; Bora, C.K.; Flater, E.E.; Street, M.D.; Redmond, J.M.; Starr, M.J.; Carpick, R.W.; Plesha, M.E. Multiscale roughness and modeling of MEMS interfaces. Tribol. Lett. 2005, 19, 37–48. [Google Scholar] [CrossRef]
- Larsen, K.P.; Ravnkilde, J.T.; Ginnerup, M.; Hansen, O. Devices for fatigue testing of electroplated nickel (MEMS). In Technical Digest. MEMS 2002 IEEE International Conference. Fifteenth IEEE International Conference on Micro Electro Mechanical Systems (Cat. No. 02CH37266); IEEE: Piscataway, NJ, USA, 2002; pp. 443–446. [Google Scholar]
- Ibl, N. Some theoretical aspects of pulse electrolysis. Surf. Technol. 1980, 10, 81–104. [Google Scholar] [CrossRef]
- Vayenas, C.G.; White, R.E.; Gamboa-Aldeco, M.E. Modern Aspects of Electrochemistry 42; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Schlesinger, M.; Paunovic, M. Modern Electroplating; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Budevski, E.; Staikov, G.; Lorenz, W. Electrocrystallization: Nucleation and growth phenomena. Electrochim. Acta 2000, 45, 2559–2574. [Google Scholar] [CrossRef]
- Ji, F.; Chen, C.; Zhao, Y.; Min, B. Optimization of Copper Electroforming Process Parameters Based on Double Hidden Layer BP Neural Network. Micromachines 2021, 12, 1157. [Google Scholar] [CrossRef]
- Singh, A.; Panda, S.; Chakraborty, D.; Pal, S. Predicting drill wear using an artificial neural network. Int. J. Adv. Manuf. Technol. 2006, 28, 456–462. [Google Scholar] [CrossRef]
- Sanjay, C.; Neema, M.; Chin, C. Modeling of tool wear in drilling by statistical analysis and artificial neural network. J. Mater. Process. Technol. 2005, 170, 494–500. [Google Scholar] [CrossRef]
- Patra, K.; Pal, S.K.; Bhattacharyya, K. Artificial neural network based prediction of drill flank wear from motor current signals. Appl. Soft Comput. 2007, 7, 929–935. [Google Scholar] [CrossRef]
- Akbari, M.; Barazandeh, F.; Barati, H. A novel approach to design and fabricate an electrothermal microgripper for cell manipulation. Sens. Actuators A Phys. 2022, 346, 113877. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Q.; Dong, H.; Xi, L.; Lin, X.; Pan, F.; Ma, Z. Electroless plating of Ni-PW coatings containing scattered Nb2O5 on sintered NdFeB substrate. Mater. Res. 2015, 18, 1089–1096. [Google Scholar] [CrossRef] [Green Version]
- Tang, L.; Han, S.; Chen, P.; Hang, T.; Ling, H.; Wu, Y.; Li, M. Influence of artificial exchange current density on microstructure of Ni films by pulse-reverse electroplating. Mater. Chem. Phys. 2022, 288, 126338. [Google Scholar] [CrossRef]
- Tseluikin, V.; Dzhumieva, A.; Tikhonov, D.; Yakovlev, A.; Strilets, A.; Tribis, A.; Lopukhova, M. Pulsed Electrodeposition and Properties of Nickel-Based Composite Coatings Modified with Graphene Oxide. Coatings 2022, 12, 656. [Google Scholar] [CrossRef]
- Kamel, M.; El_moemen, A.A.; Rashwan, S.; Bolbol, A. Electrodeposition of Nanocrystalline Copper Deposits Using Lactic Acid-Based Plating Bath. Metall 2017, 179–183. [Google Scholar]









| The Absolute Mean Value of Training Data Error (%) | The Best MSE | The Absolute Mean Value of Test Data Error (%) | Number of Neurons |
|---|---|---|---|
| 30 | 0.07731 | 34 | 2-5-5 |
| 7 | 0.00361 | 30 | 2-6-5 |
| 0.7 | 0.03020 | 3.3 | 2-7-5 |
| 8 | 0.02525 | 16 | 2-8-5 |
| 2.05 | 0.00251 | 13 | 2-9 |
| 4.15 | 0.03511 | 20 | 2-10-5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koochaksaraie, R.A.; Barazandeh, F.; Akbari, M. An Improved Optimization Model to Predict the Deposition Rate and Smoothness of Ni Pulse-Reverse Electroplating Based on ANN and Experimental Results. Metals 2023, 13, 37. https://doi.org/10.3390/met13010037
Koochaksaraie RA, Barazandeh F, Akbari M. An Improved Optimization Model to Predict the Deposition Rate and Smoothness of Ni Pulse-Reverse Electroplating Based on ANN and Experimental Results. Metals. 2023; 13(1):37. https://doi.org/10.3390/met13010037
Chicago/Turabian StyleKoochaksaraie, Reza Ahmadian, Farshad Barazandeh, and Mohammad Akbari. 2023. "An Improved Optimization Model to Predict the Deposition Rate and Smoothness of Ni Pulse-Reverse Electroplating Based on ANN and Experimental Results" Metals 13, no. 1: 37. https://doi.org/10.3390/met13010037
APA StyleKoochaksaraie, R. A., Barazandeh, F., & Akbari, M. (2023). An Improved Optimization Model to Predict the Deposition Rate and Smoothness of Ni Pulse-Reverse Electroplating Based on ANN and Experimental Results. Metals, 13(1), 37. https://doi.org/10.3390/met13010037






