Numerical Simulation of Multi-Physics Fields in Fused Magnesia Furnace
Abstract
:1. Introduction
- Based on the actual production of fused magnesium oxide, a three-dimensional transient electromagnetic heat flow multi-field coupling model is established to feedback the production state in a furnace.
- The assumption that a furnace is all magnesium oxide in many previous works is removed, and the influence of chemical reactions on temperature distribution is fully considered.
- The frequently used interpolation method is abandoned, and a more accurate two-way coupling method is selected to define the source term of the electromagnetic field equation in the form of user defined functions.
2. Mathematical Model
2.1. Multi-Physics Field Model
2.2. Simulation Assumption
- Under actual conditions, the operation mode of a fused magnesium oxide furnace is intermittent feeding. However, in the model, the calculation domain is initially filled with ore, the furnace gas diffuses upward, and the product diffuses downward; moreover, the cooling process after smelting is not included in the calculation scope.
- Chemical reactions of primary concern are considered, and very few additional reactions are ignored.
- Arc composition is considered to be a mixture of air plasma and magnesium oxide plasma, and its physical parameters obtained from [10].
- Since the mold wall thickness in the fused magnesium oxide furnace is only 3 mm, its physical model is ignored, and the fixed heat flux is replaced.
- Gas products are considered to be incompressible ideal gases.
- Plasma is considered to be a liquid with unique physical properties. Other properties are not taken into account.
3. Simulation Strategy
3.1. Geometry
3.2. Physical Properties
3.3. Boundary Conditions
3.4. Numerical Procedure
4. Results and Discussion
4.1. Model Simplification and Mesh Generation
4.2. Model Validation
4.3. Multi-Physical Field inside the Furnace
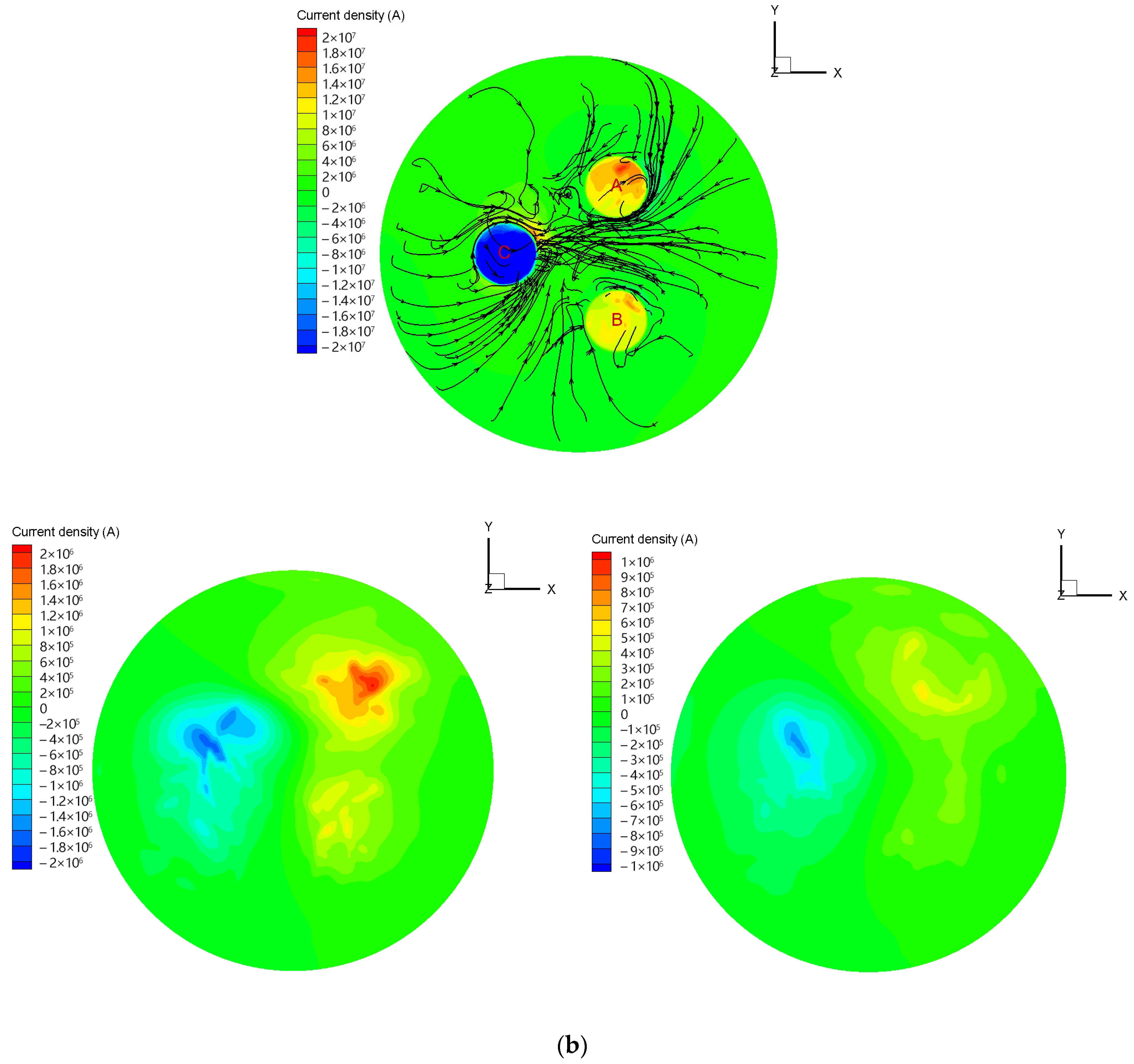
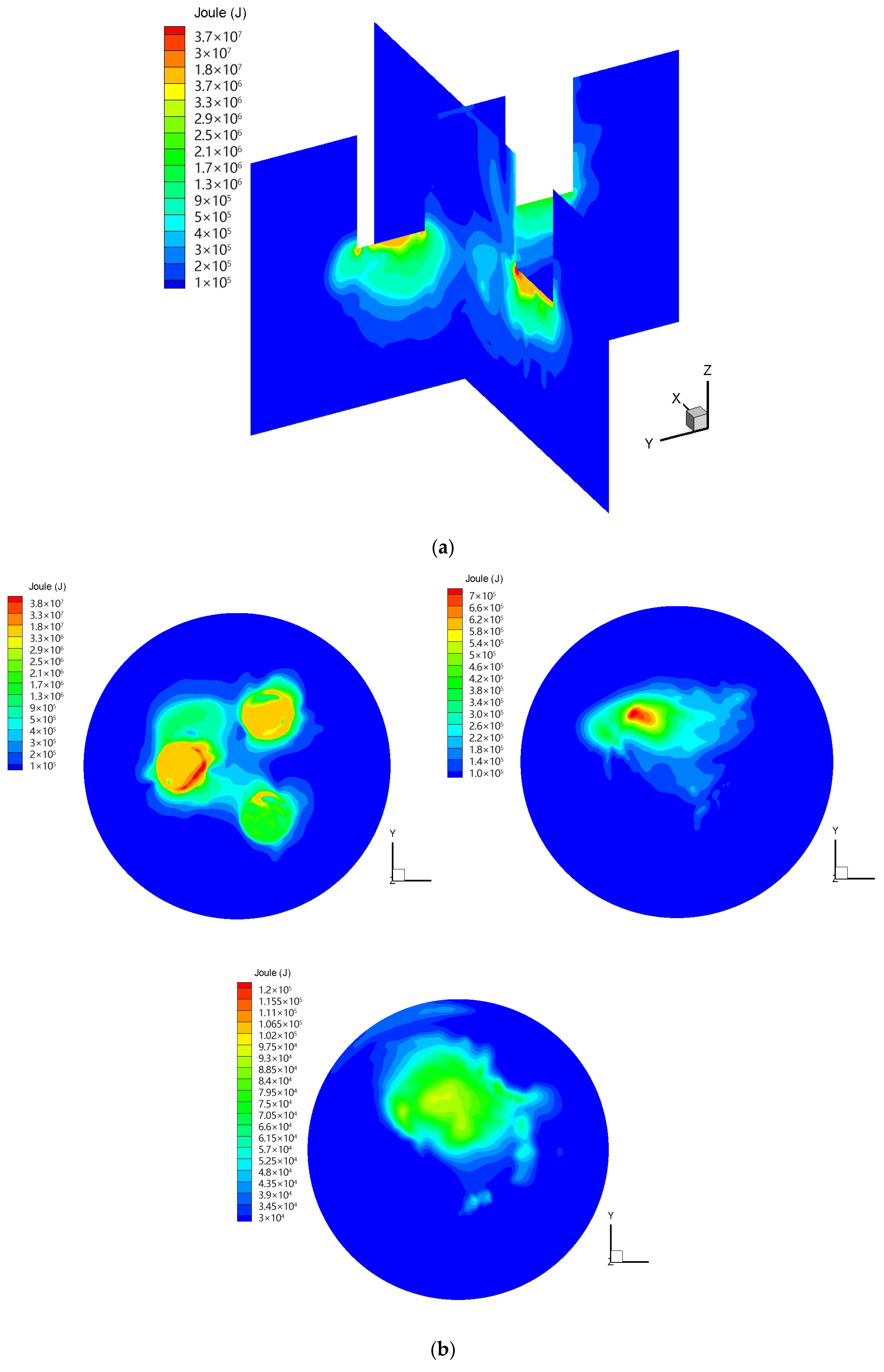
4.3.1. Electromagnetic Field Distribution
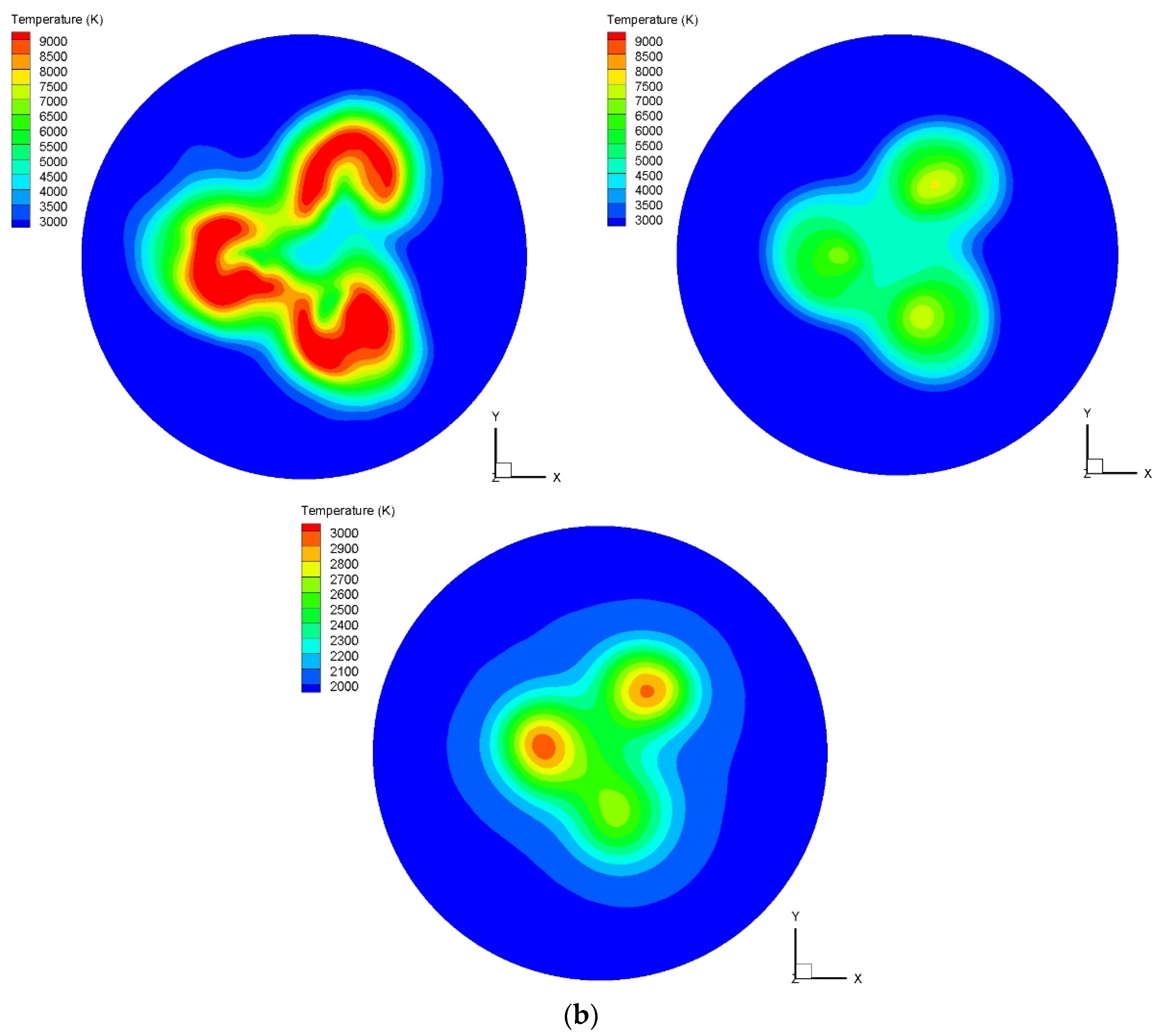
4.3.2. Arc Temperature Distribution
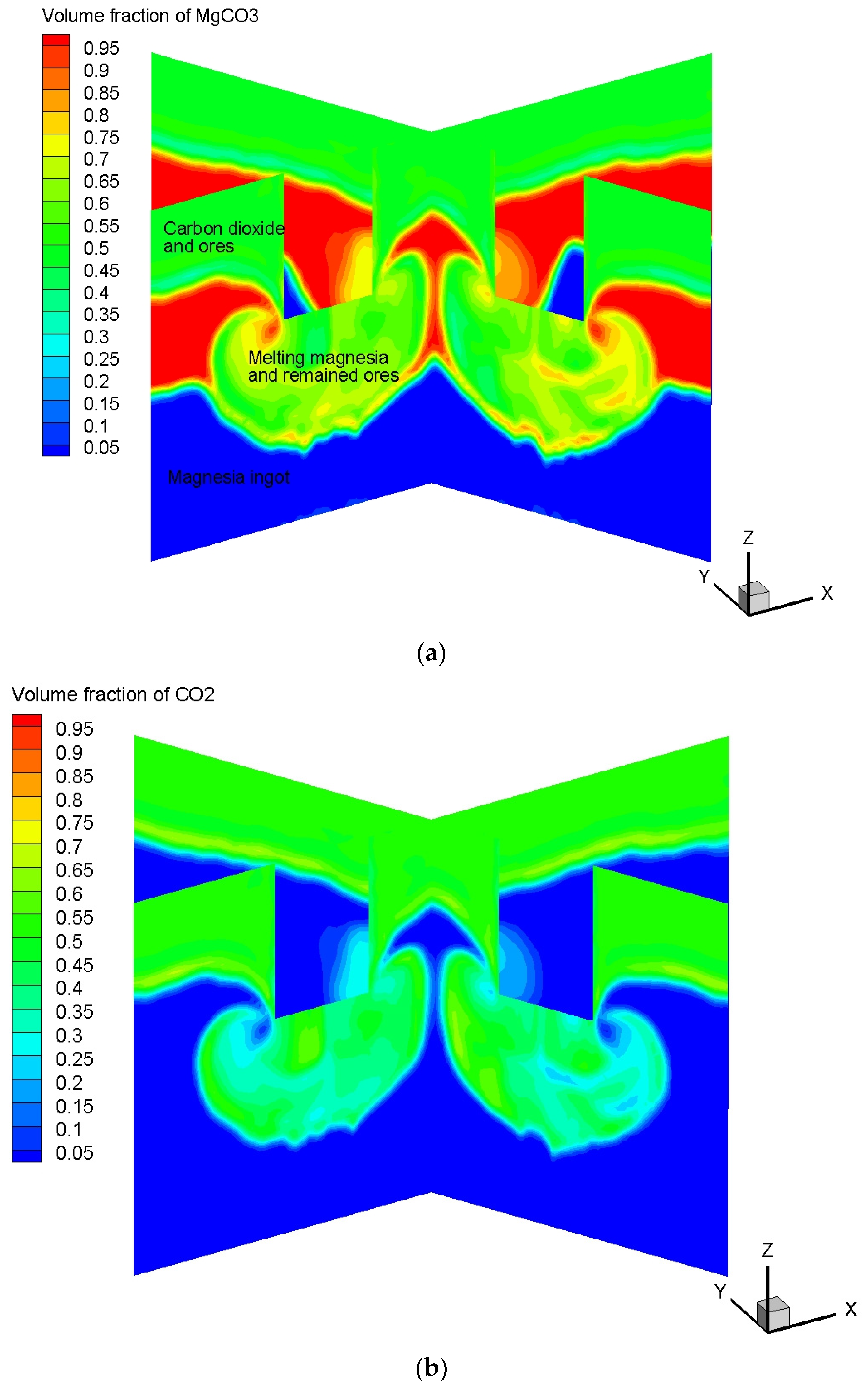
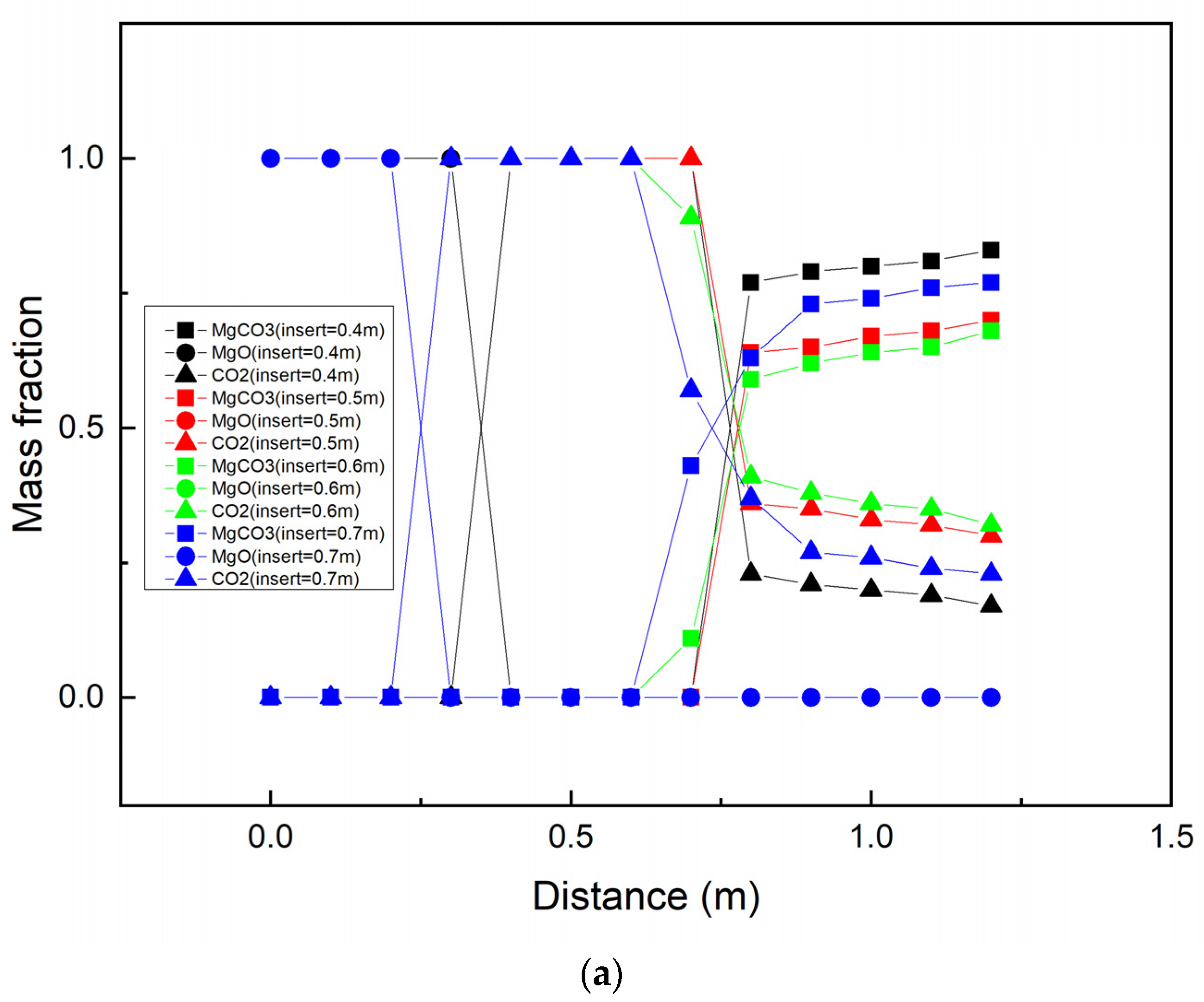
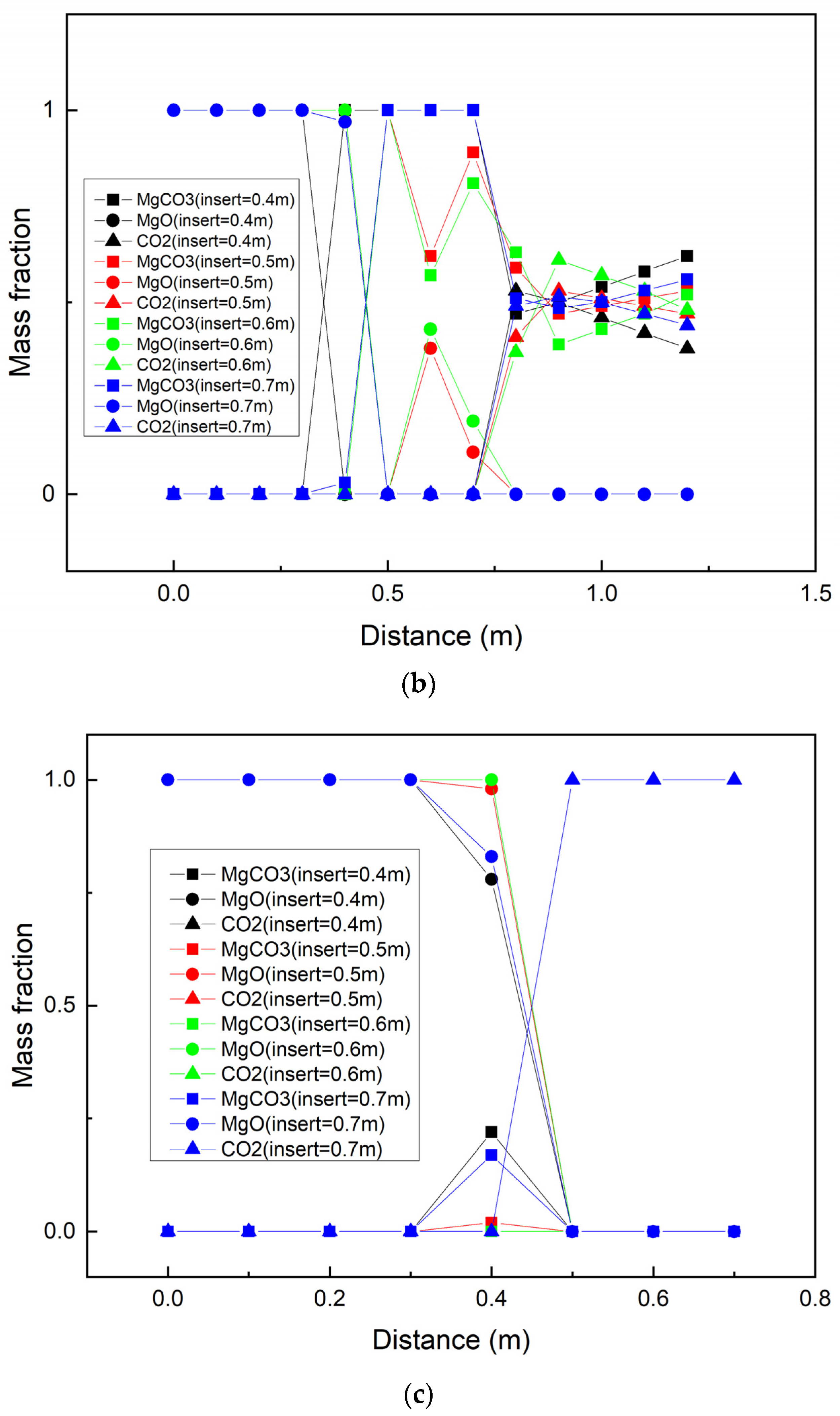
4.3.3. Reaction Distribution
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Q.; Wei, T. Development status and prospect of magnesium refractory materials in China. Refract. Ries 2013, 47, 210–214. [Google Scholar]
- Jiang, X. Study on New Energy Saving Technology of Fused Magnesia and Crystallization Process of Magnesite in Magnesite Smelting. Master’s Thesis, Northeastern University, Shenyang, China, 2011. [Google Scholar]
- Jiang, T.; Zhang, W.; Liu, S. Performance Evaluation of a Full-Scale Fused Magnesia Furnace for MgO Production Based on Energy and Exergy Analysis. Energies 2021, 15, 214. [Google Scholar] [CrossRef]
- Bowman, B.; Edels, H. Radial temperature measurements of alternating current arcs. J. Phys. D Appl. Phys. 1969, 2, 53. [Google Scholar] [CrossRef]
- Wu, X.; Feng, Y.; Li, Y.; Li, Y.; Zhang, X.; Wu, C. Numerical simulation and orthogonal analysis on coupled arc with molten pool for keyholing plasma arc weld-ing. Acta Metall. Sin. 2015, 51, 1365–1376. [Google Scholar] [CrossRef]
- Aula, M.; Demus, T.; Echterhof, T.; Huttula, M.; Pfeifer, H.; Fabritius, T. On-line Analysis of Cr2O3 Content of the Slag in Pilot Scale EAF by Measuring Optical Emission Spectrum of Electric Arc. ISIJ Int. 2017, 57, 478–486. [Google Scholar] [CrossRef] [Green Version]
- Cayo, E.H.; Alfaro, S.C.A. Aplicabilidad del monitoreo de emisiones del arco eléctrico para el control de calidad en el proceso MAG-S. Soldagem Inspeção 2011, 16, 341–349. [Google Scholar] [CrossRef] [Green Version]
- Almurr, J.; Bussière, W.; Hertzog, J.; Rochette, D. Numerical investigations on the electric arc behavior upon contact opening in a low-voltage switch under the effect of external magnetic field. Electr. Power Syst. Res. 2022, 209, 107945. [Google Scholar] [CrossRef]
- Urusov, R.M.; Urusova, I. Numerical simulation of a helical shape electric arc in the external axial magnetic field. Phys. Plasmas 2016, 23, 103502. [Google Scholar] [CrossRef]
- Chi, Z.; Zhang, W.; Yang, Q. Thermophysical properties of pure gases and mixtures at temperatures of 300–30,000 K and atmospheric pressure: Thermodynamic properties and solution of equilibrium compositions. Plasma Sci. Technol. 2021, 23, 125505. [Google Scholar] [CrossRef]
- Deng, J.; Li, Y.; Xu, Y.; Sheng, H. Numerical Simulation of Fluid Flow and Heat Transfer in a DC Non-Transferred Arc Plasma Torch Operating Under Laminar and Turbulent Conditions. Plasma Sci. Technol. 2011, 13, 201. [Google Scholar] [CrossRef] [Green Version]
- Wen, K.; Liu, X.; Zhou, K.; Liu, M.; Zhu, H.; Huang, J.; Zhang, Z.; Huang, R.; Mao, J.; Yan, X.; et al. 3D time-dependent numerical simulation for atmospheric plasma spraying. Surf. Coatings Technol. 2018, 371, 344–354. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, N.; Li, T.; Cao, Y. 3D Numerical Analysis of the Arc Plasma Behavior in a Submerged DC Electric Arc Furnace for the Production of Fused MgO. Plasma Sci. Technol. 2012, 14, 321–326. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Fu, Y.; Wang, N.; Feng, L. 3D numerical simulation of electrical arc furnaces for the MgO production. J. Mater. Process. Technol. 2014, 214, 2284–2291. [Google Scholar] [CrossRef]
- Yu, Y.; Li, B.; Yun, C.; Qi, F.; Liu, Z. Modeling on Reduction Reaction of Metal Oxides for Submerged Arc Furnace in Ferrochrome Pellets Smelting Process. Met. Mater. Trans. A 2021, 52, 3907–3919. [Google Scholar] [CrossRef]
- Xi, X.; Chen, S.; Yang, S.; Ye, M.; Li, J. Melting Characteristics of Multipiece Steel Scrap in Liquid Steel. ISIJ Int. 2021, 61, 190–199. [Google Scholar] [CrossRef]
- Logar, V.; Dovžan, D.; Škrjanc, I. Mathematical Modeling and Experimental Validation of an Electric Arc Furnace. ISIJ Int. 2011, 51, 382–391. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Yang, L.; Cheng, T.; Chen, F.; Zheng, F.; Wang, S.; Guo, Y. Fluid Flow Characteristic of EAF Molten Steel with Different Bottom-Blowing Gas Flow Rate Distributions. ISIJ Int. 2020, 60, 1957–1967. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Chen, X.; Xu, J.; Shi, L. Numerical simulation on electromagnetic field, flow field and temperature field in semisolid slurry preparation by A-EMS. Rare Met. 2010, 29, 635–641. [Google Scholar] [CrossRef]
- Wang, X.; Fan, D.; Huang, J.; Huang, Y. Numerical simulation of heat transfer and fluid flow in double electrodes TIG arc-weld pool. Acta Met. Sin. 2015, 51, 178–190. [Google Scholar]
- Bakken, J.A.; Gu, L.; Larsen, H.L.; Sevastyanenko, V.G. Numerical modeling of electric arcs. J. Eng. Phys. 1997, 70, 530–543. [Google Scholar] [CrossRef]
- Ranganathan, S.; Godiwalla, K.M. Influence of Process parameters on Reduction Contours during the production of Ferro-chromium in Submerged-arc Furnace, Canadian Metallurgical Quarterly. Can. Metall. Q. 2011, 50, 37–44. [Google Scholar] [CrossRef]
- Bowman, B. Measurements of plasma velocity distributions in free-burning DC arcs up to 2160 A. J. Phys. D Appl. Phys. 1972, 5, 1422. [Google Scholar] [CrossRef]








| Parameters | Value |
|---|---|
| Furnace height | 1.2 m |
| Furnace diameter | 1.9 m |
| Electrode diameter | 0.2 m |
| Electrode length | 1 m |
| Electrode insertion depth | 0.5 m |
| Wall thickness | 0.003 m |
| Reaction | Temperature (K) | A (min−1) | Ea (kj/mol) | Absorb Heat (kj/mol) | |
|---|---|---|---|---|---|
| 1 | MgCO3 = MgO (light burned) + CO2 | >973 | 3.22 × 106 | 79.10 | 100.59 |
| 2 | MgO (light burned) = MgO (die burned) | 973–2873 | - | - | - |
| 3 | MgO (die burned) = MgO (fused) | >2873 | - | - | - |
| Physical Parameters | Value |
|---|---|
| Temperature (K) | T |
| Density (kg/m3) | 3580 |
| Heat capacity [J/(kg·K)] | |
| Thermal conductivity [W/(m·K)] | |
| Electrical conductivity (S/m) | 19,894.5 |
| Temperature (K) | Density (Kg/m3) | Heat Conductivity (W/m·K) | Electric Conductivity (S/m) | Viscosity (Kg/m·s) | Radiation Coefficient (W/sr·m3) | Capacity (J/Kg·K) |
|---|---|---|---|---|---|---|
| 3000 | 105.999 | 0.6 | 19,894.6 | 0.00792 | 7.214 | 131.3 |
| 5000 | 89.23 | 1.01 | 115,856.3 | 0.0011 | 47.265 | 288.4 |
| 7000 | 28.26 | 1.44 | 216,795.8 | 0.0012 | 427.977 | 3601.8 |
| 9000 | 17.39 | 1.51 | 477,875.8 | 0.00065 | 1158.582 | 16,136.5 |
| 11,000 | 11.89 | 1.74 | 525,808.8 | 0.00049 | 4990.26 | 22,768.5 |
| 13,000 | 9.00 | 2.15 | 624,092.1 | 0.0004 | 9303.39 | 56,605.7 |
| Boundary | Voltage (V) | Magnetic Potential Vector (Vsm−1) | Temperature (K) |
|---|---|---|---|
| Electrode A | 5000 | ||
| Electrode B | 5000 | ||
| Electrode C | 5000 | ||
| Electrode sidewall | 2300 | ||
| Furnace top surface | |||
| Furnace sidewall | |||
| Furnace bottom |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, T.; Zhang, W. Numerical Simulation of Multi-Physics Fields in Fused Magnesia Furnace. Metals 2023, 13, 39. https://doi.org/10.3390/met13010039
Jiang T, Zhang W. Numerical Simulation of Multi-Physics Fields in Fused Magnesia Furnace. Metals. 2023; 13(1):39. https://doi.org/10.3390/met13010039
Chicago/Turabian StyleJiang, Tianchi, and Weijun Zhang. 2023. "Numerical Simulation of Multi-Physics Fields in Fused Magnesia Furnace" Metals 13, no. 1: 39. https://doi.org/10.3390/met13010039
APA StyleJiang, T., & Zhang, W. (2023). Numerical Simulation of Multi-Physics Fields in Fused Magnesia Furnace. Metals, 13(1), 39. https://doi.org/10.3390/met13010039





