Effect of Solid Concentration and Particle Size on the Flotation Kinetics and Entrainment of Quartz and Hematite
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Procedure
2.2. Flotation Kinetics Models
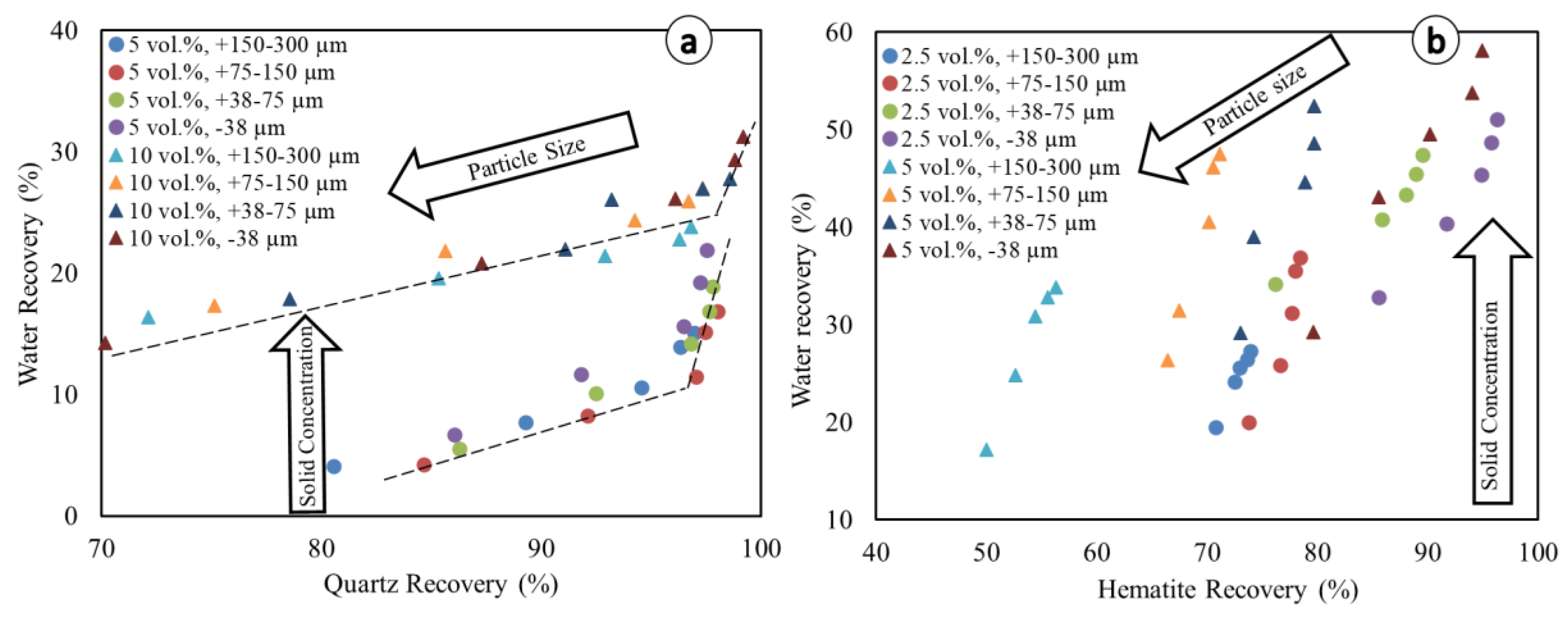
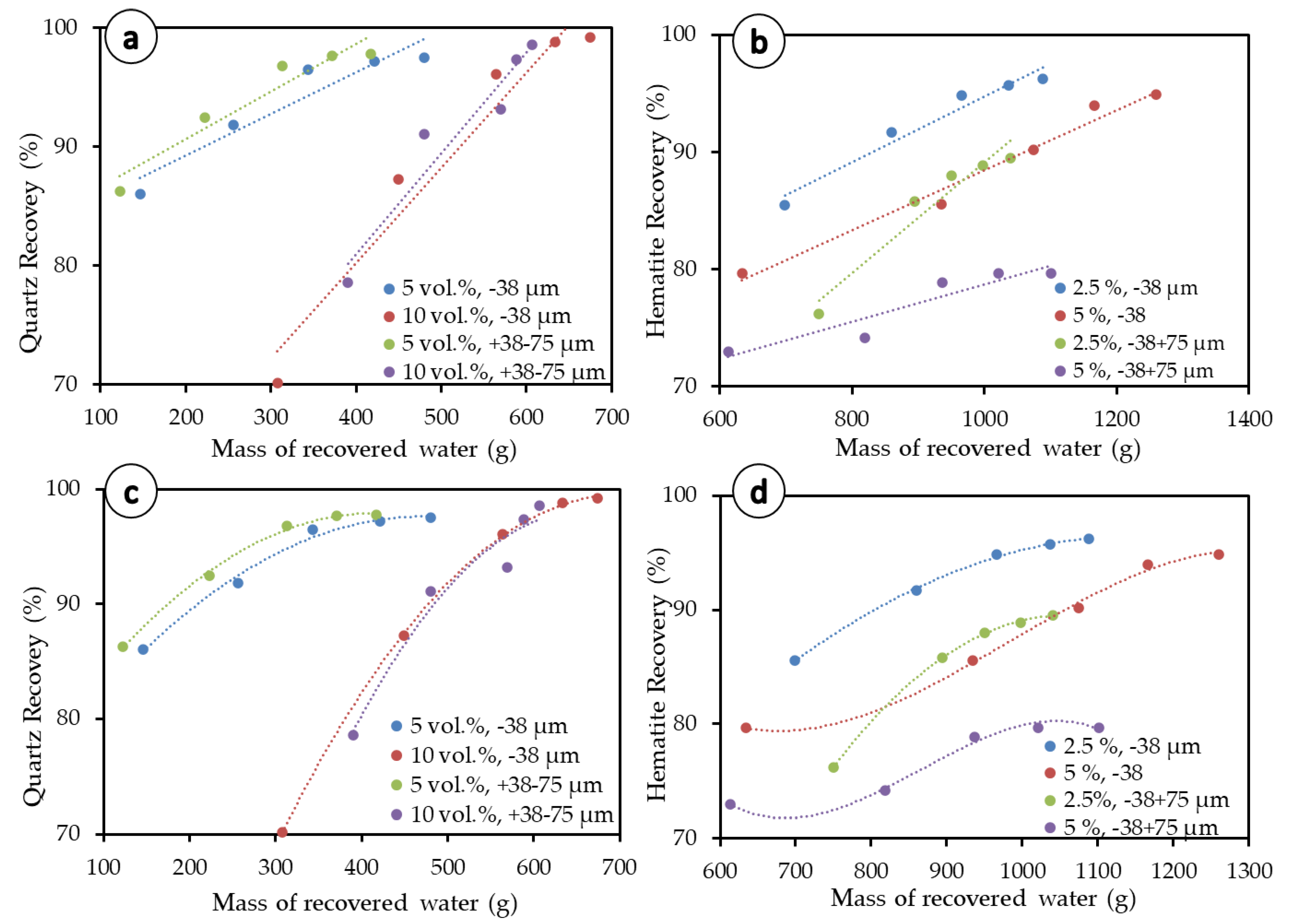
2.3. Entrainment
3. Results and Discussion
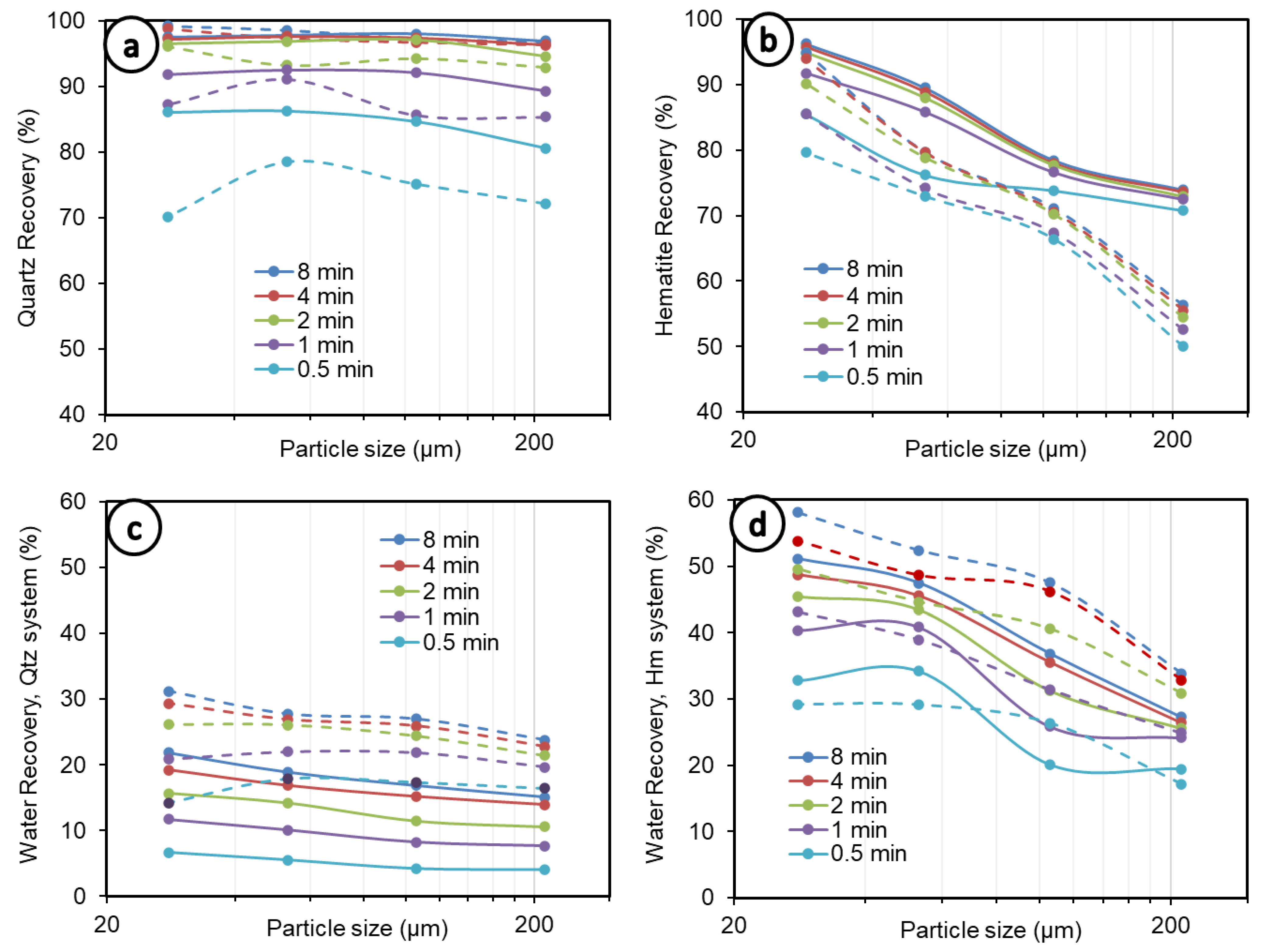
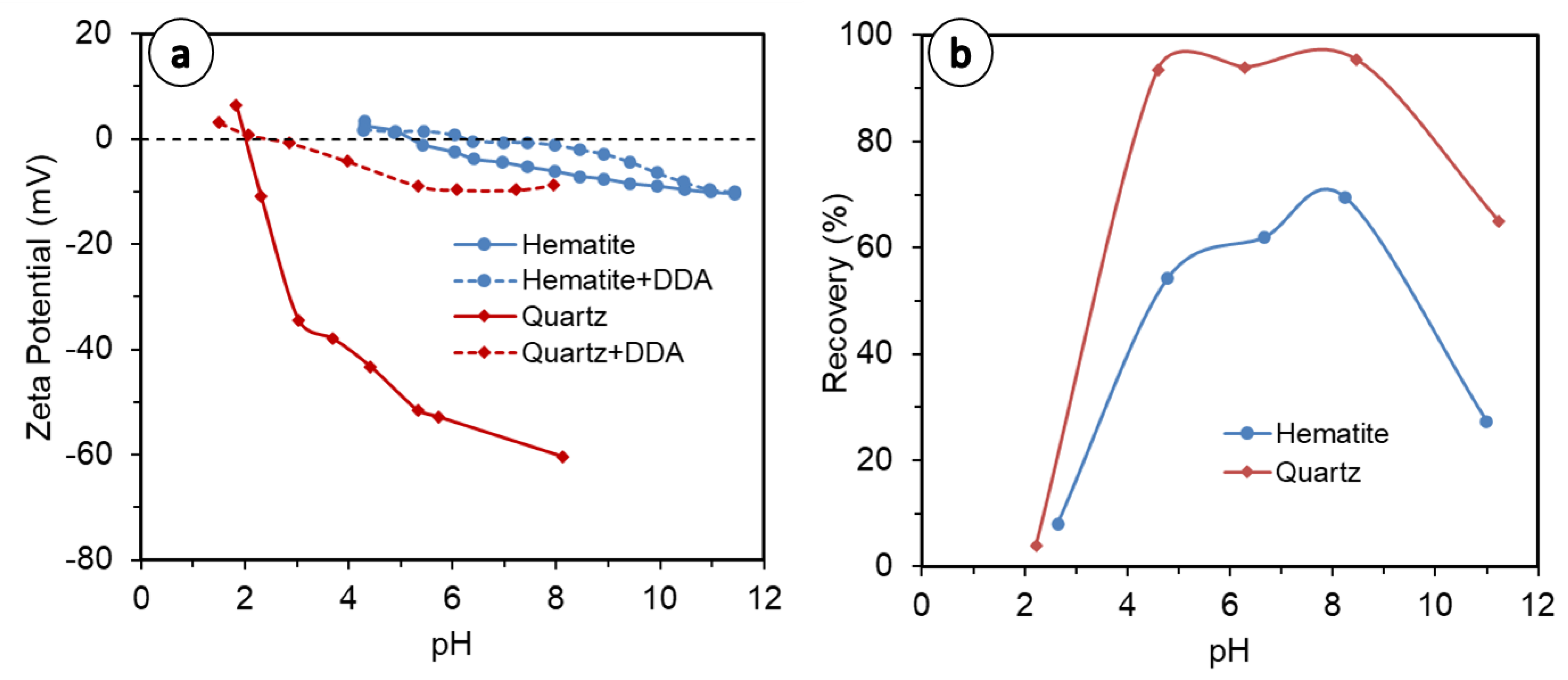
3.1. Effect of Particle Size and Solid Concentration
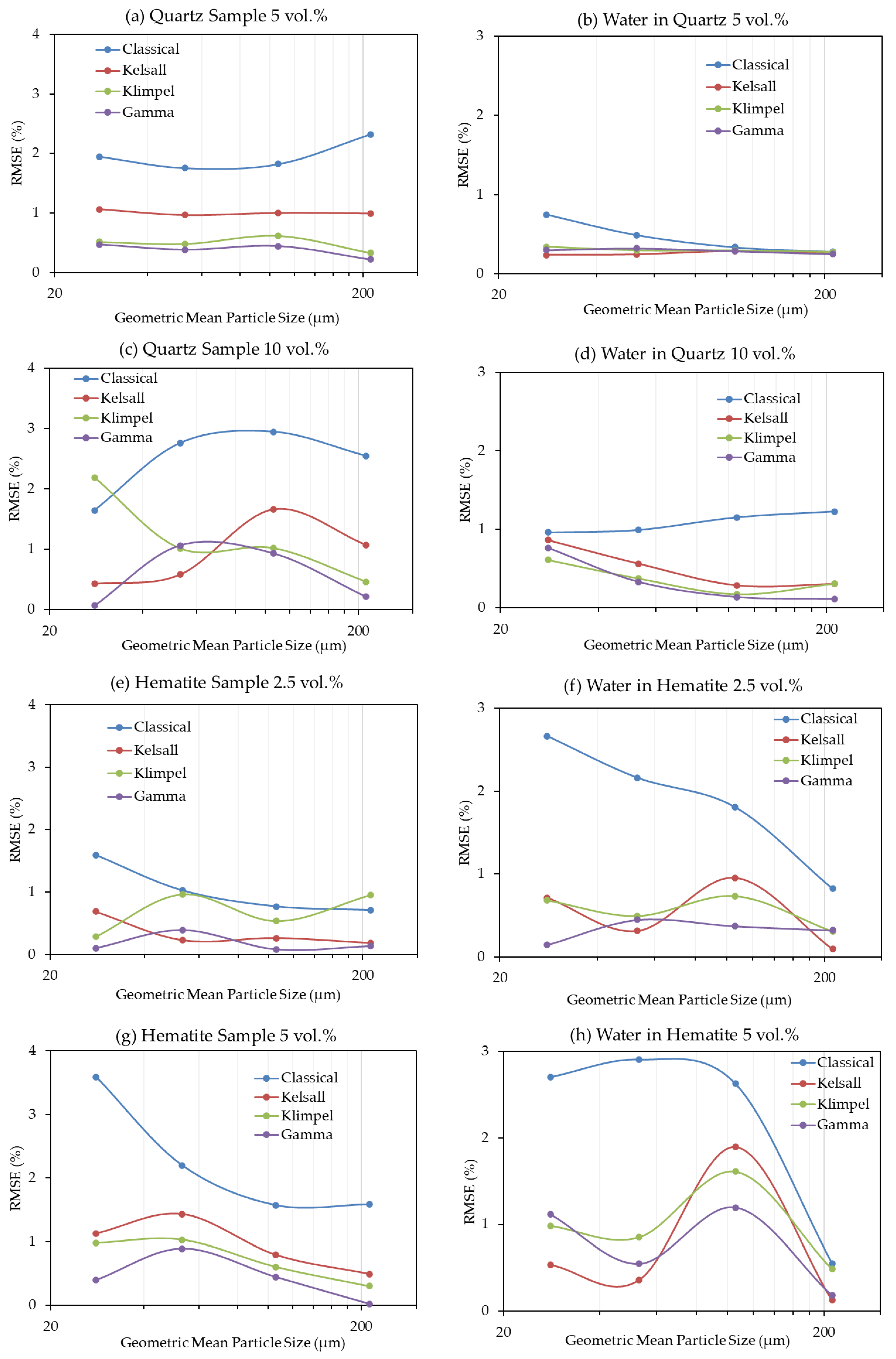
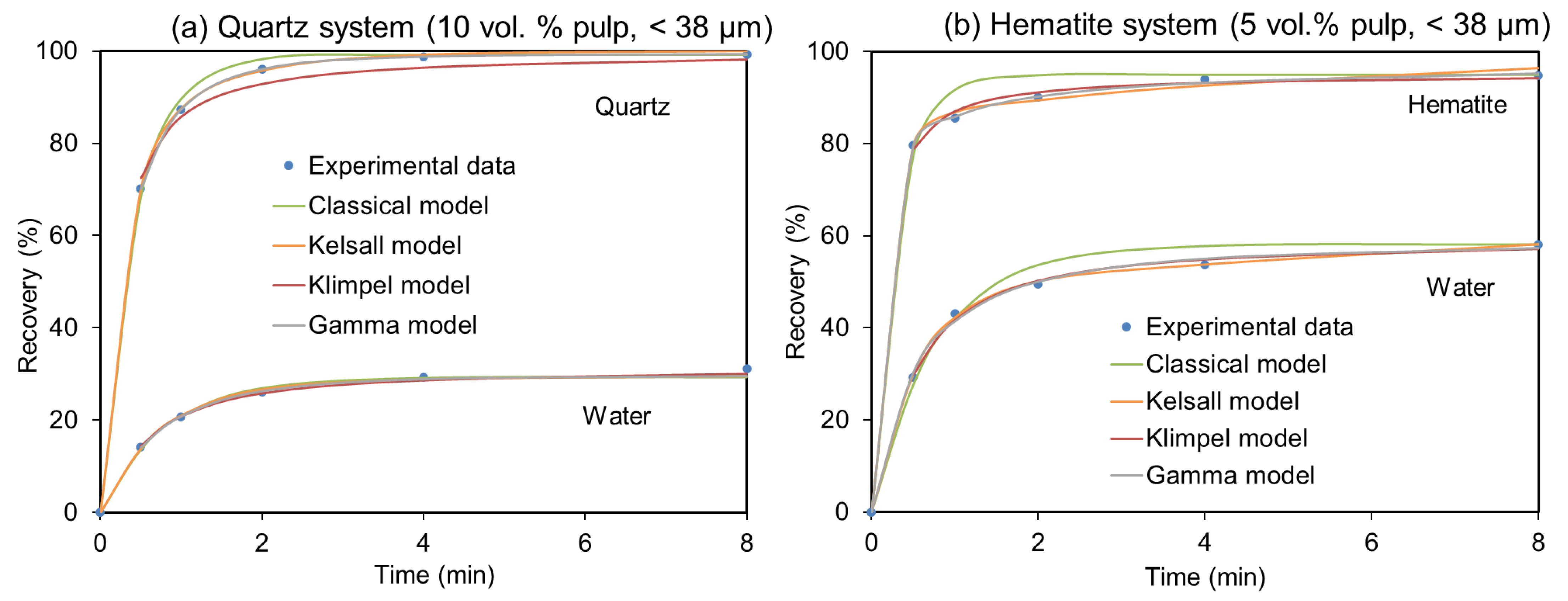
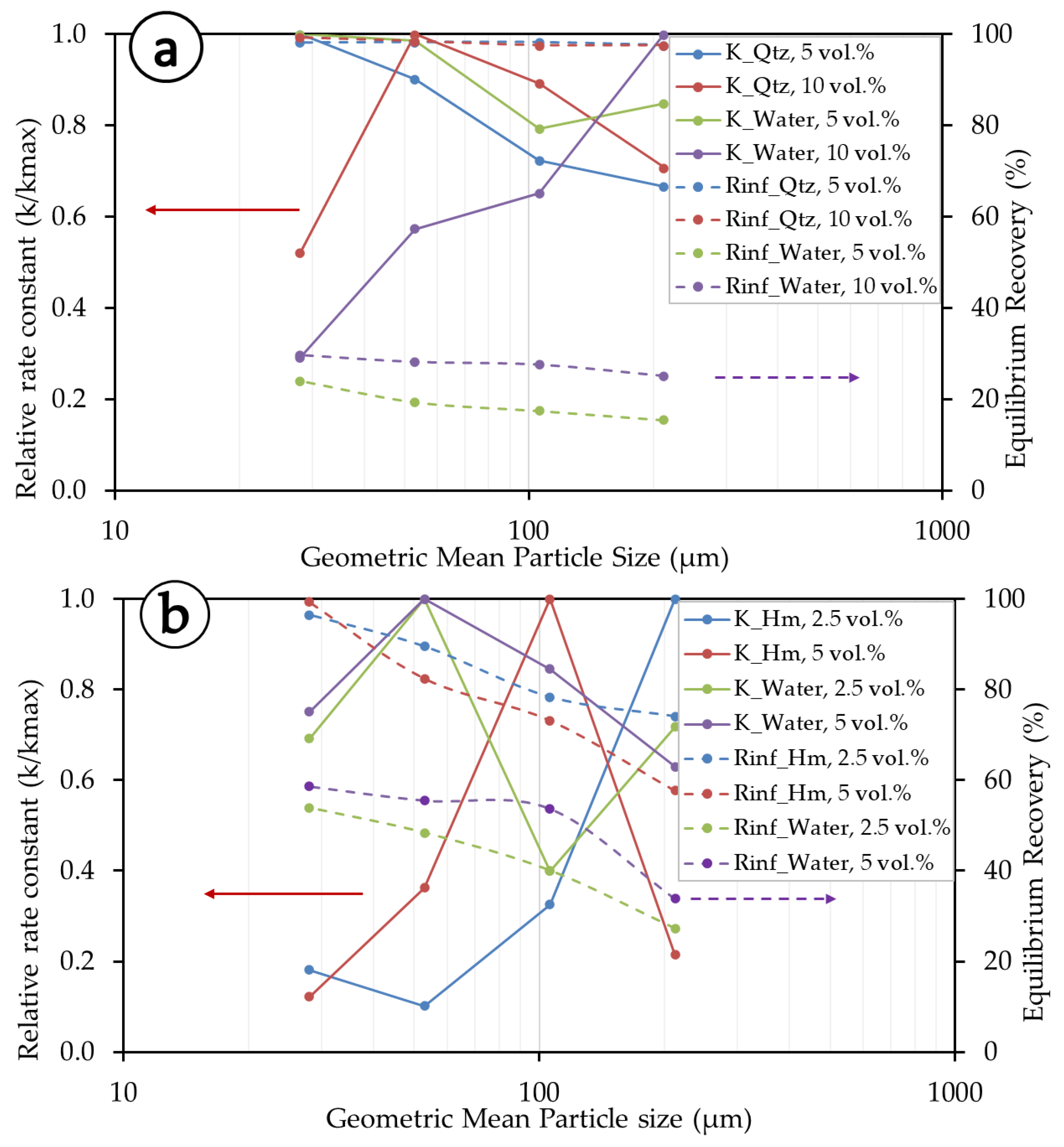
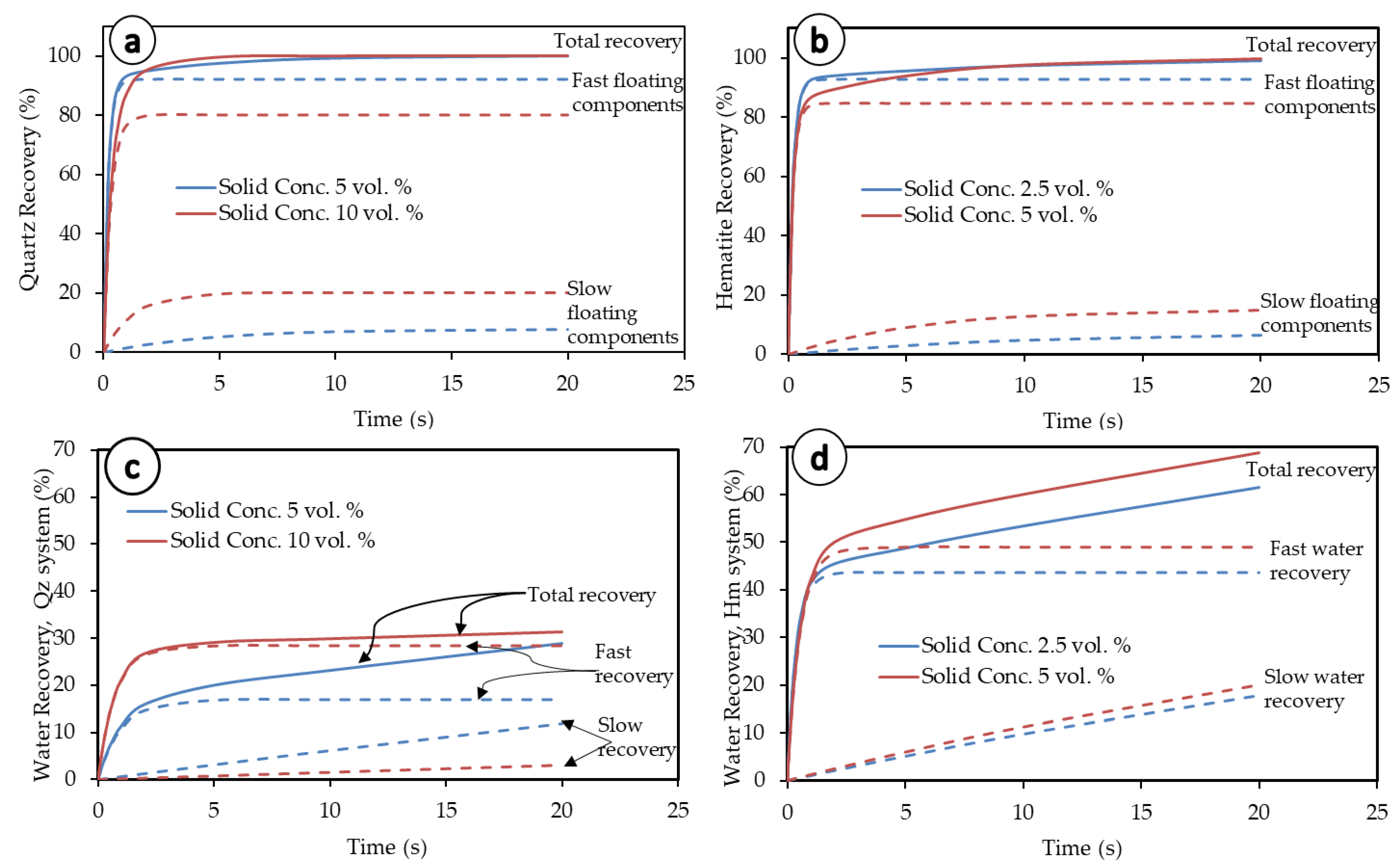
3.2. Kinetic Modeling
3.2.1. Equation Fitting
3.2.2. Kinetic Parameters
3.3. Entrainment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Filippov, L.O.; Severov, V.V.; Filippova, I.V. An Overview of the Beneficiation of Iron Ores via Reverse Cationic Flotation. Int. J. Miner. Process. 2014, 127, 62–69. [Google Scholar] [CrossRef]
- Braga, F.Y.A.; José, A.M.L.; Milhomem, F.O. Size-Dependent Kinetics of Iron Ore Reverse Flotation. Part. Sci. Technol. 2020, 38, 419–426. [Google Scholar] [CrossRef]
- Pereira, A.R.M.; Hacha, R.R.; Torem, M.L.; Merma, A.G.; Silvas, F.P.C.; Abhilash, A. Direct Hematite Flotation from an Iron Ore Tailing Using an Innovative Biosurfactant. Sep. Sci. Technol. 2021, 56, 2978–2988. [Google Scholar] [CrossRef]
- Quast, K. An Investigation of the Flotation Minimum in the Oleate Flotation of Hematite under Alkaline Conditions. Miner. Eng. 2017, 113, 71–82. [Google Scholar] [CrossRef]
- Ray, N.; Nayak, D.; Dash, N.; Rath, S.S. Utilization of Low-Grade Banded Hematite Jasper Ores: Recovery of Iron Values and Production of Ferrosilicon. Clean Technol. Environ. Policy 2018, 20, 1761–1771. [Google Scholar] [CrossRef]
- Araujo, A.C.; Viana, P.R.M.; Peres, A.E.C. Reagents in Iron Ores Flotation. Miner. Eng. 2005, 18, 219–224. [Google Scholar] [CrossRef]
- Kapiamba, K.F.; Kimpiab, M. The Effects of Partially Replacing Amine Collectors by a Commercial Frother in a Reverse Cationic Hematite Flotation. Heliyon 2021, 7, e06559. [Google Scholar] [CrossRef]
- Ma, M. Froth Flotation of Iron Ores. Int. J. Min. Eng. Miner. Process. 2012, 1, 56–61. [Google Scholar] [CrossRef]
- Nguyen, A.V. FLOTATION. In Encyclopedia of Separation Science; Wilson, I.D., Ed.; Academic Press: Oxford, UK, 2007; pp. 1–27. ISBN 978-0-12-226770-3. [Google Scholar]
- Wills, B.A.; Finch, J.A. Chapter 12—Froth Flotation. In Wills’ Mineral Processing Technology, 8th ed.; Butterworth-Heinemann: Oxford, UK, 2016; pp. 265–380. ISBN 978-0-08-097053-0. [Google Scholar]
- Runge, K. Laboratory Flotation Testing—An Essential Tool for Ore Characterisation. Flotat. Plant Optim. 2010, 19, 55–173. [Google Scholar]
- Zúñiga, H.G. La Recuperación Por Flotación Es Una Función Exponencial Del Tiempo. Boletín Soc. Nac. De Min. 1935, 47, 83–86. [Google Scholar]
- Bu, X.; Xie, G.; Peng, Y.; Ge, L.; Ni, C. Kinetics of Flotation. Order of Process, Rate Constant Distribution and Ultimate Recovery. Physicochem. Probl. Miner. Process. 2017, 53, 342–365. [Google Scholar] [CrossRef]
- Vinnett, L.; Waters, K.E. Representation of Kinetics Models in Batch Flotation as Distributed First-Order Reactions. Minerals 2020, 10, 913. [Google Scholar] [CrossRef]
- Trahar, W.J. A Rational Interpretation of the Role of Particle Size in Flotation. Int. J. Miner. Process. 1981, 8, 289–327. [Google Scholar] [CrossRef]
- Klimpel, R.R. Selection of Chemical Reagents for Flotation. In Mineral Processing Plant Design; Mullar, A.L., Bhappu, R.B., Eds.; AIME: New York, NY, USA, 1980; pp. 907–934. [Google Scholar]
- Gulsoy, O.Y. A Simple Model for the Calculation of Entrainment in Flotation. Korean J. Chem. Eng. 2005, 22, 628–634. [Google Scholar] [CrossRef]
- Kirjavainen, V.M. Application of a Probability Model for the Entrainment of Hydrophilic Particles in Froth Flotation. Int. J. Miner. Process. 1989, 27, 63–74. [Google Scholar] [CrossRef]
- Warren, L.J. Determination of the Contributions of True Flotation and Entrainment in Batch Flotation Tests. Int. J. Miner. Process. 1985, 14, 33–44. [Google Scholar] [CrossRef]
- Wang, L.; Peng, Y.; Runge, K.; Bradshaw, D. A Review of Entrainment: Mechanisms, Contributing Factors and Modelling in Flotation. Miner. Eng. 2015, 70, 77–91. [Google Scholar] [CrossRef]
- Wang, C.; Sun, C.; Liu, Q. Entrainment of Gangue Minerals in Froth Flotation: Mechanisms, Models, Controlling Factors, and Abatement Techniques—A Review. Min. Metall. Explor. 2021, 38, 673–692. [Google Scholar] [CrossRef]
- Wang, L.; Peng, Y.; Runge, K. Entrainment in Froth Flotation: The Degree of Entrainment and Its Contributing Factors. Powder Technol. 2016, 288, 202–211. [Google Scholar] [CrossRef] [Green Version]
- Ramlall, N.V. Measuring and Modelling Entrainment in Rougher and Cleaner Batch Flotation. J. S. Afr. Inst. Min. Metall. 2020, 120. [Google Scholar] [CrossRef]
- Mineralogy & Flotation: Floatability VS Selectivity Test Assessment. Mineral Processing & Metallurgy. 2016. Available online: https://www.911metallurgist.com/blog/mineralogy-flotation-floatability-selectivity (accessed on 21 July 2022).
- Rahman, R.M.; Ata, S.; Jameson, G.J. The Effect of Flotation Variables on the Recovery of Different Particle Size Fractions in the Froth and the Pulp. Int. J. Miner. Process. 2012, 106–109, 70–77. [Google Scholar] [CrossRef]
- Schubert, H. On the Optimization of Hydrodynamics in Fine Particle Flotation. Miner. Eng. 2008, 21, 930–936. [Google Scholar] [CrossRef]
- Safari, M.; Hoseinian, F.S.; Deglon, D.; Leal Filho, L.; Souza Pinto, T.C. Impact of Flotation Operational Parameters on the Optimization of Fine and Coarse Itabirite Iron Ore Beneficiation. Powder Technol. 2022, 408, 117772. [Google Scholar] [CrossRef]
- Xu, D.; Ametov, I.; Grano, S.R. Detachment of Coarse Particles from Oscillating Bubbles—The Effect of Particle Contact Angle, Shape and Medium Viscosity. Int. J. Miner. Process. 2011, 101, 50–57. [Google Scholar] [CrossRef]
- Silva, K.; Filippov, L.O.; Piçarra, A.; Flilippova, I.V.; Lima, N.; Skliar, A.; Faustino, L.; Filho, L.L. New Perspectives in Iron Ore Flotation: Use of Collector Reagents without Depressants in Reverse Cationic Flotation of Quartz. Miner. Eng. 2021, 170, 107004. [Google Scholar] [CrossRef]
- Filippov, L.O.; Silva, K.; Piçarra, A.; Lima, N.; Santos, I.; Bicalho, L.; Filippova, I.V.; Peres, A.E.C. Iron Ore Slimes Flotation Tests Using Column and Amidoamine Collector without Depressant. Minerals 2021, 11, 699. [Google Scholar] [CrossRef]
- Polat, M.; Chander, S. First-Order Flotation Kinetics Models and Methods for Estimation of the True Distribution of Flotation Rate Constants. Int. J. Miner. Process. 2000, 58, 145–166. [Google Scholar] [CrossRef]
- Sutherland, K.L. Physical Chemistry of Flotation. XI. Kinetics of the Flotation Process. J. Phys. Chem. 1948, 52, 394–425. [Google Scholar] [CrossRef]
- Brezani, I. Flotation Kinetics—Equation Fitting. Available online: https://www.mathworks.com/matlabcentral/fileexchange/28583-flotation-kinetics-equation-fitting (accessed on 5 May 2022).
- Xu, M. Modified Flotation Rate Constant and Selectivity Index. Miner. Eng. 1998, 11, 271–278. [Google Scholar] [CrossRef]
- Laplante, A.R.; Kaya, M.; Smith, H.W. The Effect of Froth on Flotation Kinetics-A Mass Transfer Approach. Miner. Process. Extr. Metall. Rev. 1989, 5, 147–168. [Google Scholar] [CrossRef]
- Fornasiero, D.; Filippov, L.O. Innovations in the Flotation of Fine and Coarse Particles. J. Phys. Conf. Ser. 2017, 879, 012002. [Google Scholar] [CrossRef] [Green Version]
- Lima, N.P.; de Souza Pinto, T.C.; Tavares, A.C.; Sweet, J. The Entrainment Effect on the Performance of Iron Ore Reverse Flotation. Miner. Eng. 2016, 96–97, 53–58. [Google Scholar] [CrossRef]
- Eskanlou, A.; Huang, Q.; Chegeni, M.H.; Khalesi, M.R.; Abdollahy, M. Determination of the Mass Transfer Rate Constant in a Laboratory Column Flotation Using the Bubble Active Surface Coefficient. Miner. Eng. 2020, 156, 106521. [Google Scholar] [CrossRef]
- Duan, J.; Fornasiero, D.; Ralston, J. Calculation of the Flotation Rate Constant of Chalcopyrite Particles in an Ore. Int. J. Miner. Process. 2003, 72, 227–237. [Google Scholar] [CrossRef]
- Rahal, K.; Manlapig, E.; Franzidis, J.-P. Effect of Frother Type and Concentration on the Water Recovery and Entrainment Recovery Relationship. Min. Metall. Explor. 2001, 18, 138–141. [Google Scholar] [CrossRef]
- Savassi, O.N.; Alexander, D.J.; Franzidis, J.P.; Manlapig, E.V. An Empirical Model for Entrainment in Industrial Flotation Plants. Miner. Eng. 1998, 11, 243–256. [Google Scholar] [CrossRef]
- Kirjavainen, V.M. Review and Analysis of Factors Controlling the Mechanical Flotation of Gangue Minerals. Int. J. Miner. Process. 1996, 46, 21–34. [Google Scholar] [CrossRef]
- Maachar, A.; Dobby, G.S. Measurement of Feed Water Recovery and Entrainment Solids Recovery in Flotation Columns. Can. Metall. Q. 1992, 31, 167–172. [Google Scholar] [CrossRef]
- Lynch, A.J.; Johnson, N.W.; Manlapig, E.V.; Thorne, C.G. Mineral and Coal Flotation Circuits: Their Simulation and Control; Elsevier: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Bu, X.; Wang, X.; Zhou, S.; Li, B.; Zhan, H.; Xie, G. Discrimination of Six Flotation Kinetic Models Used in the Conventional Flotation and Carrier Flotation of −74 Μm Coal Fines. ACS Omega 2020, 5, 13813–13821. [Google Scholar] [CrossRef]
- Liu, T.Y.; Schwarz, M.P. CFD-Based Modelling of Bubble-Particle Collision Efficiency with Mobile Bubble Surface in a Turbulent Environment. Int. J. Miner. Process. 2009, 90, 45–55. [Google Scholar] [CrossRef] [Green Version]
- Sajjad, M.; Otsuki, A. Coupling Flotation Rate Constant and Viscosity Models. Metals 2022, 12, 409. [Google Scholar] [CrossRef]
- Fan, G.; Wang, L.; Cao, Y.; Li, C. Collecting Agent–Mineral Interactions in the Reverse Flotation of Iron Ore: A Brief Review. Minerals 2020, 10, 681. [Google Scholar] [CrossRef]
- Abaka-Wood, G.B.; Addai-Mensah, J.; Skinner, W. A Study of Flotation Characteristics of Monazite, Hematite, and Quartz Using Anionic Collectors. Int. J. Miner. Process. 2017, 158, 55–62. [Google Scholar] [CrossRef]
- Suman, S.K.; Kumar, S. Reverse Flotation Studies on Iron Ore Slime by the Synergistic Effect of Cationic Collectors. Sep. Sci. Technol. 2020, 55, 1702–1714. [Google Scholar] [CrossRef]
- Wang, W.; Cong, J.; Deng, J.; Weng, X.; Lin, Y.; Huang, Y.; Peng, T. Developing Effective Separation of Feldspar and Quartz While Recycling Tailwater by HF Pretreatment. Minerals 2018, 8, 149. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Xu, X.; Duan, H.; Wang, X. QSAR Study of Amine Collectors for Iron Ore Reverse Flotation. Physicochem. Probl. Miner. Process. 2019, 55, 1059–1069. [Google Scholar] [CrossRef]
- Nguyen, A.V. Froth Flotation. In Reference Module in Chemistry, Molecular Sciences and Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 978-0-12-409547-2. [Google Scholar]
- Engelbrecht, J.A.; Woodburn, E.T. The Effects of Froth Height, Aeration Rate and Gas Precipitation on Flotation. J. S. Afr. Inst. Min. Metall 1975, 76, 125–132. [Google Scholar]
- Otsuki, A.; Barry, S.; Fornasiero, D. Rheological Studies of Nickel Oxide and Quartz/Hematite Mixture Systems. Adv. Powder Technol. 2011, 22, 471–475. [Google Scholar] [CrossRef]
- Sajjad, M.; Otsuki, A. Correlation between Flotation and Rheology of Fine Particle Suspensions. Metals 2022, 12, 270. [Google Scholar] [CrossRef]
- Michaud, D. Flotation Kinetics: Mass & Water Recovery VS Entrainment & Mineralogy. Available online: https://www.911metallurgist.com/blog/flotation-mass-water-recovery-mineralogy (accessed on 21 July 2022).

| Designation | Equation | Kinetic Parameters |
|---|---|---|
| Classical Model [13] | (2) | R∞ and k |
| Kelsall Model [15] | (3) | θ, ks and kf |
| Klimpel Model [16] | (4) | R∞ and k |
| Gamma Model [14] | (5) | R∞ and k = αk0 |
| Designation | Equation |
|---|---|
| Warren [19] | , (7) and (8), |
| Maachar and Dobby [43] | (9) |
| Ross [41] | (10) |
| Rahal et al. [40] | (11) |
| Ross and Van Deventer [20] | (12) |
| System | Solid Conc. (vol.%) | Size (µm) | R2 | y = mx + b |
|---|---|---|---|---|
| Quartz | 5 | +150–300 | 0.9183 | Rw = 0.6314 Rq − 47.534 |
| +75–150 | 0.8662 | Rw = 0.842 Rq − 67.828 | ||
| +38–75 | 0.9219 | Rw = 1.0437 Rq − 85.198 | ||
| −38 | 0.9036 | Rw = 1.1696 Rq − 94.71 | ||
| 10 | +150–300 | 0.9711 | Rw = 0.2792 Rq − 3.9576 | |
| +75–150 | 0.9833 | Rw = 0.4059 Rq − 13.157 | ||
| +38–75 | 0.9286 | Rw = 0.501 Rq − 21.845 | ||
| −38 | 0.9448 | Rw = 0.547 Rq − 25.049 | ||
| Hematite | 2.5 | +150–300 | 0.9868 | Rw = 2.4663 Rh − 154.82 |
| +75–150 | 0.9059 | Rw = 3.5921 Rh − 246.32 | ||
| +38–75 | 0.9361 | Rw = 0.9065 Rh − 35.401 | ||
| −38 | 0.9557 | Rw = 1.6056 Rh − 105.36 | ||
| 5 | +150–300 | 0.9867 | Rw = 2.7244 Rh − 118.55 | |
| +75–150 | 0.9751 | Rw = 4.3682 Rh − 263.67 | ||
| +38–75 | 0.8808 | Rw = 2.631 Rh − 160.07 | ||
| −38 | 0.9779 | Rw = 1.7583 Rh − 109.48 |
| System | Size | Density | Warren Method | Fitted Method | ||
|---|---|---|---|---|---|---|
| Linear Equation | R2 | Polynomial Equation | R2 | |||
| Quartz | −38 | 5 | y = 0.035x + 82.2 | 0.9036 | y = −0.0001x2 + 0.1048x + 72.916 | 0.9903 |
| 10 | y = 0.08x + 48.2 | 0.9448 | y = −0.0002x2 + 0.2662x + 6.1867 | 0.9998 | ||
| +38–75 | 5 | y = 0.04x + 82.6 | 0.9219 | y = −0.0001x2 + 0.1139x + 74.294 | 0.9973 | |
| 10 | y = 0.0848x + 47.0 | 0.9286 | y = −0.0003x2 + 0.348x − 16.681 | 0.9541 | ||
| Hematite | −38 | 2.5 | y = 0.0279x + 66.8 | 0.9557 | y = −5 × 10−5x2 + 0.1221x + 25.967 | 0.9989 |
| 5 | y = 0.0256x + 62.8 | 0.9779 | y = −1 × 10−7x3 + 0.0004x2 − 0.36x + 180 | 0.9965 | ||
| +38–75 | 2.5 | y = 0.0471x + 42.0 | 0.9361 | y = −0.0001x2 + 0.2998x − 68.755 | 0.9998 | |
| 5 | y = 0.0159x + 62.7 | 0.8808 | y = −4 × 10−7x3 + 0.001x2 − 0.79x + 284 | 0.9889 | ||
| Method/Model | System | Solid Conc. (vol.%) | Degree of Entrainment | Recovery by Entrainment (%) | Recovery by True Flotation (%) | |||
|---|---|---|---|---|---|---|---|---|
| −38 µm | +38–75 µm | −38 µm | +38–75 µm | −38 µm | +38–75 µm | |||
| Warren | Qz | 5 | 0.035 | 0.040 | 16.90 | 16.72 | 82.21 | 82.61 |
| 10 | 0.080 | 0.085 | 53.93 | 51.46 | 48.25 | 47.04 | ||
| Hm | 2.5 | 0.028 | 0.047 | 30.37 | 48.98 | 66.83 | 42.02 | |
| 5 | 0.026 | 0.015 | 32.27 | 17.50 | 62.85 | 62.77 | ||
| Maachar and Dobby | Qz | 5 | - | - | 6.090 | 0.585 | - | - |
| 10 | - | - | 8.689 | 0.859 | - | - | ||
| Hm | 2.5 | - | - | 13.09 | 1.468 | - | - | |
| 5 | - | - | 14.88 | 1.621 | - | - | ||
| Ross | Qz | 5 | 0.220 | 0.043 | - | - | - | - |
| 10 | 0.312 | 0.331 | - | - | - | - | ||
| Hm | 2.5 | 0.009 | 0.012 | - | - | - | - | |
| 5 | 0.013 | 0.007 | - | - | - | - | ||
| Rahal et al. | Qz | 5 | - | - | 15.50 | 8.363 | - | - |
| 10 | - | - | 25.59 | 15.810 | - | - | ||
| Hm | 2.5 | - | - | 29.56 | 26.91 | - | - | |
| 5 | - | - | 34.79 | 31.54 | - | - | ||
| Ross and Van Deventer | Qz | 5 | 0.795 | 0.487 | - | - | - | - |
| 10 | 0.795 | 0.487 | - | - | - | - | ||
| Hm | 2.5 | 0.479 | −0.305 | - | - | - | - | |
| 5 | 0.479 | −0.305 | - | - | - | - | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murhula, E.; Hashan, M.; Otsuki, A. Effect of Solid Concentration and Particle Size on the Flotation Kinetics and Entrainment of Quartz and Hematite. Metals 2023, 13, 53. https://doi.org/10.3390/met13010053
Murhula E, Hashan M, Otsuki A. Effect of Solid Concentration and Particle Size on the Flotation Kinetics and Entrainment of Quartz and Hematite. Metals. 2023; 13(1):53. https://doi.org/10.3390/met13010053
Chicago/Turabian StyleMurhula, Espoir, Mahamudul Hashan, and Akira Otsuki. 2023. "Effect of Solid Concentration and Particle Size on the Flotation Kinetics and Entrainment of Quartz and Hematite" Metals 13, no. 1: 53. https://doi.org/10.3390/met13010053
APA StyleMurhula, E., Hashan, M., & Otsuki, A. (2023). Effect of Solid Concentration and Particle Size on the Flotation Kinetics and Entrainment of Quartz and Hematite. Metals, 13(1), 53. https://doi.org/10.3390/met13010053







