Investigation of Medium Range Order Defects in CuxZr100-x (x = 50, 56, 60, 64) Metallic Glasses Using Reverse Monte Carlo Modeling
Abstract
:1. Introduction
2. Methods
2.1. Experiment
2.2. Ab Initio Molecular Dynamics Simulation
2.3. RMC Simulation
3. Results and Discussion
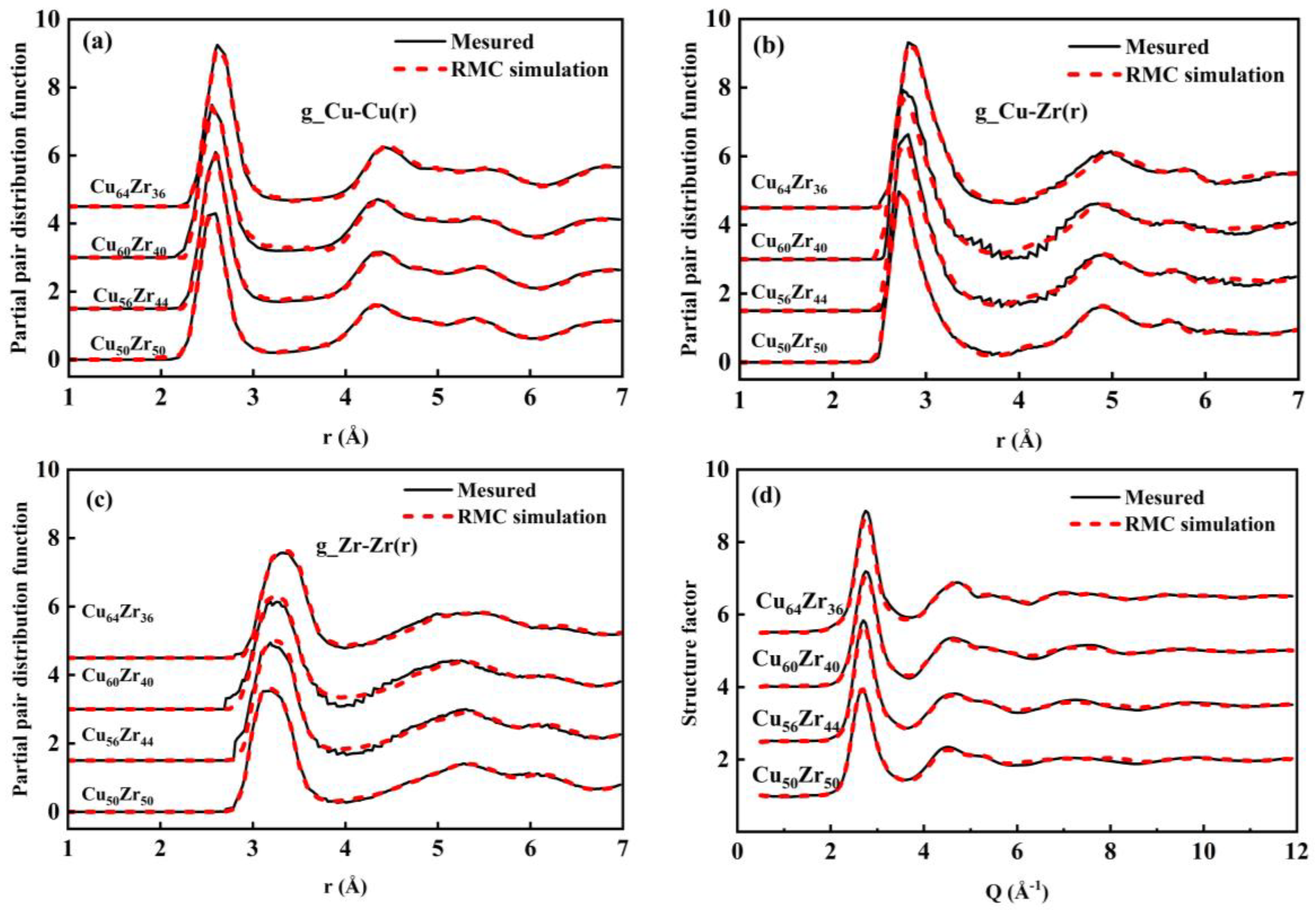
3.1. Reverse Monte Carlo Model
3.2. Short Range Structure Analysis
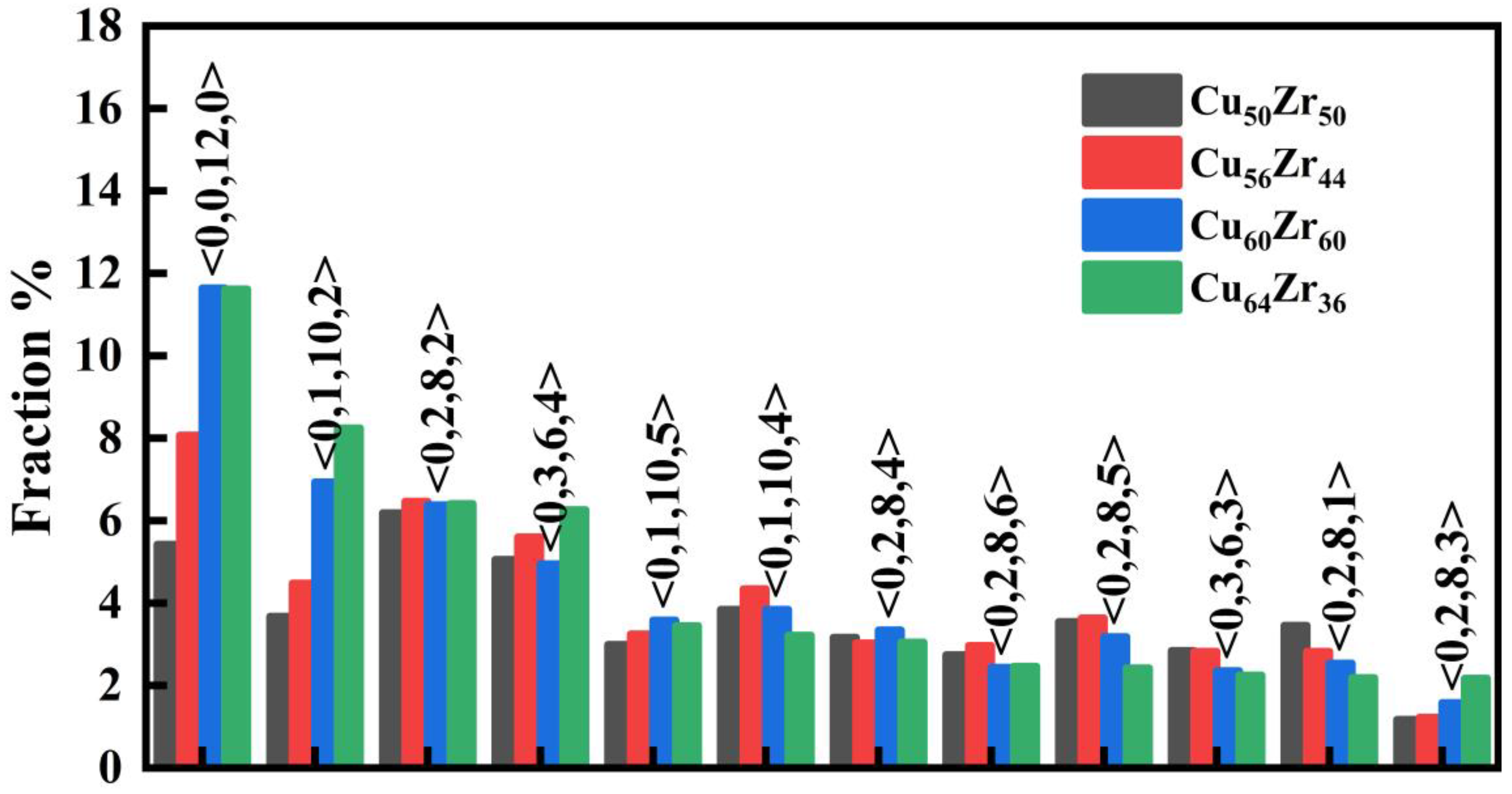
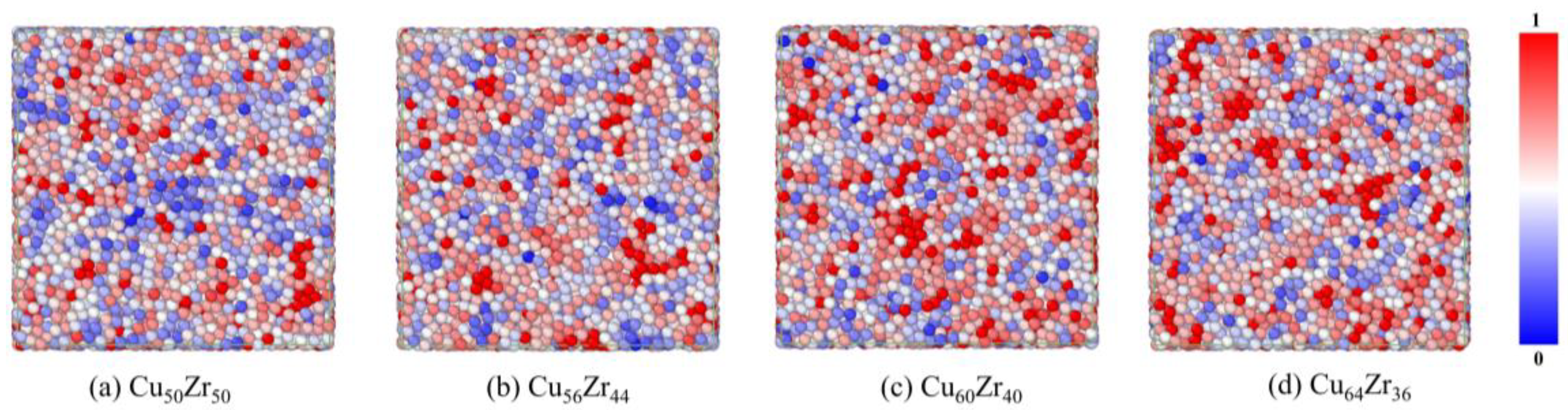
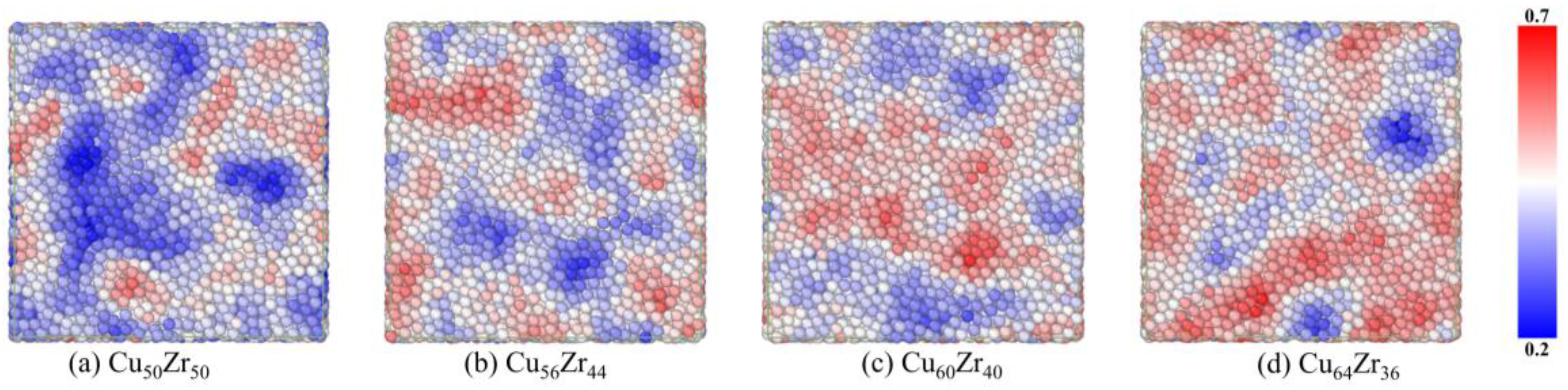
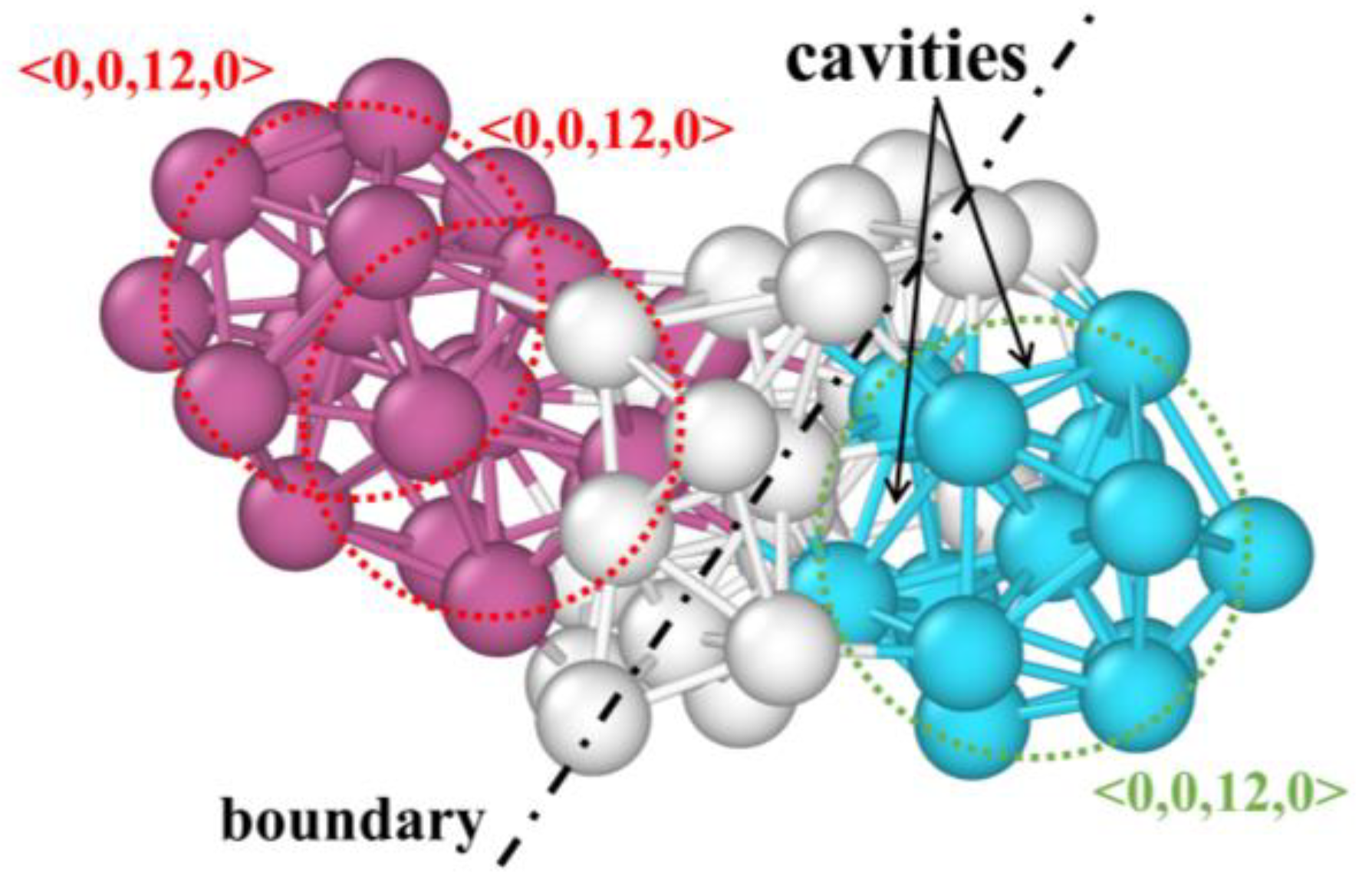
3.3. MRO and Its Defects Characterization
4. Conclusions
- (1)
- In RMC models, <0,0,12,0> and <0,1,10,2> dominates in MGs, and becomes more abundant with increasing Cu content, which makes the structures of MGs more stable.
- (2)
- Relative to the short-range order characteristic indicators (LFFS and atomic number density), new methods of describing the MRO were developed, of which as well as MRO defects show some effectiveness.
- (3)
- Using the developed MRO identification procedure, it was found that an increase in Cu content leads to an increase in full icosahedral clusters and a tendency to interconnect to form large bone regions, thus reducing the density of MRO defects. It implies that lower MRO defects may also be an important reason for the higher glass forming ability and more stable kinetic properties of Cu64Zr36 MGs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Klement, W.K.; Willens, R.H.; Duwez, P. Non-Crystalline Structure in Solidified Gold–Silicon Alloys. Nature 1960, 187, 869–870. [Google Scholar] [CrossRef]
- Schuh, C.A.; Hufnagel, T.C.; Ramamurty, U. Mechanical behavior of amorphous alloys. Acta Mater. 2007, 55, 4067–4109. [Google Scholar] [CrossRef]
- Falk, M.L.; Langer, J.S. Deformation and Failure of Amorphous Solidlike Materials. Annu. Rev. Condens. Matter Phys. 2010, 2, 353–373. [Google Scholar] [CrossRef] [Green Version]
- Wei, H.W. The Elastic Properties, Elastic Models and Elastic Perspectives of Metallic Glasses. Prog. Mater. Sci. 2012, 57, 487–656. [Google Scholar] [CrossRef]
- Wang, Q.; Ding, D.; Xia, L. Formability and Magnetic Properties of the Binary Nd-Co Amorphous Alloys. Metals 2021, 11, 1730. [Google Scholar] [CrossRef]
- Hitit, A.; Yazici, Z.O.; Şahin, H.; Öztürk, P.; Eryeşil, B.; Barut, N. Microstructure and Mechanical Properties of CoWB Based Composites Produced by Crystallization of Ni-Co-Zr-Ta-W-B Bulk Metallic Glass. Metals 2022, 12, 251. [Google Scholar] [CrossRef]
- Hirata, A.; Kang, L.J.; Fujita, T.; Klumov, B.; Matsue, K.; Kotani, M.; Yavari, A.R.; Chen, M.W. Geometric frustration of icosahedron in metallic glasses. Science 2013, 341, 376–379. [Google Scholar] [CrossRef]
- Liu, Y.H.; Wang, G.; Wang, R.J.; Zhao, D.Q.; Pan, M.X.; Wang, W.H. Super Plastic Bulk Metallic Glasses at Room Temperature. Science 2007, 315, 1385–1388. [Google Scholar] [CrossRef]
- Sheng, H.W.; Luo, W.K.; Alamgir, F.M.; Bai, J.M.; Ma, E. Atomic packing and short-to-medium-range order in metallic glasses. Nature 2006, 439, 419–425. [Google Scholar] [CrossRef]
- Yang, Z.-Y.; Wang, Y.-J.; Dai, L.-H. Susceptibility of shear banding to chemical short-range order in metallic glasses. Scr. Mater. 2019, 162, 141–145. [Google Scholar] [CrossRef]
- Cheng, Y.Q.; Ma, E. Atomic-level structure and structure–property relationship in metallic glasses. Prog. Mater. Sci. 2011, 56, 379–473. [Google Scholar] [CrossRef]
- Sun, Y.L.; Shen, J. Icosahedral ordering in Cu60Zr40 metallic glass: Molecular dynamics simulations. J. Non-Cryst. Solids 2009, 355, 1557–1560. [Google Scholar] [CrossRef]
- Wakeda, M.; Shibutani, Y. Icosahedral clustering with medium-range order and local elastic properties of amorphous metals. Acta Mater. 2010, 58, 3963–3969. [Google Scholar] [CrossRef]
- Wu, Z.W.; Li, M.Z.; Wang, W.H.; Liu, K.X. Correlation between structural relaxation and connectivity of icosahedral clusters in CuZr metallic glass-forming liquids. Phys. Rev. B 2013, 88, 054202. [Google Scholar] [CrossRef]
- Ding, J.; Cheng, Y.-Q.; Ma, E. Full icosahedra dominate local order in Cu64Zr34 metallic glass and supercooled liquid. Acta Mater. 2014, 69, 343–354. [Google Scholar] [CrossRef]
- Hu, Y.C.; Li, F.X.; Li, M.Z.; Bai, H.Y.; Wang, W.H. Five-fold symmetry as indicator of dynamic arrest in metallic glass-forming liquids. Nat. Commun. 2015, 6, 8310. [Google Scholar] [CrossRef] [Green Version]
- Peng, H.L.; Li, M.Z.; Wang, W.H. Structural signature of plastic deformation in metallic glasses. Phys. Rev. Lett. 2011, 106, 135503. [Google Scholar] [CrossRef] [Green Version]
- Tian, Z.-L.; Wang, Y.-J.; Chen, Y.; Dai, L.-H. Strain gradient drives shear banding in metallic glasses. Phys. Rev. B 2017, 96, 10. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.; Lee, C.-M.; Lee, K.-R.; Ma, E.; Lee, J.-C. Networked interpenetrating connections of icosahedra: Effects on shear transformations in metallic glass. Acta Mater. 2011, 59, 159–170. [Google Scholar] [CrossRef]
- Wu, Z.W.; Kob, W.; Wang, W.H.; Xu, L. Stretched and compressed exponentials in the relaxation dynamics of a metallic glass-forming melt. Nat. Commun. 2018, 9, 5334. [Google Scholar] [CrossRef]
- Shen, Y.; Perepezko, J.H. Al-based amorphous alloys: Glass-forming ability, crystallization behavior and effects of minor alloying additions. J. Alloy. Compd. 2017, 707, 3–11. [Google Scholar] [CrossRef] [Green Version]
- Ren, L.; Gao, T.; Ma, R.; Xie, Q.; Tian, Z.; Chen, Q.; Liang, Y.; Hu, X. The connection of icosahedral and defective icosahedral clusters in medium-range order structures of CuZrAl alloy. J. Non-Cryst. Solids 2019, 521, 119475. [Google Scholar] [CrossRef]
- Ding, J.; Cheng, Y.Q.; Ma, E. Correlating local structure with inhomogeneous elastic deformation in a metallic glass. Appl. Phys. Lett. 2012, 101, 33–36. [Google Scholar] [CrossRef]
- Hilke, S.; Rösner, H.; Wilde, G. The role of minor alloying in the plasticity of bulk metallic glasses. Scr. Mater. 2020, 188, 50–53. [Google Scholar] [CrossRef]
- Argon, A.S. Plastic deformation in metallic glasses. Acta Metall. 1979, 27, 47–58. [Google Scholar] [CrossRef]
- Falk, M.L.; Langer, J.S. Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E 1998, 57, 7192–7205. [Google Scholar] [CrossRef] [Green Version]
- Davani, F.A.; Hilke, S.; Rösner, H.; Geissler, D.; Gebert, A.; Wilde, G. Correlations between the ductility and medium-range order of bulk metallic glasses. J. Appl. Phys. 2020, 128, 015103. [Google Scholar] [CrossRef]
- Curran, D. Dynamic failure of solids. Phys. Rep. 1987, 147, 253–388. [Google Scholar] [CrossRef]
- Huang, X.; Ling, Z.; Wang, Y.J.; Dai, L.H. Intrinsic structural defects on medium range in metallic glasses. Intermetallics 2016, 75, 36–41. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Falk, M.L.; Li, J.F.; Kong, L.T. Predicting Shear Transformation Events in Metallic Glasses. Phys. Rev. Lett. 2018, 120, 125503. [Google Scholar] [CrossRef]
- Liu, Y.; Luo, J.; Huang, X. Identification of medium range order defects and their critical effect on spallation of Cu64Zr36 metallic glass. J. Alloy. Compd. 2023, 932, 167591. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, F.; Wang, C.Z.; Mendelev, M.I.; Kramer, M.J.; Ho, K.M. Cooling rates dependence of medium-range order development inCu64.5Zr35.5metallic glass. Phys. Rev. B 2015, 91, 064105. [Google Scholar] [CrossRef] [Green Version]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Feng, S.; Qi, L.; Wang, L.; Pan, S.; Ma, M.; Zhang, X.; Li, G.; Liu, R. Atomic structure of shear bands in Cu64Zr36 metallic glasses studied by molecular dynamics simulations. Acta Mater. 2015, 95, 236–243. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, X.D.; Lou, H.B.; Cao, Q.P.; Jiang, J.Z. Atomic packing in Fe-based metallic glasses. Acta Mater. 2016, 102, 116–124. [Google Scholar] [CrossRef]
- McGreevy, L.R. Reverse Monte Carlo modelling. J. Phys. Condens. Matter 2001, 13, R877. [Google Scholar] [CrossRef]
- Harada, M.; Ikegami, R.; Kumara, L.S.R.; Kohara, S.; Sakata, O. Reverse Monte Carlo modeling for local structures of noble metal nanoparticles using high-energy XRD and EXAFS. RSC Adv. 2019, 9, 29511–29521. [Google Scholar] [CrossRef] [Green Version]
- Frenkel, A.I.; Rodriguez, J.A.; Chen, J.G. ChemInform Abstract: Synchrotron Techniques for in situ Catalytic Studies: Capabilities, Challenges, and Opportunities. ChemInform 2013, 44, 2269–2280. [Google Scholar] [CrossRef]
- Clausen, B.S.; Grbk, L.; Steffensen, G.; Hansen, P.L.; Topse, H. A combined QEXAFS/XRD method for on-line, in situ studies of catalysts: Examples of dynamic measurements of Cu-based methanol catalysts. Catal. Lett. 1993, 20, 23–36. [Google Scholar] [CrossRef]
- Guo, G.-Q.; Wu, S.-Y.; Luo, S.; Yang, L. Detecting Structural Features in Metallic Glass via Synchrotron Radiation Experiments Combined with Simulations. Metals 2015, 5, 2093–2108. [Google Scholar] [CrossRef]
- Blodgett, M.E.; Kelton, K.F. Estimated partial pair correlation functions in Cu–Zr liquids. J. Non-Cryst. Solids 2015, 412, 66–71. [Google Scholar] [CrossRef] [Green Version]
- Mauro, N.A.; Fu, W.; Bendert, J.C.; Cheng, Y.Q.; Ma, E.; Kelton, K.F. Local atomic structure in equilibrium and supercooled liquid Zr(75.5)Pd(24.5). J. Chem. Phys. 2012, 137, 044501. [Google Scholar] [CrossRef] [PubMed]
- Andolina, C.M.; Williamson, P.; Saidi, W.A. Optimization and validation of a deep learning CuZr atomistic potential: Robust applications for crystalline and amorphous phases with near-DFT accuracy. J. Chem. Phys. 2020, 152, 154701. [Google Scholar] [CrossRef]
- Opletal, G.; Petersen, T.C.; Barnard, A.S.; Russo, S.P. On reverse Monte Carlo constraints and model reproduction. J. Comput. Chem. 2017, 38, 1547–1551. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.W.; Huang, L.; Wang, C.Z.; Ho, K.M.; Ding, Z.J. Structure of Cu64.5Zr35.5 metallic glass by reverse Monte Carlo simulations. J. Appl. Phys. 2014, 115, 053522. [Google Scholar] [CrossRef]
- Ziman, J.M. A theory of the electrical properties of liquid metals. I: The monovalent metals. Philos. Mag. 1961, 6, 1013–1034. [Google Scholar] [CrossRef]
- Juhás, P.; Davis, T.; Farrow, C.L.; Billinge, S.J.L. PDFgetX3: A rapid and highly automatable program for processing powder diffraction data into total scattering pair distribution functions. J. Appl. Crystallogr. 2013, 46, 560–566. [Google Scholar] [CrossRef] [Green Version]
- Ravel, B.; Newville, M. ATHENA, ARTEMIS, HEPHAESTUS: Data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron. Radiat. 2005, 12, 537–541. [Google Scholar] [CrossRef] [Green Version]
- Gereben, O.; Jóvári, P.; Temleitner, L.; Pusztai, L. A new version of the RMC++ Reverse Monte Carlo programme, aimed at investigating the structure of covalent glasses. Optoelectron. Adv. Mater.-Rapid Commun. 2007, 9, 3021–3027. [Google Scholar] [CrossRef]
- Ankudinov, A.L.; Ravel, B.; Rehr, J.J.; Conradson, S.D. Real-space multiple-scattering calculation and interpretation of x-ray-absorption near-edge structure. Phys. Rev. B 1998, 58, 7565–7576. [Google Scholar] [CrossRef]
- Kuhne, T.D.; Iannuzzi, M.; Del Ben, M.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schutt, O.; Schiffmann, F.; et al. CP2K: An electronic structure and molecular dynamics software package—Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Premier mémoire. Sur quelques propriétés des formes quadratiques positives parfaites. J. Für Die Reine Und Angew. Math. (Crelles J.) 1908, 1908, 97–102. [Google Scholar] [CrossRef]
- Peng, H.L.; Li, M.Z.; Wang, W.H.; Wang, C.Z.; Ho, K.M. Effect of local structures and atomic packing on glass forming ability in CuxZr100−x metallic glasses. Appl. Phys. Lett. 2010, 96, 021901. [Google Scholar] [CrossRef]
- Cheng, Y.Q.; Sheng, H.W.; Ma, E. Relationship between structure, dynamics, and mechanical properties in metallic glass-forming alloys. Phys. Rev. B 2008, 78, 014207. [Google Scholar] [CrossRef]
- Hwang, J.; Melgarejo, Z.H.; Kalay, Y.E.; Kalay, I.; Kramer, M.J.; Stone, D.S.; Voyles, P.M. Nanoscale structure and structural relaxation in Zr50Cu45Al5 bulk metallic glass. Phys. Rev. Lett. 2012, 108, 195505. [Google Scholar] [CrossRef] [Green Version]
- Maldonis, J.J.; Banadaki, A.D.; Patala, S.; Voyles, P.M. Short-range order structure motifs learned from an atomistic model of a Zr50Cu45Al5 metallic glass. Acta Mater. 2019, 175, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Spaepen, F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metall. 1977, 25, 407–415. [Google Scholar] [CrossRef]
- Lu, B.F.; Kong, L.T.; Laws, K.J.; Xu, W.Q.; Jiang, Z.; Huang, Y.Y.; Ferry, M.; Li, J.F.; Zhou, Y.H. EXAFS and molecular dynamics simulation studies of Cu-Zr metallic glass: Short-to-medium range order and glass forming ability. Mater. Charact. 2018, 141, 41–48. [Google Scholar] [CrossRef]


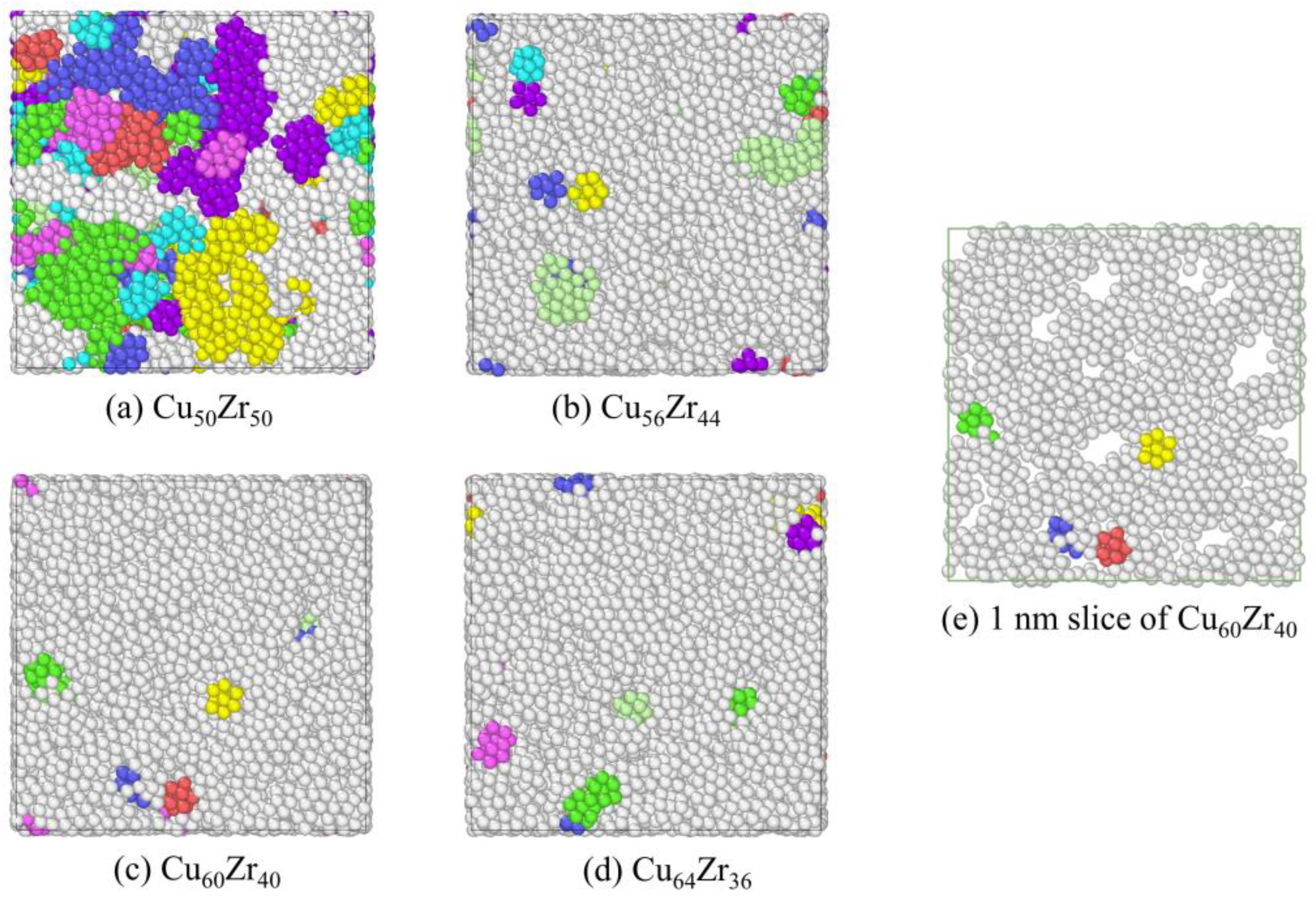
| Sample Components | Cu50Zr50 | Cu56Zr44 | Cu60Zr40 | Cu64Zr36 |
|---|---|---|---|---|
| Number of <0,0,12,0> cluster | 1065 | 1586 | 2287 | 2282 |
| Number of solid-like regions | 115 | 41 | 15 | 15 |
| Number of atoms of <0,0,12,0> cluster | 8349 | 10,823 | 13,200 | 13,745 |
| Number of atoms of bone | 2376 | 9988 | 12,936 | 13,490 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Hu, S.; Luo, J.; Hu, H.; Huang, X. Investigation of Medium Range Order Defects in CuxZr100-x (x = 50, 56, 60, 64) Metallic Glasses Using Reverse Monte Carlo Modeling. Metals 2023, 13, 70. https://doi.org/10.3390/met13010070
Liu Y, Hu S, Luo J, Hu H, Huang X. Investigation of Medium Range Order Defects in CuxZr100-x (x = 50, 56, 60, 64) Metallic Glasses Using Reverse Monte Carlo Modeling. Metals. 2023; 13(1):70. https://doi.org/10.3390/met13010070
Chicago/Turabian StyleLiu, Yuan, Shiwei Hu, Jingrun Luo, Hao Hu, and Xin Huang. 2023. "Investigation of Medium Range Order Defects in CuxZr100-x (x = 50, 56, 60, 64) Metallic Glasses Using Reverse Monte Carlo Modeling" Metals 13, no. 1: 70. https://doi.org/10.3390/met13010070
APA StyleLiu, Y., Hu, S., Luo, J., Hu, H., & Huang, X. (2023). Investigation of Medium Range Order Defects in CuxZr100-x (x = 50, 56, 60, 64) Metallic Glasses Using Reverse Monte Carlo Modeling. Metals, 13(1), 70. https://doi.org/10.3390/met13010070






