On the Determination of Elastic Properties of Indium Nitride Nanosheets and Nanotubes by Numerical Simulation
Abstract
1. Introduction
2. Materials and Methods
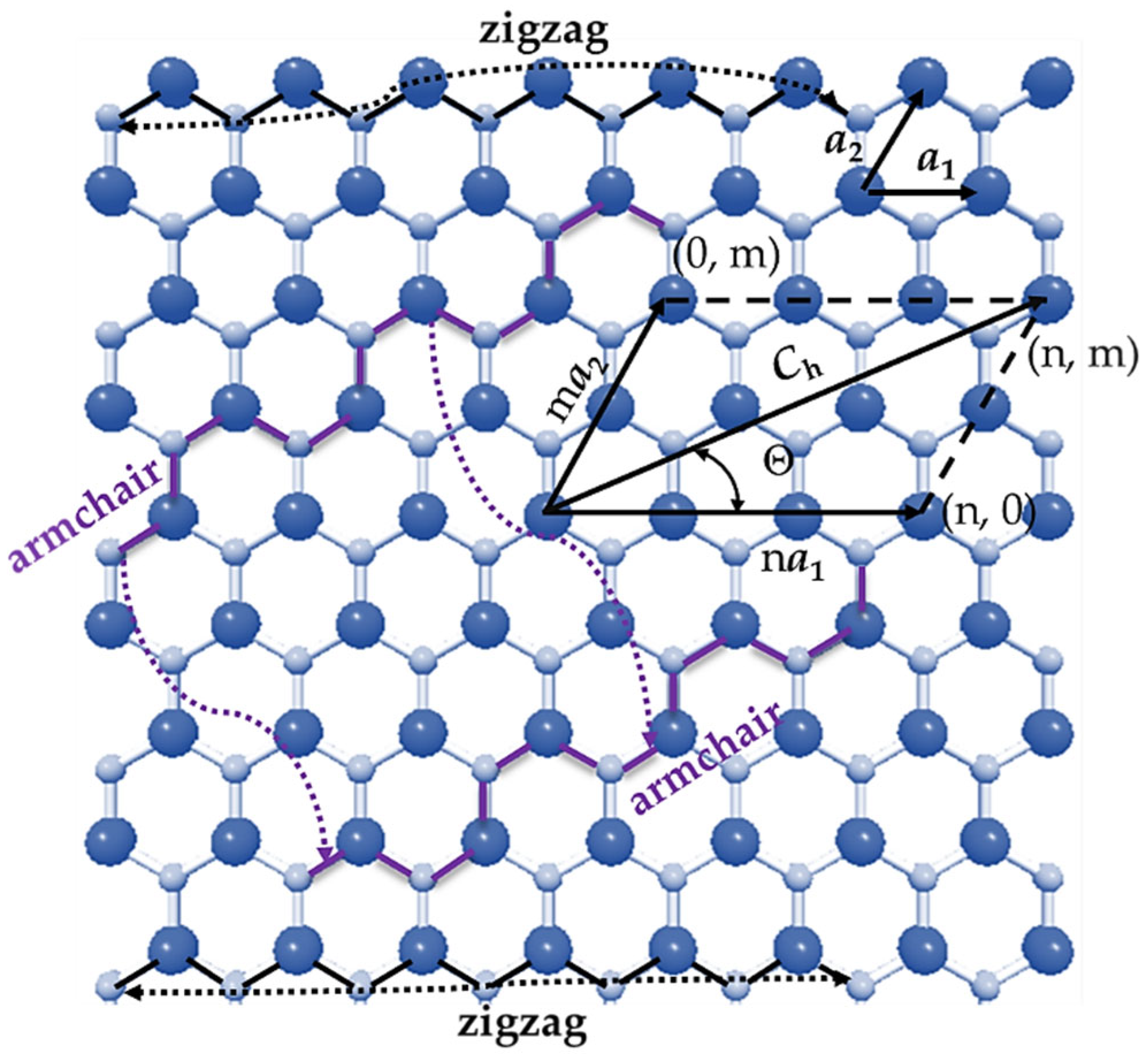
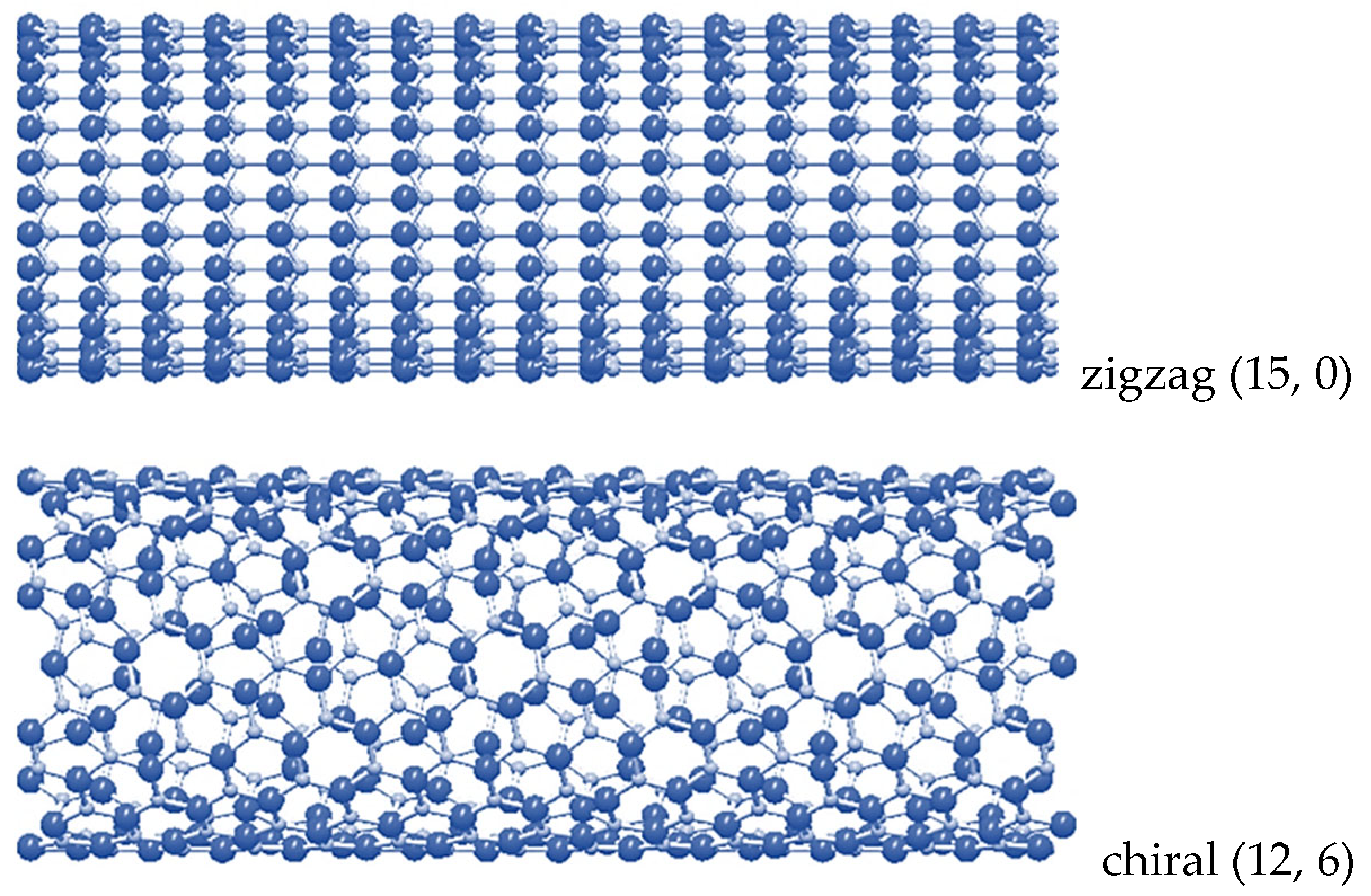
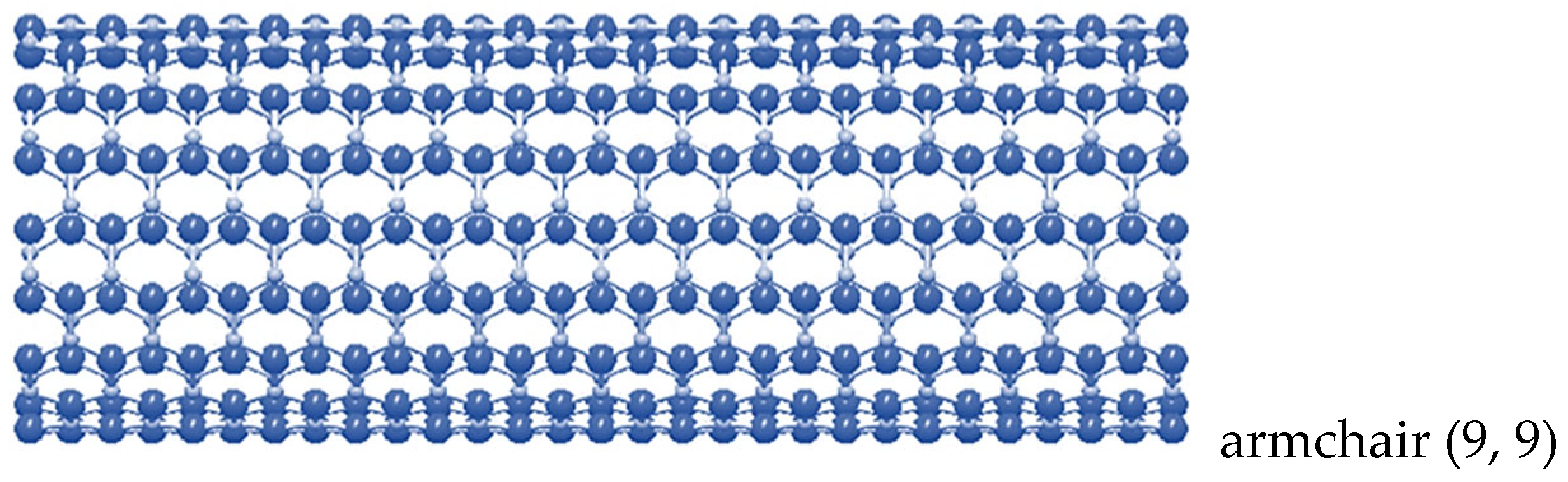
2.1. Atomic Structure of Indium Nitride Nanosheets and Nanotubes
2.2. Numerical Modeling of Elastic Properties of InNNSs and SWInNNTs
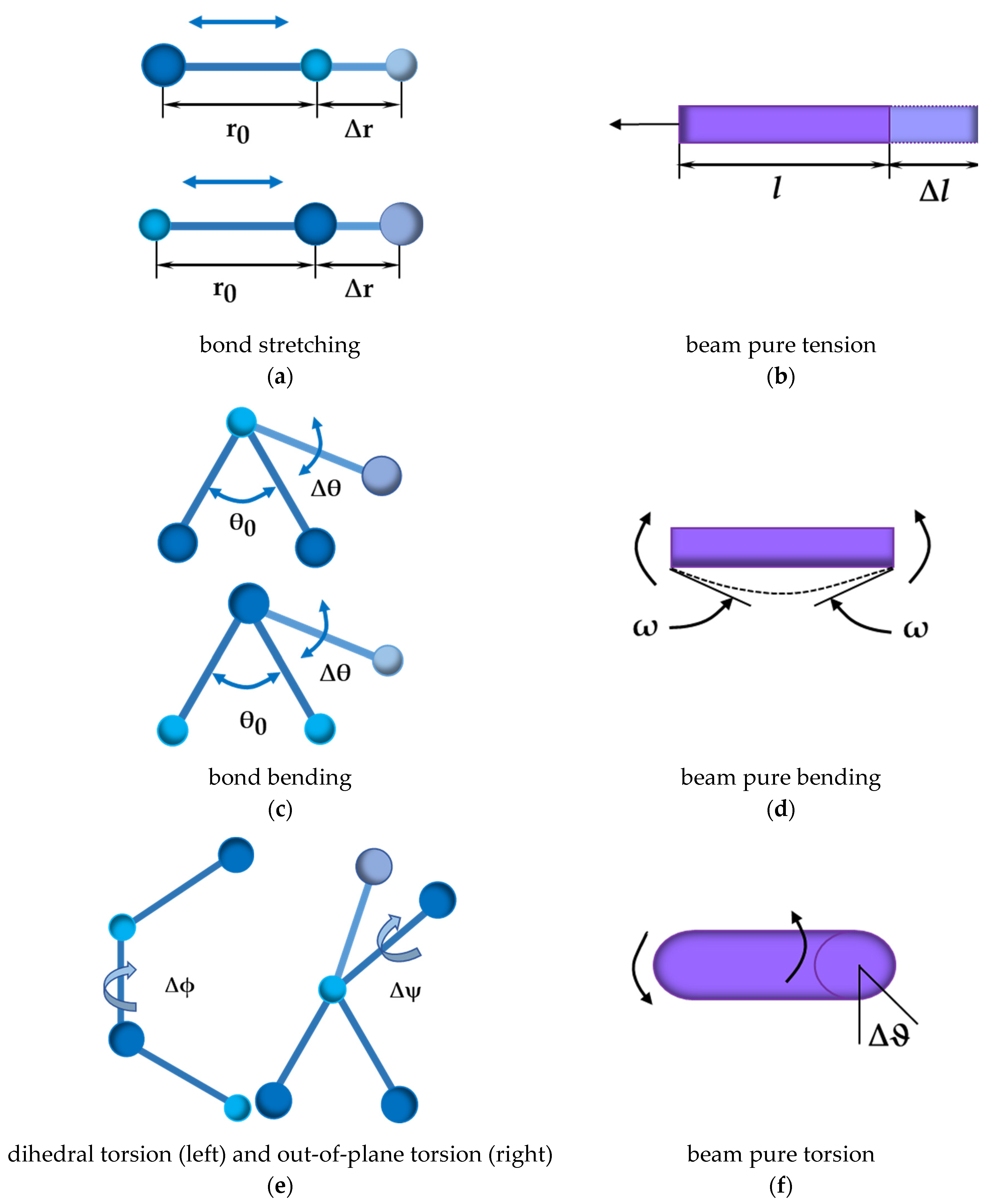
2.2.1. Input for FE Model of InN Nanostructures
- (1)
- UFF
- (2)
- DFT + MM
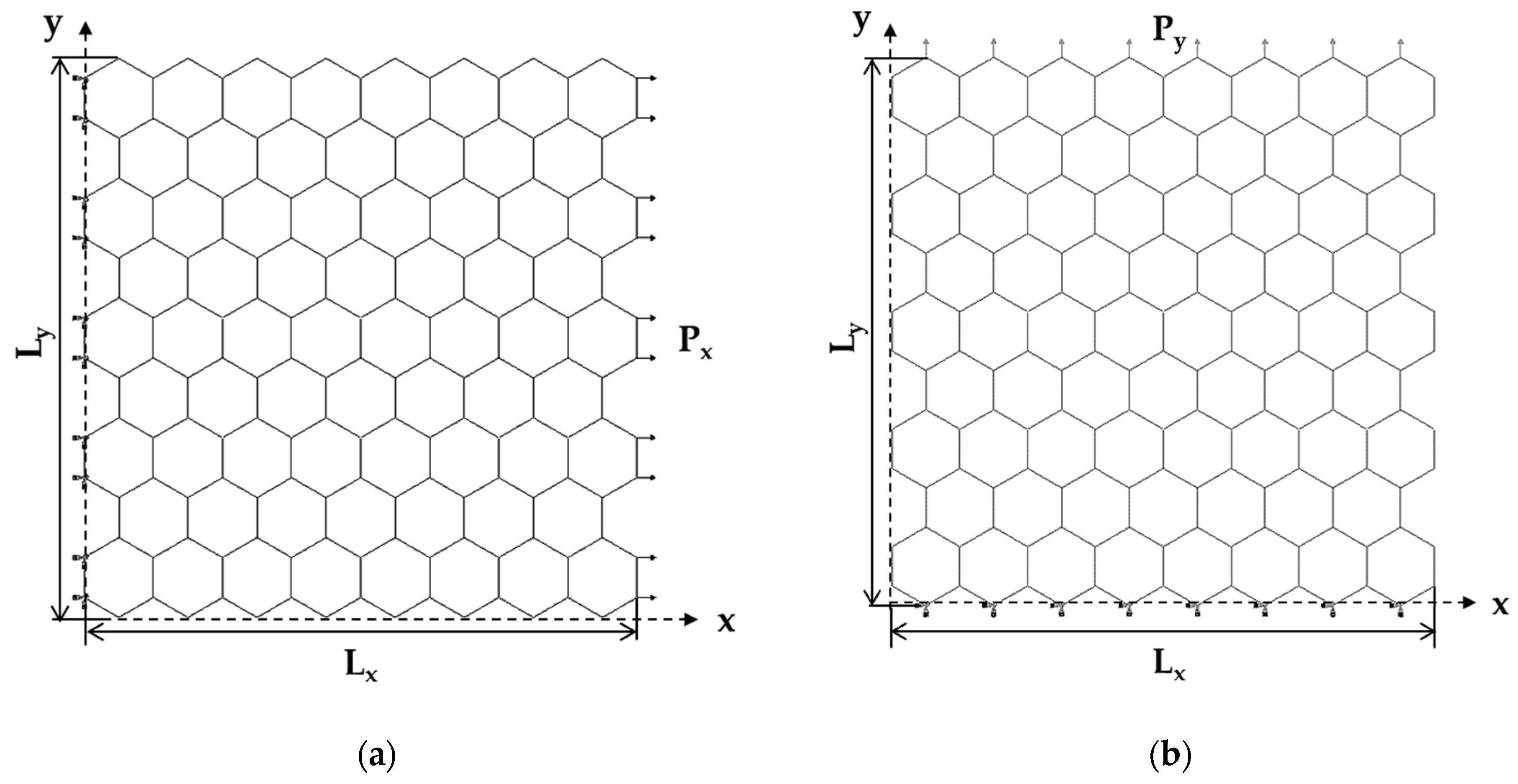
2.2.2. Geometrical Characteristics of InNNSs and SWInNNTs
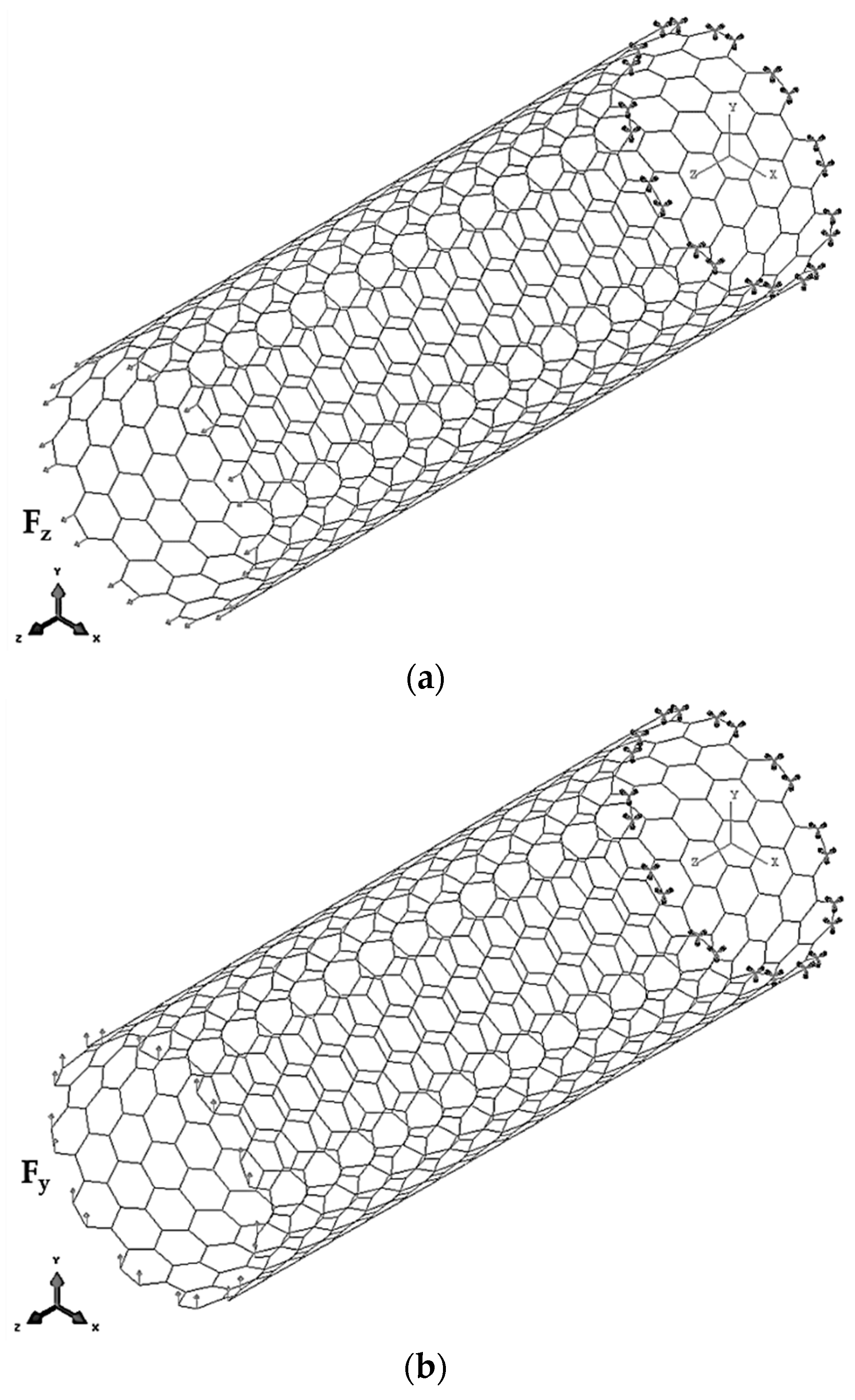
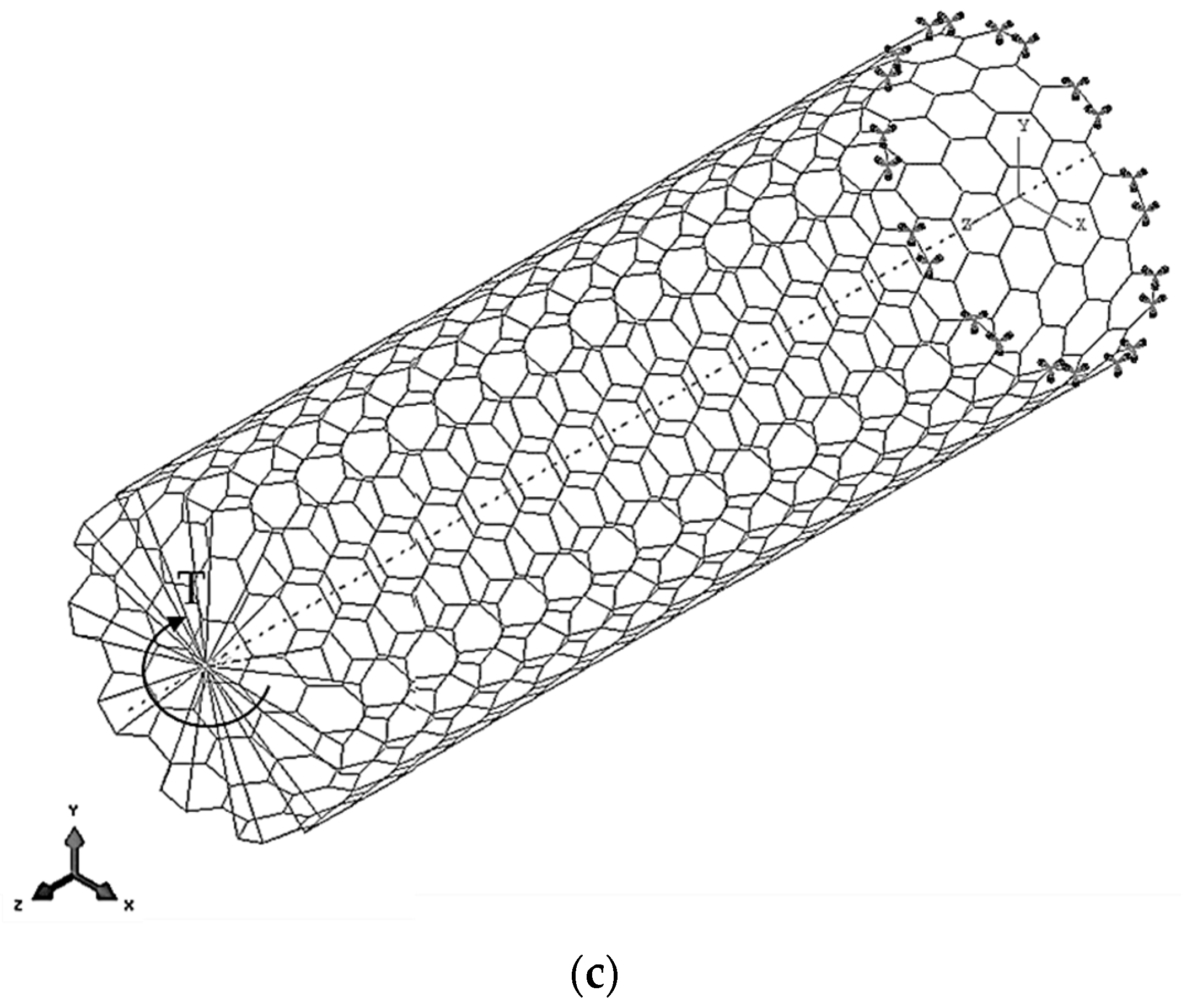
2.2.3. Finite Element Analysis and Elastic Properties of InNNSs and SWInNNTs
3. Results
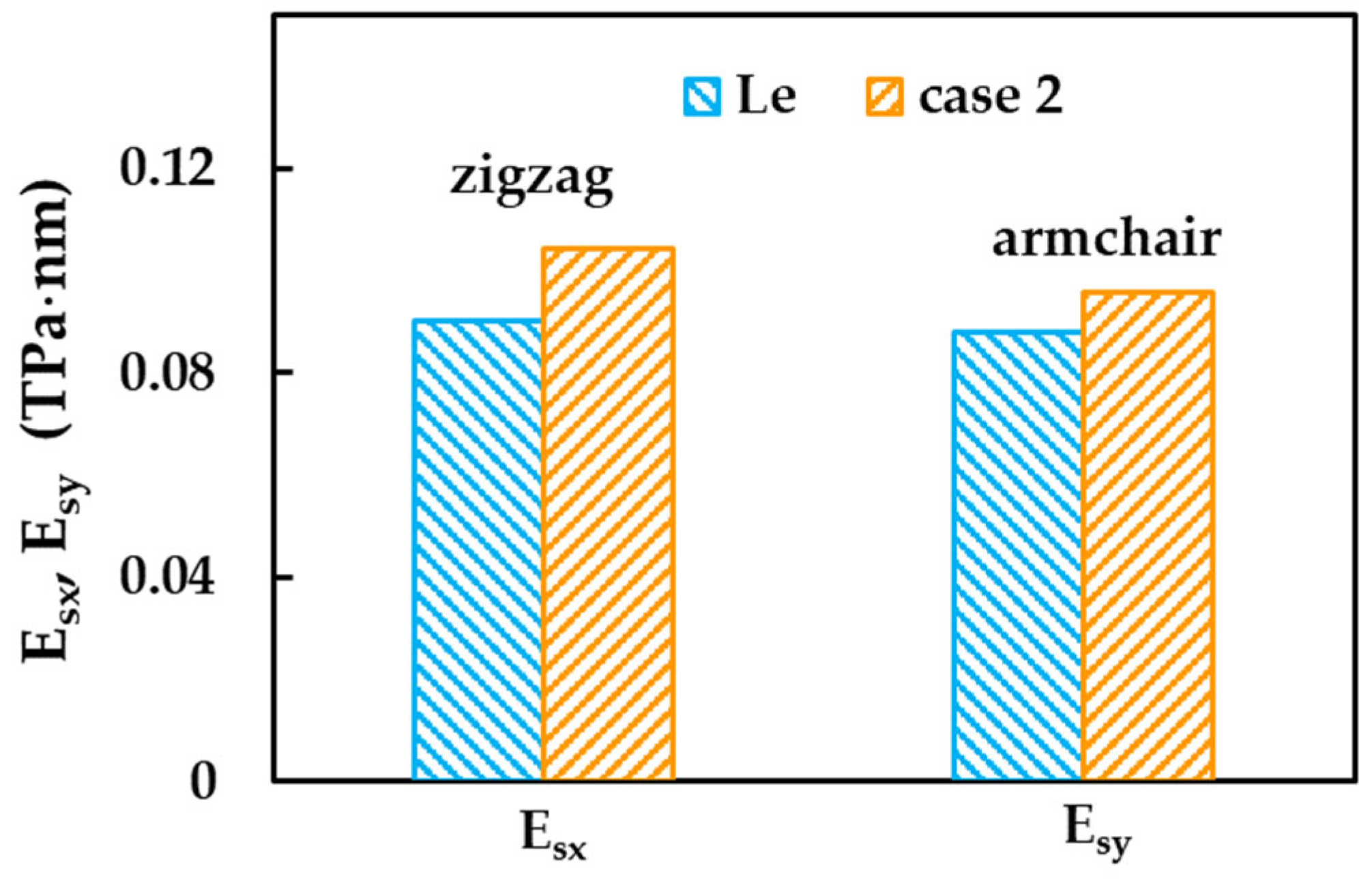
3.1. Young’s Modulus of InNNSs
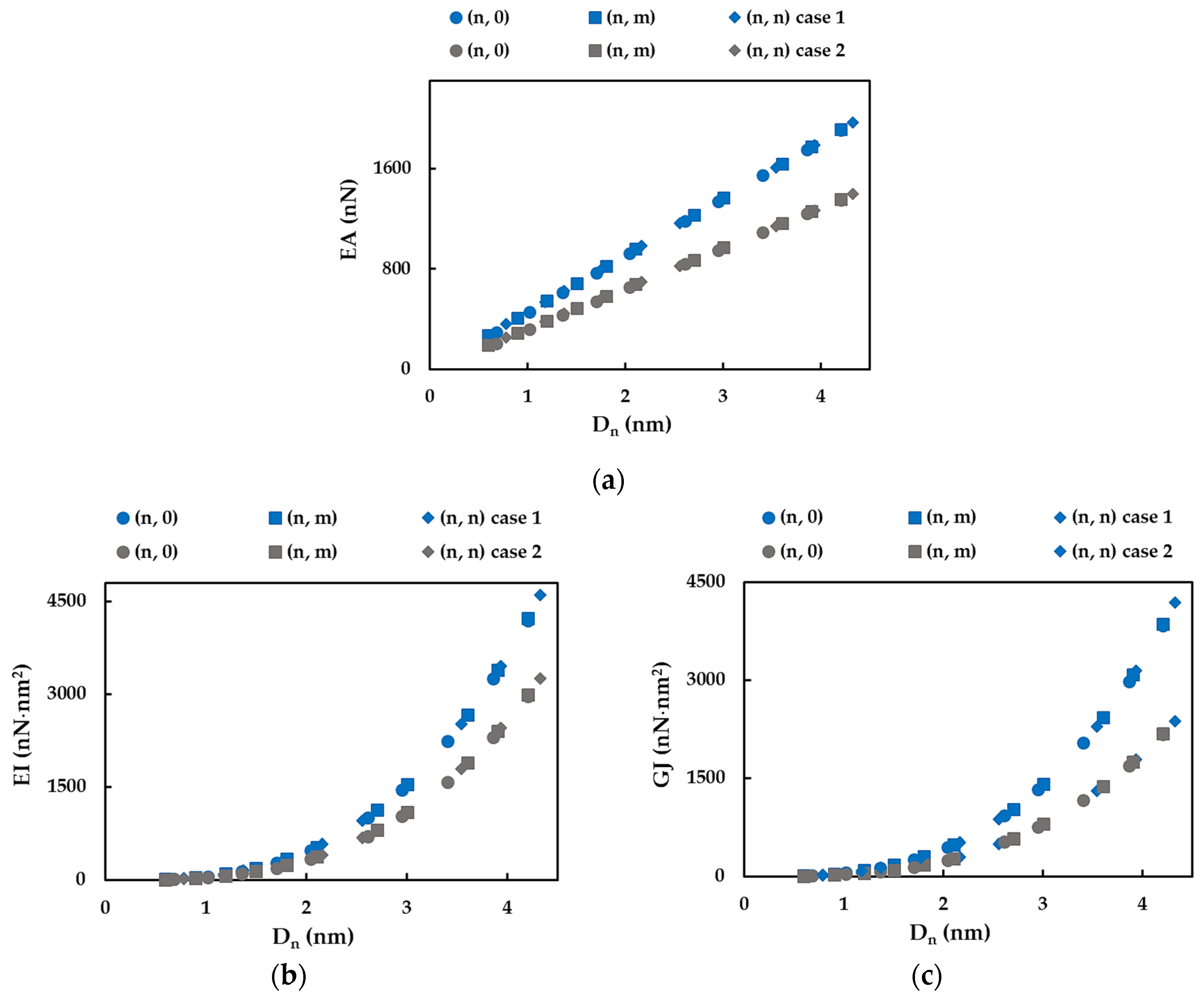
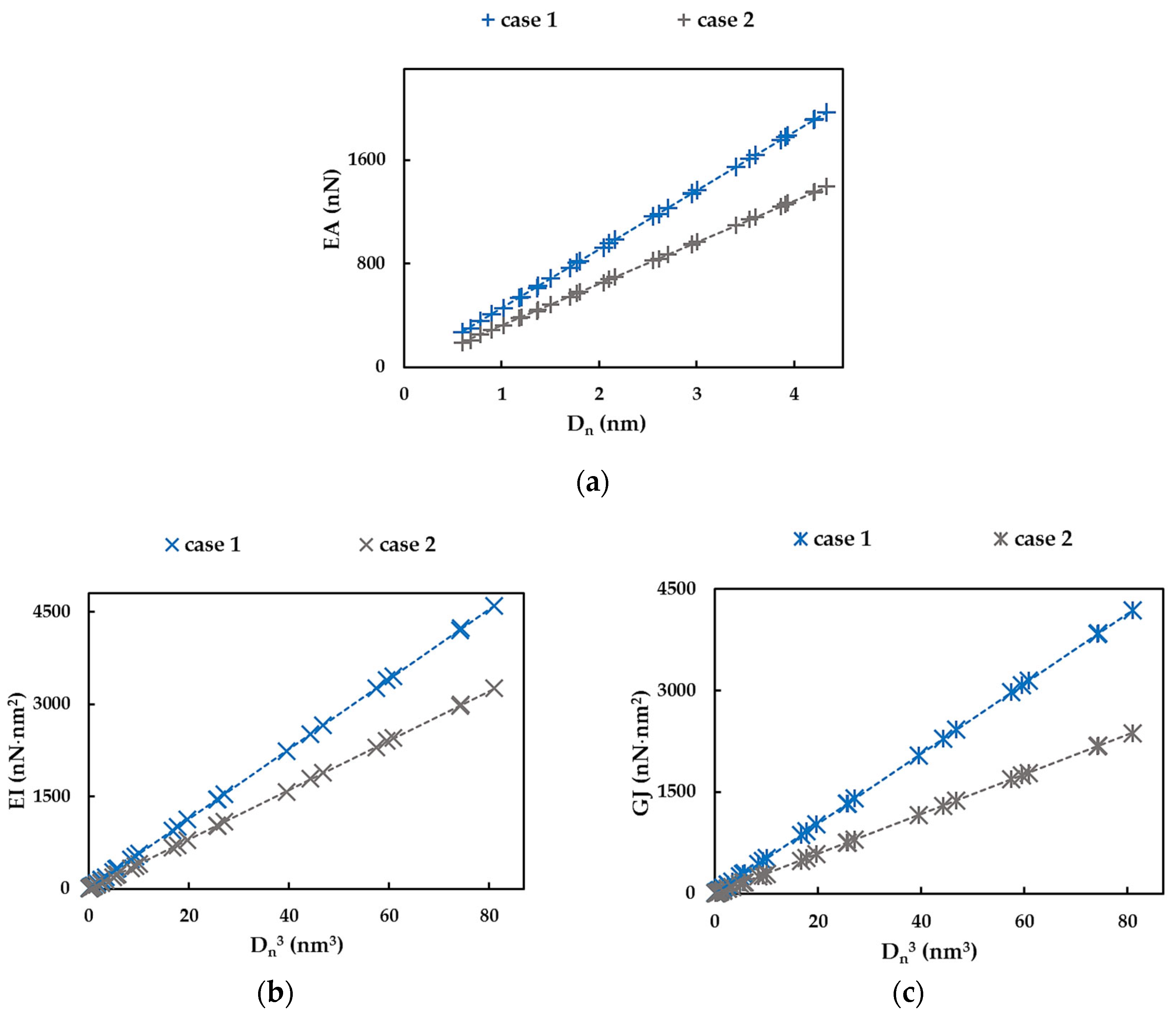
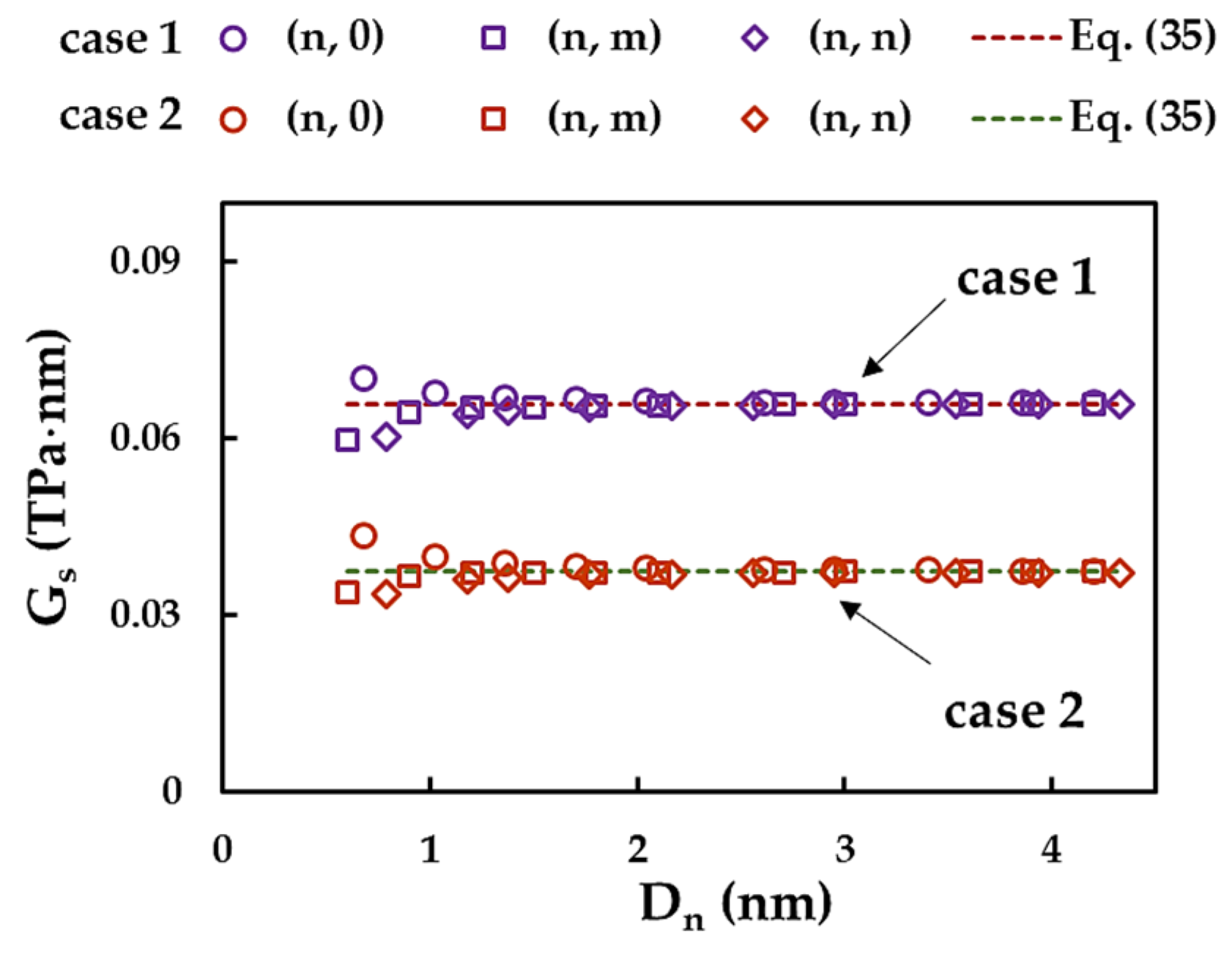
3.2. Rigidities of SWInNNTs
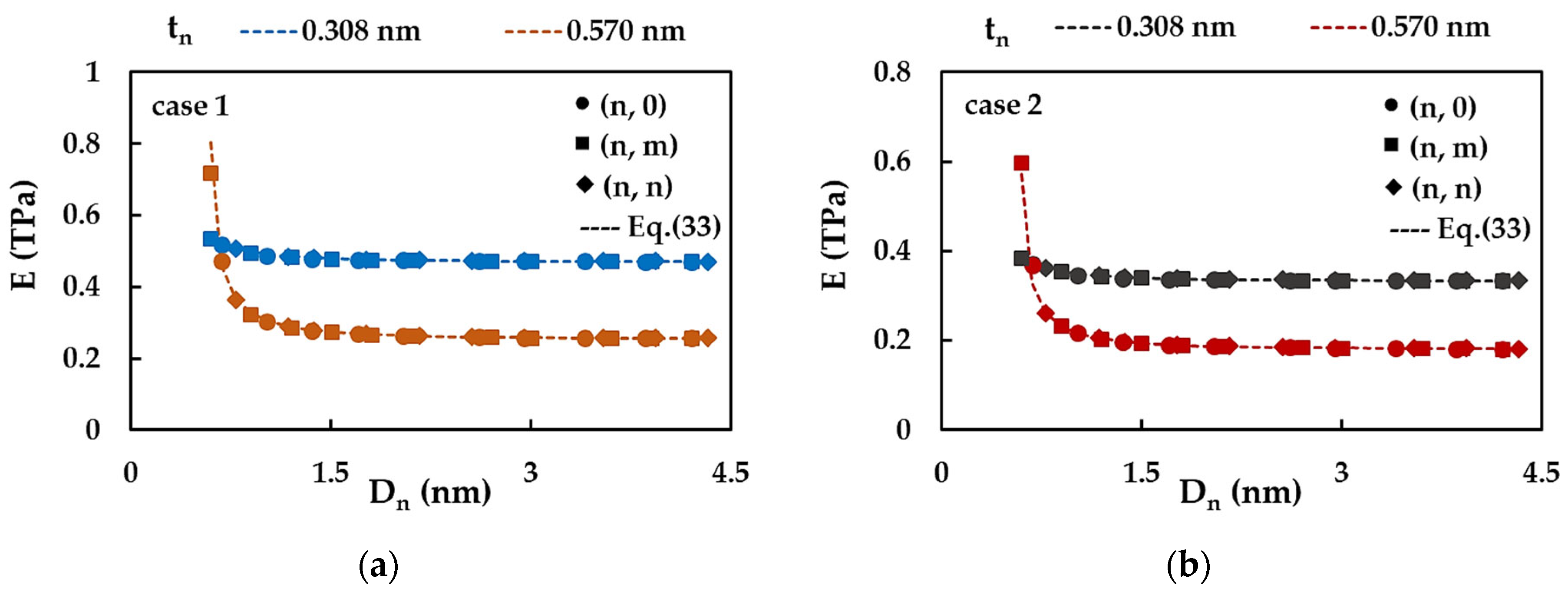
3.3. Young’s Modulus of SWInNNTs
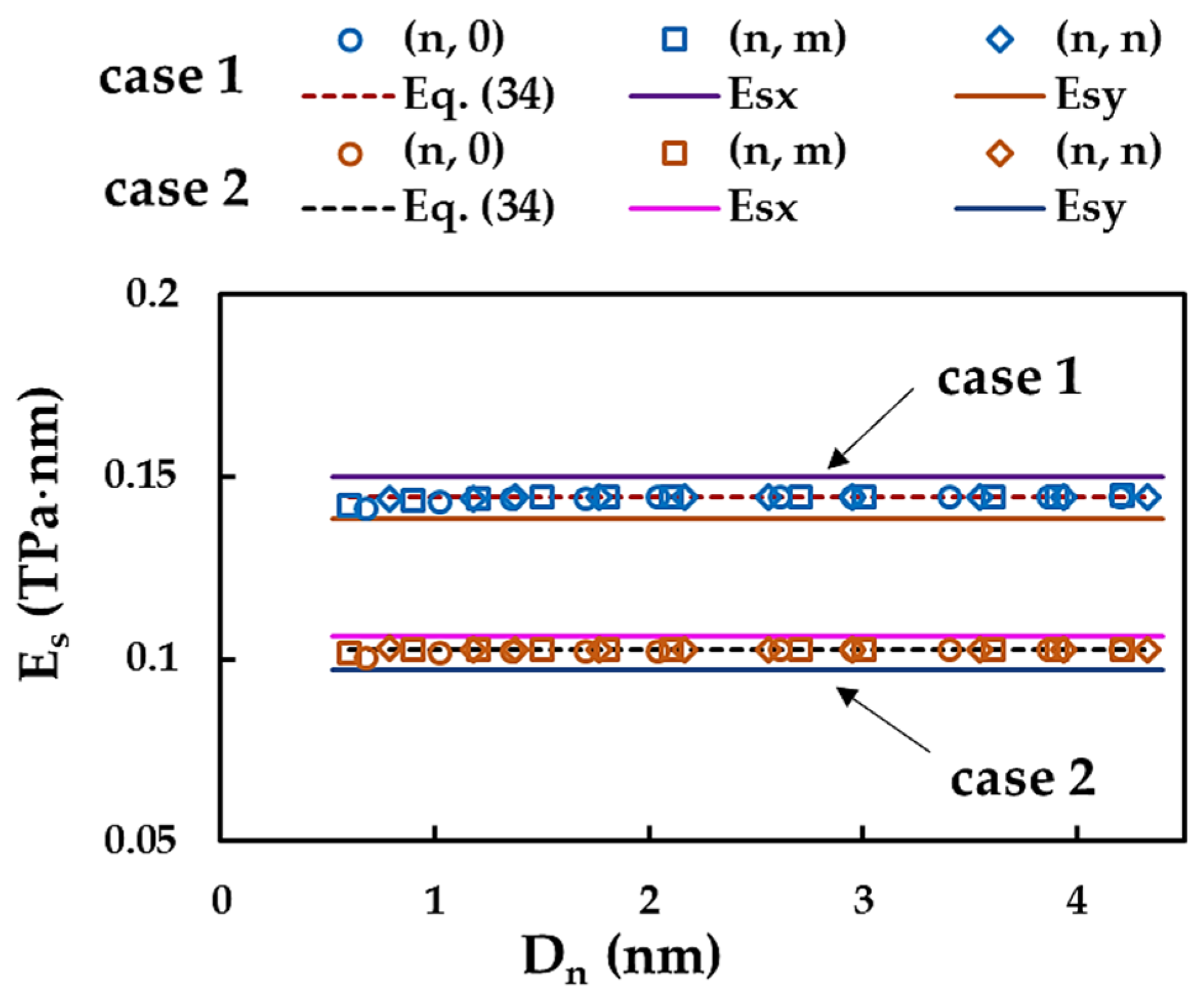
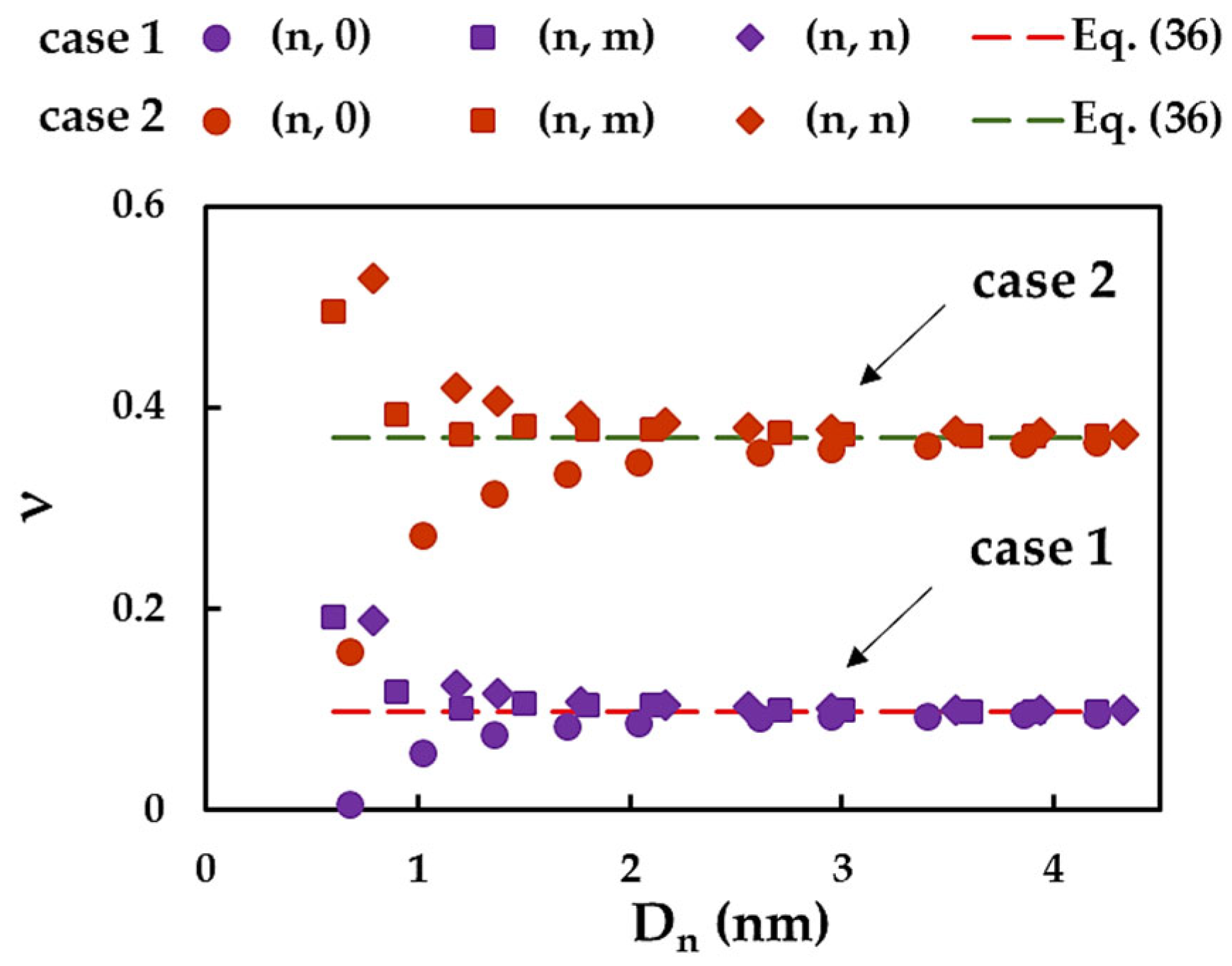
3.4. Surface Shear Modulus and Poisson’s Ratio of SWInNNTs
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chattopadhyay, S.; Ganguly, A.; Chen, K.-H.; Chen, L.-C. One-Dimensional Group III-Nitrides: Growth, Properties, and Applications in Nanosensing and Nano-Optoelectronics. Crit. Rev. Solid State Mater. Sci. 2009, 34, 224–279. [Google Scholar] [CrossRef]
- Tansley, T.L.; Foley, C.P. Electron mobility in indium nitride. Electron. Lett. 1984, 20, 1066–1068. [Google Scholar] [CrossRef]
- Wu, J.; Walukiewicz, W.; Yu, K.M.; Ager, J.W.; Haller, E.E.; Lu, H.; Schaff, W.J.; Saito, Y.; Nanishi, Y. Unusual properties of the fundamental band gap of InN. Appl. Phys. Lett. 2002, 80, 3967–3969. [Google Scholar] [CrossRef]
- Peng, Q.; Sun, X.; Wang, H.; Yang, Y.; Wene, X.; Huang, C.; Liu, S.; De, S. Theoretical prediction of a graphene-like structure of indium nitride: A promising excellent material for optoelectronics. Appl. Mater. Today 2017, 7, 169–178. [Google Scholar] [CrossRef]
- Oseki, M.; Okubo, K.; Kobayashi, A.; Ohta, J.; Fujioka, H. Field-effect transistors based on cubic indium nitride. Sci. Rep. 2014, 4, 3951. [Google Scholar] [CrossRef]
- Nakamura, S.; Mukai, T.; Senoh, M. Candela-class high brightness InGaN/AlGaN double-heterostructure blue-light emitting diodes. Appl. Phys. Lett. 1994, 64, 1687–1689. [Google Scholar]
- Nakamura, S. The roles of structural imperfections in InGaN-based bluelight-emitting diodes and laser diodes. Science 1998, 281, 956–961. [Google Scholar] [CrossRef]
- Şahin, H.; Cahangirov, S.; Topsakal, M.; Bekaroglu, E.; Akturk, E.; Senger, R.T.; Ciraci, S. Monolayer honeycomb structures of group-IV elements and III-V binary compounds: First-principles calculations. Phys. Rev. B 2009, 80, 155453. [Google Scholar] [CrossRef]
- Le, M.-Q. Atomistic Study on the tensile properties of hexagonal AlN, BN, GaN, InN and SiC sheets. J. Comput. Theor. Nanosci. 2014, 11, 1458–1464. [Google Scholar] [CrossRef]
- Yin, L.; Bando, Y.; Golberg, D.; Li, M. Growth of single-crystal indium nitride nanotubes and nanowires by controlled-carbonitridation reaction route. Adv. Mater. 2004, 16, 1833–1838. [Google Scholar] [CrossRef]
- Sardar, K.; Deepak, F.L.; Govindaraj, A.; Seikh, M.M.; Rao, C.N.R. InN nanocrystals, nanowires, and nanotubes. Small 2005, 1, 91–94. [Google Scholar] [CrossRef] [PubMed]
- Qian, Z.; Hou, S.; Zhang, J.; Li, R.; Shen, Z.; Zhao, X.; Xue, Z. Stability and electronic structure of single-walled InN nanotubes. Physica E 2005, 30, 81–85. [Google Scholar] [CrossRef]
- Mayo, S.L.; Barry, D.; Olafson, B.D.; Goddard, W.A. DREIDING: A generic force field for molecular simulations. J. Phys. Chem. 1990, 94, 8897–8909. [Google Scholar] [CrossRef]
- Rappé, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skid, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10039. [Google Scholar] [CrossRef]
- Li, C.; Chou, T.W. A structural mechanics approach for the analysis of carbon nanotubes. Int. J. Solids Struct. 2003, 40, 2487–2499. [Google Scholar] [CrossRef]
- Genoese, A.; Genoese, A.; Rizzi, N.L.; Salerno, G. Force constants of BN, SiC, AlN and GaN sheets through discrete homogenization. Meccanica 2018, 53, 593–611. [Google Scholar] [CrossRef]
- Sakharova, N.A.; Antunes, J.M.; Pereira, A.F.G.; Chaparro, B.M.; Fernandes, J.V. Elastic properties of single-walled phosphide nanotubes: Numerical Simulation Study. Nanomaterials 2022, 12, 2360. [Google Scholar] [CrossRef]
- Sakharova, N.A.; Antunes, J.M.; Pereira, A.F.G.; Chaparro, B.M.; Fernandes, J.V. On the determination of elastic properties of single-walled boron nitride nanotubes by numerical simulation. Materials 2021, 14, 3183. [Google Scholar] [CrossRef]
- Tapia, A.; Cab, C.; Hernández-Pérez, A.; Villanueva, C.; Peñuñuri, F.; Avilés, F. The bond force constants and elastic properties of boron nitride nanosheets and nanoribbons using a hierarchical modeling approach. Physica E 2017, 89, 183–193. [Google Scholar] [CrossRef]
- Sakharova, N.A.; Pereira, A.F.G.; Antunes, J.M.; Brett, C.M.A.; Fernandes, J.V. Mechanical characterization of single-walled carbon nanotubes. Numerical simulation study. Compos. B-Eng. 2015, 75, 73–85. [Google Scholar] [CrossRef]
- Pereira, A.F.G.; Antunes, J.M.; Fernandes, J.V.; Sakharova, N.A. Shear modulus and Poisson’s ratio of single-walled carbon nanotubes: Numerical evaluation. Phys. Status Solidi B 2016, 253, 366–376. [Google Scholar] [CrossRef]
- Ueno, M.; Yoshida, M.; Onodera, A.; Shimomura, O.; Takemura, K. Stability of the wurtzite-type structure under high pressure: GaN and InN. Phys. Rev. B 1994, 49, 14–21. [Google Scholar] [CrossRef] [PubMed]
- Benzarti, Z.; Sekrafi, T.; Khalfallah, A.; Bougrioua, Z.; Vignaud, D.; Evaristo, M.; Cavaleiro, A. Growth temperature effect on physical and mechanical properties of nitrogen rich InN epilayers. J. Alloys Compd. 2021, 885, 160951. [Google Scholar] [CrossRef]
- Sakharova, N.A.; Pereira, A.F.G.; Antunes, J.M. Elastic Moduli of Non-Chiral Singe-Walled Silicon Carbide Nanotubes: Numerical Simulation Study. Materials 2022, 15, 8153. [Google Scholar] [CrossRef] [PubMed]


| Case | ||||
|---|---|---|---|---|
| 1 (UFF) | 278 | 0.822 | 0.544 | 0.625 |
| 2 (DFT + MM) | 283 | 0.357 | 0.236 |
| Case | Diameter, d, nm | Formulation | * Young’s Modulus, Eb, GPa | Formulation | * Shear Modulus, Gb, GPa | Formulation | Formulation | |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.1983 | 1856 | 849 | 0.32 | ||||
| 2 | 0.1294 | 4432 | 4674 | 0.59 |
| Size | Lx, nm | Ly, nm | Number of Elements | Number of Nodes |
|---|---|---|---|---|
| 1 | 2.85 | 2.88 | 237 | 170 |
| 2 | 5.71 | 5.15 | 857 | 594 |
| 3 | 17.13 | 17.50 | 8333 | 5626 |
| 4 | 28.54 | 27.38 | 21,565 | 14,490 |
| NT Type | (n, m) | Θ° | Number of Elements | Number of Nodes | ||
|---|---|---|---|---|---|---|
| zigzag | (6, 0) | 0 | 0.681 | 20.81 | 1218 | 816 |
| (9, 0) | 1.022 | 31.31 | 2745 | 1836 | ||
| (12, 0) | 1.363 | 41.20 | 4812 | 3216 | ||
| (15, 0) | 1.704 | 52.32 | 7635 | 5100 | ||
| (18, 0) | 2.044 | 61.59 | 10,782 | 7200 | ||
| (23, 0) | 2.612 | 78.28 | 17,503 | 11,684 | ||
| (26, 0) | 2.953 | 89.40 | 22,594 | 15,080 | ||
| (30, 0) | 3.407 | 102.38 | 29,850 | 19,920 | ||
| (34, 0) | 3.862 | 115.36 | 38,114 | 25,432 | ||
| (37, 0) | 4.202 | 126.48 | 45,473 | 30,340 | ||
| chiral | (4, 2) | 19.1 | 0.601 | 20.81 | 942 | 632 |
| (6, 3) | 0.901 | 31.31 | 2106 | 1410 | ||
| (8, 4) | 1.202 | 41.20 | 3732 | 2496 | ||
| (10, 5) | 1.502 | 52.32 | 5970 | 3990 | ||
| (12, 6) | 1.803 | 61.59 | 8424 | 5628 | ||
| (14, 7) | 2.103 | 78.28 | 11,592 | 7742 | ||
| (18, 9) | 2.704 | 89.40 | 19,062 | 12,726 | ||
| (20, 10) | 3.005 | 102.38 | 23,280 | 15,540 | ||
| (24, 12) | 3.606 | 115.36 | 33,480 | 22,344 | ||
| (26, 13) | 3.906 | 126.48 | 39,546 | 26,390 | ||
| (28, 14) | 4.207 | 20.81 | 45,528 | 30,380 | ||
| armchair | (4, 4) | 30 | 0.705 | 18.38 | 1612 | 1080 |
| (6, 6) | 0.940 | 27.29 | 3624 | 2424 | ||
| (7, 7) | 1.409 | 36.13 | 4921 | 3290 | ||
| (9, 9) | 1.879 | 46.49 | 8217 | 5490 | ||
| (11, 11) | 2.114 | 54.66 | 12,023 | 8030 | ||
| (13, 13) | 2.584 | 64.47 | 16,939 | 11,310 | ||
| (15, 15) | 2.819 | 82.44 | 22,245 | 148,50 | ||
| (18, 18) | 3.289 | 90.61 | 32,634 | 21,780 | ||
| (20, 20) | 3.759 | 108.51 | 39,860 | 26,600 | ||
| (22, 22) | 4.228 | 118.39 | 48,466 | 32,340 |
| Case | Fitting Parameters | Mean Difference, % | ||||
|---|---|---|---|---|---|---|
| EA, nN | EI, nN⋅nm2 | GJ, nN⋅nm2 | ||||
| 1 | 453.96 | 56.71 | 51.67 | 0.39 | 0.69 | 0.50 |
| 2 | 321.63 | 40.14 | 29.29 | 0.47 | 0.82 | 0.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakharova, N.A.; Pereira, A.F.G.; Antunes, J.M.; Chaparro, B.M.; Fernandes, J.V. On the Determination of Elastic Properties of Indium Nitride Nanosheets and Nanotubes by Numerical Simulation. Metals 2023, 13, 73. https://doi.org/10.3390/met13010073
Sakharova NA, Pereira AFG, Antunes JM, Chaparro BM, Fernandes JV. On the Determination of Elastic Properties of Indium Nitride Nanosheets and Nanotubes by Numerical Simulation. Metals. 2023; 13(1):73. https://doi.org/10.3390/met13010073
Chicago/Turabian StyleSakharova, Nataliya A., André F. G. Pereira, Jorge M. Antunes, Bruno M. Chaparro, and José V. Fernandes. 2023. "On the Determination of Elastic Properties of Indium Nitride Nanosheets and Nanotubes by Numerical Simulation" Metals 13, no. 1: 73. https://doi.org/10.3390/met13010073
APA StyleSakharova, N. A., Pereira, A. F. G., Antunes, J. M., Chaparro, B. M., & Fernandes, J. V. (2023). On the Determination of Elastic Properties of Indium Nitride Nanosheets and Nanotubes by Numerical Simulation. Metals, 13(1), 73. https://doi.org/10.3390/met13010073






