In Situ Prediction of Metal Fatigue Life Using Frequency Change
Abstract
:1. Introduction
2. Theory and Formulation
2.1. Thermodynamics of Fatigue
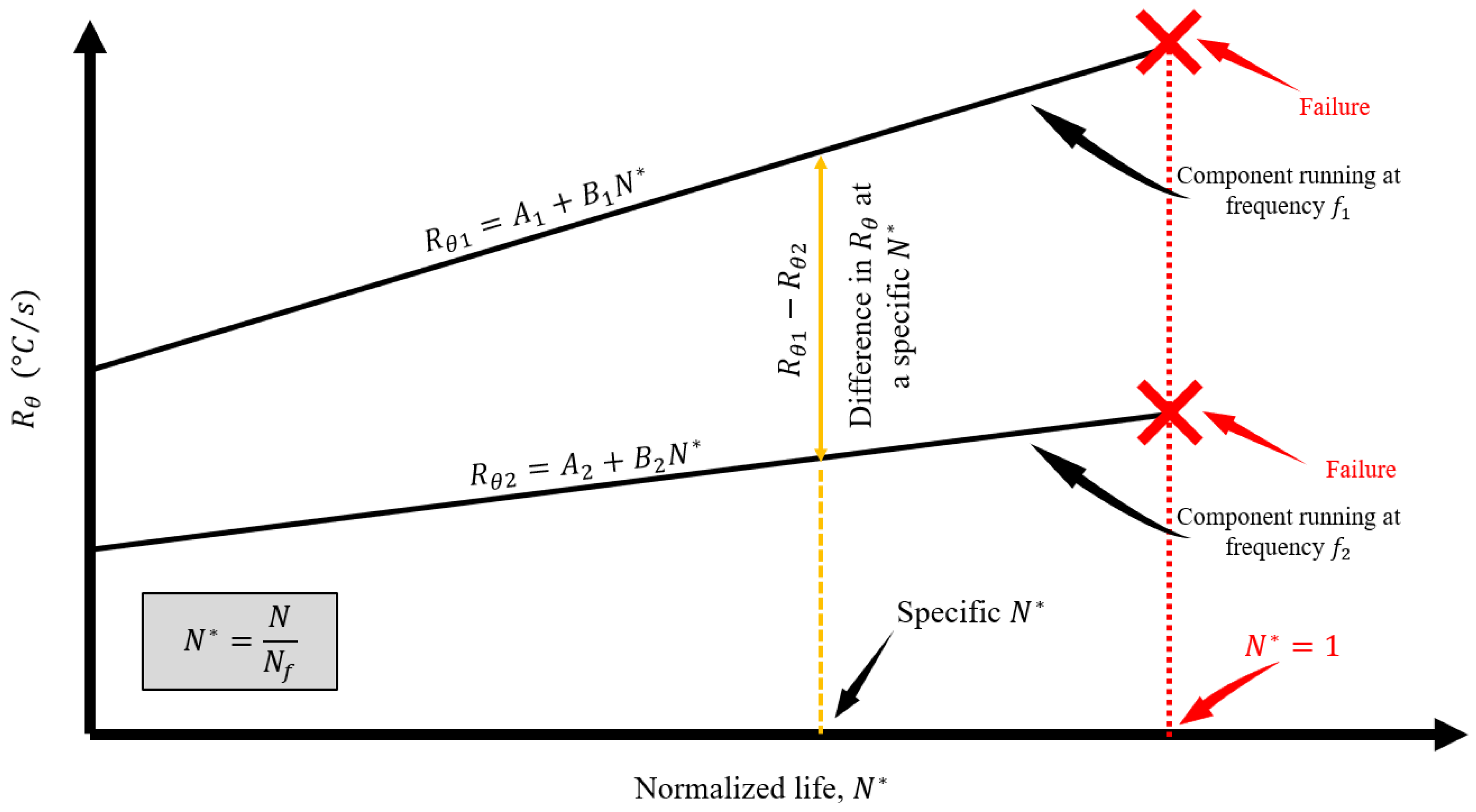
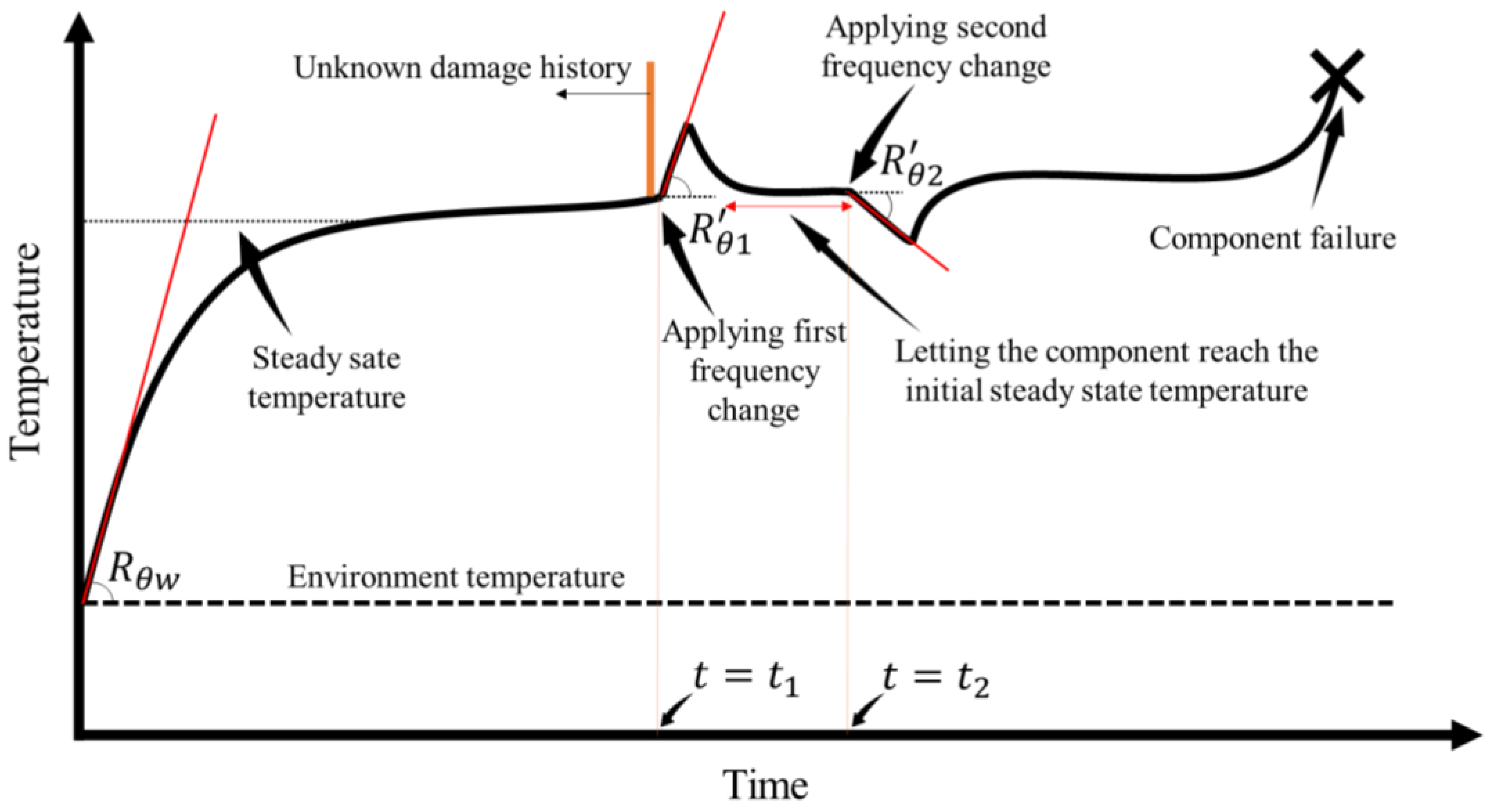
2.2. Influence of Rapid Change in Frequency
3. Experimental Verification
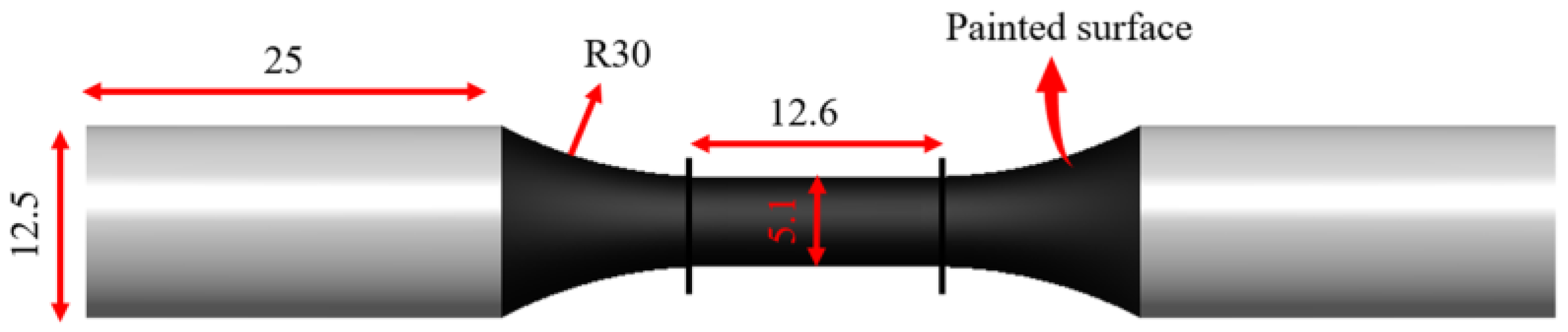
3.1. Material and Test Equipment
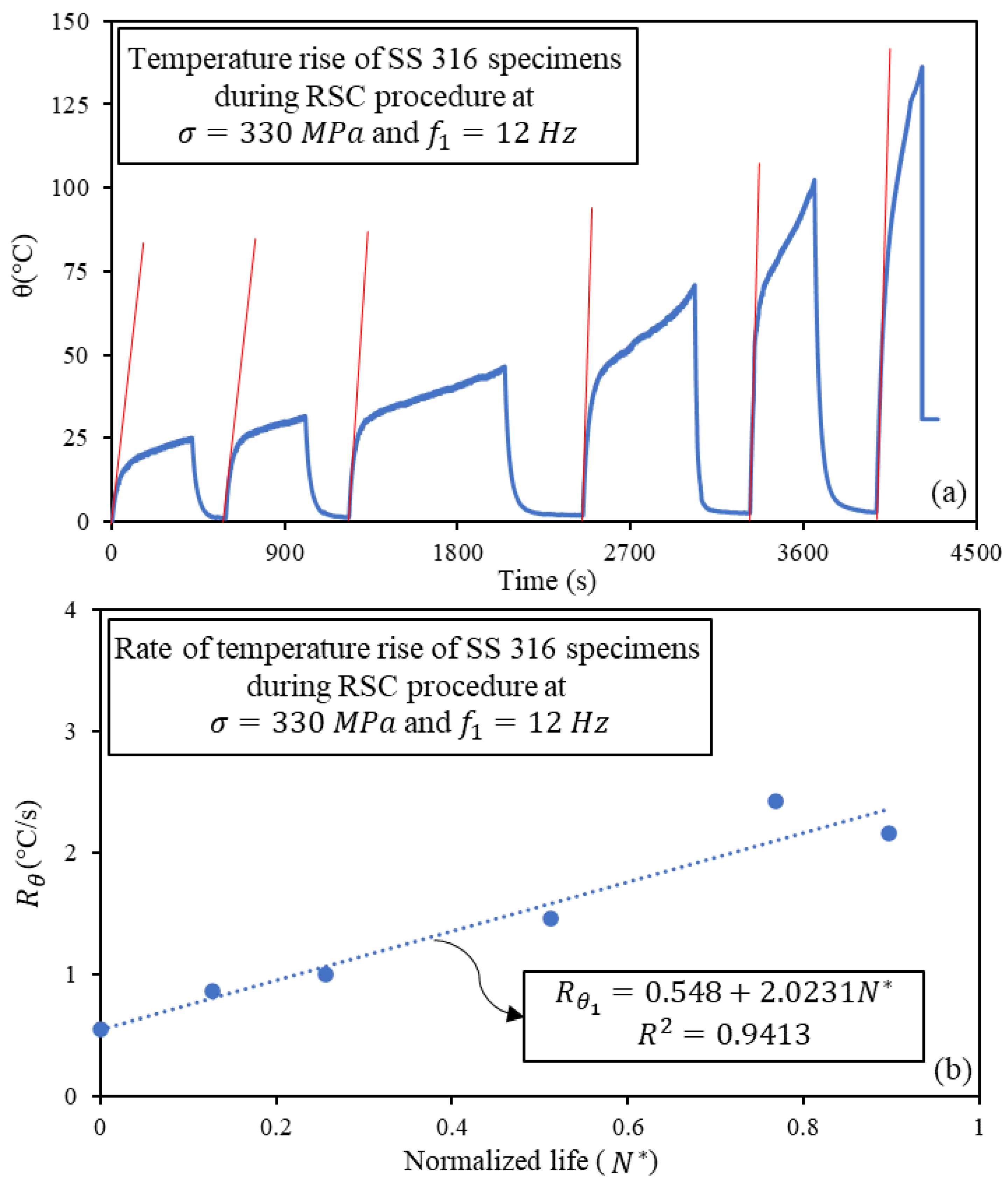
3.2. Characterization at Different Frequencies
3.3. RUL Assessment Procedure
4. Results and Discussion
4.1. Working Frequency 6 Hz
4.2. Working Frequency 8 Hz
4.3. Working Frequency 10 Hz
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmadzadeh, F.; Lundberg, J. Remaining useful life estimation. Int. J. Syst. Assur. Eng. Manag. 2014, 5, 461–474. [Google Scholar] [CrossRef]
- Bagul, Y.G. Assessment of Current Health and Remaining Useful Life of Hard Disk Drives; Northeastern University: Boston, MA, USA, 2009. [Google Scholar]
- Li, Y.; Billington, S.; Zhang, C.; Kurfess, T.; Danyluk, S.; Liang, S. Adaptive prognostics for rolling element bearing condition. Mech. Syst. Signal Process. 1999, 13, 103–113. [Google Scholar] [CrossRef]
- Oppenheimer, C.H.; Loparo, K.A. Physically based diagnosis and prognosis of cracked rotor shafts. In Proceedings of the Component and Systems Diagnostics, Prognostics, and Health Management II, Orlando, FL, USA, 16 July 2002; Volume 4733, pp. 122–132. [Google Scholar]
- Wang, W. A model to predict the residual life of rolling element bearings given monitored condition information to date. IMA J. Manag. Math. 2002, 13, 3–16. [Google Scholar] [CrossRef]
- Liao, H.; Zhao, W.; Guo, H. Predicting remaining useful life of an individual unit using proportional hazards model and logistic regression model. In Proceedings of the RAMS'06. Annual Reliability and Maintainability Symposium, Newport Beach, CA, USA, 23–26 January 2006; pp. 127–132. [Google Scholar]
- Usynin, A.V. A generic prognostic framework for remaining useful life prediction of complex engineering systems. Doctoral dissertation, The University of Tennessee, Knoxville, TN, USA, 2007. [Google Scholar]
- Kuncham, E.; Sen, S.; Kumar, P.; Pathak, H. An online model-based fatigue life prediction approach using extended Kalman filter. Theor. Appl. Fract. Mech. 2022, 117, 103143. [Google Scholar] [CrossRef]
- Lao, H.; Zein-Sabatto, S. Analysis of vibration signal’s time-frequency patterns for prediction of bearing’s remaining useful life. In Proceedings of the 33rd Southeastern Symposium on System Theory (Cat. No. 01EX460), Athens, OH, USA, 18–20 March 2001; pp. 25–29. [Google Scholar]
- El-Koujok, M.; Gouriveau, R.; Zerhouni, N. From monitoring data to remaining useful life: An evolving approach including uncertainty. In Proceedings of the 34th European Safety Reliability & Data Association, ESReDA Seminar and 2nd Joint ESReDA/ESRA Seminar on Supporting Technologies for Advanced Maintenance Informaiton Management, San Sebastian, Spain, May 2008; pp. 1–12. [Google Scholar]
- Tian, Z. An artificial neural network method for remaining useful life prediction of equipment subject to condition monitoring. J. Intell. Manuf. 2012, 23, 227–237. [Google Scholar] [CrossRef]
- Li, C.J.; Lee, H. Gear fatigue crack prognosis using embedded model, gear dynamic model and fracture mechanics. Mech. Syst. Signal Process. 2005, 19, 836–846. [Google Scholar] [CrossRef]
- Todinov, M. Limiting the probability of failure for components containing flaws. Comput. Mater. Sci. 2005, 32, 156–166. [Google Scholar] [CrossRef]
- Medjaher, K.; Tobon-Mejia, D.A.; Zerhouni, N. Remaining useful life estimation of critical components with application to bearings. IEEE Trans. Reliab. 2012, 61, 292–302. [Google Scholar] [CrossRef]
- Naderi, M.; Amiri, M.; Khonsari, M. On the thermodynamic entropy of fatigue fracture. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 423–438. [Google Scholar] [CrossRef]
- Wang, Z.R.; Yan, Z.F.; Chen, X.W.; Zhang, H.X.; Wang, S.B.; Dong, P.; Wang, W.X. Fatigue life prediction of AZ31B magnesium alloy based on fracture fatigue entropy. Mater. Sci. Technol. 2023, 39, 423–433. [Google Scholar] [CrossRef]
- Huang, J.; Li, C.; Liu, W. Investigation of internal friction and fracture fatigue entropy of CFRP laminates with various stacking sequences subjected to fatigue loading. Thin-Walled Struct. 2020, 155, 106978. [Google Scholar] [CrossRef]
- Ribeiro, P.; Petit, J.; Gallimard, L. Experimental determination of entropy and exergy in low cycle fatigue. Int. J. Fatigue 2020, 136, 105333. [Google Scholar] [CrossRef]
- Imanian, A.; Modarres, M. A thermodynamic entropy-based damage assessment with applications to prognostics and health management. Struct. Health Monit. 2018, 17, 240–254. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Khonsari, M.M. Entropic Characterization of Fatigue in Composite Materials. In Encyclopedia of Materials: Plastics and Polymers; Elsevier: Amsterdam, The Netherlands, 2022; Volume 2, pp. 147–162. [Google Scholar]
- Amooie, M.A.; Lijesh, K.; Mahmoudi, A.; Azizian-Farsani, E.; Khonsari, M.M. On the Characteristics of Fatigue Fracture with Rapid Frequency Change. Entropy 2023, 25, 840. [Google Scholar] [CrossRef] [PubMed]
- Lemaitre, J.; Chaboche, J.-L. Mechanics of Solid Materials; Cambridge University Press: New York, NY, USA, 1994. [Google Scholar]
- Halford, G. The energy required for fatigue(Plastic strain hystersis energy required for fatigue in ferrous and nonferrous metals). J. Mater. 1966, 1, 3–18. [Google Scholar]
- Jang, J.; Khonsari, M. On the evaluation of fracture fatigue entropy. Theor. Appl. Fract. Mech. 2018, 96, 351–361. [Google Scholar] [CrossRef]
- Liakat, M.; Naderi, M.; Khonsari, M.; Kabir, O. Nondestructive testing and prediction of remaining fatigue life of metals. J. Nondestruct. Eval. 2014, 33, 309–316. [Google Scholar] [CrossRef]
- ASTM Standard E466-15; Standard Practice for Conducting Force Controlled Constant Amplitude Axial Fatigue Tests of Metallic Materials. ANSI: New York, NY, USA, 2021.



| Material | Fe | C | Cr | Mo | Ni | Mn | P | S | Si |
|---|---|---|---|---|---|---|---|---|---|
| SS 316 | 82 Max | 0.08 | 18 Max | 3 Max | 14 Max | 2 | 0.045 | 0.03 | 1 |
| Material | Density (Kg/m3) | Thermal Conductivity K (W/m·K) | Specific Heat Capacity C (J/kg·K) | Young’s Modulus E (GPa) | Ultimate Strength (MPa) | Yield Strength (MPa) |
|---|---|---|---|---|---|---|
| SS 316 | 8000 * | 15.3 * | 490 * | 171 | 640 | 520 |
| Frequency (Hz) | ||
|---|---|---|
| 12 | 0.5480 | 2.0231 |
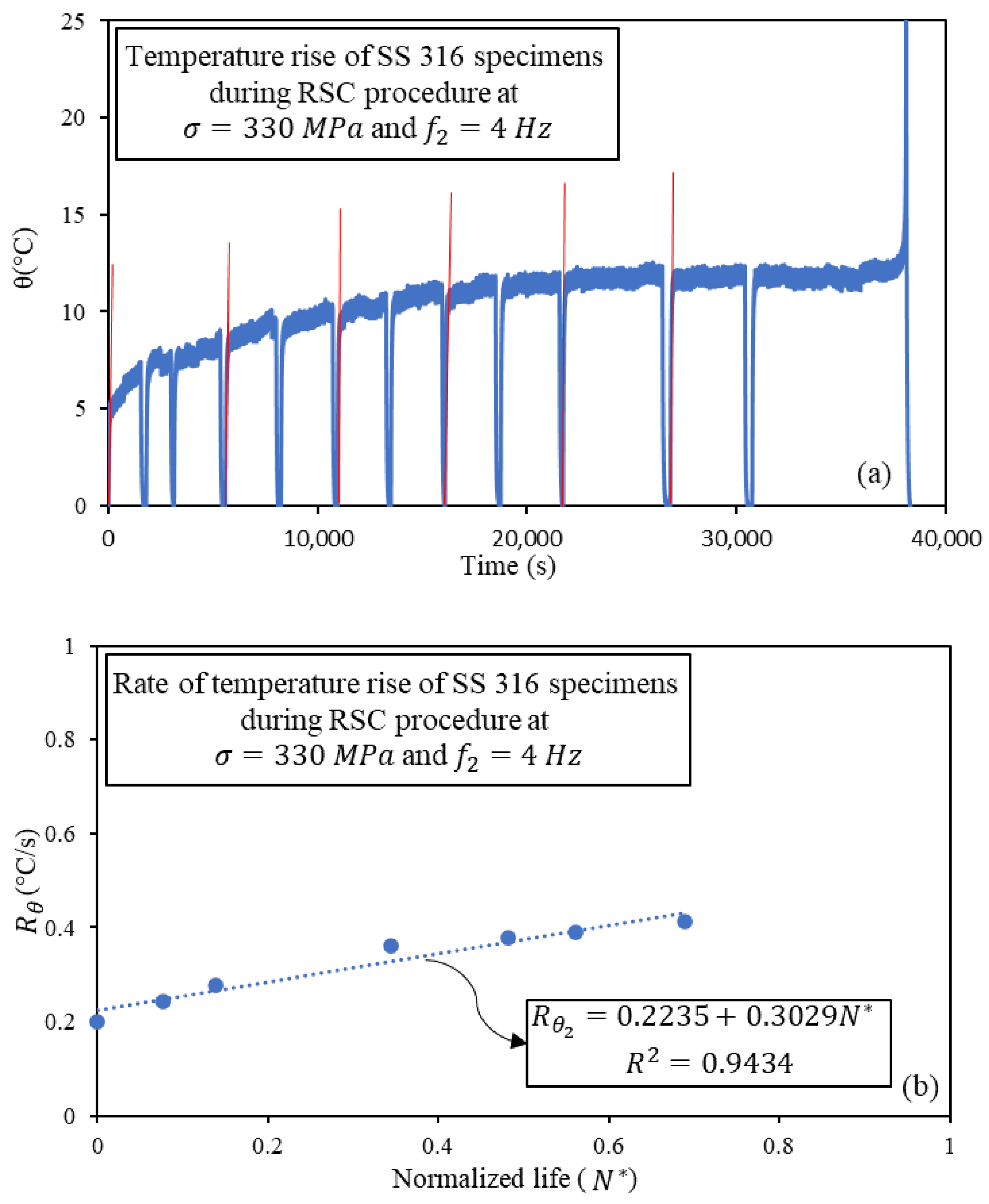
| 4 | 0.2235 | 0.3029 |
| N | Error (% of Actual Life) | ||||
|---|---|---|---|---|---|
| 10,000 | 0.3559 | 0.1186 | 0.087 | 0.023 | 6.4 |
| 30,000 | 0.4706 | 0.1470 | 0.170 | 0.066 | 10.4 |
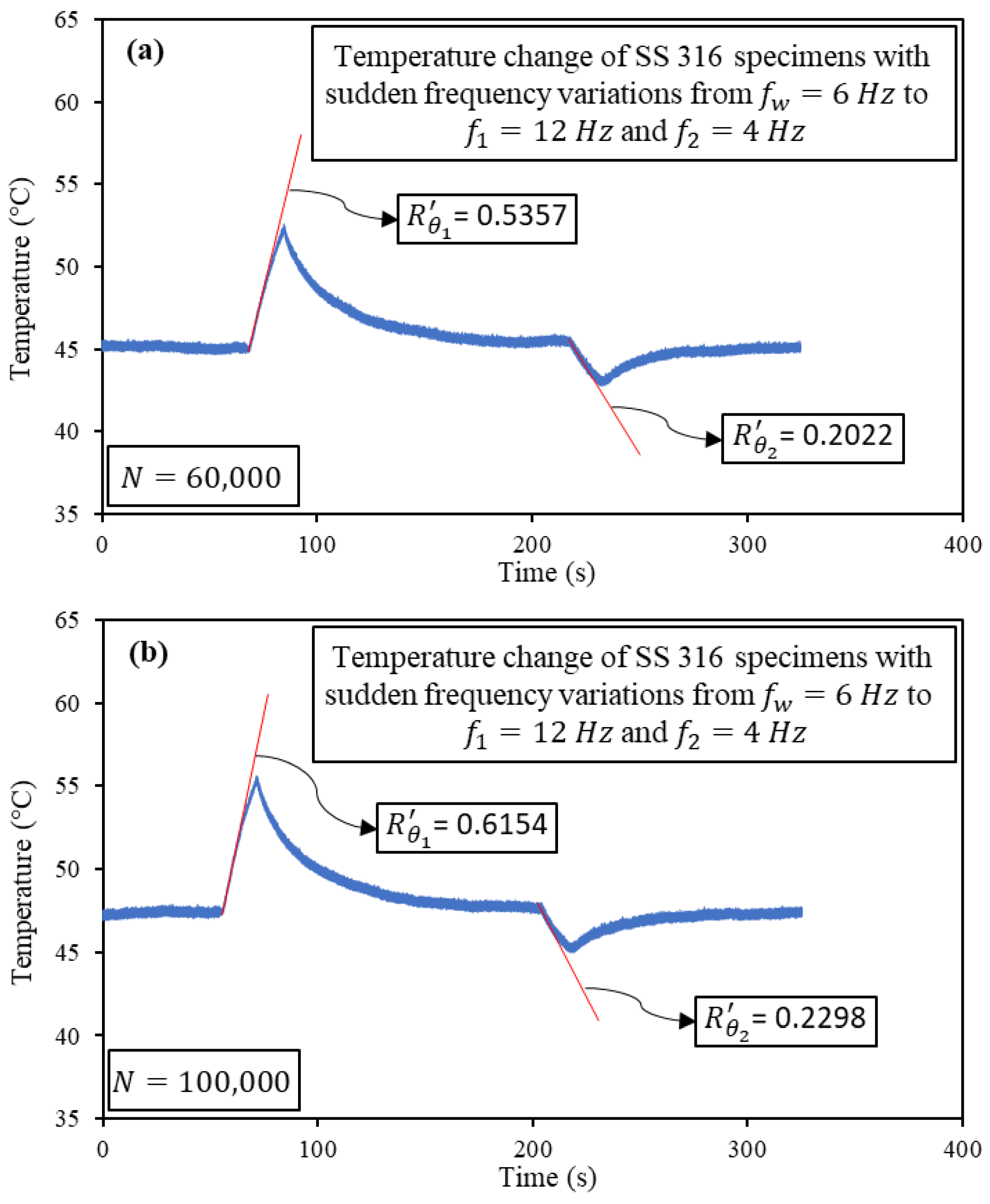
| 60,000 | 0.5357 | 0.2022 | 0.240 | 0.132 | 10.8 |
| 100,000 | 0.6154 | 0.2298 | 0.303 | 0.218 | 8.5 |
| 177,000 | 0.6513 | 0.2559 | 0.339 | 0.385 | −4.6 |
| 210,000 | 0.6691 | 0.2576 | 0.350 | 0.458 | −10.8 |
| 350,000 | 0.9206 | 0.5089 | 0.642 | 0.761 | −11.9 |
| N | Error (% of Actual Life) | ||||
|---|---|---|---|---|---|
| 10,000 | 0.2560 | 0.2626 | 0.113 | 0.036 | 7.7 |
| 30,000 | 0.3467 | 0.3208 | 0.199 | 0.105 | 9.4 |
| 72,000 | 0.3819 | 0.4883 | 0.317 | 0.250 | 6.7 |
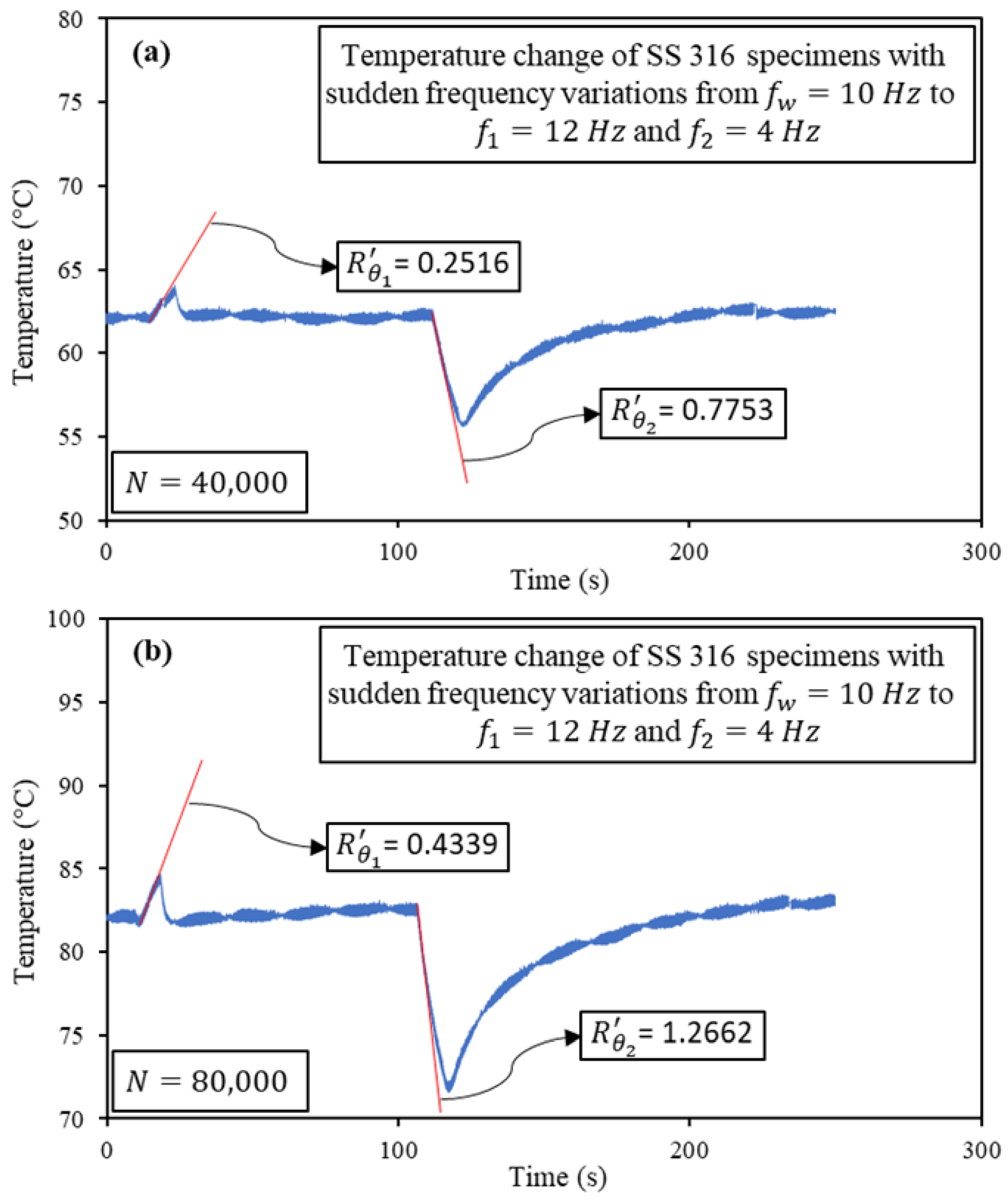
| 106,000 | 0.5122 | 0.5334 | 0.419 | 0.367 | 5.2 |
| 140,000 | 0.6581 | 0.6990 | 0.600 | 0.484 | 11.6 |
| 183,000 | 0.6986 | 0.7027 | 0.626 | 0.633 | −0.7 |
| N | Error (% of Actual Life) | ||||
|---|---|---|---|---|---|
| 10,000 | 0.0975 | 0.2660 | 0.023 | 0.096 | −7.3 |
| 33,000 | 0.2501 | 0.6905 | 0.358 | 0.302 | 5.6 |
| 40,000 | 0.2516 | 0.7753 | 0.408 | 0.366 | 4.2 |
| 45,000 | 0.2929 | 0.7958 | 0.446 | 0.412 | 3.4 |
| 55,000 | 0.3199 | 0.9194 | 0.532 | 0.503 | 2.9 |
| 65,000 | 0.3255 | 1.0113 | 0.589 | 0.595 | −0.6 |
| 80,000 | 0.4339 | 1.2662 | 0.800 | 0.732 | 6.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoudi, A.; Amooie, M.A.; Koottaparambil, L.; Khonsari, M.M. In Situ Prediction of Metal Fatigue Life Using Frequency Change. Metals 2023, 13, 1681. https://doi.org/10.3390/met13101681
Mahmoudi A, Amooie MA, Koottaparambil L, Khonsari MM. In Situ Prediction of Metal Fatigue Life Using Frequency Change. Metals. 2023; 13(10):1681. https://doi.org/10.3390/met13101681
Chicago/Turabian StyleMahmoudi, Ali, Mohammad A. Amooie, Lijesh Koottaparambil, and Michael M. Khonsari. 2023. "In Situ Prediction of Metal Fatigue Life Using Frequency Change" Metals 13, no. 10: 1681. https://doi.org/10.3390/met13101681





