Sensitivity Study of Surface Roughness Process Parameters in Belt Grinding Titanium Alloys
Abstract
:1. Introduction
- (1)
- In traditional belt grinding processes, the selection of grinding process parameters typically relies on the experience and skill level of the operators, making it difficult to ensure the quality of the finished workpieces. Therefore, this study conducted an in-depth investigation of the process parameters involved in belt grinding blades through theoretical analysis, with the aim of identifying critical process parameters and reducing the reliance on manual decision making.
- (2)
- By studying the effect of machining parameters on surface quality and categorising these parameter combinations into different intervals, it becomes possible to select machining parameters more quickly in actual production. This will help reduce preparation time, minimise the defect rate, and increase the utilisation efficiency of grinding machines.
- (3)
- By establishing a surface roughness prediction model that clarifies the relationship between surface roughness and processing parameters, it facilitates the setting of grinding process parameters. This is important for the rapid and rational selection of grinding process parameters.
2. Experiment
2.1. Methods for Solving Indicator Weights
2.2. Comprehensive Evaluation Hierarchical Model
2.3. Solving for Equilibrium Weights
2.3.1. Subjective Weight Analysis Based on Rough Set Theory
2.3.2. Objective Weight Analysis Based on Coefficient of Variation Method
2.3.3. Weight Balance Model
3. Test Conditions and Methods
3.1. Test Apparatus and Equipment
3.2. Test Material
3.3. Test Programme
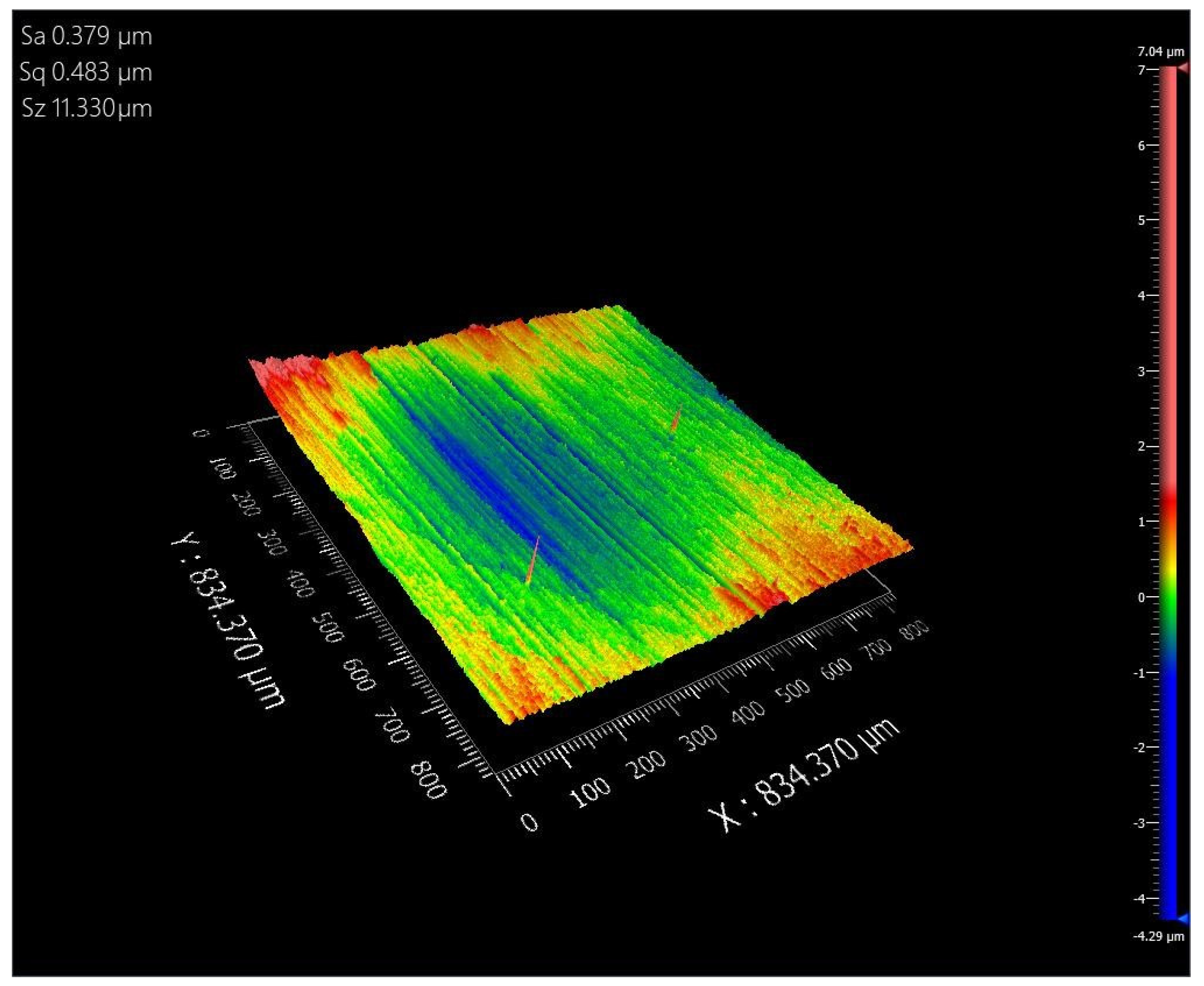
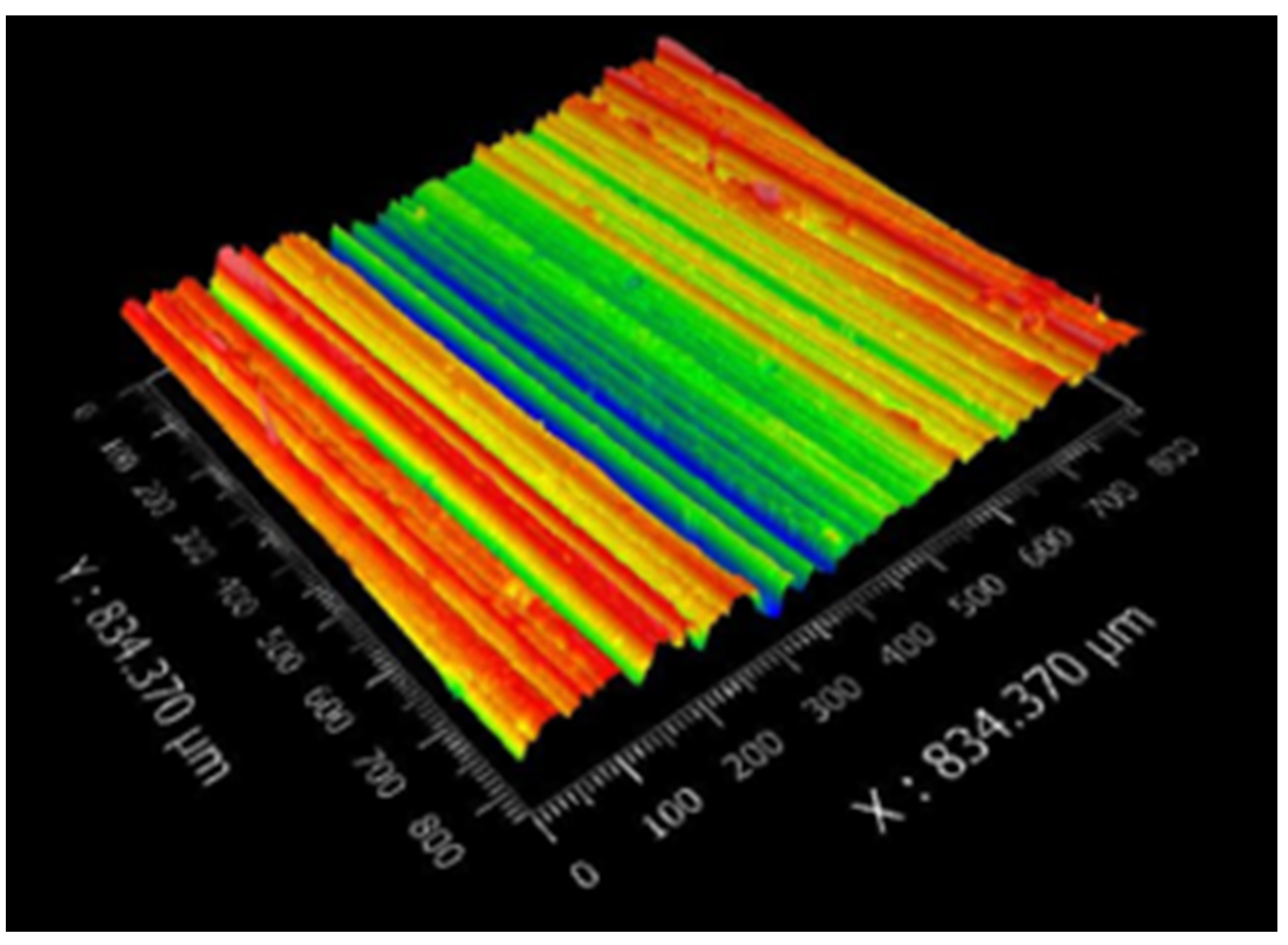
4. Test Results and Analysis
4.1. The Establishment of Empirical Formula for Surface Roughness
4.2. Analysis of Surface Roughness Process Parameters
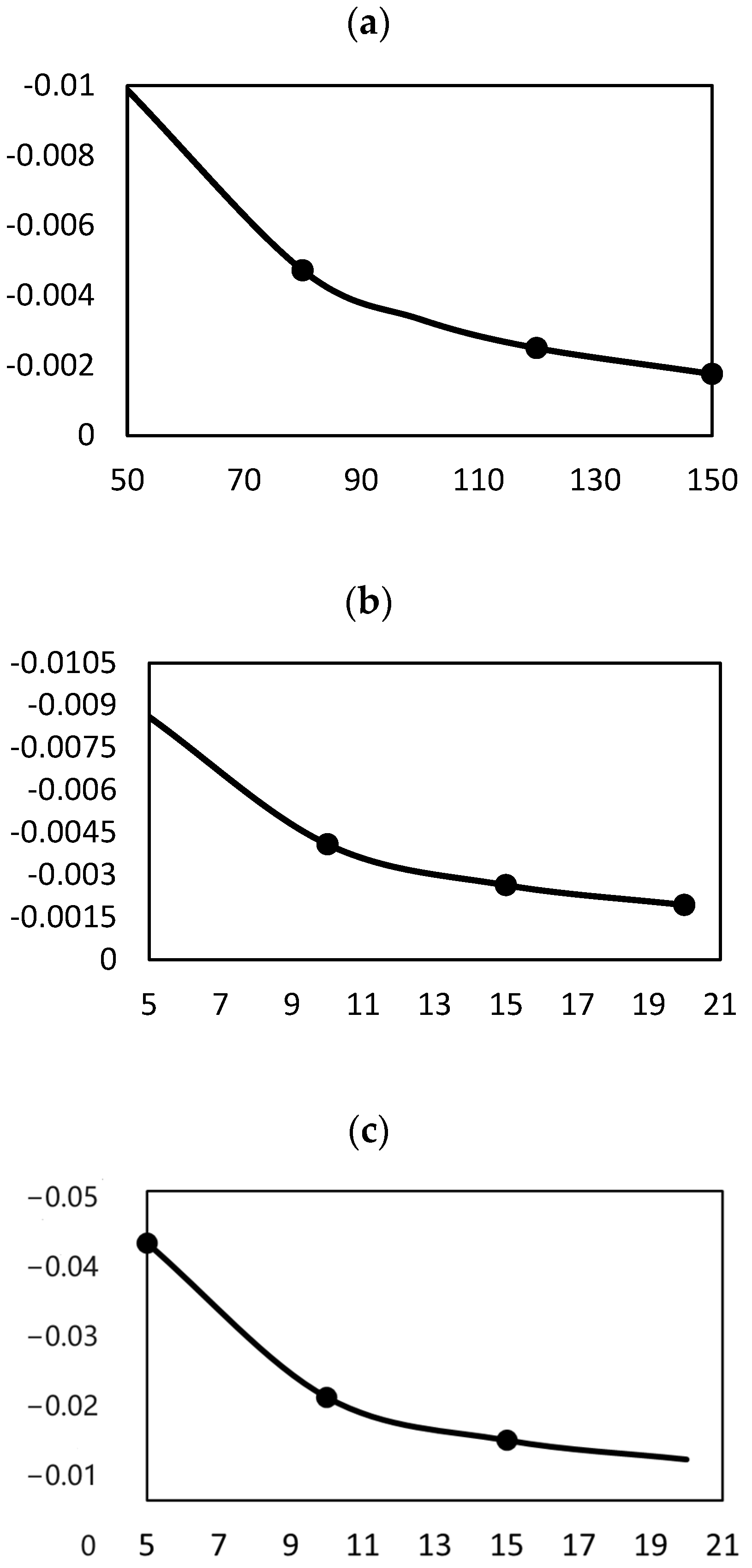
4.2.1. Sensitivity Model Calculation
4.2.2. Sensitivity Curve Analysis
4.2.3. Stable and Unstable Domains of Process Parameters
5. Process Parameter Interval Selection
6. Conclusions
- From the test of significance, it can be seen that the confidence level of the established model for the surface roughness index of titanium alloy after belt grinding was above 95%, and the correlation coefficient was 0.9547; therefore, the constructed model is accurate and reliable.
- The surface roughness of titanium alloy TC4 after abrasive belt grinding is most sensitive to changes in abrasive grain size, followed by grinding pressure and abrasive belt line speed.
- The preferred intervals for the grinding parameters were obtained: for abrasive belt grain size, the interval is from 120# to 150#; for abrasive belt line speed, it is from 15 m/s to 20 m/s; and for grinding pressure, it is from 10 N to 15 N. These intervals can control the surface roughness to be within 0.57 μm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, X.; Zhang, D.; Yang, Z.; Ren, J.; Yao, X. Study on sensitivity of GH4169 grinding surface roughness influencing parameters. Aerosp. Manuf. Technol. 2012, 55, 83–86+91. [Google Scholar]
- Shen, X.; Zhang, D.; Yao, X.; Tan, L. Research progress on surface integrity formation mechanism of titanium alloy machining. J. Aeronaut. Mater. 2021, 41, 1–16. [Google Scholar]
- Gao, C.; Wang, S.; Wang, H.; Liu, G.; Wu, G. Theoretical prediction and sensitivity analysis of surface roughness of abrasive belt grinding. Surf. Technol. 2018, 47, 295–305. [Google Scholar]
- Khellouki, A.; Rech, J.; Zahouani, H. The effect of abrasive grain’s wear and contact conditions on surface texture in belt finishing. Wear 2006, 263, 81–87. [Google Scholar]
- Bigerelle, M.; Gautier, A.; Hagege, B.; Favergeon, J.; Bounichane, B. Roughness characteristic length scales of belt finished surface. J. Mater. Process. Tech. 2009, 209, 6103–6116. [Google Scholar]
- Li, J.; Shi, Y.; He, X. Optimization of polishing process parameters of abrasive belt of aero-engine blades. Aerosp. Manuf. Technol. 2016, 59, 60–65+75. [Google Scholar]
- Tian, R.; Yao, X.; Huang, X.; Ren, J.; Zhang, D. Interval sensitivity and optimization of high-speed milling process parameters of titanium alloy for machining surface roughness. J. Aeronaut. 2010, 31, 2464–2470. [Google Scholar]
- Huang, J.; Yi, H.; Shu, A.; Tang, L.; Song, K. Visual measurement of grinding surface roughness based on feature fusion. Meas. Sci. Technol. 2023, 34, 105019. [Google Scholar] [CrossRef]
- Pan, Y.; Qiao, Y.; Wang, Y.; Liu, X.; Zhou, P. Real-time prediction of grinding surface roughness based on multi-sensor signal fusion. Int. J. Adv. Manuf. Technol. 2023, 127, 5847–5861. [Google Scholar] [CrossRef]
- Lu, E.; Guo, Y.; Zhu, X.; Wang, Y.; Ren, W.; Yang, Y. A new grinding surface roughness measurement method based on image quality algorithm and BP neural network. Surf. Topogr. Metrol. Prop. 2022, 10, 045024. [Google Scholar] [CrossRef]
- Fang, R.; Yi, H.; Shu, A.; Lv, X. Evaluation of grinding surface roughness based on gradient similarity and color similarity. Surf. Topogr. Metrol. Prop. 2022, 10, 035041. [Google Scholar] [CrossRef]
- Liu, Y.; Song, Z.; Liang, Z.; Cui, X.; Gong, Y.; Sun, X.; Dong, Z.; Yang, H.; Liu, W. Experimental investigations into groove bottom surface roughness for Zr-based bulk metallic glass by using milling. Int. J. Adv. Manuf. Technol. 2023, 125, 855–872. [Google Scholar] [CrossRef]
- Liang, X.; Lin, B.; Liu, Z.; Ma, X. Study on dispersion and attenuation of laser-induced surface acoustic wave by grinding surface roughness. Appl. Acoust. 2022, 199, 109028. [Google Scholar] [CrossRef]
- Jiang, G.; Zhao, Z.; Xiao, G.; Li, S.; Chen, B.; Zhuo, X.; Zhang, J. Study of Surface Integrity of Titanium Alloy (TC4) by Belt Grinding to Achieve the Same Surface Roughness Range. Micromachines 2022, 13, 1950. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, G.; Xiao, G.; Xu, J. Abrasive belt grinding force and its influence on surface integrity. Mater. Manuf. Process. 2022, 38, 888–897. [Google Scholar] [CrossRef]
- Shao, B.; Peng, Y.; Zhang, C.; Lu, X.; Yang, W.; Huang, X. Research on the optimal allocation method of nitrogen-rich gas based on entropy weight improved TOPSIS theory. J. Aerodyn. 2023, 1–9. [Google Scholar] [CrossRef]
- Zhong, R.; Qin, X.; Lai, M.; Hu, W.; Xia, C.; Lu, N.; Xiao, Z. Research on the evaluation method of energy efficiency management level of hydropower station based on AHP and TOPSIS. China Rural. Water Conserv. Hydropower 2023, 1–11. [Google Scholar] [CrossRef]
- Zhan, X.; Shu, L.; Liu, T.; Fan, Z. An aero-engine maintainability assessment method based on improved TOPSIS. Comput. Meas. Control 2023, 117, 1–9. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, Z. Safety risk evaluation of assembly building construction based on AHP-TOPSIS. Chongqing Constr. 2022, 21, 67–70. [Google Scholar]
- He, L.; Du, M.; Zhang, J.; Du, Y. Dynamic evaluation of water resources carrying capacity based on improved TOPSIS. China Rural Water Conserv. Hydropower 2023, 1–6. [Google Scholar] [CrossRef]
- Liang, Y.; Gao, G.; Li, X.; Luo, Z.; Song, S.; Huang, S. Optimisation of mining methods for deep thick and large ore bodies based on AHP-TOPSIS comprehensive evaluation. Mod. Min. Ind. 2022, 38, 85–88. [Google Scholar]
- Han, R.; Guo, X.; Liu, X.; He, L.; Li, G.; Wang, X. Application of entropy weight-based TOPSIS method in comprehensive evaluation of Perilla frutescens. Mol. Plant Breed. 1–13. Available online: http://kns.cnki.net/kcms/detail/46.1068.S.20221009.1420.026.html (accessed on 26 October 2023).
- Zhu, J.; Cui, X. Evaluation of China’s comprehensive marine strength based on entropy weight TOPSIS model. Sci. Ind. 2022, 22, 283–289. [Google Scholar]
- Li, Y. Application of digital image technology in machining surface roughness detection. Foshan Ceram. 2023, 33, 54–56. [Google Scholar]
- Yang, D.; Yu, J.; Gao, M.; Wu, J.; Tu, L.; An, Q. Optimisation of machining parameters of 1J50 soft magnetic alloy based on milling force and surface roughness. Tool Technol. 2022, 56, 49–54. [Google Scholar]
- Xiao, G.; Chen, S.; Li, S.; Chen, B.; Zhuo, X.; Huang, Y. Study on the effect of abrasive wear on the surface integrity of TC17 by abrasive belt grinding. Aerosp. Manuf. Technol. 2022, 65, 26–33. [Google Scholar]
- Ren, H.; Li, J.; Xie, L. Inclined feed method for robotic belt grinding of aero-engine blades. Form. Technol. Prod. Mod. 2021, 38, 42–49. [Google Scholar]
- Song, W.-W.; Huang, Y.; Xiao, G.-J.; Song, S.-Y.; Zhang, Y.-D. Study on the formation of surface topography and its prediction in TC17 titanium alloy belt grinding. Aviat. Manuf. Technol. 2021, 64, 56–62. [Google Scholar]
- Yuan, L. Quality and Efficiency Improvement Method and Experimental Research On Aircraft Blade Abrasive Belt Grinding. Master’s Thesis, Chongqing University, Chongqing, China, 2021. [Google Scholar]
- Tian, F.; Si, D.; Li, L. Prediction and validation of surface roughness in abrasive belt grinding. Tool Technol. 2021, 55, 96–100. [Google Scholar]
- Wang, H.; Luo, M. Influence of abrasive belt grinding parameters on the depth of material removal. J. Fujian Eng. Coll. 2021, 19, 524–531. [Google Scholar]
- Dong, H.; Yang, H.; Sun, X.; Dong, Z.; Liu, Y. Prediction of surface roughness of screw belt grinding based on improved neural network algorithm. Surf. Technol. 2022, 51, 275–283. [Google Scholar]
- Duan, J.; Zhou, Z.; An, J.; Gao, F.; Li, Y.; Huai, W. Study on contact characteristics of blade belt grinding based on contact wheel flexibility regulation. J. Mech. Eng. 2023, 59, 354–365. [Google Scholar]
- Hu, C. Research on Diamond Belt Grinding Mechanism and Surface Quality of SiCp/Al composites. Master’s Thesis, Chongqing University, Chongqing, China, 2021. [Google Scholar]
- Kong, X.; Hu, G.; Liu, B.; Dong, Z.; Ci, Y.; Wang, M. Optimisation analysis of cutting force and surface roughness in titanium alloy turning. Tool Technol. 2022, 56, 20–25. [Google Scholar]
- Liu, C.; Wu, L.; Yang, F.; Hong, K.; Zhang, F.; Liu, X. Conditional impact analysis method based on the comparison of interval values of distribution parameters. J. Wuhan Eng. Vocat. Tech. Coll. 2021, 33, 1–7. [Google Scholar]
- Wang, X. A three-parameter interval grey number multi-attribute decision-making method based on improved TOPSIS. Syst. Sci. Math. 2021, 41, 1328–1338. [Google Scholar]
- Qiao, H.; Hu, S.; Xiang, Y.; Liu, S.; Zhang, L. Research on the Analysis and Prediction Model of Machining Parameters of Titanium Alloy by Abrasive Belt. Metals 2023, 13, 1085. [Google Scholar] [CrossRef]
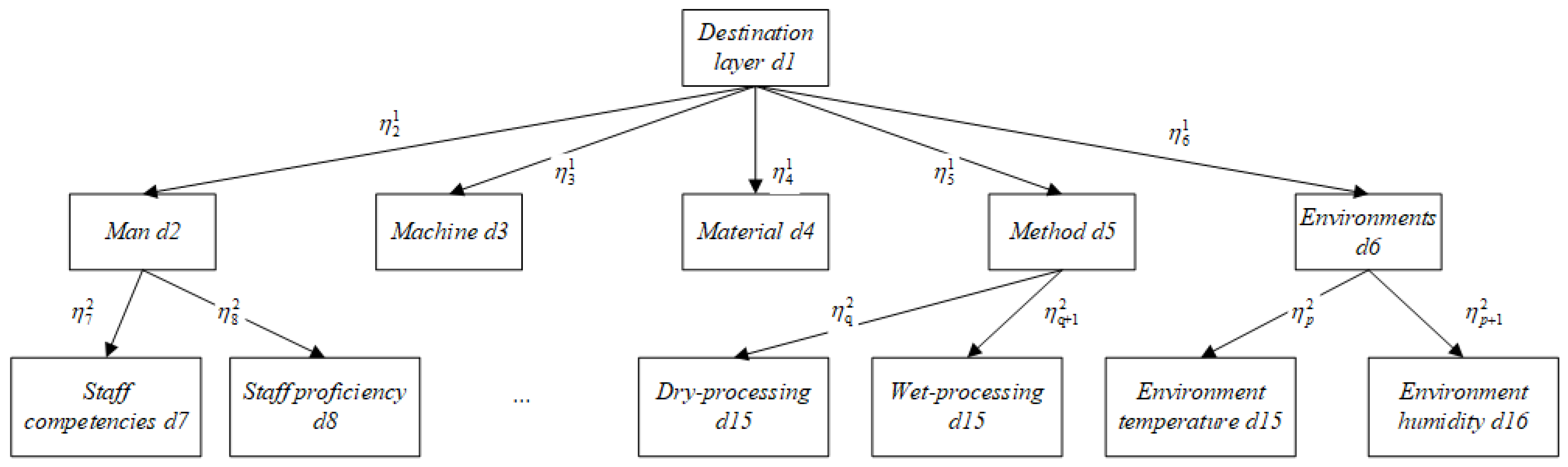






| Factor | Man | Machine | Material | Method | Environment | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Employee Skills (D1) | Employee Proficiency (D2) | Feed Rate (D3) | Grinding Pressure (D4) | Belt Line Speed (D5) | Grit Size of Abrasive Belts (D6) | Dry Processing (D7) | Wet Processing (D8) | Processing Environment Temperature (D9) | Processing Environment Humidity (D10) | |
| Norm | 60% | 80% | 50% | 90% | 80% | 60% | 60% | 50% | 70% | 50% |
| Factor | Human | Machine | Material | Method | Environment | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Employee Skill (D1) | Employee Proficiency (D2) | Feed Rate (D3) | Grinding Pressure (D4) | Belt Line Speed (D5) | Grit Size of Abrasive Belts (D6) | Dry Processing (D7) | Wet Processing (D8) | Processing Environment Temperature (D9) | Processing Environment Humidity (D10) | |
| Norm | 11.3% | 10.1% | 6.1% | 9.1% | 10.6% | 22.6% | 6.2% | 8.3% | 6.4% | 5.4% |
| Abrasive Belt Model | Abrasive Material | Abrasive Grain Size | Abrasive Belt Size (Circumference × Width) |
|---|---|---|---|
| TJ113 | Aluminium oxide | 80# | 1510 mm × 25 mm |
| TJ113 | Aluminium oxide | 120# | 1510 mm × 25 mm |
| TJ113 | Aluminium oxide | 150# | 1510 mm × 25 mm |
| No. | P | Vs | F | Ra |
|---|---|---|---|---|
| 1 | 80# | 10 | 5 | 0.863 |
| 2 | 80# | 15 | 10 | 0.662 |
| 3 | 80# | 20 | 15 | 0.573 |
| 4 | 120# | 10 | 10 | 0.491 |
| 5 | 120# | 15 | 15 | 0.469 |
| 6 | 120# | 20 | 5 | 0.658 |
| 7 | 150# | 10 | 15 | 0.452 |
| 8 | 150# | 15 | 5 | 0.579 |
| 9 | 150# | 20 | 10 | 0.434 |
| Process Parameters | Stable Domain | Unstable Domain |
|---|---|---|
| Abrasive particle size P(#) | [120, 150] | [80, 120] |
| Abrasive belt line speed Vs (m/s) | [15, 20] | [10, 15] |
| Grinding pressure F(N) | [10, 15] | [5, 10] |
| Process Parameter | Preferred Interval for Process Parameters | Stable or Unstable Domains | Surface Roughness Variation Range |
|---|---|---|---|
| Abrasive particle size, P(#) | [120, 150] | Stable domain | 0.488~0.539 |
| Abrasive belt line speed, Vs (m/s) | [15, 20] | Stable domain | 0.555~0.570 |
| Grinding pressure, F(N) | [10, 15] | Stable domain | 0.498~0.529 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, Y.; Hu, S.; Qiao, H. Sensitivity Study of Surface Roughness Process Parameters in Belt Grinding Titanium Alloys. Metals 2023, 13, 1825. https://doi.org/10.3390/met13111825
Shang Y, Hu S, Qiao H. Sensitivity Study of Surface Roughness Process Parameters in Belt Grinding Titanium Alloys. Metals. 2023; 13(11):1825. https://doi.org/10.3390/met13111825
Chicago/Turabian StyleShang, Yueru, Sibo Hu, and Hu Qiao. 2023. "Sensitivity Study of Surface Roughness Process Parameters in Belt Grinding Titanium Alloys" Metals 13, no. 11: 1825. https://doi.org/10.3390/met13111825
APA StyleShang, Y., Hu, S., & Qiao, H. (2023). Sensitivity Study of Surface Roughness Process Parameters in Belt Grinding Titanium Alloys. Metals, 13(11), 1825. https://doi.org/10.3390/met13111825






