Creep–Fatigue Life Estimation of Gr.91 Steel and Its Welded Joints
Abstract
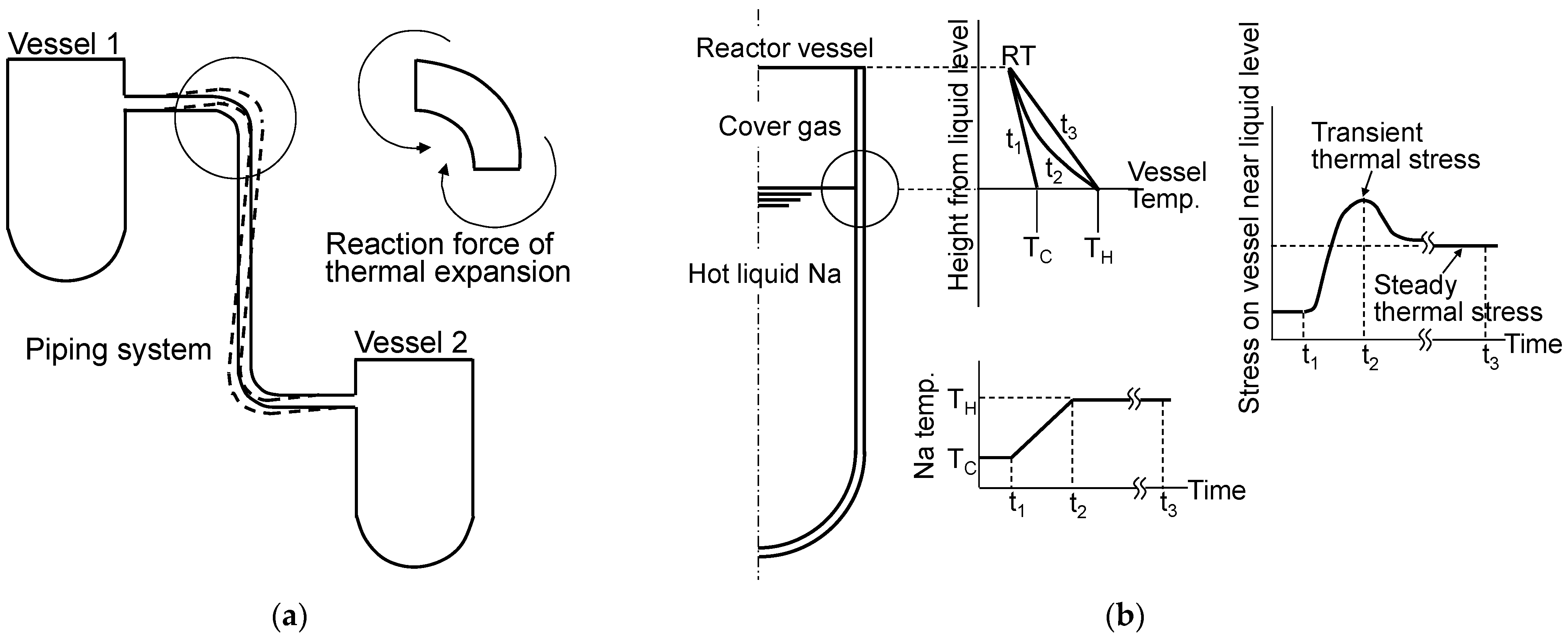
:1. Introduction
2. Creep–Fatigue Life Estimation of Gr.91 Steel
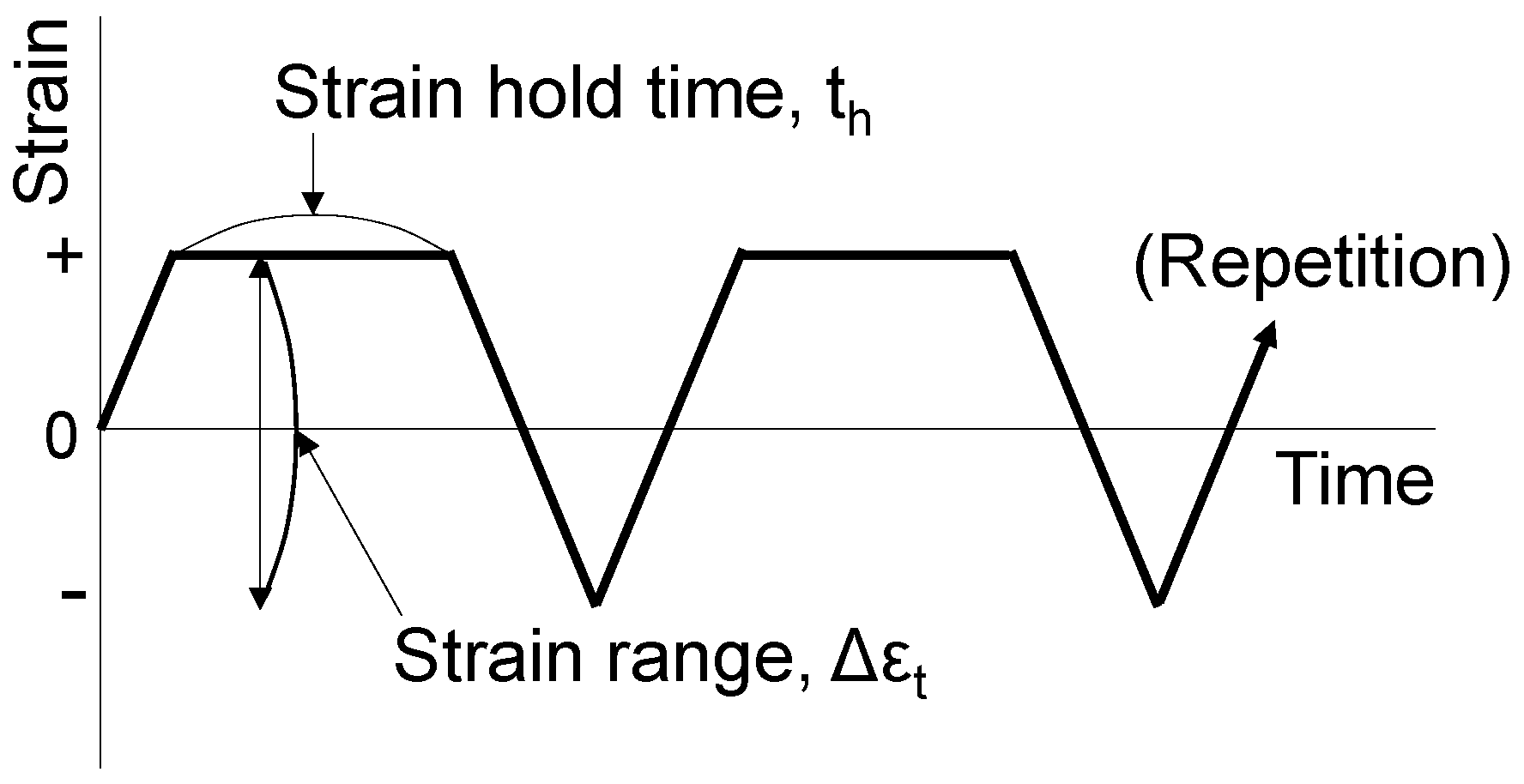
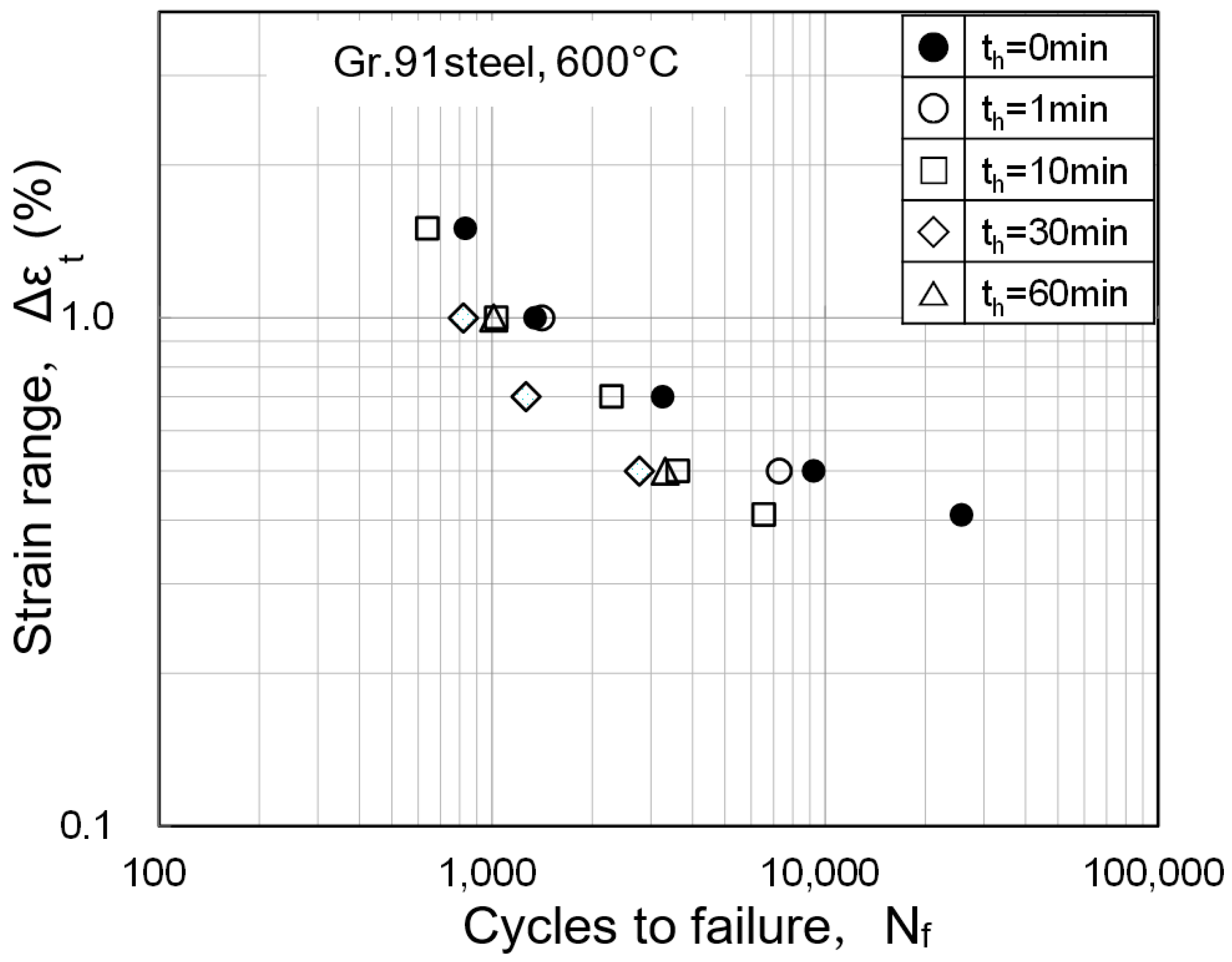
2.1. Creep–Fatigue Test Results
2.2. Creep–Fatigue Life Estimation Results
2.3. Discussions of the Creep–Fatigue Interaction
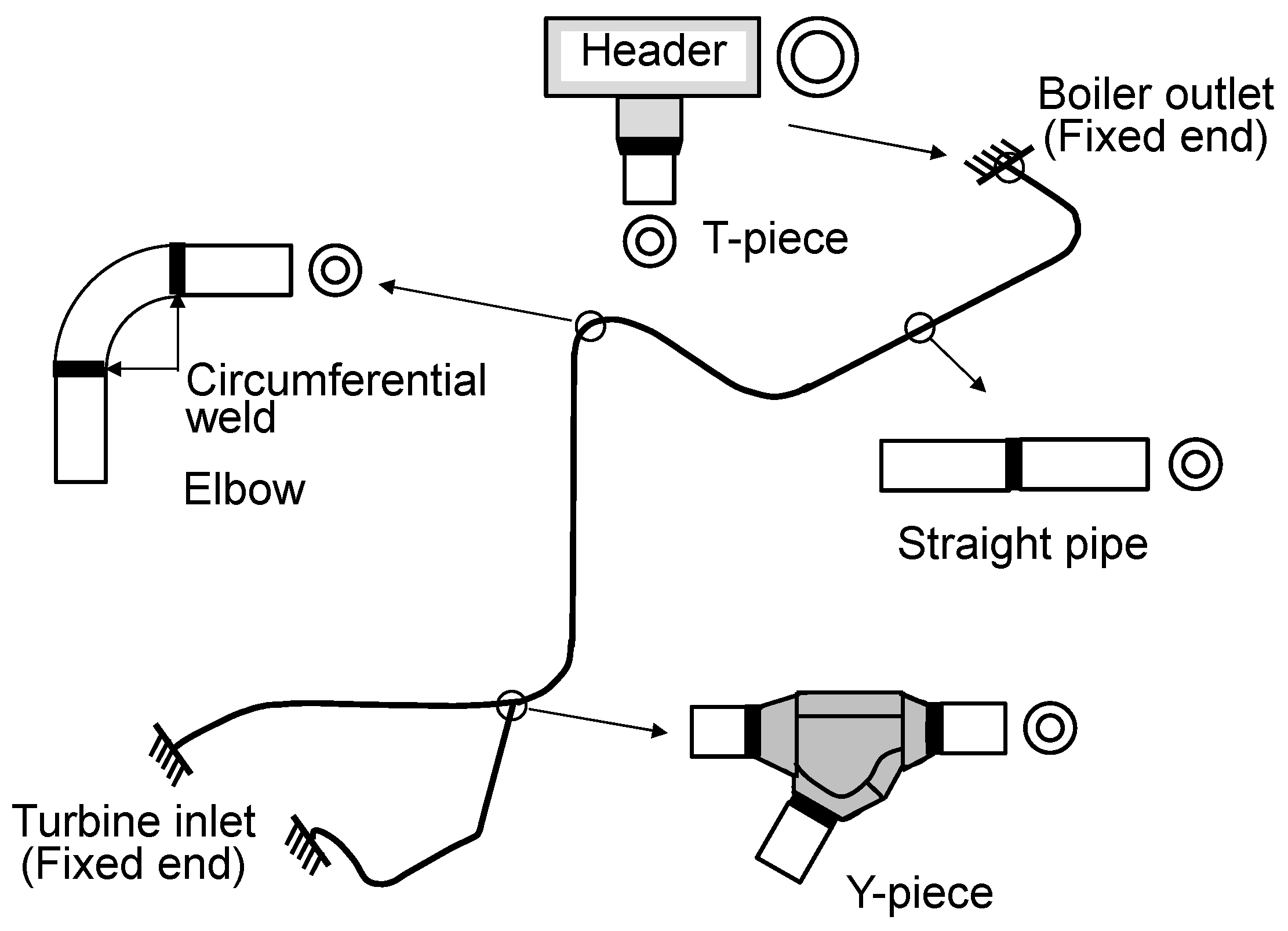
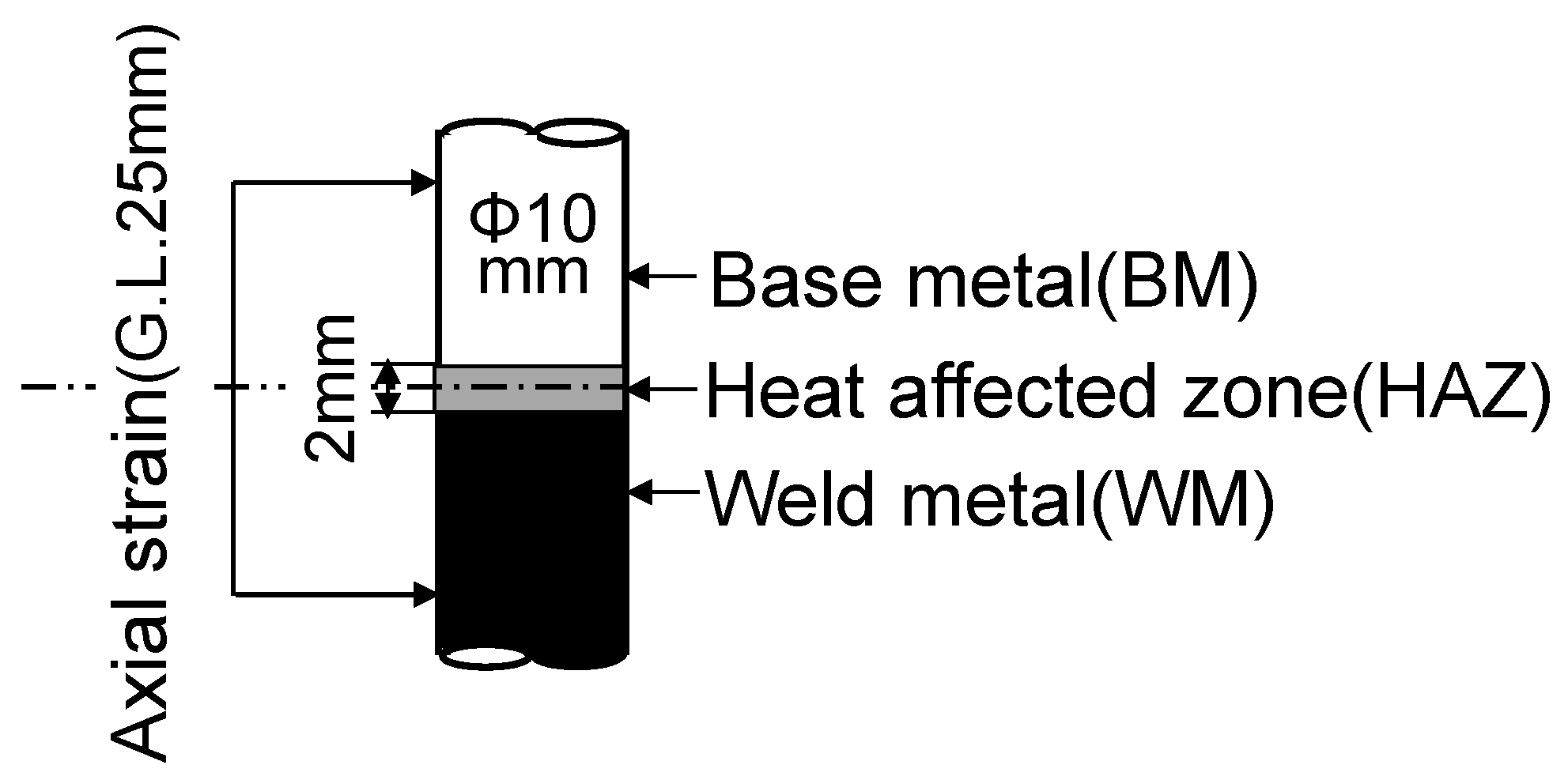
3. Creep–Fatigue Life Estimation of Gr.91 Steel Welded Joints
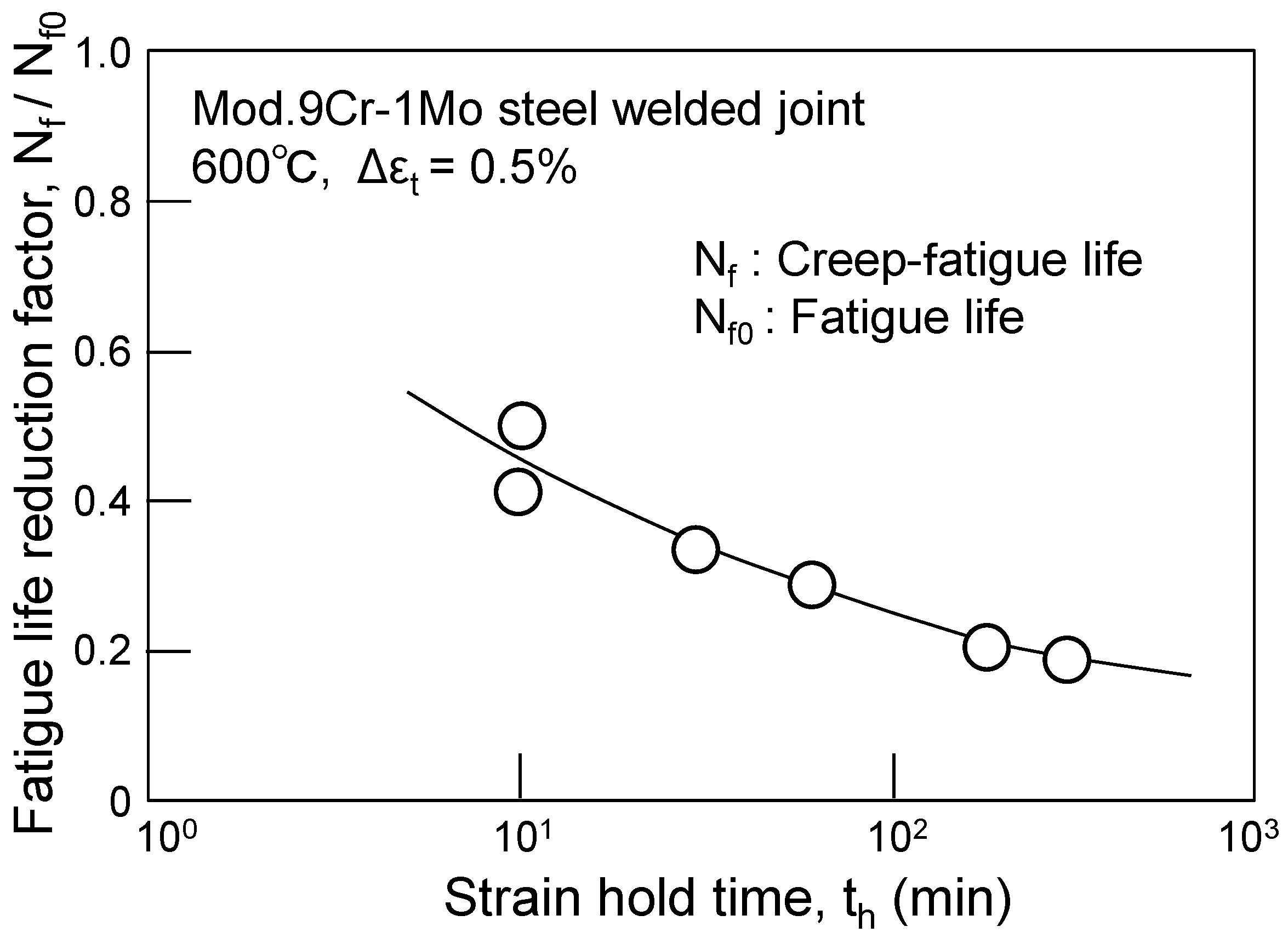
3.1. Creep–Fatigue Test Results
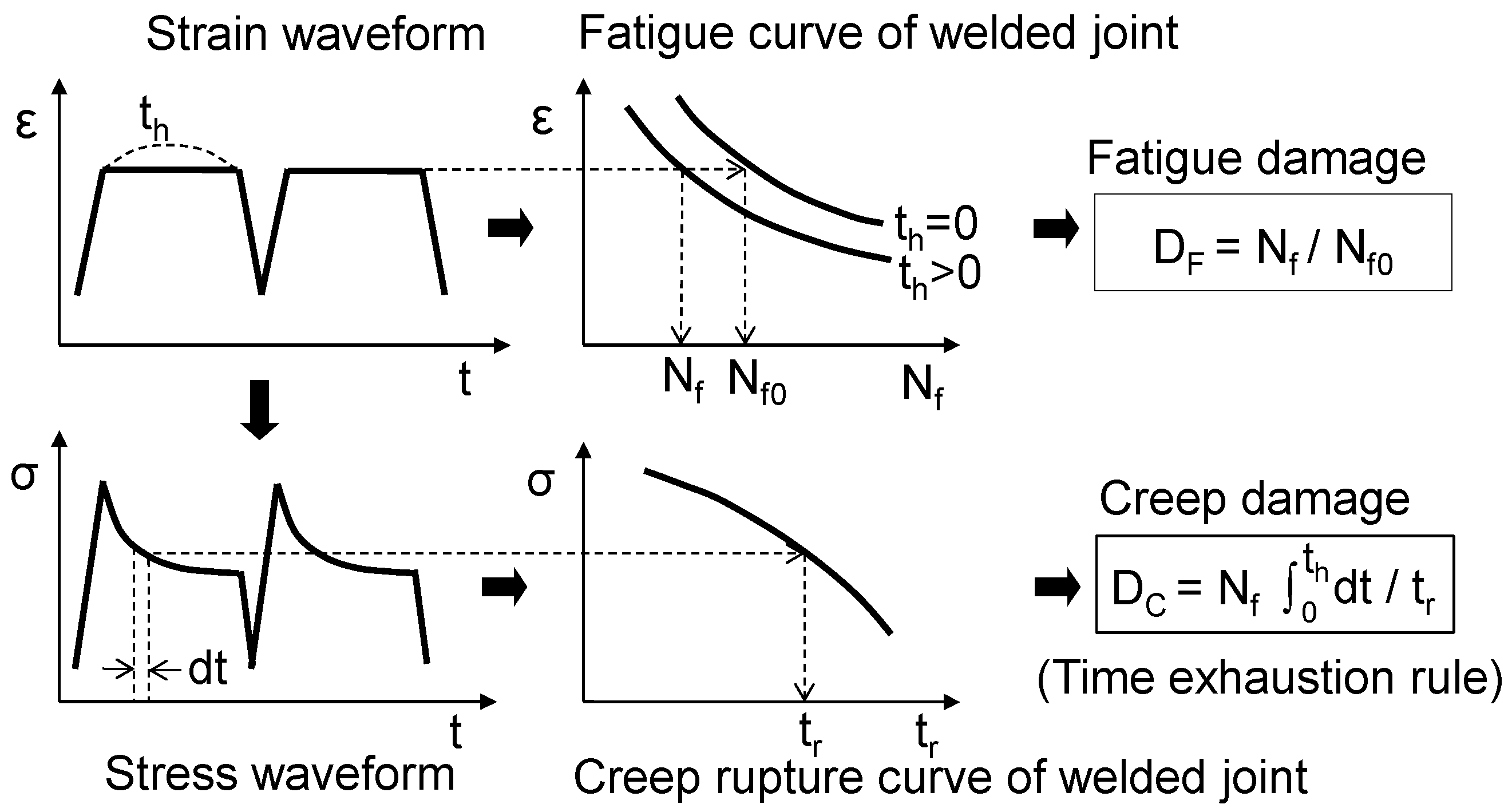
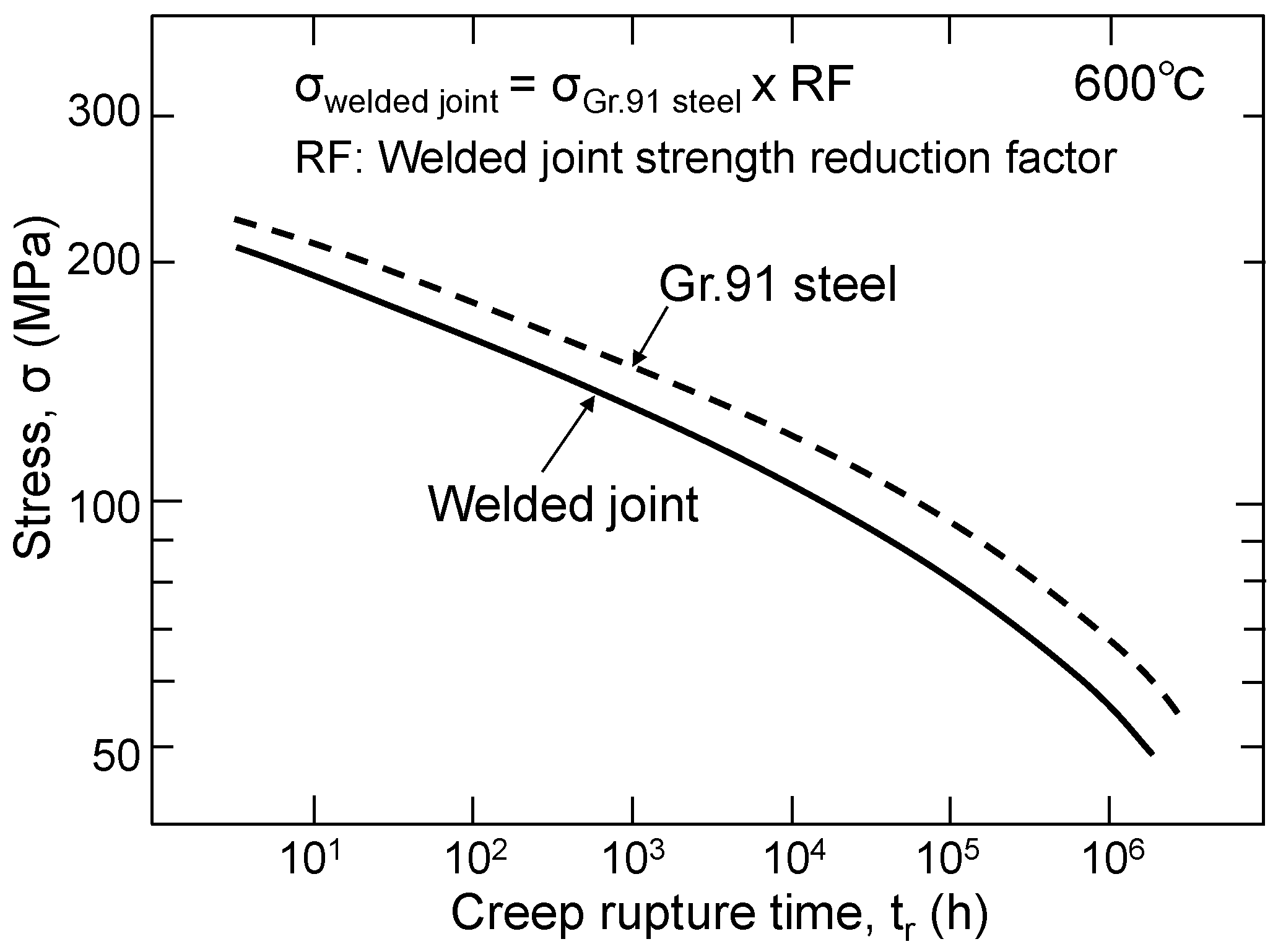
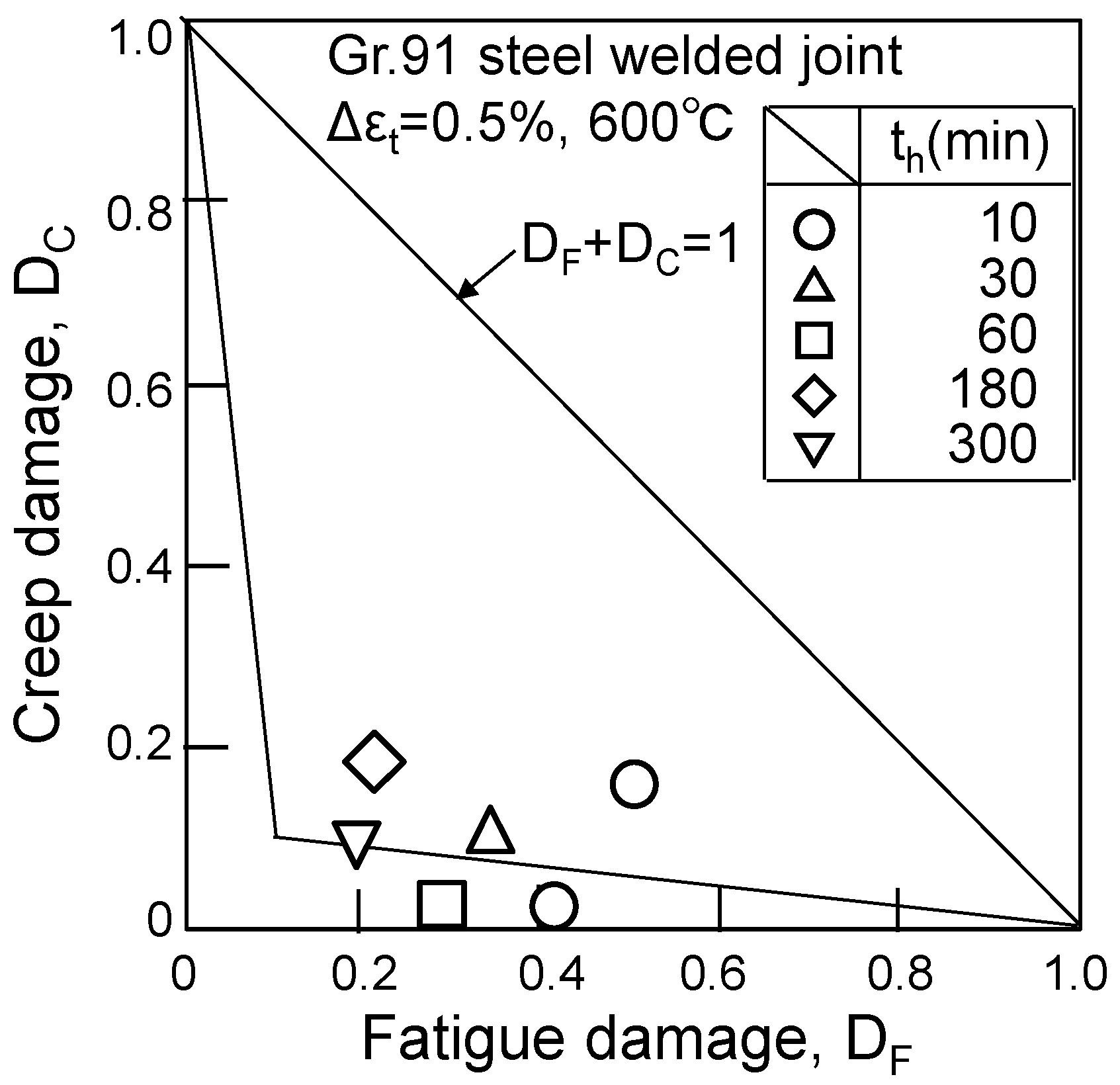
3.2. Creep–Fatigue Life Estimation Results
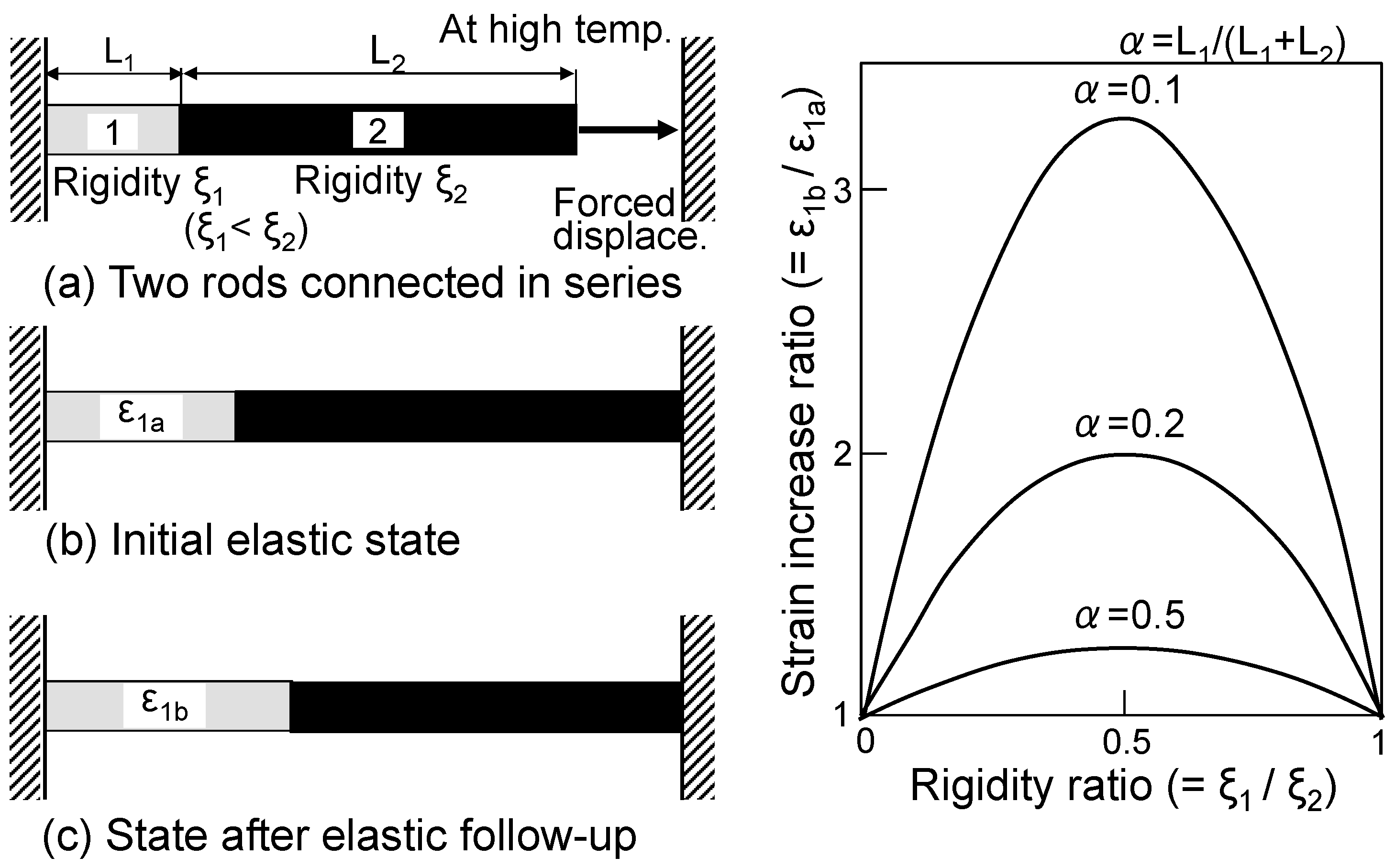
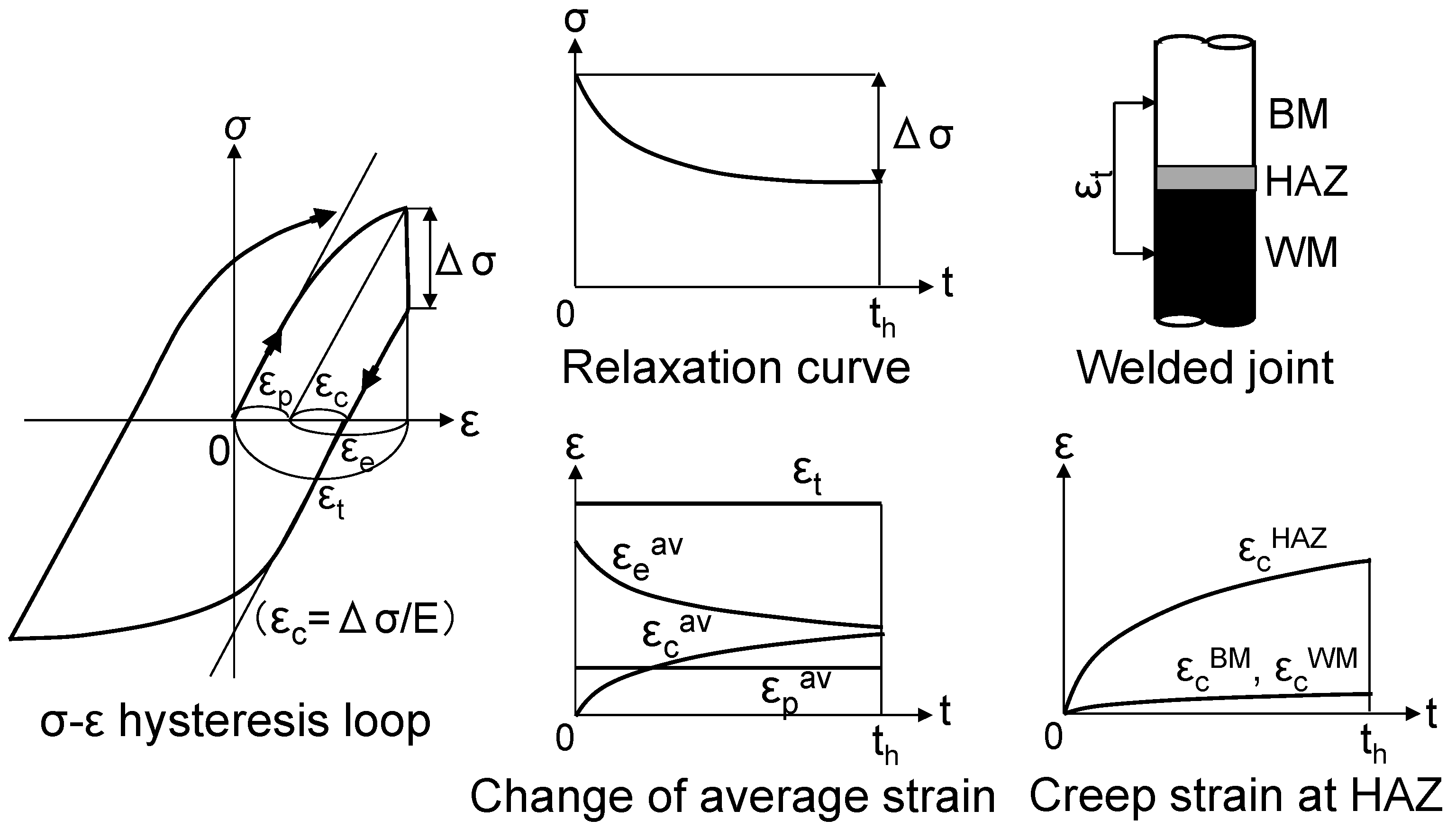
3.3. Discussion of the Elastic Follow-Up Phenomena
4. Conclusions
- (1)
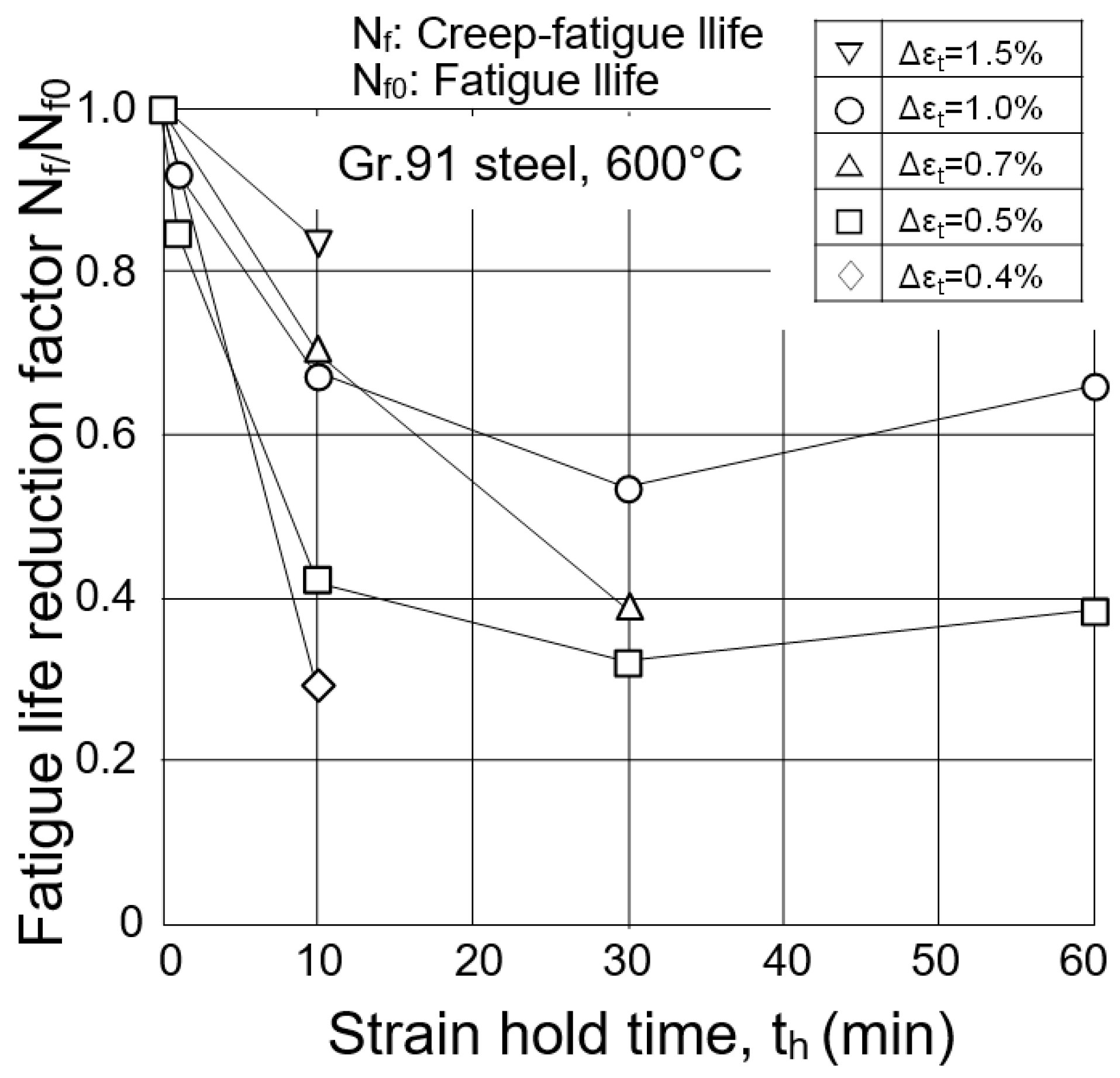
- In a series of creep–fatigue tests of Gr.91 steel at 600 °C, the fatigue life decreased with the tensile strain holding, and the smaller the strain range, the smaller the fatigue life reduction factor. The minimum life reduction factor was approximately 0.3. Furthermore, the longer the strain hold time, the smaller the fatigue life reduction factor, but it tended to saturate at a strain holding of about 30 min.
- (2)
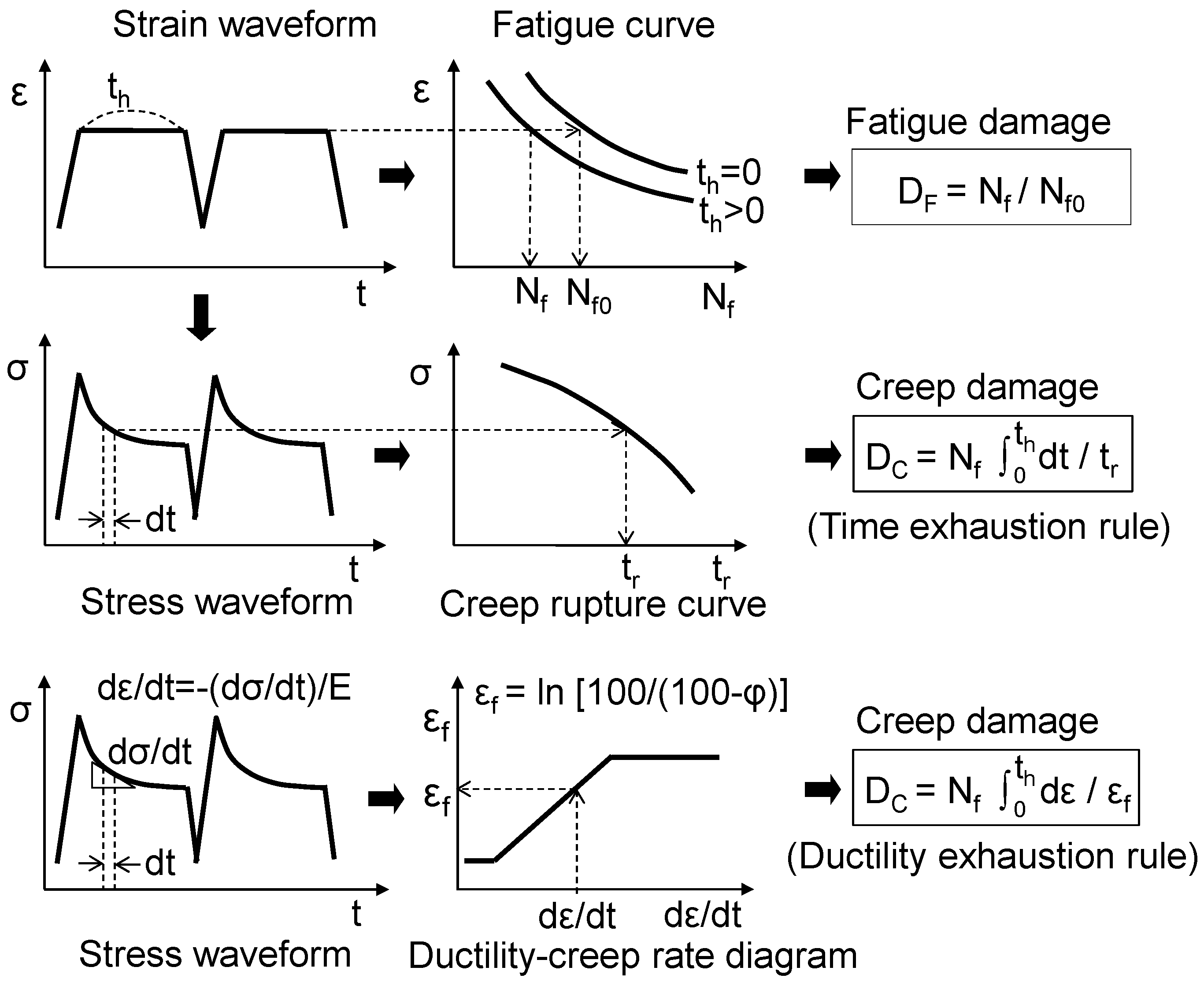
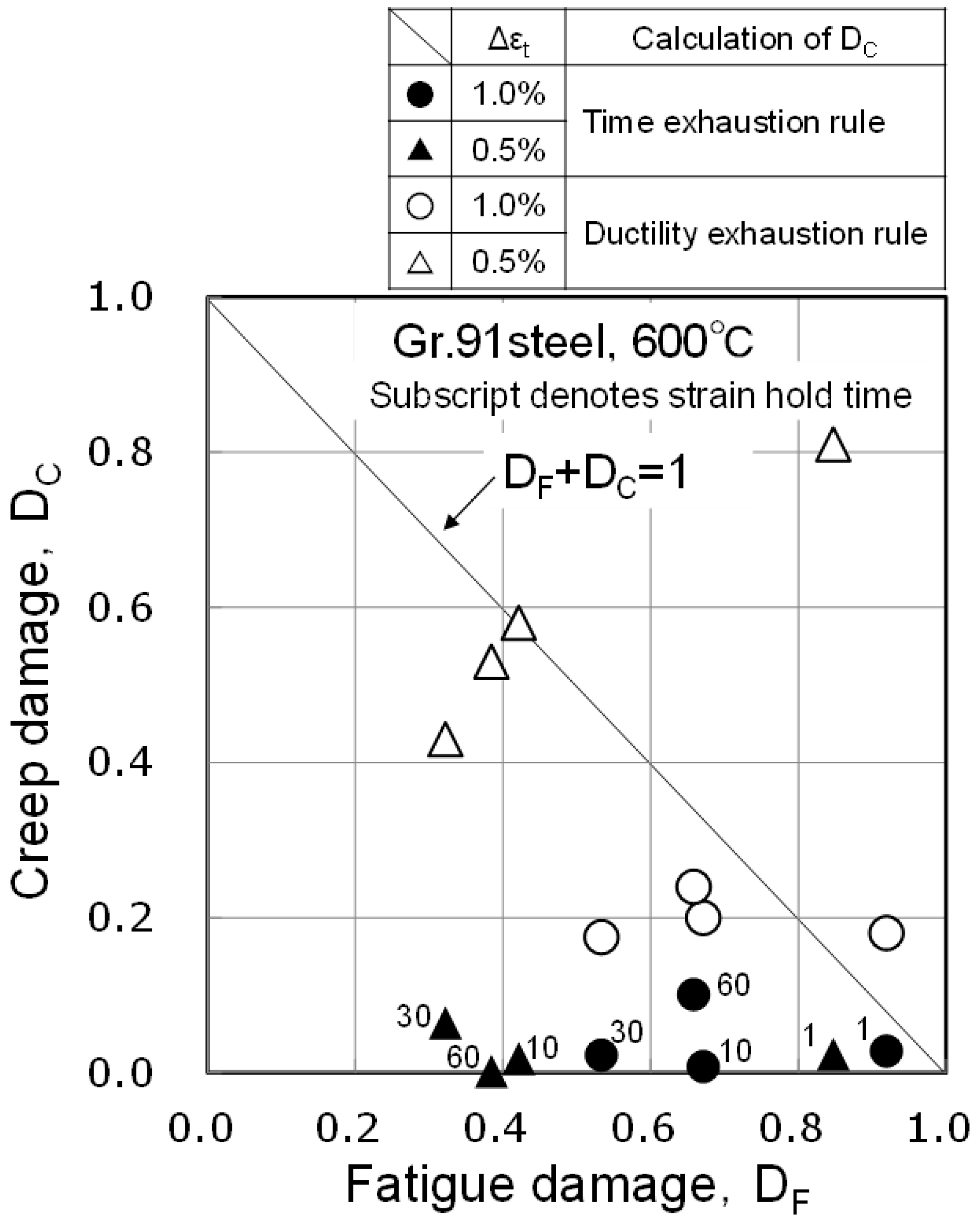
- The test pieces fractured when the linear summation of the accumulated fatigue damage and the creep damage calculated using the time exhaustion rule was much less than 1. One of the reasons is that the creep damage was underestimated, but another important reason is that the effect of the creep–fatigue interaction was not considered. In this material at 600 °C, the damage due to the creep–fatigue interaction is considered to be quite large.
- (3)
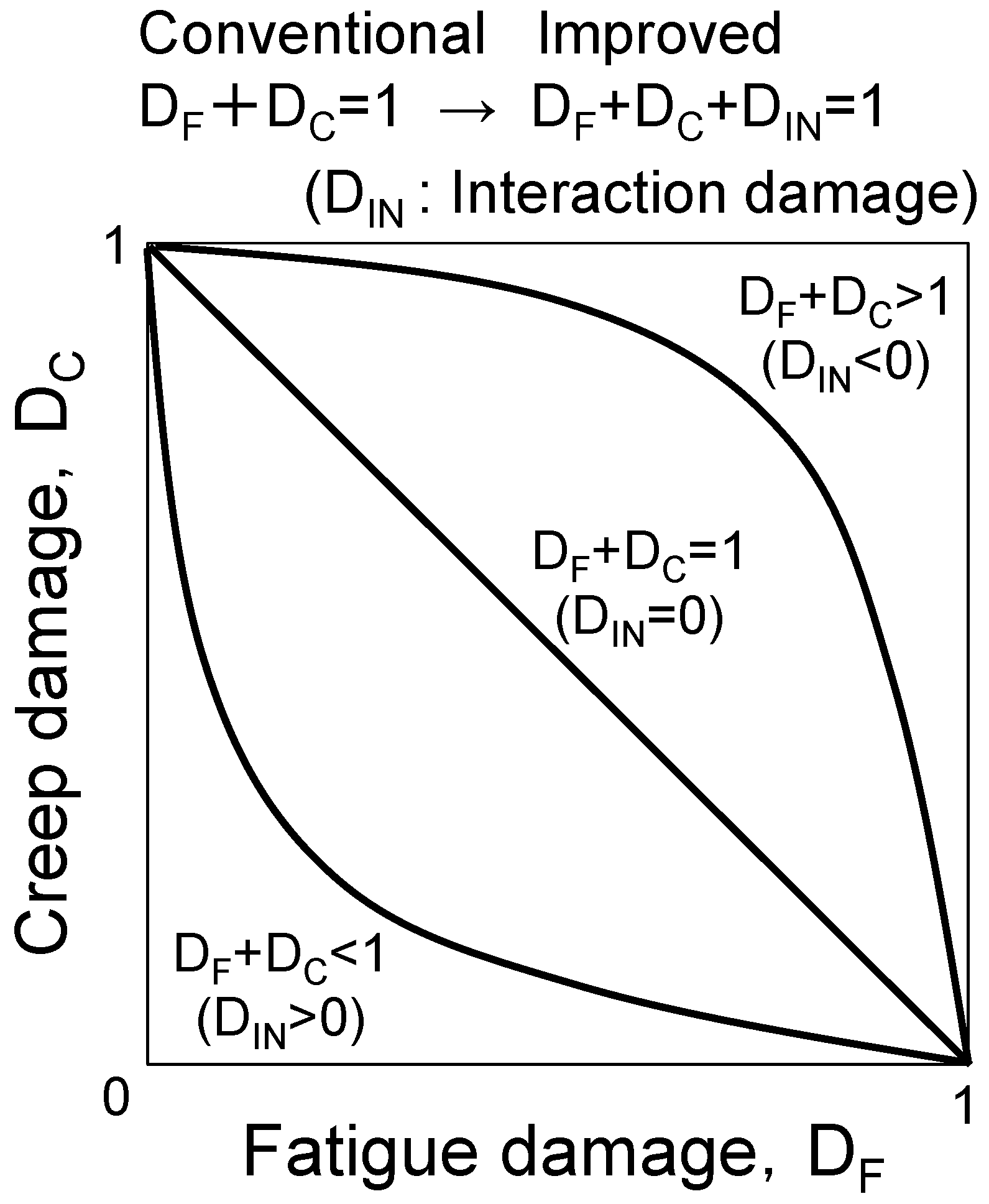
- The creep–fatigue life should be estimated using the linear summation rule of the fatigue damage, the creep damage, and the creep–fatigue interaction damage. In the future, it will be necessary to clarify the creep–fatigue interaction mechanism and define the damage value.
- (4)
- In a series of creep–fatigue tests of Gr.91 steel welded joints in the strain range of 0.5% at 600 °C, the fatigue life decreased with the tensile strain holding. The longer the strain hold time, the lower the fatigue life, and the minimum fatigue life reduction factor was approximately 0.2 in the case of the 300 min strain holding. All the test pieces fractured in the fine-grained HAZ.
- (5)
- The creep–fatigue life of the welded joint was estimated using the linear damage summation rule of the fatigue damage and the creep damage of the HAZ, which was the fracture location. All the test pieces fractured when the linear summation of the fatigue damage and the creep damage was considerably less than 1. One possible reason is the influence of the elastic follow-up phenomena peculiar to welded joints.
- (6)
- The creep strain in the HAZ may increase due to the transfer of the elastic strain from the base metal and the weld metal according to the elastic follow-up phenomena during the strain holding. In the future, it will be important to quantitatively evaluate the increase in the creep strain in the HAZ in order to estimate the creep–fatigue life of welded joints.
Funding
Data Availability Statement
Conflicts of Interest
References
- Wada, Y. Design of elevated temperature components 5, FBR. J. Soc. Mater. Sci. Jpn. 1987, 36, 127–132. [Google Scholar]
- Bender, T.; Klenk, A.; Weihe, S. Creep-fatigue assessment of martensitic welds based on numerically determined local deformation. Mater. Test. 2023, 65, 815–823. [Google Scholar] [CrossRef]
- Ando, M.; Takaya, S. Creep–fatigue evaluation method for weld joints of Mod.9Cr–1Mo steel. Part I: Proposal of the evaluation method based on finite element analysis and uniaxial testing. Nucl. Eng. Des. 2017, 323, 463–473. [Google Scholar] [CrossRef]
- Veerababu, J.; Goyal, S.; Nagesha, A. Studies on creep-fatigue interaction behaviour of Grade 92 steel and its weld joints. Int. J. Fatigue 2021, 149, 106307. [Google Scholar] [CrossRef]
- Egner, W.; Sulich, P.; Mroziński, S.; Egner, H. Modelling thermo-mechanical cyclic behaviour of P91 steel. Int. J. Plast. 2020, 135, 102820. [Google Scholar] [CrossRef]
- Nonaka, I. Creep-Fatigue Life Estimation of Circumferential Welds in Thermal High Energy Piping Systems. Manuscript Submitted for Publication. Available online: https://www.tandfonline.com/journals/ymht20 (accessed on 1 May 2023).
- Nonaka, I.; Torihata, S.; Kihara, S. Prediction of creep-fatigue lives for FBR and boiler materials based on ductility exaustion concept. Mater. Sci. Res. Int. 1997, 3, 44–48. [Google Scholar]
- Nomura, K.; Kubushiro, K. Creep-fatigue property for a long term tensile strain hold of Ni-based alloy HR6W. In Proceedings of the 56th Symposium on Strength of Materials at High Temperature, Okazaki, Japan, 6–7 December 2018; pp. 118–121. [Google Scholar]
- NIMS Fatigue Data Sheet, No.113; National Institute for Materials Science: Tsukuba, Japan, 2011.
- Kobayashi, K.; Hayakawa, M.; Kimura, M. Creep-fatigue interaction properties of Ni-based superalloy 617. Acta Met. Sin. (Engl. Lett.) 2011, 24, 115–131. [Google Scholar]
- Robinson, E.L. Effect of Temperature Variation on the Long Time Rupture Strength of Steels. Trans. ASME 1952, 74, 777. [Google Scholar] [CrossRef]
- Taira, S. IUTAM Colloquium; Springer: New York, NY, USA, 1962; p. 96. [Google Scholar]
- Nonaka, I.; Kitagawa, M.; Torihata, S. Feasibility study on ductility exhaustion approach for creep-fatigue damage assessment of FBR 316 stainless steel using published data. J. Soc. Mater. Sci. Jpn. 1995, 44, 41–45. [Google Scholar] [CrossRef]
- Takahashi, Y.; Yaguchi, M. Modification of ductility exhaustion-type creep-fatigue life prediction method based on re-definition of creep damage and application to high-chromium steels. J. Soc. Mater. Sci. Jpn. 2005, 54, 168–173. [Google Scholar] [CrossRef]
- Spindler, M.W.; Payten, W.M. Advanced ductility exhaustion methods for the calculation of creep damage during creep-fatigue cycling. J. ASTM Int. Sel. Tech. Pap. 1539 2011, 8, 102–127. [Google Scholar]
- An Assessment Procedure for High Temperature Response of Structures, R5; Nuclear Electric: Berkeley, UK, 1995; Issue 1.
- Yagi, K.; Kubo, K.; Tanaka, C. Chiaki. Evaluation of creep-fatigue interaction by linear damage rule and appearance of fracture for SUS 304 stainless steel subjected to combined creep-fatigue tests. J. Soc. Mater. Sci. Jpn. 1979, 29, 928–934. [Google Scholar] [CrossRef]
- Kubo, K.; Kanemaru, O.; Yagi, K. Relationship between ceep damage mode and creep-fatigue interaction for SUS 321 steel. J. Soc. Mater. Sci. Jpn. 1993, 42, 1–7. [Google Scholar] [CrossRef]
- Yokobori, T.; Ichikawa, M.; Yokobori, A.T., Jr. Interaction of Fatigue and creep. J. Jpn. Soc. Strength Fract. Mater. 1973, 9, 13–20. [Google Scholar] [CrossRef]
- Nonaka, I.; Torihata, S.; Kihara, S.; Umaki, H. Creep-fatigue life evaluation for weldments of modified 9Cr-1Mo steel at boiler temperature. Mater. High Temp. 1998, 15, 107–111. [Google Scholar] [CrossRef]
- Brinkman, C.R.; Maziasz, P.J.; Keys, B.L.P.; Upiton, H.D. Oak Ridge National Laboratory Report, No. ORNL/9Cr/90-1; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1990.
- Ando, Y.; Okabayashi, K. Structural Design of Nuclear Plant; University of Tokyo Press: Tokyo, Japan, 1977; pp. 192–197. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nonaka, I. Creep–Fatigue Life Estimation of Gr.91 Steel and Its Welded Joints. Metals 2023, 13, 1880. https://doi.org/10.3390/met13111880
Nonaka I. Creep–Fatigue Life Estimation of Gr.91 Steel and Its Welded Joints. Metals. 2023; 13(11):1880. https://doi.org/10.3390/met13111880
Chicago/Turabian StyleNonaka, Isamu. 2023. "Creep–Fatigue Life Estimation of Gr.91 Steel and Its Welded Joints" Metals 13, no. 11: 1880. https://doi.org/10.3390/met13111880
APA StyleNonaka, I. (2023). Creep–Fatigue Life Estimation of Gr.91 Steel and Its Welded Joints. Metals, 13(11), 1880. https://doi.org/10.3390/met13111880




