Development of a High-Frequency Test System to Study the Wear of Ultrasonic Welding Tools
Abstract
:1. Introduction
2. Materials and Methods
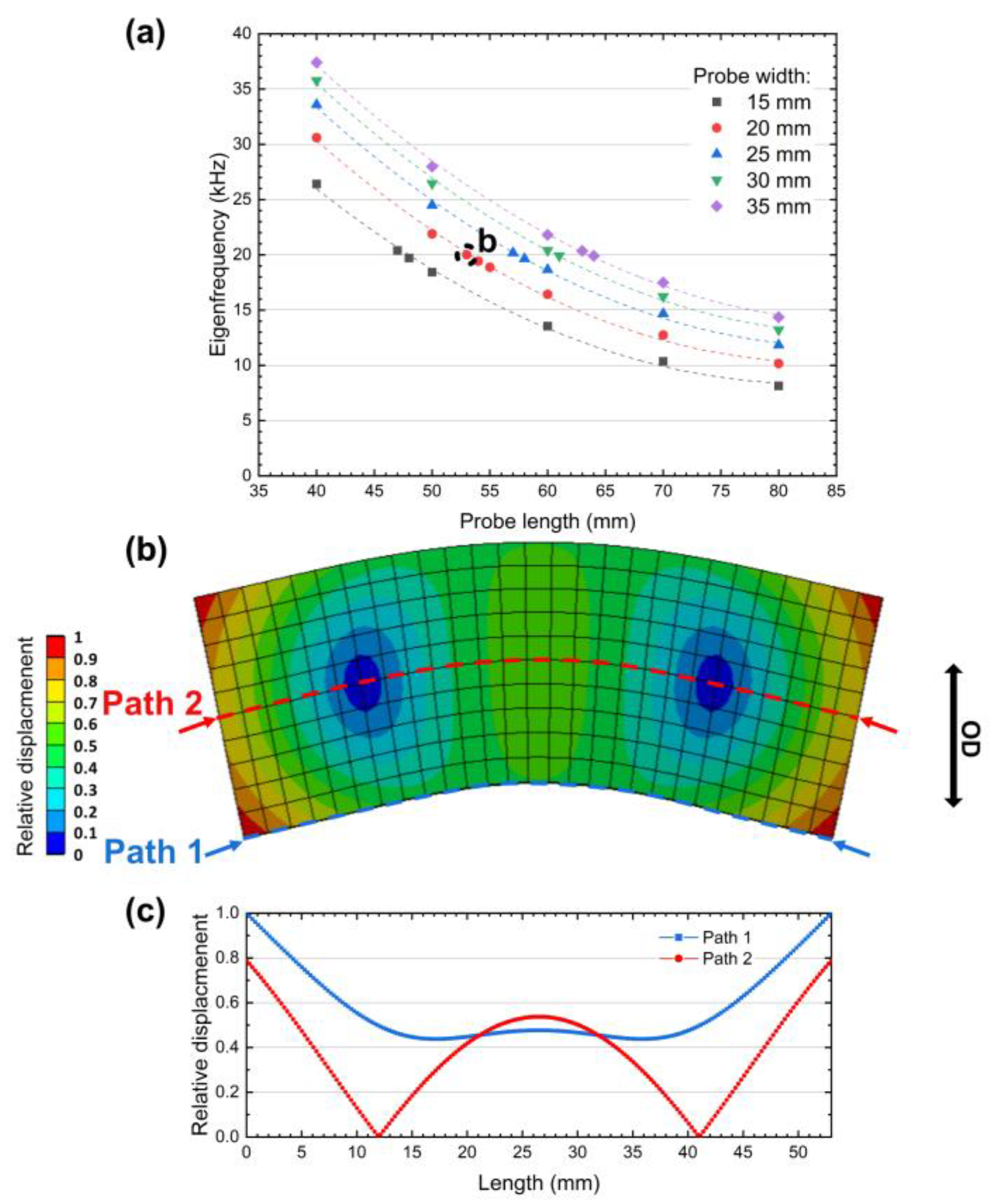
2.1. Base Material and Specimen Design
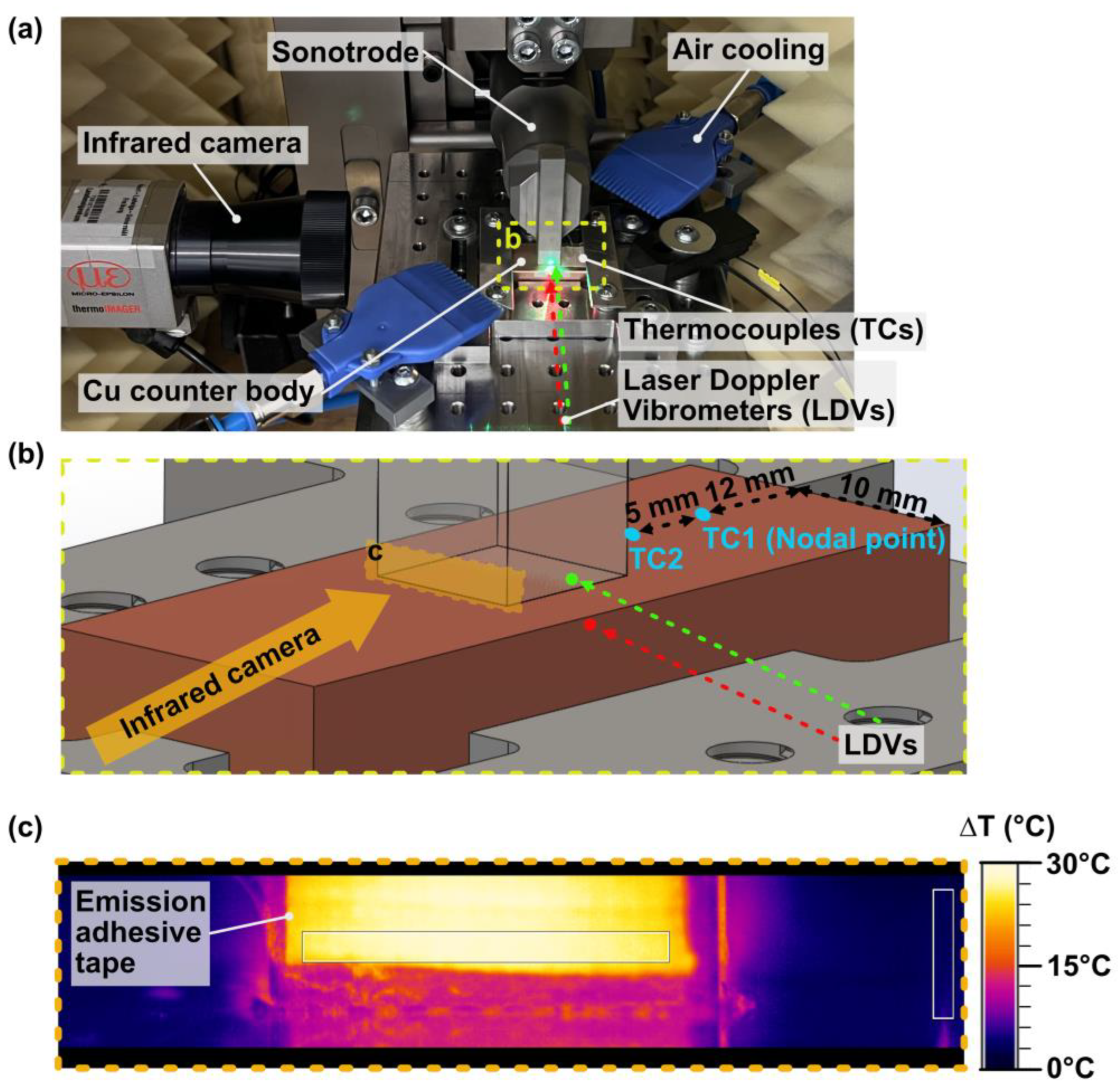
2.2. Test System with In-Situ Measurements
3. Results and Discussion
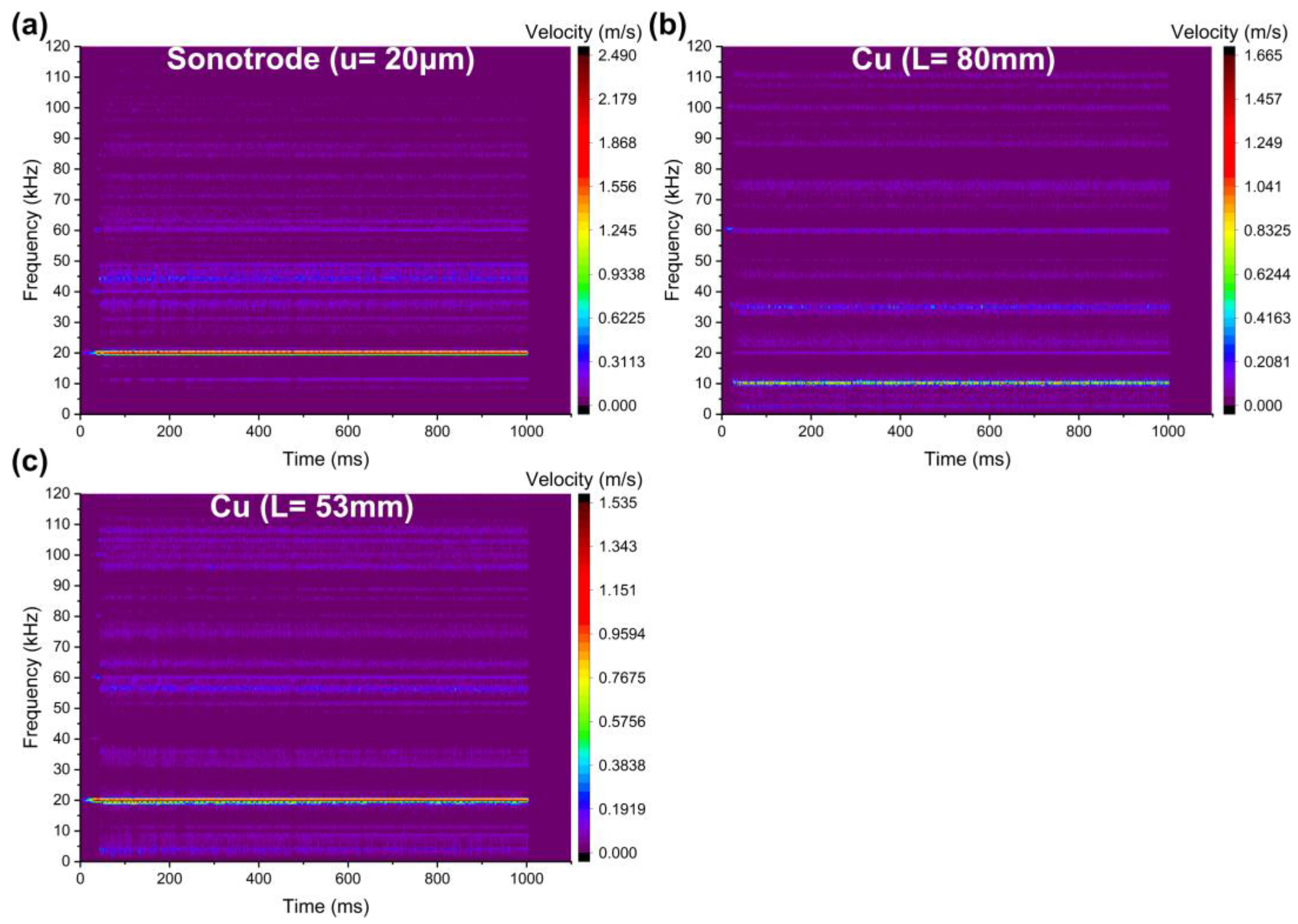
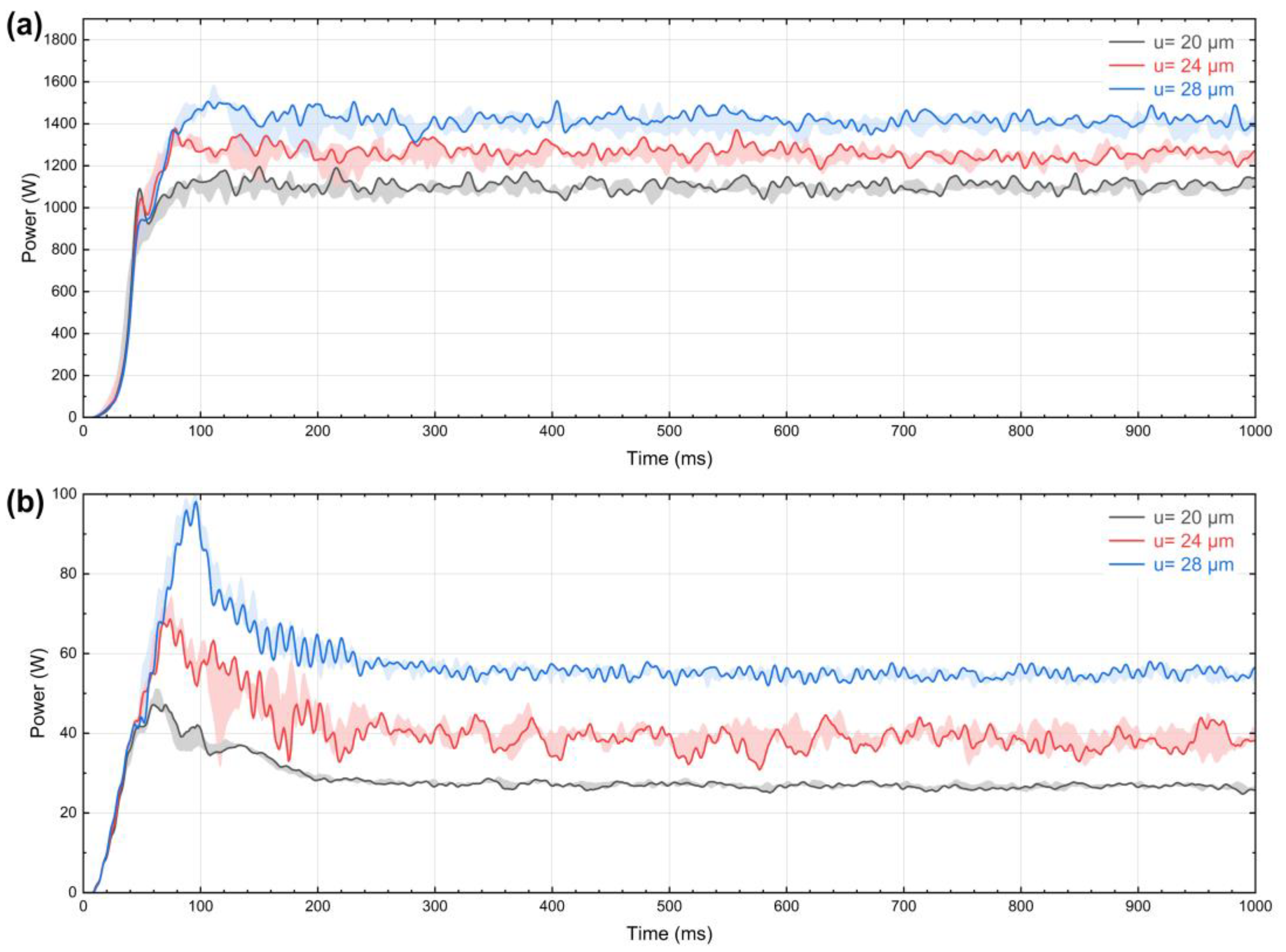
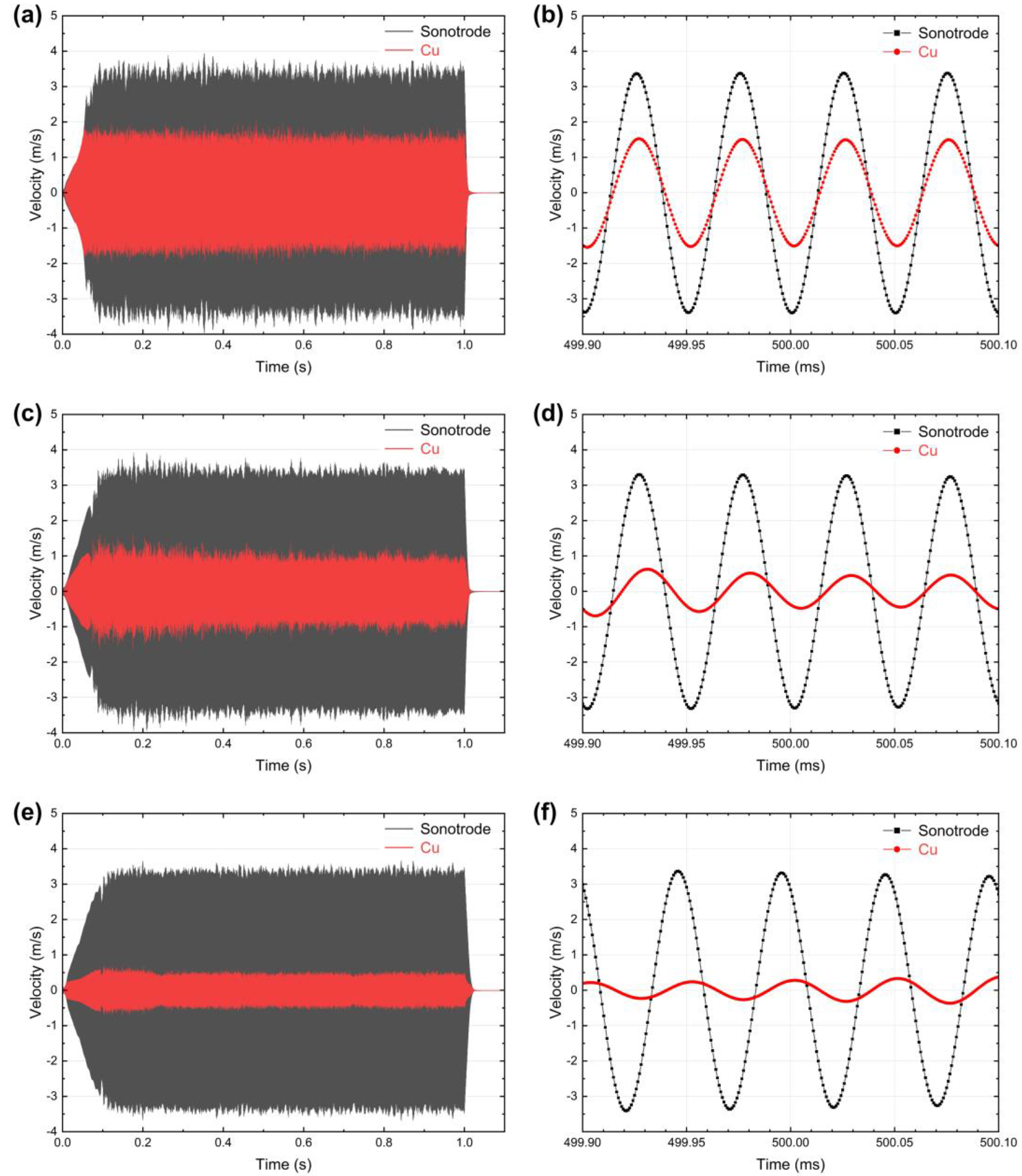
3.1. Validation of the Oscillation Behavior
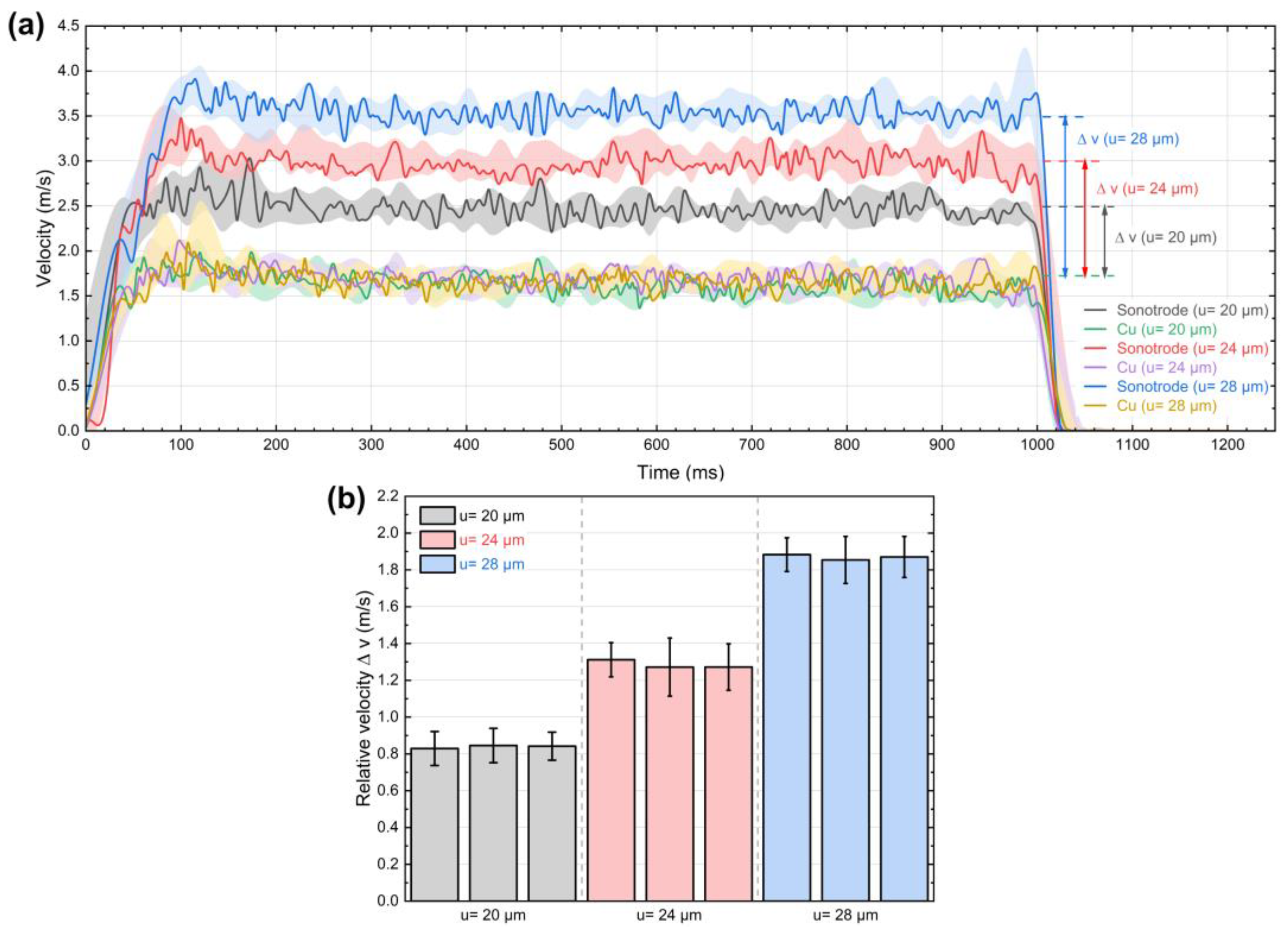
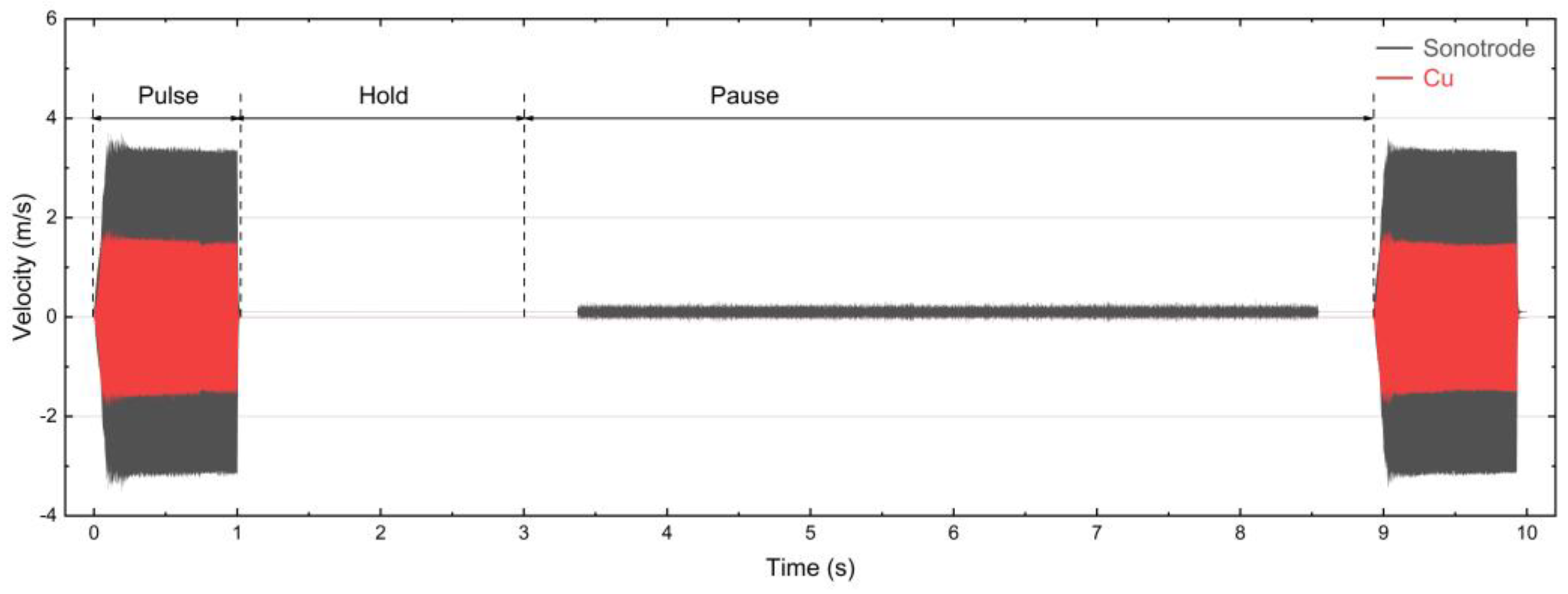
3.2. Relative Motion at the Sonotrode/Cu Interface
3.3. Estimation of the Frictional Force
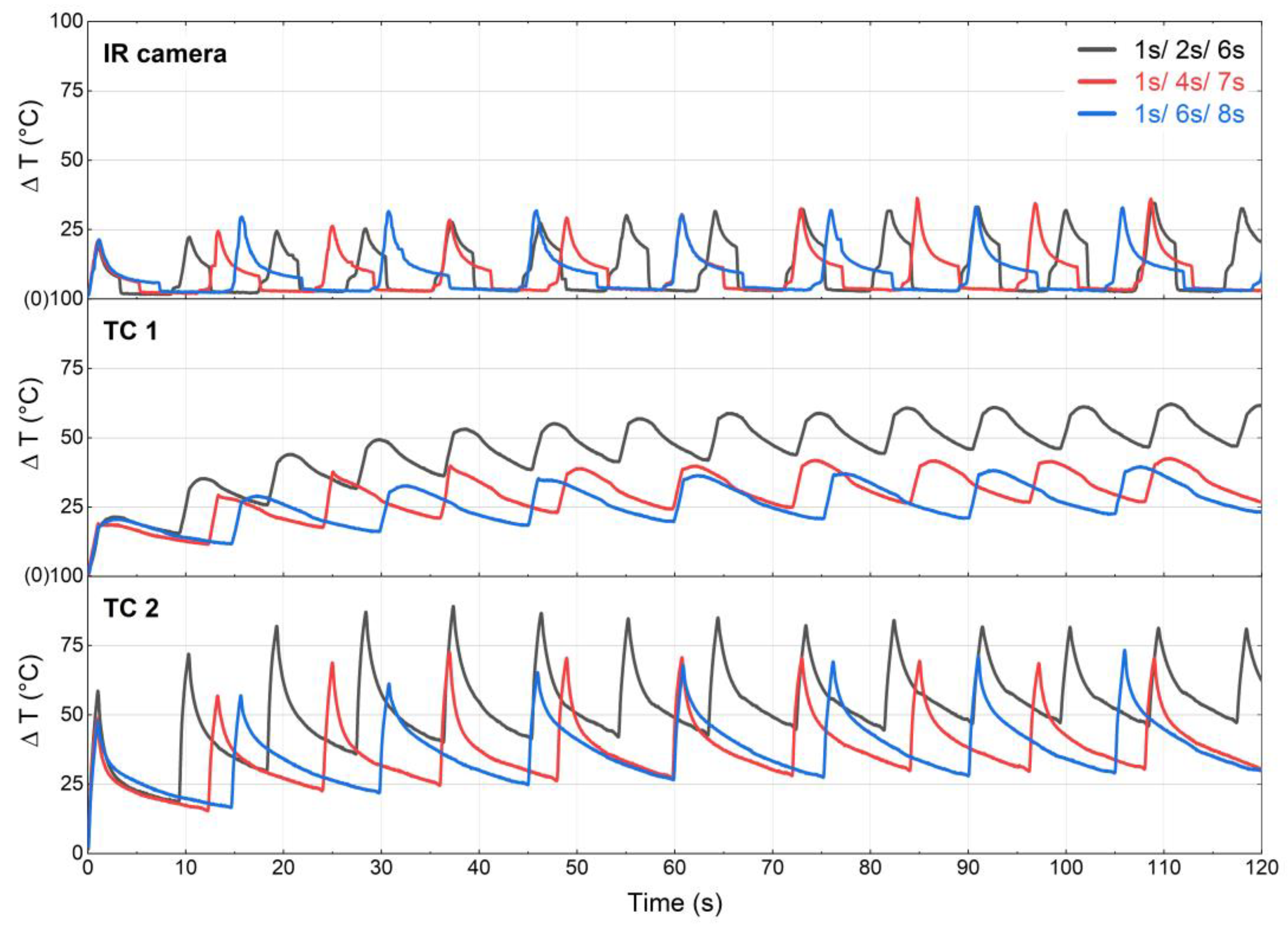
3.4. Temperature Development during Continuous Testing
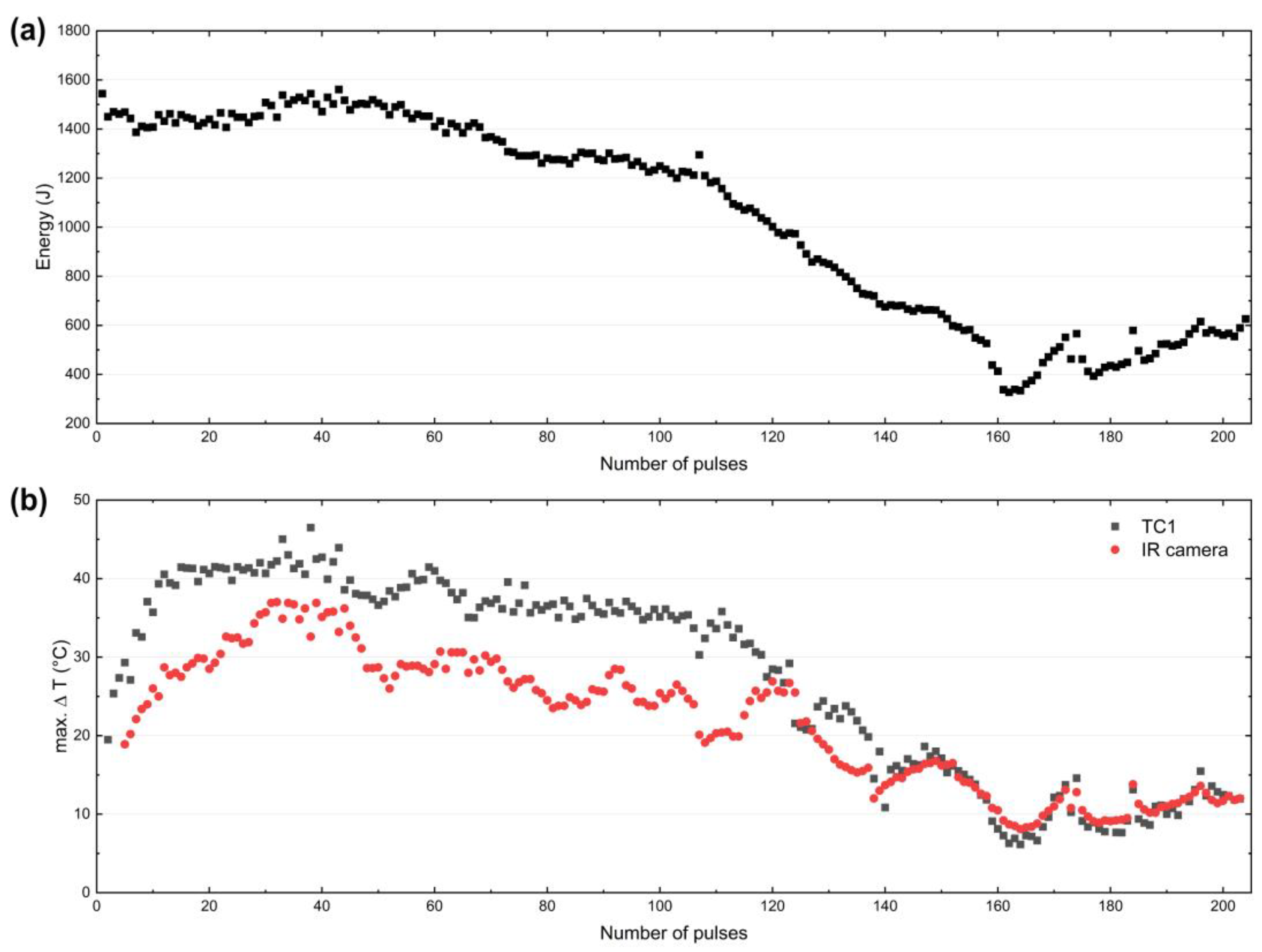
3.5. Failure of the Cu Counter Body
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lambiase, F.; Balle, F.; Blaga, L.A.; Liu, F.; Amancio-Filho, S.T. Friction-Based Processes for Hybrid Multi-Material Joining. Compos. Struct. 2021, 266, 113828. [Google Scholar] [CrossRef]
- Martinsen, K.; Hu, S.J.; Carlson, B.E. Joining of Dissimilar Materials. CIRP Ann. Manuf. Technol. 2015, 64, 679–699. [Google Scholar] [CrossRef]
- Zhang, C.; Li, H.; Liu, Q.; Huang, C.; Zhou, K. Ultrasonic Welding of Aluminum to Steel: A Review. Metals 2023, 13, 29. [Google Scholar] [CrossRef]
- Mirza, F.A.; Macwan, A.; Bhole, S.D.; Chen, D.L.; Chen, X.G. Microstructure, Tensile and Fatigue Properties of Ultrasonic Spot Welded Aluminum to Galvanized High-Strength-Low-Alloy and Low-Carbon Steel Sheets. Mater. Sci. Eng. A 2017, 690, 323–336. [Google Scholar] [CrossRef]
- Macwan, A.; Kumar, A.; Chen, D. Ultrasonic Spot Welded 6111-T4 Aluminum Alloy to Galvanized High-Strength Low-Alloy Steel: Microstructure and Mechanical Properties. Mater. Des. 2017, 113, 284–296. [Google Scholar] [CrossRef]
- Peng, H.; Chen, D.L.; Guo, S.F.; Hong, H.; Zheng, K.H.; Bai, X.F.; Li, D.Y.; Jiang, X.Q. Dissimilar Ultrasonic Spot Welding of Rare-Earth Containing ZEK100 Magnesium-to-Aluminum Alloy with a Zinc Interlayer: Microstructural Evolution and Mechanical Properties. J. Manuf. Process. 2023, 92, 422–434. [Google Scholar] [CrossRef]
- Feng, M.N.; Luo, Z. Interface Morphology and Microstructure of High-Power Ultrasonic Spot Welded Mg/Al Dissimilar Joint. Sci. Technol. Weld. Join. 2019, 24, 63–78. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, J.; Gao, J.; Xiao, Y.; Luo, G.; Shen, Q. Microstructure and Texture Evolution of Aluminum and Titanium Ultrasonic Welded Joints. Mater. Charact. 2023, 195, 112542. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Liu, Z.; Yang, Y.; Li, Y.; Luo, Z. Ultrasonic Welding of Metal to Fiber-Reinforced Thermoplastic Composites: A Review. J. Manuf. Process. 2023, 85, 702–712. [Google Scholar] [CrossRef]
- Zwicker, M.F.R.; Moghadam, M.; Zhang, W.; Nielsen, C.V. Automotive Battery Pack Manufacturing—A Review of Battery to Tab Joining. J. Adv. Join. Process. 2020, 1, 100017. [Google Scholar] [CrossRef]
- Cai, W.; Daehn, G.S.; Vivek, A.; Li, J.; Khan, H.; Mishra, R.S.; Komarasamy, M. A State-of-the-Art Review on Solid-State Metal Joining. J. Manuf. Sci. Eng. Trans. ASME 2019, 141, 031012. [Google Scholar] [CrossRef]
- Lee, S.S.; Hyung Kim, T.; Hu, S.J.; Cai, W.; Abell, J.A. Joining Technologies for Automotive Lithium-Ion Battery Manufacturing: A Review. In Proceedings of the ASME 2010 International Manufacturing Science and Engineering Conference, Erie, PA, USA, 12–15 October 2010; pp. 541–549. [Google Scholar] [CrossRef]
- Lee, S.S.; Hyung Kim, T.; Jack Hu, S.; Cai, W.; Abell, J.A.; Li, J. Characterization of Joint Quality in Ultrasonic Welding of Battery Tabs. J. Manuf. Sci. Eng. 2013, 135, 021004. [Google Scholar] [CrossRef]
- Pati, P.R.; Das, S.; Satpathy, M.P.; Routara, B.C.; Sahoo, S.K.; Bhuyan, S.K. Ultrasonic Spot Welding of Al-Cu Sheets: A Comprehensive Study. Mater. Today Proc. 2020, 33, 5168–5173. [Google Scholar] [CrossRef]
- Komiyama, K.; Sasaki, T.; Watanabe, Y. Effect of Tool Edge Geometry in Ultrasonic Welding. J. Mater. Process. Technol. 2016, 229, 714–721. [Google Scholar] [CrossRef]
- Liesegang, M.; Yu, Y.; Beck, T.; Balle, F. Sonotrodes for Ultrasonic Welding of Titanium/Cfrp-Joints—Materials Selection and Design. J. Manuf. Mater. Process. 2021, 5, 61. [Google Scholar] [CrossRef]
- Shin, H.S.; De Leon, M. Parametric Study in Similar Ultrasonic Spot Welding of A5052-H32 Alloy Sheets. J. Mater. Process. Technol. 2015, 224, 222–232. [Google Scholar] [CrossRef]
- Du, P.; Chen, W.; Deng, J.; Li, K.; Liu, Y. Effects of Knurl Tooth Angle on Mechanical and Thermal Behaviors of Aluminum Ultrasonic Welding. Ultrasonics 2020, 108, 106207. [Google Scholar] [CrossRef]
- Das, A.; Masters, I.; Williams, D. Process Robustness and Strength Analysis of Multi-Layered Dissimilar Joints Using Ultrasonic Metal Welding. Int. J. Adv. Manuf. Technol. 2019, 101, 881–900. [Google Scholar] [CrossRef]
- Singh, A.R.; Sudarsan, C.; Das, A.; Hazra, S.; Panda, S.K. Process Optimization and Characterization of Ultra-Thin Dissimilar Sheet Material Joints for Battery Applications Using Ultrasonic Welding. J. Mater. Eng. Perform. 2022, 31, 4133–4149. [Google Scholar] [CrossRef]
- Ni, Z.; Yang, J.J.; Gao, Z.T.; Hao, Y.X.; Chen, L.F.; Ye, F. Joint Formation in Ultrasonic Spot Welding of Aluminum to Copper and the Effect of Particle Interlayer. J. Manuf. Process. 2020, 50, 57–67. [Google Scholar] [CrossRef]
- Satpathy, M.P.; Das Mohapatra, K.; Sahoo, A.K.; Sahoo, S.K. Parametric Investigation on Microstructure and Mechanical Properties of Ultrasonic Spot Welded Aluminium to Copper Sheets. IOP Conf. Ser. Mater. Sci. Eng. 2018, 338, 012024. [Google Scholar] [CrossRef]
- Li, J.; Balle, F. In-Situ Observation of the Bond Formation Process during Ultrasonic Metal Welding of Al / Cu Joints Using Laser Doppler Vibrometry. J. Manuf. Process. 2023, 106, 1–11. [Google Scholar] [CrossRef]
- Lee, S.S.; Hyung Kim, T.; Jack Hu, S.; Cai, W.; Abell, J.A. Analysis of Weld Formation in Multilayer Ultrasonic Metal Welding Using High-Speed Images. J. Manuf. Sci. Eng. 2015, 137, 031016. [Google Scholar] [CrossRef]
- Gester, A.; Wagner, G.; Pöthig, P.; Bergmann, J.P.; Fritzsche, M. Analysis of the Oscillation Behavior during Ultrasonic Welding of EN AW-1070 Wire Strands and EN CW004A Terminals. Weld. World 2022, 66, 567–576. [Google Scholar] [CrossRef]
- Shao, C.; Hyung Kim, T.; Jack Hu, S.; Jin, J.; Abell, J.A.; Patrick Spicer, J. Tool Wear Monitoring for Ultrasonic Metal Welding of Lithium-Ion Batteries. J. Manuf. Sci. Eng. 2015, 138, 051005. [Google Scholar] [CrossRef]
- Balz, I.; Rosenthal, E.; Reimer, A.; Turiaux, M.; Schiebahn, A.; Reisgen, U. Analysis of the Thermo-Mechanical Mechanism during Ultrasonic Welding of Battery Tabs Using High-Speed Image Capturing. Weld. World 2019, 63, 1573–1582. [Google Scholar] [CrossRef]
- Nazir, Q.; Shao, C. Online Tool Condition Monitoring for Ultrasonic Metal Welding via Sensor Fusion and Machine Learning. J. Manuf. Process. 2021, 62, 806–816. [Google Scholar] [CrossRef]
- Spaltmann, D.; Hartelt, M.; Woydt, M. Triboactive Materials for Dry Reciprocating Sliding Motion at Ultra-High Frequency. Wear 2009, 266, 167–174. [Google Scholar] [CrossRef]
- Spaltmann, D.; Hartelt, M.; Woydt, M. Ultra-High Frequency Tribometer for Reciprocating Sliding Motion. Tribo Test 2007, 13, 153–164. [Google Scholar] [CrossRef]
- Lu, Y.; Song, H.; Taber, G.A.; Foster, D.R.; Daehn, G.S.; Zhang, W. In-Situ Measurement of Relative Motion during Ultrasonic Spot Welding of Aluminum Alloy Using Photonic Doppler Velocimetry. J. Mater. Process. Technol. 2016, 231, 431–440. [Google Scholar] [CrossRef]
- Arimoto, K.; Sasaki, T.; Doi, Y.; Kim, T. Ultrasonic Bonding of Multi-Layered Foil Using a Cylindrical Surface Tool. Metals 2019, 9, 505. [Google Scholar] [CrossRef]
- Li, H.; Cao, B. Effects of Welding Pressure on High-Power Ultrasonic Spot Welding of Cu/Al Dissimilar Metals. J. Manuf. Process. 2019, 46, 194–203. [Google Scholar] [CrossRef]
- Fujii, H.T.; Endo, H.; Sato, Y.S.; Kokawa, H. Interfacial Microstructure Evolution and Weld Formation during Ultrasonic Welding of Al Alloy to Cu. Mater. Charact. 2018, 139, 233–240. [Google Scholar] [CrossRef]


| Young’s Modulus | Poisson’s Ratio | Mass Density |
|---|---|---|
| 1.27 GPa | 0.34 | 8940 kg/m3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Rienks, M.; Balle, F. Development of a High-Frequency Test System to Study the Wear of Ultrasonic Welding Tools. Metals 2023, 13, 1935. https://doi.org/10.3390/met13121935
Li J, Rienks M, Balle F. Development of a High-Frequency Test System to Study the Wear of Ultrasonic Welding Tools. Metals. 2023; 13(12):1935. https://doi.org/10.3390/met13121935
Chicago/Turabian StyleLi, Junqi, Michael Rienks, and Frank Balle. 2023. "Development of a High-Frequency Test System to Study the Wear of Ultrasonic Welding Tools" Metals 13, no. 12: 1935. https://doi.org/10.3390/met13121935
APA StyleLi, J., Rienks, M., & Balle, F. (2023). Development of a High-Frequency Test System to Study the Wear of Ultrasonic Welding Tools. Metals, 13(12), 1935. https://doi.org/10.3390/met13121935








