Inverse Magnetocaloric Effect in Heusler Ni44.4Mn36.2Sn14.9Cu4.5 Alloy at Low Temperatures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Samples Characterization
2.2. Computational Methods
3. Results
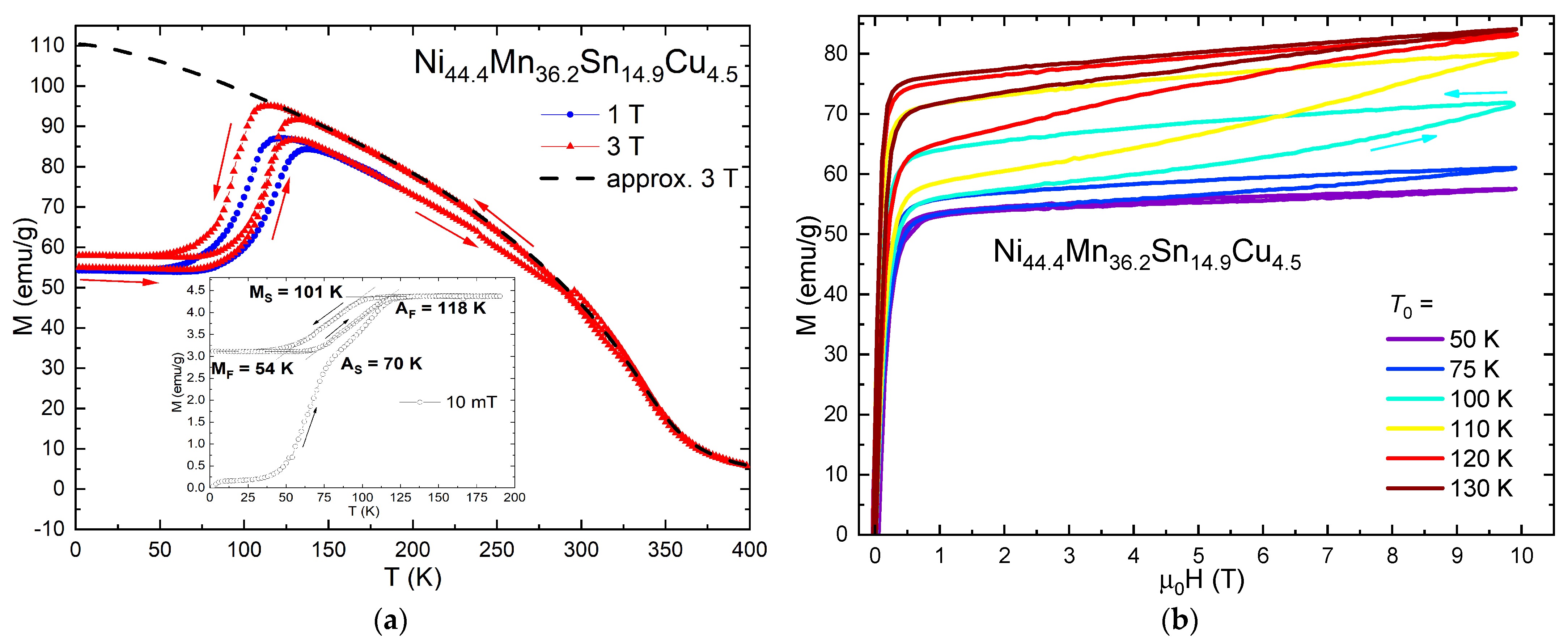
3.1. Indirect MCE Estimation
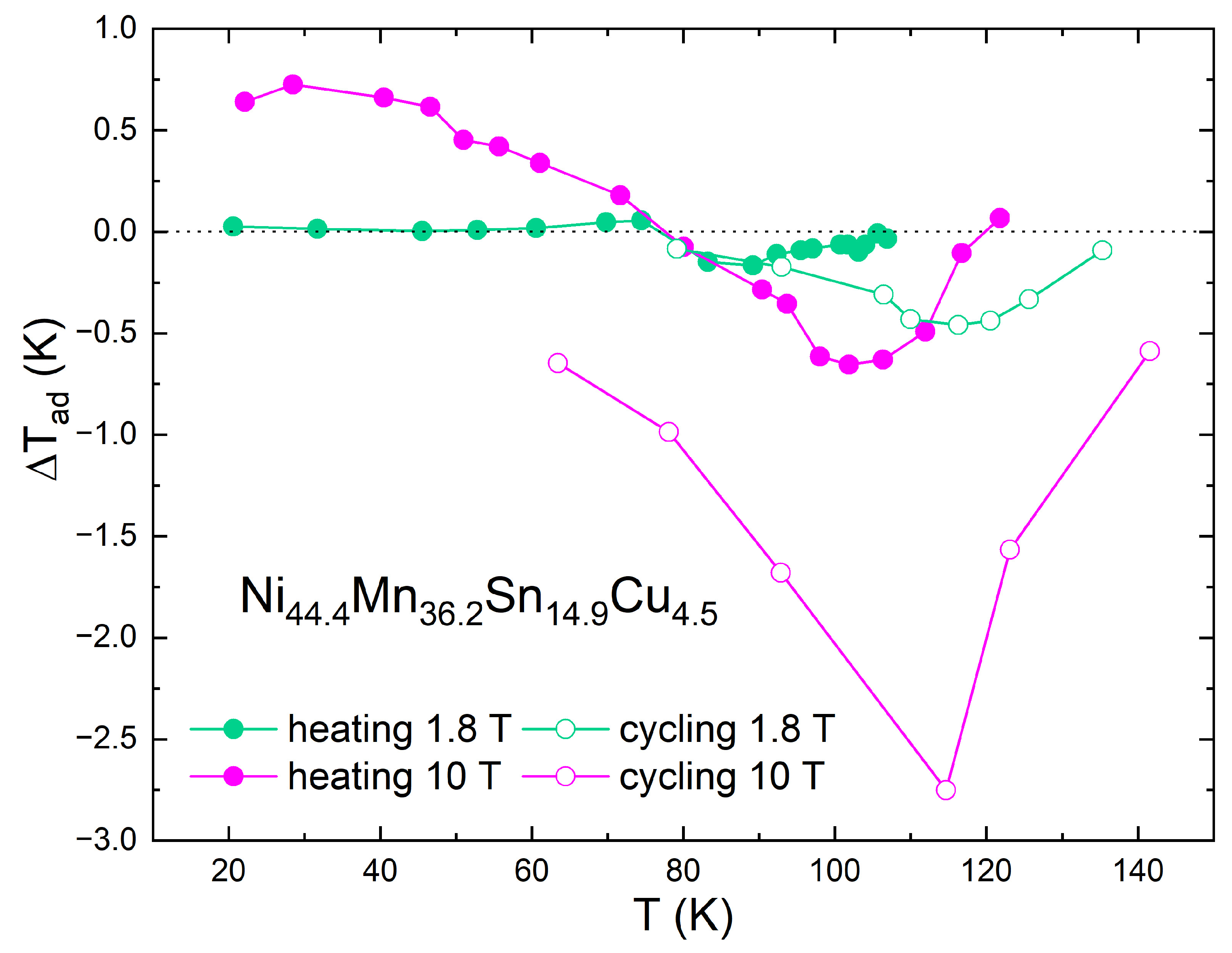
3.2. Direct MCE Measurements
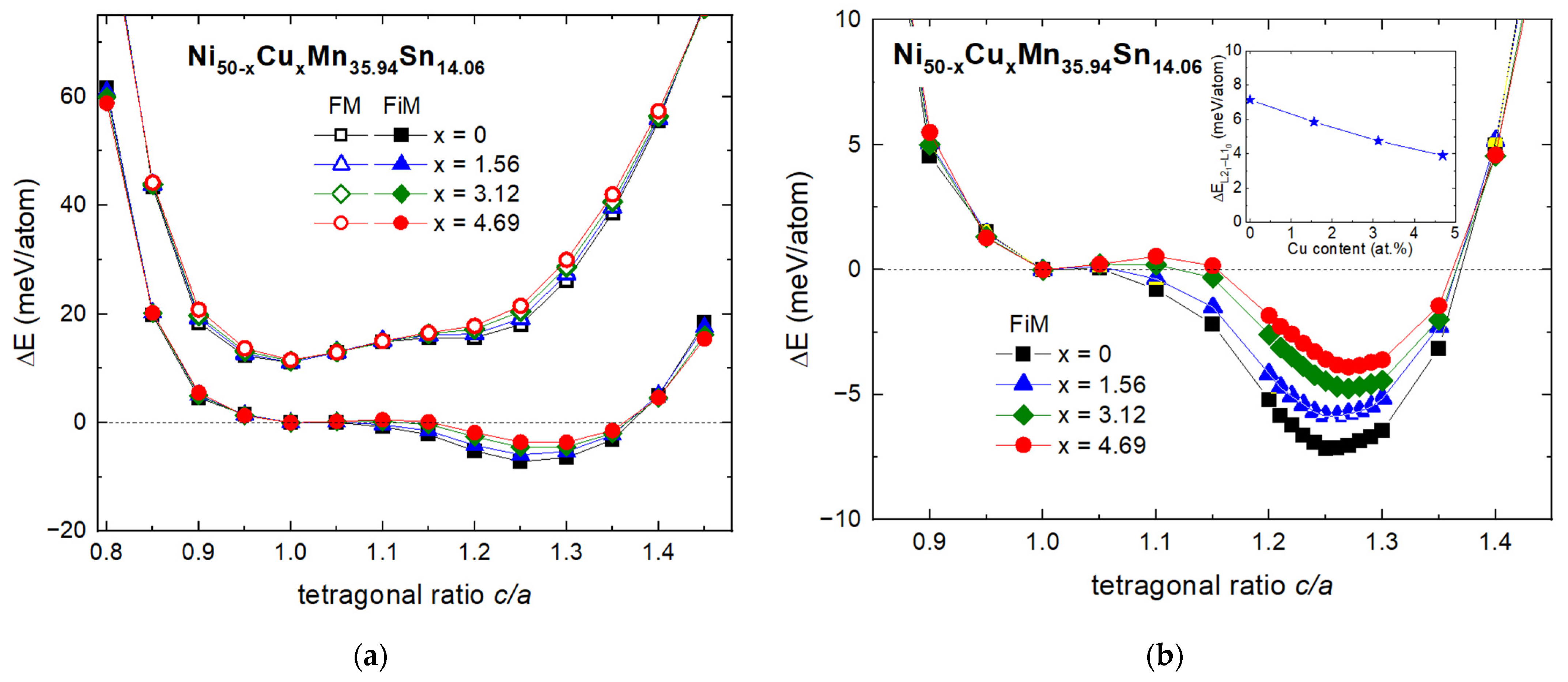
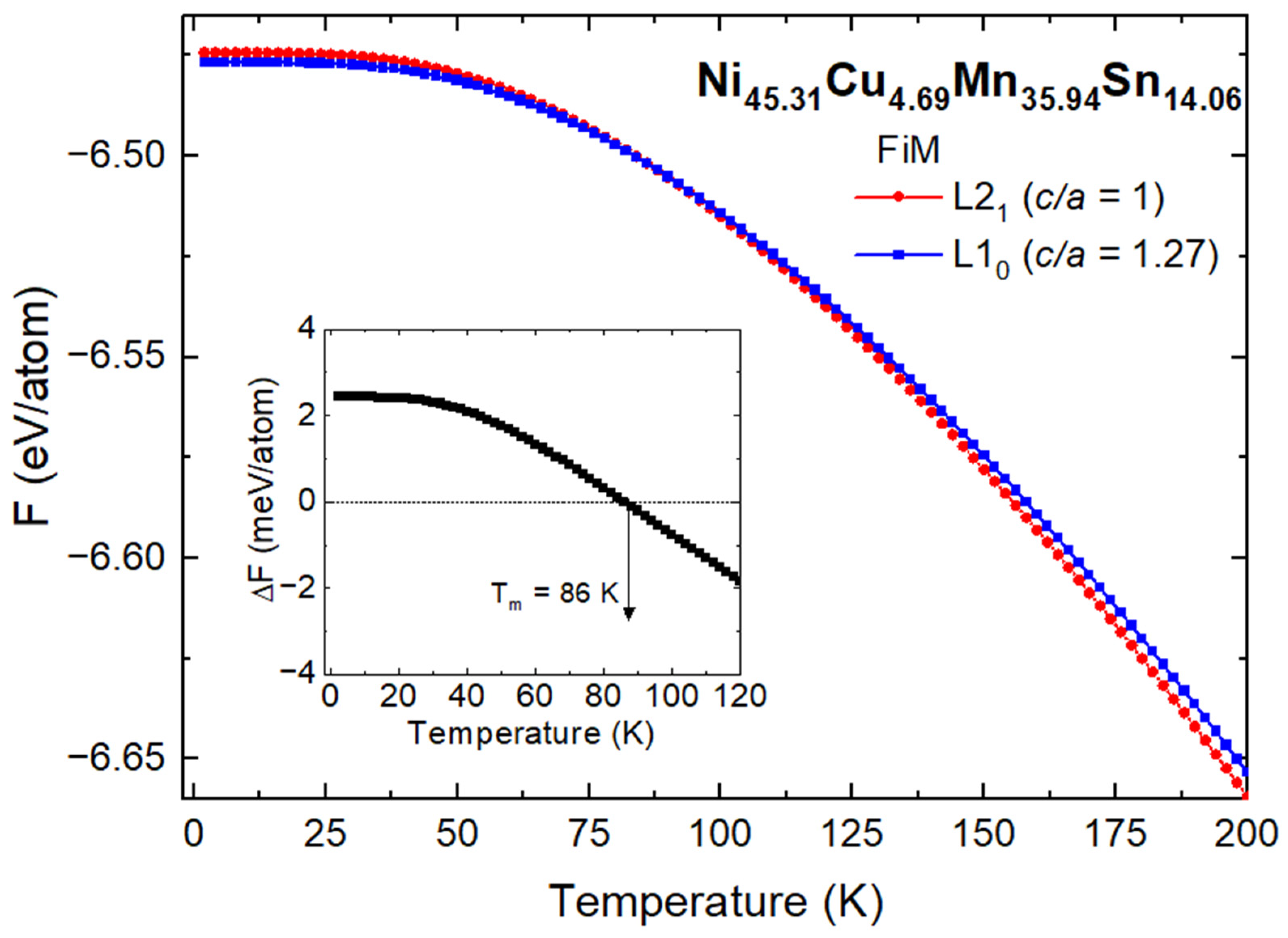
3.3. Computational Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Giauque, W.F.; MacDougall, D.P. Attainment of Temperatures Below 1 Absolute by Demagnetization of Gd2(SO4)3·8H2O. Phys. Rev. 1933, 43, 768. [Google Scholar] [CrossRef]
- Koshkid’ko, Y.S.; Dilmieva, E.T.; Kamantsev, A.P.; Mashirov, A.V.; Cwik, J.; Kol’chugina, N.B.; Koledov, V.V.; Shavrov, V.G. Magnetocaloric Materials for Low-Temperature Magnetic Cooling. J. Commun. Technol. Electron. 2023, 68, 379–388. [Google Scholar] [CrossRef]
- Tishin, A.M.; Spichkin, Y.I. The Magnetocaloric Effect and Its Applications; IOP Publisher: Bristol, UK, 2003; p. 476. [Google Scholar]
- Belov, K.P. The Magnetothermal Phenomena in Rare-Earth Magnetics; Nauka: Moscow, Russia, 1990. [Google Scholar]
- Khovaylo, V.V.; Taskaev, S.V. Magnetic Refrigeration: From Theory to Applications. Encycl. Smart Mater. 2022, 5, 407–417. [Google Scholar]
- Tang, X.; Sepehri-Amin, H.; Terada, N.; Martin-Cid, A.; Kurniawan, I.; Kobayashi, S.; Kotani, Y.; Takeya, H.; Lai, J.; Matsushita, Y.; et al. Magnetic refrigeration material operating at a full temperature range required for hydrogen liquefaction. Nat. Commun. 2022, 13, 1817. [Google Scholar] [CrossRef] [PubMed]
- Aziz, M. Liquid Hydrogen: A Review on Liquefaction, Storage, Transportation, and Safety. Energies 2021, 14, 5917. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, Y.J.; Niu, E.; Yang, L.H.; Shen, J.; Hu, F.X.; Sun, J.R.; Shen, B.G. Large magnetocaloric effects of RFeSi (R = Tb and Dy) compounds for magnetic refrigeration in nitrogen and natural gas liquefaction. Appl. Phys. Lett. 2013, 103, 202412. [Google Scholar] [CrossRef]
- Timmerhaus, K.D.; Reed, R.P. Cryogenic Engineering: Fifty Years of Progress; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Andreenko, A.S.; Belov, K.P.; Nikitin, S.A.; Tishin, A.M. Magnetocaloric effects in rare-earth magnetic materials. Sov. Phys. Usp. 1989, 32, 649–664. [Google Scholar] [CrossRef]
- Zheng, X.Q.; Xu, Z.Y.; Zhang, B.; Hu, F.X.; Shen, B.G. The normal and inverse magnetocaloric effect in RCu2 (RB = Tb, Dy, Ho, Er) compounds. J. Magn. Magn. Mater. 2017, 421, 448–452. [Google Scholar] [CrossRef]
- Kuchin, A.G.; Iwasieczko, W.; Platonov, S.P. The magnetocaloric effect in R2Fe17 intermetallics with different types of magnetic phase transition. Low Temp. Phys. 2015, 41, 985–989. [Google Scholar] [CrossRef]
- Kamantsev, A.P.; Koshkidko, Y.S.; Taskaev, S.V.; Khovaylo, V.V.; Koshelev, A.V.; Cwik, J.; Shavrov, V.G. Inverse Magnetocaloric Effect and Kinetic Arrest Behavior in As-Cast Gd2In at Cryogenic Temperatures. J. Supercond. Nov. Magn. 2022, 35, 2181–2186. [Google Scholar] [CrossRef]
- Kuchin, A.G.; Platonov, S.P.; Mukhachev, R.D.; Lukoyanov, A.V.; Volegov, A.S.; Gaviko, V.S.; Yakovleva, M.Y. Large Magnetic Entropy Change in GdRuSi Optimal for Magnetocaloric Liquefaction of Nitrogen. Metals 2023, 13, 290. [Google Scholar] [CrossRef]
- Nikitin, S.A.; Skokov, K.P.; Koshkid’ko, Y.S.; Pastushenkov, Y.G.; Ivanova, T.I. Giant Rotating Magnetocaloric Effect in the Region of Spin-Reorientation Transition in the NdCo5 Single Crystal. Phys. Rev. Lett. 2010, 105, 137205. [Google Scholar] [CrossRef] [PubMed]
- Moon, J.Y.; Kim, M.K.; Oh, D.G.; Kim, J.H.; Shin, H.J.; Choi, Y.J.; Lee, N. Anisotropic magnetic properties and giant rotating magnetocaloric effect in double-perovskite Tb2CoMnO6. Phys. Rev. B 2018, 98, 174424. [Google Scholar] [CrossRef]
- Koshkid’ko, Y.; Cwik, J.; Dilmieva, E.; Pandey, S.; Quetz, A.; Aryal, A.; Dubenko, I.; Ali, N.; Granovsky, A.; Lähderanta, E.; et al. Inverse magnetocaloric effects in metamagnetic Ni-Mn-In-based alloys in high magnetic fields. J. Alloys Compd. 2017, 695, 3348–3352. [Google Scholar] [CrossRef]
- Konoplyuk, S.M.; Kokorin, V.V.; Mashirov, A.V.; Kamantsev, A.P.; Koledov, V.V.; Shavrov, V.G.; Koshelev, A.V. Direct measurements of adiabatic temperature change in Ni49.9Mn37.03Sb12.3Fe0.77 alloy due to magnetocaloric effect in the temperature range of martensitic transformation. IEEE Trans. Magn. 2018, 54, 2500204. [Google Scholar] [CrossRef]
- Sokolovskiy, V.V.; Nachinova, D.V.; Buchel’nikov, V.D.; Dilmieva, E.T.; Koshkidko, Y.S.; Emelyanova, S.M.; Marchenkova, E.B.; Marchenkov, V.V. Magnetic and magnetocaloric properies of Heusler alloys Ni-Mn-Sn with an excess of Mn within the theoreticaland experimental approaches. Chel. Phys.-Math. J. 2020, 5, 493–503. [Google Scholar] [CrossRef]
- Lekkla, P.; Jantaratana, P.; Chotibhawaris, T. Magnetocaloric Effect in CoFe-Electroplated Ni50Mn33In16Cr1 Alloy. Metals 2022, 12, 2137. [Google Scholar] [CrossRef]
- Dadda, K.; Alleg, S.; Souilah, S.; Daza, J.; Saurina, J.; Suñol, J.-J.; Bessais, L.; Hlil, E.-K. Microstructure, Critical Behavior and Magnetocaloric Properties of Melt-Spun Ni51.82Mn32.37In15.81. Magnetochemistry 2022, 8, 179. [Google Scholar] [CrossRef]
- Marchenkov, V.V.; Emelyanova, S.M.; Marchenkova, E.B. Martensitic Transformation Temperatures and Hall Effect in Ni47−xMn41+xIn12 (x = 0, 1, 2) Alloys. Materials 2023, 16, 672. [Google Scholar] [CrossRef]
- Beckmann, B.; Koch, D.; Pfeuffer, L.; Gottschall, T.; Taubel, A.; Adabifiroozjaei, E.; Miroshkina, O.N.; Riegg, S.; Niehoff, T.; Kani, N.A.; et al. Dissipation losses limiting first-order phase transition materials in cryogenic caloric cooling: A case study on all-d-metal Ni (-Co)-Mn-Ti Heusler alloys. Acta Mater. 2023, 246, 118695. [Google Scholar] [CrossRef]
- Dincer, I.; Yüzüak, E.; Elerman, Y. Influence of irreversibility on inverse magnetocaloric and magnetoresistance properties of the (Ni, Cu)50Mn36Sn14 alloys. J. Alloys Compd. 2010, 506, 508–512. [Google Scholar] [CrossRef]
- Gaifullin, R.Y.; Kirilyuk, K.K.; Safarov, I.M.; Musabirov, I.I. Structure of Ni44.4Mn36.2Sn14.9Cu4.5 alloy applicable for thermomechanical treatment. Lett. Mater. 2023, 13, 164–170. [Google Scholar] [CrossRef]
- Nizhankovskii, V.I.; Lugansky, L.B. Vibrating sample magnetometer with a step motor. Meas. Sci. Technol. 2007, 18, 1533. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane- wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopo-tentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Ebert, H.; Ködderitzsch, D.; Minár, J. Calculating condensed matter properties using the KKR-Green’s function method-recent developments and applications. Rep. Prog. Phys. 2011, 74, 096501. [Google Scholar] [CrossRef]
- Landau, D.; Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics; Cambridge University Press: Cambridge, UK, 2021; p. 578. [Google Scholar]
- Koshkid’ko, Y.S.; Dilmieva, E.T.; Cwik, J.; Rogacki, K.; Kowalska, D.; Kamantsev, A.P.; Koledov, V.V.; Mashirov, A.V.; Shavrov, V.G.; Valkov, V.I.; et al. Giant reversible adiabatic temperature change and isothermal heat transfer of MnAs single crystals studied by direct method in high magnetic fields. J. Alloys Comp. 2019, 798, 810–819. [Google Scholar] [CrossRef]
- Koshkid’ko, Y.S.; Ćwik, J.; Ivanova, T.I.; Nikitin, S.A.; Miller, M.; Rogacki, K. Magnetocaloric properties of Gd in fields up to 14 T. J. Magn. Magn. Mater. 2017, 433, 234–238. [Google Scholar] [CrossRef]
- Moruzzi, V.L.; Janak, J.F.; Schwarz, K. Calculated thermal properties of metals. Phys. Rev. B 1988, 37, 790–799. [Google Scholar] [CrossRef]
- Sokolovskiy, V.V.; Buchelnikov, V.D.; Zagrebin, M.A.; Entel, P.; Sahool, S.; Ogura, M. First-principles investigation of chemical and structural disorder in magnetic Ni2Mn1+xSn1−x Heusler alloys. Phys. Rev. B 2012, 86, 134418. [Google Scholar] [CrossRef]
- Kuz’min, M.D. Landau-type parametrization of the equation of state of a ferromagnet. Phys. Rev. B 2008, 77, 184431. [Google Scholar] [CrossRef]
- Gottschall, T.; Skokov, K.P.; Frincu, B.; Gutfleisch, O. Large reversible magnetocaloric effect in Ni-Mn-In-Co. Appl. Phys. Lett. 2015, 106, 021901. [Google Scholar] [CrossRef]
- Timofeeva, E.; Panchenko, E.; Zherdeva, M.; Tokhmetova, A.; Chumlyakov, Y.I. The Cyclic Stability of the Superelasticity in Quenched and Aged Ni44Fe19Ga27Co10 Single Crystals. Metals 2023, 13, 1538. [Google Scholar] [CrossRef]
- Bhale, P.; Ari-Gur, P.; Noebe, R.D.; Ren, Y.; Madiligama, A.; Devaraj, R.; Cook, M.S. Effect of Melt-Spinning Parameters on the Structure and Properties of Ni55.5Mn18.8Ga24Si1.7 Heusler Alloy Ribbons. Materials 2023, 16, 6590. [Google Scholar] [CrossRef] [PubMed]
- Bachagha, T.; Chakaravarthy, R.; Ren, W.; Saurina, J.; Suñol, J.-J. Structural, Magnetocaloric, and Magnetic Properties in Heusler Ni50Mn35In10X5 (X = Ga, Fe and Al) Alloys. Metals 2023, 13, 1913. [Google Scholar] [CrossRef]
- Zhang, Y.; Hao, W.; Hu, C.; Wang, X.; Zhang, X.; Li, L. Rare-Earth-Free Mn30Fe20−xCuxAl50 Magnetocaloric Materials with Stable Cubic CsCl-Type Structure for Room-Temperature Refrigeration. Adv. Funct. Mater. 2023, 2310047. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, P.; Zhu, J.; Yan, S.; Zhang, J.; Li, L. The emergence of considerable room temperature magnetocaloric performances in the transition metal high-entropy alloys. Mater. Today Phys. 2023, 32, 101031. [Google Scholar] [CrossRef]
- Nambiar, S.S.; Murthy, B.R.N.; Karthik, B.M.; Sharma, S.; Prasanna, A.A. Investigation on Magnetization, Magnetocalory, Magnetoresistance, and Electric Properties of Ni-Mn Based Heusler Alloy. J. Compos. Sci. 2023, 7, 5. [Google Scholar] [CrossRef]




| Phase | Parameters | x = 0 | x = 1.56 | x = 3.12 | x = 4.69 |
|---|---|---|---|---|---|
| FiM cubic (c/a = 1) | a0 (Å) | 5.953 | 5.955 | 5.959 | 5.963 |
| (K) | 316 | 308 | 293 | 282 | |
| FiM tetragonal (c/a = 1.27) | at (Å) | 5.526 | 5.513 | 5.502 | 5.500 |
| c (Å) | 6.908 | 6.947 | 6.988 | 6.994 | |
| c/a | 1.25 | 1.26 | 1.27 | 1.27 | |
| (K) | 333 | 325 | 308 | 295 |
| x | Mn1-Ni | Mn2-Ni | Mn1-Mn1 | Mn2-Mn2 | Mn1-Mn2 | TC (MC) | TC (MFA) |
|---|---|---|---|---|---|---|---|
| FiM cubic structure | |||||||
| 0 | 2.961 | 2.341 | 1.082 | −0.936 | −6.065 | 425 | 423.4 |
| 1.56 | 2.977 | 2.364 | 1.201 | −0.837 | −5.925 | 430 | 433.5 |
| 3.12 | 2.988 | 2.384 | 1.492 | −0.772 | −5.859 | 452 | 444.8 |
| 4.69 | 2.999 | 2.402 | 1.702 | −0.678 | −5.722 | 464 | 453.1 |
| FiM tetragonal structure | |||||||
| 0 | 3.514 | 2.308 | 2.035 | 1.859 | −21.902 | 484 | 544.9 |
| 1.56 | 3.502 | 2.299 | 1.985 | 1.826 | −21.513 | 506 | 547.5 |
| 3.12 | 3.495 | 2.294 | 1.942 | 1.798 | −21.071 | 514 | 549.6 |
| 4.69 | 3.489 | 2.287 | 1.906 | 1.779 | −20.598 | 523 | 551.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamantsev, A.P.; Koshkid’ko, Y.S.; Gaifullin, R.Y.; Musabirov, I.I.; Koshelev, A.V.; Mashirov, A.V.; Sokolovskiy, V.V.; Buchelnikov, V.D.; Ćwik, J.; Shavrov, V.G. Inverse Magnetocaloric Effect in Heusler Ni44.4Mn36.2Sn14.9Cu4.5 Alloy at Low Temperatures. Metals 2023, 13, 1985. https://doi.org/10.3390/met13121985
Kamantsev AP, Koshkid’ko YS, Gaifullin RY, Musabirov II, Koshelev AV, Mashirov AV, Sokolovskiy VV, Buchelnikov VD, Ćwik J, Shavrov VG. Inverse Magnetocaloric Effect in Heusler Ni44.4Mn36.2Sn14.9Cu4.5 Alloy at Low Temperatures. Metals. 2023; 13(12):1985. https://doi.org/10.3390/met13121985
Chicago/Turabian StyleKamantsev, Alexander P., Yuriy S. Koshkid’ko, Ruslan Yu. Gaifullin, Irek I. Musabirov, Anatoliy V. Koshelev, Alexey V. Mashirov, Vladimir V. Sokolovskiy, Vasiliy D. Buchelnikov, Jacek Ćwik, and Vladimir G. Shavrov. 2023. "Inverse Magnetocaloric Effect in Heusler Ni44.4Mn36.2Sn14.9Cu4.5 Alloy at Low Temperatures" Metals 13, no. 12: 1985. https://doi.org/10.3390/met13121985
APA StyleKamantsev, A. P., Koshkid’ko, Y. S., Gaifullin, R. Y., Musabirov, I. I., Koshelev, A. V., Mashirov, A. V., Sokolovskiy, V. V., Buchelnikov, V. D., Ćwik, J., & Shavrov, V. G. (2023). Inverse Magnetocaloric Effect in Heusler Ni44.4Mn36.2Sn14.9Cu4.5 Alloy at Low Temperatures. Metals, 13(12), 1985. https://doi.org/10.3390/met13121985














