Web Bend-Buckling of Steel Plate Girders Reinforced by Two Longitudinal Stiffeners with Various Cross-Section Shapes
Abstract
:1. Introduction
2. Existing Design Standards
2.1. AASHTO LRFD Standards
2.2. Eurocode 3 Standard
3. Methodology
3.1. Elastic Buckling Analysis
3.2. Problem Statement for Optimization of Longitudinally Stiffened Plate Girders
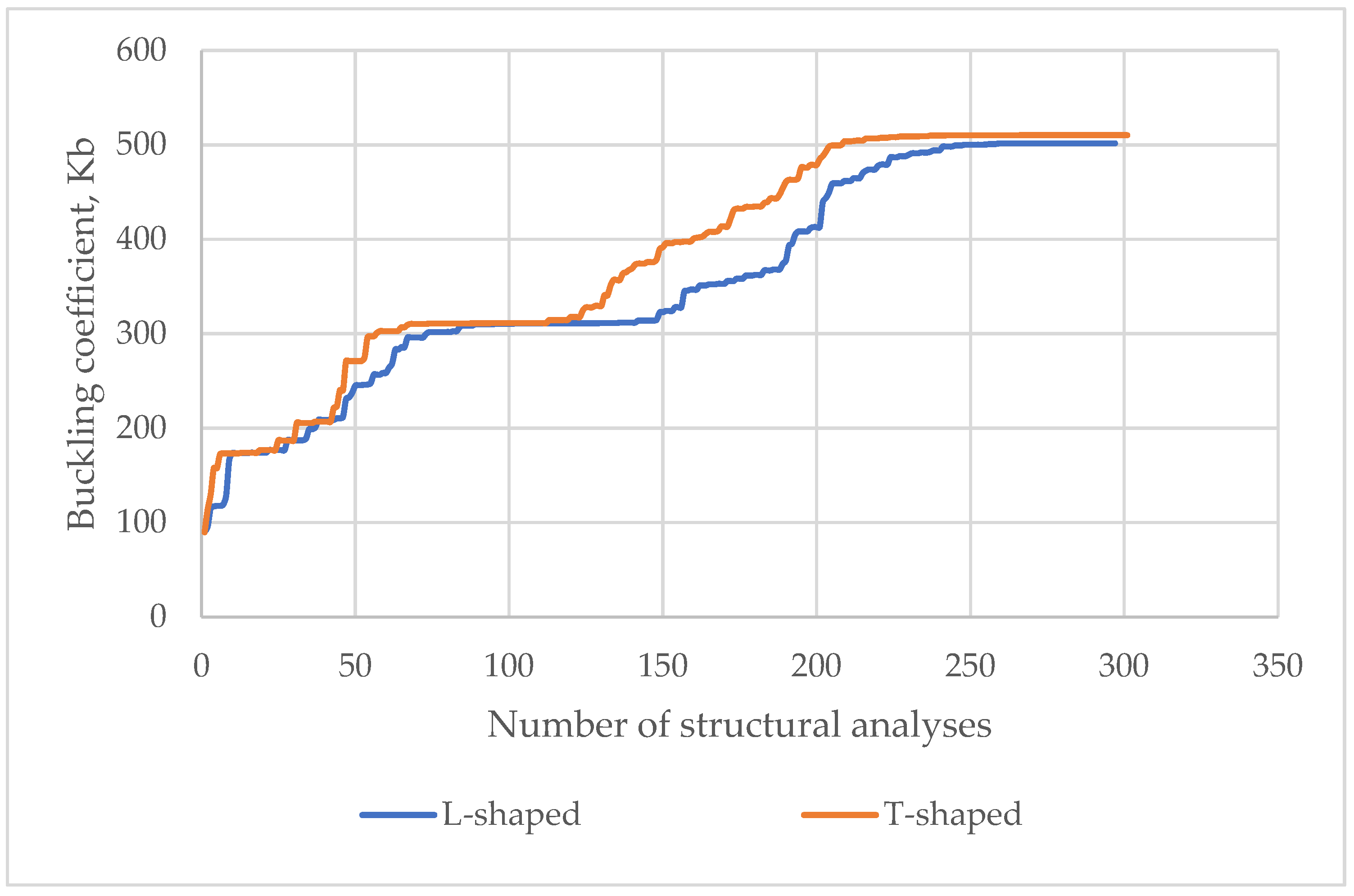
3.3. Optimization Procedure
- 1.
- Establish a Matlab function so that an Abaqus input file (*inp) is automatically created when it runs inside Matlab;
- 2.
- Define input variables (longitudinal stiffener positions) in the Matlab function above;
- 3.
- Define the objective function mentioned in Section 3.2 for the optimization problem;
- 4.
- Build a main Matlab function consisting of the starting point value for the solution, lower and upper bound values of the stiffener position, and an optimization algorithm (using the fmincon function available in Matlab). The starting point is an initial guess and can be any arbitrary selection which satisfies the lower and upper bounds as well as any other constraints that may apply;
- 5.
- Compute the objective function defined in step 3;
- 6.
- Perform the optimization procedure;
- 7.
- Check the stopping criterion. This criterion is a maximization of kb. If the criterion is satisfied, the optimization procedure will complete. Otherwise, it will go to the next step;
- 8.
- Change the design variable value to create a new Abaqus input file;
- 9.
- Run the analysis in Abaqus again;
- 10.
- Repeat steps 6–9 until convergence is attained, satisfying the specific tolerance;
- 11.
- The optimization result obtained is the final solution.
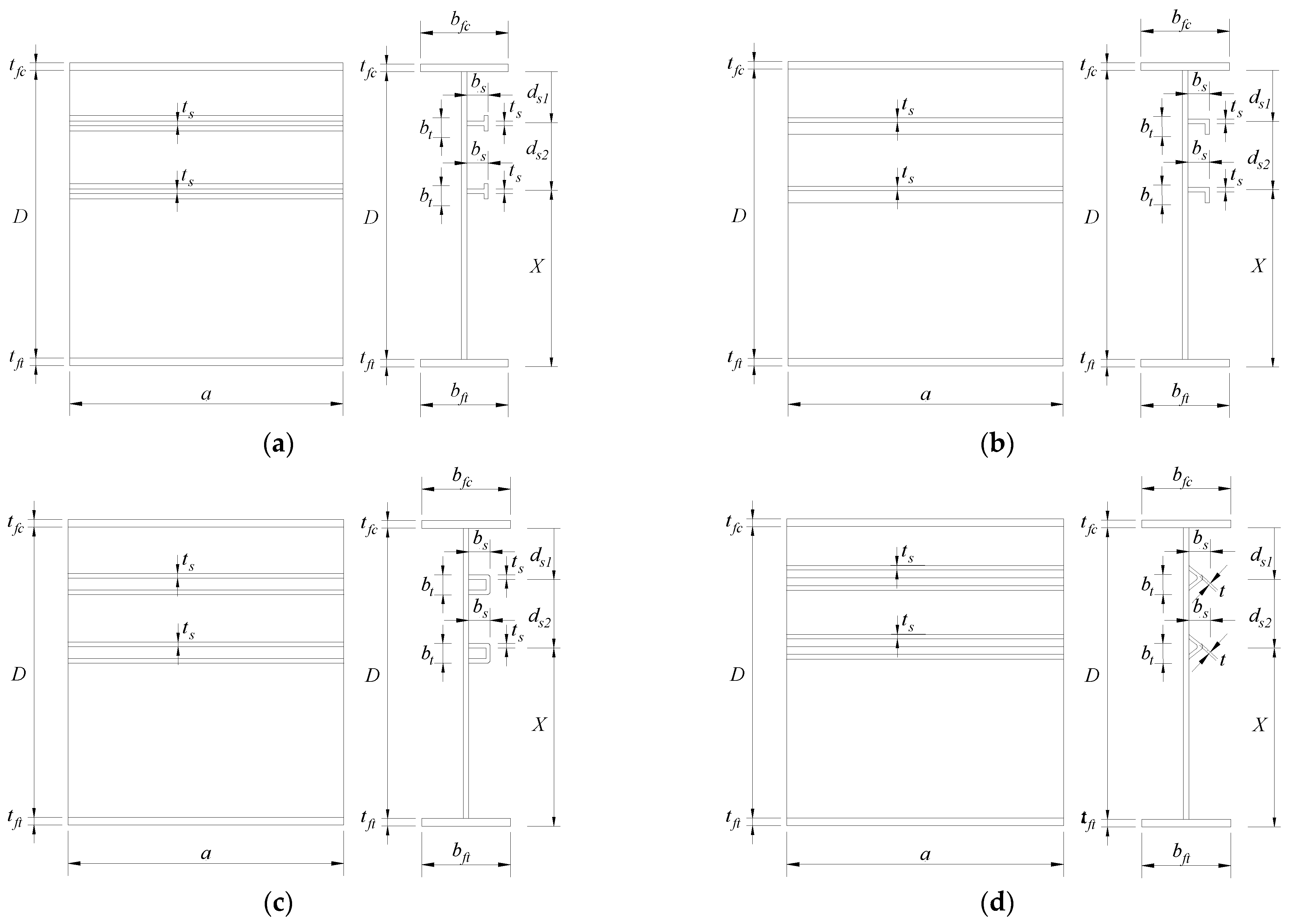
4. Finite Element Modeling
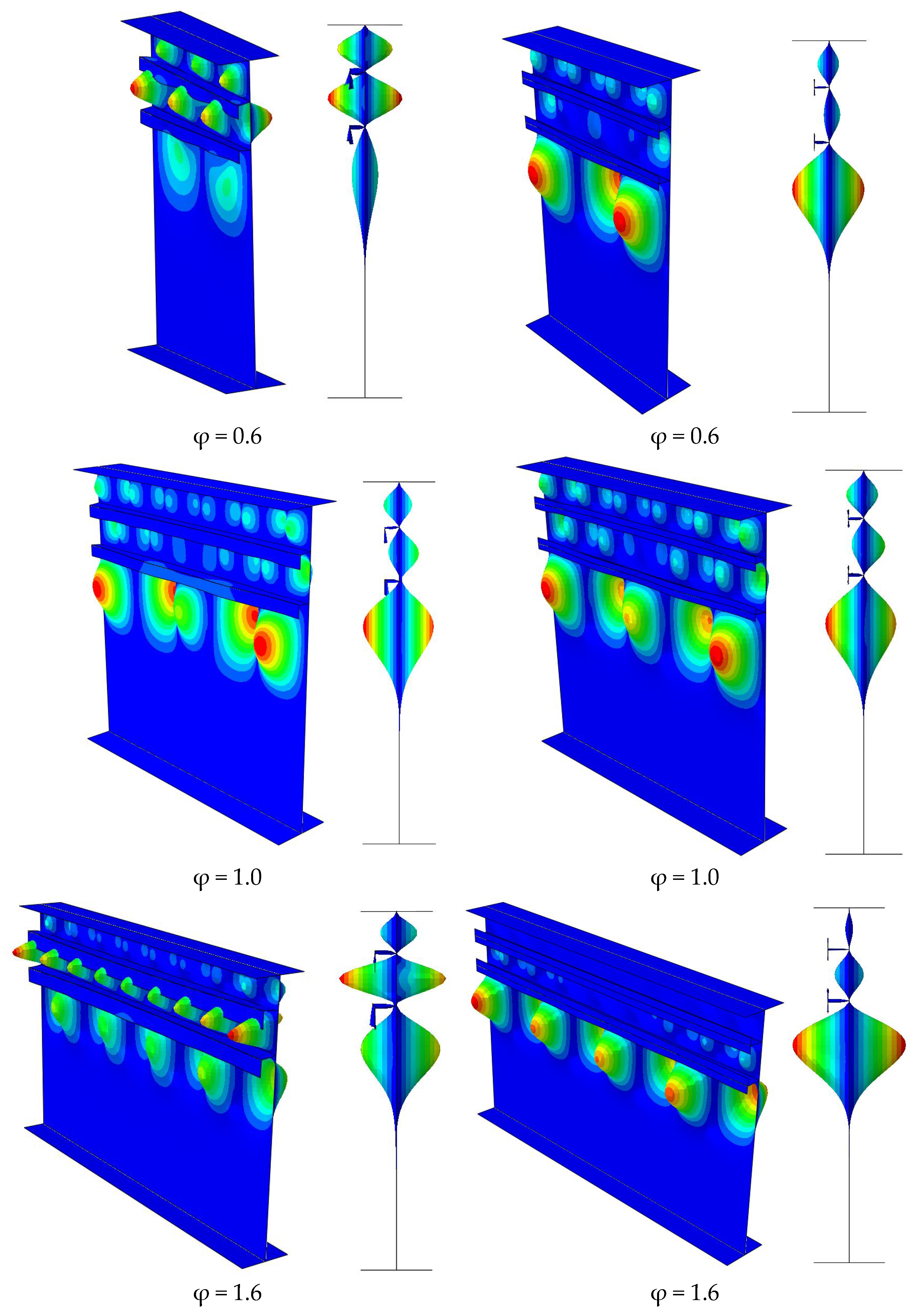
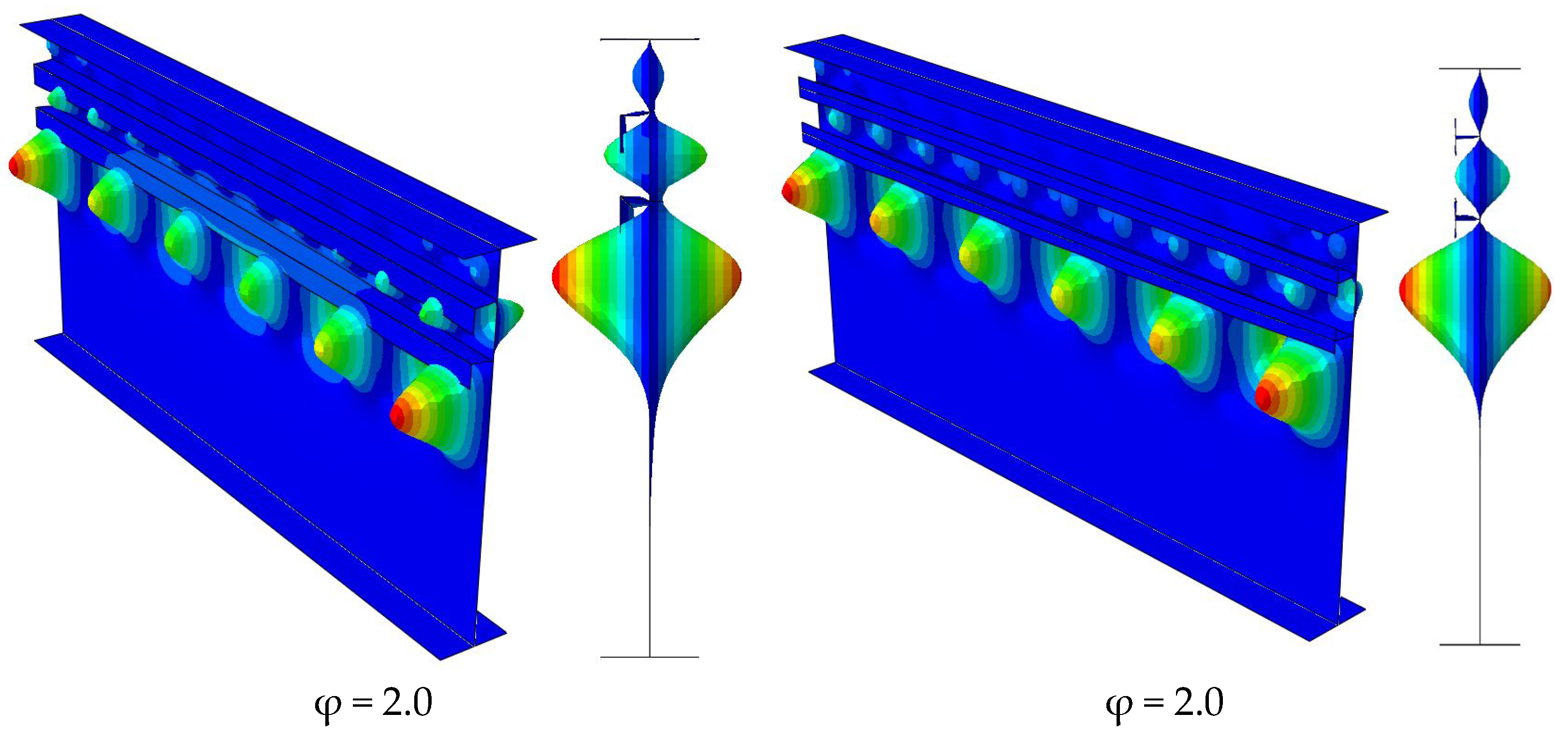
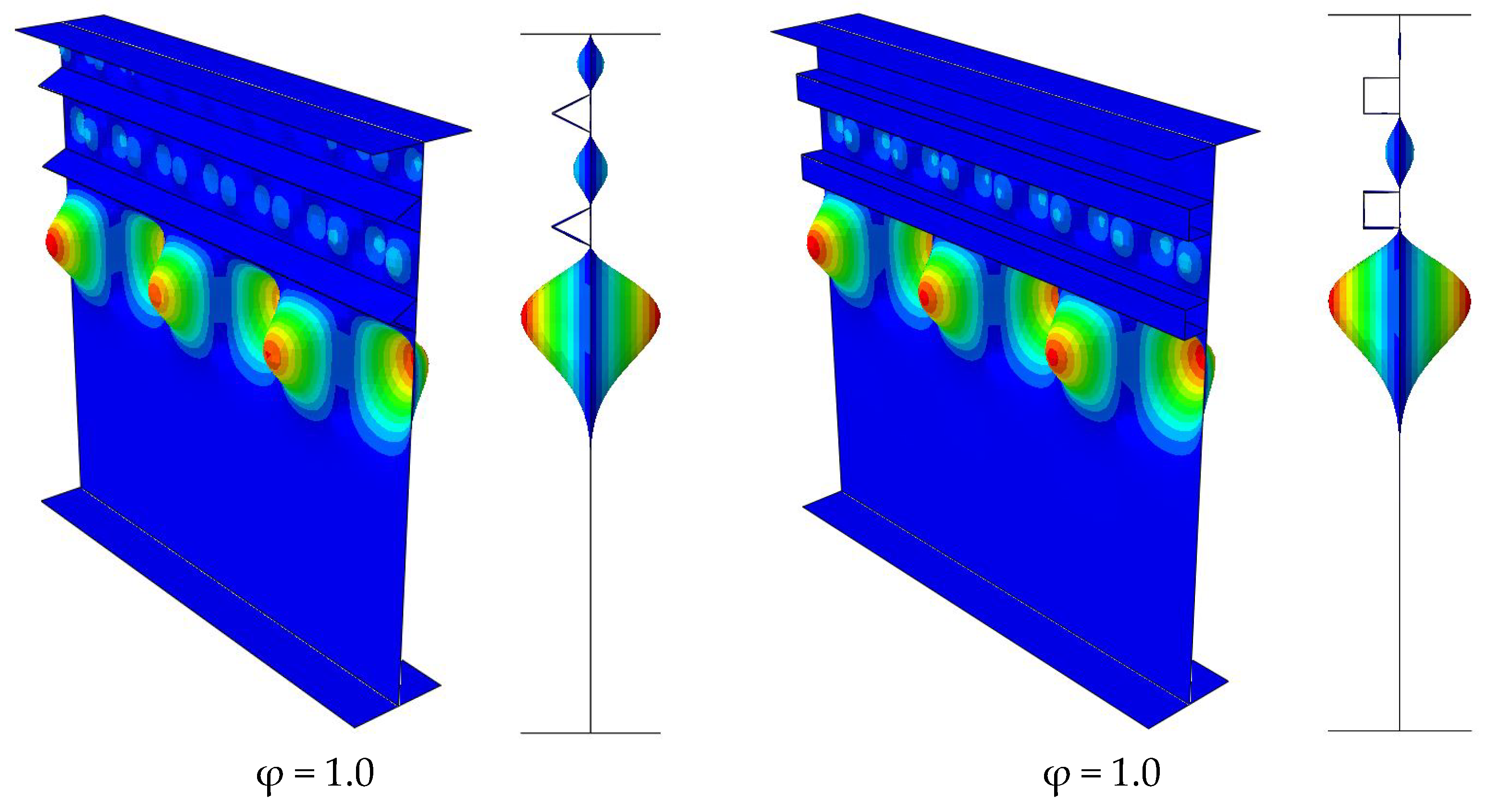
5. Optimum Location of 2 Stiffeners with Open Cross-Section Types
6. Optimum Location of Two Stiffeners with Closed Cross-Section Types
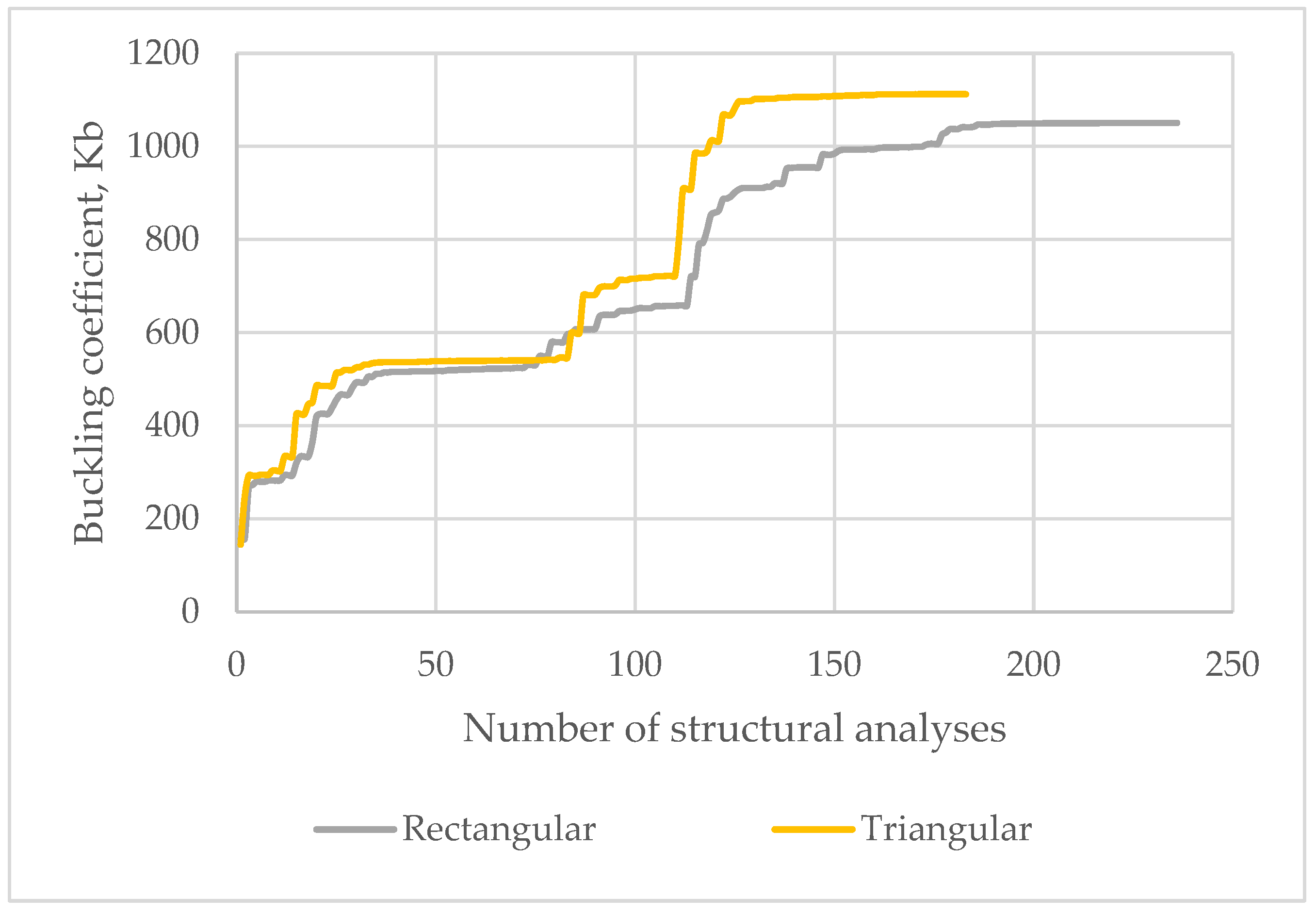
7. Comparison of the Efficiency of Longitudinal Stiffener Types
8. Conclusions
- -
- The optimum positions of the stiffeners with open cross-section shapes (T- and L-shaped) are around 0.25Dc and 0.55Dc, which are similar to the optimum location of the flat stiffener.
- -
- The optimum positions of the stiffeners with closed cross-section shapes (triangular and rectangular shapes) are around 0.23Dc and 0.54Dc, which are slightly different to the stiffeners with open cross-sections.
- -
- The bend-buckling coefficient of the stiffened girder with stiffeners with a triangular cross-section shape is highest, while that with a flat cross-section shape is lowest in all considered stiffener types.
- -
- The required web thickness of the girder web reinforced by two stiffeners with closed section shapes is remarkably reduced compared with those reinforced by two stiffeners with open cross-section shapes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Haffar, M.Z.; Kövesdi, B.; Adany, S. Buckling of compressed plates with closed-section longitudinal stiffeners: Two new mathematical models for resistance prediction. Structures 2021, 33, 3526–3539. [Google Scholar] [CrossRef]
- Kovesdi, B.; Haffar, M.; Adany, S. Buckling resistance of longitudinally stiffened plates: Eurocode-based design for col-umn-like and interactive behavior of plates with closed-section stiffeners. Thin-Walled Struct. 2021, 159, 107266. [Google Scholar] [CrossRef]
- Loaiza, N.; Graciano, C.; Casanova, E. Web slenderness for longitudinally stiffened I-girders subjected to patch loading. J. Constr. Steel Res. 2019, 162, 105737. [Google Scholar] [CrossRef]
- Demari, F.E.; Mezzomo, G.P.; Pravia, Z.M.C. Numerical study of slender I-girders with one longitudinal stiffener under patch loading. J. Constr. Steel Res. 2020, 167, 105964. [Google Scholar] [CrossRef]
- Truong, V.-H.; Papazafeiropoulos, G.; Vu, Q.-V.; Pham, V.-T.; Kong, Z. Predicting the patch load resistance of stiffened plate girders using machine learning algorithms. Ocean Eng. 2021, 240, 109886. [Google Scholar] [CrossRef]
- Truong, V.-H.; Papazafeiropoulos, G.; Pham, V.-T.; Vu, Q.-V. Effect of multiple longitudinal stiffeners on ultimate strength of steel plate girders. Structures 2019, 22, 366–382. [Google Scholar] [CrossRef]
- Chen, Z.; Yuan, H. Local buckling behaviour of longitudinally stiffened stainless steel plate girders under combined bending and shear. Thin-Walled Struct. 2023, 184, 110541. [Google Scholar] [CrossRef]
- Azhari, M.; Bradford, M. Local buckling of I-section beams with longitudinal web stiffeners. Thin-Walled Struct. 1993, 15, 1–13. [Google Scholar] [CrossRef]
- Alinia, M.; Moosavi, S. A parametric study on the longitudinal stiffeners of web panels. Thin-Walled Struct. 2008, 46, 1213–1223. [Google Scholar] [CrossRef]
- Vu, Q.-V.; Papazafeiropoulos, G.; Graciano, C.; Kim, S.-E. Optimum linear buckling analysis of longitudinally multi-stiffened steel plates subjected to combined bending and shear. Thin-Walled Struct. 2018, 136, 235–245. [Google Scholar] [CrossRef]
- Vu, Q.-V.; Truong, V.-H.; Papazafeiropoulos, G.; Graciano, C.; Kim, S.-E. Bend-buckling strength of steel plates with multiple longitudinal stiffeners. J. Constr. Steel Res. 2019, 158, 41–52. [Google Scholar] [CrossRef]
- Elbanna, A.; Ramadan, H.; Mourad, S. Buckling enhancement of longitudinally and vertically stiffened plate girders. J. Eng. Appl. Sci. 2014, 61, 351–370. [Google Scholar]
- HKim, S.; Park, Y.; Kim, B.; Kim, K. Numerical investigation of buckling strength of longitudinally stiffened web of plate girders subjected to bending. Struct. Eng. Mech. 2018, 65, 141–154. [Google Scholar]
- Hoàn, P.; Trung, P.; Vi, V. Nghiên cứu xác định vị trí tối ưu của sườn tăng cường dọc của dầm cầu thép chịu uốn. Tạp chí Khoa học Công nghệ Xây dựng. NUCE 2020, 14, 29–38. [Google Scholar]
- Kim, S.-E.; Papazafeiropoulos, G.; Graciano, C.; Truong, V.-H.; Do, Q.T.; Kong, Z.; Vu, Q.-V. Optimal design of longitudinal stiffeners of unsymmetric plate girders subjected to pure bending. Ocean Eng. 2021, 221, 108374. [Google Scholar] [CrossRef]
- Cho, E.-Y.; Shin, D.-K. Elastic web bend-buckling analysis of longitudinally stiffened I-section girders. Int. J. Steel Struct. 2011, 11, 297–313. [Google Scholar] [CrossRef]
- AASHTO. AASHTO LRFD Bridge Design Specifications, 7th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2014. [Google Scholar]
- Rockey, K.; Cook, I. Optimum reinforcement by two longitudinal stiffeners of a plate subjected to pure bending. Int. J. Solids Struct. 1965, 1, 79–92. [Google Scholar] [CrossRef]
- Rockey, K.; Cook, I. The buckling under pure bending of a plate girder reinforced by multiple longitudinal stiffeners. Int. J. Solids Struct. 1965, 1, 147–156. [Google Scholar] [CrossRef]
- Kim, B.J.; Park, Y.; Kim, K.; Choi, B. Web bend-buckling strength of plate girders with two longitudinal web stiffeners. Struct. Eng. Mech. 2019, 69, 383–397. [Google Scholar]
- Maiorana, E.; Pellegrino, C.; Modena, C. Influence of longitudinal stiffeners on elastic stability of girder webs. J. Constr. Steel Res. 2010, 67, 51–64. [Google Scholar] [CrossRef]
- Papazafeiropoulos, G.; Vu, Q.-V.; Nguyen, V.-S.; Truong, V.-H. Optimum location of a single longitudinal stiffener with various cross-section shapes of steel plate girders under bending loading. J. Sci. Technol. Civ. Eng. (STCE)—NUCE 2022, 16, 65–75. [Google Scholar] [CrossRef]
- Papazafeiropoulos, G.; Muñiz-Calvente, M.; Martínez-Pañeda, E. Abaqus2Matlab: A suitable tool for finite element post-processing. Adv. Eng. Softw. 2017, 105, 9–16. [Google Scholar] [CrossRef]
- ABAQUS. Analysis User’s Manual, Version 6.14; Dassault Systems: Los Angeles, CA, USA, 2014.
- MathWorks, Inc. MATLAB R2017b; MathWorks, Inc.: Natick, MA, USA, 2017. [Google Scholar]
- Frank, K.H.; Helwig, T.A. Buckling of webs in unsymmetric plate girders. Eng. J. Second Quart. 1995, 32, 43–53. [Google Scholar]
- CEN. EN 1993-1-5; Eurocode 3: Design of Steel Structures-Part 1-5: Plated Structural Elements. European Committee for Standardization: Brussels, Belgium, 2006.
- Byrd, R.H.; Gilbert, J.C.; Nocedal, J. A trust region method based on interior point techniques for nonlinear programming. Math. Program. 2000, 89, 149–185. [Google Scholar] [CrossRef]
- Byrd, R.H.; Hribar, M.E.; Nocedal, J. An Interior Point Algorithm for Large-Scale Nonlinear Programming. SIAM J. Optim. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- Waltz, R.; Morales, J.; Nocedal, J.; Orban, D. An interior algorithm for nonlinear optimization that combines line search and trust region steps. Math. Prograhm. 2006, 107, 391–408. [Google Scholar] [CrossRef]
- Pham, V.T.; Vu, Q.V.; Papazafeiropoulos, G.; Ngo, V.T. Efficiency of Abaqus2Matlab toolbox for structural optimization problems. IOP Conf. Ser. Mater. Sci. Eng. 2020, 869, 022025. [Google Scholar] [CrossRef]
- Ghorashi, M.; Askarian, A.; Gashtasby, M. Optimal design of stiffened plates for buckling under in-plane forces and bending moments. In Proceedings of the Eighth International Conference on the Application of Artificial Intelligence to Civil and Structural Engineering Computing, Stirling, UK, 19–21 September 2001; pp. 83–84. [Google Scholar]
- Silva, D.A.B.; Filho, J.O.F.; Barreto, R. Numerical study for optimization of the buckling behavior of longitudinally stiffened plates under pure bending. In Proceedings of the 1st International Congress on Structural Integrity and Maintenance—SIM 2021, Online, 8–9 April 2021. [Google Scholar]
- Papazafeiropoulos, G.; Vu, Q.-V.; Truong, V.-H.; Luong, M.-C.; Pham, V.-T. Prediction of buckling coefficient of stiffened plate girders using deep learning algorithm. Lect. Notes Civ. Eng. 2019, 54, 1143–1148. [Google Scholar] [CrossRef]





| Stiffener Type | φ | ds1/Dc | ds2/Dc | kb | Note |
|---|---|---|---|---|---|
| Flat-shaped | 1.0 | 0.244 | 0.566 | 437.02 | [15] |
| T-shaped | 1.0 | 0.25 | 0.55 | 501.62 | Present study |
| L-shaped | 1.0 | 0.25 | 0.55 | 500.25 | Present study |
| φ | Stiffener Type | ds1/Dc | ds2/Dc | kb |
|---|---|---|---|---|
| 0.6 | T-shaped | 0.25 | 0.55 | 501.48 |
| L-shaped | 0.25 | 0.55 | 500.1 | |
| 1.0 | T-shaped | 0.25 | 0.55 | 501.62 |
| L-shaped | 0.25 | 0.55 | 500.25 | |
| 1.6 | T-shaped | 0.24 | 0.53 | 582.76 |
| L-shaped | 0.24 | 0.53 | 578.59 | |
| 2.0 | T-shaped | 0.24 | 0.53 | 582.96 |
| L-shaped | 0.24 | 0.53 | 579.32 |
| φ | Stiffener Types | ds1/Dc | ds2/Dc | kb |
|---|---|---|---|---|
| 0.6 | Triangular | 0.23 | 0.55 | 1109.33 |
| Rectangular | 0.23 | 0.54 | 1049.47 | |
| 1.0 | Triangular | 0.23 | 0.55 | 1112.28 |
| Rectangular | 0.23 | 0.54 | 1050.66 |
| Stiffener Type | D (mm) | kb | tmin (mm) |
|---|---|---|---|
| Flat-shaped | 3000 | 437.02 | 5.85 |
| T-shaped | 3000 | 501.62 | 5.46 |
| L-shaped | 3000 | 500.25 | 5.47 |
| Triangular | 3000 | 1112.28 | 3.67 |
| Rectangular | 3000 | 1050.66 | 3.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Kong, Z.; Dinh, B.H.; Nguyen, H.-H.; Cao, T.-S.; Papazafeiropoulos, G.; Vu, Q.-V. Web Bend-Buckling of Steel Plate Girders Reinforced by Two Longitudinal Stiffeners with Various Cross-Section Shapes. Metals 2023, 13, 323. https://doi.org/10.3390/met13020323
Peng Y, Kong Z, Dinh BH, Nguyen H-H, Cao T-S, Papazafeiropoulos G, Vu Q-V. Web Bend-Buckling of Steel Plate Girders Reinforced by Two Longitudinal Stiffeners with Various Cross-Section Shapes. Metals. 2023; 13(2):323. https://doi.org/10.3390/met13020323
Chicago/Turabian StylePeng, Yongli, Zhengyi Kong, Ba Huu Dinh, Huu-Hue Nguyen, Truong-Son Cao, George Papazafeiropoulos, and Quang-Viet Vu. 2023. "Web Bend-Buckling of Steel Plate Girders Reinforced by Two Longitudinal Stiffeners with Various Cross-Section Shapes" Metals 13, no. 2: 323. https://doi.org/10.3390/met13020323
APA StylePeng, Y., Kong, Z., Dinh, B. H., Nguyen, H.-H., Cao, T.-S., Papazafeiropoulos, G., & Vu, Q.-V. (2023). Web Bend-Buckling of Steel Plate Girders Reinforced by Two Longitudinal Stiffeners with Various Cross-Section Shapes. Metals, 13(2), 323. https://doi.org/10.3390/met13020323








