First-Principles Calculation and Kink-Dislocation Dynamics Simulation on Dislocation Plasticity in TiZr-Based Concentrated Solid-Solution Alloys
Abstract
:1. Introduction
2. Methodology
2.1. First-Principles Calculation
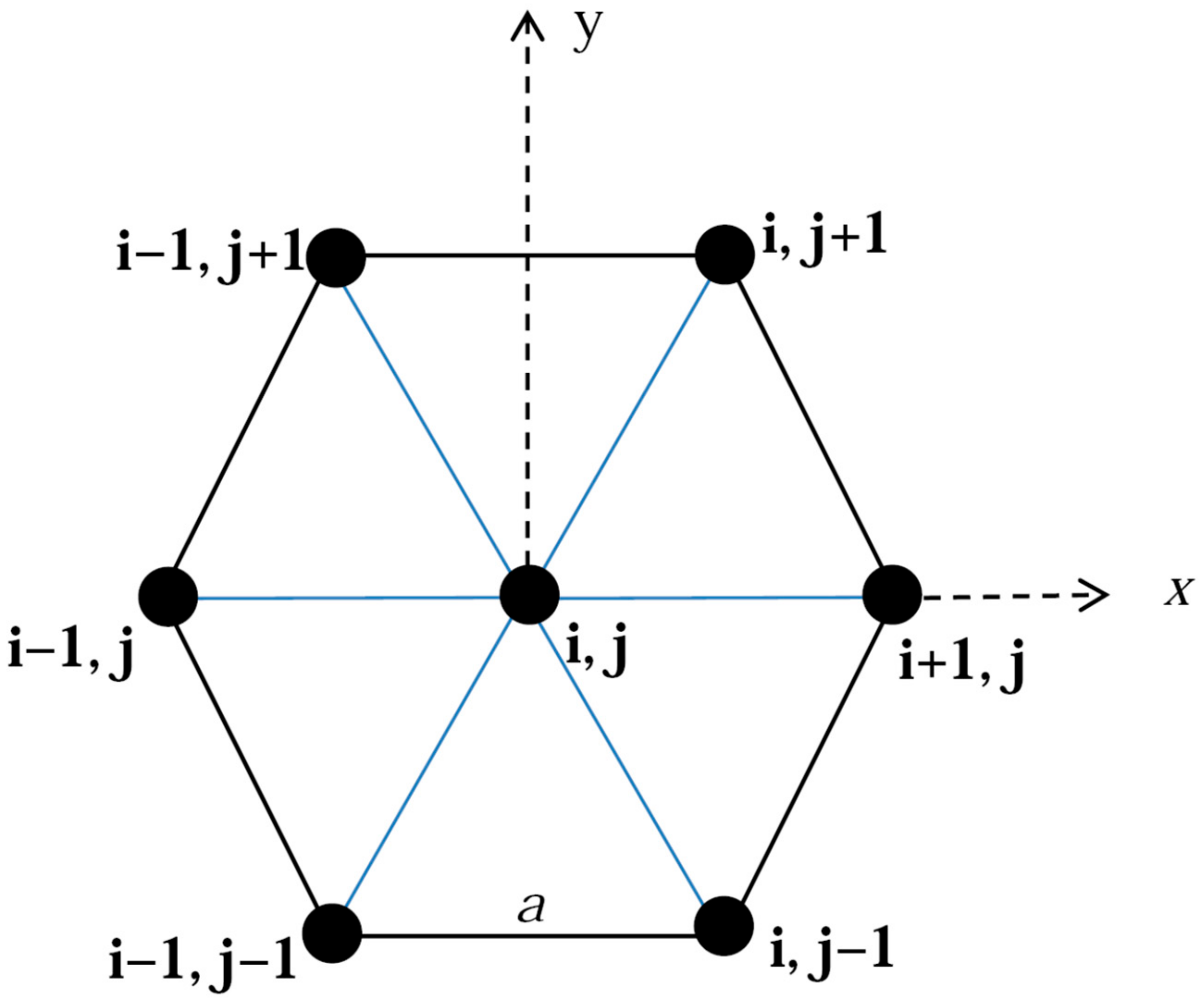
2.2. Simulation of Dislocation Kinetics by a Kink-Dislocation Model
3. Results and Discussion
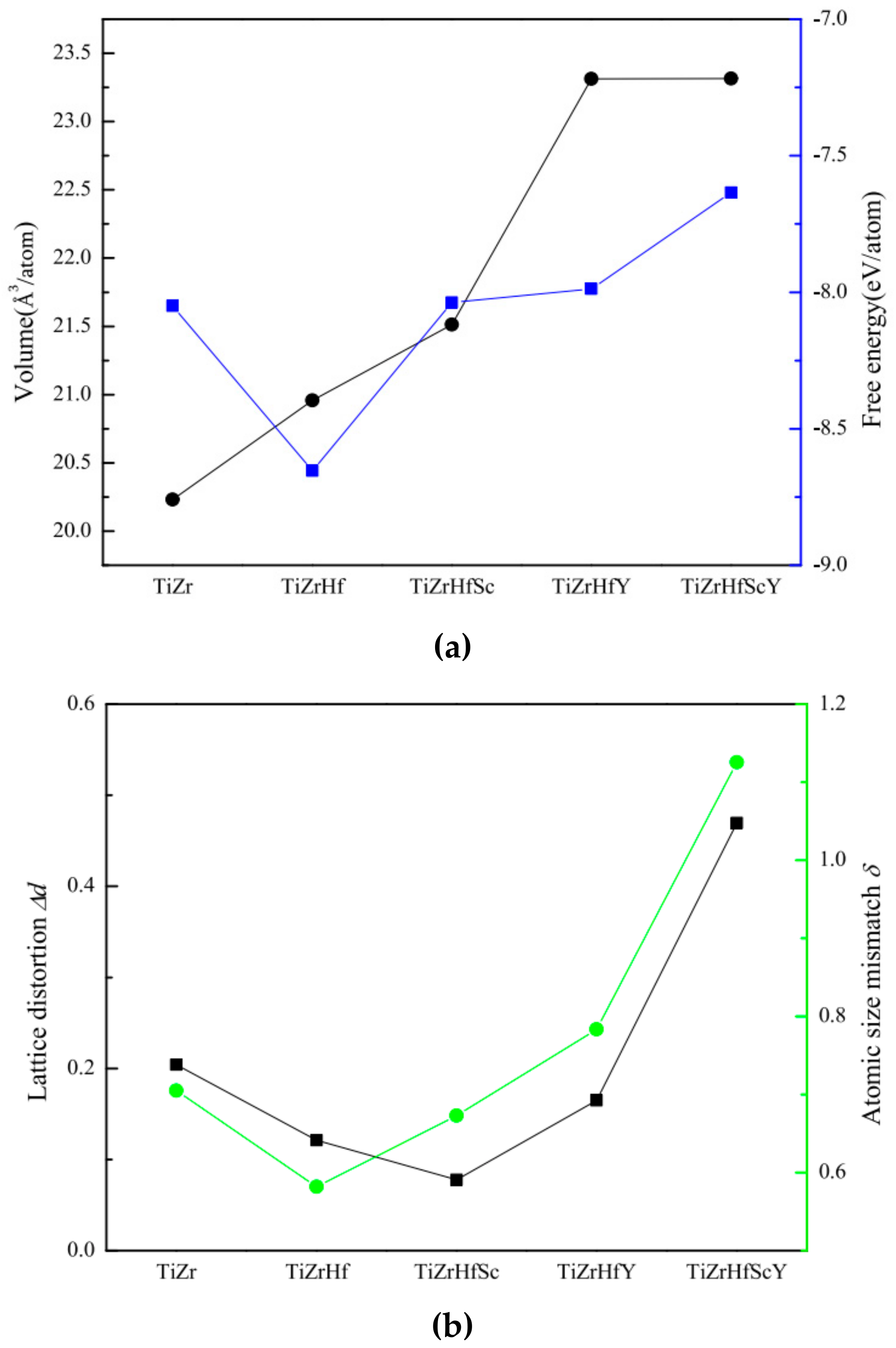
3.1. Lattice Parameters and Lattice Distortion of HCP CSAs
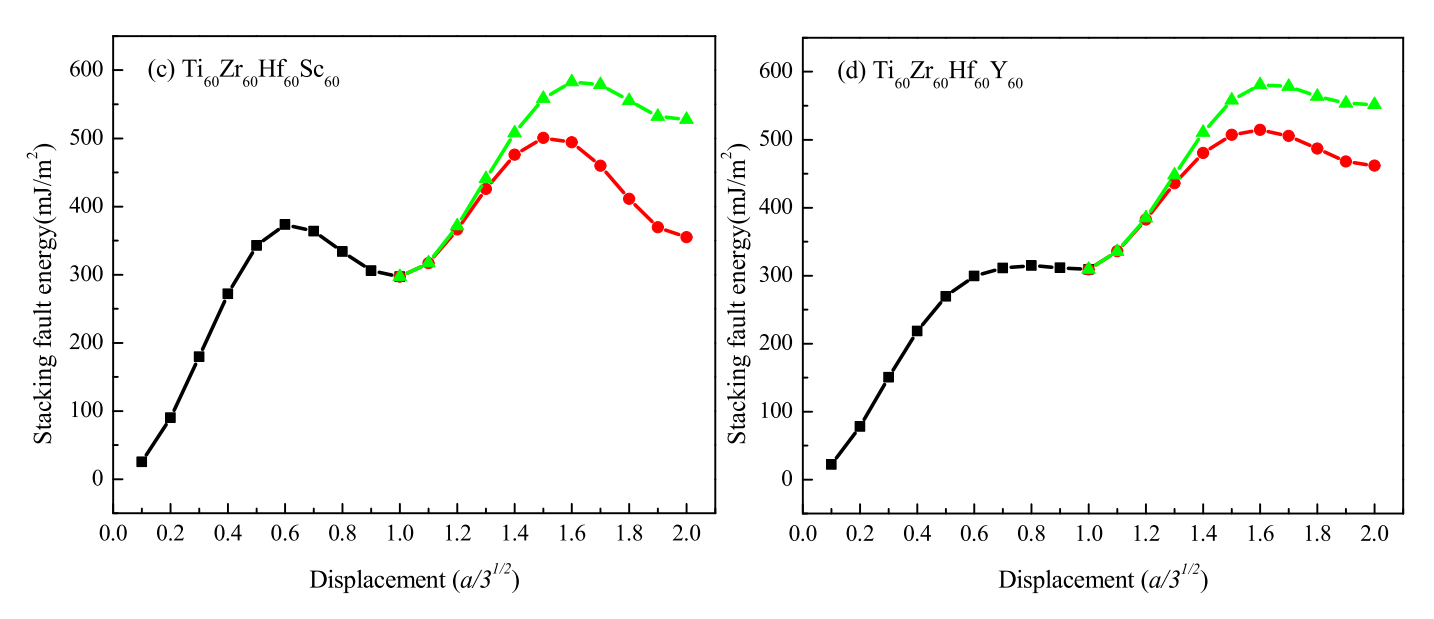
3.2. Deformation Mechanisms in HCP CSAs
3.3. Mesoscopic Studies on Dislocation Plasticity of CSAs
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Stocks, G.M.; Jin, K.; Lu, C.; Bei, H.; Sales, B.C.; Wang, L.; Béland, L.K.; Stoller, R.E.; Samolyuk, G.D.; et al. Influence of chemical disorder on energy dissipation and defect evolution in concentrated solid solution alloys. Nat. Commun. 2015, 6, 8736. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Bei, H.; Pharr, G.M.; George, E.P. Temperature dependence of the mechanical properties of equiatomic solid solution alloys with face-centered cubic crystal structures. Acta Mater. 2014, 81, 428–441. [Google Scholar] [CrossRef]
- Gao, M.C.; Zhang, C.; Gao, P.; Zhang, F.; Ouyang, L.; Widom, M.; Hawk, J. Thermodynamics of concentrated solid solution alloys. Curr. Opin. Solid State Mater. Sci. 2017, 21, 238–251. [Google Scholar] [CrossRef]
- Gao, L.; Chen, R.; Han, E. Solid solution strengthening behaviors in binary Mg–Y single phase alloys. J. Alloy Compd. 2009, 472, 234–240. [Google Scholar] [CrossRef]
- Huang, Y.-S.; Chen, L.; Lui, H.-W.; Cai, M.-H.; Yeh, J.-W. Microstructure, hardness, resistivity and thermal stability of sputtered oxide films of AlCoCrCu0.5NiFe high-entropy alloy. Mater. Sci. Eng. A 2007, 457, 77–83. [Google Scholar] [CrossRef]
- Senkov, O.N.; Scott, J.M.; Senkova, S.V.; Miracle, D.B.; Woodward, C.F. Microstructure and room temperature properties of a high-entropy TaNbHfZrTi alloy. J. Alloys Compd. 2011, 509, 6043–6048. [Google Scholar] [CrossRef]
- Manzoni, A.; Daoud, H.; Mondal, S.; van Smaalen, S.; Völkl, R.; Glatzel, U.; Wanderka, N. Investigation of phases in Al23Co15Cr23Cu8Fe15Ni16 and Al8Co17Cr17Cu8Fe17Ni33 high entropy alloys and comparison with equilibrium phases predicted by Thermo-Calc. J. Alloy Compd. 2013, 552, 430–436. [Google Scholar] [CrossRef]
- Murty, B.S.; Yeh, J.-W.; Ranganathan, S.; Bhattacharjee, P. High-Entropy Alloys; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Zhang, Y.; Zuo, T.T.; Tang, Z.; Gao, M.C.; Dahmen, K.A.; Liaw, P.K.; Lu, Z.P. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 2014, 61, 1–93. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Tsai, C.-W.; Juan, C.-C.; Chuang, M.-H.; Yeh, J.-W.; Chin, T.-S.; Chen, S.-K. Amorphization of equimolar alloys with HCP elements during mechanical alloying. J. Alloy Compd. 2010, 506, 210–215. [Google Scholar] [CrossRef]
- Youssef, K.M.; Zaddach, A.J.; Niu, C.; Irving, D.L.; Koch, C.C. A Novel Low-Density, High-Hardness, High-entropy Alloy with Close-packed Single-phase Nanocrystalline Structures. Mater. Res. Lett. 2014, 3, 95–99. [Google Scholar] [CrossRef]
- Gao, M.C.; Zhang, B.; Guo, S.; Qiao, J.; Hawk, J. High-entropy alloys in hexagonal close-packed structure. Metall. Mater. Trans. A 2016, 47, 3322–3332. [Google Scholar] [CrossRef]
- Gao, M.C.; Alman, D.E. Searching for Next Single-Phase High-Entropy Alloy Compositions. Entropy 2013, 15, 4504–4519. [Google Scholar] [CrossRef]
- Takeuchi, A.; Amiya, K.; Wada, T.; Yubuta, K.; Zhang, W. High-Entropy Alloys with a Hexagonal Close-Packed Structure Designed by Equi-Atomic Alloy Strategy and Binary Phase Diagrams. JOM 2014, 66, 1984–1992. [Google Scholar] [CrossRef]
- Feuerbacher, M.; Heidelmann, M.; Thomas, C. Hexagonal high-entropy alloys. Mater. Res. Lett. 2015, 3, 1–6. [Google Scholar] [CrossRef]
- Huang, T.; Jiang, H.; Lu, Y.; Wang, T.; Li, T. Effect of Sc and Y addition on the microstructure and properties of HCP-structured high-entropy alloys. Appl. Phys. A 2019, 125, 180. [Google Scholar] [CrossRef]
- Rogal, Ł.; Czerwinski, F.; Jochym, P.; Litynska-Dobrzynska, L. Microstructure and mechanical properties of the novel Hf25Sc25Ti25Zr25 equiatomic alloy with hexagonal solid solutions. Mater. Des. 2016, 92, 8–17. [Google Scholar] [CrossRef]
- Zhang, F.; Zhao, S.; Jin, K.; Bei, H.; Popov, D.; Park, C.; Neuefeind, J.C.; Weber, W.J.; Zhang, Y. Pressure-induced fcc to hcp phase transition in Ni-based high entropy solid solution alloys. Appl. Phys. Lett. 2017, 110, 011902. [Google Scholar] [CrossRef]
- Niu, C.; LaRosa, C.R.; Miao, J.; Mills, M.J.; Ghazisaeidi, M. Magnetically-driven phase transformation strengthening in high entropy alloys. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Basu, S.; Li, Z.; Pradeep, K.G.; Raabe, D. Strain Rate Sensitivity of a TRIP-Assisted Dual-Phase High-Entropy Alloy. Front. Mater. 2018, 5, 30. [Google Scholar] [CrossRef]
- Siegel, D.J. Generalized stacking fault energies, ductilities, and twinnabilities of Ni and selected Ni alloys. Appl. Phys. Lett. 2005, 87, 121901. [Google Scholar] [CrossRef]
- Achmad, T.L.; Fu, W.; Chen, H.; Zhang, C.; Yang, Z.-G. Effects of alloying elements concentrations and temperatures on the stacking fault energies of Co-based alloys by computational thermodynamic approach and first-principles calculations. J. Alloy Compd. 2017, 694, 1265–1279. [Google Scholar] [CrossRef]
- Achmad, T.L.; Fu, W.; Chen, H.; Zhang, C.; Yang, Z.-G. First-principles calculations of generalized-stacking-fault-energy of Co-based alloys. Comput. Mater. Sci. 2016, 121, 86–96. [Google Scholar] [CrossRef]
- MacLaren, J.M.; Gonis, A.; Schadler, G. First-principles calculation of stacking-fault energies in substitutionally disordered alloys. Phys. Rev. B 1992, 45, 14392–14395. [Google Scholar] [CrossRef]
- Zhao, S.; Stocks, G.M.; Zhang, Y. Stacking fault energies of face-centered cubic concentrated solid solution alloys. Acta Mater. 2017, 134, 334–345. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhuang, Y.; Hu, A.; Kai, J.; Liu, C. The origin of negative stacking fault energies and nano-twin formation in face-centered cubic high entropy alloys. Scr. Mater. 2016, 130, 96–99. [Google Scholar] [CrossRef]
- Zunger, A.; Wei, S.H.; Ferreira, L.; Bernard, J. Special quasirandom structures. Phys. Rev. Lett. 1990, 65, 353–356. [Google Scholar] [CrossRef] [PubMed]
- van de Walle, A.; Tiwary, P.; de Jong, M.; Olmsted, D.; Asta, M.; Dick, A.; Shin, D.; Wang, Y.; Chen, L.-Q.; Liu, Z.-K. Efficient stochastic generation of special quasirandom structures. Calphad 2013, 42, 13–18. [Google Scholar] [CrossRef]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Wisesa, P.; McGill, K.A.; Mueller, T. Efficient generation of generalized Monkhorst-Pack grids through the use of informatics. Phys. Rev. B 2016, 93, 155109. [Google Scholar] [CrossRef]
- Zheng, G. Molecular dynamics and first-principles studies on the deformation mechanisms of nanostructured cobalt. J. Alloy Compd. 2010, 504, S467–S471. [Google Scholar] [CrossRef]
- Frenkel, J.; Kontorova, T. On the theory of plastic deformation and twinning. Izv. Akad. Nauk. SSSR Seriya Fiz. 1939, 1, 137–149. [Google Scholar]
- Lomdahl, P.S.; Srolovitz, D.J. Dislocation Generation in the Two-Dimensional Frenkel-Kontorova Model at High Stresses. Phys. Rev. Lett. 1986, 57, 2702–2705. [Google Scholar] [CrossRef]
- Srolovitz, D.; Lomdahl, P. Dislocation dynamics in the 2-D Frenkel-Kontorova model. Phys. D Nonlinear Phenom. 1986, 23, 402–412. [Google Scholar] [CrossRef]
- Song, H.; Tian, F.; Hu, Q.-M.; Vitos, L.; Wang, Y.; Shen, J.; Chen, N. Local lattice distortion in high-entropy alloys. Phys. Rev. Mater. 2017, 1, 023404. [Google Scholar] [CrossRef]
- Spedding, F.H.; Daane, A.H.; Herrmann, K.W. The crystal structures and lattice parameters of high-purity scandium, yttrium and the rare earth metals. Acta Crystallogr. 1956, 9, 559–563. [Google Scholar] [CrossRef]
- Raffy, C.; Furthmüller, J.; Bechstedt, F. Properties of hexagonal polytypes of group-IV elements from first-principles calculations. Phys. Rev. B 2002, 66, 075201. [Google Scholar] [CrossRef]

| Alloy Systems | This Work | Experimental | |||
|---|---|---|---|---|---|
| a | c | c/a | a | c | |
| TiZr | 3.092 | 4.875 | 1.577 | - | - |
| TiZrHf | 3.138 | 4.917 | 1.567 | 3.162 a | 4.997 a |
| TiZrHfSc | 3.166 | 4.958 | 1.566 | 3.184 b 3.198 a | 5.013 b 5.046 a |
| TiZrHfY | 3.251 | 5.091 | 1.566 | - | - |
| TiZrHfScY | 3.254 | 5.086 | 1.563 | - | - |
| Elements | Lattice Constants (Å) | c/a | Radius (Å) | Tm (℃) | Valence Configurations |
|---|---|---|---|---|---|
| Ti | a = 2.9509 c = 4.6826 | 1.59 | 1.462 | 1670 | 3p63d24s2 |
| Zr | a = 3.232 c = 5.147 | 1.59 | 1.603 | 1850 | 4s24p64d35s1 |
| Hf | a = 3.193 c = 5.052 | 1.57 | 1.578 | 2150 | 5p65d26s2 |
| Sc | a = 3.2899 c = 5.2529 | 1.59 | 1.641 | 1539 | 3s23p63d24s1 |
| Y | a = 3.6451 c = 5.7305 | 1.57 | 1.802 | 1526 | 4s24p64d15s2 |
| Alloy Systems | γUSF (mJ/m2) | γSF (mJ/m2) | γUT (mJ/m2) | γUFCC (mJ/m2) | γUT − γSF (mJ/m2) | γUFCC − γSF (mJ/m2) |
|---|---|---|---|---|---|---|
| TiZr | 235 | 216 | 384 | 396 | 168 | 180 |
| TiZrHf | 357 | 331 | 513 | 599 | 182 | 268 |
| TiZrHfSc | 374 | 297 | 500 | 583 | 203 | 286 |
| TiZrHfY | 314 | 309 | 514 | 580 | 205 | 271 |
| TiZrHfScY | 271 | 199 | 379 | 521 | 180 | 322 |
| TiZr | TiZrHf | TiZrHfSc | TiZrHfY | TiZrHfScY | |
|---|---|---|---|---|---|
| G (GPa) | 70.6 | 79.2 | 85.5 | 71.4 | 78.8 |
| Shear strength τy (MPa) | 311.5 ± 1.4 | 280.4 ± 1.0 | 342.3 ± 1.5 | 178.8 ± 1.0 | 275.2 ± 1.2 |
| Yield strength σy (MPa) | - | 773 | 1001 | 554 | 793 |
| τdis (MPa) | - | 257.6 | 333.6 | 184.6 | 264.3 |
| εp (%) | - | 17.0 | 21.9 | 17.7 | 15.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zheng, G. First-Principles Calculation and Kink-Dislocation Dynamics Simulation on Dislocation Plasticity in TiZr-Based Concentrated Solid-Solution Alloys. Metals 2023, 13, 351. https://doi.org/10.3390/met13020351
Liu Y, Zheng G. First-Principles Calculation and Kink-Dislocation Dynamics Simulation on Dislocation Plasticity in TiZr-Based Concentrated Solid-Solution Alloys. Metals. 2023; 13(2):351. https://doi.org/10.3390/met13020351
Chicago/Turabian StyleLiu, Yu, and Guangping Zheng. 2023. "First-Principles Calculation and Kink-Dislocation Dynamics Simulation on Dislocation Plasticity in TiZr-Based Concentrated Solid-Solution Alloys" Metals 13, no. 2: 351. https://doi.org/10.3390/met13020351
APA StyleLiu, Y., & Zheng, G. (2023). First-Principles Calculation and Kink-Dislocation Dynamics Simulation on Dislocation Plasticity in TiZr-Based Concentrated Solid-Solution Alloys. Metals, 13(2), 351. https://doi.org/10.3390/met13020351






