Intelligent Systems to Optimize and Predict Machining Performance of Inconel 825 Alloy
Abstract
1. Introduction
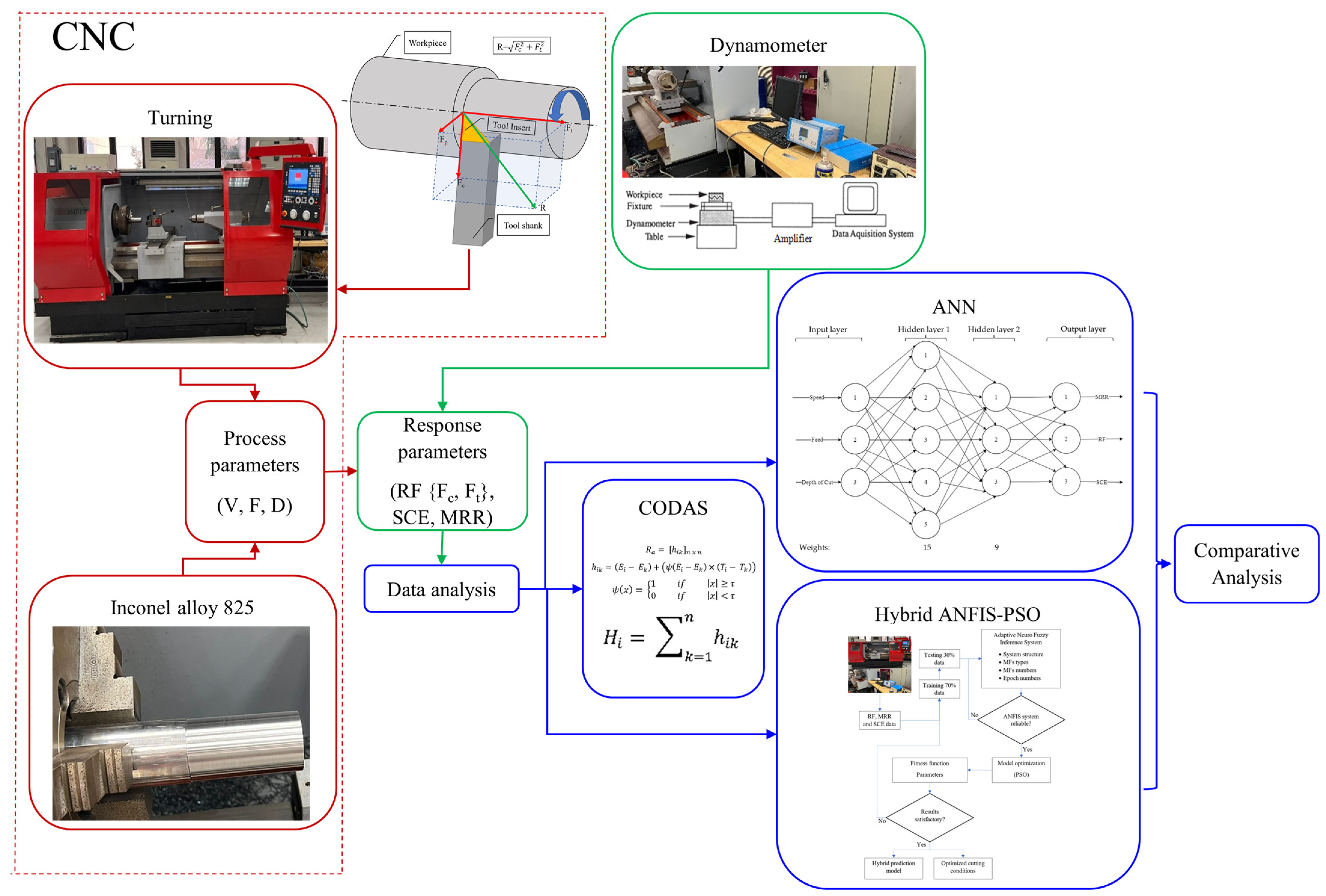
2. Materials and Methods
Design of Experiment
3. Results and Discussion
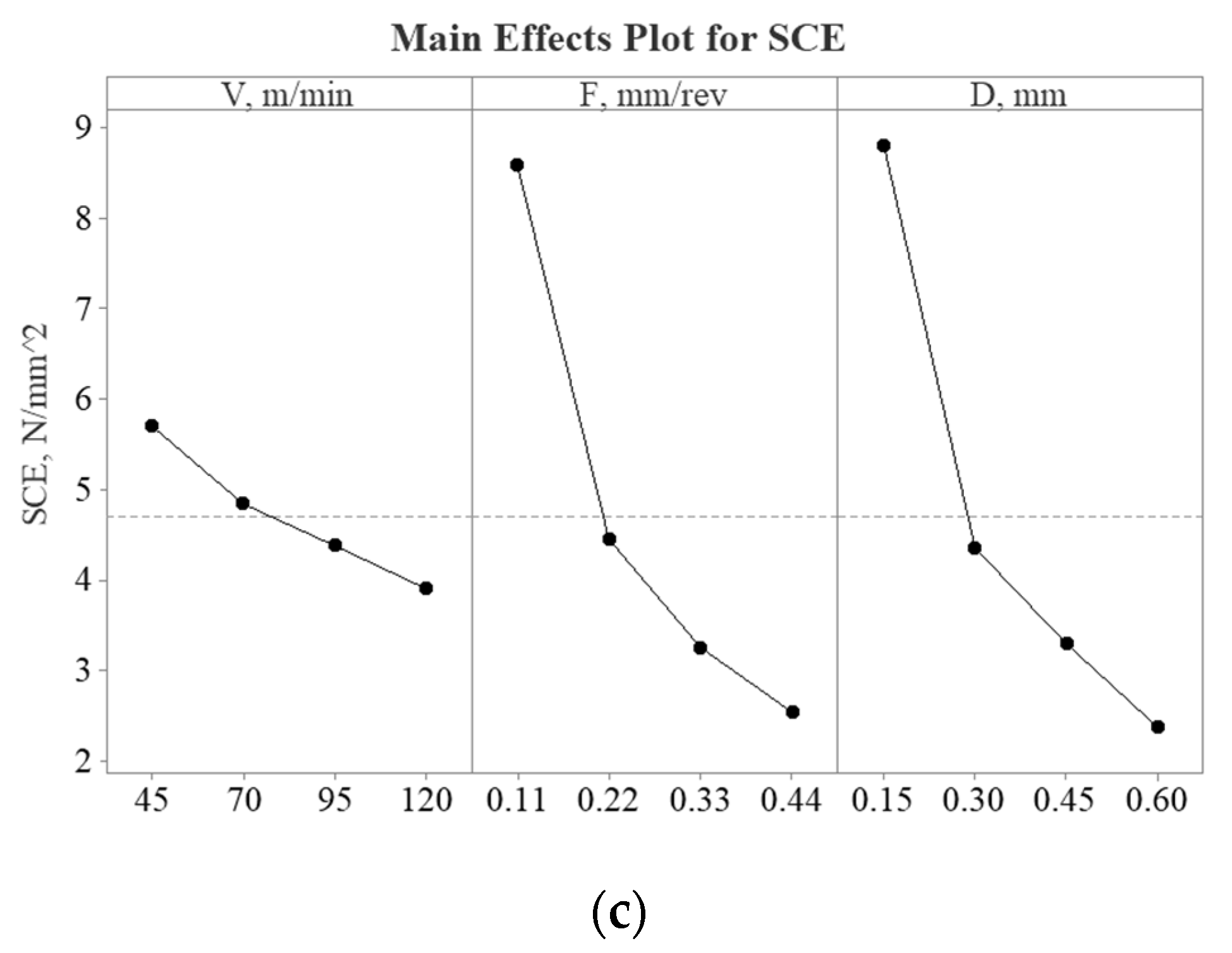
3.1. Effect of Input Parameters
3.2. Combinative Distance-Based Assesment Method
3.3. Optimization of Neural Network Parameters
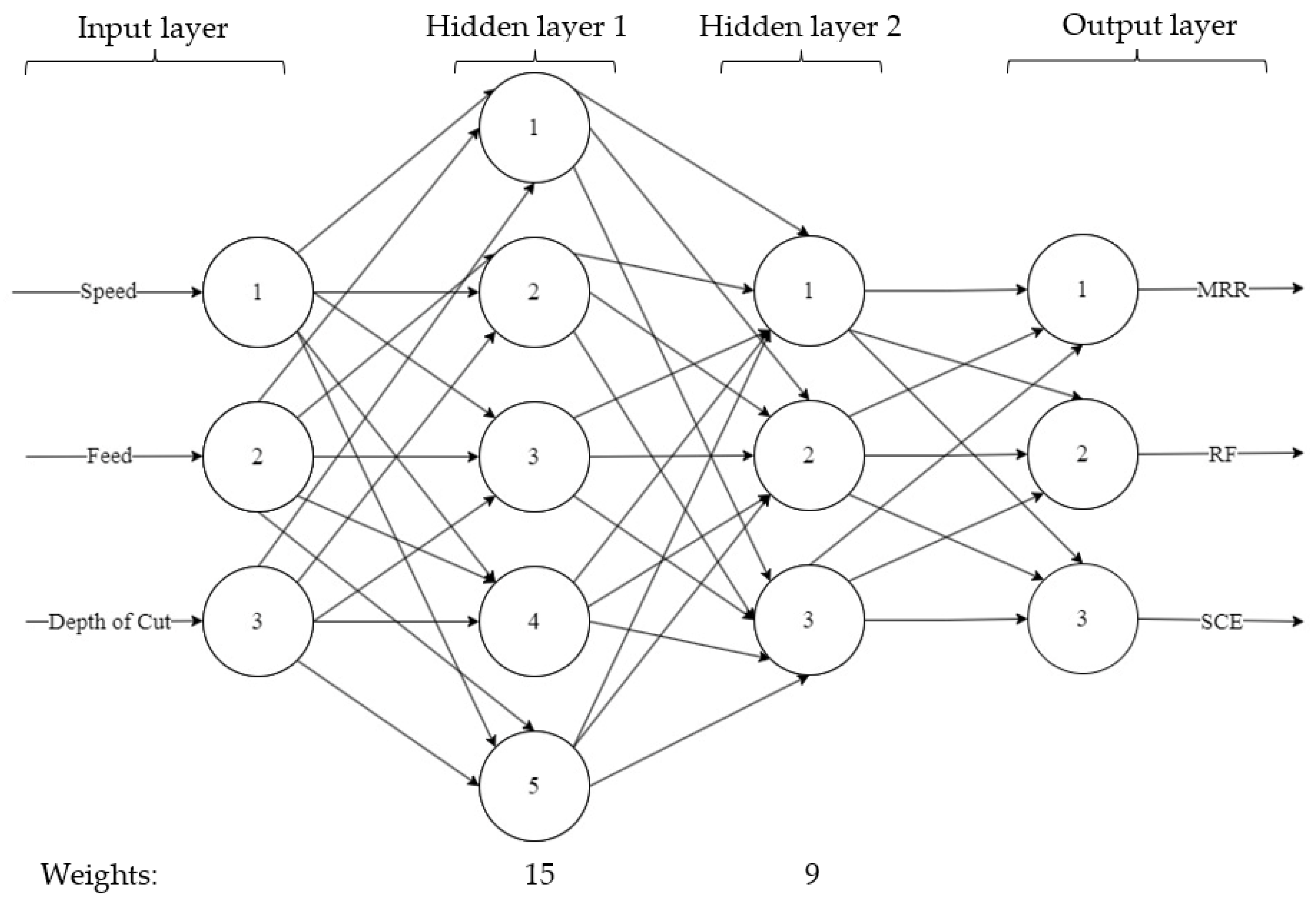
3.3.1. ANN
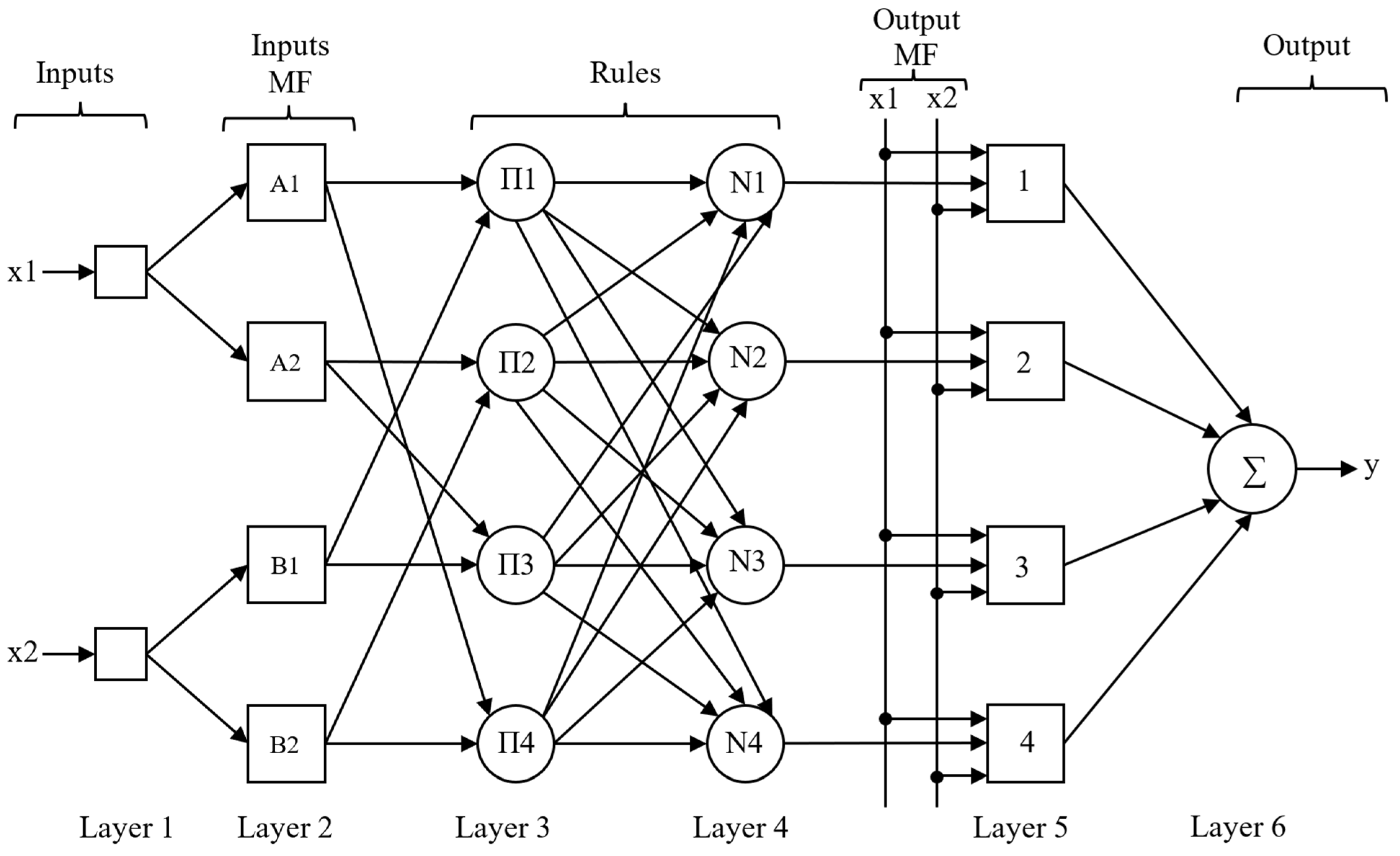
3.3.2. Adaptive Neuro-Fuzzy Inference System
- Rule 1: IF x1 is A1 AND x2 is B1 THEN y = f1 = k10 + k11x1 + k12x2
- Rule 2: IF x1 is A2 AND x2 is B2 THEN y = f2 = k20 + k21x1 + k22x2
- Rule 3: IF x1 is A2 AND x2 is B1 THEN y = f3 = k30 + k31x1 + k32x2
- Rule 4: IF x1 is A1 AND x2 is B2 THEN y = f4 = k40 + k41x1 + k42x2
3.3.3. Model Efficiency and Performance Criteria
3.4. Particle Swarm Optimization of ANFIS Method
4. Conclusions
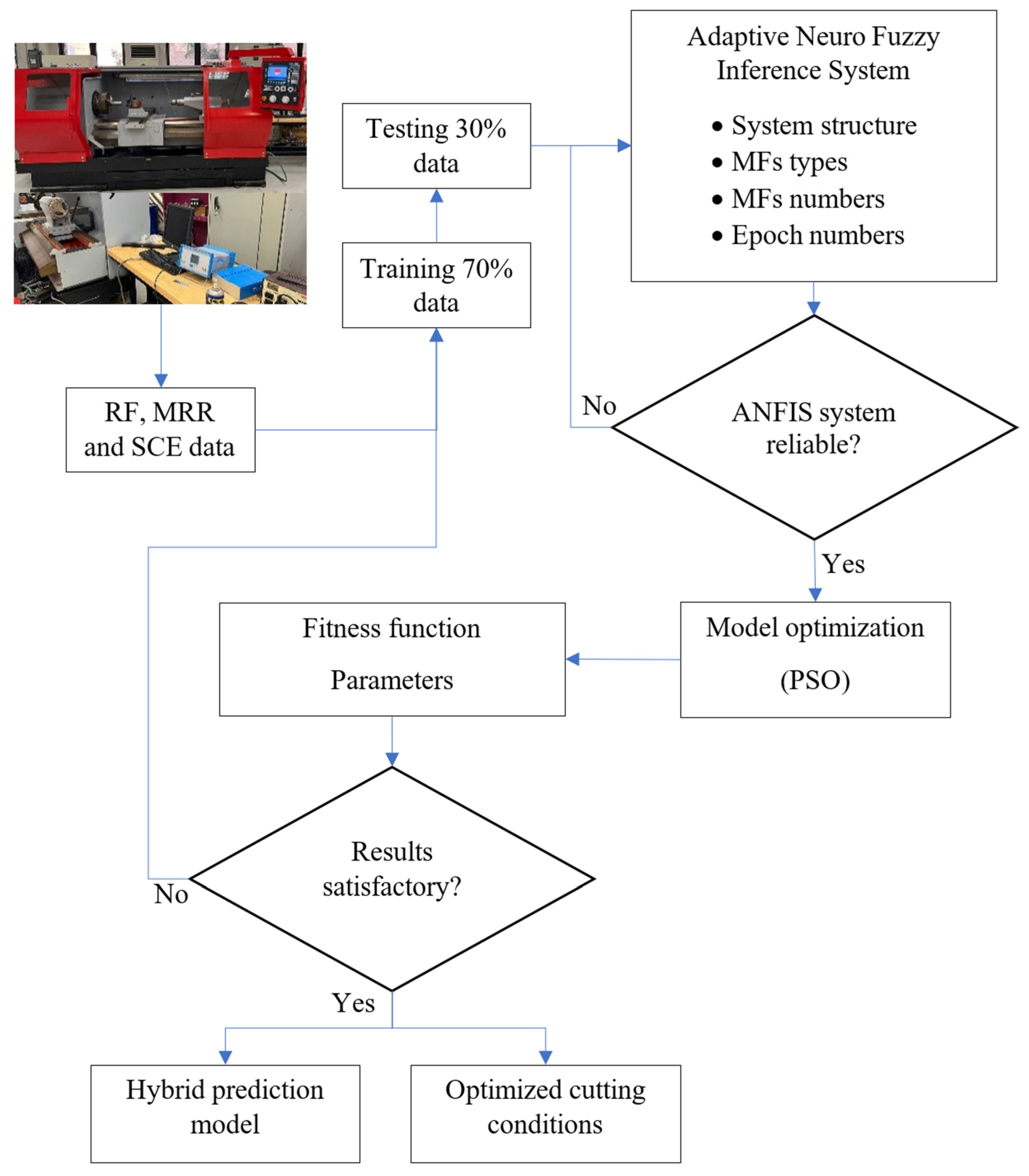
- As shown in Figure 2, optimized parameters can be used for machining the 825-super alloy by increasing the cutting speed to 120 m/min, feed rate to 0.44 mm/rev, and depth of cut to 0.4 mm which consequently will increase the metal removal rate, reduce energy consumption, and satisfy the requirements of green manufacturing.
- Given in Table 6, the optimized parameters resulted by the CODAS to improve Inconel 825 machinability (i.e., increase MRR and decrease SCE) were to set the cutting speed to 70 m/min, feed rate to 0.33 mm/rev, and depth of cut to 0.6 mm.
- In Table 10, the ANFIS-PSO model shows that minimizing RF optimum parameters were 82 m/min cutting speed, 0.11 mm/rev feed rate, and 0.15 m depth of cut. To maximize MRR, ANFIS-PSO resulted the factors to be set at 101 m/min cutting speed, 0.43 mm/rev feed rate, and 0.54 mm depth of cut. Lastly, to minimize SCE, the optimum levels were 45 m/min cutting speed, 0.44 mm/rev, and 0.6 mm depth of cut.
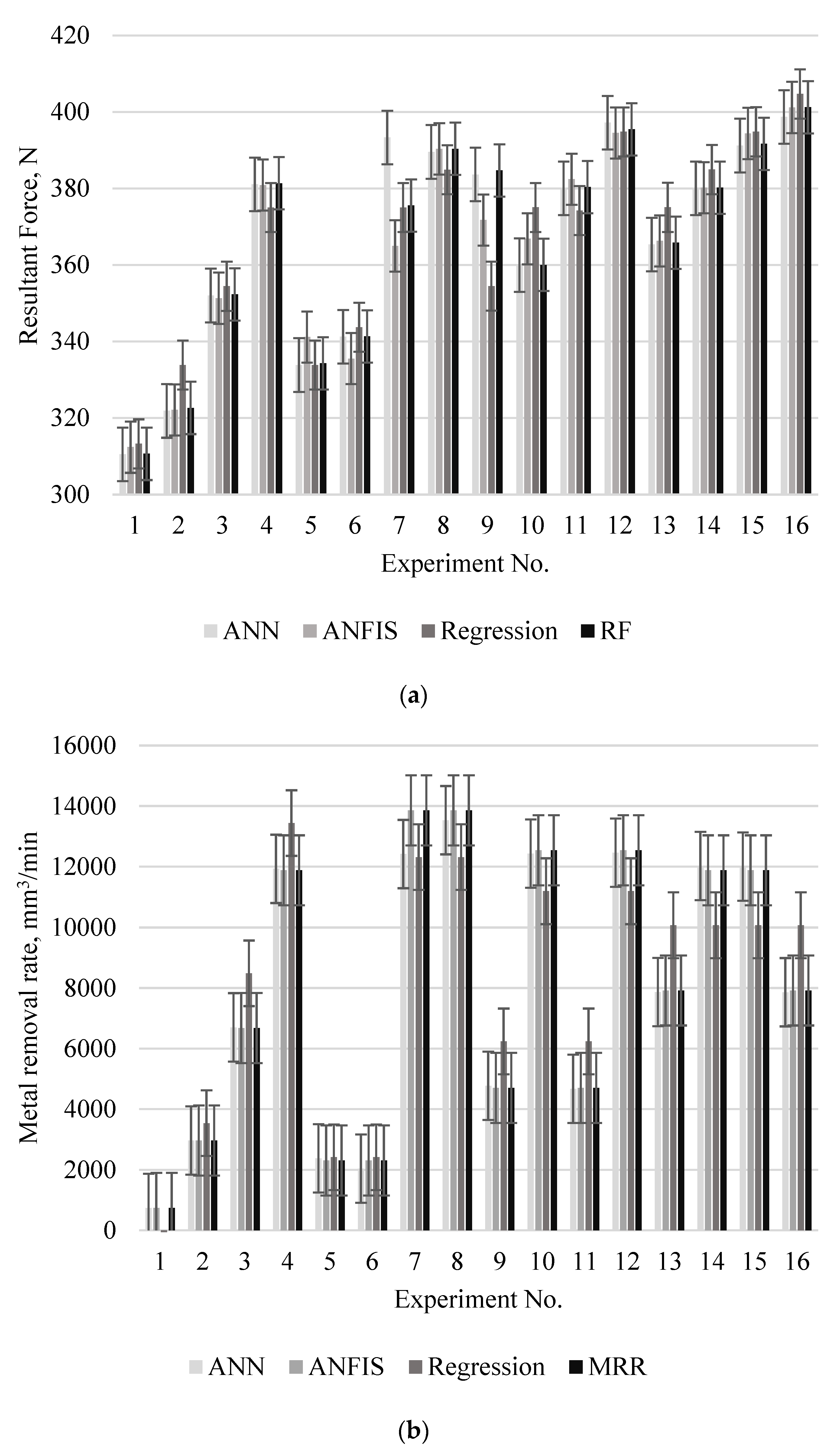
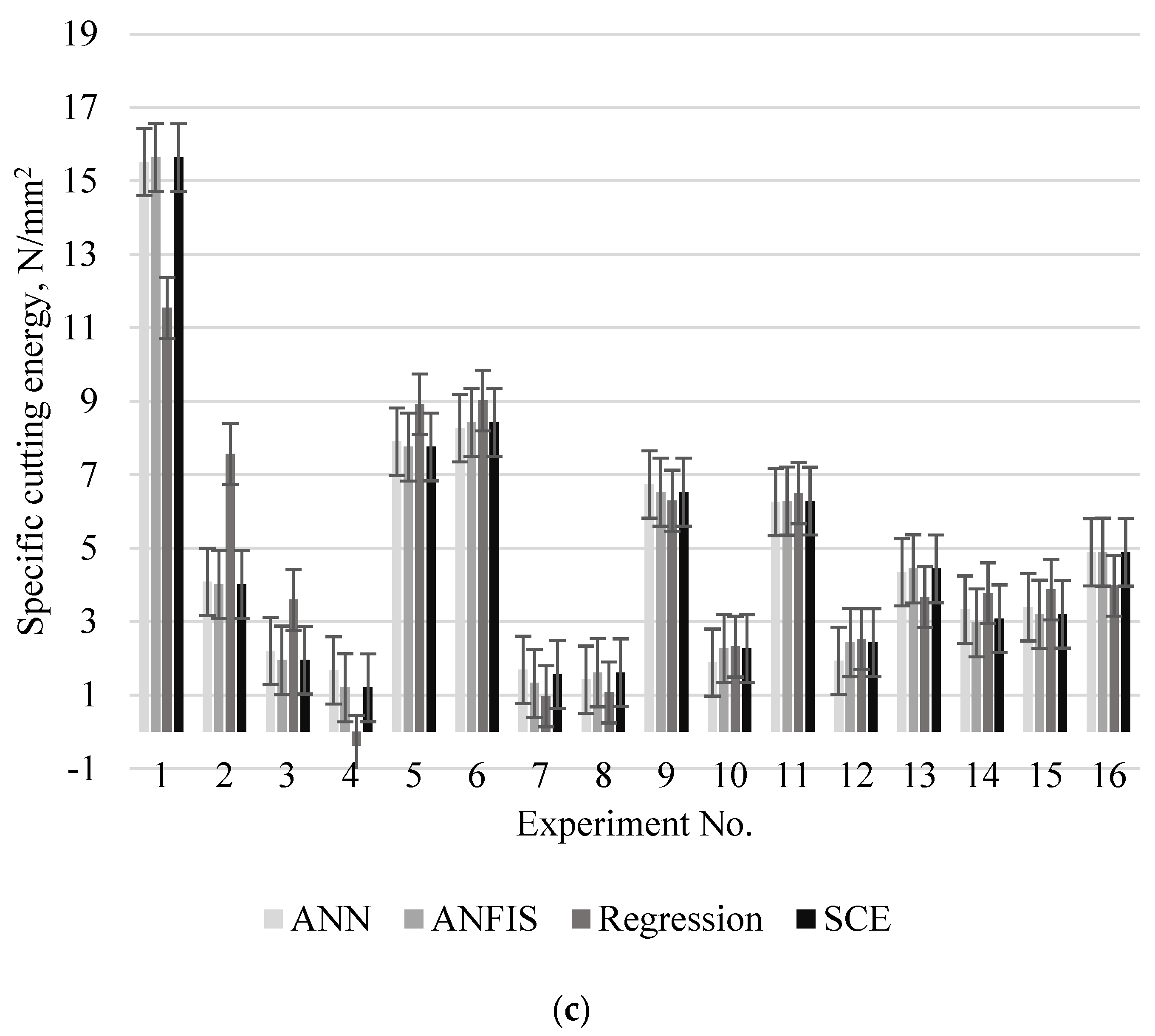
- Considering statistical errors and based on the provided data in Figure 6, the hybrid model ANFIS-PSO has proved to be a better method based on comparison to other predictive models on the time factor, the lower discrepancy in assessment, and having good computational efficiency.
- According to results and the literature, data-driven models have shown high potential in predicting and measuring machining parameters more accurately compared to analytical and statistical methods. The developed hybrid ANFIS-PSO method can be implemented for different super alloy in complex machining processes, including grinding, milling, and non-traditional machining processes. Further analysis of workpiece surface roughness, chip formation, and cutting temperature must be considered to increase the intelligence of the proposed prediction model.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pawade, R.S.; Sonawane, H.A.; Joshi, S.S. An analytical model to predict specific shear energy in high-speed turning of Inconel 718. Int. J. Mach. Tools Manuf. 2009, 49, 979–990. [Google Scholar] [CrossRef]
- Thakur, A.; Gangopadhyay, S.; Maity, K.P.; Sahoo, S.K. Evaluation on Effectiveness of CVD and PVD Coated Tools during Dry Machining of Incoloy 825. Tribol. Trans. 2016, 59, 1048–1058. [Google Scholar] [CrossRef]
- Reddy, M.C.; Venkata Rao, K.; Suresh, G. An experimental investigation and optimization of energy consumption and surface defects in wire cut electric discharge machining. J. Alloy. Compd. 2021, 861, 158582. [Google Scholar] [CrossRef]
- Singh, A.; Anandita, S.; Gangopadhyay, S. Microstructural Analysis and Multiresponse Optimization During ECM of Inconel 825 Using Hybrid Approach. Mater. Manuf. Process. 2015, 30, 842–851. [Google Scholar] [CrossRef]
- Thakur, A.; Mohanty, A.; Gangopadhyay, S.; Maity, K.P. Tool Wear and Chip Characteristics during Dry Turning of Inconel 825. Procedia Mater. Sci. 2014, 5, 2169–2177. [Google Scholar] [CrossRef]
- Rahul; Abhishek, K.; Datta, S.; Biswal, B.B.; Mahapatra, S.S. Machining performance optimization for electro-discharge machining of Inconel 601, 625, 718 and 825: An integrated optimization route combining satisfaction function, fuzzy inference system and Taguchi approach. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 3499–3527. [Google Scholar] [CrossRef]
- Mohanty, S.D.; Mahapatra, S.S.; Mohanty, R.C.; Khuntia, S.K.; Mohapatra, J.A. Perceptive Approach for Multi-objective Optimization of Die-Sinking EDM Process Parameters with Utility Concept and Taguchi Method for Sustainable Machining. In Proceedings of the Recent Advances in Mechanical Engineering; Springer: Singapore, 2023; pp. 133–141. [Google Scholar]
- Murthi, C.S.; Arunachalam, V.P. Optimization of High-speed CNC Face Milling of Inconel 825 Alloy, Using Box Behnken based Response Surface Methodology. J. Balk. Tribol. Assoc. 2018, 24, 586–599. [Google Scholar]
- Saravanakumar, A.; Rajeshkumar, L.; Sisindri Reddy, G.; Narashima Prasad, K.; Pranava Adithya, M.; Suryaprakash Reddy, P.; Harsha Vardhan, P.; Bala Narasimhudu, P. Multi-response Optimization of Turning Parameters for AZ91D Magnesium Alloy Using Gray-Based Taguchi Approach. Proceedings of Recent Advances in Mechanical Engineering; Springer: Singapore, 2023; pp. 389–397. [Google Scholar]
- Cesén, M.; Vila, C.; Ayabaca, C.; Zambrano, I.; Valverde, J.; Fuentes, P. Cost optimization of the AISI-1018 turning process under sustainable manufacturing. Mater. Today Proc. 2022, 49, 58–63. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Amiri, M.; Zavadskas, E.K.; Hooshmand, R.; Antuchevičienė, J. Fuzzy extension of the CODAS method for multi-criteria market segment evaluation. J. Bus. Econ. Manag. 2017, 18, 1–19. [Google Scholar] [CrossRef]
- Mathew, M.; Sahu, S. Comparison of new multi-criteria decision making methods for material handling equipment Selection. Manag. Sci. Lett. 2018, 8, 139–150. [Google Scholar] [CrossRef]
- Stojčić, M.; Zavadskas, E.K.; Pamučar, D.; Stević, Ž.; Mardani, A. Application of MCDM Methods in Sustainability Engineering: A Literature Review 2008–2018. Symmetry 2019, 11, 350. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. A new combinative distance-based assessment (CODAS) method for multi-criteria decision-making. Econ. Comput. Econ. Cybern. Stud. Res. 2016, 50, 25–44. [Google Scholar]
- Bolturk, E. Pythagorean fuzzy CODAS and its application to supplier selection in a manufacturing firm. J. Enterp. Inf. Manag. 2018, 31, 550–564. [Google Scholar] [CrossRef]
- Sofuoğlu, M.A. A new hybrid decision-making strategy of cutting fluid selection for manufacturing environment. Sādhanā 2021, 46, 94. [Google Scholar] [CrossRef]
- Adalı, E.A.; Tuş, A. Hospital site selection with distance-based multi-criteria decision-making methods. Int. J. Healthc. Manag. 2021, 14, 534–544. [Google Scholar] [CrossRef]
- Kumari, A.; Acherjee, B. Selection of non-conventional machining process using CRITIC-CODAS method. Mater. Today Proc. 2022, 56, 66–71. [Google Scholar] [CrossRef]
- Karthik Pandiyan, G.; Prabaharan, T.; Jafrey Daniel James, D.; Sivalingam, V. Machinability Analysis and Optimization of Electrical Discharge Machining in AA6061-T6/15wt.% SiC Composite by the Multi-criteria Decision-Making Approach. J. Mater. Eng. Perform. 2022, 31, 3741–3752. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Kumar, V.; Singh, N.K. Study of Machining of Inconel 825 Super Alloy Using Powder Mixed EDM Process. Mater. Today Proc. 2018, 5, 18129–18134. [Google Scholar] [CrossRef]
- Muhammad, R. A Fuzzy Logic Model for the Analysis of Ultrasonic Vibration Assisted Turning and Conventional Turning of Ti-Based Alloy. Materials 2021, 14, 6572. [Google Scholar] [CrossRef]
- Riaz, A.A.; Muhammad, R.; Ullah, N.; Hussain, G.; Alkahtani, M.; Akram, W. Fuzzy Logic-Based Prediction of Drilling-Induced Temperatures at Varying Cutting Conditions along with Analysis of Chips Morphology and Burrs Formation. Metals 2021, 11, 277. [Google Scholar] [CrossRef]
- Muthuram, N.; Frank, F.C. Optimization of machining parameters using artificial Intelligence techniques. Mater. Today Proc. 2021, 46, 8097–8102. [Google Scholar] [CrossRef]
- Shivakoti, I.; Kibria, G.; Pradhan, P.M.; Pradhan, B.B.; Sharma, A. ANFIS based prediction and parametric analysis during turning operation of stainless steel 202. Mater. Manuf. Process. 2019, 34, 112–121. [Google Scholar] [CrossRef]
- Sofuoglu, M.A.; Orak, S. Prediction of stable cutting depths in turning operation using soft computing methods. Appl. Soft Comput. 2016, 38, 907–921. [Google Scholar] [CrossRef]
- Sada, S.O.; Ikpeseni, S.C. Evaluation of ANN and ANFIS modeling ability in the prediction of AISI 1050 steel machining performance. Heliyon 2021, 7, e06136. [Google Scholar] [CrossRef]
- Gopal, M. The Effect of Machining Parameters and Optimization of Temperature Rise in Turning Operation of Aluminium-6061 Using RSM and Artificial Neural Network. Period. Polytech. Mech. Eng. 2021, 65, 141–150. [Google Scholar] [CrossRef]
- Chiu, H.W.; Lee, C.H. Intelligent Machining System Based on CNC Controller Parameter Selection and Optimization. IEEE Access 2020, 8, 51062–51070. [Google Scholar] [CrossRef]
- Kennametal. KCUX. NPR/L. Available online: https://www.kennametal.com/us/en/products/fam.kcux-nprl.100002164.html?pdpQuery=KCU10:relevance:obsoleteFacet:false:allCategoriesKMT:47535256&sort=&pageSize=16&category=undefined (accessed on 2 February 2023).
- Thakur, A.; Dewangan, S.; Patnaik, Y.; Gangopadhyay, S. Prediction of Work Hardening during Machining Inconel 825 Using Fuzzy Logic Method. Procedia Mater. Sci. 2014, 5, 2046–2053. [Google Scholar] [CrossRef]
- Thakur, A.; Gangopadhyay, S.; Mohanty, A. Investigation on Some Machinability Aspects of Inconel 825 During Dry Turning. Mater. Manuf. Process. 2015, 30, 1026–1034. [Google Scholar] [CrossRef]
- Daramola, O.O.; Tlhabadira, I.; Olajide, J.L.; Daniyan, I.A.; Sadiku, E.R.; Masu, L.; VanStaden, L.R. Process Design for Optimal Minimization of Resultant Cutting Force during the Machining of Ti-6Al-4V: Response Surface Method and Desirability Function Analysis. Procedia CIRP 2019, 84, 854–860. [Google Scholar] [CrossRef]
- Chen, Z.; Lin Peng, R.; Zhou, J.; M’Saoubi, R.; Gustafsson, D.; Moverare, J. Effect of machining parameters on cutting force and surface integrity when high-speed turning AD 730™ with PCBN tools. Int. J. Adv. Manuf. Technol. 2019, 100, 2601–2615. [Google Scholar] [CrossRef]
- Buddaraju, K.M.; Sastry, G.R.K.; Kosaraju, S.; Saxena, K.K. Experimental studies and mathematical modelling of Inconel 600 with CVD coated TiN/TiCN/Al2O3/ZrCN inserts under dry machining Conditions. Indian J. Eng. Mater. Sci. 2022, 29, 385–393. [Google Scholar]
- Venkatesan, K.; Manivannan, K.; Devendiran, S.; Mathew, A.T.; Ghazaly, N.M.; Aadhavan; Bennyg, S.M.N. Study of Forces, Surface Finish and Chip Morphology on Machining of Inconel 825. In Proceedings of the 14th Global Congress on Manufacturing and Management (GCMM-2018), Brisbane, QLD, Australia, 5–7 December 2019; pp. 611–618. [Google Scholar]
- Thakur, A.; Gangopadhyay, S.; Maity, K.P. Effect of cutting speed and CVD multilayer coating on machinability of Inconel 825. Surf. Eng. 2014, 30, 516–523. [Google Scholar] [CrossRef]
- Cagan, S.C.; Buldum, B.B. Machinability investigation of Incoloy 825 in high-speed turning under dry conditions. Mater. -Rio De Jan. 2021, 26, e13066. [Google Scholar] [CrossRef]
- Gupta, M.K.; Pruncu, C.I.; Mia, M.; Singh, G.; Singh, S.; Prakash, C.; Sood, P.K.; Gill, H.S. Machinability Investigations of Inconel-800 Super Alloy under Sustainable Cooling Conditions. Materials 2018, 11, 2088. [Google Scholar] [CrossRef]
- Vasudevan, H.; Rajguru, R.; Jain, S.; Kaklotar, M.; Desai, J.; Mathur, S. Optimization of Machining Parameters in the Turning Operation of Inconel 825 Using Grey Relation Analysis. In Proceedings of the International Conference on Intelligent Manufacturing and Automation: ICIMA 2018; Springer: Singapore, 2019; pp. 413–424. [Google Scholar]
- Venkata Rao, K.; Parimi, S.; Suvarna Raju, L.; Suresh, G. Modelling and optimization of weld bead geometry in robotic gas metal arc-based additive manufacturing using machine learning, finite-element modelling and graph theory and matrix approach. Soft Comput. 2022, 26, 3385–3399. [Google Scholar] [CrossRef]
- de Almeida, R.; Goh, Y.M.; Monfared, R.; Steiner, M.T.A.; West, A. An ensemble based on neural networks with random weights for online data stream regression. Soft Comput. 2020, 24, 9835–9855. [Google Scholar] [CrossRef]
- Naresh, C.; Bose, P.S.C.; Rao, C.S.P. Artificial neural networks and adaptive neuro-fuzzy models for predicting WEDM machining responses of Nitinol alloy: Comparative study. SN Appl. Sci. 2020, 2, 314. [Google Scholar] [CrossRef]
- Ali, S. (Ed.) Introductory Chapter: Which Membership Function is Appropriate in Fuzzy System? In Fuzzy Logic Based in Optimization Methods and Control Systems and Its Applications; IntechOpen: Rijeka, Croatia, 2018; p. Ch. 1. [Google Scholar]
- Acayaba, G.M.A.; Escalona, P.M.d. Prediction of surface roughness in low speed turning of AISI316 austenitic stainless steel. CIRP J. Manuf. Sci. Technol. 2015, 11, 62–67. [Google Scholar] [CrossRef]
- Ghordoyee Milan, S.; Roozbahani, A.; Arya Azar, N.; Javadi, S. Development of adaptive neuro fuzzy inference system –Evolutionary algorithms hybrid models (ANFIS-EA) for prediction of optimal groundwater exploitation. J. Hydrol. 2021, 598, 126258. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; IEEE: Piscataway, NJ, USA, 2000; pp. 39–43. [Google Scholar]
- Heris, M.K. Evolutionary ANFIS Training in MATLAB. Yarpiz 2015. [Google Scholar]
- Thamrin, I. Analysis of the effect of the cutting speed on specific cutting energy in turning process. In Proceedings of the Sriwijaya international Conference on Science, Engineering, and Technology, Palembang, Indonesia, 25–26 October 2019. [Google Scholar]


| Properties | Values |
|---|---|
| Poisson’s ratio | 0.29–0.34 |
| Density (gm/cm3) | 8.14 |
| Yield strength (MPa) | 310 |
| Hardness Brinell (HB) | 190–240 |
| Elongation (%) | 45 |
| Tensile strength (MPa) | 690 |
| Melting point °C | 1370–1400 |
| Factors | Level 1 | Level 2 | Level 3 | Level 4 |
|---|---|---|---|---|
| Cutting speed, V, m/min | 45 | 70 | 95 | 120 |
| Feed rate, F, mm/rev | 0.11 | 0.22 | 0.33 | 0.44 |
| Depth of cut, D, mm | 0.15 | 0.3 | 0.45 | 0.6 |
| Exp. No. | V m/min | F mm/rev | D mm | Fc N | Ft N | Resultant Force N | MRR mm3/min | SCE N/mm2 |
|---|---|---|---|---|---|---|---|---|
| 1 | 45 | 0.11 | 0.15 | 258 | 173 | 310.63 | 742.50 | 15.64 |
| 2 | 45 | 0.22 | 0.3 | 265 | 184 | 322.62 | 2970 | 4.02 |
| 3 | 45 | 0.33 | 0.45 | 290 | 200 | 352.28 | 6682.50 | 1.95 |
| 4 | 45 | 0.44 | 0.6 | 317 | 212 | 381.36 | 11,880 | 1.20 |
| 5 | 70 | 0.11 | 0.3 | 256 | 215 | 334.31 | 2310 | 7.76 |
| 6 | 70 | 0.22 | 0.15 | 278 | 198 | 341.30 | 2310 | 8.42 |
| 7 | 70 | 0.33 | 0.6 | 310 | 212 | 375.55 | 13,860 | 1.57 |
| 8 | 70 | 0.44 | 0.45 | 319 | 225 | 390.37 | 13,860 | 1.61 |
| 9 | 95 | 0.11 | 0.45 | 323 | 209 | 384.72 | 4702.50 | 6.53 |
| 10 | 95 | 0.22 | 0.6 | 300 | 199 | 360.00 | 12,540 | 2.27 |
| 11 | 95 | 0.33 | 0.15 | 311 | 219 | 380.37 | 4702.50 | 6.28 |
| 12 | 95 | 0.44 | 0.3 | 321 | 231 | 395.48 | 12,540 | 2.43 |
| 13 | 120 | 0.11 | 0.6 | 293 | 219 | 365.80 | 7920 | 4.44 |
| 14 | 120 | 0.22 | 0.45 | 305 | 227 | 380.21 | 11,880 | 3.08 |
| 15 | 120 | 0.33 | 0.3 | 317 | 230 | 391.65 | 11,880 | 3.20 |
| 16 | 120 | 0.44 | 0.15 | 323 | 238 | 401.21 | 7920 | 4.89 |
| Resultant Force ANOVA | |||||||
|---|---|---|---|---|---|---|---|
| Factors | DF | Seq SS | Adj SS | Adj MS | F-Value | p-Value | Contribution |
| Cutting speed | 3 | 4676.9 | 4676.9 | 1558.95 | 16.9 | 0.002 | 41.66% |
| Feed rate | 3 | 5108.6 | 5108.6 | 1702.87 | 18.46 | 0.002 | 45.52% |
| Depth of cut | 3 | 885.1 | 885.1 | 295.05 | 3.2 | 0.105 | 7.89% |
| Residual error | 6 | 553.4 | 553.4 | 92.23 | - | - | 4.93% |
| Total | 15 | 11,224 | - | - | - | - | 100.00% |
| Fitness statistics | R2 = 0.95 | Adjusted R2 = 0.88 | |||||
| Metal removal rate ANOVA | |||||||
| Factors | DF | Seq SS | Adj SS | Adj MS | F-Value | p-Value | Contribution |
| Cutting speed | 3 | 39,625,988 | 39,625,988 | 13,208,663 | 2.49 | 0.158 | 12.33% |
| Feed rate | 3 | 124,894,688 | 124,894,688 | 41,631,563 | 7.85 | 0.017 | 38.88% |
| Depth of cut | 3 | 124,894,688 | 124,894,688 | 41,631,563 | 7.85 | 0.017 | 38.88% |
| Residual error | 6 | 31,839,638 | 31,839,638 | 5,306,606 | - | - | 9.91% |
| Total | 15 | 321,255,000 | - | - | - | - | 100.00% |
| Fitness statistics | R2 = 0.9 | Adjusted R2 = 0.75 | |||||
| Specific cutting energy ANOVA | |||||||
| Factors | DF | Seq SS | Adj SS | Adj MS | F-Value | p-Value | Contribution |
| Cutting speed | 3 | 17,026,069 | 17,026,069 | 5,675,356 | 1.21 | 0.384 | 3.44% |
| Feed rate | 3 | 2.13 × 108 | 2.13 × 108 | 70,922,810 | 15.1 | 0.003 | 43.05% |
| Depth of cut | 3 | 2.36 × 108 | 2.36 × 108 | 78,785,716 | 16.77 | 0.003 | 47.81% |
| Residual error | 6 | 28,185,704 | 28,185,704 | 4,697,617 | - | - | 5.70% |
| Total | 15 | 4.94 × 108 | - | - | - | - | 100.00% |
| Fitness statistics | R2 = 0.94 | Adjusted R2 = 0.86 | |||||
| Process Parameters | Beneficial | Non Beneficial | ||||
|---|---|---|---|---|---|---|
| Speed m/min | Feed mm/rev | Depth mm | Metal Removal Rate mm3/min | Resultant Force N | Specific Cutting Energy N/mm2 | |
| Weights | - | - | - | 0.5 | 0.15 | 0.35 |
| Min | 45 | 0.11 | 0.15 | 477 | 310.63 | 112.07 |
| Max | 120 | 0.44 | 0.6 | 8910 | 401.21 | 1459.39 |
| Exp. (i|j) | Weight Criteria | 0.15 | 0.5 | 0.35 | Ei | Ti | Assessment Score | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Normalization | Weight Normalization | |||||||||
| RF N | MRR mm3/min | SCE N/mm2 | RF N | MRR mm3/min | SCE N/mm2 | Hi | Rank | |||
| 1 | 1.000 | 0.054 | 0.077 | 0.150 | 0.027 | 0.027 | 0.034 | 0.034 | −4.122 | 16 |
| 2 | 0.963 | 0.214 | 0.299 | 0.144 | 0.107 | 0.104 | 0.115 | 0.186 | −2.838 | 13 |
| 3 | 0.882 | 0.482 | 0.615 | 0.132 | 0.241 | 0.215 | 0.286 | 0.419 | −0.124 | 8 |
| 4 | 0.815 | 0.857 | 1.000 | 0.122 | 0.429 | 0.350 | 0.516 | 0.731 | 3.568 | 3 |
| 5 | 0.929 | 0.167 | 0.155 | 0.139 | 0.083 | 0.054 | 0.067 | 0.107 | −3.602 | 14 |
| 6 | 0.910 | 0.167 | 0.143 | 0.137 | 0.083 | 0.050 | 0.064 | 0.100 | −3.642 | 14 |
| 7 | 0.827 | 1.000 | 0.764 | 0.124 | 0.500 | 0.268 | 0.531 | 0.722 | 3.813 | 1 |
| 8 | 0.796 | 1.000 | 0.745 | 0.119 | 0.500 | 0.261 | 0.528 | 0.710 | 3.764 | 2 |
| 9 | 0.807 | 0.339 | 0.184 | 0.121 | 0.170 | 0.064 | 0.148 | 0.185 | −2.320 | 12 |
| 10 | 0.863 | 0.905 | 0.529 | 0.129 | 0.452 | 0.185 | 0.454 | 0.597 | 2.575 | 4 |
| 11 | 0.817 | 0.339 | 0.191 | 0.122 | 0.170 | 0.067 | 0.148 | 0.189 | −2.309 | 11 |
| 12 | 0.785 | 0.905 | 0.494 | 0.118 | 0.452 | 0.173 | 0.450 | 0.573 | 2.506 | 5 |
| 13 | 0.849 | 0.571 | 0.270 | 0.127 | 0.286 | 0.095 | 0.268 | 0.338 | −0.410 | 9 |
| 14 | 0.817 | 0.857 | 0.390 | 0.123 | 0.429 | 0.136 | 0.416 | 0.518 | 1.968 | 6 |
| 15 | 0.793 | 0.857 | 0.375 | 0.119 | 0.429 | 0.131 | 0.415 | 0.509 | 1.946 | 7 |
| 16 | 0.774 | 0.571 | 0.245 | 0.116 | 0.286 | 0.086 | 0.266 | 0.318 | −0.446 | 10 |
| Negative ideal solution | 0.116 | 0.027 | 0.027 | - | - | - | - | |||
| Layer Number | Equation | Layer Number | Equation |
|---|---|---|---|
| 1 | 4 | ||
| 2 | 5 | yi(5) = xi(5) [ki + kix1 + kix2] = [ki0 + ki1x1 + ki2x2] | |
| 3 | 6 | ||
| Membership function equations | Triangular = | ||
| Trapezoidal = | |||
| Gaussian = | |||
| Bell-shaped = | |||
| Sigmodal = | |||
| Exp. No. | Resultant Force, N | Metal Removal Rate, mm3/min | Specific Cutting Energy, N/mm2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Real | ANN | ANFIS | Real | ANN | ANFIS | Real | ANN | ANFIS | |
| 7 | 376 | 393 | 365 | 13,860 | 12,418 | 13,859 | 1.566 | 1.689 | 1.326 |
| 14 | 380 | 380 | 380 | 11,880 | 12,023 | 11,879 | 3.081 | 3.328 | 2.968 |
| Avg. RE% | 2.32 | 1.49 | 5.81 | 0.0003 | 7.97 | 9.46 | |||
| RMSE% | 3.16 | 2.09 | 8.38 | 0.0003 | 7.80 | 8.70 | |||
| MAE% | 2.26 | 1.50 | 6.49 | 0.0003 | 7.40 | 8.19 | |||
| MAPE% | 2.33 | 1.49 | 5.81 | 0.0003 | 7.97 | 9.46 | |||
| No. | Parameters | Value |
|---|---|---|
| 1 | Population size | 100 |
| 2 | Epoch | 50 |
| 2 | Inertia weight | 1 |
| 3 | Inertia weight damping ratio | 0.99 |
| 4 | No. of iterations | 1000 |
| 5 | Number of variables | 3 |
| 6 | Personal learning coefficient (C1) | 1 |
| 7 | Global learning coefficient (C2) | 2 |
| 8 | Lower range | 45 m/min, 0.11 mm/rev, 0.15 mm |
| 9 | Upper range | 120 m/min, 0.44 mm/rev, 0.6 mm |
| Response | Speed m/min | Feed mm/rev | Depth mm | Predicted | Actual | % RE |
|---|---|---|---|---|---|---|
| Resultant force | 82 | 0.11 | 0.15 | 242 | N/A | |
| MRR | 101 | 0.43 | 0.54 | 24,145 | N/A | |
| SCE | 45 | 0.44 | 0.6 | 1.20 | 1.20 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Tamimi, A.A.; Sanjay, C. Intelligent Systems to Optimize and Predict Machining Performance of Inconel 825 Alloy. Metals 2023, 13, 375. https://doi.org/10.3390/met13020375
Al-Tamimi AA, Sanjay C. Intelligent Systems to Optimize and Predict Machining Performance of Inconel 825 Alloy. Metals. 2023; 13(2):375. https://doi.org/10.3390/met13020375
Chicago/Turabian StyleAl-Tamimi, Abdulsalam Abdulaziz, and Chintakindi Sanjay. 2023. "Intelligent Systems to Optimize and Predict Machining Performance of Inconel 825 Alloy" Metals 13, no. 2: 375. https://doi.org/10.3390/met13020375
APA StyleAl-Tamimi, A. A., & Sanjay, C. (2023). Intelligent Systems to Optimize and Predict Machining Performance of Inconel 825 Alloy. Metals, 13(2), 375. https://doi.org/10.3390/met13020375






