Theoretical Forming Limit Diagram Based on Induced Stress in the Thickness Direction

Abstract

The conventional theoretical forming limit diagram (FLD) based on the plane stress state has defects due to the neglect of the stress in the thickness direction of the sheet. It is urgent to study the FLD which considers the stress in the thickness direction. Through the finite element simulation, it is further confirmed that the stress in the thickness direction will be induced in the deformation process. At the same time, the effect of the induced stress in the thickness direction on FLD is not the same as that always applied stress in the thickness direction during the deformation process. Based on the Modified Maximum Force Criterion (MMFC) instability theory, C-H instability theory, Mises and Hill48 yield criterion, the effects of the two stresses on FLD are compared. The induced stress in the thickness direction also affects the sensitivity of the coefficient of normal anisotropy $r$, but does not significantly change the effect of the stress-strain index $n$ on Forming Limit Curves (FLC). The theoretical calculations of the three materials TRIP780, AA5182, and 5754O are compared with the experimental data, which proves that the FLD which considers induced stress in the thickness direction is more accurate than the FLD of the plane stress.

1. Introduction

Forming limit is an important performance index and process parameter in sheet metal forming. It reflects the maximum degree of deformation that can be achieved before tensile instability during processing, which is one of the main basis for process and mold design. A forming limit diagram (FLD) has been developed to determine the sheet forming limit. FLD can not only distinguish between safety points and failure points but also avoid failure problems in the actual forming process. Therefore, it is widely used in industrial production and promotes the development of sheet metal forming technology.

Keeler [1] (pp. 25–48) and Goodwin [2] (pp. 380–397) first proposed the FLD composed of ultimate strain, which consists of primary strain and secondary strain (two perpendicular directions along the plane of the sheet). Hiller [3] (p. 282) and Negroni [4] (p. 387) et al. proved that FLD is related to strain path according to Swift instability criterion. Korhonen [5] (pp. 303–309) assumed that instability is related to the previous strain history and the strain increment ratio at the time of instability. The Swift instability criterion is used in the positive strain ratio zone, and the Hill instability criterion is used in the negative strain ratio zone to establish the FLD. Lee and Kobayashi [6] (pp. 277–290) used the M-K criterion to analyze the forming limit under complex strain paths and found that only considering the initial necking belt orientation perpendicular to the direction of the maximum principal stress would result in a high FLD.

FLD and its associated analytical and experimental techniques have been widely used for 40 years. Traditional FLD predictions are based on plane stress loading conditions, and the effects of stress in the thickness direction are often ignored. However, the sheet will establish non-negligible normal stress in the thickness direction during the deformation process. For example, normal stress becomes more significant in processes such as bulging. Therefore, in the study of sheet-forming properties, it is necessary to consider the influence of stress in the thickness direction, and further research is urgently needed.

Gotoh et al. [7] (pp. 123–132) proposed an analytical expression. Due to the presence of compressive stress in the thickness direction, the plane strain forming limit in the strain space is improved. They theoretically proved that the out-of-plane stress (even if only one-tenth of the yield stress) can increase the forming ultimate strain. Therefore, it can be used to delay the fracture of the specimen during the stamping process. Smith et al. [8] (pp. 1567–1583) developed a new model that takes into account the effects of compressive stress, so the predicted forming performance is much more accurate than predicted by the Gotoh model. Nurcheshmeh and Green [9] (pp. 213–226) extended the M-K model to a three-dimensional stress state for predicting FLC with different through-thickness stress values. Allwood and Shoule [10] (pp. 1207–1230) proposed a more general forming limit diagram, including positive stress in the thickness direction and shear stress in the thickness direction. Matin and Smith [11] (pp. 671–690) improved the existing model and discussed the effect of stress in thickness direction on FLD. Mozhdeh Erfanian and Ramin Hashemi [12] (pp. 316–326) continuously applied constant stress in the thickness direction, and analyzed the influence of normal stress through the thickness on different forming limit diagrams.

With the development of computer technology and the maturity of finite element technology, the actual forming process of the sheet can be simulated. The results show that even in simple uniaxial tension and biaxial tension tests, the stress in the thickness direction appears during the deformation process. It indicates that stress in the thickness direction is universal. And the appearance of the stress in the thickness direction is induced as the sheet is deformed. This is different from the artificially applied stress in the normal direction, the results may be very different.

In the engineering stress-strain curve, when the engineering stress reaches the maximum value, the material will not immediately fail but will continue to deform. The applied stress remains constant at the maximum level until localized necking occurs. When the loading force is reduced, the sample is broken. Therefore, the maximum force criterion is not a sufficient condition for predicting fracture, and more factors should be included to improve accuracy. Based on this point of view, Hora proposed the revised maximum force criterion (MMFC) [13,14,15,16,17,18]. The MMFC model takes into account the factors of additional tensile stress caused by material necking, which delays localized necking or cracking. Since the model takes into account more factors, its prediction of sheet metal forming is more accurate. Moreover, when predicting the theoretical forming limit (FLD), the model only applies the yield criterion and the stress-strain relationship that the material satisfies, and does not require too many material parameters, so it is also more streamlined.

Through computer simulation, it is proved that the sheet material will induce stress in the thickness direction during the deformation process. The forming limit is calculated based on the MMFC instability criterion and the induced stress thickness direction. The traditional forming limit model is extended to a three-dimensional stress state to predict the forming limit curve of sheet metal based on induced stress in the thickness direction.

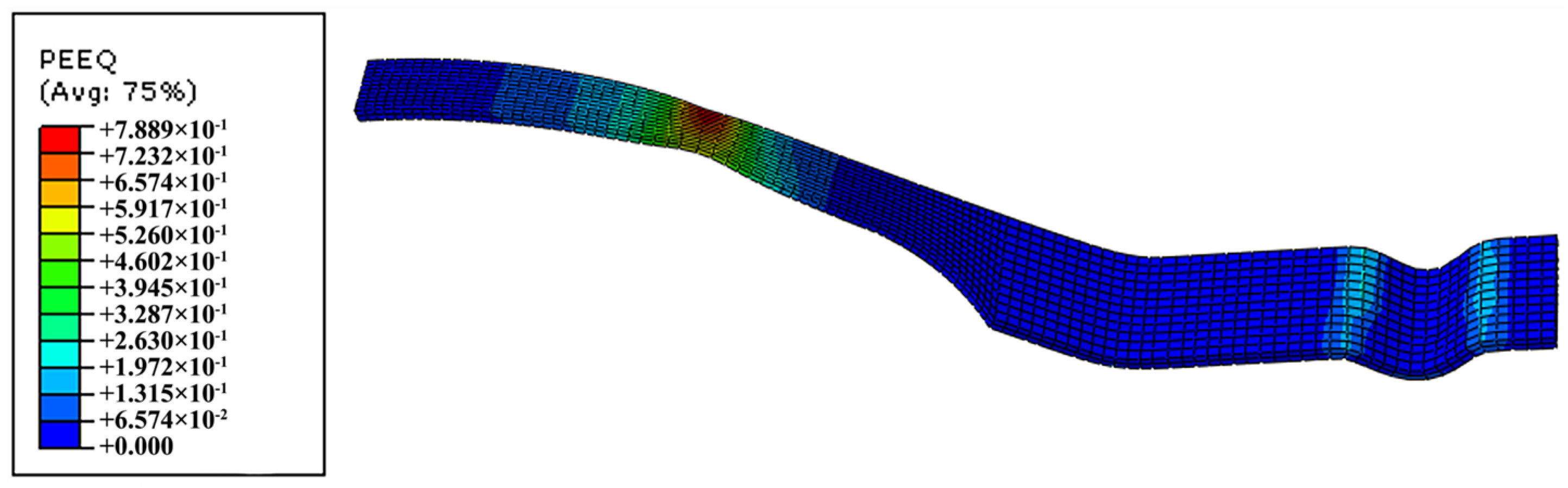
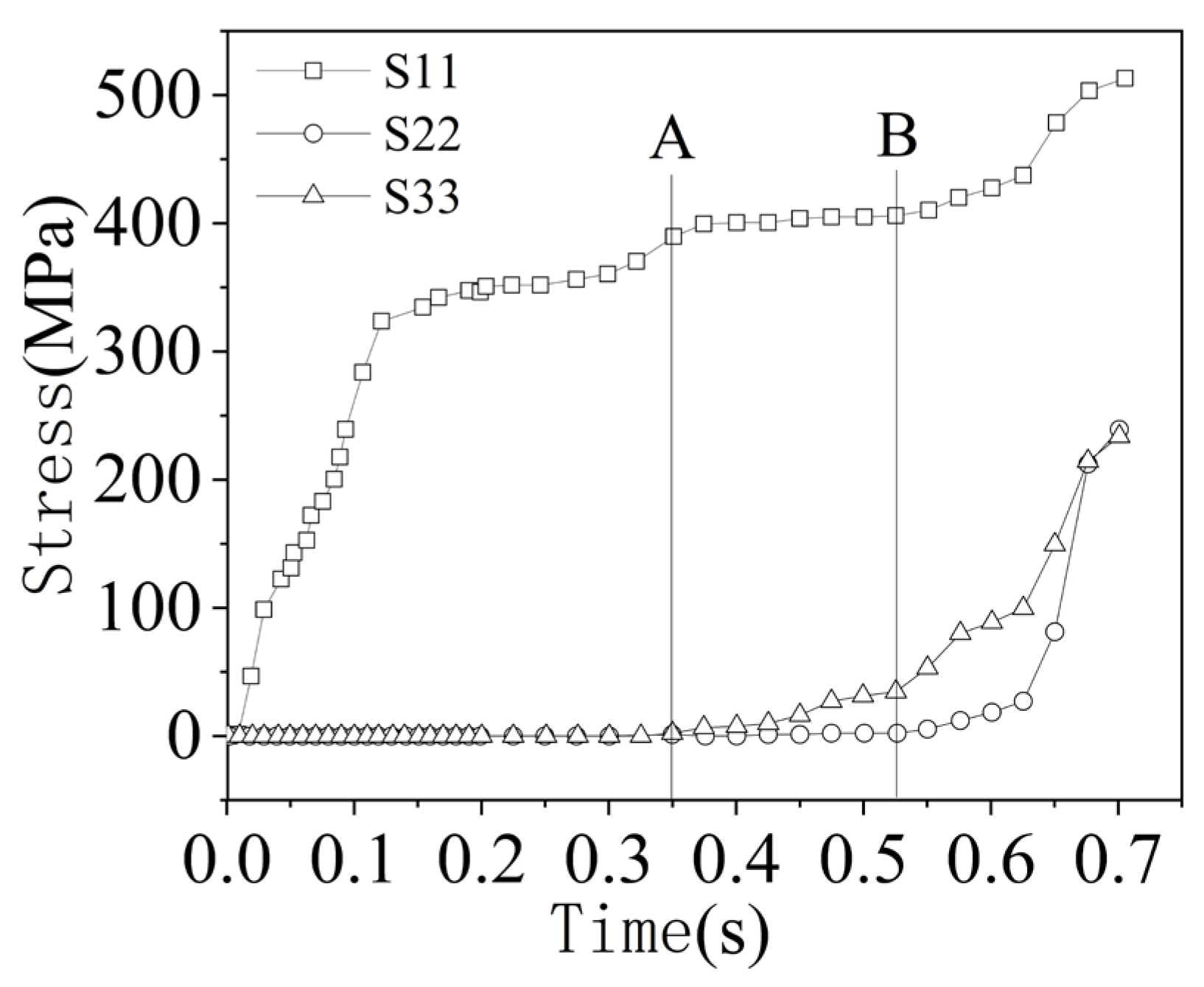
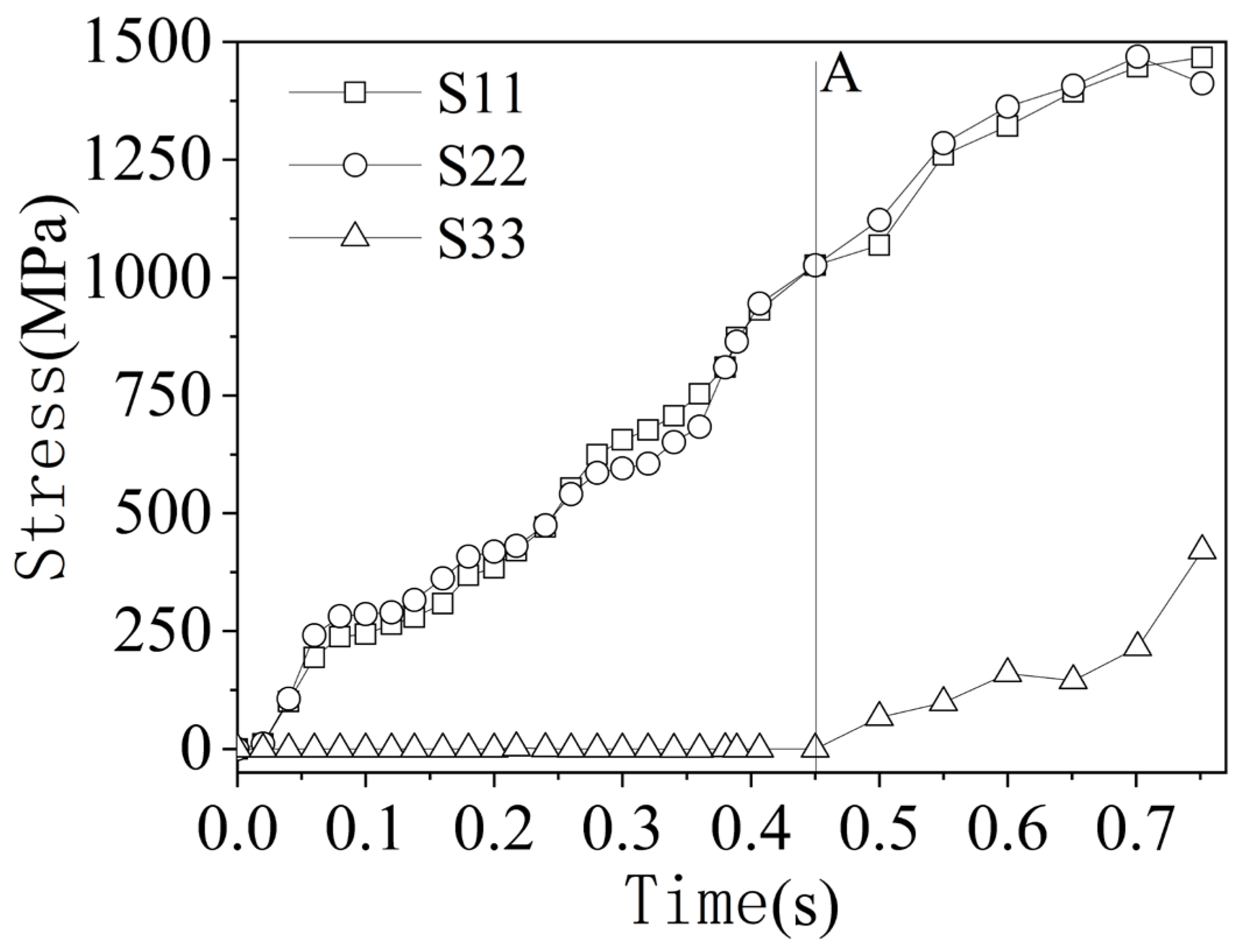
2. Finite Element Simulation to Verify the Existence of Stress in the Thickness Direction

To verify that the material will induce stress in the thickness direction during the deformation process, the finite element simulation of uniaxial tension and hemispherical bulging is carried out. The equivalent plastic strain (PEEQ) results obtained by the finite element simulation are shown in Figure 1 and Figure 2. The material used for the simulation is Trip 780, and the thickness of the sheet is 1 mm. In order to confirm the actual conditions of sheet deformation, a solid element is selected which is more precise.

According to the simulation results, the main stresses S11, S22 and S33 in the three directions where necking occurs are extracted, and the schematic diagram of the stress changing with time is drawn, as shown in Figure 3. Before point A, the sheet is always in a state of uniaxial stress, that is, it is only affected by the principle stress S11. When the stress curve reaches point A, the stress S33 in the thickness direction appears inside the sheet. Then the sheet continues to deform. When the curve reaches point B, the minor stress in the direction of vertical principle stress also appears, and the sheet is in a triaxial stress state. The principal stress in the three directions of the neck point is also extracted, as shown in Figure 4. With the deformation of the sheet, the stress S33 in the thickness direction appears after the curve reaches point A. It can be concluded that the sheet is not only affected by plane stress during the deformation process, and the stress in the thickness direction is induced as the deformation progresses.

The tensile stress in the thickness direction is induced during the deformation of the sheet, which is caused by the mutual restraint between the particles. The thickness of the sheet becomes thinner in the process of deformation. When the deformation reaches a certain extent, the sheet locally becomes thinner. This thinning trend is limited by nearby materials, which induces stress in the thickness direction.

And when the ratio of thickness to width of the sheet metal is constant, the stress in the thickness direction appears first than the minor stress in the sheet. Therefore, the forming limit diagram which considers plane stress only has an error.

3. Theoretical Basis

3.1. C-H Instability Criterion

According to C-H instability theory, the process of metal sheet material from initial deformation to fracture needs to go through yield, dispersed instability stage, concentrated instability stage, and fracture stage. The main failure stage of material strength mainly occurs in concentrated instability stage. For uniaxial tension, when the material deformation reaches the concentrated instability stage, the deformation mainly occurs in the main strain direction, while the compressive strain increment in the width direction gradually decreases, and this trend becomes more and more obvious as the deformation increases. When $d{\epsilon }_2\to 0$, concentrated instability occurs, that is, the material is about to fracture, which is the theoretical basis of C-H instability criterion.

3.1.1. Solution of Relevant Parameters of Sheet Metal Yield Function

Applying the Hosford criterion, when $r=1$, $a=2$, the yield criterion degenerates to the isotropic Mises yield criterion; When $a=2$ it becomes anisotropic quadratic Hill48 yield criterion. The Hosford criterion expression is:

$$(r+1){\sigma }_e^a=|{\sigma }_1-{\sigma }_3{|}^a+|{\sigma }_2-{\sigma }_3{|}^a+r|{\sigma }_1-{\sigma }_2{|}^a$$

(1)

Set $\raisebox{1ex}{${\sigma }_2$}\!\left/ \!\raisebox{-1ex}{${\sigma }_1$}\right.=\alpha$,$\raisebox{1ex}{${\sigma }_3$}\!\left/ \!\raisebox{-1ex}{${\sigma }_1$}\right.=\chi$, so:

$${\sigma }_e^{}={\sigma }_1{\left\{\frac{\left[{\left(1-\chi \right)}^a+{\left(\alpha -\chi \right)}^a+r{\left(1-\alpha \right)}^a\right]}{\left(r+1\right)}\right\}}^{\frac{1}{a}}$$

Set ${\sigma }_e^{}={\sigma }_1\varphi$, including:

$$\varphi ={\left\{\frac{\left[{\left(1-\chi \right)}^a+{\left(\alpha -\chi \right)}^a+r{\left(1-\alpha \right)}^a\right]}{\left(r+1\right)}\right\}}^{\frac{1}{a}}$$

The stress change of sheet metal under external force is:

$$d{\epsilon }_e=\frac{\partial {\sigma }_e}{\partial {\sigma }_1}d{\sigma }_1+\frac{\partial {\sigma }_e}{\partial {\sigma }_2}d{\sigma }_2+\frac{\partial {\sigma }_e}{\partial {\sigma }_3}d{\sigma }_3={\beta }_{1}d{\sigma }_1+{\beta }_{2}d{\sigma }_2+{\beta }_{3}d{\sigma }_3$$

(2)

where:

$${\beta }_1=\frac{\partial {\sigma }_e}{\partial {\sigma }_1}=\frac{\partial \left({\sigma }_1\varphi \right)}{\partial {\sigma }_1}=\varphi +{\sigma }_1\left(\frac{\partial \varphi }{\partial \alpha }\frac{\partial \alpha }{\partial {\sigma }_1}+\frac{\partial \varphi }{\partial \chi }\frac{\partial \chi }{\partial {\sigma }_1}\right)$$

$${\beta }_2=\frac{\partial {\sigma }_e}{\partial {\sigma }_2}=\frac{\partial \left({\sigma }_1\varphi \right)}{\partial {\sigma }_2}=\frac{\varphi }{\alpha }+\frac{{\sigma }_2}{\alpha }\frac{\partial \varphi }{\partial \alpha }\frac{\partial \alpha }{\partial {\sigma }_2}-\frac{{\sigma }_2\varphi }{{\alpha }^2}\frac{\partial \alpha }{\partial {\sigma }_2}=\frac{\varphi }{\alpha }+\left(\frac{\partial \varphi }{\partial \alpha }-\frac{\varphi }{\alpha }\right){\sigma }_1\frac{\partial \alpha }{\partial {\sigma }_2}$$

$${\beta }_3=\frac{\partial {\sigma }_e}{\partial {\sigma }_3}=\frac{\partial \left({\sigma }_1\varphi \right)}{\partial {\sigma }_3}=\frac{\varphi }{\chi }+\frac{{\sigma }_3}{\chi }\frac{\partial \varphi }{\partial \chi }\frac{\partial \chi }{\partial {\sigma }_3}-\frac{{\sigma }_3\varphi }{{\chi }^2}\frac{\partial \chi }{\partial {\sigma }_3}=\frac{\varphi }{\chi }+\left(\frac{\partial \varphi }{\partial \chi }-\frac{\varphi }{\chi }\right){\sigma }_3\frac{\partial \chi }{\partial {\sigma }_3}$$

Because:

$$\begin{array}{l}\frac{\partial \varphi }{\partial \alpha }={\left(\frac{1}{r+1}\right)}^{\frac{1}{a}}{\left[{\left(1-\chi \right)}^a+{\left(\alpha -\chi \right)}^a+r{\left(1-\alpha \right)}^a\right]}^{\left(\frac{1}{a}-1\right)}\left[{\left(\alpha -\chi \right)}^{\left(a-1\right)}-r{\left(1-\alpha \right)}^{\left(a-1\right)}\right]\\ ={\left(\frac{1}{r+1}\right)}^{\frac{1}{a}}{\varphi }_2^{\left(\frac{1}{a}-1\right)}{\varphi }_1\end{array}$$

$$\begin{array}{l}\frac{\partial \varphi }{\partial \chi }={\left(\frac{1}{r+1}\right)}^{\frac{1}{a}}{\left[{\left(1-\chi \right)}^a+{\left(\alpha -\chi \right)}^a+r{\left(1-\alpha \right)}^a\right]}^{\left(\frac{1}{a}-1\right)}\left[-{\left(1-\chi \right)}^{\left(a-1\right)}-{\left(\alpha -\chi \right)}^{\left(a-1\right)}\right]\\ ={\left(\frac{1}{r+1}\right)}^{\frac{1}{a}}{\varphi }_2^{\left(\frac{1}{a}-1\right)}{\varphi }_3\end{array}$$

$$\left\{\begin{array}{l}\frac{\partial \alpha }{\partial {\sigma }_1}=\frac{\partial \left({\sigma }_2/{\sigma }_1\right)}{\partial {\sigma }_1}=-\frac{{\sigma }_2}{{\sigma }_1^2}=-\frac{\alpha }{{\sigma }_1}\\ \frac{\partial \alpha }{\partial {\sigma }_2}=\frac{1}{{\sigma }_1}\\ \frac{\partial \chi }{\partial {\sigma }_1}=\frac{\partial \left({\sigma }_3/{\sigma }_1\right)}{\partial {\sigma }_1}=-\frac{{\sigma }_3}{{\sigma }_1^2}=-\frac{\chi }{{\sigma }_1}\\ \frac{\partial \chi }{\partial {\sigma }_3}=\frac{1}{{\sigma }_1}\end{array}\right.$$

So, it is concluded that:

$$\left\{\begin{array}{l}{\beta }_1=\varphi \left(1-\frac{\alpha {\varphi }_1}{{\varphi }_2}-\frac{\chi {\varphi }_3}{{\varphi }_2}\right)\\ {\beta }_2=\frac{\varphi {\varphi }_1}{{\varphi }_2}\\ {\beta }_3=\frac{\varphi {\varphi }_3}{{\varphi }_2}\end{array}\right.$$

Set:

$$f=|{\sigma }_1-{\sigma }_3{|}^a+|{\sigma }_2-{\sigma }_3{|}^a+r|{\sigma }_1-{\sigma }_3{|}^a$$

Because Drucker formula:

$$\frac{d{\epsilon }_1}{\frac{\partial f}{\partial {\sigma }_1}}=\frac{d{\epsilon }_2}{\frac{\partial f}{\partial {\sigma }_2}}=\frac{d{\epsilon }_3}{\frac{\partial f}{\partial {\sigma }_3}}=\frac{d{\epsilon }_e}{\frac{\partial f}{\partial {\sigma }_e}}=dc$$

(3)

The following formula is obtained:

$$\begin{array}{l}\frac{\partial f}{\partial {\sigma }_1}=a{\left({\sigma }_1-{\sigma }_3\right)}^{\left(a-1\right)}+ar{\left({\sigma }_1-{\sigma }_2\right)}^{\left(a-1\right)}=a|{\sigma }_1{|}^{\left(a-1\right)}\left[{\left(1-\chi \right)}^{\left(a-1\right)}+r{\left(1-\alpha \right)}^{\left(a-1\right)}\right]\\ =a{\varphi }_4|{\sigma }_1{|}^{\left(a-1\right)}\end{array}$$

$$\begin{array}{l}\frac{\partial f}{\partial {\sigma }_2}=a|{\sigma }_2-{\sigma }_3{|}^{\left(a-1\right)}-r|{\sigma }_1-{\sigma }_2{|}^{\left(a-1\right)}=a|{\sigma }_1{|}^{\left(a-1\right)}\left[{\left(\alpha -\chi \right)}^{\left(a-1\right)}-ar{\left(1-\alpha \right)}^{\left(a-1\right)}\right]\\ =a{\varphi }_1|{\sigma }_1{|}^{\left(a-1\right)}\end{array}$$

$$\frac{\partial f}{\partial {\sigma }_3}=-\left(\frac{\partial f}{\partial {\sigma }_1}+\frac{\partial f}{\partial {\sigma }_2}\right)=-\left(a{\varphi }_4|{\sigma }_1{|}^{\left(a-1\right)}+a{\varphi }_1|{\sigma }_1{|}^{\left(a-1\right)}\right)=-a\left({\varphi }_1+{\varphi }_4\right)|{\sigma }_1{|}^{\left(a-1\right)}$$

The scale factor $dc$ can be obtained by the following method. During deformation, the shaping work per unit volume of sheet metal can be expressed as:

$$dw={\sigma }_{e}d{\epsilon }_e={\sigma }_{ij}^{\prime }d{\epsilon }_{ij}={\sigma }_{ij}^{\prime }\cdot dc\cdot \frac{\partial f}{\partial {\sigma }_{ij}}$$

where ${\sigma }_{ij}^{\prime }$ is the stress tensor. Therefore:

$$d{\epsilon }_e=\frac{a}{{\sigma }_e}dc\left[{\sigma }_1^{\prime }{\varphi }_4+{\sigma }_2^{\prime }{\varphi }_1-{\sigma }_3^{\prime }({\varphi }_1+{\varphi }_4)\right]|{\sigma }_1{|}^{\left(a-1\right)}=a\cdot dc\cdot |{\sigma }_1{|}^{\left(a-1\right)}$$

(4)

From formula Equation (4), we can get:

$$dc=\frac{d{\epsilon }_e}{a\cdot \frac{{\varphi }_2}{\varphi }\cdot |{\sigma }_1{|}^{\left(a-1\right)}}$$

(5)

By combining Equation (5) formula and Equation (3) formula, we can get:

$$\frac{\partial f}{\partial {\sigma }_e}=a\cdot \frac{{\varphi }_1}{{\varphi }_2}\cdot |{\sigma }_1{|}^{\left(a-1\right)}$$

Taking the above results into formula Equation (3), we can get:

$$\frac{d{\epsilon }_1}{{\varphi }_4}=\frac{d{\epsilon }_2}{{\varphi }_1}=\frac{-d{\epsilon }_3}{{\varphi }_1+{\varphi }_4}=\frac{\varphi d{\epsilon }_e}{{\varphi }_2}$$

(6)

Corresponding results:

$$\frac{{\epsilon }_1}{{\varphi }_4}=\frac{{\epsilon }_2}{{\varphi }_1}=\frac{-{\epsilon }_3}{{\varphi }_1+{\varphi }_4}=\frac{\varphi {\epsilon }_e}{{\varphi }_2}$$

Including:

$$\left\{\begin{array}{l}{\varphi }_1={\left(\alpha -\chi \right)}^{\left(a-1\right)}-r{\left(1-\alpha \right)}^{\left(a-1\right)}\\ {\varphi }_2={\left(1-\chi \right)}^a+{\left(\alpha -\chi \right)}^a+r{\left(1-\alpha \right)}^a\\ {\varphi }_3=-{\left(1-\chi \right)}^{\left(a-1\right)}-{\left(\alpha -\chi \right)}^{\left(a-1\right)}\\ {\varphi }_4={\left(1-\chi \right)}^{\left(a-1\right)}+r{\left(1-\alpha \right)}^{\left(a-1\right)}\end{array}\right.$$

The hardening law of sheet metal is:

$${\sigma }_e=k{\epsilon }_e^n$$

(7)

The deformation resistance of the material can be obtained from the differential Equation (7):

$$d{\sigma }_e=\frac{n}{{\epsilon }_e}{\sigma }_{e}d{\epsilon }_e$$

(8)

The deformation resistance of the material during stable deformation is equal to the stress increment, that is, the formula Equation (8) is equal to the Equation (2):

$$\frac{n}{{\epsilon }_e}{\sigma }_{e}d{\epsilon }_e={\beta }_{1}d{\sigma }_1+{\beta }_{2}d{\sigma }_2+{\beta }_{3}d{\sigma }_3$$

(9)

3.1.2. Calculation of the Limit Strain of Considered Dispersion Instability

According to the Considered instability criteria:

$$d{p}_1=0 \mathrm{or} d{\sigma }_1={\sigma }_{1}d{\epsilon }_1$$

If the sheet ratio is loaded, i.e., $\alpha =const$,then:

$$\frac{d{\sigma }_2}{d{\sigma }_1}=\frac{{\sigma }_2}{{\sigma }_1}=\alpha \mathrm{and} \frac{d{\sigma }_3}{d{\sigma }_1}=\frac{{\sigma }_3}{{\sigma }_1}=\chi$$

Substitute Equations (7) and (8) into Equation (9) and note the relationship Equation (6). The limit strain expression satisfying the Considered criterion can be obtained:

$$\left\{\begin{array}{l}{\epsilon }_{ed}=\frac{{\varphi }_2}{\varphi {\varphi }_4}\cdot n\\ {\epsilon }_{1d}=\frac{\varphi {\varphi }_4}{{\varphi }_2}{\epsilon }_{cd}=n\\ {\epsilon }_{2d}=\frac{\varphi {\varphi }_1}{{\varphi }_2}{\epsilon }_{cd}=\frac{{\varphi }_1}{{\varphi }_4}n\end{array}\right.$$

3.1.3. Calculation of Limit Strain of Concentrated Instability

According to the C-H instability criterion, assuming that the strain path begins to drift to the plane strain state when the load is kept constant at the maximum level during the deformation of the material, that is, the secondary strain gradually approaches zero, and then the sheet metal will have concentrated instability, then:

$$\left\{\begin{array}{l}d{\rho }_1=0\\ d{\sigma }_1=\sigma d{\epsilon }_1\\ d{\epsilon }_2=0\end{array}\right.$$

(10)

Substitute the first item in Equation (10) into Equation (9) to get:

$$\frac{n}{{\epsilon }_e}{\sigma }_{e}d{\epsilon }_e={\beta }_1{\sigma }_{1}d{\epsilon }_1+{\beta }_{2}d{\sigma }_2+{\beta }_{3}d{\sigma }_3$$

$$d{\sigma }_2=\frac{1}{{\beta }_2}\left[\frac{n}{{\epsilon }_e}{\sigma }_{e}d{\epsilon }_e-\left({\beta }_1+\chi {\beta }_3\frac{d{\epsilon }_e}{d{\epsilon }_1}\right){\sigma }_{1}d{\epsilon }_1\right]$$

The formula Equations (1) and (6) can be obtained as follows:

$$d{\sigma }_2=\frac{\varphi }{{\beta }_2}\left[\frac{n}{{\epsilon }_e}-\left({\beta }_1-\chi {\beta }_3\frac{{\varphi }_1+{\varphi }_4}{{\varphi }_4}\right)\frac{{\varphi }_3}{\varphi 2}\right]{\sigma }_{1}d{\epsilon }_e$$

(11)

$$d{\sigma }_1={\sigma }_{1}d{\epsilon }_1=\frac{\varphi \cdot {\varphi }_4}{{\varphi }_2}{\sigma }_{1}d{\epsilon }_e$$

(12)

In the drift stage, the limit strain value of concentrated instability can be obtained by gradually integrating Equations (11) and (12) with iterative method. If $d{\epsilon }_2$ approaches 0 infinitely (truncation error $d{\epsilon }_2\le 0.00001$ is specified in this paper), the operation is terminated:

$${\epsilon }_{1n}={\epsilon }_{1d}+{\displaystyle \sum _{i=1}^{N-1}d{\epsilon }_1}$$

$${\epsilon }_{2n}={\epsilon }_{2d}+{\displaystyle \sum _{i=1}^{N-1}d{\epsilon }_2}$$

3.2. MMFC Instability Criterion

The MMFC instability criterion states that the material does not immediately become unstable when the stress reaches the maximum value. At this time, the strain ratio $\beta$ begins to change, the material is unstable when $\beta \to 0$. The detailed calculation process can refer to the literature [19] (pp. 267–279). And the main theoretical basis is: Stress ${\sigma }_{11}$ is a function of strain ratio $\beta =d{\epsilon }_2/d{\epsilon }_1$. Therefore, the stress increment $d{\sigma }_1$ can be expressed as

$$d{\sigma }_1=\frac{\partial {\sigma }_1}{\partial {\epsilon }_1}d{\epsilon }_1+\frac{\partial {\sigma }_1}{\partial \beta }d\beta$$

(13)

The original maximum force condition is:

$$dF=d({\sigma }_{1}A)+{\sigma }_{1}dA>0$$

(14)

Substitute Equation (13) into Equation (14) to get Equation (15):

$$\frac{\partial {\sigma }_1}{\partial {\epsilon }_1}d{\epsilon }_1+\frac{\partial {\sigma }_1}{\partial \beta }d\beta >{\sigma }_{1}d{\epsilon }_1$$

(15)

In the case of $\partial {\sigma }_1/\partial {\epsilon }_1>{\sigma }_1$, $d\beta$ is zero and $\beta$ remains the same, that is, the state of uniform deformation. During the deformation process, the stress increases with the influence of work hardening, the hardening rate $\partial {\sigma }_1/\partial {\epsilon }_1$ gradually decreases for most metal materials. When the $\partial {\sigma }_1/\partial {\epsilon }_1>{\sigma }_1$ condition is reached, $\beta$ will change correspondingly to keep the stability of the equilibrium state.

Set

$$\beta =\frac{\mathrm{\Delta }{\epsilon }_2}{\mathrm{\Delta }{\epsilon }_1}=\frac{d{\epsilon }_2}{d{\epsilon }_1}$$

$$\left\{\begin{array}{l}{\sigma }_1=f(\alpha ,x)\overline{\sigma }\\ \mathrm{\Delta }\overline{\epsilon }=g(\beta )\mathrm{\Delta }{\epsilon }_1\end{array}\right.$$

$$\left\{\begin{array}{l}H=\overline{\sigma }=H(\overline{\epsilon })\\ H^{\prime }=\frac{\overline{\sigma }}{\overline{\epsilon }}\end{array}\right.$$

Set $\beta$ as the strain increment ratio, $\alpha =\raisebox{1ex}{${\sigma }_2$}\!\left/ \!\raisebox{-1ex}{${\sigma }_1$}\right.$ and $\chi =\raisebox{1ex}{${\sigma }_3$}\!\left/ \!\raisebox{-1ex}{${\sigma }_1$}\right.$ as the stress ratio, where $\chi$ is the medium that introduces the stress in the thickness direction. In general, as long as the yield function $F\left({\sigma }_{1,}{\sigma }_2\right)=0$ is given. Then $\partial {\sigma }_1/\partial {\epsilon }_1$ and $\partial {\sigma }_1/\partial \beta$ can be calculated accordingly as

$$\frac{\partial {\sigma }_1}{\partial {\epsilon }_1}=\frac{\partial {\sigma }_1}{\partial \overline{\sigma }}\frac{\partial \overline{\sigma }}{\partial \overline{\epsilon }}\frac{\partial \overline{\epsilon }}{\partial {\epsilon }_1}=f(\alpha ,x)g(\beta )H^{\prime }$$

$$\frac{\partial {\sigma }_1}{\partial \beta }=\frac{\partial {\sigma }_1}{\partial \alpha }\frac{\partial \alpha }{\partial \beta }=f(\alpha ,x)\overline{\sigma }H{\displaystyle /}\left(\frac{\partial \beta }{\partial \alpha }\right)$$

Equation (15) is converted to

$$\frac{\partial {\sigma }_1}{\partial {\epsilon }_1}+\frac{\partial {\sigma }_1}{\partial \beta }\frac{\partial \beta }{\partial {\epsilon }_1}>{\sigma }_1$$

Then the correction formula of the maximum force criterion is obtained.

3.3. Mises Yield Criterion

R. Von Mises obtained the Mises yield criterion by revised and refining Treaca’s conclusions. The Mises yield criterion can be expressed as:

$$\begin{array}{l}{\left({\sigma }_x-{\sigma }_y\right)}^2+{\left({\sigma }_y-{\sigma }_z\right)}^2+{\left({\sigma }_z-{\sigma }_x\right)}^2\\ +6\left({\tau }_{xy}{}^2+{\tau }_{yz}{}^2+{\tau }_{zx}{}^2\right)=2{\overline{\sigma }}^2\end{array}$$

The principal stress state expression is:

$${\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_3-{\sigma }_1\right)}^2=2{\overline{\sigma }}^2$$

$$\beta =\mathrm{\Delta }{\epsilon }_2/\mathrm{\Delta }{\epsilon }_1=\frac{\frac{\partial f}{\partial {\sigma }_2}}{\frac{\partial f}{\partial {\sigma }_1}}=\frac{-1+2\alpha -\chi }{2-\alpha -\chi }$$

$$f\left(\alpha ,\chi \right)=\frac{1}{\sqrt{\frac{1}{2}\left[{\left(1-\alpha \right)}^2+{\left(\alpha -\chi \right)}^2+{\left(\chi -1\right)}^2\right]}}$$

$$g\left(\beta \right)=\frac{\sqrt{\frac{1}{2}\left[{(\chi -1)}^2+{\left(\alpha -\chi \right)}^2+{\left(1-\alpha \right)}^2\right]}}{2-\alpha -\chi }$$

3.4. HILL48 Yield Criterion

According to the Mises yield criterion, Hill proposed a yield criterion with the ability to describe anisotropy. That is, by adding some parameters to the yield function, the position of the material’s actual yield point can be more accurate. The equivalent stress is expressed as:

$$\begin{array}{l}f=F{\left({\sigma }_{yy}-{\sigma }_{zz}\right)}^2+G{\left({\sigma }_{zz}-{\sigma }_{xx}\right)}^2+H{\left({\sigma }_{xx}-{\sigma }_{yy}\right)}^2\\ \begin{array}{cc}& \end{array}+2L{\sigma }_{yz}{}^2+2M{\sigma }_{zx}{}^2+2N{\sigma }_{xy}{}^2\end{array}$$

where $x$, $y$, $z$ are the principal axes of three orthogonal directions, where $F$, $G$, $H$, $L$, $M$, and $N$ are anisotropic parameters. The corresponding principal stress state expression is:

$$f=F{\left({\sigma }_{yy}-{\sigma }_{zz}\right)}^2+G{\left({\sigma }_{zz}-{\sigma }_{xx}\right)}^2+H{\left({\sigma }_{xx}-{\sigma }_{yy}\right)}^2$$

Assume that the material only has differences in the thickness direction.

Set $r=\frac{H}{G}$. Then the yield criterion [20] (pp. 45–53) can be written as

$$\left(r+1\right)\overline{\sigma }={\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_1-{\sigma }_3\right)}^2+r{\left({\sigma }_1-{\sigma }_2\right)}^2$$

Set $\alpha =\raisebox{1ex}{${\sigma }_2$}\!\left/ \!\raisebox{-1ex}{${\sigma }_1$}\right.$,$\chi =\raisebox{1ex}{${\sigma }_3$}\!\left/ \!\raisebox{-1ex}{${\sigma }_1$}\right.$,

$$\beta =\mathrm{\Delta }{\epsilon }_2/\mathrm{\Delta }{\epsilon }_1=\frac{\frac{\partial f}{\partial {\sigma }_2}}{\frac{\partial f}{\partial {\sigma }_1}}=\frac{\alpha -\chi -r+r\cdot \alpha }{1-\chi +r-r\cdot \alpha }$$

$$f\left(\alpha ,\chi \right)=\frac{r+1}{\sqrt{{\left(1-\chi \right)}^2+{\left(\alpha -\chi \right)}^2+r{\left(1-\alpha \right)}^2}}$$

$$g\left(\beta \right)=\frac{\sqrt{\left[{\left(1-\chi \right)}^2+{\left(\alpha -\chi \right)}^2+r{\left(1-\alpha \right)}^2\right]\cdot \left(r+1\right)}}{1-\chi +r-r\cdot \alpha }$$

4. Calculation Results and Discussion

4.1. Always Apply Stress in the Thickness Direction during Sheet Deformation

For a typical steel TRIP780, the hardening curve is described by the swift model [21] (pp. 2370–2378).

Table 1. Swift constitutive equation coefficient.

$\mathit{K}$	$\mathit{n}$	${\mathit{\epsilon }}_0$
1503.6	0.273	0.0083

is the coefficient of the constitutive equation.

The Swift constitutive equation expression is:

$$\overline{\sigma }=K{\left({\overline{\epsilon }}_p+{\epsilon }_0\right)}^n$$

The FLD of introducing the stress in the thickness direction by the proportional method is shown in Figure 5 and Figure 6. The $\chi$ shown in the figure is the ratio of the stress in the thickness direction to the principal stress, $\chi$ which is a negative value, that is, compressive stress in the thickness direction is introduced; $\chi$ is a positive value, that is, the tensile stress is introduced in the thickness direction; $\chi =0$ means no stress in the thickness direction. The value of $\chi$ increases, indicating that the stress in the thickness direction increases.

Compared with the plane stress state, the height of FLC does not change significantly after the stress in the thickness direction was introduced, but the length of the curve changes significantly. In the tension and compression zone on the left side, the compressive stress in the thickness direction increases, the FLC becomes shorter, and the ultimate strain of the corresponding strain state decreases; In the biaxial tension zone on the right side, the compressive stress in the thickness direction increases, and the FLC becomes longer, indicating that the ultimate strain of the corresponding strain state increases. When the tension stress in the thickness direction is introduced, the conclusion is reversed.

The FLD of introducing the stress in the thickness direction by the constant method is shown in Figure 7 and Figure 8. ${\sigma }_3$ is always constant during material deformation, and the greater the value of ${\sigma }_3$, the greater the stress in the thickness direction.

The changing trend of the FLC is similar to the proportional method when the stress in the thickness direction is introduced by the constant method. As the compressive stress in the thickness direction increases, the curve of the tension and compression zone on the left side becomes shorter, and the curve of the biaxial tension zone on the right side becomes longer; However, when the compressive stress in the thickness direction increases in a form of constant, the curve shifts slightly to the lower right as a whole, and resulting in the curve on the left side increases slightly and a small increase in the forming limit; The curve on the right side drops slightly and the range of forming limits is also slightly reduced. When the tension stress in the thickness direction is introduced, the conclusion is reversed. And in the biaxial tension zone on the right side, the curve gradually closes.

4.2. Sheet Material Is Induced Stress in the Thickness Direction during Deformation

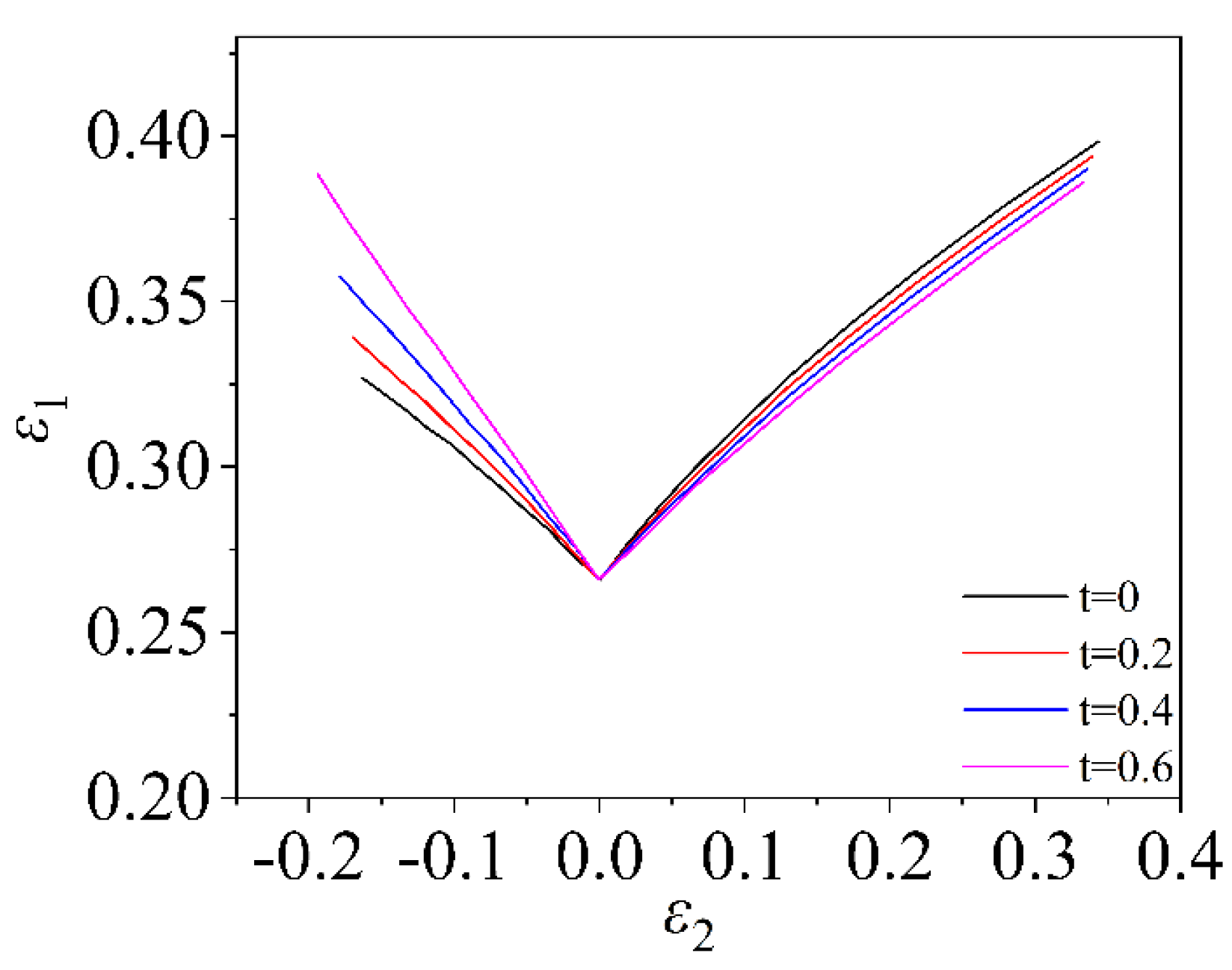
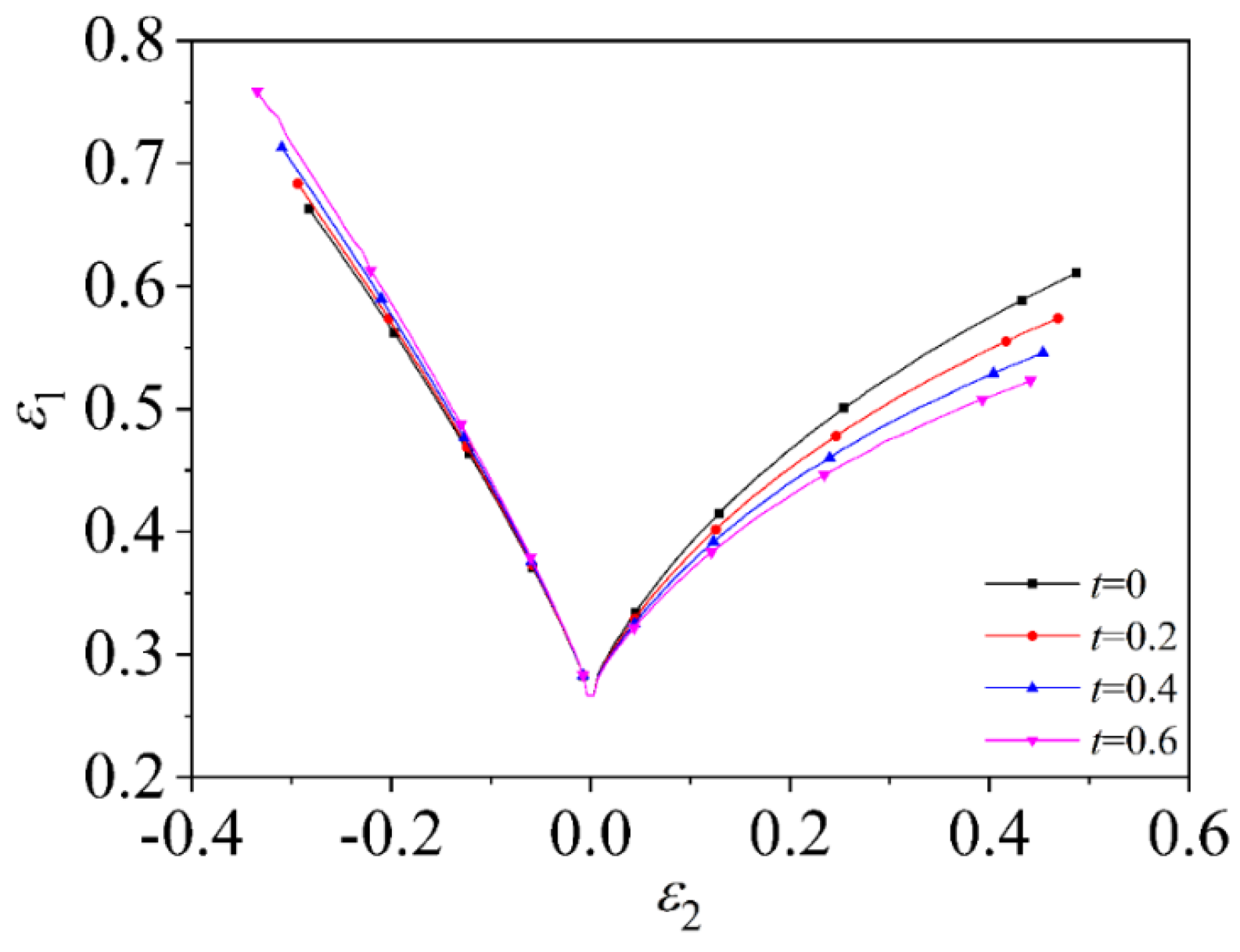
4.2.1. Induced Stress in Thickness Direction Based on MMFC Instability Model

Due to the principle of volume invariably, the deformation of the sheet in the planar direction is maintained by thinning in the thickness direction during the uniaxial tension or biaxial tension experiments. When the thickness of the material begins to thin, due to the mutual restraint between the particles, there will be a force to prevent the thinning. Moreover, when the material begins to neck, this force that opposes thinning will be very obvious, that is, the induced tensile stress in the thickness direction.

After the material becomes load instability, the flow constraint force between the material particles is increasing, and the strain state gradually drifts to the plane strain state, that is, the strain increment ratio $\beta$ gradually approaches zero. Therefore, the stress ratio α is not loaded according to the initial stress ratio at this stage but changes at any time. According to the change of the ratio of the minor stress to the principal stress, the relationship between $\mathrm{\Delta }\chi$ and $\mathrm{\Delta }\alpha$ is established and then accumulates the sum.

For the material TRIP780, the Swift constitutive equation is used, and the stress in the thickness direction is considered to solve the theoretical FLD, as shown in Figure 9 and Figure 10.

Compared with applying the stress in the thickness direction all the time in the deformation process, the FLC which considers the induced stress in the thickness direction has changed significantly. As can be seen from the figure, the plane strain point of the FLC does not change. In the tension and compression zone, when the given multiple $t$ increases (the same loading time, larger stress in the thickness direction is induced inside the sheet), the FLC is significantly increased, and the range of forming limits is increased; the curve gradually becomes longer as $t$ increases. The curve is the longest when $t=0.6$, indicating that the ultimate strain of the corresponding strain state increases.

4.2.2. Induced Stress in Thickness Direction Based on C-H Instability Model

The C-H instability criterion [22] considers when $d{\epsilon }_2\to 0$, $\beta \to 0$, the material is about to break. It is assumed that the stress in the thickness direction is induced in the concentrated instability phase. The intermediate process of iterative calculation is:

$${\epsilon }_e={\epsilon }_{ed}+{\displaystyle \sum _{i=1}^{N-1}d{\epsilon }_e}$$

$${\sigma }_1^{\prime }=1+{\displaystyle \sum _{i=1}^{N-1}d{\sigma }_1^{\prime }}$$

$${\sigma }_2^{\prime }={\alpha }_d+{\displaystyle \sum _{i=1}^{N-1}d{\sigma }_2^{\prime }}$$

$$\alpha =\frac{{\sigma }_2^{\prime }}{{\sigma }_1^{\prime }}$$

$$\mathrm{\Delta }\alpha =\left|\alpha -{\alpha }^{\prime }\right|$$

$$\mathrm{\Delta }\chi =t\cdot \mathrm{\Delta }\alpha$$

$$\chi =\chi +\mathrm{\Delta }\chi$$

$$d{\epsilon }_1=\frac{\phi {\phi }_3}{{\phi }_2}d{\epsilon }_e$$

$$d{\epsilon }_2=\frac{\phi {\phi }_1}{{\phi }_2}d{\epsilon }_e$$

$${\epsilon }_1={\epsilon }_{1d}+{\displaystyle \sum _{i=1}^{N-1}d{\epsilon }_1}$$

$${\epsilon }_2={\epsilon }_{2d}+{\displaystyle \sum _{i=1}^{N-1}d{\epsilon }_2}$$

When $d{\epsilon }_2$ is less than a certain value, the operation is stopped (this article specifies the truncation error $d{\epsilon }_2\le 0.00001$). The main strain value at this time is the ultimate strain value when the sheet material is localized necking:

$${\epsilon }_{1n}^{*}={\epsilon }_{1d}+{\displaystyle \sum _{i=1}^{N-1}d{\epsilon }_1}$$

$${\epsilon }_{2n}^{*}={\epsilon }_{2d}+{\displaystyle \sum _{i=1}^{N-1}d{\epsilon }_2}$$

Figure 11 is a FLD based on the C-H instability criterion and the Hill48 yield criterion when considering the induced stress in the thickness direction. Figure 12 is a FLD based on the C-H instability criterion and the Mises yield criterion when considering the induced stress in the thickness direction. Compared with MMFC instability criterion, the overall change trend of FLD based on C-H model is similar. The curve of the tension and compressed zone increases as $t$ increases, so the forming limit increases; The curve of the biaxial tension zone decreases as $t$ increases and becomes shorter; However, on the left side, the slope of the FLC which is based on the C-H instability model rises very small, so the curve change is not obvious; while the slope of the curve on the right side is more obvious.

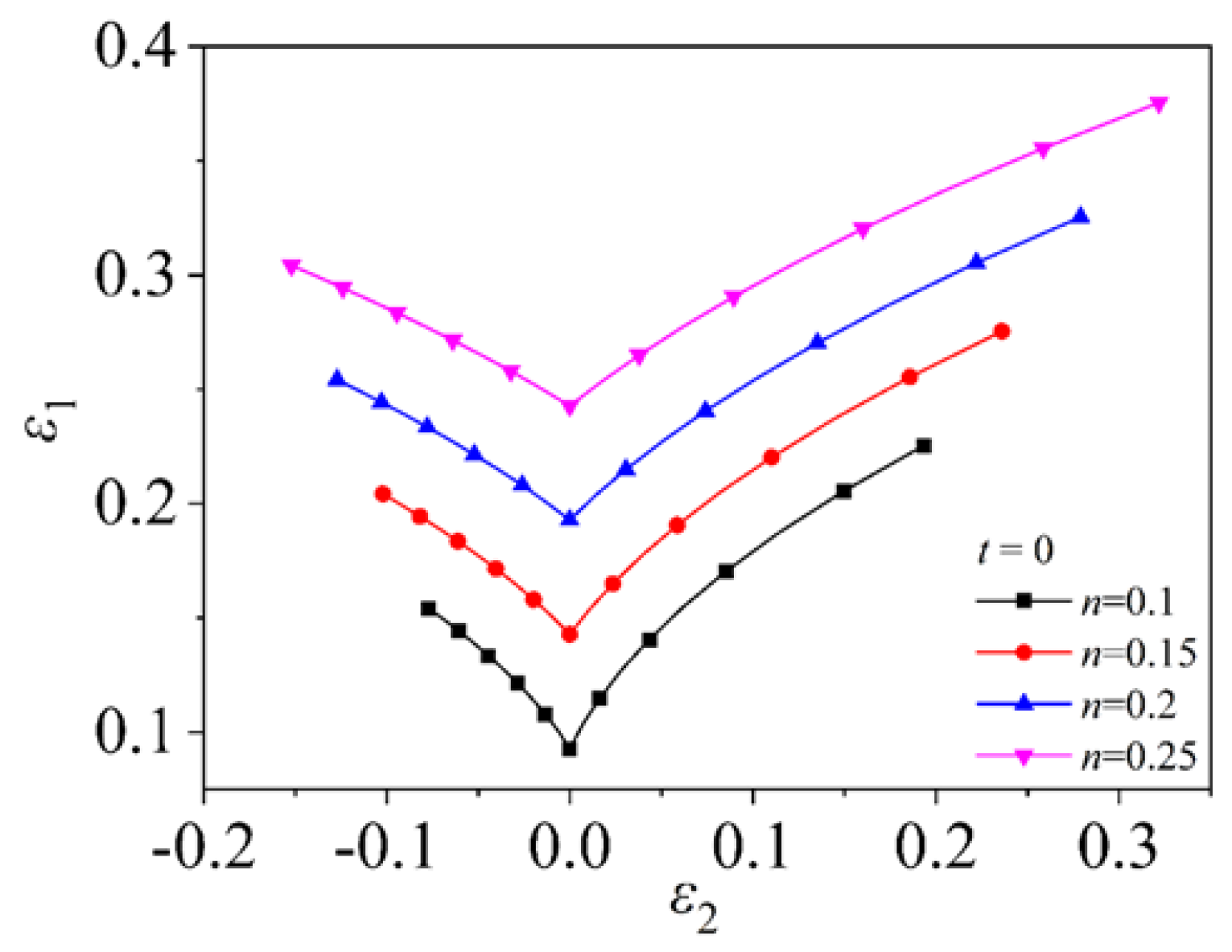
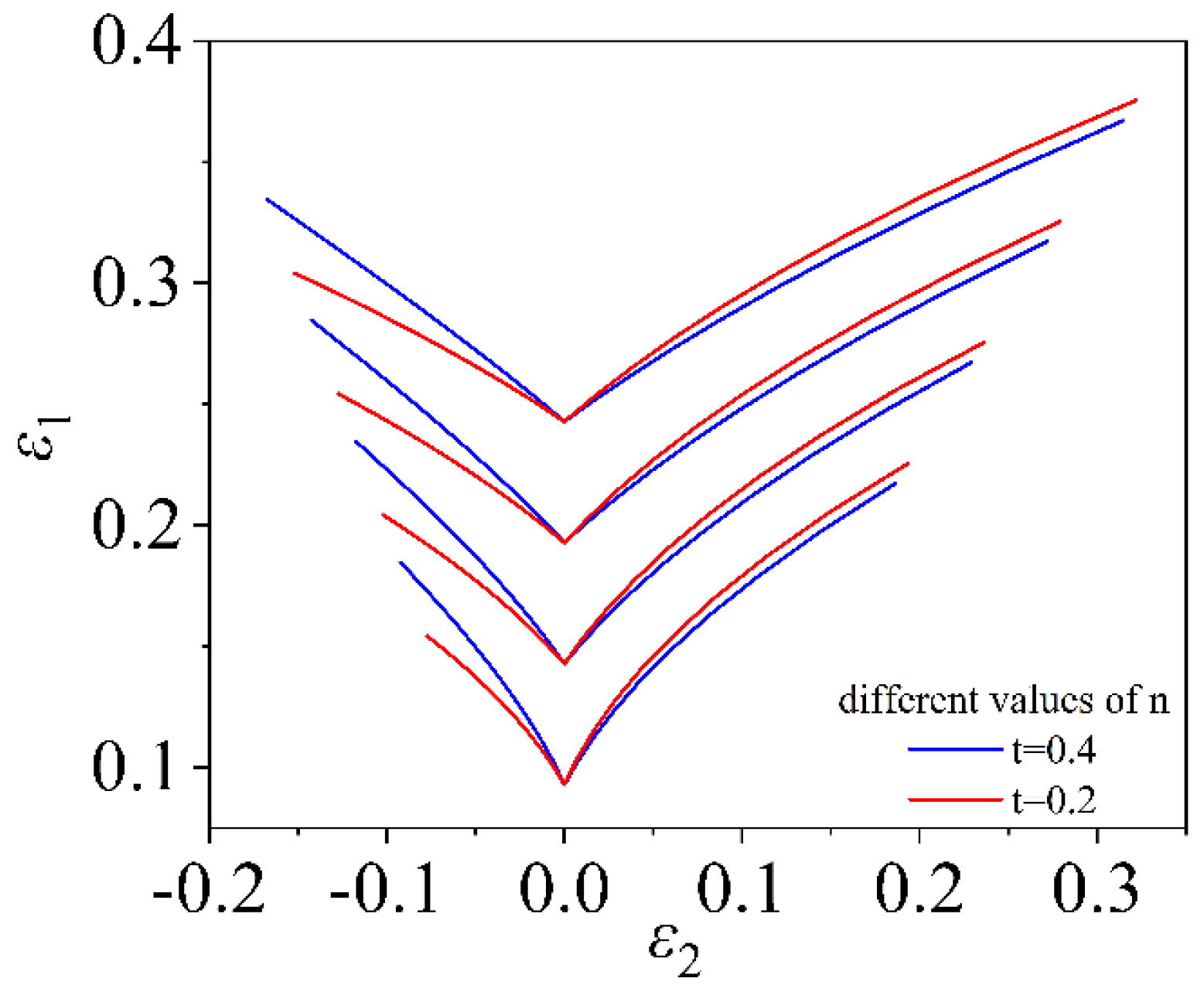
4.2.3. Effect of Strain Hardening Exponent $n$ on Forming Limit

The strain hardening index $n$ is the strain-strengthening ability of the material during deformation. The larger the value of $n$, the stronger the strain-hardening ability. Figure 13 and Figure 14 show the FLD for different values of $n$ based on the Mises yield criterion and the MMFC instability criterion. The forming limit curve shifts upwards significantly as the value of $n$ increases and the range of forming limits increases. Considering the induced stress in the thickness direction does not significantly change the effect of the $n$ on the forming limit, only affecting the overall change of the curve, as shown in Figure 15.

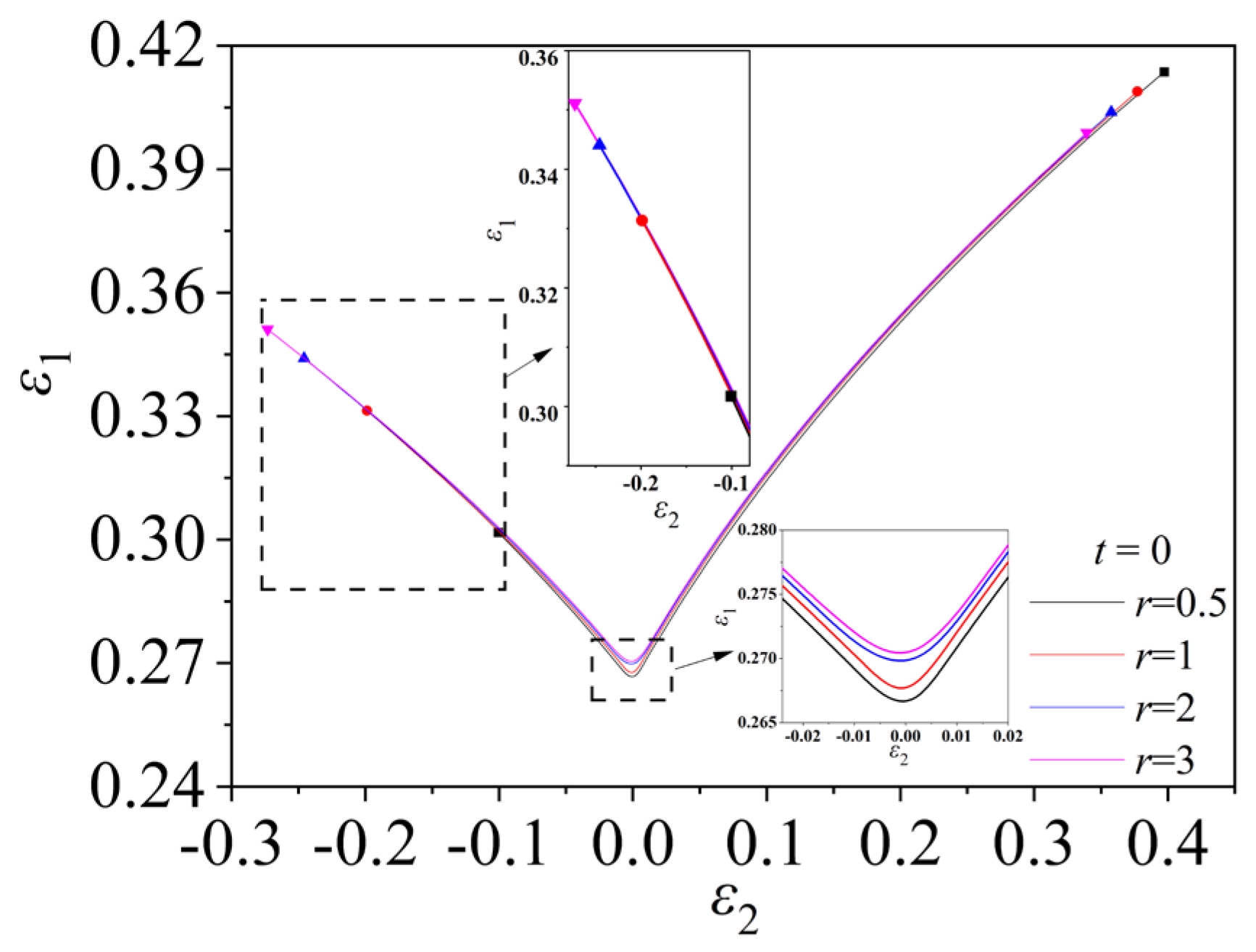
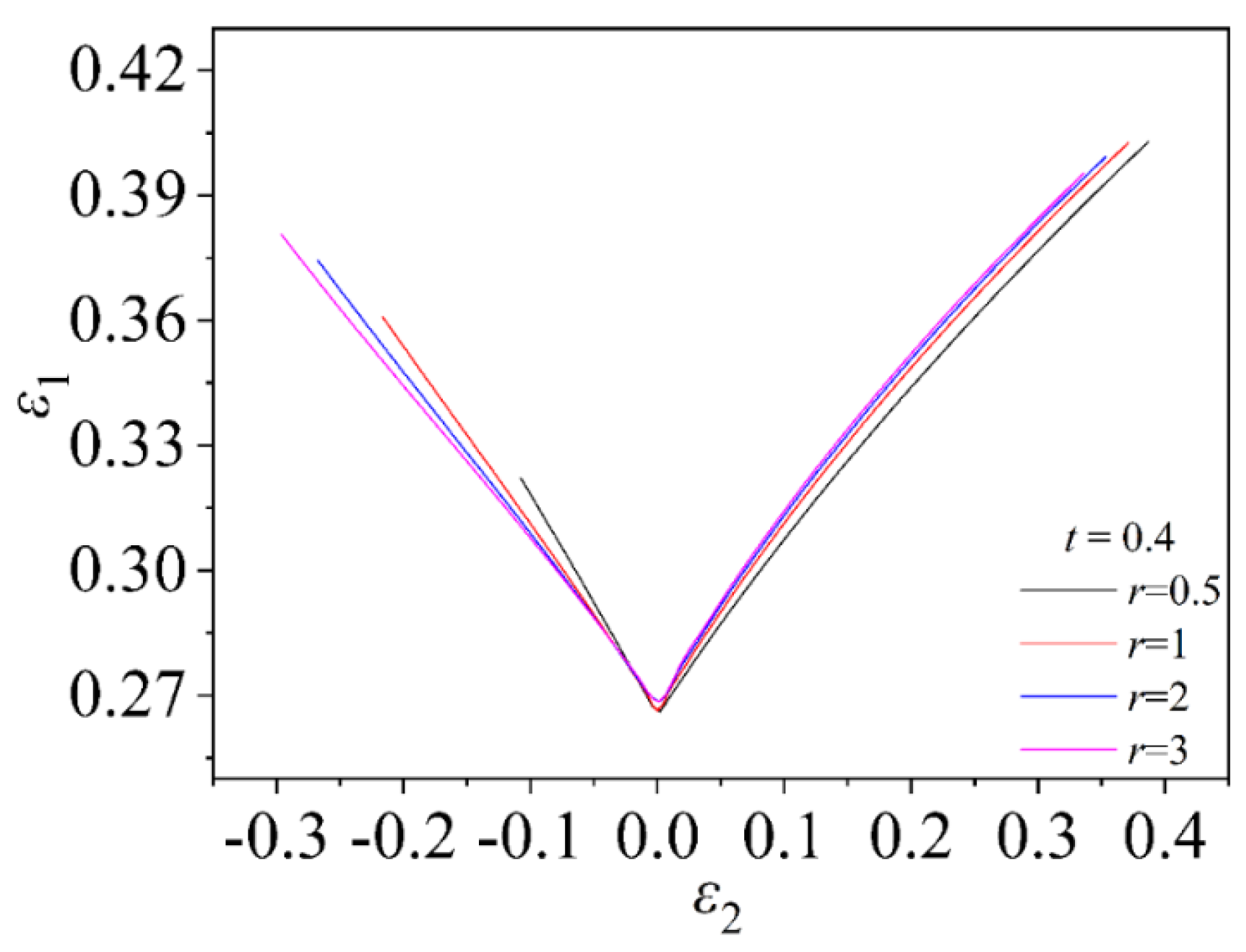
4.2.4. The Effect of Coefficient of Normal Anisotropy $r$ on Forming Limit

The coefficient of normal anisotropy $r$ reflects the difference between the plane direction and the thickness direction of the sheet during the deformation process. After considering the induced stress in the thickness direction, the effect of the $r$ on the FLD has changed significantly.

For the MMFC instability criterion, when the thickness direction stress is not considered, the change of the $r$ hardly changes the slope of the curve, but significantly affects the length of the curve. The FLC of the tension and compression zone increases with the increase in $r$, and the curve of the biaxial tension zone becomes shorter as the $r$ increases, as shown in Figure 16. For this, the C-H instability criterion shows the same. The difference is that the $r$ significantly affects the slope of the biaxial tension zone on the right side of the curve, as shown in Figure 17. The value of $r$ increases and the slope decreases, indicating that the normal anisotropy is more pronounced, and the easier the material reaches the forming limit.

When considering the induced stress in the thickness direction, the slope of the FLC based on the MMFC criterion also changes significantly. The slope of the curve on the left side increases with the increase in $r$; the curve on the right-side increases with the value of $r$ decreasing, as shown in Figure 18. Based on the C-H criterion, the sensitivity of the $r$ value to the forming limit curve decreases with the induced stress in the thickness direction. By comparing Figure 17 and Figure 19, it can be seen that the slope of the curve on the right side is closer considering the induced stress in the thickness direction.

5. Verification of the Forming Curve after Induced Thick Stress

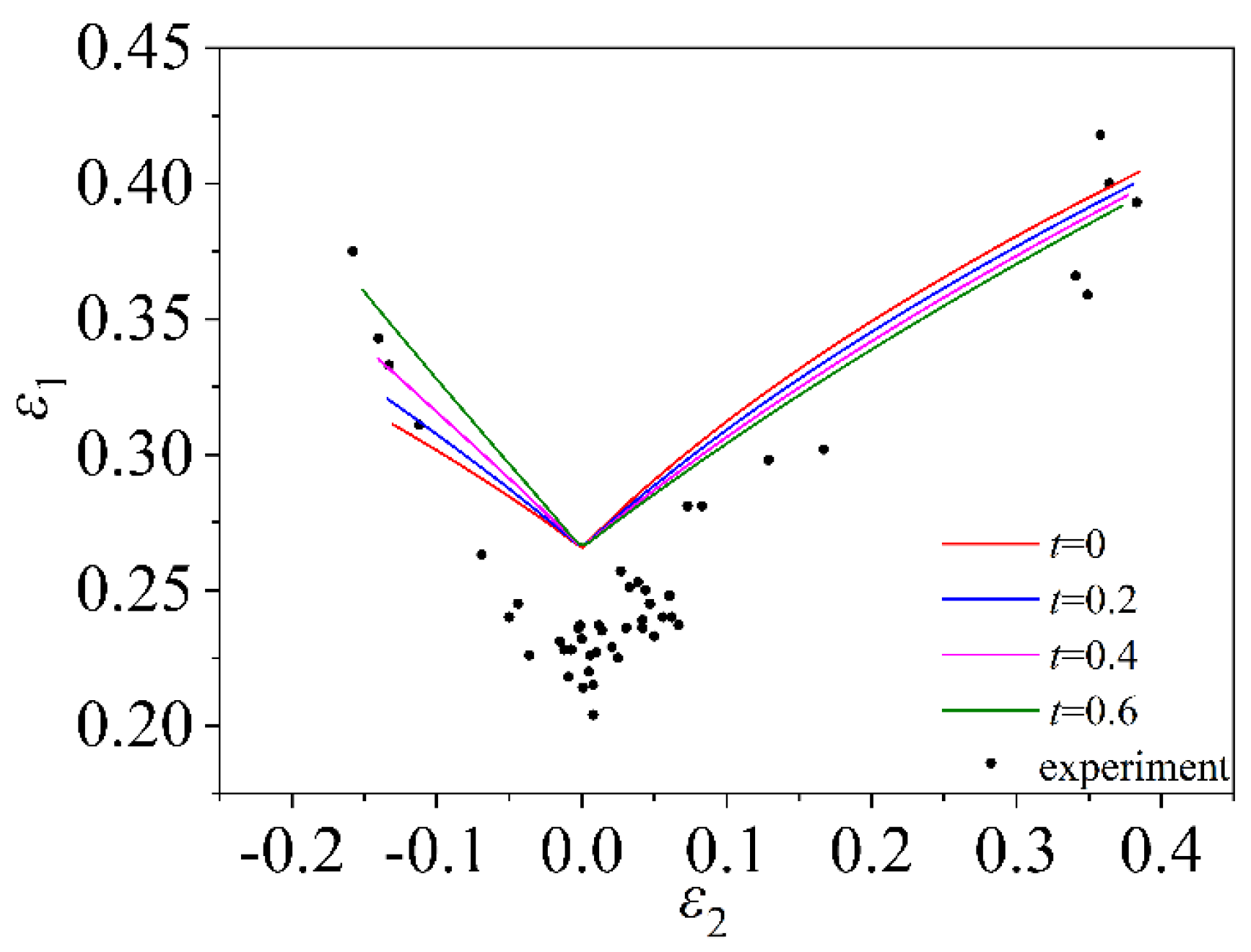
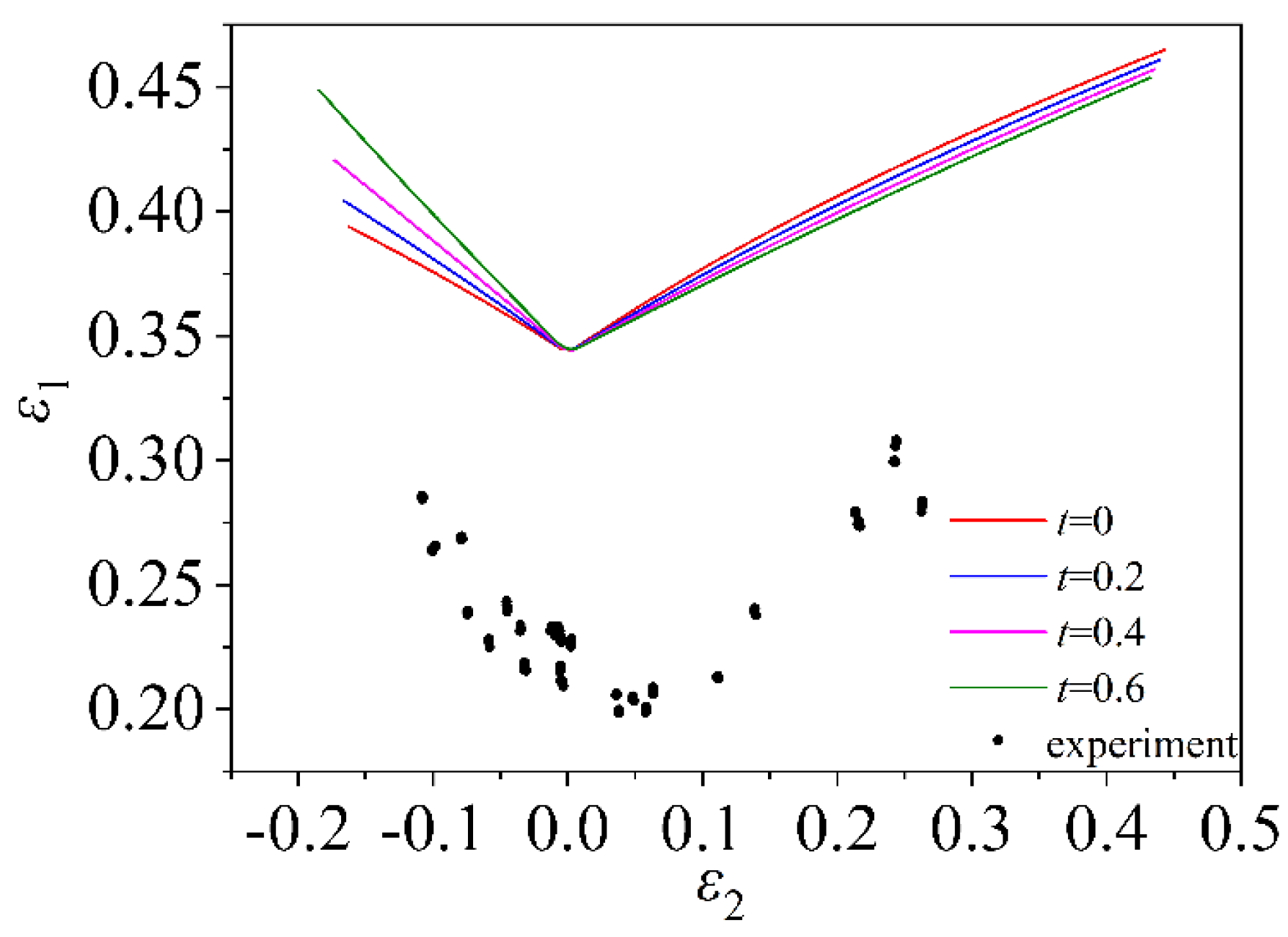
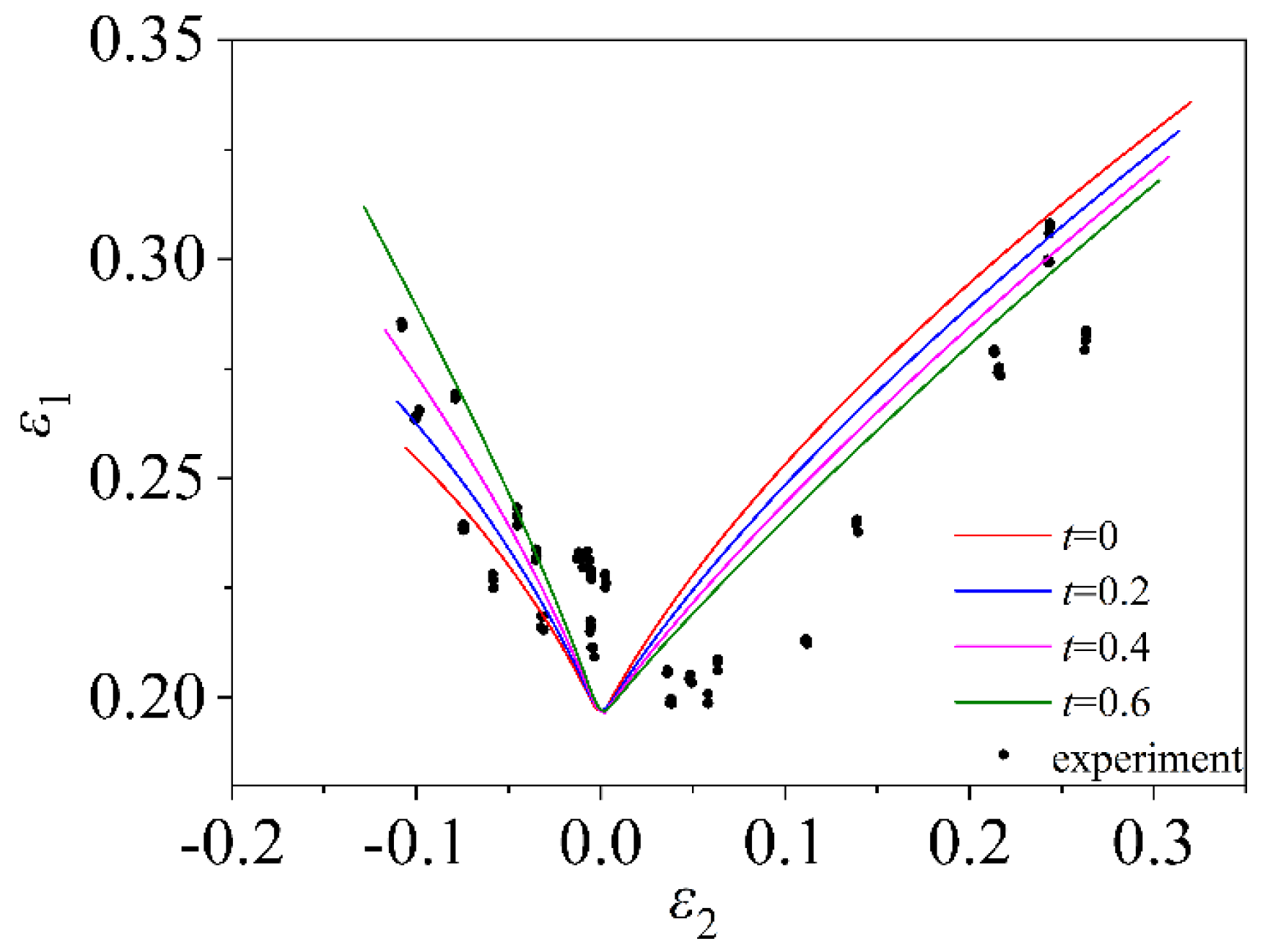
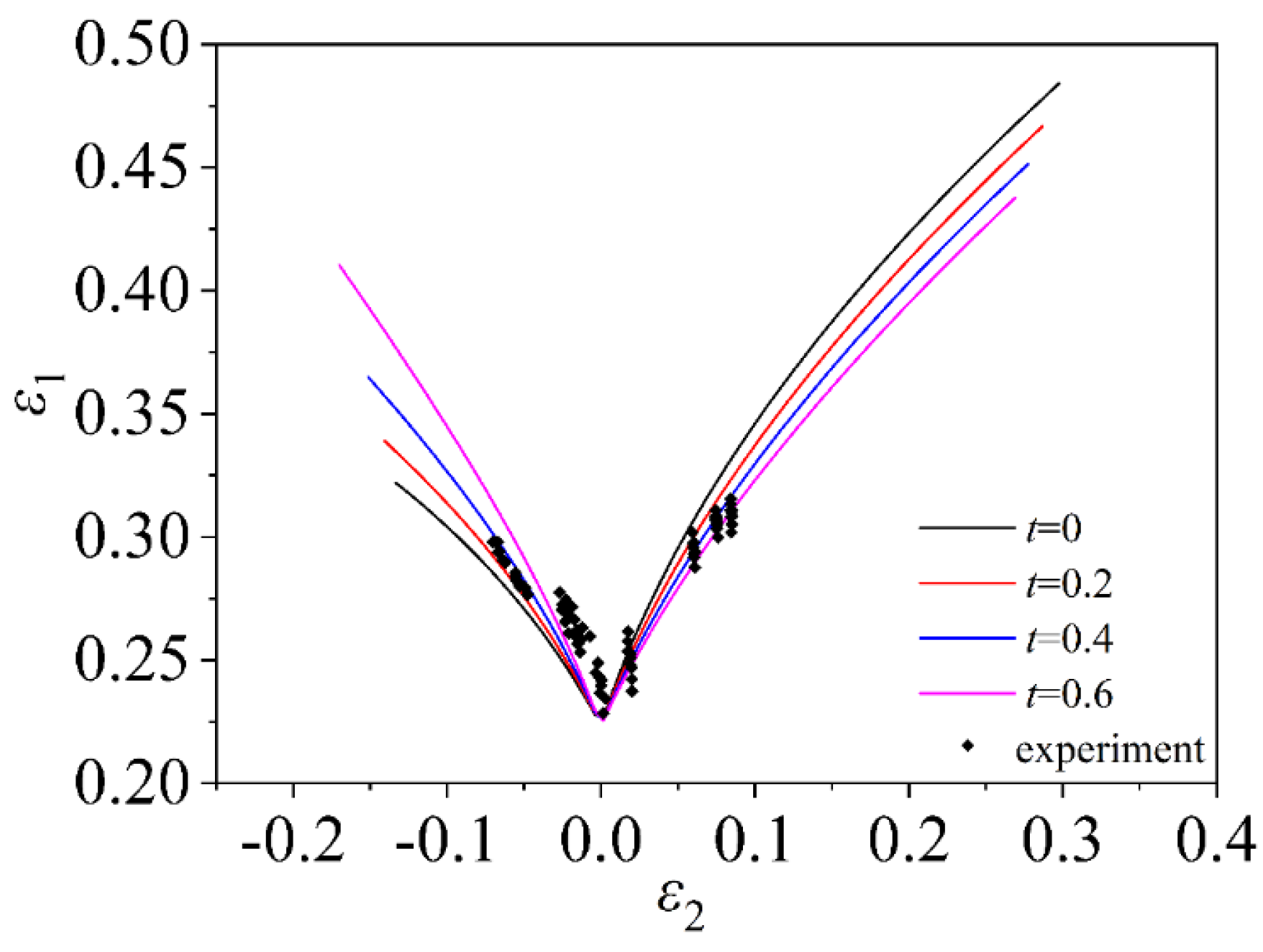
5.1. Forming Curve Verification of Material TRIP780

In order to verify whether the forming limit under the induced stress in the thickness direction is closer to the experimental results, the FLD of the material TRIP780 and the material AA5182 were calculated and compared with the experimental data which using the Swift constitutive equation and the modified Voce constitutive equation and the more accurate anisotropic yield criterion Hill48 yield criterion. The constitutive equation coefficients and the forming limit experimental data are taken from the data published by NUMISHEET 2013.

The mechanical properties of the material TRIP780 are shown in

Table 2. Mechanical properties of material TRIP780.

${\mathit{\sigma }}_0/\mathbf{MPa}$	${\mathit{\sigma }}_{45}/\mathbf{MPa}$	${\mathit{\sigma }}_{90}/\mathbf{MPa}$	${\mathit{\sigma }}_{\mathbf{b}}/\mathbf{MPa}$	${\mathit{r}}_0$	${\mathit{r}}_{45}$	${\mathit{r}}_{90}$
463.5	460.8	497.5	488.1	0.71	0.920	0.830

.

The modified Voce constitutive equation expression is as:

$$\overline{\sigma }=A-B\exp \left(-C{\overline{\epsilon }}_p\right)+D{\overline{\epsilon }}_p$$

The coefficients of the constitutive equation are shown in

Table 3. Modified Voce constitutive equation coefficient of material TRIP780.

A	B	C	D
910	479.9	14.240	334.788

.

The stress-strain curve of the material TRIP780 is obtained according to the constitutive equation of the material, and the forming limit curves with different constitutive equations are as follows:

As shown in Figure 20, the two stress-strain relationships coincide with each other during the uniform deformation stage, and they diverge after the non-uniform deformation point. As the number of deformations increases, it can be seen that the slope of the Swift stress-strain relationship is higher than the modified Voce. In other words, the hardening rate of the material based on the Swift stress-strain relationship is higher than the hardening rate of the material based on the modified Voce relationship. Higher material hardening rates may result in higher forming limits. Therefore, the forming limit calculated based on the Swift relationship is higher than the forming limit based on the modified Voce relationship.

As shown in Figure 21 and Figure 22, considering the induced stress in thickness direction during the deformation process, as the value of t increases, and the forming limit curve gradually moves closer to the experimental data. It is shown that after considering the induced stress in the thickness direction, the material forming is indeed closer to the actual forming conditions, and the accuracy of the theoretical forming limit curve is improved.

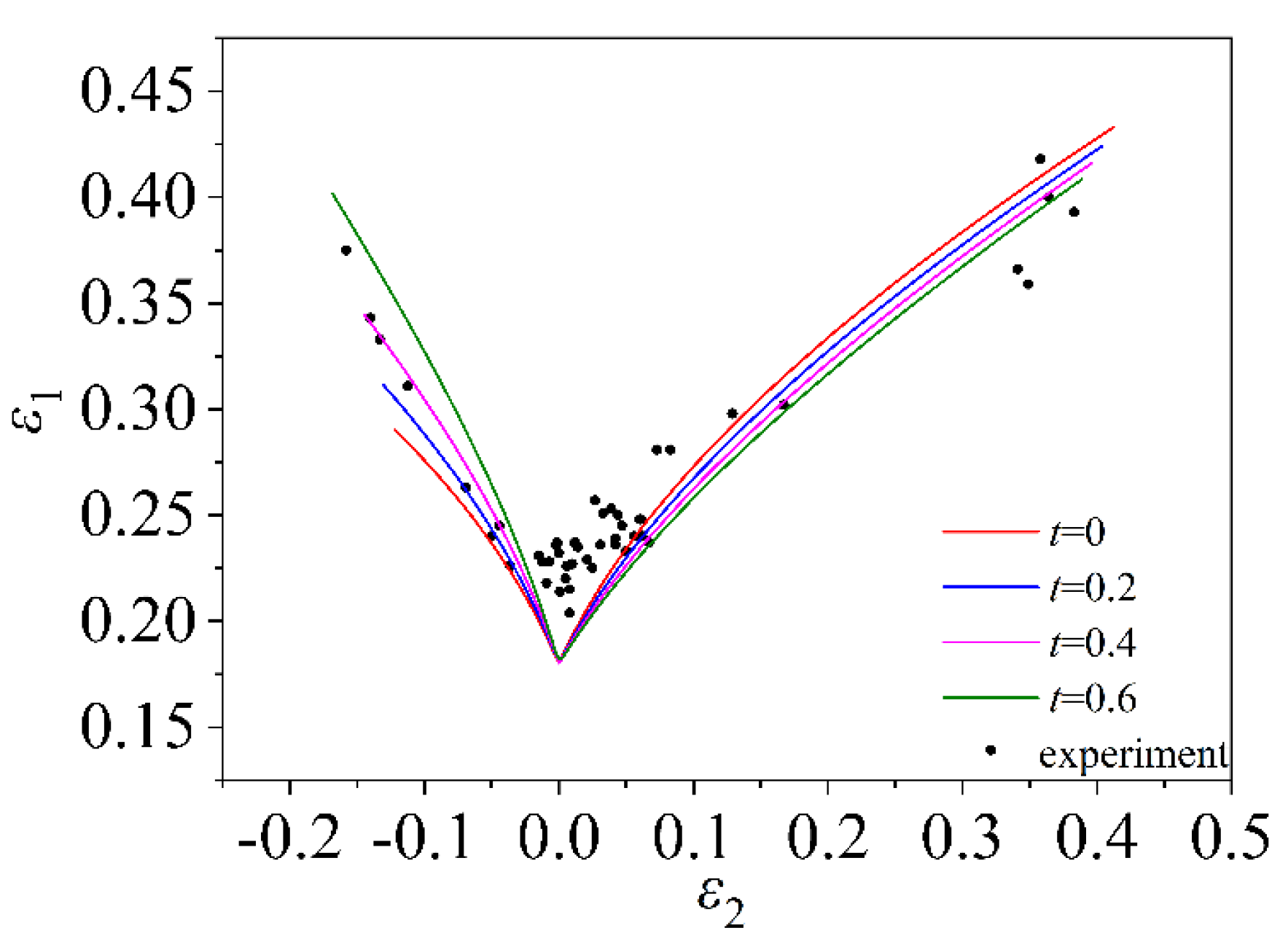
5.2. Forming Curve Verification of Material AA5182

The mechanical properties of the material AA5182 are shown in

Table 4. Mechanical properties of material AA5182.

${\mathit{\sigma }}_0/\mathbf{MPa}$	${\mathit{\sigma }}_{45}/\mathbf{MPa}$	${\mathit{\sigma }}_{90}/\mathbf{MPa}$	${\mathit{\sigma }}_{\mathbf{b}}/\mathbf{MPa}$	${\mathit{r}}_0$	${\mathit{r}}_{45}$	${\mathit{r}}_{90}$
126.4	123.3	127.8	114.2	0.699	0.766	0.755

.

The constitutive equation coefficients are shown in

Table 5. Swift constitutive equation coefficients of material AA5182.

$\mathit{K}$	$\mathit{n}$	${\mathit{\epsilon }}_0$
615.3	0.363	0.00761

and

Table 6. Modified Voce constitutive equation coefficients of material AA5182.

A	B	C	D
432.7	316.0	8.393	−173.946

.

The stress-strain curve of material AA5182 is obtained according to the constitutive equation of the material, and the forming limit curves with different constitutive equations are as follows:

As shown in Figure 23, both modified Voce and Swift stress-strain relations can accurately describe the curve of the elastic deformation region during uniaxial tension. However, the FLD calculated based on the modified Voce constitutive equation is different from that based on the stress-strain relation of Swift. Since the experimental data of the non-uniform deformation stage cannot be obtained, the material constants of the two stress-strain relations can only be obtained by fitting the experimental data of the uniform deformation process [22]. Therefore, the accuracy of modified Voce and Swift stress-strain relationship in describing the deformation behavior of non-uniform deformation cannot be guaranteed. However, the calculation process of forming limits includes uniform and non-uniform deformation processes. Further comparison of the modified Voce and Swift flow stress-strain relationships is shown in Figure 24 and Figure 25. For material AA5182, the forming limit of the material can be more accurately described based on the modified Voce constitutive equation; The Swift constitutive equation has a higher hardening rate, which causes the FLC to deviate greatly from the actual experimental data. It can be seen from Figure 25 that the theoretical prediction of FLC is better than the experimental data after considering the induced stress in the thickness direction during the deformation process.

5.3. Forming Curve Verification of Material 5754O

The mechanical properties of the material 5754O are shown in

Table 7. Mechanical properties of material 5754O.

${\mathit{\sigma }}_0/\mathbf{MPa}$	${\mathit{\sigma }}_{45}/\mathbf{MPa}$	${\mathit{\sigma }}_{90}/\mathbf{MPa}$	${\mathit{\sigma }}_{\mathbf{b}}/\mathbf{MPa}$	${\mathit{r}}_0$	${\mathit{r}}_{45}$	${\mathit{r}}_{90}$
108.671	108.678	113.385	110.041	0.707	0.894	0.956

.

The coefficients of the constitutive equation are shown in

Table 8. Swift constitutive equation coefficients of material 5754O.

$\mathit{K}$	$\mathit{n}$	${\mathit{\epsilon }}_0$
474.9	0.3236	0.0068

and

Table 9. Voce constitutive equation coefficients of material 5754O.

A	B	C
99.69	189.20	12.01

.

The stress-strain curve of material 5754O is obtained according to the constitutive equation of the material, and the forming limit curves with different constitutive equations are as follows.

The stress-strain curve is shown in Figure 26. For material 5754O, the Voce stress-strain relationship with a low hardening rate is used to solve the theoretical FLD. As shown in the Figure 27, it is further confirmed that the FLC which considers the induced stress in the thickness direction is more consistent with the experimental data, and the accuracy of the FLD under the induced stress in the thickness direction is verified.

6. Conclusions

(1)

In this paper, solid element is used to simulate the bulging test of hemispherical punch, and the principal stresses S11, S22 and S33 in three directions are extracted from the finite element simulation results. It is confirmed that the thick stress is induced during the plastic deformation of sheet metal.

(2)

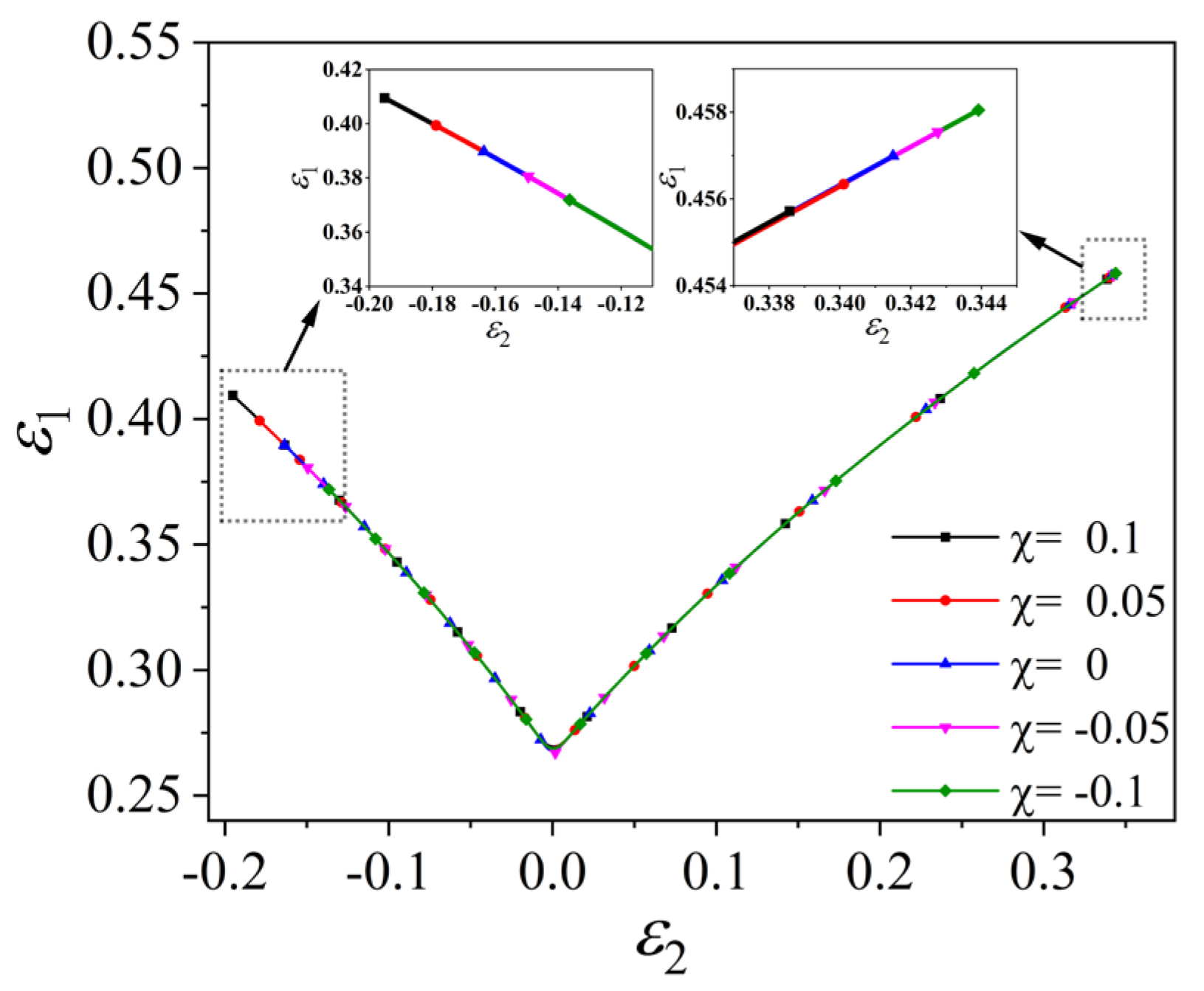
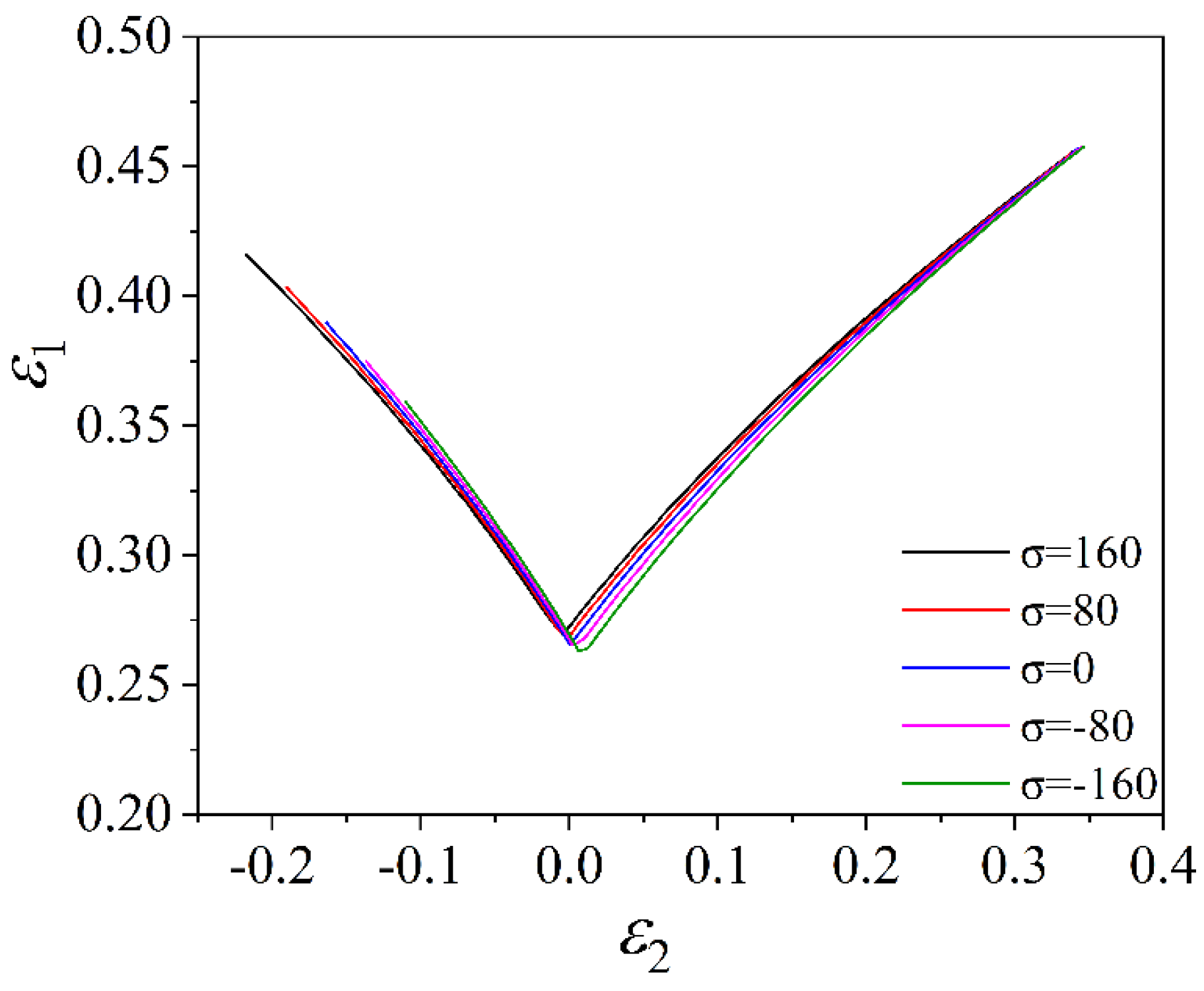
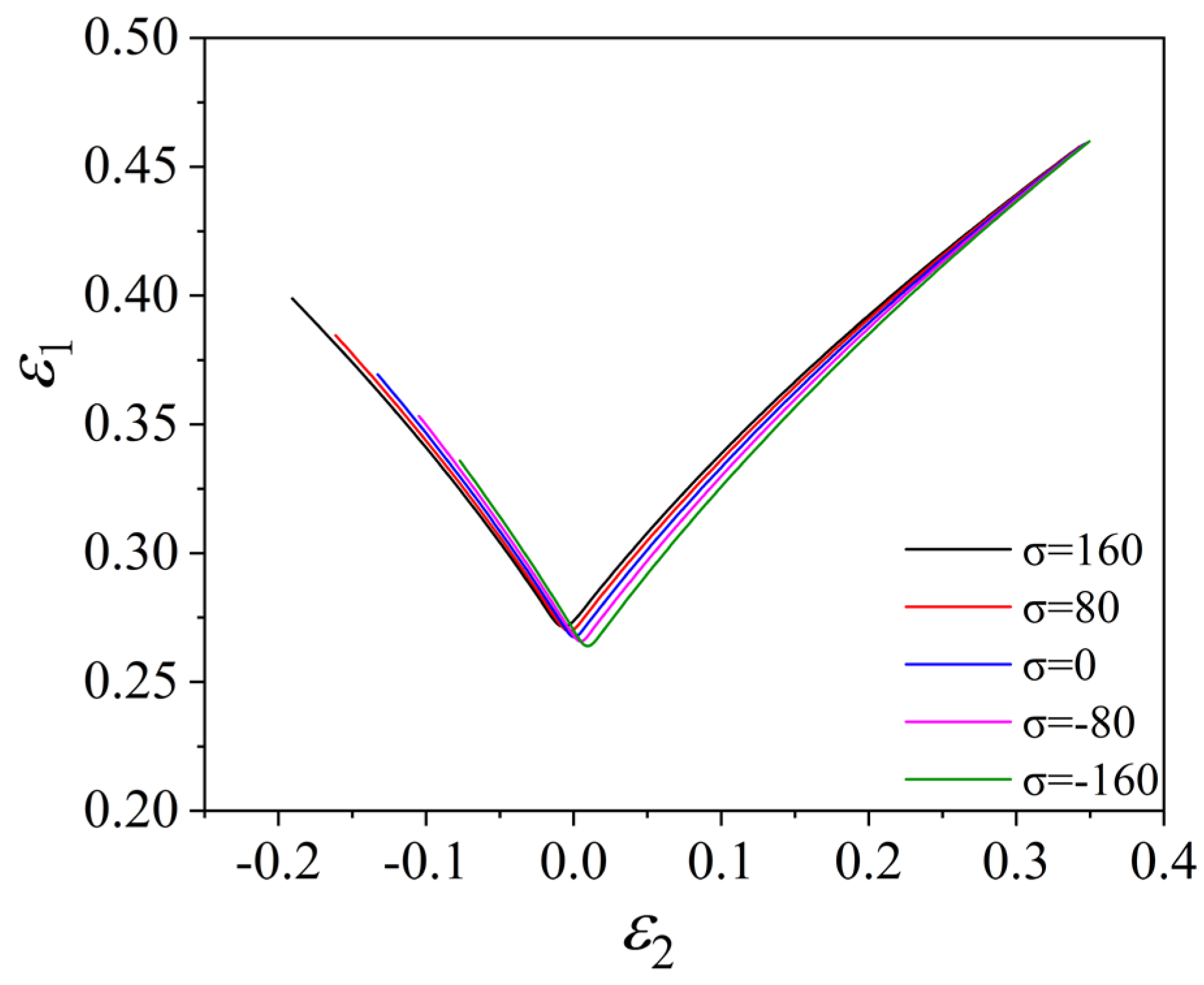
When solving the theoretical forming limit, the conclusion that the stress in the thickness direction is always applied to the sheet and the stress in the thickness direction is induced during the deformation of the sheet is not exactly the same. In this paper, the study of induced thick stress shows that the influence of induced stress in thickness direction on FLD during deformation process is not only reflected in the length of the curve but also affects the height. The FLC of the tension and compression zone is significantly increased compared with the plane strain state, and as the strain increases, the degree of elevation also increases. The FLC decreases in the biaxial tension zone, and the degree of decrease gradually becomes stable with the increase in strain. Appropriate methods should be used in the project to predict the theoretical limit curve of the sheet metal.

(3)

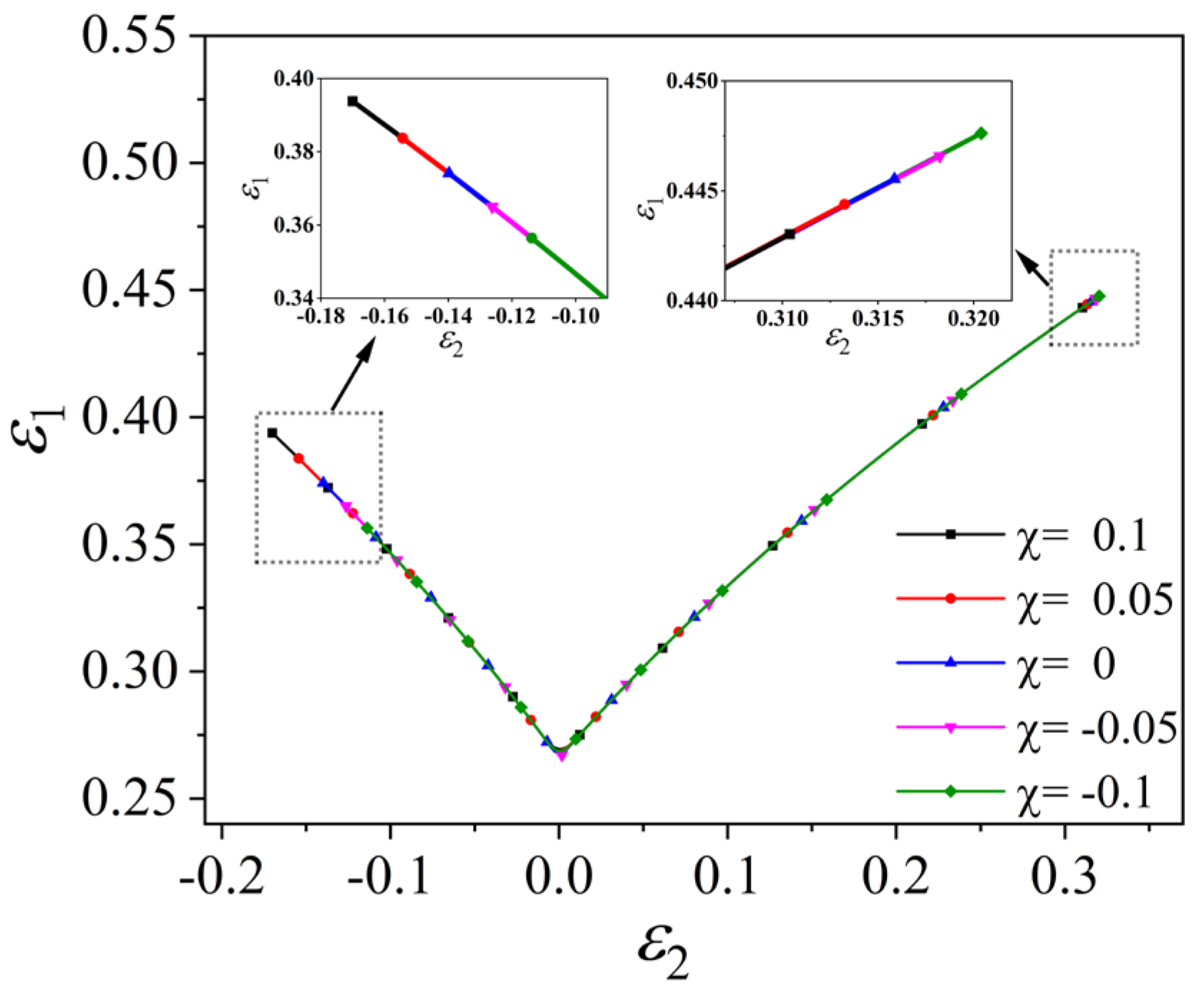
This study shows that the induced stress in the thickness direction does not significantly change the effect of $n$ on FLD, but significantly changes the sensitivity of $r$ to FLD. The method of always applying stress in the thickness direction does not significantly change the effect of $r$ and $n$ values on FLD, but only changes the overall change of the curve. In addition, FLC increases with the increase in $n$ value, which is the effect of $n$ value itself on FLD. The larger the $n$ value, the longer the FLC. This result is also consistent with the results of other theoretical models.

(4)

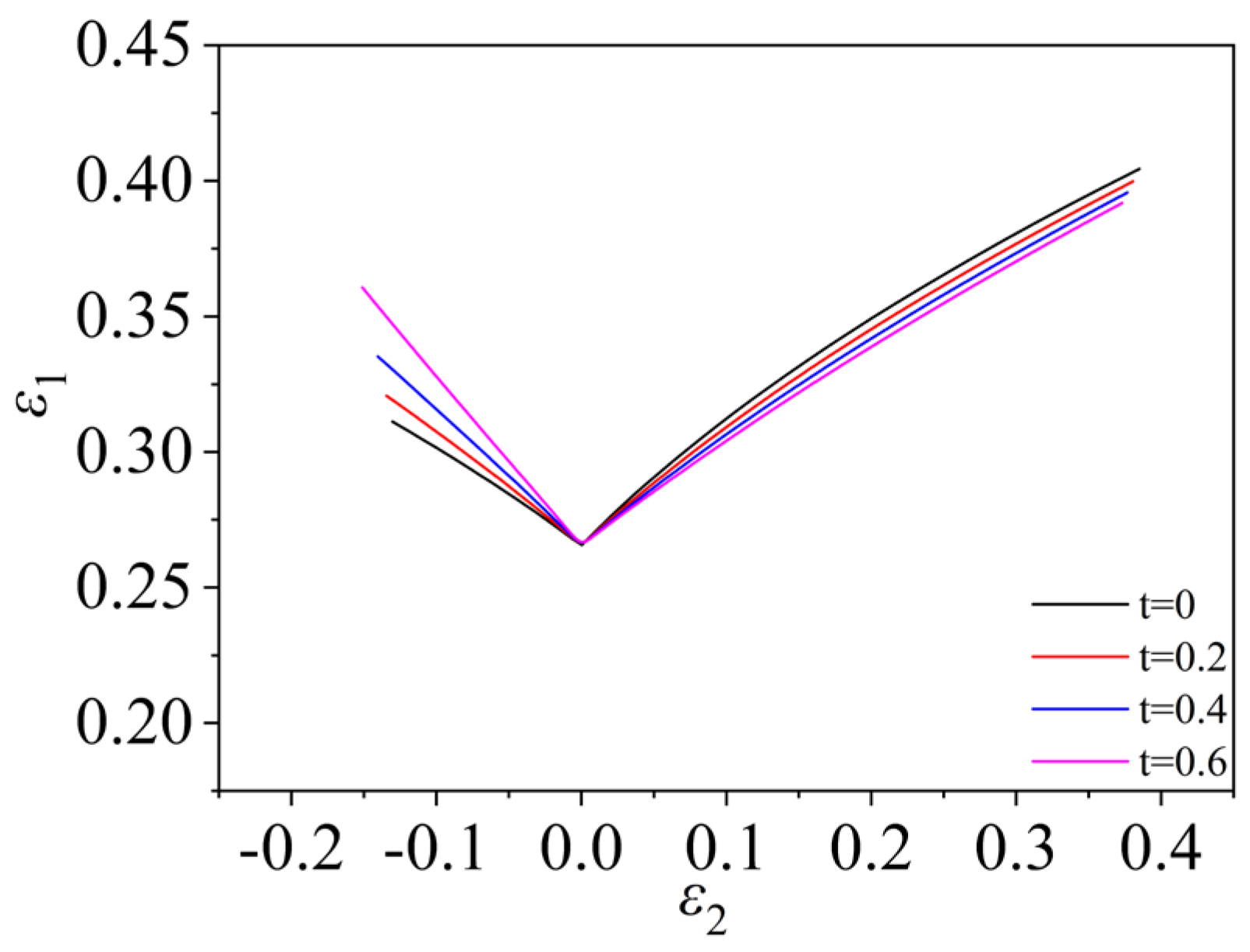
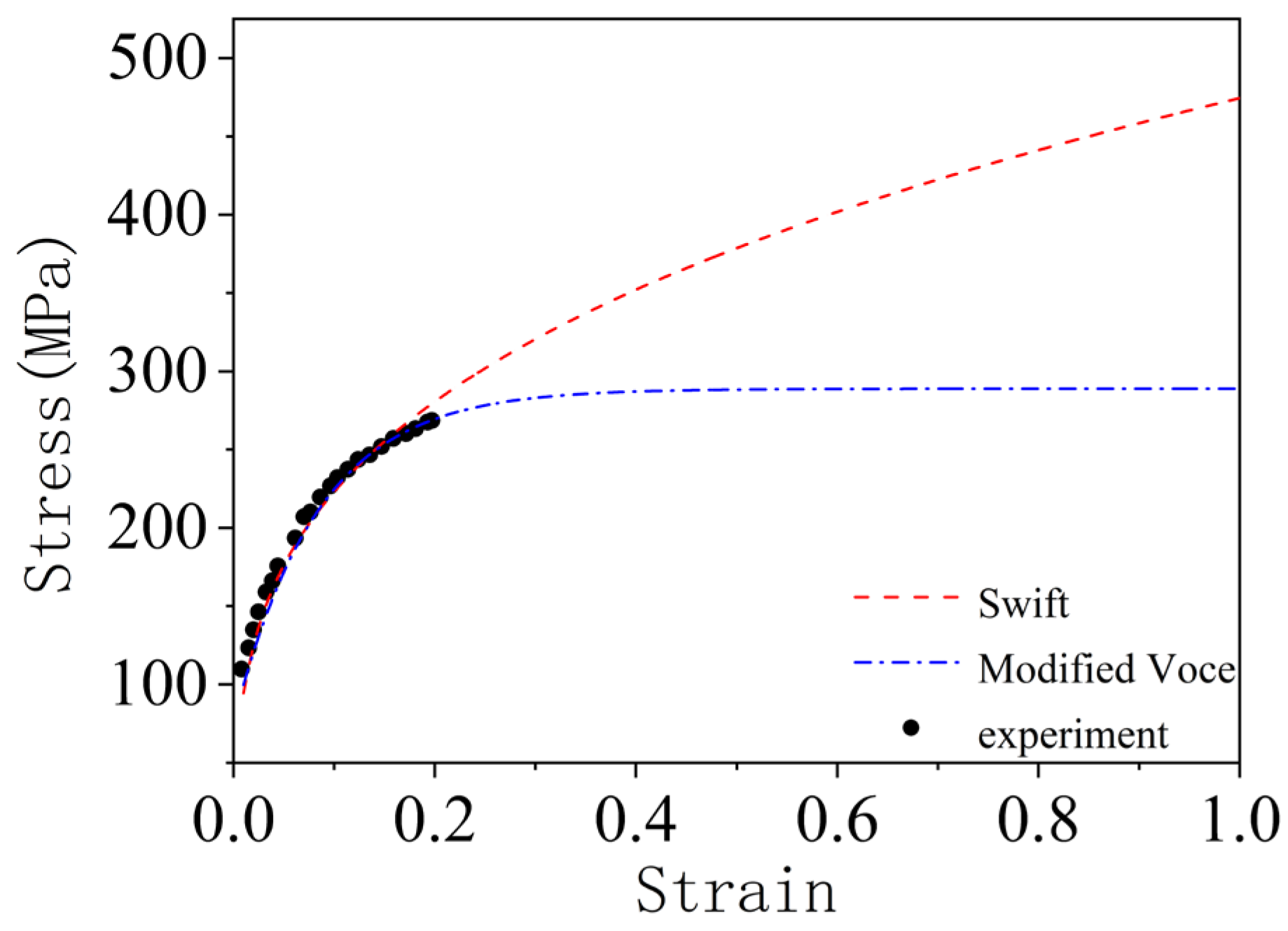
Even with a more accurate anisotropic yield function, the stress-strain relationship plays an important role in forming limits [22]. The two flow stress-strain relationships described in this paper, Swift stress-strain relationship and modified Voce stress-strain relationship can accurately describe the deformation behavior of uniform strain, but the resulting forming limits are very different. Therefore, in calculating the sheet forming limit, in addition to choosing the appropriate yield criterion, an appropriate stress-strain relationship should be used.

(5)

The stress in the thickness direction must be induced during the deformation of the sheet. By comparing the theoretical calculation of the three materials TRIP780, AA5182 and 5754O with the experimental data, it is found that the FLC which considers the induced stress in the thickness direction is more consistent with the experimental data, and the prediction accuracy is higher. It is proved that the FLD which only considers the plane stress state is defective, so it is important to consider the induced stress in the thickness direction when predicting the theoretical FLD.