Biaxial Deformation Behavior of AZ31 Magnesium Alloy along RD and Diagonal Direction Degree between TD and ND
Abstract
:1. Introduction
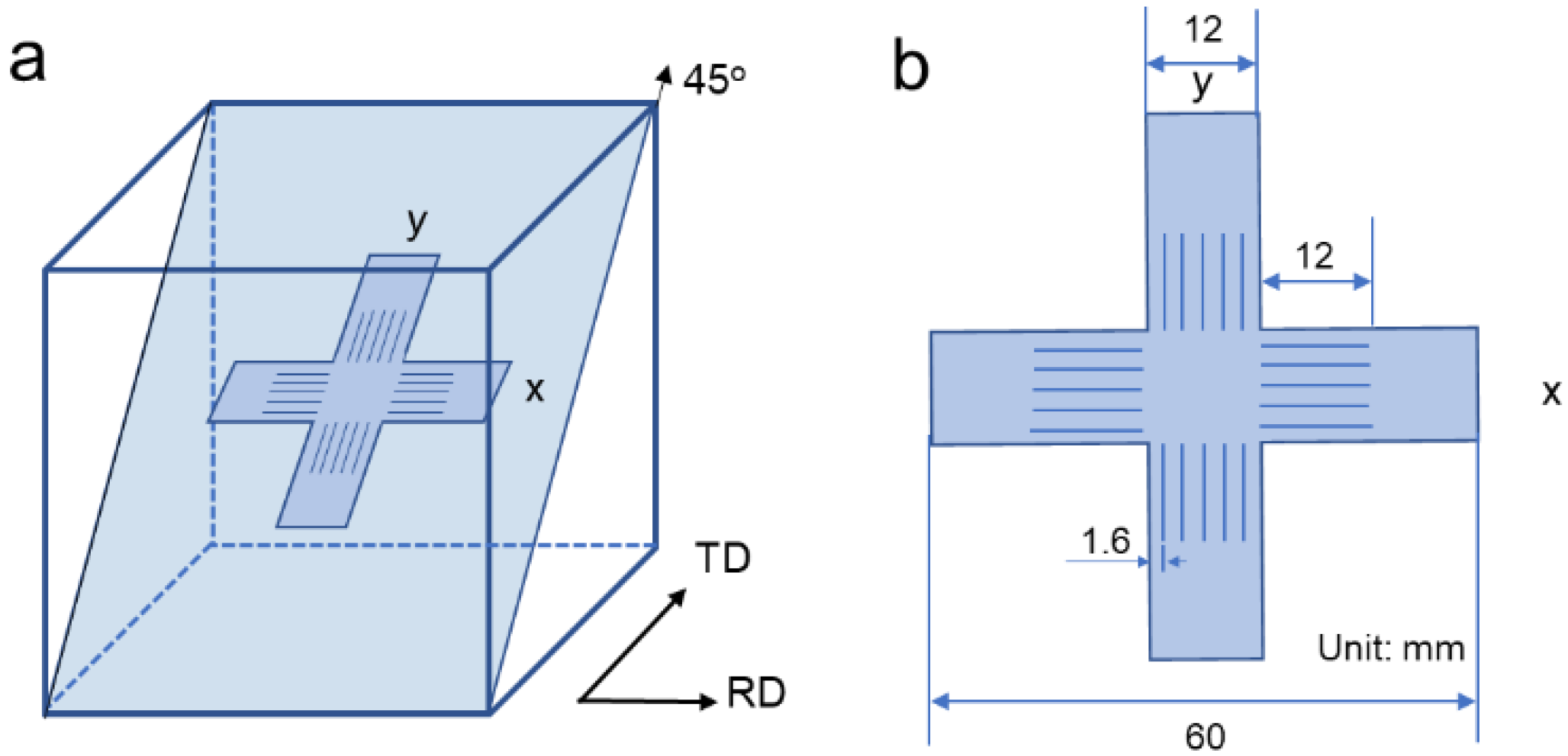
2. Materials and Methods
2.1. Material and Mechanical Tests
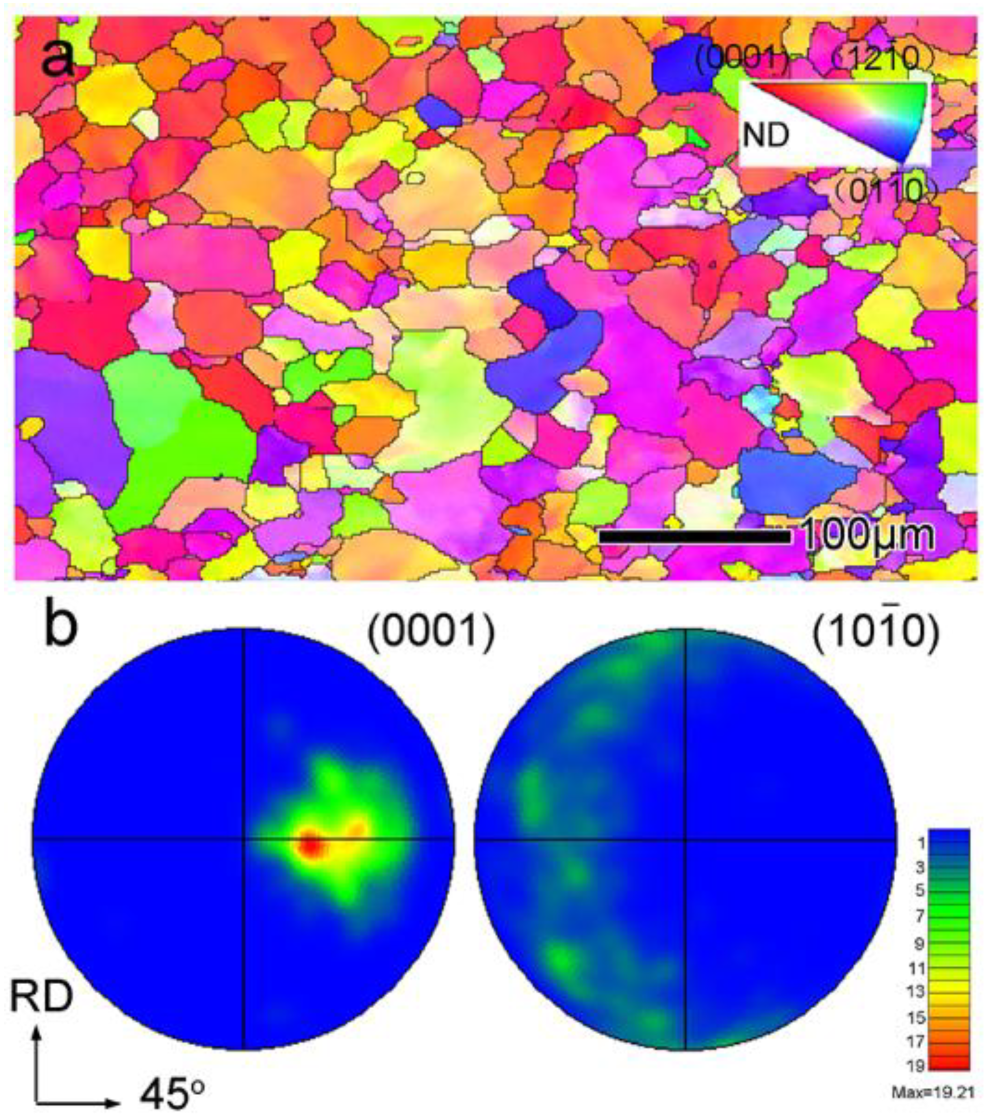
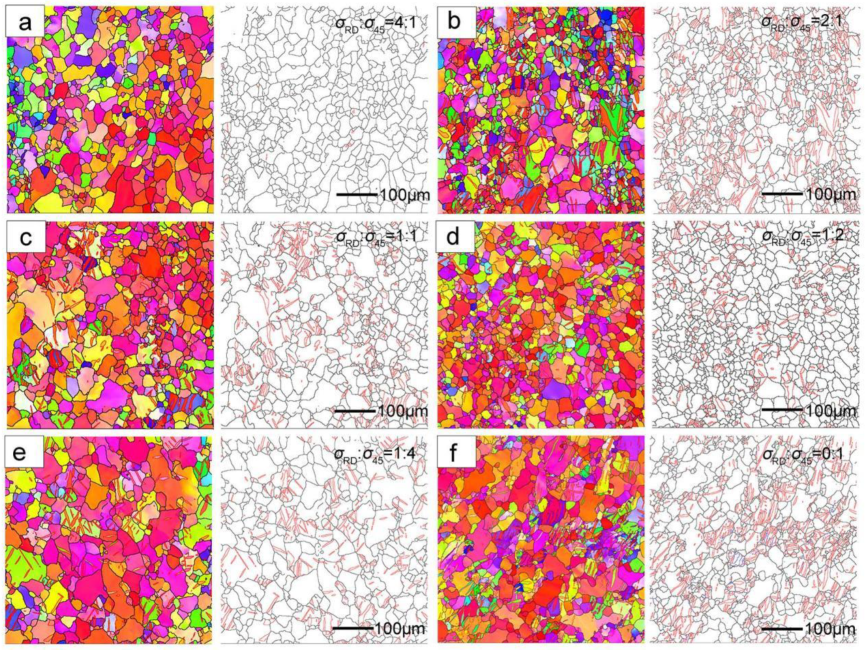
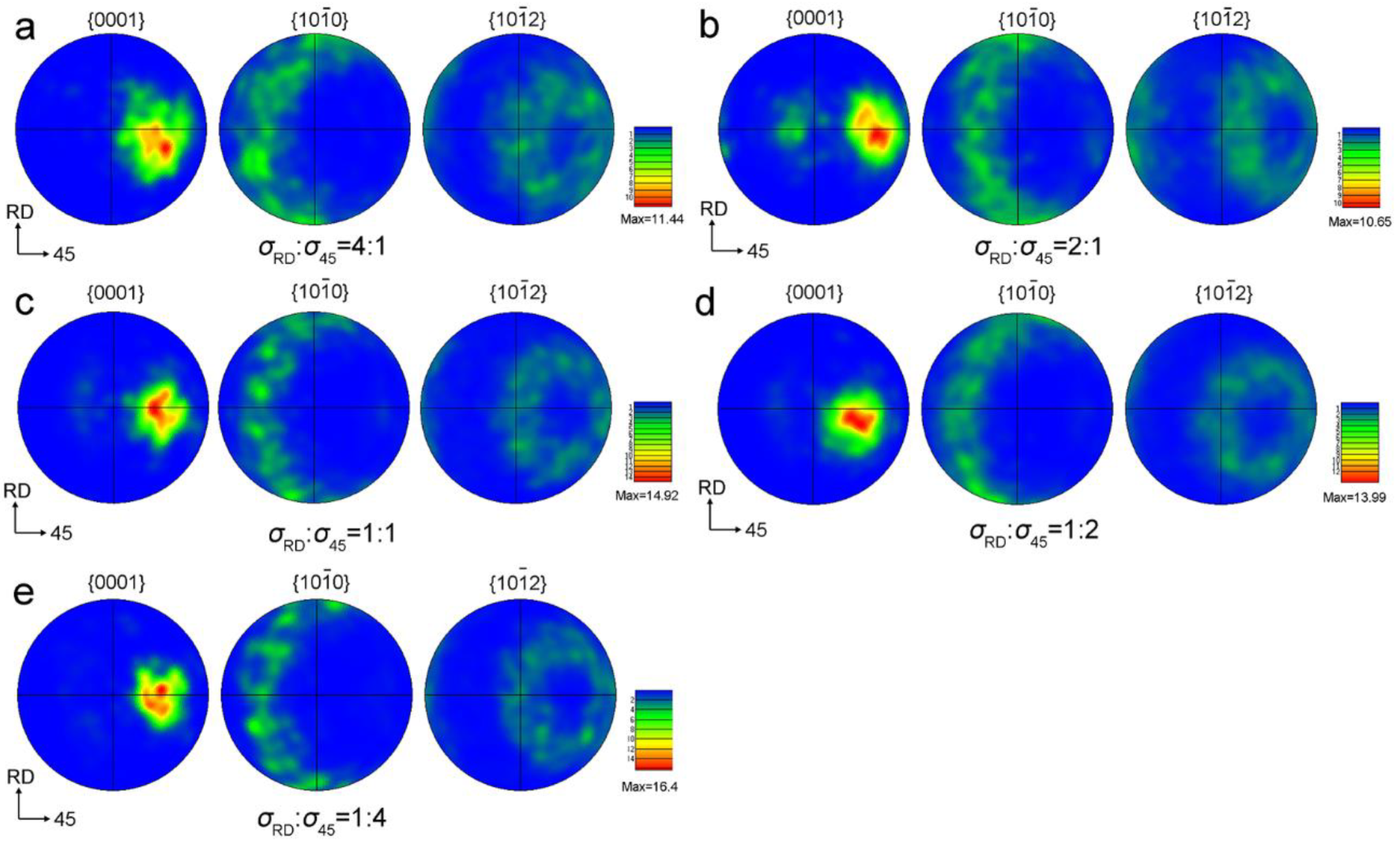
2.2. Characterization of Microstructure and Texture
3. Results
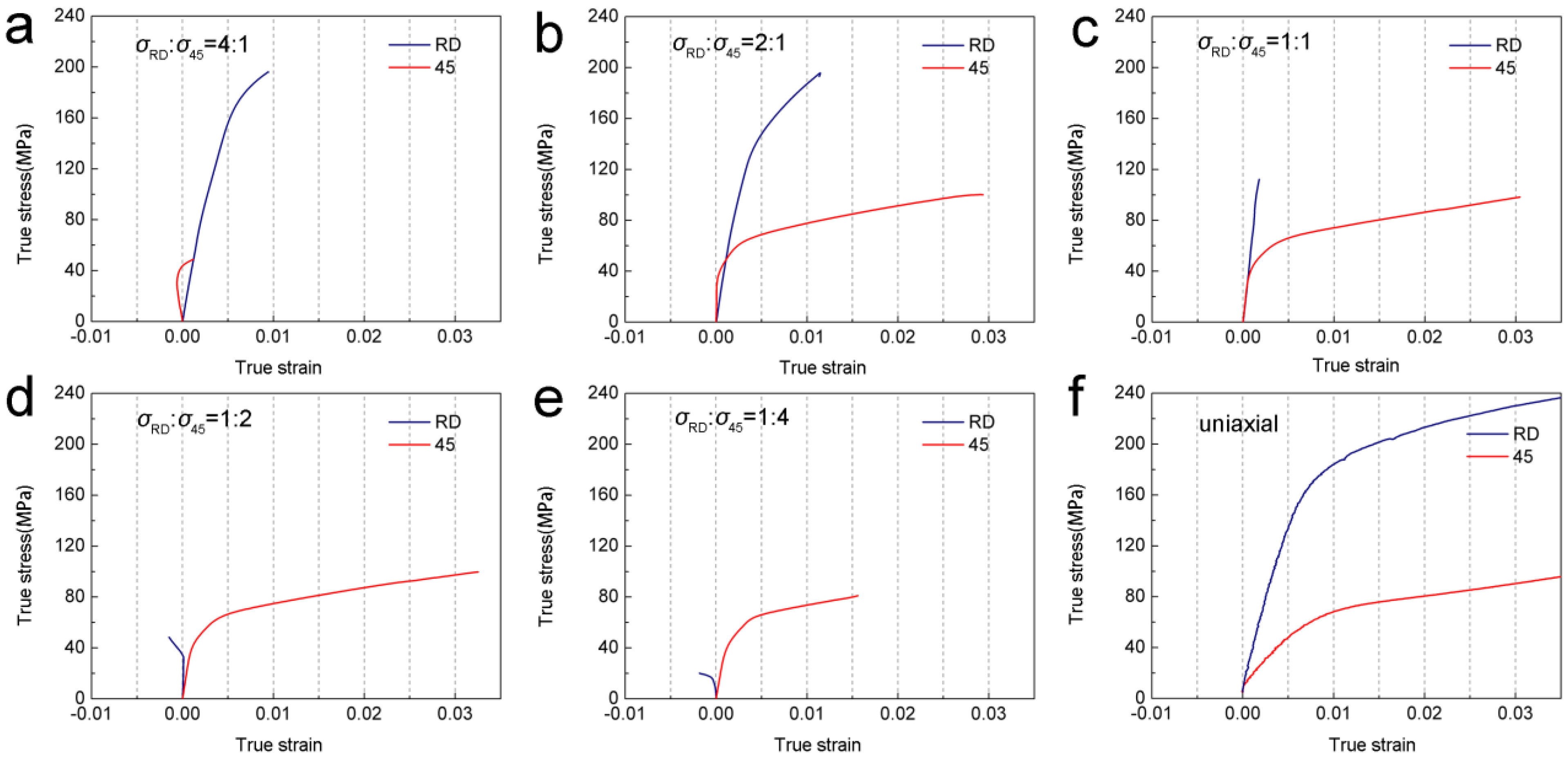
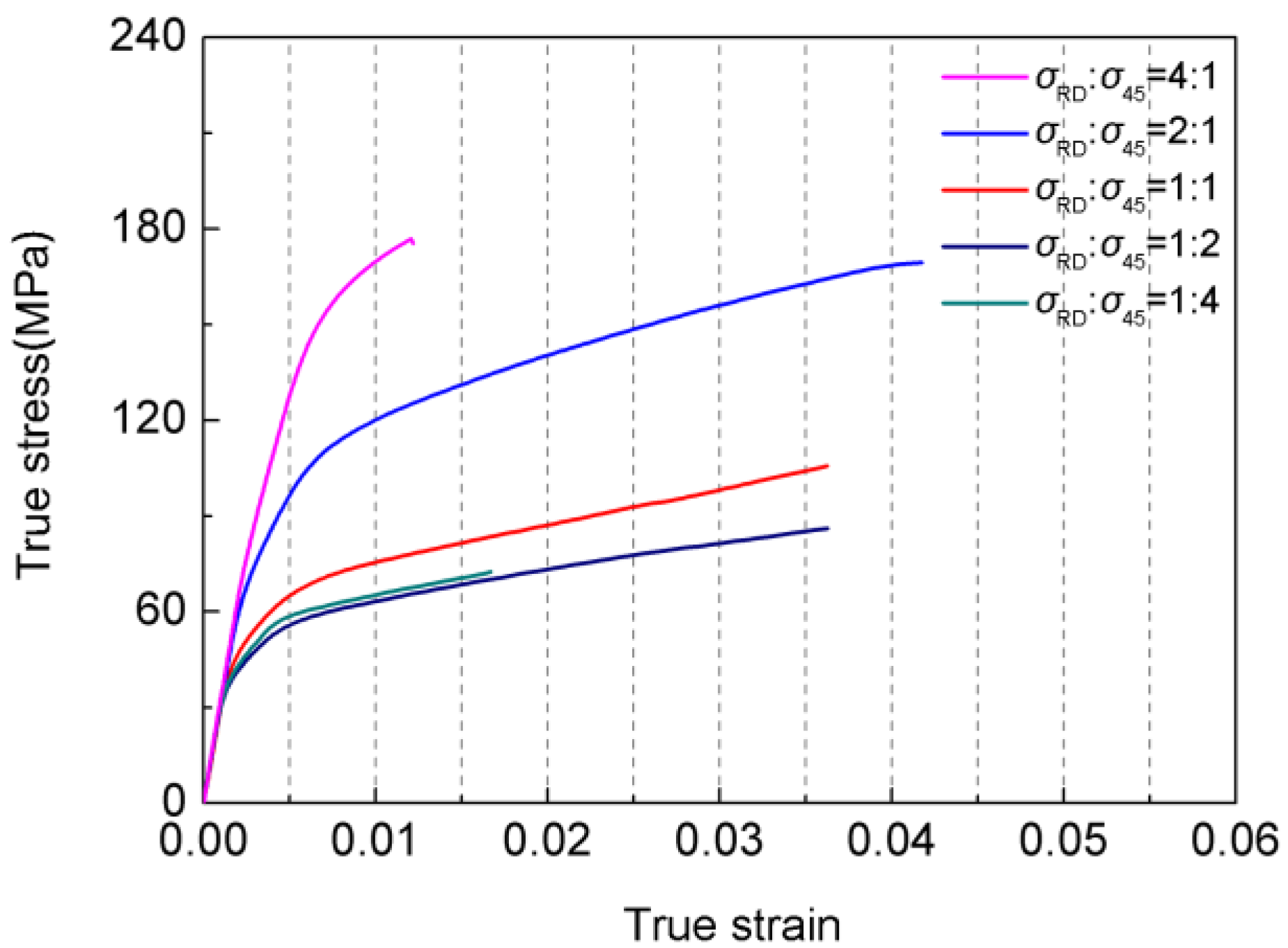
3.1. Mechanical Behavior
3.2. Twinning Behavior
4. Discussion
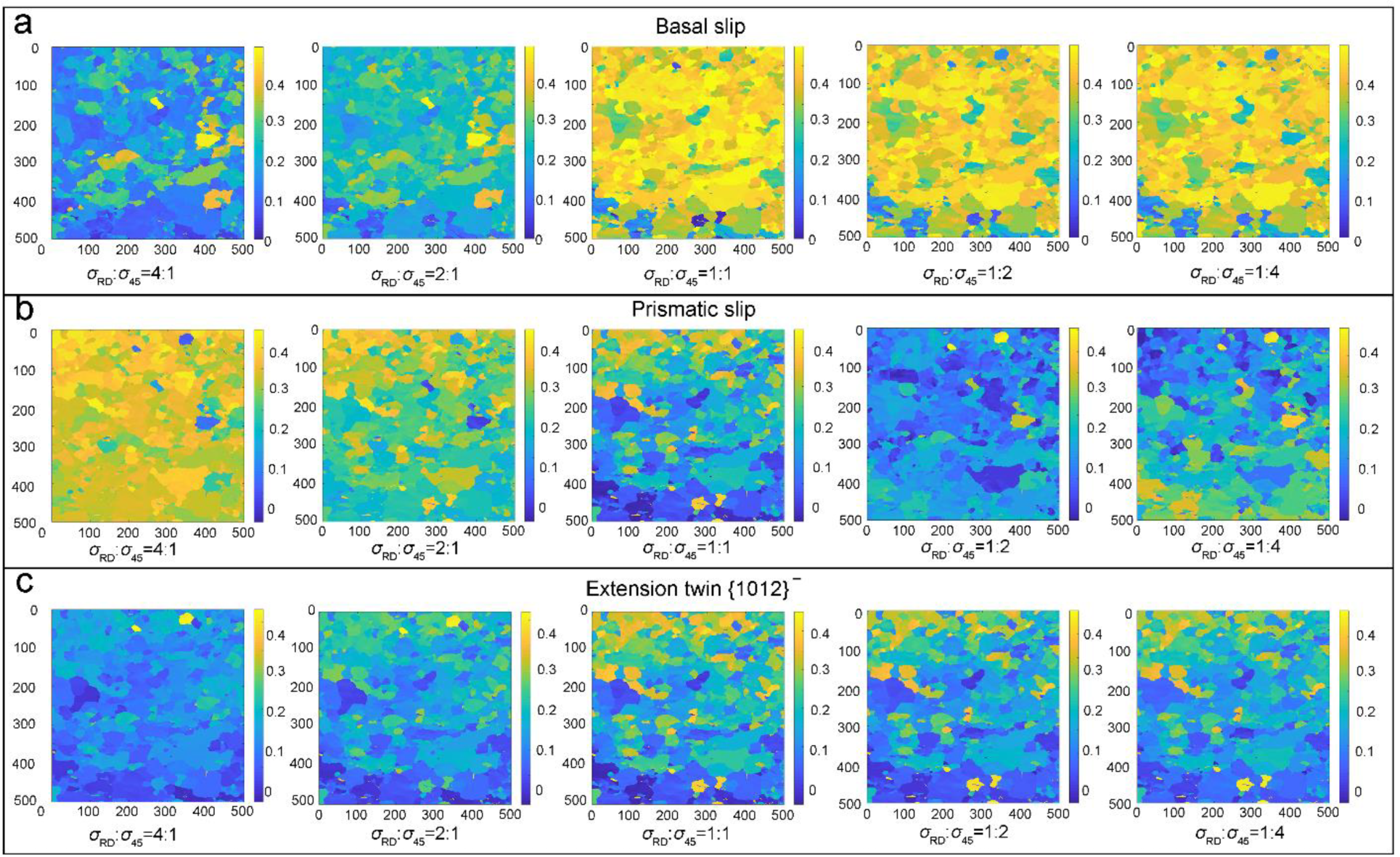
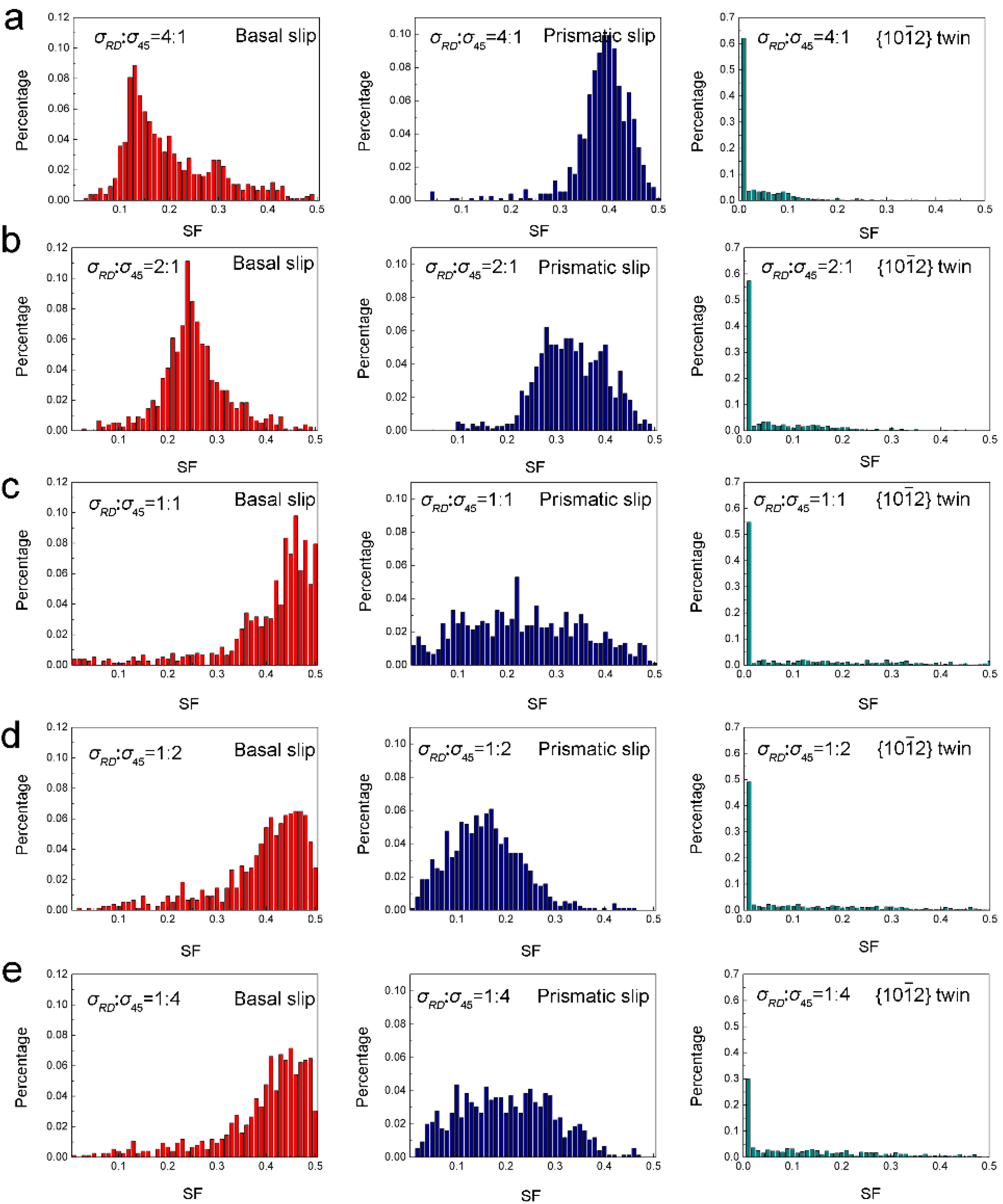
4.1. Twinning and Slip Behavior under Biaxial Tension
4.1.1. Schmid Factor Analysis of the Twinning System
4.1.2. Contribution of the Twinning to Plastic Deformation
4.1.3. Activities of Slip Systems in the Deformation
4.2. Effect of the Deformation Mechanism on the Flow Stress
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kuji, C.; Soyama, H. Mechanical Surface Treatment of Titanium Alloy Ti6Al4V Manufactured by Direct Metal Laser Sintering Using Laser Cavitation. Metals 2023, 13, 181. [Google Scholar] [CrossRef]
- Li, Y.; Han, T.; Chu, Z.; Xue, C.; Yang, Q.; Zhao, X.; Gao, H. Effect of Loading Direction on the Tensile Properties and Texture Evolution of AZ31 Magnesium Alloy. Crystals 2021, 11, 1193. [Google Scholar] [CrossRef]
- Pérez, P.; Medina, J.; Vega, M.F.; Garcés, G.; Adeva, P. Control of the Microstructure in a Al5Co15Cr30Fe25Ni25 High Entropy Alloy through Thermo-Mechanical and Thermal Treatments. Metals 2023, 13, 180. [Google Scholar] [CrossRef]
- Čapek, J.; Panzner, T.; Sofinowski, K.; Drozdenko, D.; Máthis, K. In Situ Neutron Diffraction and Acoustic Emission during the Biaxial Loading of AZ31 Alloy. In Magnesium Technology 2018; Orlov, D., Joshi, V., Solanki, K.N., Neelameggham, N.R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 199–202. [Google Scholar]
- Thirumalai, R.; Senthilkumaar, J.S.; Selvarani, P.; Ramesh, S. Machining characteristics of Inconel 718 under several cutting conditions based on Taguchi method. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2012, 227, 1889–1897. [Google Scholar] [CrossRef]
- Wang, H.; Wu, P.D.; Gharghouri, M.A. Effects of basal texture on mechanical behaviour of magnesium alloy AZ31B sheet. Mater. Sci. Eng. A 2010, 527, 3588–3594. [Google Scholar] [CrossRef]
- Chun, Y.B.; Davies, C.H.J. Investigation of Prism <a> Slip in Warm-Rolled AZ31 Alloy. Metall. Mater. Trans. A 2011, 42, 4113–4125. [Google Scholar]
- Zhao, B.; Wu, W.; Zhi, J.; Su, C.; Yao, T. Effect of CeO2 Content on Melting Performance and Microstructure of CaO-Al2O3-SiO2-MgO Refining Slag. Metals 2023, 13, 179. [Google Scholar] [CrossRef]
- Zhang, J.; Xin, S.; Zhang, Y.; Guo, P.; Sun, H.; Li, T.; Qin, C. Effects of Elements on the Microstructure and Mechanical Properties of AlCoCrFeNiTi High-Entropy Alloys. Metals 2023, 13, 178. [Google Scholar] [CrossRef]
- Sun, X.; Liu, P.; Jiang, Z.; Yang, Y.; Wang, Z.; Mu, Z. Analysis of Design Method and Mechanical Properties of Plug-In Composite Shear Wall. Metals 2023, 13, 177. [Google Scholar] [CrossRef]
- Máthis, K.; Čapek, J.; Zdražilová, Z.; Trojanová, Z. Investigation of tension—Compression asymmetry of magnesium by use of the acoustic emission technique. Mater. Sci. Eng. A 2011, 528, 5904–5907. [Google Scholar] [CrossRef]
- Máthis, K.; Csiszár, G.; Čapek, J.; Gubicza, J.; Clausen, B.; Lukáš, P.; Vinogradov, A.; Agnew, S.R. Effect of the loading mode on the evolution of the deformation mechanisms in randomly textured magnesium polycrystals—Comparison of experimental and modeling results. Int. J. Plast. 2015, 72, 127–150. [Google Scholar] [CrossRef]
- Xiong, Y.; Yu, Q.; Jiang, Y. Deformation of extruded ZK60 magnesium alloy under uniaxial loading in different material orientations. Mater. Sci. Eng. A 2018, 710, 206–213. [Google Scholar] [CrossRef]
- Barnett, M.R.; Ghaderi, A.; da Fonseca, J.Q.; Robson, J.D. Influence of orientation on twin nucleation and growth at low strains in a magnesium alloy. Acta Mater. 2014, 80, 380–391. [Google Scholar] [CrossRef]
- Ma, Q.; El Kadiri, H.; Oppedal, A.L.; Baird, J.C.; Li, B.; Horstemeyer, M.F.; Vogel, S.C. Twinning effects in a rod-textured AM30 Magnesium alloy. Int. J. Plast. 2012, 29, 60–76. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, M.; Gan, M.; Wang, X.; Gu, C.; Tu, J. Rapid Electrodeposition and Corrosion Behavior of Zn Coating from a Designed Deep Eutectic Solvent. Metals 2023, 13, 172. [Google Scholar] [CrossRef]
- Hong, S.-G.; Park, S.H.; Lee, C.S. Role of {10–12} twinning characteristics in the deformation behavior of a polycrystalline magnesium alloy. Acta Mater. 2010, 58, 5873–5885. [Google Scholar] [CrossRef]
- Lou, X.Y.; Li, M.; Boger, R.K.; Agnew, S.R.; Wagoner, R.H. Hardening evolution of AZ31B Mg sheet. Int. J. Plast. 2007, 23, 44–86. [Google Scholar] [CrossRef]
- Chapuis, A.; Wang, B.; Liu, Q. A comparative study between uniaxial compression and plane strain compression of Mg–3Al–1Zn alloy using experiments and simulations. Mater. Sci. Eng. A 2014, 597, 349–358. [Google Scholar] [CrossRef]
- Wang, H.; Raeisinia, B.; Wu, P.D.; Agnew, S.R.; Tomé, C.N. Evaluation of self-consistent polycrystal plasticity models for magnesium alloy AZ31B sheet. Int. J. Solids Struct. 2010, 47, 2905–2917. [Google Scholar] [CrossRef]
- Wang, B.; Xin, R.; Huang, G.; Liu, Q. Effect of crystal orientation on the mechanical properties and strain hardening behavior of magnesium alloy AZ31 during uniaxial compression. Mater. Sci. Eng. A 2012, 534, 588–593. [Google Scholar] [CrossRef]
- Knezevic, M.; Levinson, A.; Harris, R.; Mishra, R.K.; Doherty, R.D.; Kalidindi, S.R. Deformation twinning in AZ31: Influence on strain hardening and texture evolution. Acta Mater. 2010, 58, 6230–6242. [Google Scholar] [CrossRef]
- Wang, H.; Wu, P.D.; Wang, J.; Tomé, C.N. A crystal plasticity model for hexagonal close packed (HCP) crystals including twinning and de-twinning mechanisms. Int. J. Plast. 2013, 49, 36–52. [Google Scholar] [CrossRef]
- Xie, S.; Yuan, X.; Liu, F.; Zhao, B. Control of Copper Content in Flash Smelting Slag and the Recovery of Valuable Metals from Slag—A Thermodynamic Consideration. Metals 2023, 13, 153. [Google Scholar] [CrossRef]
- Molodov, K.D.; Al-Samman, T.; Molodov, D.A.; Gottstein, G. On the role of anomalous twinning in the plasticity of magnesium. Acta Mater. 2016, 103, 711–723. [Google Scholar] [CrossRef]
- Luo, J.R.; Godfrey, A.; Liu, W.; Liu, Q. Twinning behavior of a strongly basal textured AZ31 Mg alloy during warm rolling. Acta Mater. 2012, 60, 1986–1998. [Google Scholar] [CrossRef]
- Molodov, K.D.; Al-Samman, T.; Molodov, D.A.; Gottstein, G. Mechanisms of exceptional ductility of magnesium single crystal during deformation at room temperature: Multiple twinning and dynamic recrystallization. Acta Mater. 2014, 76, 314–330. [Google Scholar] [CrossRef]
- Tomlinson, P.; Azizi-Alizamini, H.; Poole, W.J.; Sinclair, C.W.; Gharghouri, M.A. Biaxial Deformation of the Magnesium Alloy AZ80. Metall. Mater. Trans. A 2013, 44, 2970–2983. [Google Scholar] [CrossRef]
- Kuwabara, T.; Ikeda, S.; Kuroda, K. Measurement and analysis of differential work hardening in cold-rolled steel sheet under biaxial tension. J. Mater. Process. Technol. 1998, 80–81, 517–523. [Google Scholar] [CrossRef]
- Cheng, Y.; Fu, Y.; Xin, Y.; Chen, G.; Wu, P.; Huang, X.; Liu, Q. twinning behavior under biaxial tension of Mg–3Al–1Zn plate. Int. J. Plast. 2020, 132, 102754. [Google Scholar] [CrossRef]
- Kim, H.L.; Bang, W.K.; Chang, Y.W. Effect of initial texture on deformation behavior of AZ31 magnesium alloy sheets under biaxial loading. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2012, 552, 245–251. [Google Scholar] [CrossRef]
- Van Petegem, S.; Wagner, J.; Panzner, T.; Upadhyay, M.V.; Trang, T.T.T.; Van Swygenhoven, H. In-situ neutron diffraction during biaxial deformation. Acta Mater. 2016, 105, 404–416. [Google Scholar] [CrossRef]
- Steglich, D.; Jeong, Y.; Andar, M.O.; Kuwabara, T. Biaxial deformation behaviour of AZ31 magnesium alloy: Crystal-plasticity-based prediction and experimental validation. Int. J. Solids Struct. 2012, 49, 3551–3561. [Google Scholar] [CrossRef]
- Godet, S.; Jiang, L.; Luo, A.; Jonas, J. Use of Schmid factors to select extension twin variants in extruded magnesium alloy tubes. Scr. Mater. 2006, 55, 1055–1058. [Google Scholar] [CrossRef]
- Jonas, J.J.; Mu, S.; Al-Samman, T.; Gottstein, G.; Jiang, L.; Martin, Ė. The role of strain accommodation during the variant selection of primary twins in magnesium. Acta Mater. 2011, 59, 2046–2056. [Google Scholar] [CrossRef]
- Xia, D.; Chen, X.; Huang, G.; Jiang, B.; Tang, A.; Yang, H.; Gavras, S.; Huang, Y.; Hort, N.; Pan, F. Calculation of Schmid factor in Mg alloys: Influence of stress state. Scr. Mater. 2019, 171, 31–35. [Google Scholar] [CrossRef]
- Hutchinson, W.B.; Barnett, M.R. Effective values of critical resolved shear stress for slip in polycrystalline magnesium and other hcp metals. Scr. Mater. 2010, 63, 737–740. [Google Scholar] [CrossRef]
- Yu, H.; Li, C.; Xin, Y.; Chapuis, A.; Huang, X.; Liu, Q. The mechanism for the high dependence of the Hall-Petch slope for twinning/slip on texture in Mg alloys. Acta Mater. 2017, 128, 313–326. [Google Scholar] [CrossRef]
- Zhang, J.; Xi, G.; Wan, X.; Fang, C. The dislocation-twin interaction and evolution of twin boundary in AZ31 Mg alloy. Acta Mater. 2017, 133, 208–216. [Google Scholar] [CrossRef]

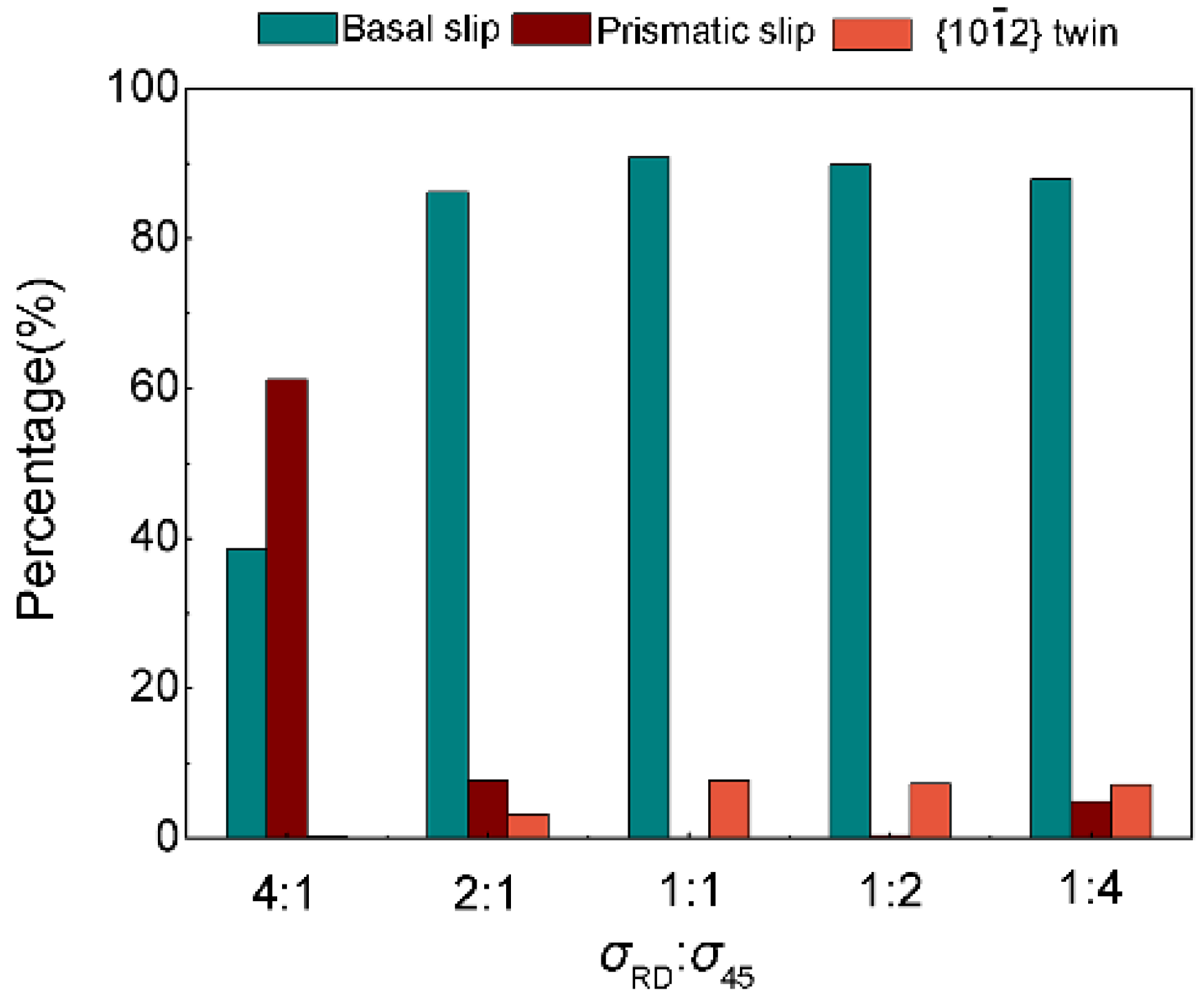
| 4:1 | 2:1 | 1:1 | 1:2 | 1:4 | 0:1 | |
|---|---|---|---|---|---|---|
| RD strain | 0.449% | 0.79% | 0% | −0.16% | −0.5% | _ |
| 45° strain | 0.11% | 2.85% | 2.87% | 3.05% | 2.87% | 3% |
| Equ-strain | 0.7% | 3.7% | 3.38% | 3.38% | 3.5% | 3% |
| TV | 0.831% | 18.9% | 12.3% | 7% | 8.8% | 15.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, J.; Fu, Y.; Cheng, Y.; He, Q.; Zhao, L.; Xin, Y.; Chen, G.; Wu, P.; Liu, Q. Biaxial Deformation Behavior of AZ31 Magnesium Alloy along RD and Diagonal Direction Degree between TD and ND. Metals 2023, 13, 845. https://doi.org/10.3390/met13050845
Mao J, Fu Y, Cheng Y, He Q, Zhao L, Xin Y, Chen G, Wu P, Liu Q. Biaxial Deformation Behavior of AZ31 Magnesium Alloy along RD and Diagonal Direction Degree between TD and ND. Metals. 2023; 13(5):845. https://doi.org/10.3390/met13050845
Chicago/Turabian StyleMao, Jiale, Yuanjie Fu, Yao Cheng, Qiuju He, Lingyu Zhao, Yunchang Xin, Gang Chen, Peidong Wu, and Qing Liu. 2023. "Biaxial Deformation Behavior of AZ31 Magnesium Alloy along RD and Diagonal Direction Degree between TD and ND" Metals 13, no. 5: 845. https://doi.org/10.3390/met13050845
APA StyleMao, J., Fu, Y., Cheng, Y., He, Q., Zhao, L., Xin, Y., Chen, G., Wu, P., & Liu, Q. (2023). Biaxial Deformation Behavior of AZ31 Magnesium Alloy along RD and Diagonal Direction Degree between TD and ND. Metals, 13(5), 845. https://doi.org/10.3390/met13050845







