Efficient Roll-Forming Simulation Using Non-Conformal Meshes with Hanging Nodes Handled by Lagrange Multipliers
Abstract
:1. Introduction
2. Method: Lagrange Multipliers and Hanging Nodes
3. Results and Discussion
3.1. 2D Verification Tests
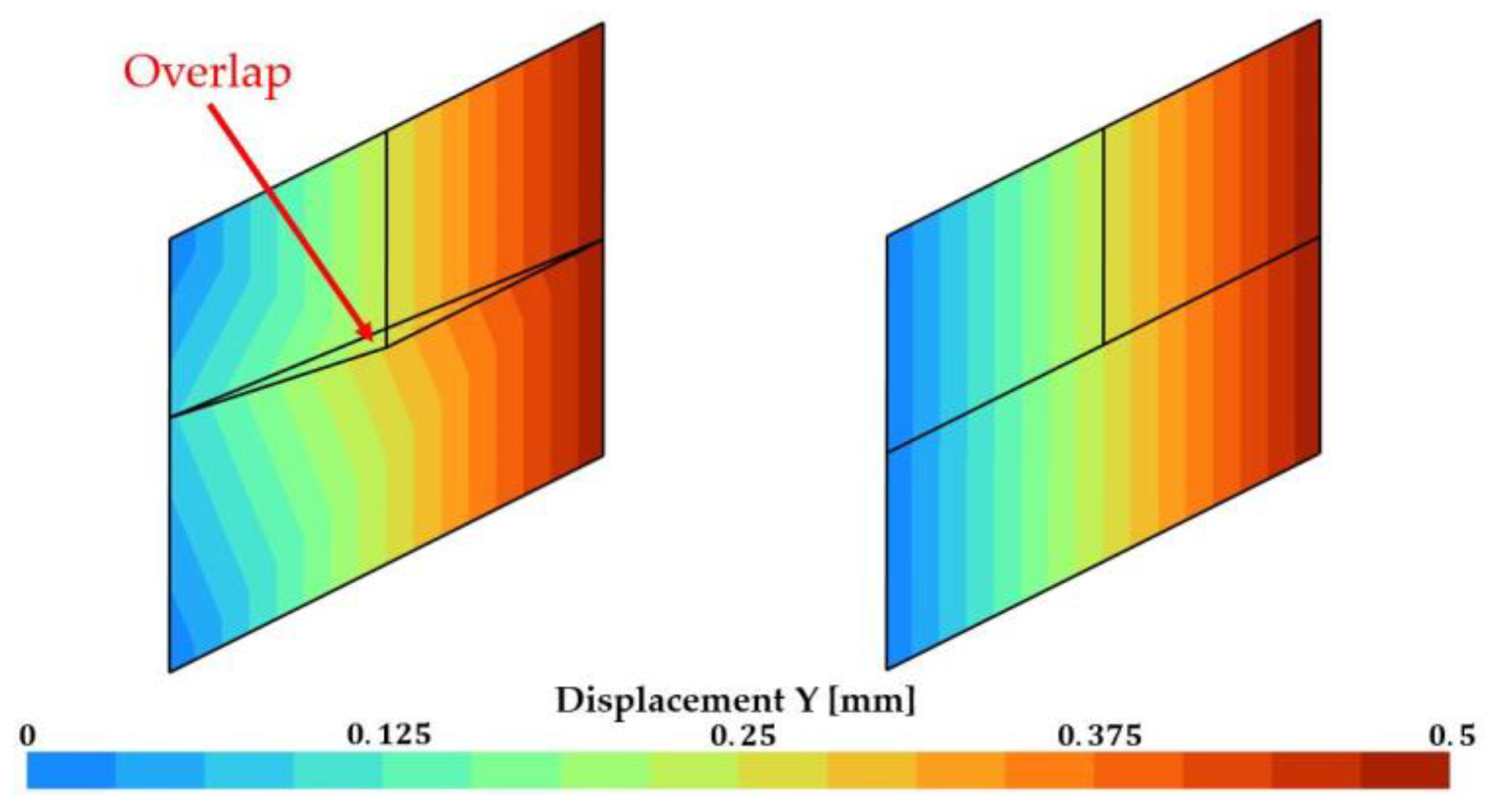
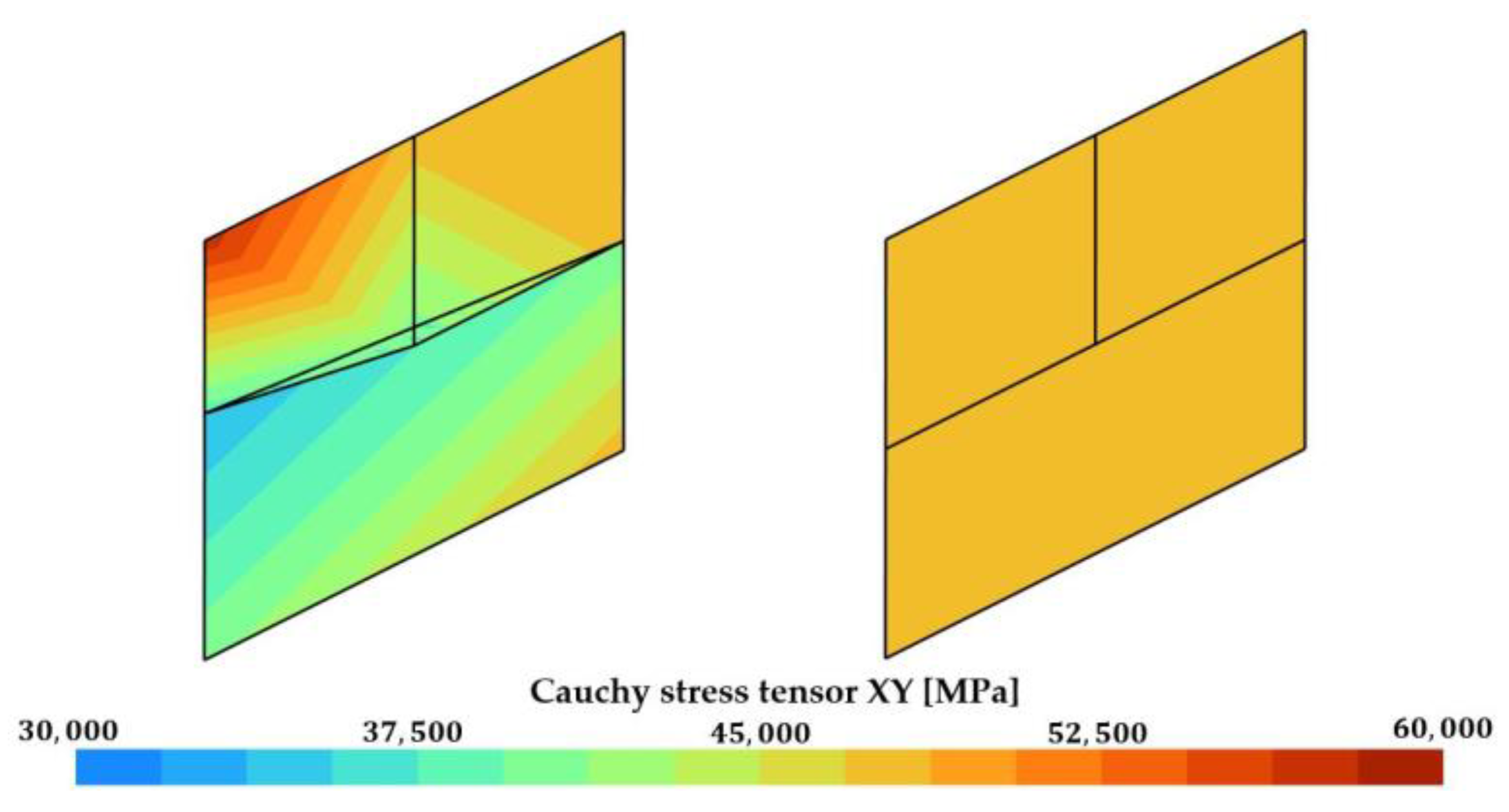
3.1.1. Cube Submitted to Simple Shear
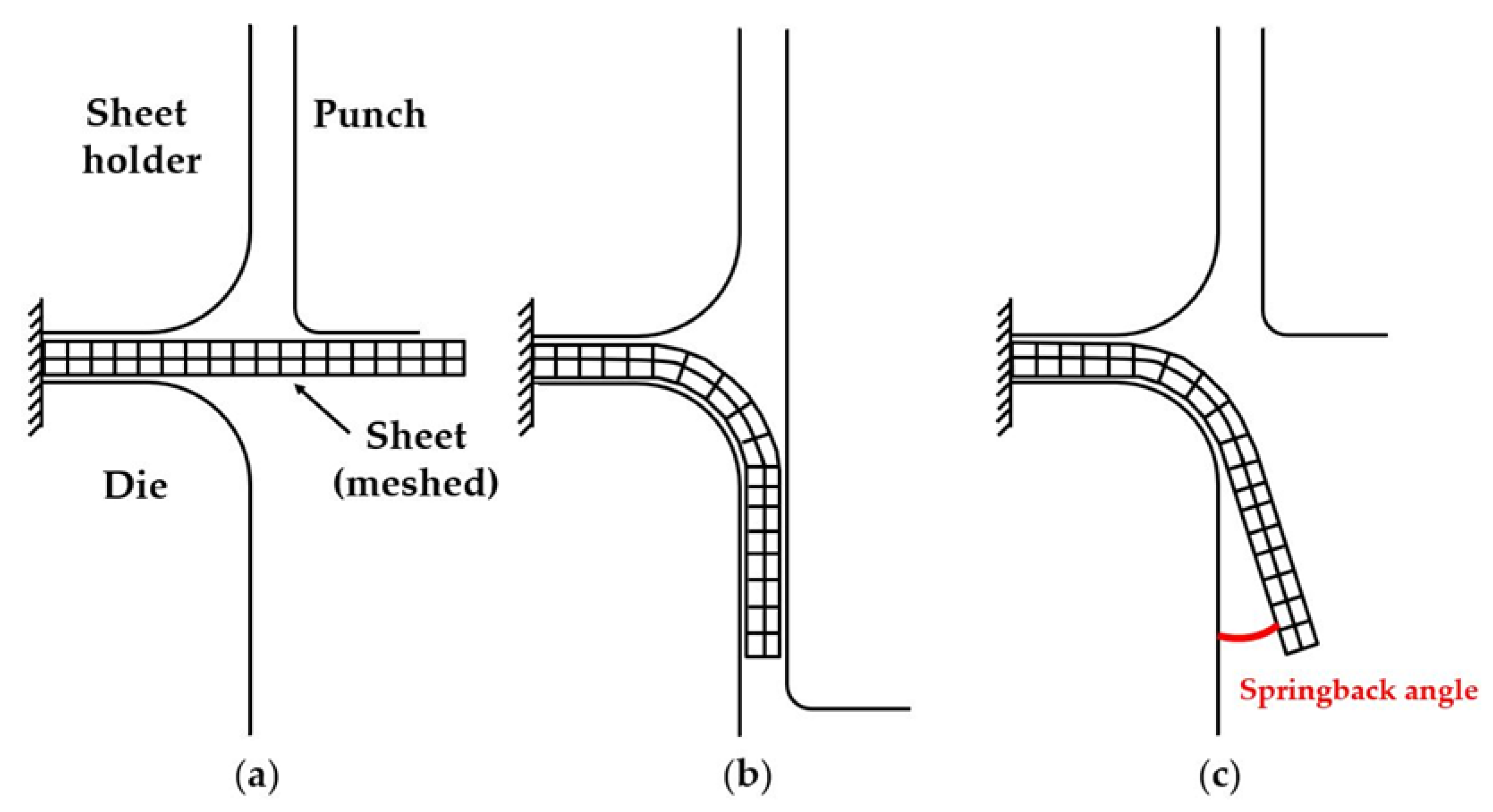
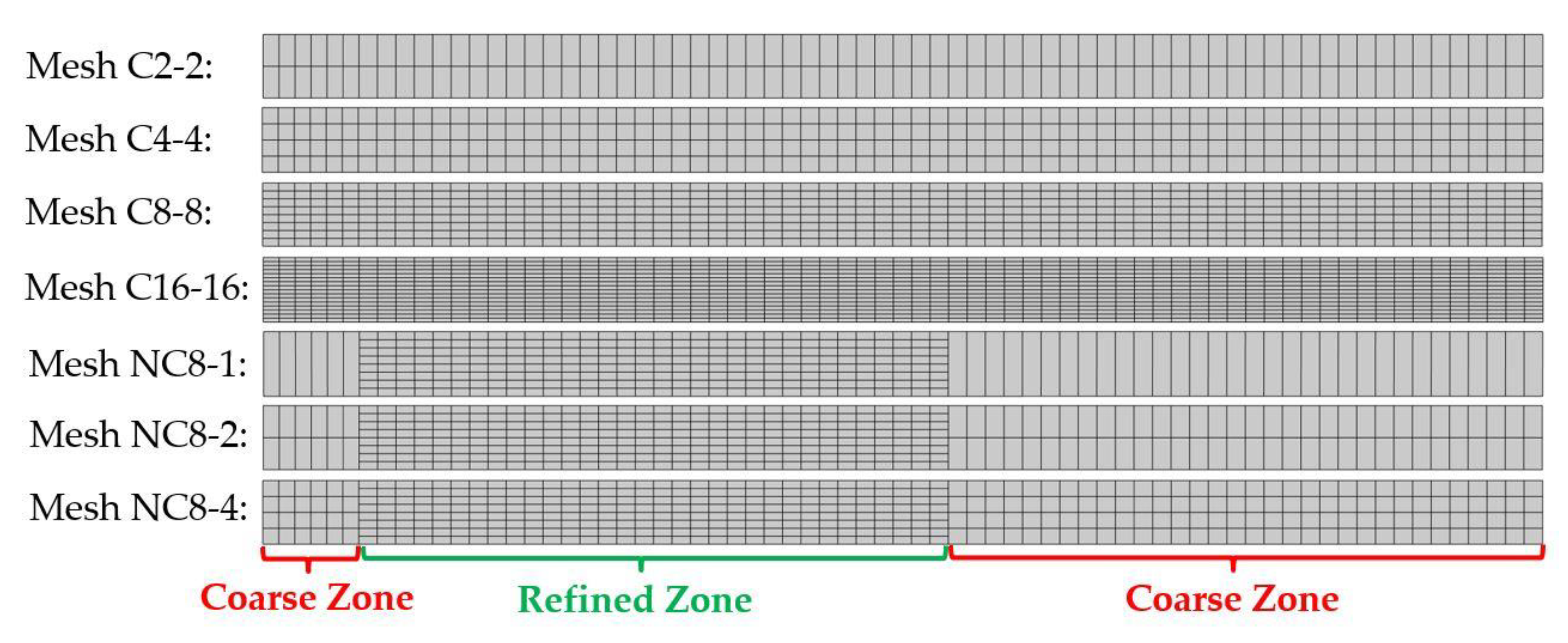
3.1.2. 2D Flanging of a Metal Sheet
3.2. 3D Roll Forming Applications
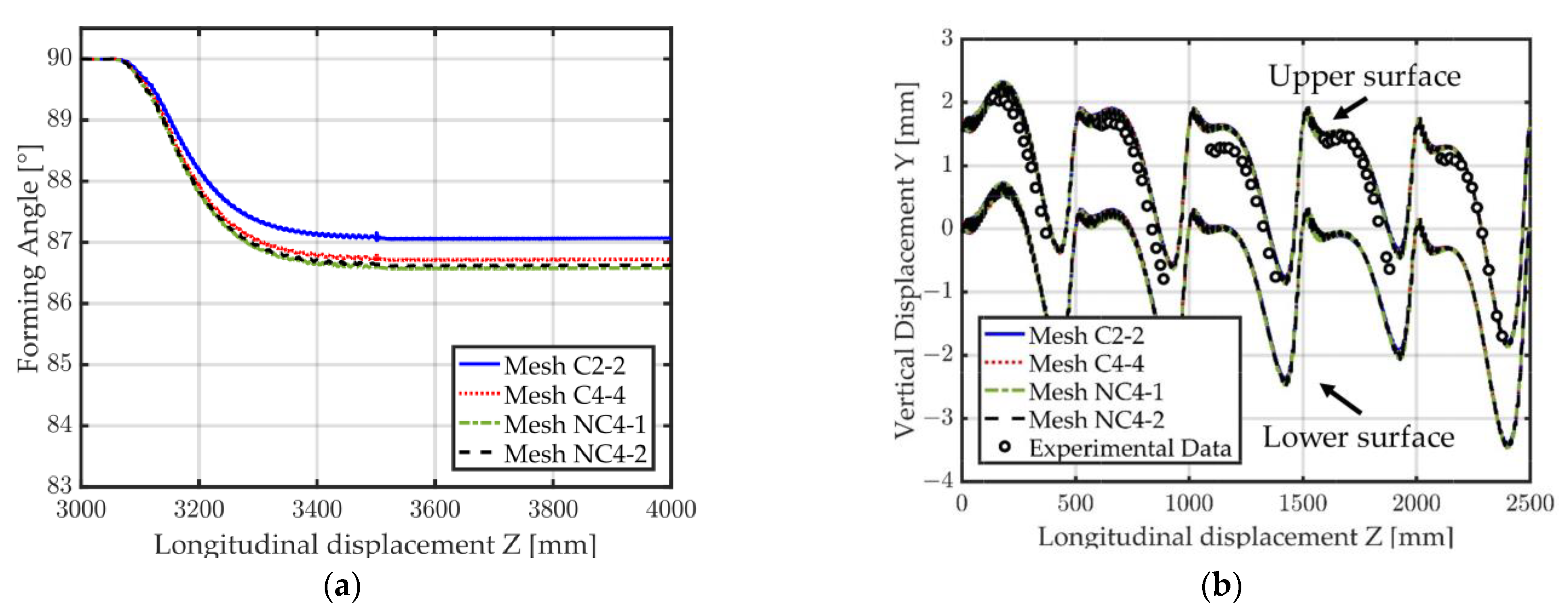
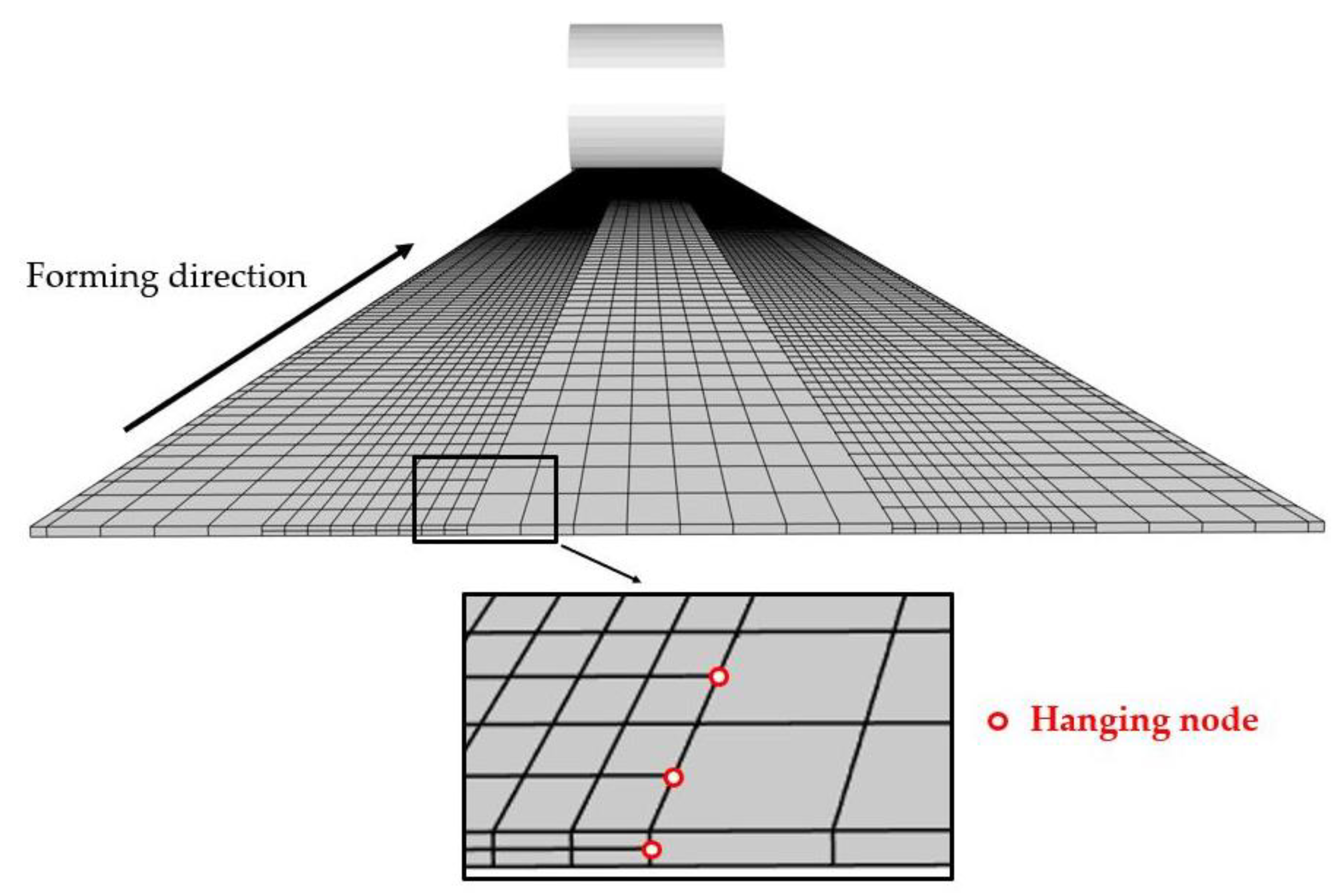
3.2.1. Forming of a U-Channel
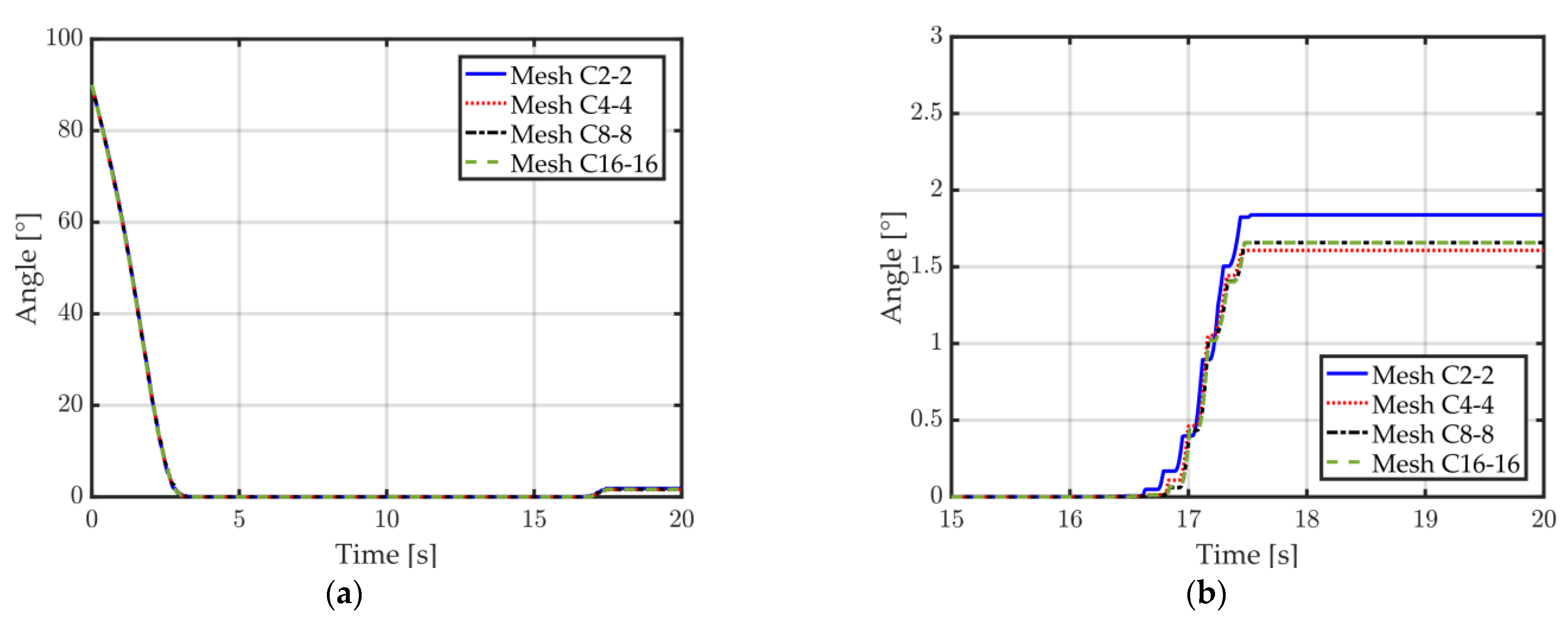
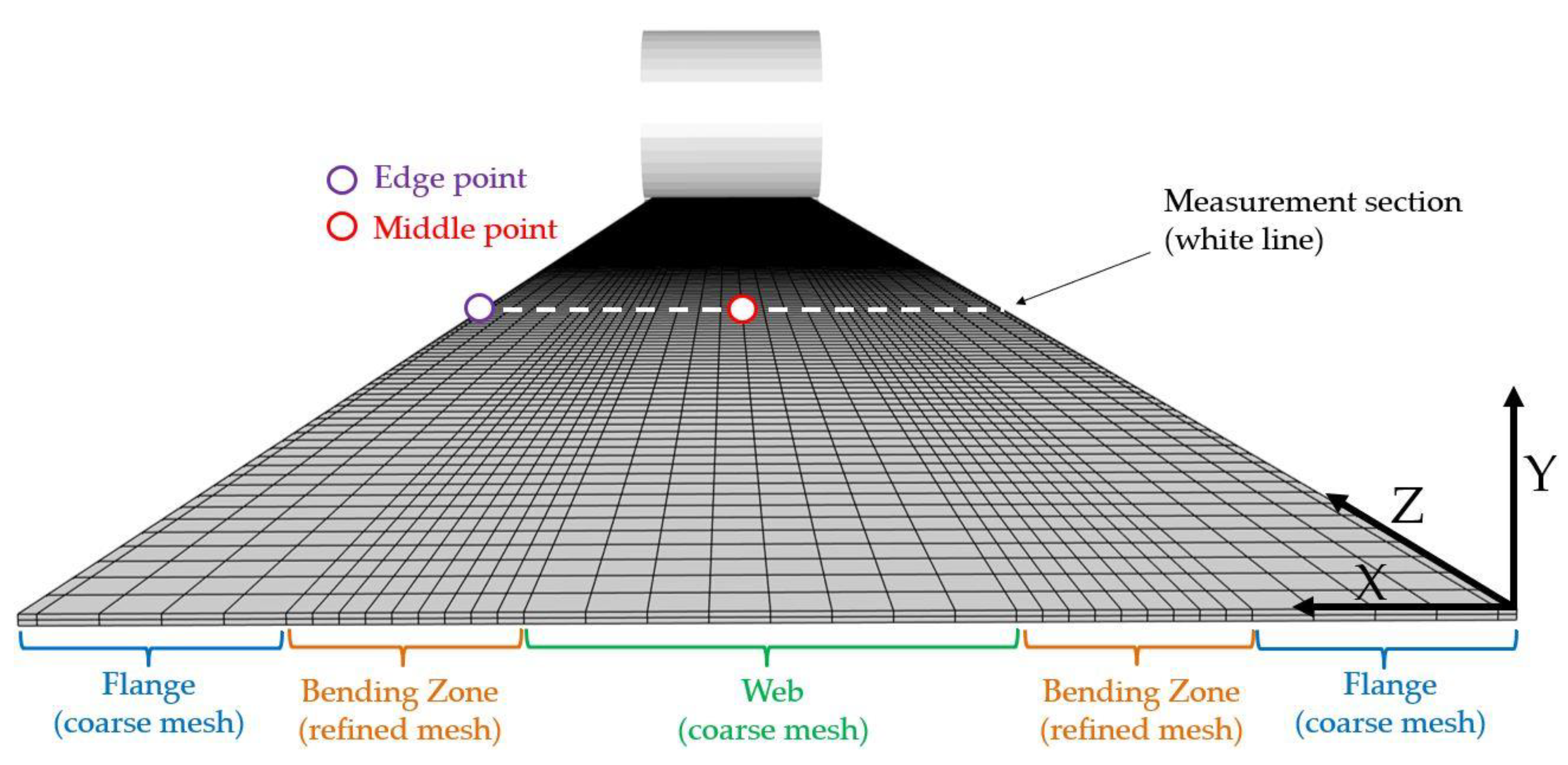
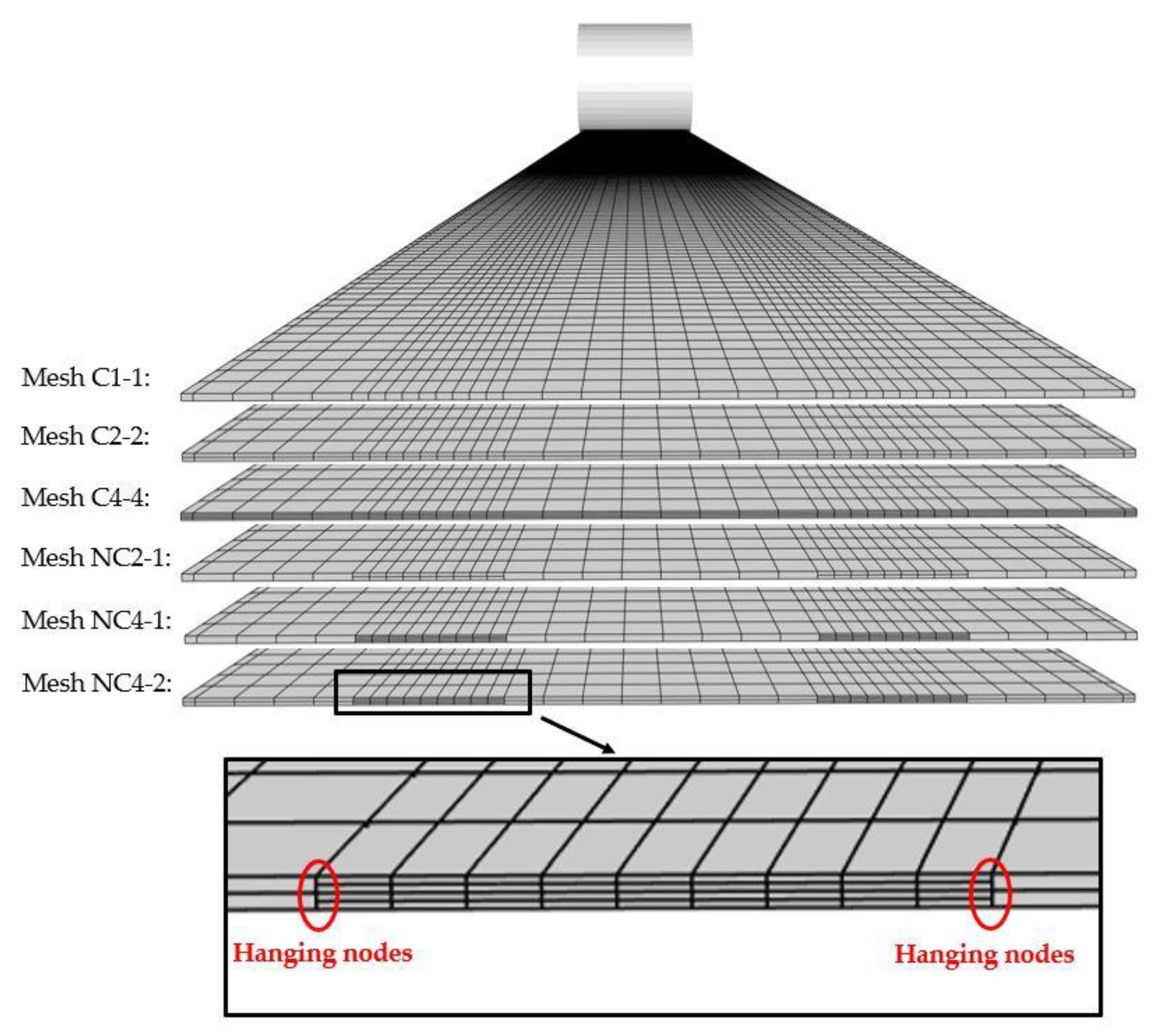
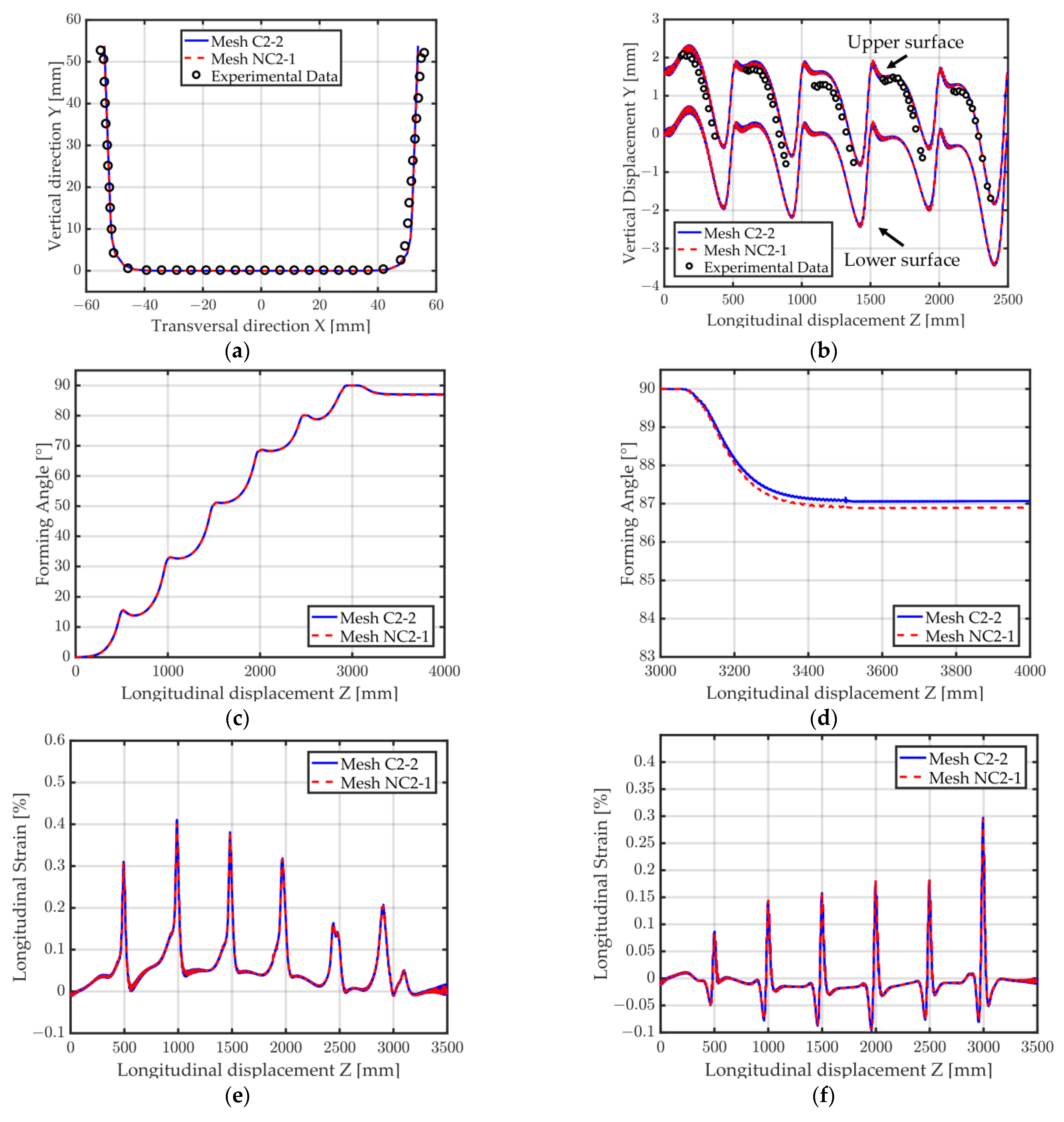
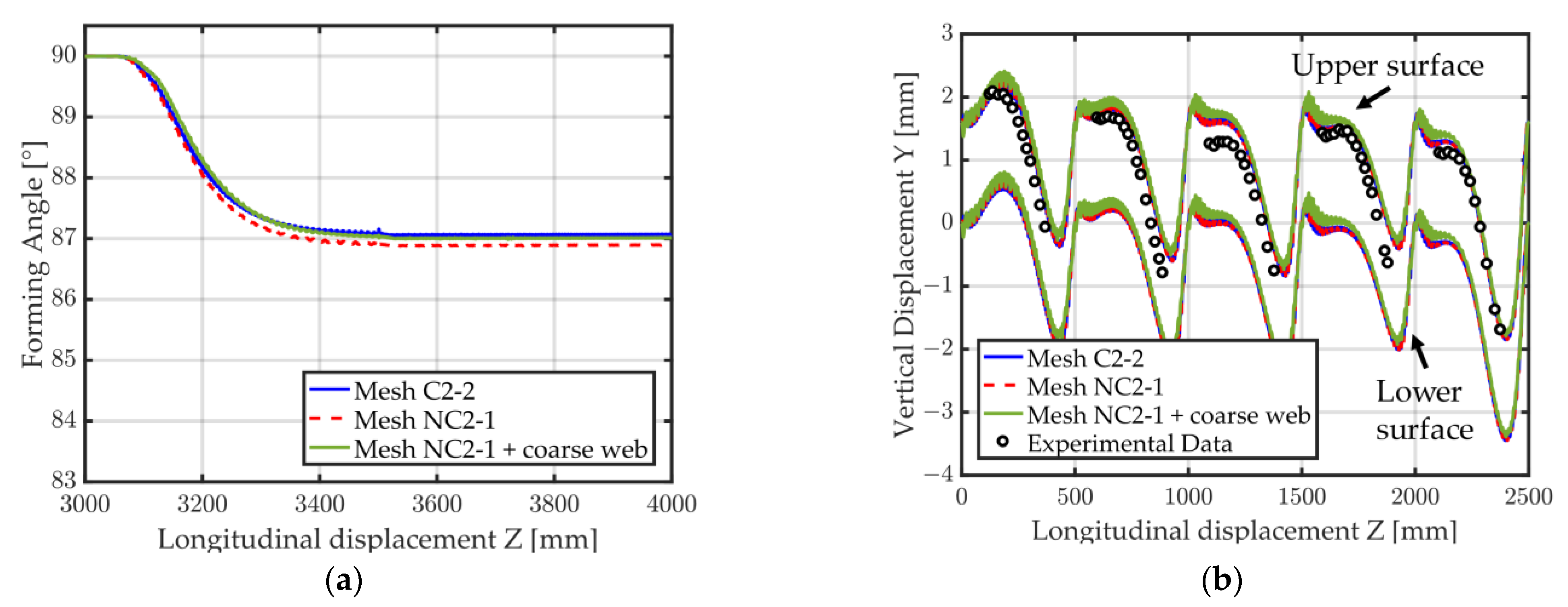
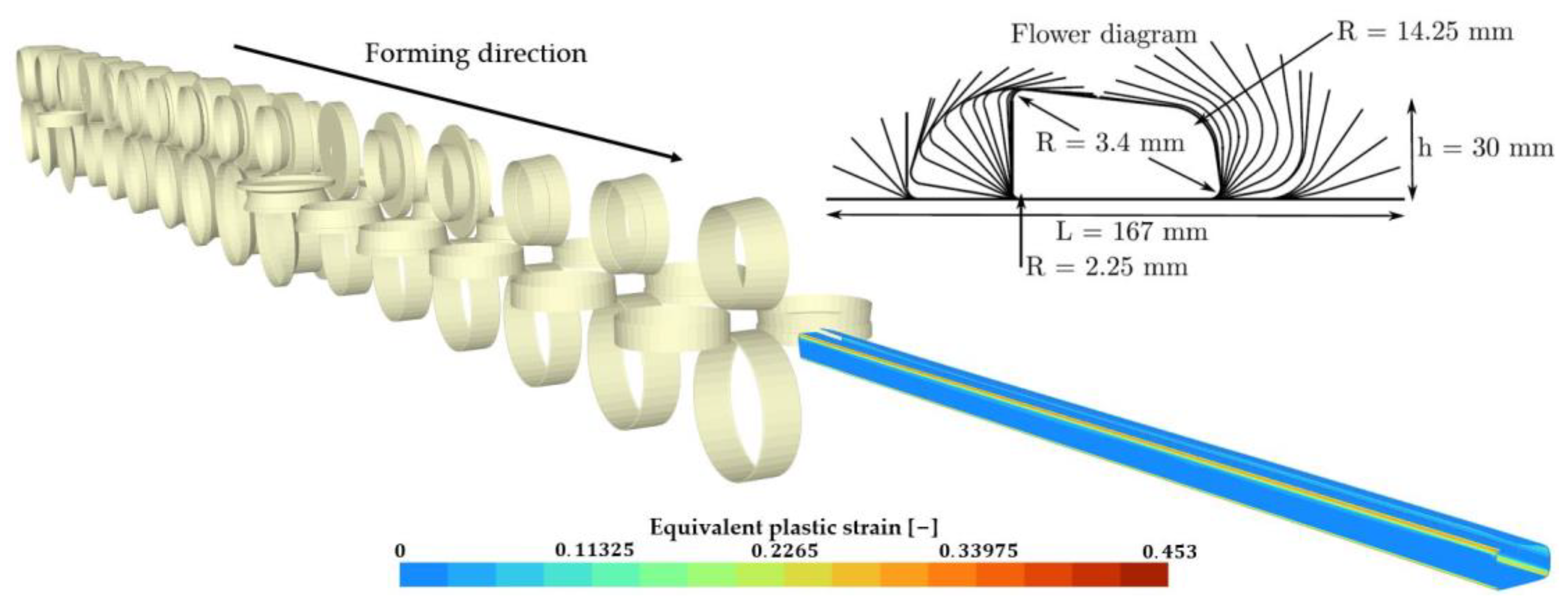
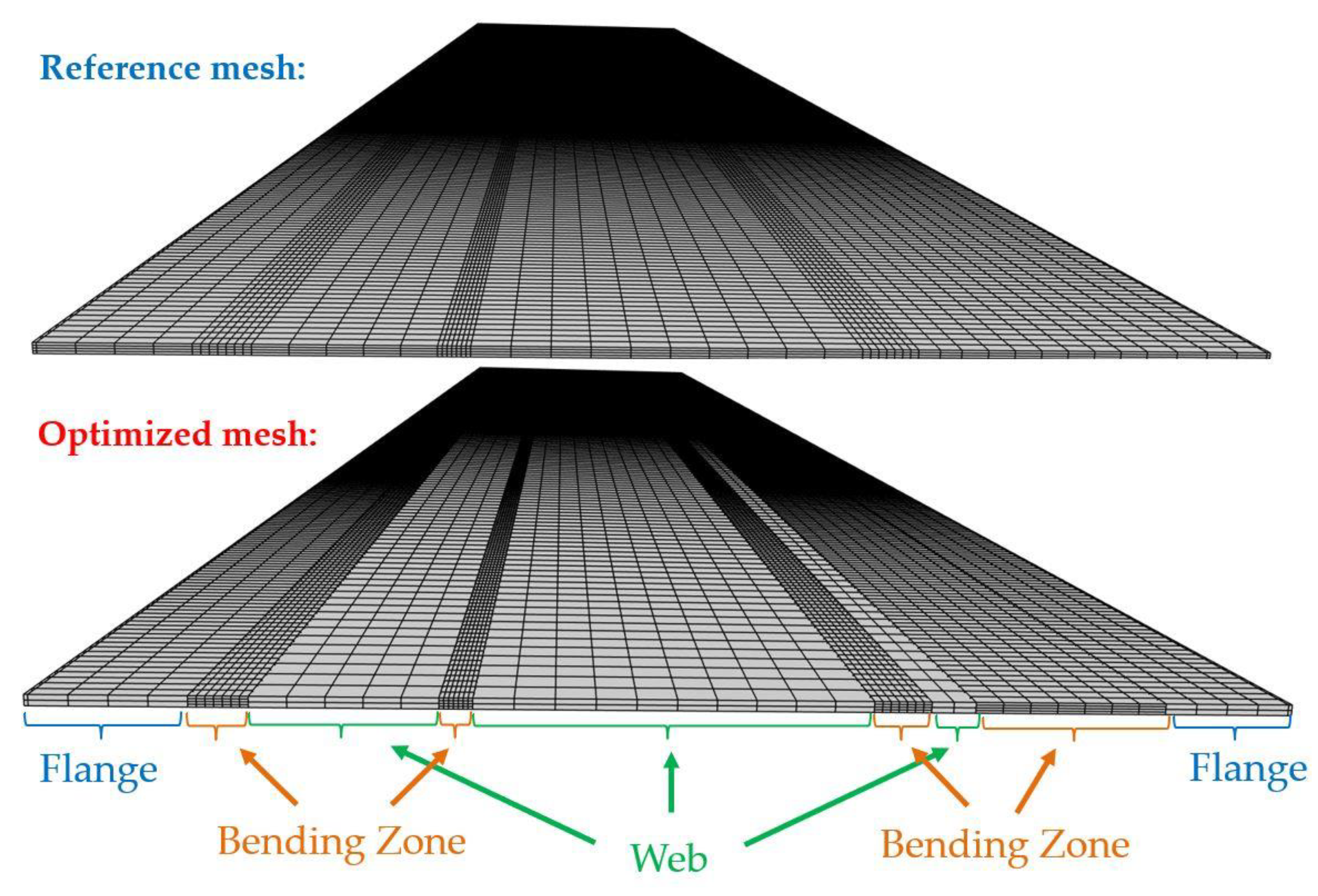
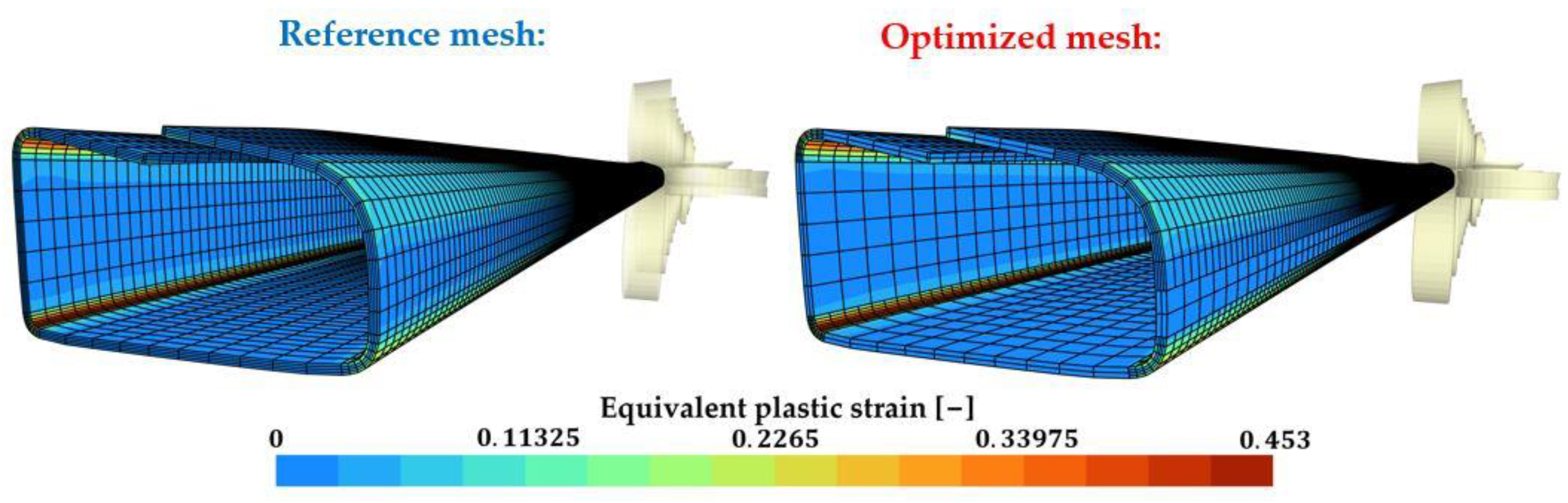
3.2.2. Forming of a Tubular Rocker Panel
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Viet, B.Q.; Boman, R.; Papeleux, L.; Wouters, P.; Kergen, R.; Daolio, G.; Duroux, P.; Flores, P.; Habraken, A.; Ponthot, J.-P. Springback and twist prediction of roll formed parts. In Proceedings of the IDDRG 2006 International Deep Drawing Research Group, Drawing the Things to Come, Trends and Advances in Sheet Metal Forming, Porto, Portugal, 19–21 June 2006. [Google Scholar]
- Boman, R.; Ponthot, J.P. Continuous roll forming simulation using arbitrary Lagrangian Eulerian formalism. Key Eng. Mater. 2011, 473, 564–571. [Google Scholar] [CrossRef]
- Crutzen, Y.; Boman, R.; Papeleux, L.; Ponthot, J.-P. Lagrangian and arbitrary Lagrangian Eulerian simulations of complex roll-forming processes. Comptes Rendus Mec. 2016, 344, 251–266. [Google Scholar] [CrossRef]
- Crutzen, Y.; Boman, R.; Papeleux, L.; Ponthot, J.-P. Continuous roll forming including in-line welding and post-cut within an ALE formalism. Finite Elem. Anal. Des. 2018, 143, 11–31. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, H.; Li, Q.; Guan, Y. Finite element simulation of flexible roll forming with supplemented material data and the experimental verification. Chin. J. Mech. Eng. 2016, 29, 342–350. [Google Scholar] [CrossRef]
- Tsang, K.S.; Ion, W.; Blackwell, P.; English, M. Validation of a finite element model of the cold roll forming process on the basis of 3D geometric accuracy. Proc. Eng. 2017, 207, 1278–1283. [Google Scholar] [CrossRef]
- Lun, F.; Li, R.; Li, M.; Qiu, N.; Xue, P. Forming load in flexible rolling process for sheet metal parts. Int. J. Adv. Manuf. Technol. 2015, 77, 1333–1344. [Google Scholar] [CrossRef]
- Joo, B.; Lee, H.; Kim, D.; Moon, Y. A study on forming characteristics of roll forming process with high strength steel. AIP Conf. Proc. 2011, 1383, 1034–1040. [Google Scholar] [CrossRef]
- Falsafi, J.; Demirci, E.; Silberschmidt, V. Numerical study of strain-rate effect in cold rolls forming of steel. J. Phys. Conf. Ser. 2013, 451, 012041. [Google Scholar] [CrossRef]
- Kasaei, M.M.; Moslemi Naeini, H.; Abbaszadeh, B.; Roohi, A.H.; Silva, M.B.; Martins, P.A. On the prediction of wrinkling in flexible roll forming. Int. J. Adv. Manuf. Technol. 2021, 113, 2257–2275. [Google Scholar] [CrossRef]
- Mohammdi Najafabadi, H.; Moslemi Naeini, H.; Safdarian, R.; Kasaei, M.; Akbari, D.; Abbaszadeh, B. Effect of forming parameters on edge wrinkling in cold roll forming of wide profiles. Int. J. Adv. Manuf. Technol. 2019, 101, 181–194. [Google Scholar] [CrossRef]
- Tajik, Y.; Naeini, H.M.; Tafti, R.A.; Bidabadi, B.S. A strategy to reduce the twist defect in roll-formed asymmetrical-channel sections. Thin-Walled Struct. 2018, 130, 395–404. [Google Scholar] [CrossRef]
- Li, K.; Carden, W.; Wagoner, R. Simulation of springback. Int. J. Mech. Sci. 2002, 44, 103–122. [Google Scholar] [CrossRef]
- Ghiabakloo, H.; Kim, J.; Kang, B.-S. An efficient finite element approach for shape prediction in flexibly-reconfigurable roll forming process. Int. J. Mech. Sci. 2018, 142, 339–358. [Google Scholar] [CrossRef]
- Görtan, M.O.; Vucic, D.; Groche, P.; Livatyali, H. Roll forming of branched profiles. J. Mater. Process. Technol. 2009, 209, 5837–5844. [Google Scholar] [CrossRef]
- Groche, P.; Mueller, C.; Traub, T.; Butterweck, K. Experimental and numerical determination of roll forming loads. Steel Res. Int. 2014, 85, 112–122. [Google Scholar] [CrossRef]
- Luo, Z.; Sun, M.; Zhang, Z.; Lu, C.; Zhang, G.; Fan, X. Finite element analysis of circle-to-rectangle roll forming of thick-walled rectangular tubes with small rounded corners. Int. J. Mater. Form. 2022, 15, 73. [Google Scholar] [CrossRef]
- Essa, A.; Abeyrathna, B.; Rolfe, B.; Weiss, M. Prototyping of straight section components using incremental shape rolling. Int. J. Adv. Manuf. Technol. 2022, 121, 3883–3901. [Google Scholar] [CrossRef]
- Min, J.; Wang, J.; Lian, J.; Liu, Y.; Hou, Z. Laser-Assisted Robotic Roller Forming of Ultrahigh-Strength Steel QP1180 with High Precision. Materials 2023, 16, 1026. [Google Scholar] [CrossRef]
- Liang, C.; Li, S.; Liang, J.; Li, J. Method for Controlling Edge Wave Defects of Parts during Roll Forming of High-Strength Steel. Metals 2022, 12, 53. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.-M.; Li, S.-F.; Chen, W.-J. Cold Roll Forming Process Design for Complex Stainless-Steel Section Based on COPRA and Orthogonal Experiment. Materials 2022, 15, 8023. [Google Scholar] [CrossRef]
- Xing, M.; Wang, H.; Liu, J.; Fu, Y.; Du, F. Application of Mean Modulus in Three-Point Bending and Roll Forming. Materials 2023, 16, 2571. [Google Scholar] [CrossRef]
- Badia, S.; Baiges, J. Adaptive finite element simulation of incompressible flows by hybrid continuous-discontinuous Galerkin formulations. SIAM J. Sci. Comput. 2013, 35, A491–A516. [Google Scholar] [CrossRef]
- Houston, P.; Schötzau, D.; Wihler, T.P. An hp-adaptive mixed discontinuous Galerkin FEM for nearly incompressible linear elasticity. Comput. Methods Appl. Mech. Eng. 2006, 195, 3224–3246. [Google Scholar] [CrossRef]
- Cockburn, B.; Kanschat, G.; Schötzau, D.; Schwab, C. Local discontinuous Galerkin methods for the Stokes system. SIAM J. Numer. Anal. 2002, 40, 319–343. [Google Scholar] [CrossRef]
- Baiges, J.; Bayona, C. Refficientlib: An Efficient Load-Rebalanced Adaptive Mesh Refinement Algorithm for High-Performance Computational Physics Meshes. SIAM J. Sci. Comput. 2017, 39, C65–C95. [Google Scholar] [CrossRef]
- Bangerth, W.; Hartmann, R.; Kanschat, G. deal. II—A general-purpose object-oriented finite element library. ACM Trans. Math. Softw. TOMS 2007, 33, 24-es. [Google Scholar] [CrossRef]
- Zander, N.; Bog, T.; Kollmannsberger, S.; Schillinger, D.; Rank, E. Multi-level hp-adaptivity: High-order mesh adaptivity without the difficulties of constraining hanging nodes. Comput. Mech. 2015, 55, 499–517. [Google Scholar] [CrossRef]
- Di Stolfo, P.; Schröder, A.; Zander, N.; Kollmannsberger, S. An easy treatment of hanging nodes in hp-finite elements. Finite Elem. Anal. Des. 2016, 121, 101–117. [Google Scholar] [CrossRef]
- Dana, S. Augmented lagrangian for treatment of hanging nodes in hexahedral meshes. arXiv 2018, arXiv:1809.04031. [Google Scholar] [CrossRef]
- Fries, T.P.; Byfut, A.; Alizada, A.; Cheng, K.W.; Schröder, A. Hanging nodes and XFEM. Int. J. Numer. Methods Eng. 2011, 86, 404–430. [Google Scholar] [CrossRef]
- Metafor Website. Available online: http://metafor.ltas.ulg.ac.be (accessed on 27 March 2023).
- Ponthot, J.-P. Unified stress update algorithms for the numerical simulation of large deformation elasto-plastic and elasto-viscoplastic processes. Int. J. Plast. 2002, 18, 91–126. [Google Scholar] [CrossRef]
- Belytschko, T.; Liu, W.K.; Moran, B.; Elkhodary, K. Nonlinear Finite Elements for Continua and Structures; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Flores, P.; Habraken, A. Material Identification of Dual Phase Steel DP1000; Tech. Rep.; University of Liège: Liège, Belgium, 2005. [Google Scholar]
- Flores, P. Development of Experimental Equipment and Identification Procedures for Sheet Metal Constitutive Laws. Ph.D. Thesis, University of Liège, Liège, Belgium, 2005. [Google Scholar]
- Data M Sheet Metal Solutions GmbH, COPRA RF. Available online: http://www.datam.de/en/products-solutions/roll-forming/ (accessed on 27 March 2023).
- Simo, J.; Armero, F.; Taylor, R. Improved versions of assumed enhanced strain tri-linear elements for 3D finite deformation problems. Comput. Methods Appl. Mech. Eng. 1993, 110, 359–386. [Google Scholar] [CrossRef]
- Bui, Q.; Papeleux, L.; Ponthot, J.-P. Numerical simulation of springback using enhanced assumed strain elements. J. Mater. Process. Technol. 2004, 153, 314–318. [Google Scholar] [CrossRef]
- Adam, L.; Ponthot, J.-P. Thermomechanical modeling of metals at finite strains: First and mixed order finite elements. Int. J. Solids Struct. 2005, 42, 5615–5655. [Google Scholar] [CrossRef]







| Mesh Name | Number of Elements | Number of Hanging Nodes | CPU Time (1 Core) | ||
|---|---|---|---|---|---|
| C2-2 | 2 | 2 | 140 | 0 | 23 s |
| C4-4 | 4 | 4 | 280 | 0 | 35 s |
| C8-8 | 8 | 8 | 560 | 0 | 62 s |
| C16-16 | 16 | 16 | 1120 | 0 | 102 s |
| NC8-1 | 8 | 1 | 294 | 14 | 35 s |
| NC8-2 | 8 | 2 | 332 | 12 | 37 s |
| NC8-4 | 8 | 4 | 408 | 8 | 48 s |
| Mesh Name | Number of Elements | Number of Hanging Nodes | CPU Time (12 Cores) | ||
|---|---|---|---|---|---|
| C1-1 | 1 | 1 | 7200 | 0 | 5 h 00 m |
| C2-2 | 2 | 2 | 14,400 | 0 | 10 h 8 m |
| C4-4 | 4 | 4 | 28,800 | 0 | 24 h 21 m |
| NC2-1 | 2 | 1 | 10,800 | 808 | 6 h 27 m |
| NC4-1 | 4 | 1 | 18,000 | 2424 | 10 h 58 m |
| NC4-2 | 4 | 2 | 21,600 | 1616 | 13 h 58 m |
| Mesh Name | Number of Elements | Number of Hanging Nodes | CPU Time (12 Cores) |
|---|---|---|---|
| Reference mesh | 77,440 | 0 | 2 d 15 h 9 m |
| Optimized mesh | 52,448 | 8832 | 1 d 6 h 33 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laruelle, C.; Boman, R.; Papeleux, L.; Ponthot, J.-P. Efficient Roll-Forming Simulation Using Non-Conformal Meshes with Hanging Nodes Handled by Lagrange Multipliers. Metals 2023, 13, 895. https://doi.org/10.3390/met13050895
Laruelle C, Boman R, Papeleux L, Ponthot J-P. Efficient Roll-Forming Simulation Using Non-Conformal Meshes with Hanging Nodes Handled by Lagrange Multipliers. Metals. 2023; 13(5):895. https://doi.org/10.3390/met13050895
Chicago/Turabian StyleLaruelle, Cédric, Romain Boman, Luc Papeleux, and Jean-Philippe Ponthot. 2023. "Efficient Roll-Forming Simulation Using Non-Conformal Meshes with Hanging Nodes Handled by Lagrange Multipliers" Metals 13, no. 5: 895. https://doi.org/10.3390/met13050895
APA StyleLaruelle, C., Boman, R., Papeleux, L., & Ponthot, J.-P. (2023). Efficient Roll-Forming Simulation Using Non-Conformal Meshes with Hanging Nodes Handled by Lagrange Multipliers. Metals, 13(5), 895. https://doi.org/10.3390/met13050895








