Relationship of Internal Stress Fields with Self-Organization Processes in Hadfield Steel under Tensile Load
Abstract
:1. Introduction
2. Materials and Methods
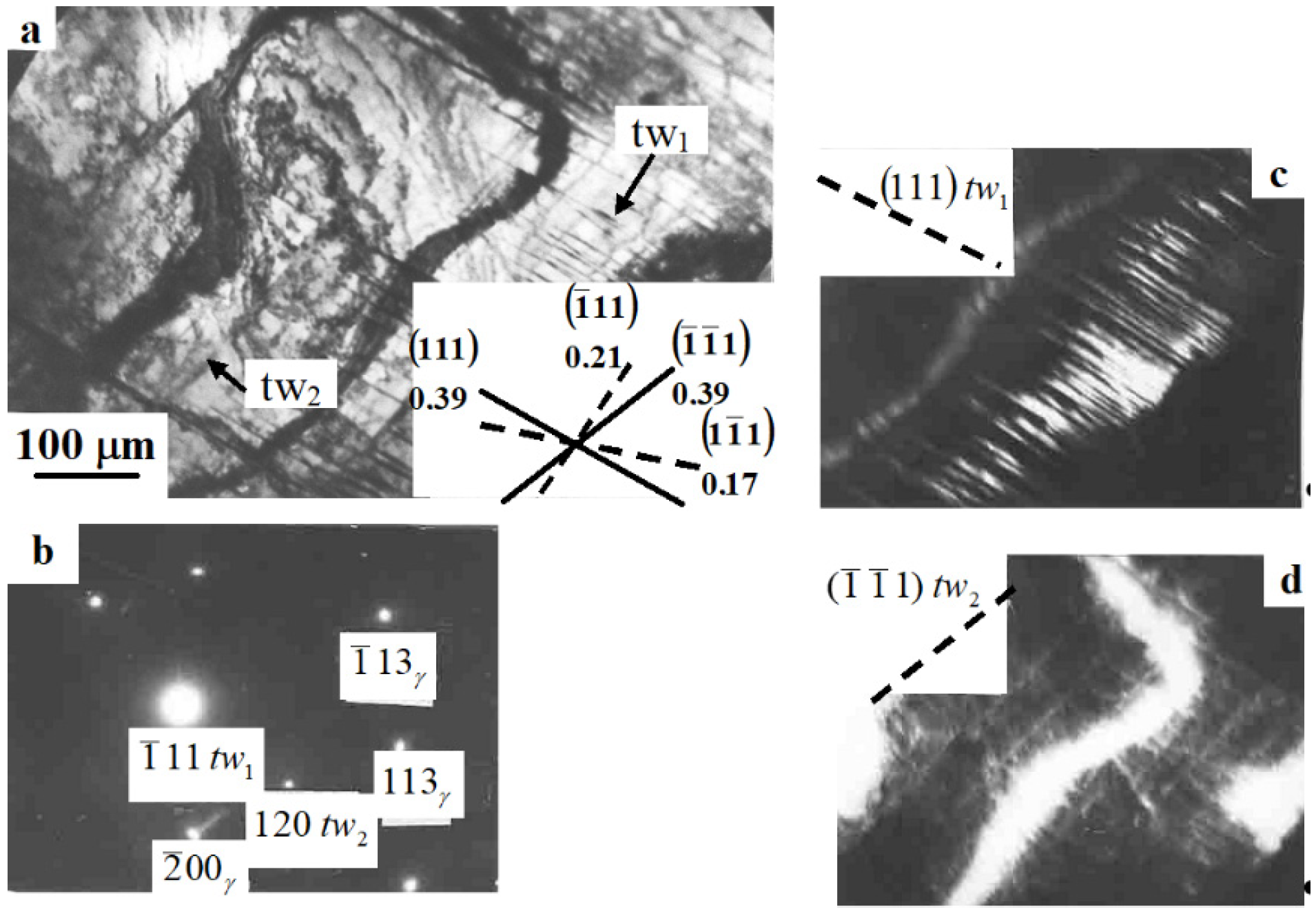
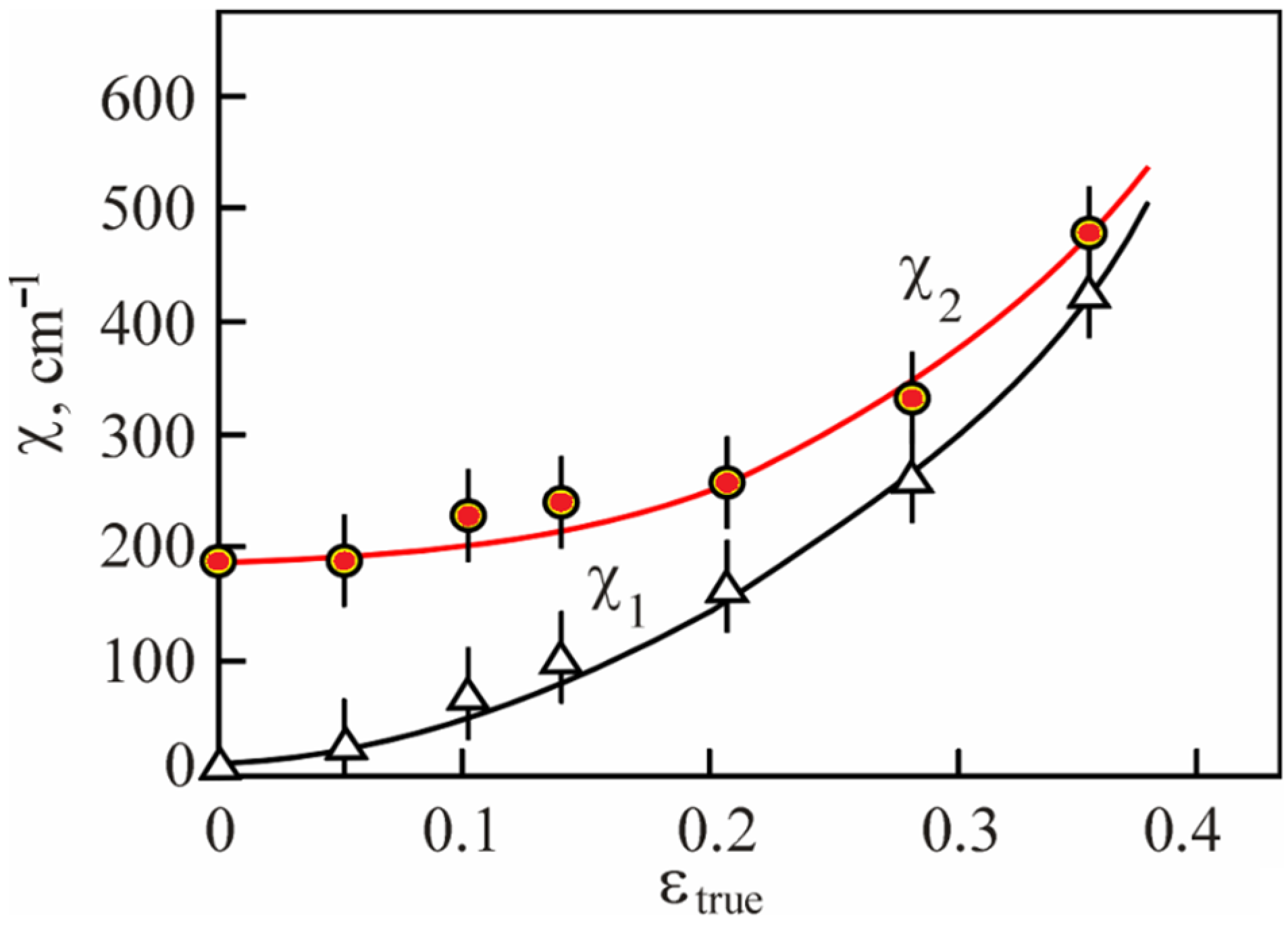
3. Results
4. Discussion
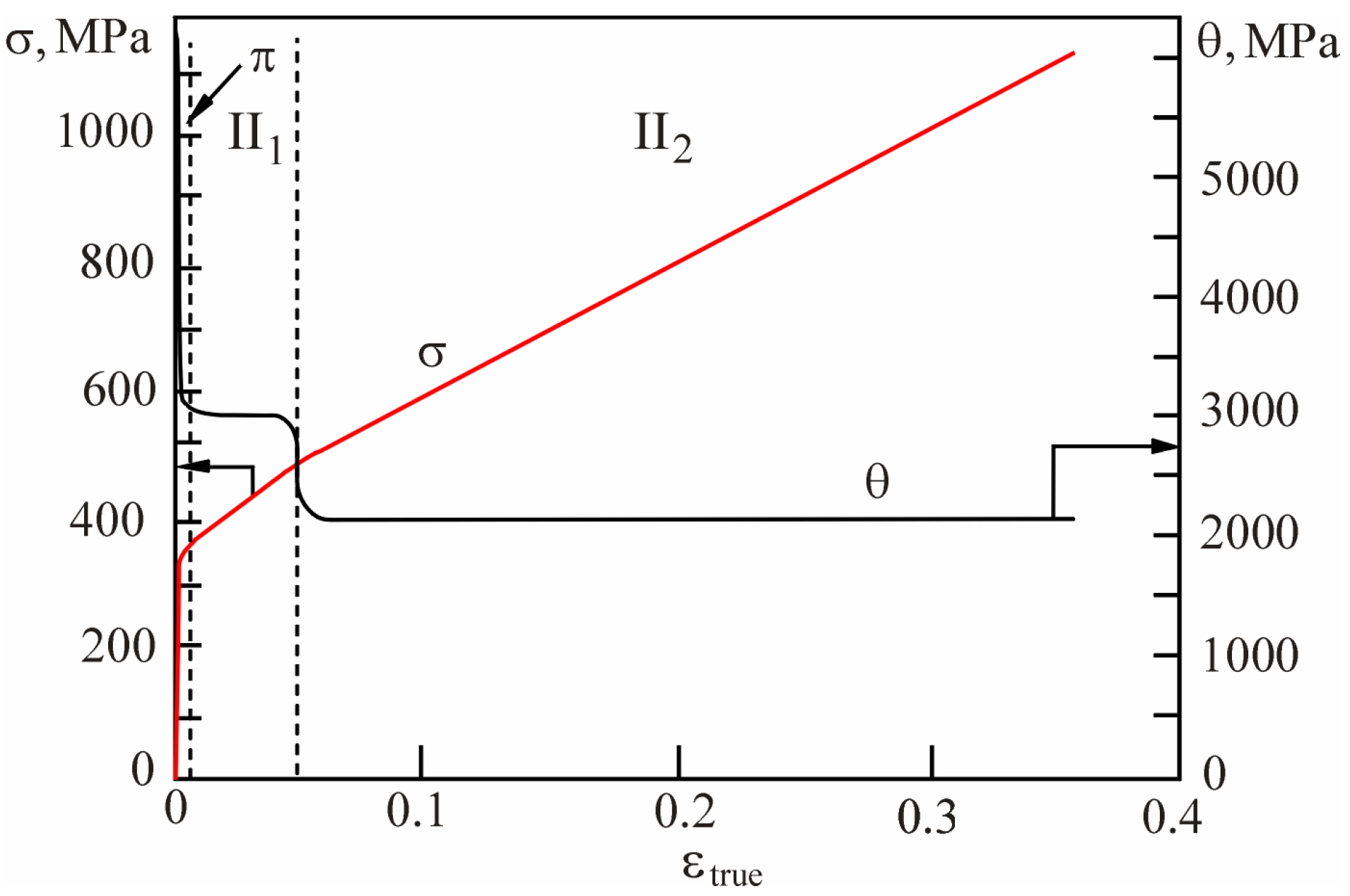
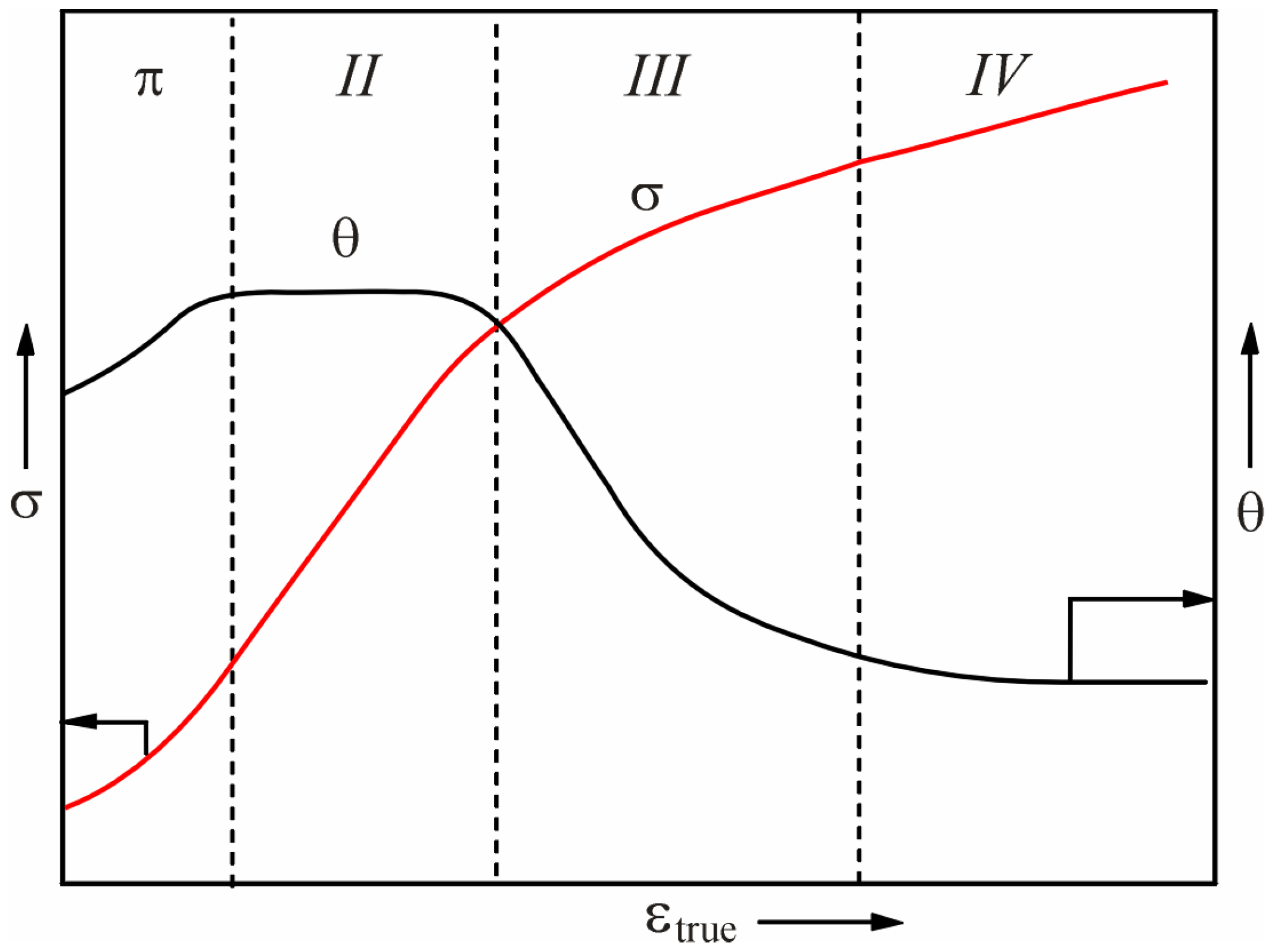
4.1. The ‘σ–ε’ and ‘θ–ε’ Dependences
4.2. Mechanisms Providing the High Hardening of the Hadfield Steel
4.3. Features of Strain Hardening and Self-Organization Processes in the Hadfield Steel during Plastic Deformation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bogachev, I.N.; Egolaev, V.F. Structure and Properties of Ferromanganese Alloys; Metallurgy: Moscow, Russia, 1973. (In Russian) [Google Scholar]
- Sokolov, O.G.; Katsov, K.B. Ferromanganese Alloys; Naukova Dumka: Kiev, Russia, 1982. (In Russian) [Google Scholar]
- Korshunov, L.G. Structural transformations during friction and wear resistance of austenitic steels. Phys. Met. Met. Sci. 1992, 8, 3–21. (In Russian) [Google Scholar]
- Gasik, M.I. Manganese; Metallurgy: Moscow, Russia, 1992. (In Russian) [Google Scholar]
- Wang, X.G.; Wang, L.; Huang, M.X. Kinematic and thermal characteristics of Lüders and Portevin-Le Châtelier bands in a medium Mn transformation-induced plasticity steel. Acta Mater. 2017, 124, 17–29. [Google Scholar] [CrossRef]
- Wang, X.G.; Wang, L.; Huang, M.X. In-situ evaluation of Lüders band associated with martensitic transformation in a medium Mn transformation-induced plasticity steel. Mater. Sci. Eng. A 2016, 674, 59–63. [Google Scholar] [CrossRef]
- Qiu, H.; Inoue, T.; Ueji, R. Experimental measurement of the variables of Lüders deformation in hot-rolled steel via digital image correlation. Mater. Sci. Eng. A 2020, 790, 139756. [Google Scholar] [CrossRef]
- Zhang, M.; Li, L.; Ding, J.; Wu, Q.; Wang, Y.-D.; Almer, J.; Guo, F.; Ren, Y. Temperature-dependent micromechanical behavior of medium-Mn transformation-induced-plasticity steel studied by in situ synchrotron X-ray diffraction. Acta Mater. 2017, 141, 294–303. [Google Scholar] [CrossRef]
- Kwok, T.W.J.; Rahman, K.M.; Xu, X.; Bantounas, I.; Kelleher, J.F.; Dasari, S.; Alam, T.; Banerjee, R.; Dye, D. Design of a high strength, high ductility 12 wt% Mn medium manganese steel with hierarchical deformation behavior. Mater. Sci. Eng. A 2020, 782, 139258. [Google Scholar] [CrossRef]
- Wang, J.-J.; Hui, W.-J.; Xie, Z.-Q.; Zhang, Y.-J.; Zhao, X.-L. Influence of pre-strain on microstructural characteristics and tensile deformation behaviour of a cold-rolled Al-containing medium Mn steel. J. Mater. Sci. 2020, 55, 5296–5310. [Google Scholar] [CrossRef]
- Jeong, M.S.; Park, T.M.; Choi, S.; Lee, S.-J.; Han, J. Recovering the ductility of medium-Mn steel by restoring the original microstructure. Scr. Mater. 2021, 190, 16–21. [Google Scholar] [CrossRef]
- Yan, S.; Li, T.; Liang, T.; Chen, J.; Zhao, Y.; Liu, X. By controlling recrystallization degree: A plain medium Mn steel overcoming Lüders deformation and low yield-to-tensile ratio simultaneously. Mater. Sci. Eng. A 2019, 758, 79–85. [Google Scholar] [CrossRef]
- Benzing, J.T.; Liu, Y.; Zhang, X.; Luecke, W.E.; Ponge, D.; Dutta, A.; Oskay, C.; Raabe, D.; Wittig, J.E. Experimental and numerical study of mechanical properties of multi-phase medium-Mn TWIP-TRIP steel: Influences of strain rate and phase constituents. Acta Mater. 2019, 177, 250–265. [Google Scholar] [CrossRef]
- De Cooman, B.C.; Gibbs, P.; Lee, S.; Matlock, D.K. Transmission electron microscopy analysis of yielding in ultrafine-grained medium Mn transformation-induced plasticity steel. Metall. Mater. Trans. A 2013, 44, 2563–2572. [Google Scholar] [CrossRef]
- Ma, J.; Liu, H.; Lu, Q.; Zhong, Y.; Wang, L.; Shen, Y. Transformation kinetics of retained austenite in the tensile Lüders strain range in medium Mn steel. Scr. Mater. 2019, 169, 1–5. [Google Scholar] [CrossRef]
- Korshunov, L.G.; Chernenko, N.L. Effect of aluminum on structural transformations and wear resistance of Hadfield steel under friction. Phys. Met. Met. Sci. 2018, 119, 746–752. (In Russian) [Google Scholar]
- Ma, Y. Medium-manganese steels processed by austenite-reverted-transformation annealing for automotive applications. Mater. Sci. Technol. 2017, 33, 1713–1727. [Google Scholar] [CrossRef]
- Lee, Y.-K.; Han, J. Current opinion in medium manganese steel. Mater. Sci. Technol. 2015, 31, 843–856. [Google Scholar] [CrossRef]
- Gulyaev, A.P. Pure Steel; Metallurgy: Moscow, Russia, 1966. (In Russian) [Google Scholar]
- Volynova, T.F. High Manganese Steels and Alloys; Metallurgy: Moscow, Russia, 1988. (In Russian) [Google Scholar]
- Lü, Y.; Hutchinson, B.; Molodov, D.A.; Gottstein, G. Effect of deformation and annealing on the formation and reversion of ε-martensite in an Fe–Mn–C alloy. Acta Mater. 2010, 58, 3079–3090. [Google Scholar] [CrossRef]
- Tsakiris, V.; Edmonds, D.V. Martensite and deformation twinning in austenitic steels. Mater. Sci. Eng. A 1999, 273–275, 430–436. [Google Scholar] [CrossRef]
- Park, K.-T.; Jin, K.G.; Han, S.H.; Hwang, S.W.; Choi, K.; Lee, C.S. Stacking fault energy and plastic deformation of fully austenitic high manganese steels: Effect of Al addition. Mater. Sci. Eng. A 2010, 527, 3651–3661. [Google Scholar] [CrossRef]
- Karaman, I.; Sehitoglu, H.; Chumlyakov, Y.I.; Maier, H.J.; Kireeva, I.V. Extrinsic stacking faults and twinning in hadfield manganese steel single crystals. Scr. Mater. 2001, 44, 337–343. [Google Scholar] [CrossRef]
- Nikulina, A.A.; Smirnov, A.I.; Velikoselskaya, E.Y. Structural changes in Hadfield steel under cold deformation. Surface X-ray Synchrotron Neutron Res. 2013, 2, 82–88. (In Russian) [Google Scholar] [CrossRef]
- Wan, X.; Liu, G.; Yang, Z.; Chen, H. Flash annealing yields a strong and ductile medium Mn steel with heterogeneous microstructure. Scr. Mater. 2021, 198, 113819. [Google Scholar] [CrossRef]
- Popova, N.A.; Klopotov, A.A.; Nikonenko, E.L.; Trishkina, L.I.; Cherkasova, T.V.; Volokitin, G.G.; Loskutov, O.V.; Borodin, V.I.; Potekaev, A.I. Strengthening mechanisms and specifics of strain stages in high-manganese austenitic Hadfield steel. Basic Probl. Mater. Sci. 2022, 19, 423–436. (In Russian) [Google Scholar] [CrossRef]
- Panin, V.E. Physical mesomechanics of materials. Solid State Mech. 1999, 5, 88–107. (In Russian) [Google Scholar] [CrossRef]
- Golenkov, V.A.; Malinin, V.G.; Malinina, N.A. Structural-Analytical Mesomechanics and Its Applications; Mechanical Engineering: Moscow, Russia, 2009. (In Russian) [Google Scholar]
- Barannikova, S.A.; Zuev, L.B. On the features of patterns of localization of plastic deformation at the yield point in single crystals of Hadfield steel. Lett. J. Tech. Phys. 2008, 34, 24–32. (In Russian) [Google Scholar]
- Noskov, F.M.; Kveglis, L.I.; Volochaev, M.N.; Jess, A.V. Scale invariance of the structure of steel 110G13L during self-organization caused by plastic deformation. Fundam. Probl. Mod. Mater. Sci. 2016, 13, 292–303. (In Russian) [Google Scholar]
- Ivanova, V.S.; Balankin, A.S.; Bunin, I.Z.; Oksoghoev, A.A. Synergetics and Fractals in Materials Science; Science: Moscow, Russia, 1994. (In Russian) [Google Scholar]
- Haken, H. Synergetics; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Bobbili, R.; Madhu, V. Flow and fracture characteristics of near alpha titanium alloy. J. Alloy. Compd. 2016, 684, 162–170. [Google Scholar] [CrossRef]
- Trishkina, L.I.; Cherkasova, T.V.; Popova, N.A.; Koneva, N.A.; Gromov, V.E.; Aksenova, K.V. Dislocation Ensemble: Scalar Dislocation Density and Its Components; TSUAB: Tomsk, Russia, 2019. (In Russian) [Google Scholar]
- Saltykov, S.A. Steriometric Metallography; Metallurgy: Moscow, Russia, 1970. (In Russian) [Google Scholar]
- Koneva, N.A.; Kozlov, E.V. Physical nature of stages of plastic deformation. Sov. Phys. J. 1990, 2, 89–106. (In Russian) [Google Scholar] [CrossRef]
- Trefilov, V.I. Strain Hardening and Fracture of Polycrystalline Metals, 2nd ed.; Naukova Dumka: Kiev, Russia, 1989. (In Russian) [Google Scholar]
- Koneva, N.A.; Kozlov, E.V. Modern picture of the stages of plastic deformation. Russ. Phys. J. 2004, 8, 90–98. (In Russian) [Google Scholar]
- Glezer, A.M.; Kozlov, E.V.; Koneva, N.A.; Popova, N.A.; Kurzina, I.A. Plastic Deformation of Nanostructured Materials; Taylor & Francis Group: London, UK, 2017. [Google Scholar]
- Klopotov, A.A.; Potekaev, A.I.; Ustinov, A.M.; Ivanov, Y.F.; Abzaev, Y.A.; Kulagina, V.V. Relationships between characteristics of deformation behavior and evolution of deformation fields in aluminum under uniaxial tension. Russ. Phys. J. 2021, 64, 574–580. [Google Scholar] [CrossRef]
- Narita, N.; Yamamoto, A.; Umemoto, T.; Takamura, J.I. Anelastic effect due to deformation twins in Cu-Ge alloy crystals. J. Jpn. Inst. Met. 1978, 42, 1190–1199. [Google Scholar] [CrossRef]
- Miura, S.; Takamura, J.J.; Narita, N. Orientation dependence of the flow stress for twinning in silver crystals. In Proceedings of the International Conference on Strength of Metals and Alloys, Tokyo, Japan, 4–8 September 1967; pp. 555–562. [Google Scholar]
- Jafarian, H.R.; Sabzi, M.; Mousavi Anijdan, S.H.; Eivani, A.R.; Park, N. The influence of austenitization temperature on microstructural developments, mechanical properties, fracture mode and wear mechanism of Hadfield high manganese steel. J. Mater. Res. Technol. 2021, 10, 819–831. [Google Scholar] [CrossRef]
- Adler, P.H.; Olson, G.B.; Owen, W.S. Strain hardening of Hadfield manganese steel. Metall. Mater. Trans. A 1986, 17, 1725–1737. [Google Scholar] [CrossRef]
- Zhilkashinova, A.M.; Skakov, M.K.; Popova, N.A. Relationship between the coefficient of strain hardening and plastic deformation of Hadfield austenitic steel. Bull. Sci. Sib. 2011, 1, 686–691. (In Russian) [Google Scholar]
- Zhang, L.; Guo, P.; Wang, G.; Liu, S. Serrated flow and failure behaviors of a Hadfield steel at various strain rates under extensometer-measured strain control tensile load. Journal of Materials Research and Technology. 2020, 9, 1500–1508. [Google Scholar] [CrossRef]
- Chen, C.; Lv, B.; Feng, X.; Zhang, F.; Beladi, H. Strain hardening and nanocrystallization behaviors in Hadfield steel subjected to surface severe plastic deformation. Mater. Sci. Eng. A 2018, 729, 178–184. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, C.; Lv, B.; Ma, H.; Farabi, E.; Beladi, H. Effect of pre-deformation mode on the microstructures and mechanical properties of Hadfield steel. Mater. Sci. Eng. A 2019, 743, 251–258. [Google Scholar] [CrossRef]
- Hutchinson, B.; Ridley, N. On dislocation accumulation and work hardening in Hadfield steel. Scr. Mater. 2006, 55, 299–302. [Google Scholar] [CrossRef]
- Park, J.; Jo, M.C.; Song, T.; Kim, H.S.; Sohn, S.S.; Lee, S. Ultra-high strength and excellent ductility in multi-layer steel sheet of austenitic hadfield and martensitic hot-press-forming steels. Mater. Sci. Eng. A 2019, 759, 320–328. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, F.C.; Wang, F.; Liu, H.; Yu, B.D. Effect of N+Cr alloying on the microstructures and tensile properties of Hadfield steel. Mater. Sci. Eng. A 2017, 679, 95–103. [Google Scholar] [CrossRef]
- Lambakahar, O.O.; Pascal, Y.I. Dislocation structure and strain hardening of high-manganese steel. Sov. Phys. J. 1973, 7, 26–30. (In Russian) [Google Scholar]
- Lambakahar, O.O.; Pascal, Y.I. On the nature of strain hardening of high-manganese austenitic steels. I. Sov. Phys. J. 1977, 1, 158. (In Russian) [Google Scholar]
- Lychagin, D.V.; Filippov, A.V.; Novitskaya, O.S.; Kolubaev, A.V.; Moskvichev, E.N.; Fortunata, S.V.; Chumlyakov, Y.I. Deformation and wear of Hadfield steel single crystals under dry sliding friction. Wear 2022, 488–489, 204126. [Google Scholar] [CrossRef]
- Shtremel, M.A.; Kovalenko, I.A. On the hardening mechanism of Hadfield steel. Phys. Met. Met. Sci. 1987, 63, 172–180. (In Russian) [Google Scholar]
- Georgieva, I.Y.; Gulyaev, A.A.; Kondratieva, E.Y. Deformation twinning and mechanical properties of austenitic manganese steels. Met. Sci. Therm. Treat. Met. 1976, 8, 56–58. (In Russian) [Google Scholar] [CrossRef]
- Gulyaev, A.A.; Tyapkin, Y.D.; Golikov, V.A.; Zharinova, V.S. The fine structure of Hadfield steel. Met. Sci. Therm. Treat. Met. 1985, 6, 14–18. (In Russian) [Google Scholar] [CrossRef]
- Chumlyakov, Y.I.; Shehitoglu, H.; Kireeva, I.V.; Litvinova, E.I.; Astafurova, E.G.; Kalashnikov, I.S. Plastic deformation of Hadfield steel single crystals. Rep. Russ. Acad. Sci. 1998, 361, 185–188. (In Russian) [Google Scholar]
- Karaman, I.; Sehitoglu, H.; Gall, K.; Chumlyakov, Y.I. On the deformation mechanisms in single crystal Hadfield manganese steels. Scr. Mater. 1998, 38, 1009–1015. [Google Scholar] [CrossRef]
- Litvinova, E.I.; Kireeva, I.V.; Zakharova, E.G.; Luzginova, N.V.; Chumlyakov, Y.I.; Sehitoglu, H.; Karaman, I. Twinning in single crystals of Hadfield steel. Phys. Mesomech. 1999, 2, 115–121. (In Russian) [Google Scholar]
- Chumlyakov, Y.I.; Kireeva, I.V.; Litvinova, E.I.; Zakharova, E.G.; Luzginova, N.V.; Efimenko, S.P.; Seyhitoglu, H.; Karaman, I. Twinning in single crystals of Hadfield steel. Rep. Russ. Acad. Sci. 2000, 371, 45–48. (In Russian) [Google Scholar]
- Koneva, N.A. Nature of plastic deformation stages. Soros Educ. J. 1998, 35, 99–105. (In Russian) [Google Scholar]
- Koneva, N.A.; Kozlov, E.V. Dislocation structure and physical mechanisms of hardening of metallic materials. In Perspective Materials; Merson, D.L., Ed.; TSU and MISiS: Tula, Russia, 2006; pp. 267–320. (In Russian) [Google Scholar]
- Koneva, N.A.; Kozlov, E.V. Patterns of substructural hardening. Sov. Phys. J. 1991, 3, 56–70. (In Russian) [Google Scholar]
- Koneva, N.A.; Kozlov, E.V. Physics of substructural hardening. Bull. TSUAB 1999, 1, 21–35. (In Russian) [Google Scholar]
- Strunin, B.N. On the distribution of internal stresses in the case of a random arrangement of dislocations. Phys. Solid State 1967, 9, 805–812. (In Russian) [Google Scholar]
- Hirsh, P.B.; Howie, A.; Nicholson, R.B.; Pashley, D.W.; Whelan, M.J. Electron Microscopy of Thin Crystals; Butterworths: London, UK, 1965. [Google Scholar]
- Kozlov, E.V.; Lychagin, D.V.; Popova, N.A.; Trishkina, L.I.; Koneva, N.A. Long-range stress fields and their role in the deformation of structurally inhomogeneous materials. In Physics of Strength of Heterogeneous Materials; Physical-Technical Institute: Leningrad, Russia, 1988; pp. 3–13. (In Russian) [Google Scholar]
- Cottrell, A.H. Dislocations and Plastic Flow in Crystals; Clarendon Press: Oxford, UK, 1953. [Google Scholar]
- Zhilkashinova, A.M.; Skakov, M.K.; Kozlov, E.V.; Popova, N.A. Investigation of the influence of C and Mn on the structural-phase state of the 110G13L hardened steel matrix. Bull. Natl. Acad. Sci. Repub. Kazakhstan. Phys.-Math. Ser. 2008, 2, 13–16. (In Russian) [Google Scholar]
- Zhilkashinova, A.M.; Skakov, M.K.; Popova, N.A. Second phases formed in Fe-Mn-C alloys. Issues Mater. Sci. 2010, 64, 48–54. (In Russian) [Google Scholar]
- Popov, L.E.; Koneva, N.A.; Tereshko, I.V. Strain Hardening of Ordered Alloys; Metallurgy: Moscow, Russia, 1979. (In Russian) [Google Scholar]
- Mitchel, T.E. Dislocations and plasticity in single crystals of face-central cubic metals and alloys. In Progress in Applied Material Research; A Heywood Book: London, UK, 1964; Volume 6, pp. 117–237. [Google Scholar]
- Nabarro, F.R.N.; Basinski, Z.S.; Holt, D.B. The plasticity of pure single crystals. Adv. Phys. 1964, 13, 193–323. [Google Scholar] [CrossRef]
- Friedel, J. Dislocations; Pergamon Press: Oxford, UK, 1964. [Google Scholar] [CrossRef]
- Staker, M.R.; Holt, D.L. The dislocation cell size and dislocation density in copper deformed at temperatures between 25 and 700 °C. Acta Metall. 1972, 20, 569–579. [Google Scholar] [CrossRef]
- Nes, E. Modelling of work hardening and stress saturation in FCC metals. Prog. Mater. Sci. 1997, 41, 129–193. [Google Scholar] [CrossRef]
- Raj, S.V.; Pharr, G.M. A compilation and analysis of data for the stress dependence of the subgrain size. Mater. Sci. Eng. 1986, 81, 217–237. [Google Scholar] [CrossRef]
- Kozlov, E.V.; Trishkina, L.I.; Daneliya, G.V.; Tsypin, M.I. Effect of the solid-solution concentration on the type and parameters of the dislocation structure formed in deformation of Cu-Mn alloys. Sov. Phys. J. 1991, 10, 60–66. (In Russian) [Google Scholar] [CrossRef]
- Koneva, N.A.; Lychagin, D.V.; Starenchenko, V.A.; Kozlov, E.V. Patterns of the formation and evolution of the cellular dislocation substructure of FCC metals and single-phase solid solutions and their quantification. Deform. Fract. Mater. 2006, 9, 24–32. (In Russian) [Google Scholar]
- Holt, D.L. Dislocation cell formation in metals. J. Appl. Phys. 1970, 41, 3197–3201. [Google Scholar] [CrossRef]
- Zeger, A. Mechanisms of sliding and hardening in cubic face-centered and hexagonal close-packed metals. In Dislocations and Mechanical Properties of Crystals; Publishing House of Foreign Literature: Moscow, Russia, 1960; pp. 179–268. (In Russian) [Google Scholar]
- Kozlov, E.V.; Popova, N.A.; Koneva, N.A. The role of geometrically necessary dislocations in the micro-range of grain and fragment sizes. Perspect. Mater. 2011, 12, 231–237. (In Russian) [Google Scholar]
- Kozlov, E.V.; Popova, N.A.; Koneva, N.A. Dislocation structure and its components in steel of martensite class. News. Ferrous Metallurgy. 2015, 58, 61–70. [Google Scholar] [CrossRef]

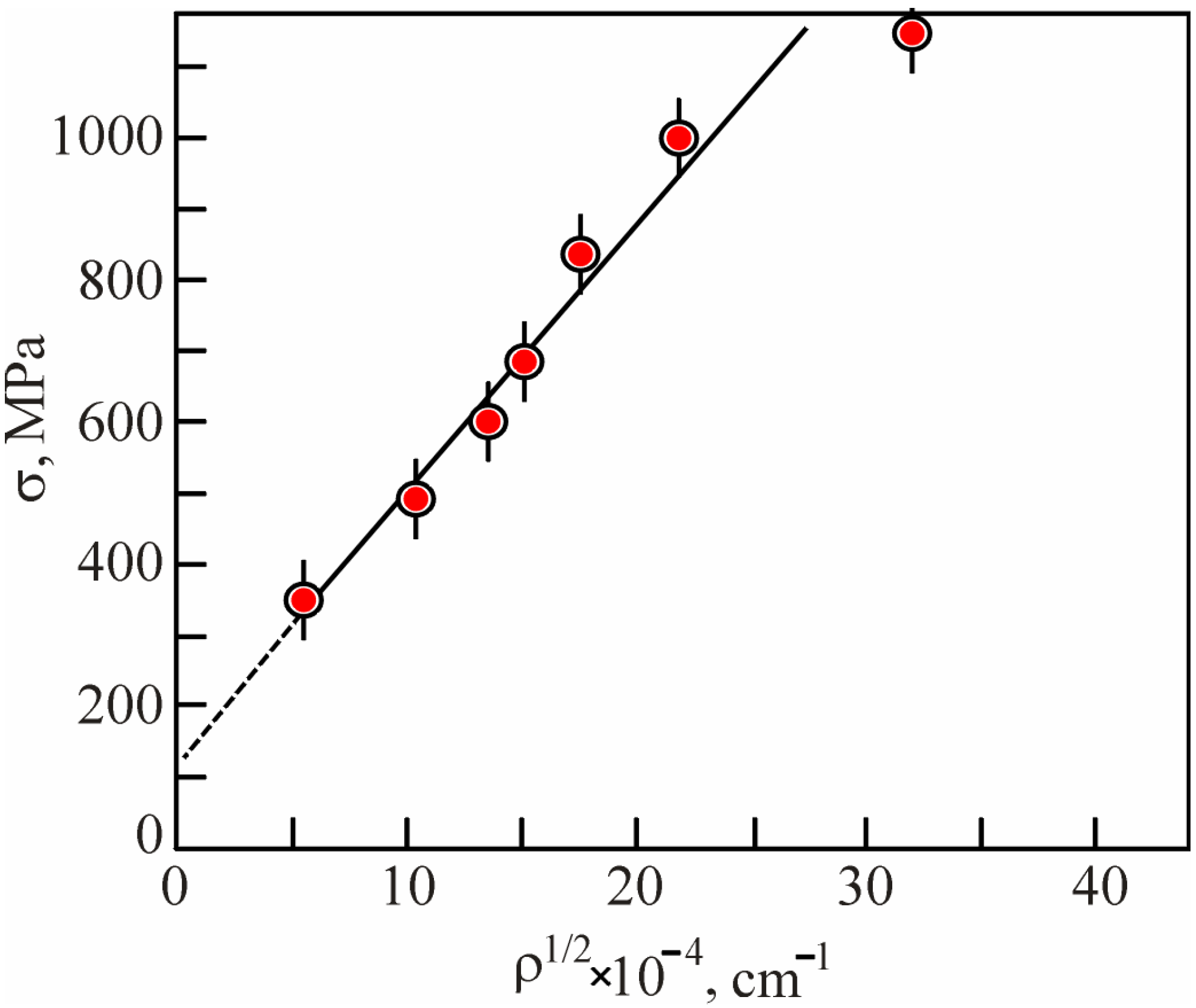
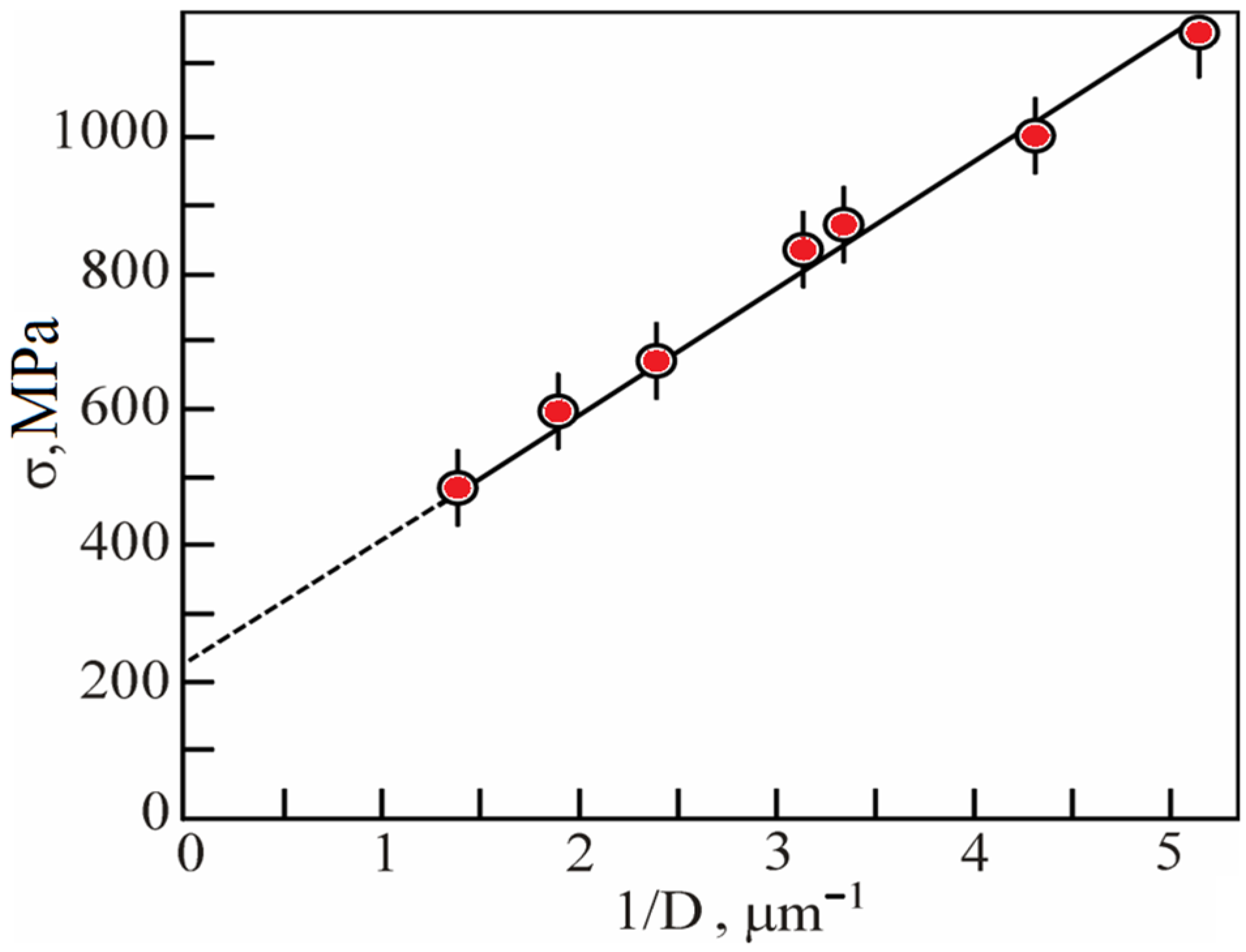
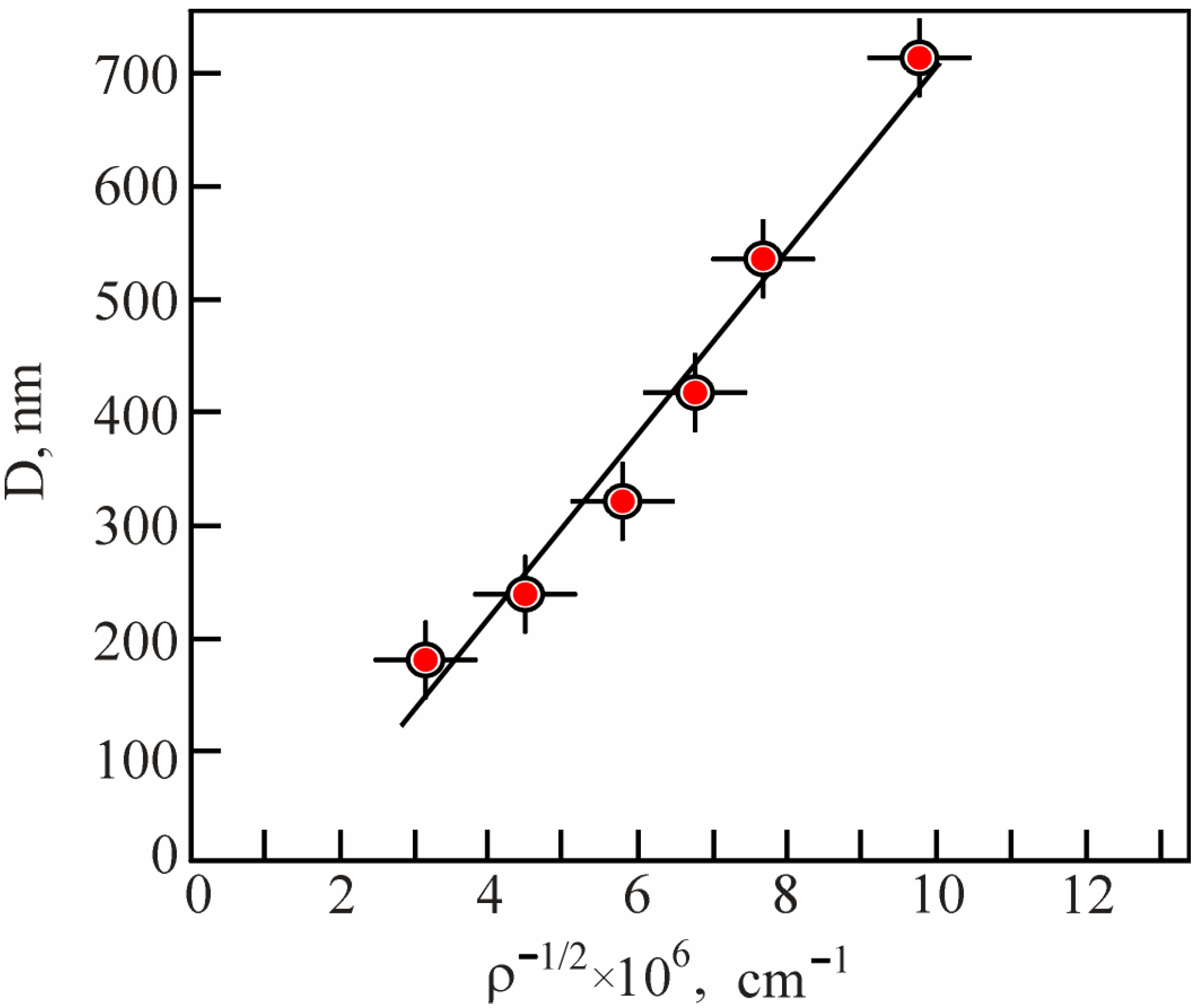


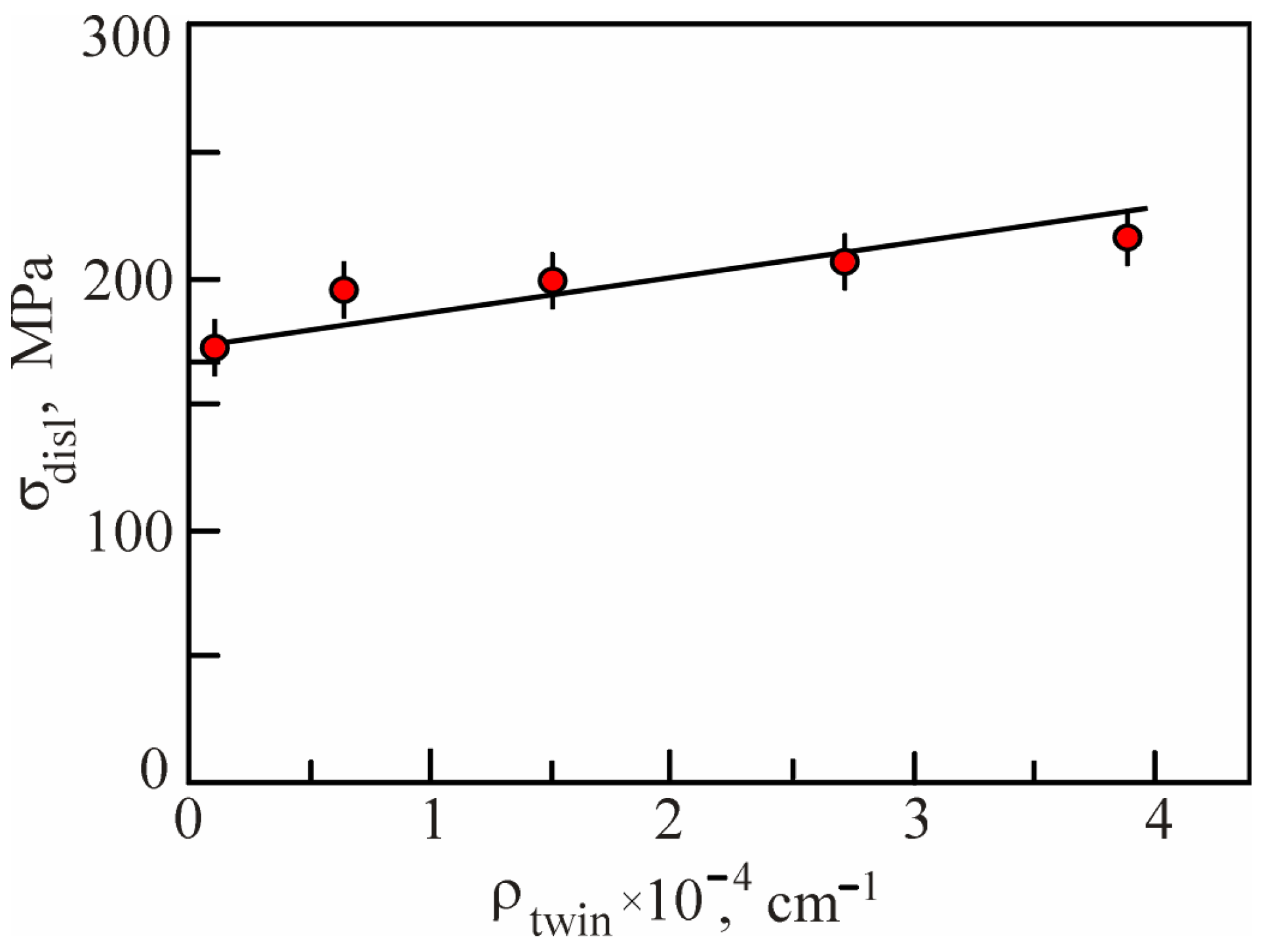
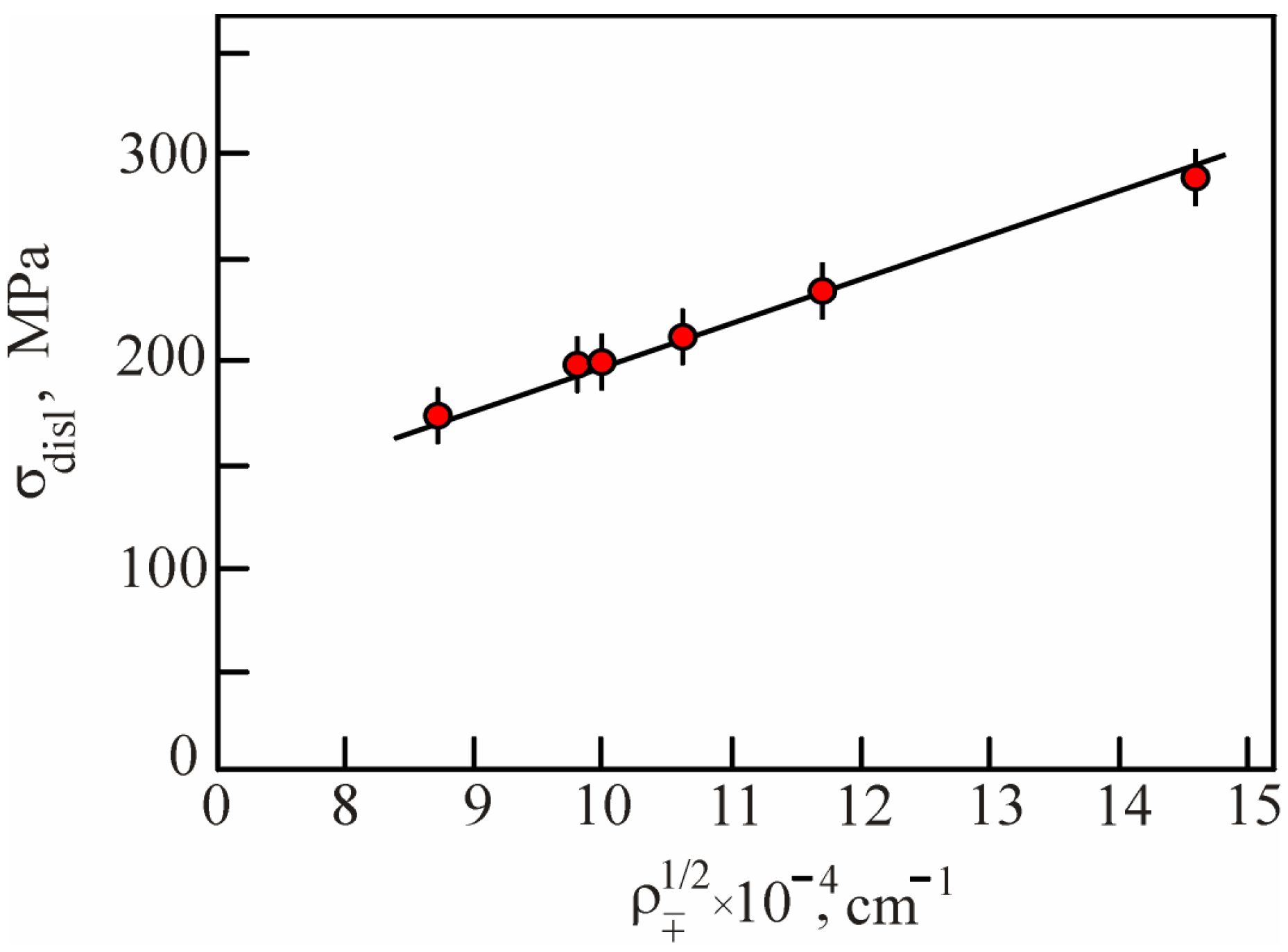
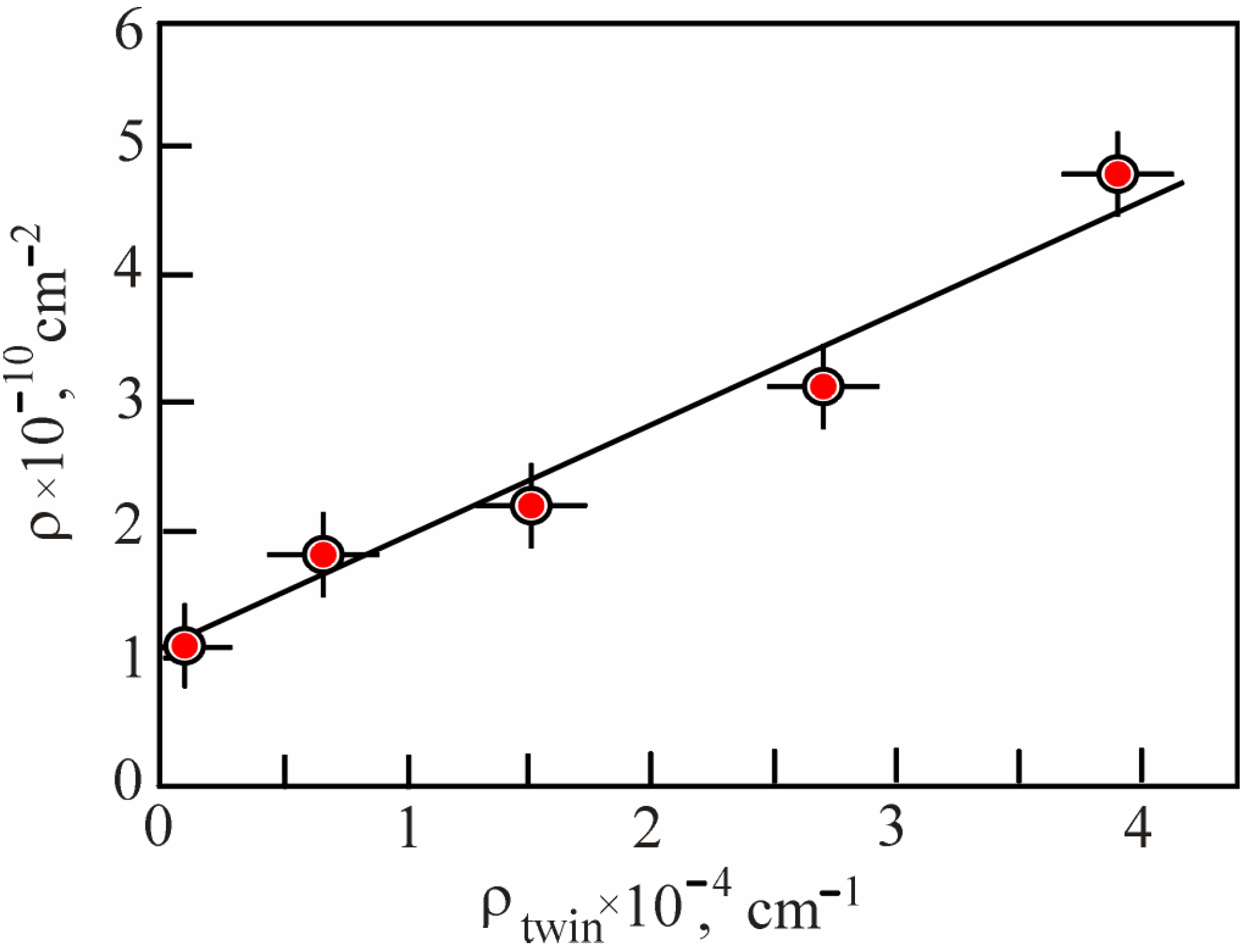
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popova, N.; Slobodyan, M.; Klopotov, A.; Nikonenko, E.; Potekaev, A.; Borodin, V. Relationship of Internal Stress Fields with Self-Organization Processes in Hadfield Steel under Tensile Load. Metals 2023, 13, 952. https://doi.org/10.3390/met13050952
Popova N, Slobodyan M, Klopotov A, Nikonenko E, Potekaev A, Borodin V. Relationship of Internal Stress Fields with Self-Organization Processes in Hadfield Steel under Tensile Load. Metals. 2023; 13(5):952. https://doi.org/10.3390/met13050952
Chicago/Turabian StylePopova, Natalyi, Mikhail Slobodyan, Anatoliy Klopotov, Elena Nikonenko, Alexander Potekaev, and Vladislav Borodin. 2023. "Relationship of Internal Stress Fields with Self-Organization Processes in Hadfield Steel under Tensile Load" Metals 13, no. 5: 952. https://doi.org/10.3390/met13050952
APA StylePopova, N., Slobodyan, M., Klopotov, A., Nikonenko, E., Potekaev, A., & Borodin, V. (2023). Relationship of Internal Stress Fields with Self-Organization Processes in Hadfield Steel under Tensile Load. Metals, 13(5), 952. https://doi.org/10.3390/met13050952








