Offline Feed-Rate Scheduling Method for Ti–Al Alloy Blade Finishing Based on a Local Stiffness Estimation Model
Abstract
1. Introduction
1.1. Online Feed-Rate Scheduling Method
1.2. Offline Feed-Rate Scheduling Method
1.2.1. MRR-Based Feed-Rate Optimization
1.2.2. Feed-Speed Optimization Based on Cutting Force
1.2.3. Power-Based Feed-Rate Optimization
1.2.4. Feed-Rate Schedule Based on Geometric and Kinematic Constraints
1.3. Suppression of Deformation Error in the Machining of Thin-Walled Parts
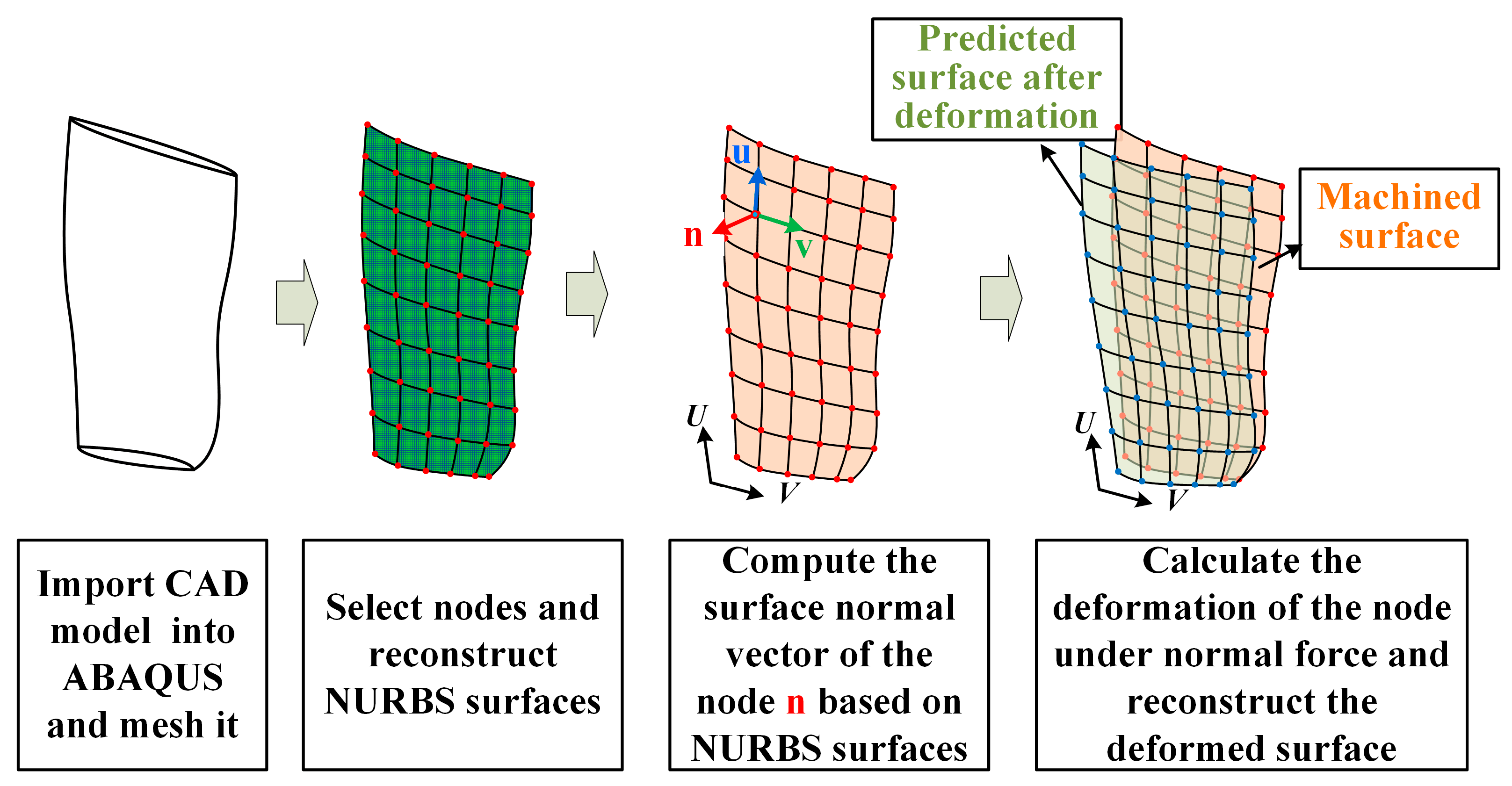
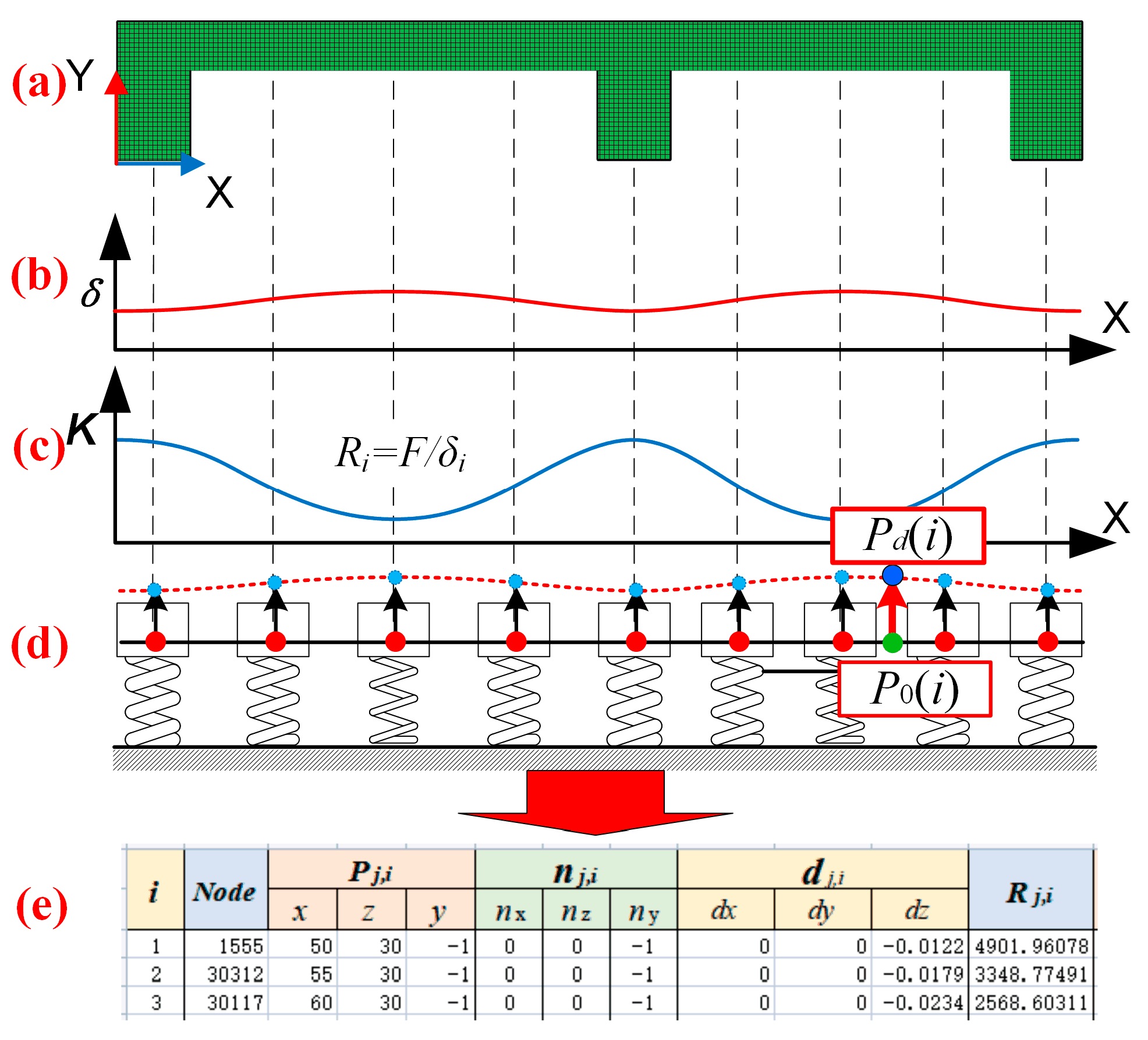
2. Local Stiffness Estimation Model of Thin-Walled Parts
3. Cutting-Force Prediction Model Considering the Effect of Cutting Angle
4. Feed-Rate Scheduling Method for Thin-Walled Blade Finishing
4.1. Identification of the Machining Process Based on the CLSF
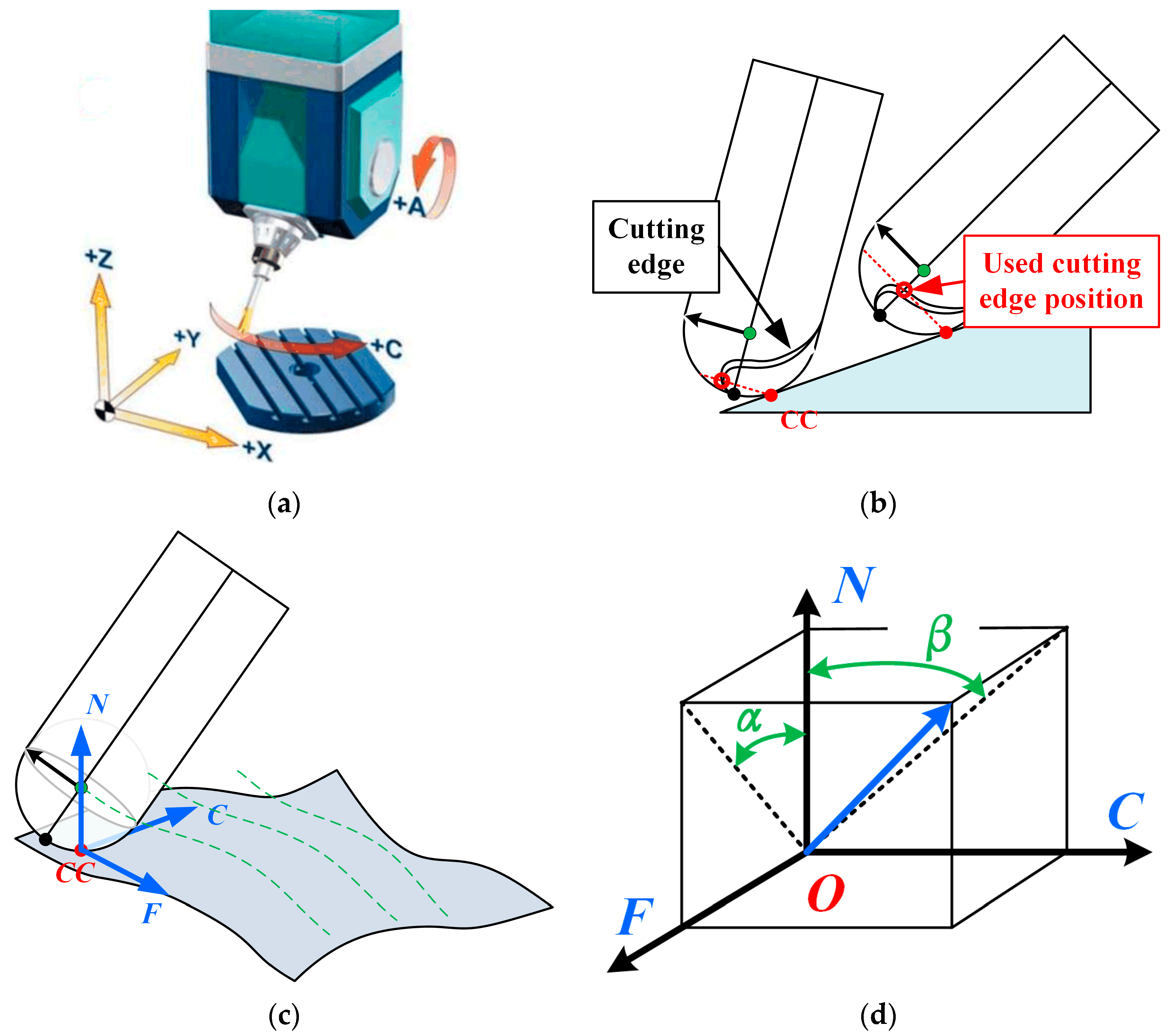
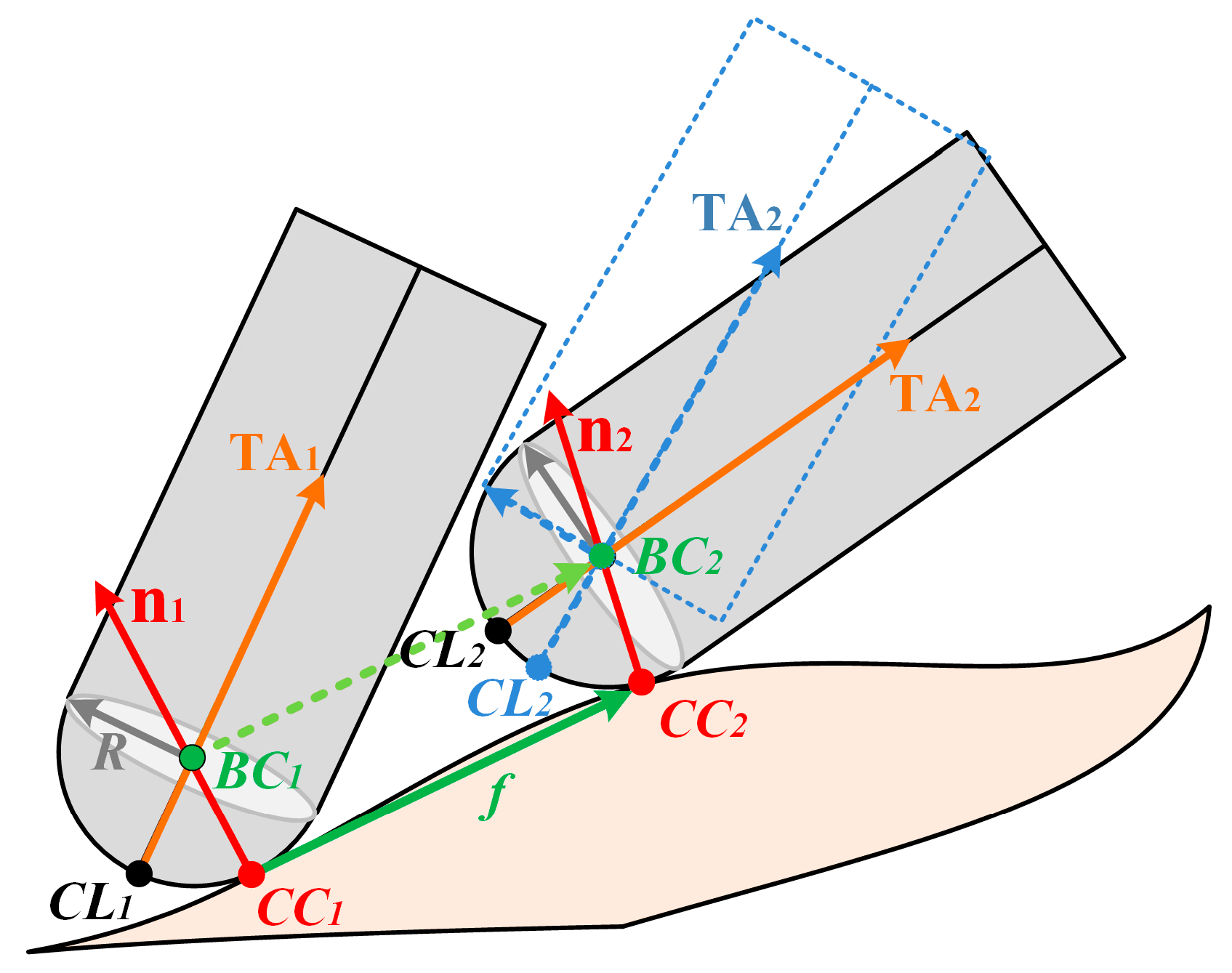
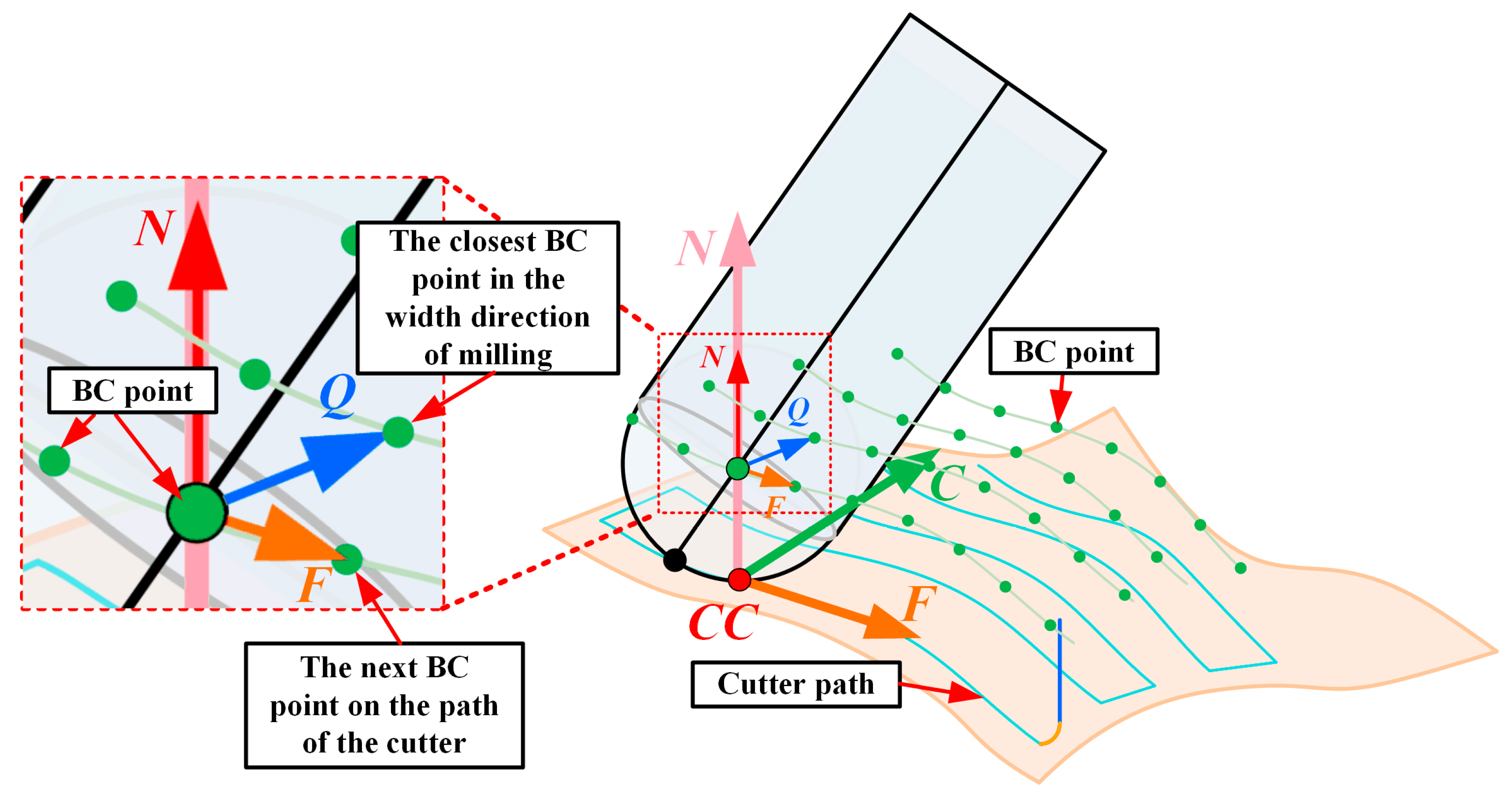
4.1.1. Determining CC Points and the CSCS
4.1.2. Determining the Angle between the TA and the Machined Surface in the CSCS
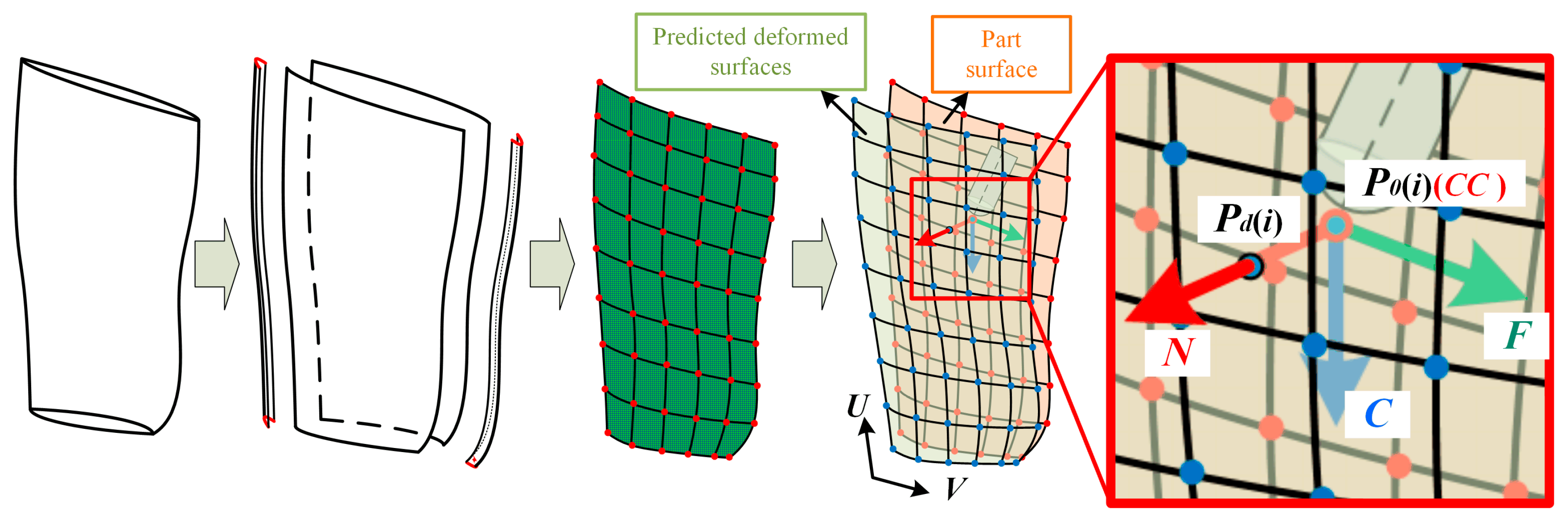
4.1.3. Local Stiffness Estimation and Machining Deformation Prediction at the CC Point
4.2. Feed-Rate Optimization Constraint
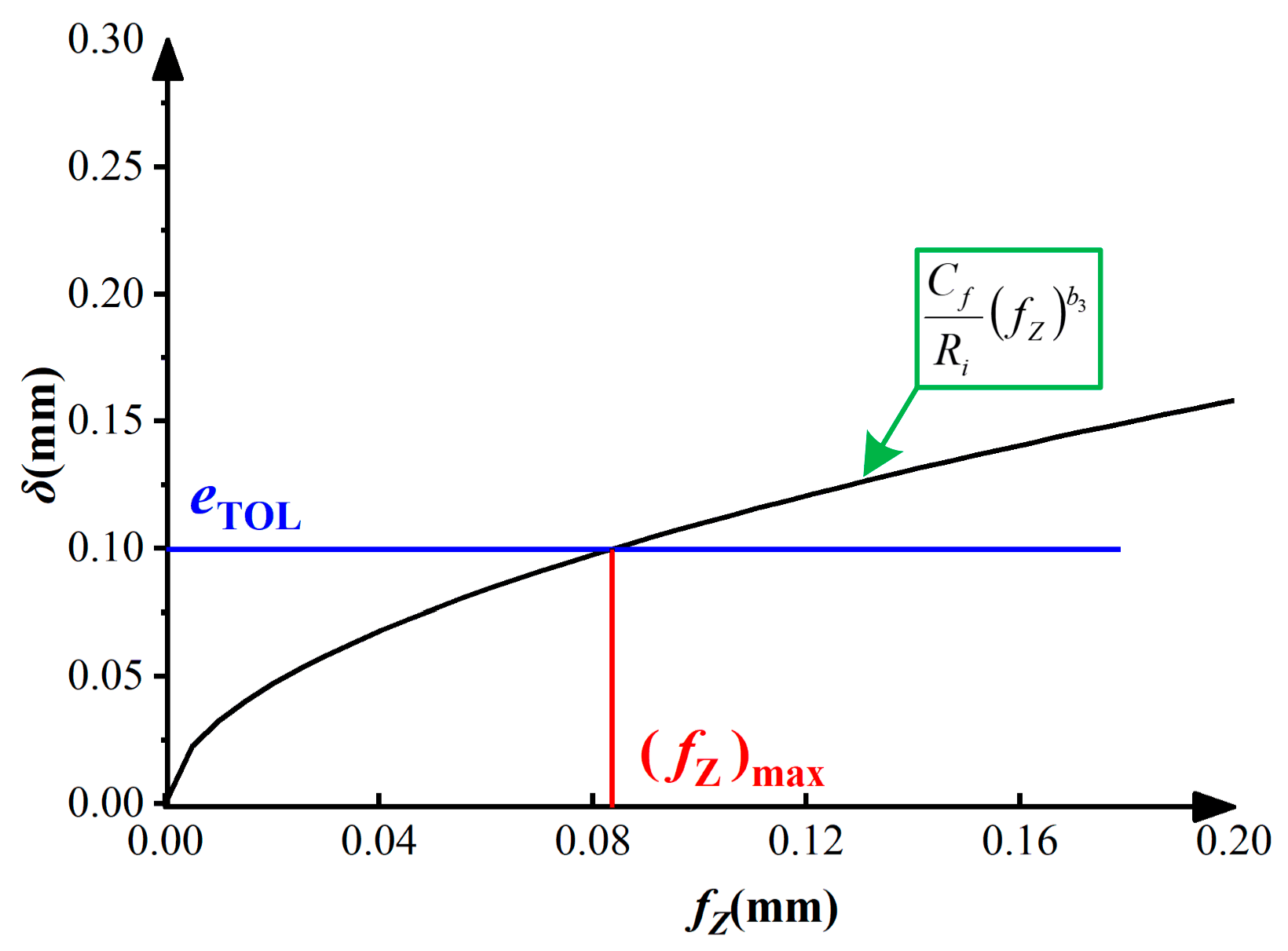
4.2.1. Constraints on Machining Deformation Based on Local Stiffness Estimation
4.2.2. Acceleration Distance Constraint
4.2.3. Feed-Speed Range Constraint
4.3. The Execution Process of Feed-Rate Scheduling
5. Simulation and Experimental Verification
5.1. Experimental Setup
5.2. Establishment of Milling-Force Estimation Model
5.3. Local Stiffness Estimation Model of the Blade and Its Performance Analysis
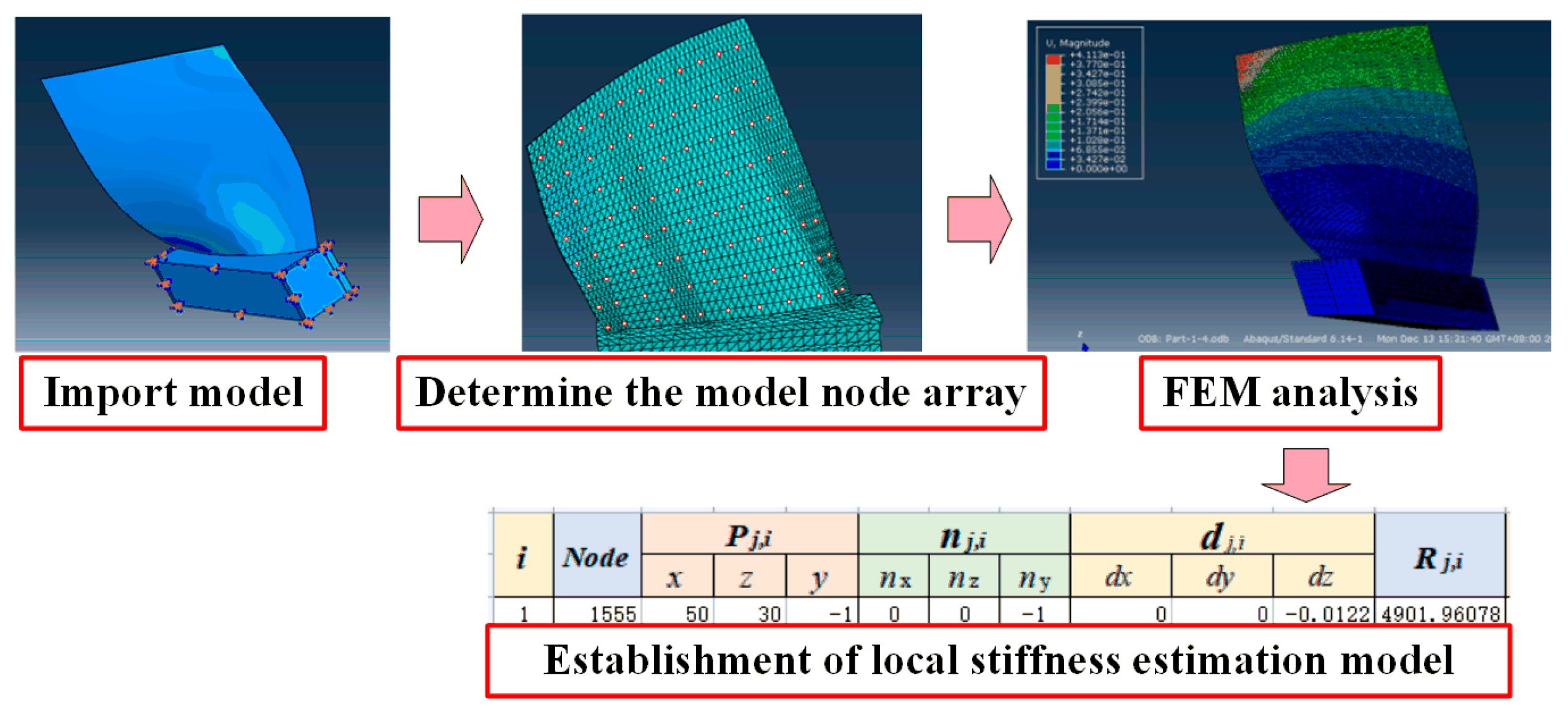
5.3.1. Local Stiffness Estimation Model of the Blade
5.3.2. Analysis of Prediction Accuracy and Efficiency of the Model
5.4. Application Verification of Feed-Rate Scheduling Method
6. Conclusions
- A machining method with constant cutting parameters is constrained by the machining deformation error during the machining of thin-walled blades, resulting in conservative machining parameters and low machining efficiency.
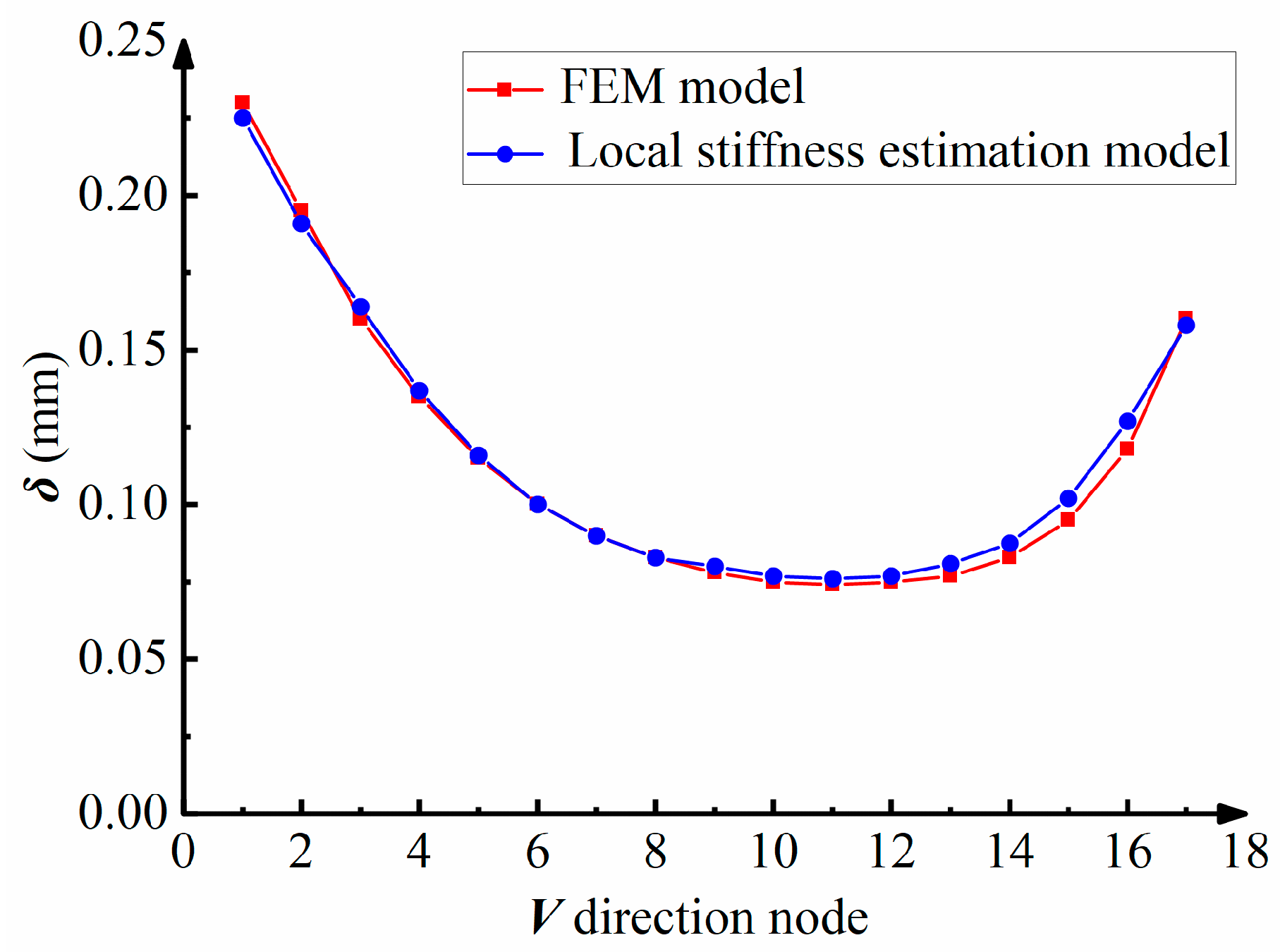
- Compared with the FEM-based model, the maximum prediction error of the established local stiffness estimation model is less than 3%, but the calculation time is reduced by 99%. This shows that the proposed local stiffness estimation model has a higher computational efficiency and flexibility.
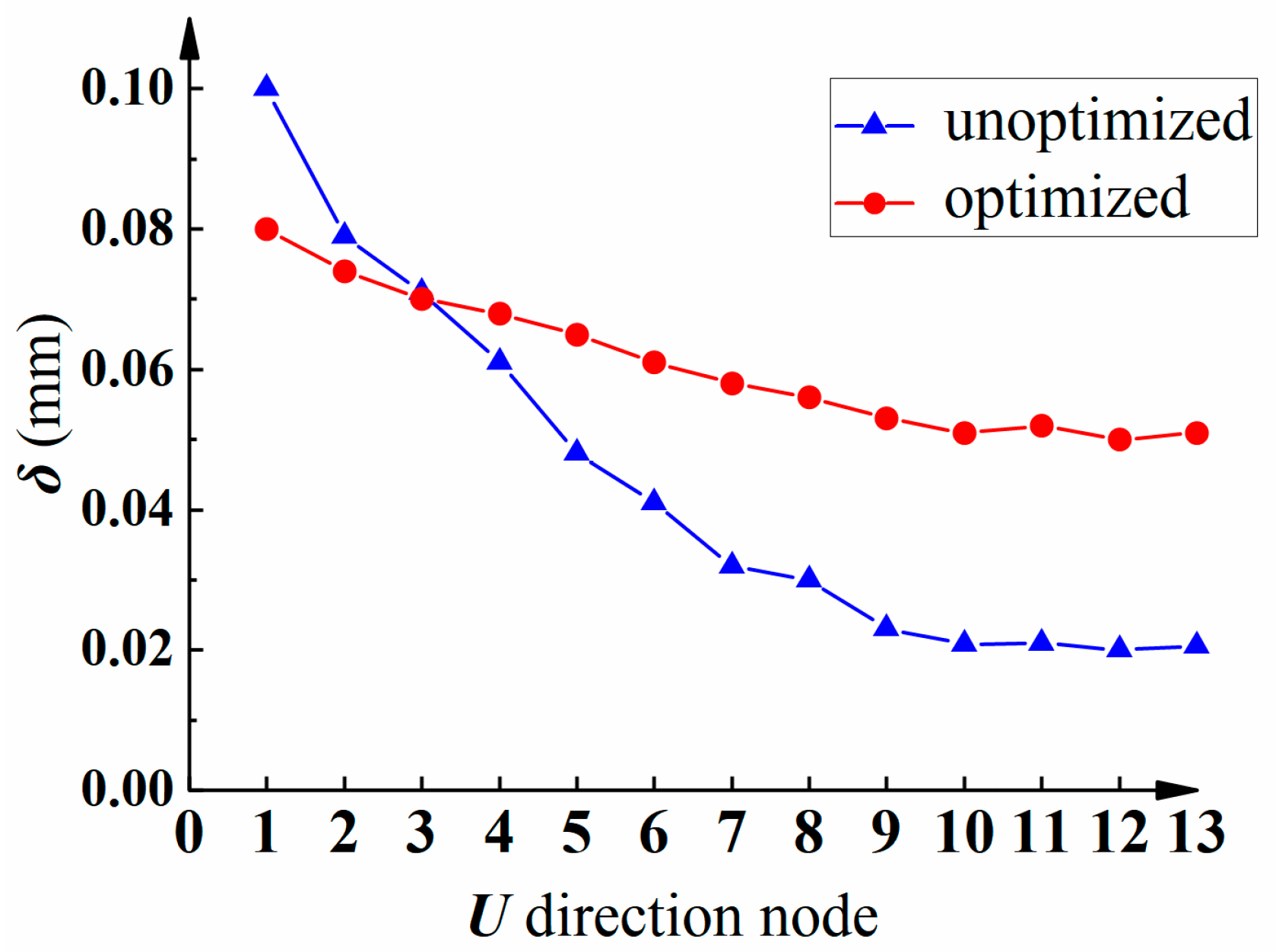
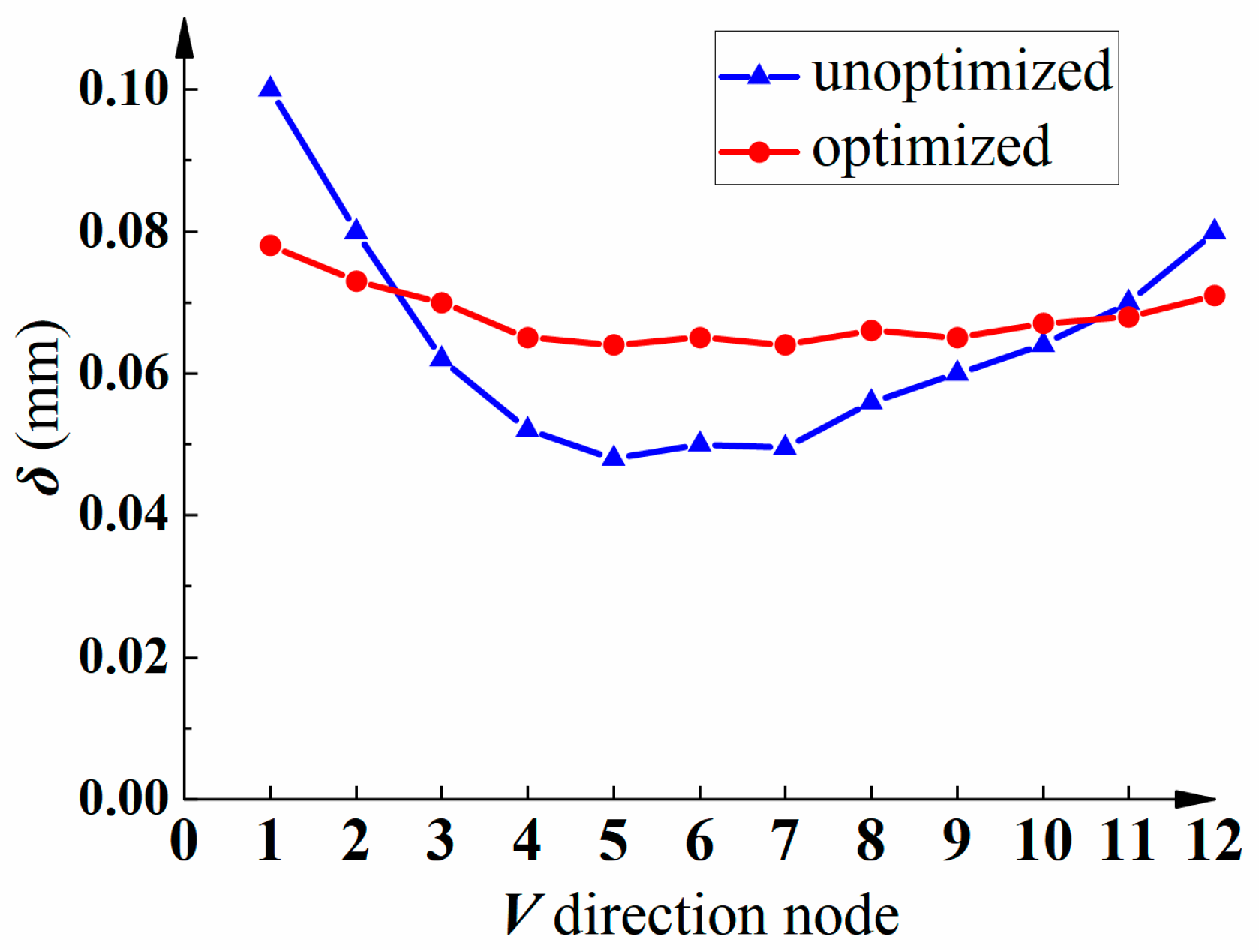
- The proposed offline feed-rate scheduling method increases the machining efficiency by 23% and reduces the machining error by 20%. This shows that the proposed method can reasonably allocate the feed rate and improve the machining efficiency of parts while ensuring the machining accuracy of thin-walled blades.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kurt, M.; Bagci, E. Feedrate optimisation/scheduling on sculptured surface machining: A comprehensive review, applications and future directions. Int. J. Adv. Manuf. Technol. 2011, 55, 1037–1067. [Google Scholar] [CrossRef]
- Adams, O.; Klocke, F.; Schwenzer, M.; Stemmler, S.; Abel, D. Model-based predictive force control in milling—System identification. Procedia Technol. 2016, 26, 214–220. [Google Scholar] [CrossRef]
- Han, Z.; Jin, H.; Fu, Y.; Fu, H. Cutting deflection control of the blade based on real-time feedrate scheduling in open modular architecture CNC system. Int. J. Adv. Manuf. Technol. 2017, 90, 2567–2579. [Google Scholar] [CrossRef]
- Jang, D.; Kim, K.; Jung, J. Voxel-based virtual multi-axis machining. Int. J. Adv. Manuf. Technol. 2000, 16, 709–713. [Google Scholar] [CrossRef]
- Layegh, K.S.E.; Erdim, H.; Lazoglu, I. Offline force control and feedrate scheduling for complex free form surfaces in 5-axis milling. Procedia CIRP 2012, 1, 96–101. [Google Scholar]
- Woo, W.-S.; Curtis, D.; Bagni, C.; Lee, C.-M.; Lee, J.-H.; Kim, D.-H. Productivity enhancement of aircraft turbine disk using a two-step strategy based on tool-path planning and NC-code optimization. Metals 2022, 12, 567. [Google Scholar] [CrossRef]
- Käsemodel, R.B.; de Souza, A.F.; Voigt, R.; Basso, I.; Rodrigues, A.R. CAD/CAM interfaced algorithm reduces cutting force, roughness, and machining time in free-form milling. Int. J. Adv. Manuf. Technol. 2020, 107, 1883–1900. [Google Scholar] [CrossRef]
- Ghosh, T.; Wang, Y.; Martinsen, K.; Wang, K. A surrogate-assisted optimization approach for multi-response end milling of aluminum alloy AA3105. Int. J. Adv. Manuf. Technol. 2020, 111, 2419–2439. [Google Scholar] [CrossRef]
- Park, H.; Qi, B.; Dang, D.; Park, D.Y. Development of smart machining system for optimizing feedrates to minimize machining time. J. Comp. Des. Eng. 2018, 5, 299–304. [Google Scholar] [CrossRef]
- Wang, L.P.; Yuan, X.; Si, H.; Duan, F.Y. Feedrate scheduling method for constant peak cutting force in five-axis flank milling process. Chin. J. Aeronaut. 2020, 33, 2055–2069. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, M.; Zhang, D.; Wu, B. A force-measuring-based approach for feed rate optimization considering the stochasticity of machining allowance. Int. J. Adv. Manuf. Technol. 2018, 97, 2545–2556. [Google Scholar] [CrossRef]
- Osorio-Pinzon, J.C.; Abolghasem, S.; Marañon, A.; Casas-Rodriguez, J.P. Cutting parameter optimization of Al-6063-O using numerical simulations and particle swarm optimization. Int. J. Adv. Manuf. Technol. 2020, 111, 2507–2532. [Google Scholar] [CrossRef]
- Xu, G.; Chen, J.; Zhou, H.; Yang, J.; Hu, P.; Dai, W. Multi-objective feedrate optimization method of end milling using the internal data of the CNC system. Int. J. Adv. Manuf. Technol. 2019, 101, 715–731. [Google Scholar] [CrossRef]
- Xie, J.; Zhao, P.; Hu, P.; Yin, Y.; Zhou, H.; Chen, J.; Yang, J. Multi-objective feed rate optimization of three-axis rough milling based on artificial neural network. Int. J. Adv. Manuf. Technol. 2021, 114, 1323–1339. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, Y.; Liu, G.; Zhang, Y. Feedrate optimization method based on machining allowance optimization and constant power constraint. Int. J. Adv. Manuf. Technol. 2021, 115, 3345–3360. [Google Scholar] [CrossRef]
- Du, X.; Huang, J.; Zhu, L.-M.; Ding, H. An error-bounded B-spline curve approximation scheme using dominant points for CNC interpolation of micro-line toolpath. Robot. Comput. Integr. Manuf. 2020, 64, 101930. [Google Scholar] [CrossRef]
- Li, H.; Jiang, X.; Huo, G.; Su, C.; Wang, B.; Hu, Y.; Zheng, Z. A novel feedrate scheduling method based on Sigmoid function with chord error and kinematic constraints. Int. J. Adv. Manuf. Technol. 2022, 119, 1531–1552. [Google Scholar] [CrossRef]
- Song, D.N.; Ma, J.W.; Zhong, Y.G.; Xiao, D.; Yao, J.J.; Zhou, C. A fully real-time spline interpolation algorithm with axial jerk constraint based on FIR filtering. Int. J. Adv. Manuf. Technol. 2021, 113, 1873–1886. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, P.; Zhao, M.; Zhang, H. Dynamic feedrate optimization for parametric toolpath with data-based tracking error prediction. Mech. Syst. Signal Process. 2019, 120, 221–233. [Google Scholar] [CrossRef]
- Lamikiz, A.; López de Lacalle, L.N.; Sánchez, J.A.; Salgado, M.A. Cutting force estimation in sculptured surface milling. Int. J. Mach. Tools Manuf. 2004, 44, 1511–1526. [Google Scholar] [CrossRef]
- Calleja, A.; Alonso, M.A.; Fernández, A.; Tabernero, I.; Ayesta, I.; Lamikiz, A.; López de Lacalle, L.N. Flank milling model for tool path programming of turbine blisks and compressors. Int. J. Prod. Res. 2014, 53, 3354–3369. [Google Scholar] [CrossRef]
- Calleja, A.; Bo, P.; González, H.; Bartoň, M.; López de Lacalle, L.N. Highly accurate 5-axis flank CNC machining with conical tools. Int. J. Adv. Manuf. Technol. 2018, 97, 1605–1615. [Google Scholar] [CrossRef]
- Salgado, M.A.; López de Lacalle, L.N.; Lamikiz, A.; Muñoa, J.; Sánchez, J.A. Evaluation of the stiffness chain on the deflection of end-mills under cutting forces. Int. J. Mach. Tools Manuf. 2005, 45, 727–739. [Google Scholar] [CrossRef]
- López de Lacalle, L.N.; Lamikiz, A.; Sánchez, J.A.; Salgado, M.A. Toolpath selection based on the minimum deflection cutting forces in the programming of complex surfaces milling. Int. J. Mach. Tools Manuf. 2007, 47, 388–400. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, D.; Zhang, Y.; Wu, B. The variable radial depth of cut in finishing machining of thin-walled blade based on the stable-state deformation field. Int. J. Adv. Manuf. Technol. 2021, 113, 141–158. [Google Scholar] [CrossRef]
- Wang, J.; Ibaraki, S.; Matsubara, A. A cutting sequence optimization algorithm to reduce the workpiece deformation in thin-wall machining. Precis. Eng. 2017, 50, 506–514. [Google Scholar] [CrossRef]
- Campa, F.J.; Lopez de Lacalle, L.N.; Celaya, A. Chatter avoidance in the milling of thin floors with bull-nose end mills: Model and stability diagrams. Int. J. Mach. Tools Manuf. 2011, 51, 43–53. [Google Scholar] [CrossRef]
- Rozylo, P.; Debski, H. Effect of eccentric loading on the stability and load-carrying capacity of thin-walled composite profiles with top-hat section. Compos. Struct. 2020, 245, 112388. [Google Scholar] [CrossRef]
- Wysmulski, P.; Debski, H.; Falkowicz, K.; Rozylo, P. The influence of load eccentricity on the behavior of thin-walled compressed composite structures. Compos. Struct. 2019, 213, 98–107. [Google Scholar] [CrossRef]
- Hailong, M.; Aijun, T.; Shubo, X.; Tong, L. Finite element simulation of bending thin-walled parts and optimization of cutting parameters. Metals 2023, 13, 115. [Google Scholar] [CrossRef]
- Wu, L.; Wang, A.; Xing, W.; Wang, K. Adaptive sampling method for thin-walled parts based on on-machine measurement. Int. J. Adv. Manuf. Technol. 2022, 122, 2577–2592. [Google Scholar] [CrossRef]
- Fei, J.; Xu, F.; Lin, B.; Huang, T. State of the art in milling process of the flexible workpiece. Int. J. Adv. Manuf. Technol. 2020, 109, 1695–1725. [Google Scholar] [CrossRef]
- Tunc, L.T. Rapid extraction of machined surface data through inverse geometrical solution of tool path information. Int. J. Adv. Manuf. Technol. 2016, 87, 353–362. [Google Scholar] [CrossRef]
- Gerhard, W.; Boyer, R.R.; Collings, E.W. Material Properties Handbook: Titanium Alloys; ASM International: Materials Park, OH, USA, 1994. [Google Scholar]
- Liu, D.; Shi, Y.; Lin, X.; Xian, C.; Gu, Z. Polishing surface integrity of TC17 aeroengine blades. J. Mech. Sci. Technol. 2020, 34, 689–699. [Google Scholar] [CrossRef]
- Fernandez-Valdivielso, A.; de Lacalle, L.N.L.; Urbikain, G.; Rodriguez, A. Detecting the key geometrical features and grades of carbide inserts for the turning of nickel-based alloys concerning surface integrity. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 3725–3742. [Google Scholar] [CrossRef]









| Spindle speed | 6000 rpm | Rotation range of axis A | +60°~−100° |
| Spindle power | 37 KW | Rotation range of axis B | 0°~360° |
| Table area | 1000 × 1000 mm | Maximum feed acceleration | 0.5 g |
| The maximum speed of axis A/B | 6 rpm |
| Density (g/cm3) | 4.55 |
| Tensile strength (Mpa) | 1960 |
| Yield strength (Mpa) | 1890 |
| Poisson ratio | 0.3 |
| Young’s modulus (Gpa) | 223 |
| Tooth Number | Diameter (mm) | Spiral Angle (Deg) | Tool Length | Material |
|---|---|---|---|---|
| 4 | 10 | 30 | 70 | sintered carbide integral tool |
| No. | ap | ae | f | v | α | β | Fx(N) | Fy(N) | Fz(N) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.1 | 0.3 | 0.04 | 25 | 0 | 0 | 24.952 | 22.156 | 36.138 |
| 2 | 0.1 | 0.6 | 0.06 | 50 | 10 | 10 | 53.579 | 41.669 | 62.926 |
| 3 | 0.1 | 0.9 | 0.08 | 75 | 20 | 20 | 77.578 | 40.894 | 86.847 |
| 4 | 0.1 | 1.2 | 0.1 | 100 | 30 | 30 | 137.825 | 62.397 | 175.167 |
| 5 | 0.1 | 1.5 | 0.12 | 150 | 40 | 40 | 171.599 | 80.063 | 250.637 |
| 6 | 0.2 | 0.3 | 0.06 | 75 | 30 | 40 | 60.034 | 41.426 | 57.549 |
| 7 | 0.2 | 0.6 | 0.08 | 100 | 40 | 0 | 92.342 | 8.581 | 60.314 |
| 8 | 0.2 | 0.9 | 0.1 | 150 | 0 | 10 | 182.964 | 333.842 | 570.216 |
| 9 | 0.2 | 1.2 | 0.12 | 25 | 10 | 20 | 87.063 | 67.242 | 106.534 |
| 10 | 0.2 | 1.5 | 0.04 | 50 | 20 | 30 | 53.969 | 32.364 | 84.573 |
| 11 | 0.3 | 0.3 | 0.08 | 150 | 10 | 30 | 47.621 | 80.625 | 77.361 |
| 12 | 0.3 | 0.6 | 0.1 | 25 | 20 | 40 | 42.561 | 37.534 | 63.967 |
| 13 | 0.3 | 0.9 | 0.12 | 50 | 30 | 0 | 54.134 | 8.144 | 41.193 |
| 14 | 0.3 | 1.2 | 0.04 | 75 | 40 | 10 | 62.403 | 8.786 | 60.334 |
| 15 | 0.3 | 1.5 | 0.06 | 100 | 0 | 20 | 72.648 | 152.171 | 222.876 |
| 16 | 0.6 | 0.3 | 0.1 | 50 | 40 | 20 | 46.397 | 20.209 | 68.932 |
| 17 | 0.6 | 0.6 | 0.12 | 75 | 0 | 30 | 80.075 | 151.223 | 209.186 |
| 18 | 0.6 | 0.9 | 0.04 | 100 | 10 | 40 | 87.212 | 112.896 | 183.542 |
| 19 | 0.6 | 1.2 | 0.06 | 150 | 20 | 0 | 208.071 | 39.102 | 123.514 |
| 20 | 0.6 | 1.5 | 0.08 | 25 | 30 | 10 | 139.775 | 52.221 | 133.549 |
| 21 | 0.8 | 0.3 | 0.12 | 100 | 20 | 10 | 157.748 | 82.535 | 105.263 |
| 22 | 0.8 | 0.6 | 0.04 | 150 | 30 | 20 | 162.991 | 62.011 | 175.294 |
| 23 | 0.8 | 0.9 | 0.06 | 25 | 40 | 30 | 68.951 | 16.973 | 99.564 |
| 24 | 0.8 | 1.2 | 0.08 | 50 | 0 | 40 | 69.809 | 129.175 | 262.953 |
| 25 | 0.8 | 1.5 | 0.1 | 75 | 10 | 0 | 296.587 | 318.279 | 323.219 |
| Ω (r/min) | ap (mm) | ae (mm) | Vf (mm/min) | fZ (mm) | vC (m/min) | |
|---|---|---|---|---|---|---|
| finishing | 2500 | 0.8 | 0.6 | 600 | 0.06 | 78.5 |
| Unoptimized (min) | Optimized (min) | Optimized Efficiency (%) | |
|---|---|---|---|
| Time consumption | 124 | 95 | 23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Wang, A.; Xing, W. Offline Feed-Rate Scheduling Method for Ti–Al Alloy Blade Finishing Based on a Local Stiffness Estimation Model. Metals 2023, 13, 987. https://doi.org/10.3390/met13050987
Wu L, Wang A, Xing W. Offline Feed-Rate Scheduling Method for Ti–Al Alloy Blade Finishing Based on a Local Stiffness Estimation Model. Metals. 2023; 13(5):987. https://doi.org/10.3390/met13050987
Chicago/Turabian StyleWu, Long, Aimin Wang, and Wenhao Xing. 2023. "Offline Feed-Rate Scheduling Method for Ti–Al Alloy Blade Finishing Based on a Local Stiffness Estimation Model" Metals 13, no. 5: 987. https://doi.org/10.3390/met13050987
APA StyleWu, L., Wang, A., & Xing, W. (2023). Offline Feed-Rate Scheduling Method for Ti–Al Alloy Blade Finishing Based on a Local Stiffness Estimation Model. Metals, 13(5), 987. https://doi.org/10.3390/met13050987





