Estimation of Component Activities and Molar Excess Gibbs Energy of 19 Binary Liquid Alloys from Partial Pair Distribution Functions in Literature
Abstract
:1. Introduction
2. Thermodynamic Models and Calculating Parameters
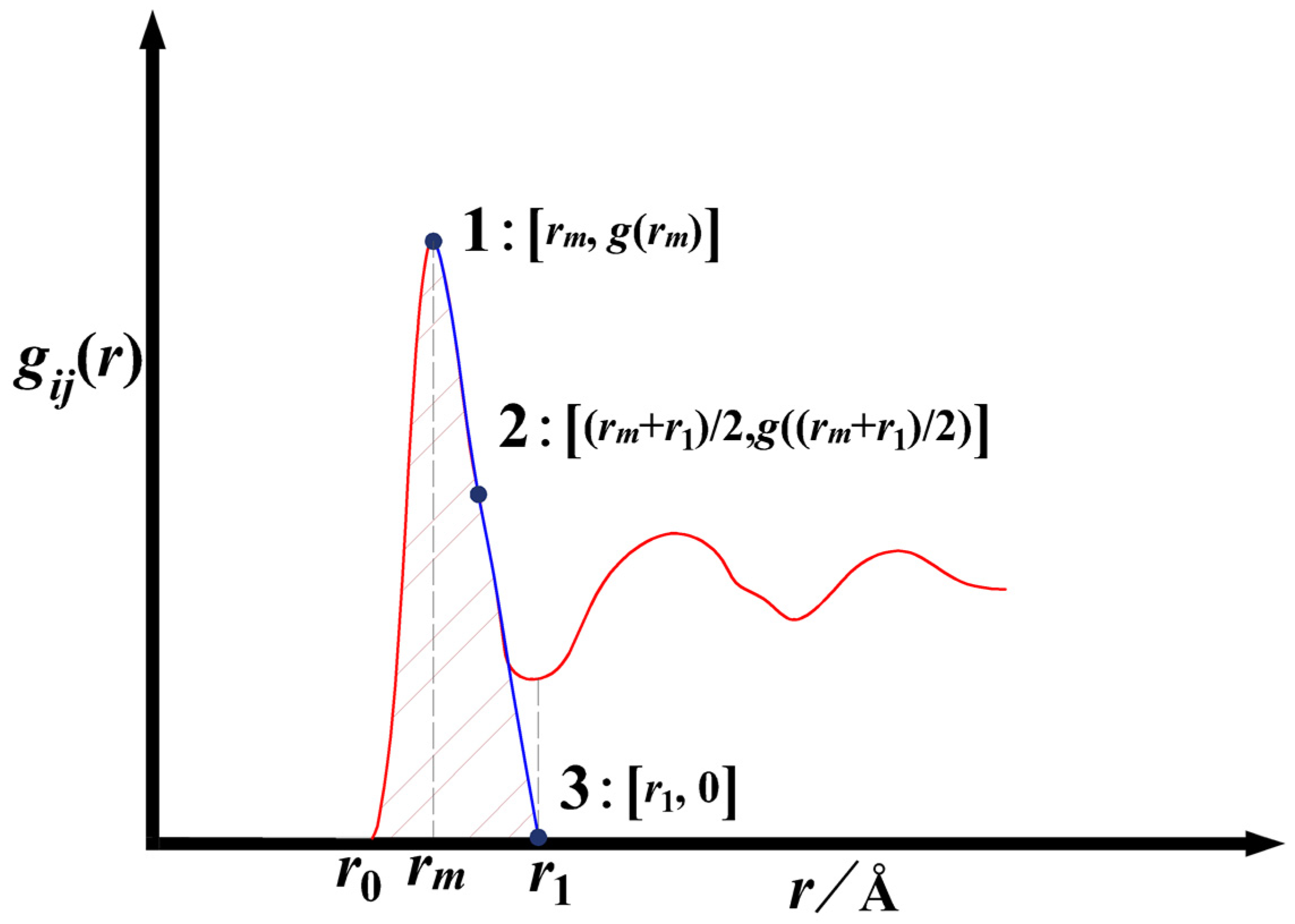
2.1. Obtaining Local Structure Parameters from Partial Pair Distribution Function
2.2. Thermodynamic Model
2.2.1. Four-Parameter Molecular Interaction Volume Model (MIVM)
2.2.2. Regular Solution Model (RSM)
2.2.3. Wilson’s Model
2.2.4. Nonrandom Two-Liquid (NRTL) Model
2.2.5. Quasi-Chemical Model (QCM)
3. Results and Discussion
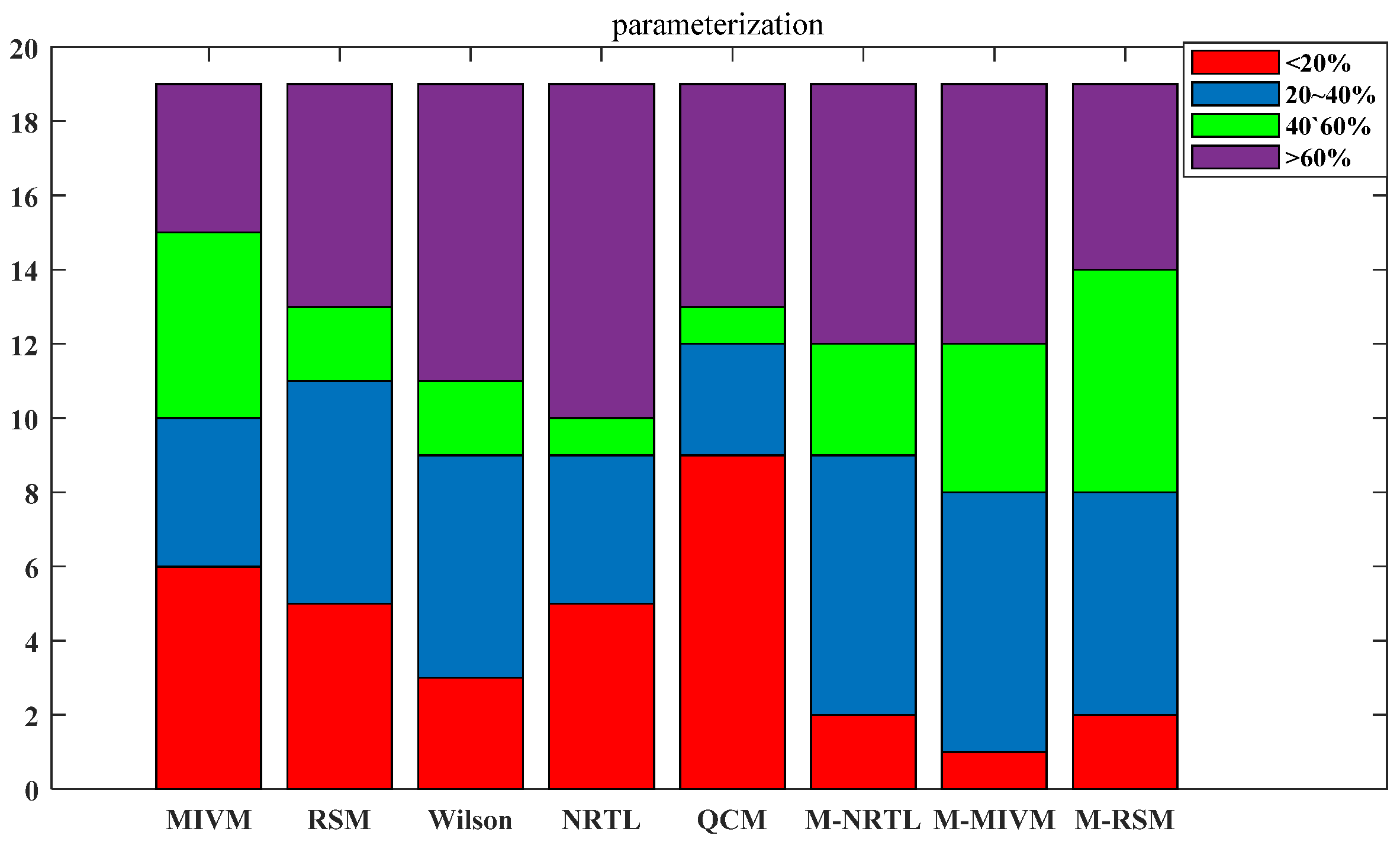
3.1. Calculation of Thermodynamic Model Parameters
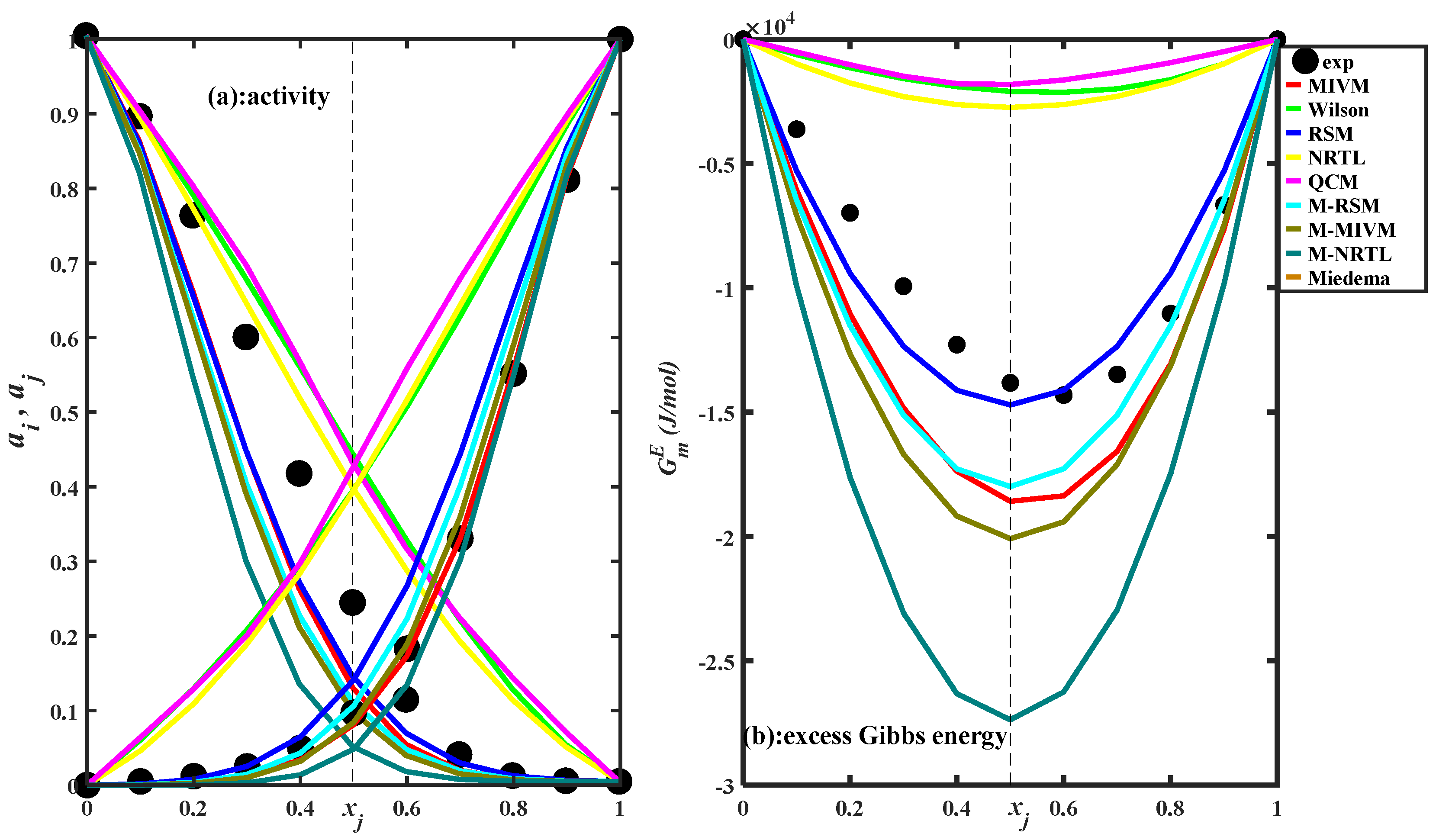
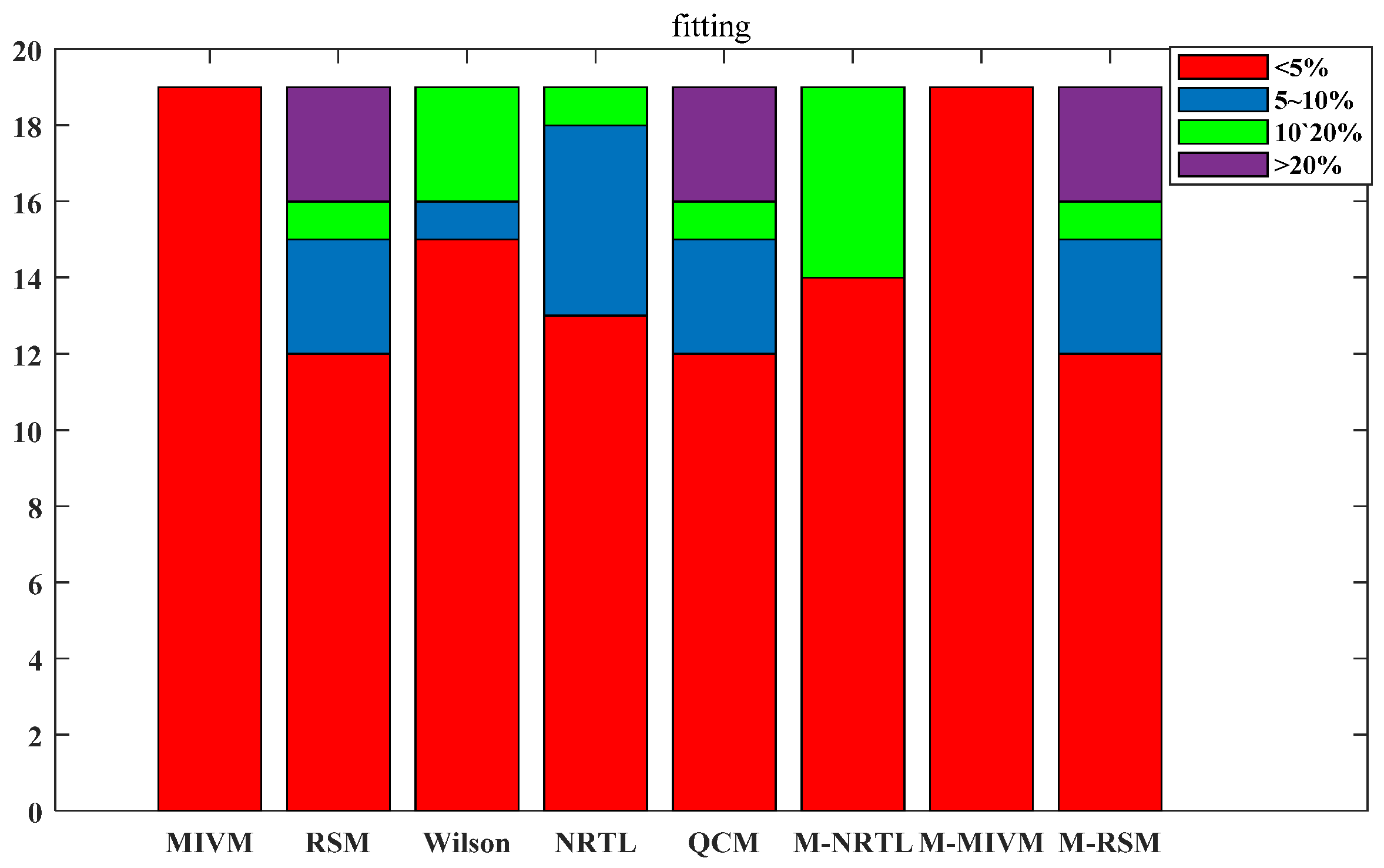
3.2. Estimating Thermodynamic Values
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Aij, Aji | Wilson’s model parameters |
| Bij, Bji, λij, λji | molecular interaction volume model (MIVM) parameters |
| Ψij,Ψji | modify molecular interaction volume model (MIVM) and modify regular solution model parameters |
| molar excess Gibbs energy, J/mol | |
| Pii(r), Pjj(r), Pij(r) | probability density function of pairs i-i, j-j, i-j |
| R | gas constant, 8.314 J/(K·mol) |
| T | absolute temperature, K |
| Vmi,Vmj | molar volume of i and j, cm3/mol |
| Zii, Zjj, Zij, Zjj | local coordination number (the first subscript represents the central atom; the second subscript represents the surrounding atom) |
| Zi, Zj | the first coordination number of i and j |
| average coordination number of liquid alloy | |
| Z0, Zc | the parameters in the first-order multinomial expression of Z |
| ai, aj | activity of component i and j |
| gii(r), gjj(r), gij(r), gji(r) | local partial pair distribution functions. gij(r) is the probability of finding atom j in the spherical shell in the interval r to r + dr centered on atom i. gii(r), gjj(r) and gji(r) have similar meanings. |
| r0 | position of the starting coordinate of pair distribution function is not 0, Å |
| rm | position of the first peak of the partial pair distribution function, Å |
| r1 | coordinate of the valley of the partial pair distribution function, Å |
| k | Boltzmann constant, 1.38 × 10−23 J/K |
| xii, xij, xjj, xji | local molecular fractions |
| xi, xj | molar fractions of i and j |
| u, v | Gaussian function width parameter |
| W | regular solution model parameter |
| εii(r), εjj(r), εij(r), εjj(r) | local pair potential function, J |
| εii, εij, εij, εjj | molecular pair potential, J |
| ω, β | quasi chemical model parameters |
| σ | short-range ordering |
| τij, τji, αij | nonrandom two-liquid model parameters |
| ρ0 | average number density Å−3 |
| γi, γj | activity coefficient of i, j |
| P1, P2 | parameters of the first order linear equation |
| AIMD | ab initio molecular dynamics |
| ARD | average relative deviation |
| MIVM | molecular interaction volume model |
| M-MIVM | modify molecular interaction volume model |
| M-RSM | modify regular solution model |
| NRTL | nonrandom two-liquid |
| PPDF | partial pair distribution function |
| L-PPDF | local partial pair distribution function |
| QCM | quasi-chemical model |
| UNIQUAC | universal quasi-chemical theory |
| RSM | regular solution model |
| STGE | Scientific Group Thermodata Group Europe |
References
- Su, Y.; Duan, S.C.; Guo, H.J.; Guo, J. Thermodynamic Properties Prediction of Fe-Al-Ti Alloys Based on Atom and Molecule Coexistence Theory. Phys. Met. Metallogr. 2022, 123, 1287–1298. [Google Scholar] [CrossRef]
- Islam, M.R.; Tanveer, S.; Chen, C.C. Modeling swelling behavior of hydrogels in aqueous organic solvents. Chem. Eng. Sci. 2021, 242, 116744. [Google Scholar] [CrossRef]
- Mounir, A.; Messnaoui, B.; Dinane, A.; Samaouali, A. New thermodynamic data for KNO3-sucrose-water ternary system: Water activity, osmotic coefficient, activity coefficient, excess Gibbs energy, solubility and transfer Gibbs energy at 298.15 K. Fluid Phase Equilib. 2020, 506, 112399. [Google Scholar] [CrossRef]
- Ha, C.; Kim, Y.M.; Woo, S.K.; Maawad, E.; Letzig, D.; Yi, S. Analysis of the dislocation activity of Mg-Zn-Y alloy using synchrotron radiation under tensile loading. J. Synchrotron Radiat. 2023, 30, 1–7. [Google Scholar] [CrossRef]
- Zhang, M.; Zhu, Z.Y.; Zhang, L.S.; Gao, M.R.; Gao, J.; Du, M.K.; Wang, B.Y. Understanding microstructure evolution and corrosion behavior of wire arc cladding inconel 625 Superalloy by thermodynamic approaches. J. Alloys Compd. 2023, 947, 169530. [Google Scholar] [CrossRef]
- Chen, L.L.; Li, T.; Zhang, J.P.; Wang, Y.A.; Kong, L.X.; Xu, B.Q.; Yang, B.; Wu, M.Z. Modeling and measurement of vapor-liquid equilibrium of In-Pb and In-Pb-Sn alloy systems in vacuum distillation. Vacuum 2023, 207, 111556. [Google Scholar] [CrossRef]
- Zhu, Y.Q.; Chen, Z.J.; Zhang, H.M.; Ma, W.H.; Wu, J.J. The effect of Ni on Fe and Al impurities by MIVM model for the silicon production. Energy 2022, 254, 124459. [Google Scholar] [CrossRef]
- Wang, S.L.; Hou, K.; Zhang, Z.W.; Huang, S.X.; Liu, X.Y.; He, M.G. Vapor-liquid equilibrium for dimethyl ether and three imidazolium ionic liquids as working pairs in absorption-refrigeration cycle. J. Mol. Liq. 2023, 380, 121742. [Google Scholar] [CrossRef]
- Xue, Q.; Kang, R.; Klionsky, D.J.; Tang, D.L.; Liu, J.B.; Chen, X. Copper metabolism in cell death and autophagy. Autophagy, 2023; just accepted. [Google Scholar]
- Wang, S.P.; Chen, L.L.; Xu, B.Q.; Jiang, W.L.; Kong, L.X.; Yang, B.; Xiong, H.; Qu, C.; Zhang, T.; Zhang, S.H.; et al. Theoretical calculation and experimental investigation on vacuum gasification separation of Ag-Cu-Au ternary alloy. J. Alloys Compd. 2023, 948, 169685. [Google Scholar] [CrossRef]
- El Guendouzi, M.; Benbiyi, A.; Dinane, A.; Azougen, R. Determination of water activities and osmotic and activity coefficients of the system NaCl-BaCl2-H2O at 298.15 K. Calphad 2003, 27, 375–381. [Google Scholar] [CrossRef]
- Hu, J.X.; Peng, D.L.; Huang, X.Y.; Wang, N.L.; Liu, B.Q.; Di, D.L.; Liu, J.F.; Qu, Q.L.; Pei, D. COSMO-SAC and QSPR combined models: A flexible and reliable strategy for screening the extraction efficiency of deep eutectic solvents. Sep. Purif. Technol. 2023, 315, 123699. [Google Scholar] [CrossRef]
- Zhao, X.; Cheng, S.X.; Koh, Y.P.; Kelly, B.D.; McKenna, G.B.; Simon, S.L. Prediction of the Synergistic Glass Transition Temperature of Coamorphous Molecular Glasses Using Activity Coefficient Models. Mol. Pharmaceut. 2021, 18, 3439–3451. [Google Scholar] [CrossRef] [PubMed]
- Sum, A.K.; Sandler, S.I. Use of ab initio methods to make phase equilibria predictions using activity coefficient models. Fluid Phase Equilib. 1999, 158, 375–380. [Google Scholar] [CrossRef]
- Wilson, G.M. Vapor-Liquid Equilibrium. XI. A New Expression for the Excess Free Energy of Mixing. J. Am. Chem. Soc. 1963, 86, 127–130. [Google Scholar] [CrossRef]
- Raabe, G.; Koehler, J. Use of ab initio interaction energies for the prediction of phase equilibria in the system nitrogen-ethane. Phys. Chem. Chem. Phys. 2002, 6, 926–930. [Google Scholar] [CrossRef]
- Neiman, M.; Cheng, H.; Parekh, V. A critical assessment on two predictive models of binary vapor liquid equilibrium. Phys. Chem. Chem. Phys. 2004, 13, 3474–3483. [Google Scholar] [CrossRef]
- Haghtalab, A.; Yousefi, J.S. A new insight to validation of local composition models in binary mixtures using molecular dynamic simulation. AIChE J. 2015, 1, 275–286. [Google Scholar] [CrossRef]
- Ravichandran, A.; Khare, R.; Chen, C.C. Predicting NRTL binary interaction parameters from molecular simulations. AIChE J. 2018, 64, 2758–2769. [Google Scholar] [CrossRef]
- Ravichandran, A.; Tun, H.; Khare, R.; Chen, C.C. Prediction of thermodynamic properties of organic mixtures: Combining molecular simulations with classical thermodynamics. Fluid Phase Equilib. 2020, 523, 1–10. [Google Scholar] [CrossRef]
- Dorini, T.T.; Eleno, L. Liquid Bi–Pb; Bi–Li alloys: Mining thermodynamic properties from ab-initio molecular dynamics calculations using thermodynamic models. Calphad 2019, 67, 101687. [Google Scholar] [CrossRef]
- Guggenheim, E.A. Statistical thermodynamics of co-operative systems (a generalization of the quasi-chemical method). Trans. Faraday Soc. 1948, 44, 263–271. [Google Scholar] [CrossRef]
- Tao, D.P. A new model of thermodynamics of liquid mixtures and its application to liquid alloys. Thermochim. Acta 2000, 363, 105–113. [Google Scholar] [CrossRef]
- Hildebrand, J.H. Solubility. XII. regular solutions. J. Am. Chem. Soc. 1929, 51, 66–80. [Google Scholar] [CrossRef]
- Renon, H.; Prausnitz, J.M. Local Composition Thermodynamic Excess Functions for Liquid Mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Zernike, F.; Prins, J.A. Die Beugung von Röntgenstrahlen in Flüssigkeiten als Effekt der Molekülanordnung. Z. Phys. A Hadron. Nucl. 1927, 41, 184–194. [Google Scholar] [CrossRef]
- Acree, W.E. Comments on excess molar volumes reported in “Study of short range and long range molecular interactions in binary liquid mixtures of N,N—dimethylformamide (DMF) and 1-propanol”. J Mol. Liq. 2022, 360, 118832. [Google Scholar] [CrossRef]
- Mokshin, A.V.; Khusnutdinoff, R.M.; Galimzyanov, B.N.; Brazhkin, V.V. Extended Short-Range Order Determines the Overall Structure of Liquid Gallium. Phys. Chem. Chem. Phys. 2020, 22, 4122–4129. [Google Scholar] [CrossRef]
- Roik, O.S.; Yakovenko, O.M.; Kashirina, Y.O.; Kazimirov, V.P.; Sokol’Skii, V.E.; Rebenko, M.Y.; Galushko, S.M.; Golovataya, N.V. The short-range order in liquid Al-Co-Sn alloys. Phys. Chem. Liq. 2022, 60, 625–635. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.; Tao, D. Development of a Non-Integral Form of Coordination Number Equation Based on Pair Distribution Function; Gaussian Function. Metals 2023, 13, 384. [Google Scholar] [CrossRef]
- Khambholja, S.G.; Abhishek, A. Structure factor and radial distribution function of liquid Pb83Li17. DAE Solid State Phys. Symp. 2019, 2020, 030365. [Google Scholar] [CrossRef]
- Su, Y.; Wang, X.D.; Cao, Q.P.; Zhang, D.X.; Jiang, J.Z. Different Thermal Responses of Local Structures in Pd43Cu27Ni10P20 Alloy from Glass to Liquid. J. Phys. Chem. C 2020, 124, 19817–19828. [Google Scholar] [CrossRef]
- Waseda, Y. The Structure of Non-Crystalline Materials: Liquids and Amorphous Solids; McGraw-Hill International Book: New York, NY, USA, 1980; pp. 47–49. [Google Scholar]
- Mikolaj, P.G.; Pings, C.J. The Use of the Coordination Number in the Interpretation of Fluid Structure. Phys. Chem. Liq. 1968, 1, 93–108. [Google Scholar] [CrossRef]
- Cahoon, J.R. The first coordination number for liquid metals. Can. J. Phys. 2004, 82, 291–301. [Google Scholar] [CrossRef]
- Liu, J.H.; Zhang, L. Structural and Thermodynamic Behaviors of CumAgn (m + n = 144–147) Nanoalloys during Cooling: Implications for Nanoparticle Structure Control. ACS Appl. Nano Mater. 2023, 6, 6388–6397. [Google Scholar] [CrossRef]
- Gosh, R.C.; Pandit, A.; Sarkar, S. A comparative study on surface tension, diffusion coefficient and shear viscosity coefficient of liquid transition metals. J. Non-Cryst. Solids 2023, 606, 122176. [Google Scholar] [CrossRef]
- Davidson, N. Statistical Mechanics; Series in Advanced Chemistry; McGraw Hill: New York, NY, USA, 1962; pp. 474–475. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and Its Applications; Wiley: Hoboken, NJ, USA, 1950; pp. 220–222. [Google Scholar]
- Iida, T.; Guthrie, R. The Physical Properties of Liquid Metals; Oxford University Press: Oxford, UK, 1988; pp. 71–72. [Google Scholar]
- Nakanishi, K.; Okazaki, S.; Ikari, K.; Higuchi, T.; Tanaka, H. Free Energy of Mixing, Phase Stability, and Local Composition in Lennard-Jones Liquid Mixtures. J. Chem. Phys. 1982, 76, 629–636. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E.; Devonshire, A.F. Critical phenomena in gases-I. Proc. R. Soc. Ser. A Math. Phys. Eng. Sci. 1937, 163, 53–70. [Google Scholar]
- Guggenheim, E.A. Application of Statistical Mechanics; Oxford University Press: Oxford, UK, 1966; p. 211. [Google Scholar]
- Cheremisina, E.; Gao, X.; Ueda, S.; Kitamura, S.; Yamashina, R.; Schenk, J. Experimental Determination of the MnO Activity Coefficient in High-Manganese Slags Using the Chemical Equilibrium Method. Metals 2021, 11, 1190. [Google Scholar] [CrossRef]
- Sui, Y.R.; Ding, Z.X.; Zhai, C.; Lin, H.S.; Wu, W. Crystallization-free and low-cost deep eutectic solvents for absorption thermal battery utilizing ultra-low-grade energy. Energy Convers. Manag. 2023, 284, 116984. [Google Scholar] [CrossRef]
- Prausnitz, J.M.; Lichtenthaler, R.N.; Azevedo, E. Molecular Thermodynamics of Fluid-Phase Equilibria; Prentice-Hall: Hoboken, NJ, USA, 1999; p. 296. [Google Scholar]
- Tsilifis, P.; Browning, W.J.; Wood, T.E.; Newton, P.K.; Ghanem, R.G. The Stochastic Quasi-chemical Model for Bacterial Growth: Variational Bayesian Parameter Update. J. Nonlinear Sci. 2018, 28, 371–393. [Google Scholar] [CrossRef]
- Tao, D.P. The universal characteristics of a thermodynamic model to conform to the Gibbs-Duhem equation. Sci. Rep. 2016, 6, 35792. [Google Scholar] [CrossRef] [PubMed]
- Voigtmann, T.; Kolland, G.; Kobatake, H.; Brillo, J.; Peng, H.L. Structural and dynamical properties of liquid Al-Au alloys. Phys. Rev. B 2015, 92, 184–201. [Google Scholar]
- Roik, O.S.; Samsonnikov, O.V.; Kazimirov, V.P.; Sokolskii, V.E.; Galushko, S.M. Medium-range order in Al-based liquid binary alloys. J. Mol. Liq. 2010, 151, 42–49. [Google Scholar] [CrossRef]
- Kbirou, M.; Mazroui, M.; Hasnaoui, A. Atomic packing and fractal behavior of Al-Co metallic glasses. J. Alloys Compd. 2018, 735, 464–472. [Google Scholar] [CrossRef]
- Roik, O.S.; Yakovenko, O.M.; Kazimirov, V.P.; Bilovodska, O.O.; Sokolskii, V.E. RMC simulations of the liquid Al Ge alloys. J. Mol. Liq. 2016, 220, 155–160. [Google Scholar] [CrossRef]
- Faruk, M.M.; Bhuiyan, G.M. Investigation of segregation for Al-In liquid binary alloys. Phys. B Condens. Matter 2013, 422, 56–63. [Google Scholar] [CrossRef]
- Wang, C.C.; Wong, C.H. Short-to-medium range order of Al-Mg metallic glasses studied by molecular dynamics simulations. J. Alloys Compd. 2011, 509, 10222–10229. [Google Scholar] [CrossRef]
- Qin, J.; Pan, S.; Qi, Y.; Gu, T. The structure and thermodynamic properties of liquid Al-Si alloys by ab initio molecular dynamics simulation. J. Non-Cryst. Solids 2016, 433, 31–37. [Google Scholar] [CrossRef]
- Roik, O.S.; Yakovenko, O.M.; Kazimirov, V.P.; Sokolskii, V.E.; Golovataya, N.V.; Kashirina, Y.O. Structure of liquid AlSn alloys. J. Mol. Liq. 2021, 330, 115570. [Google Scholar] [CrossRef]
- Souto, J.; Alemany, M.M.G.; Gallego, L.J.; González, L.E.; González, D.J. Static structure, microscopic dynamics and electronic properties of the liquid Bi–Pb alloy. An ab initio molecular dynamics study. J. Nucl. Mater 2011, 411, 163–170. [Google Scholar] [CrossRef]
- Chen, S.; Ma, J.; Dai, Y.; Yang, J.; Zhang, J.; Dong, Q.; Han, Y.; Xing, H.; Sun, B. Atomic-scale simulations of the local structures of molten Ni1-xCox and Ni1-xFex. J. Non-Cryst. Solids 2018, 481, 470–478. [Google Scholar] [CrossRef]
- Korkmaz, S.D.; Korkmaz, Ş. A study for structure and inter-diffusion coefficient of liquid K1−x Cs x metal alloys. Phys. Chem. Liq. 2011, 49, 801–810. [Google Scholar] [CrossRef]
- Faruk, M.M.; Bhuiyan, G.M.; Biswas, A.; Hossain, M.S. Study of microscopic origin of segregation for Fe x Cu1x and CuxCo1-x liquid binary alloys. J. Chem. Phys. 2014, 140, 134505. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Qin, J.Y.; Gu, T.K. The structure of liquid Mg-Cu binary alloys. J. Non-Cryst. Solids 2010, 356, 1587–1592. [Google Scholar] [CrossRef]
- Guo, F.; Tian, Y.; Qin, J.; Xu, R.; Sun, Y. Structure of liquid Cu-Sb alloys by ab initio molecular dynamics simulations, high temperature X-ray diffraction, and resistivity. J. Mater Sci. 2013, 48, 4438–4445. [Google Scholar] [CrossRef]
- Jakse, N.; Nguyen, T.; Pasturel, A. Local order and dynamic properties of liquid and undercooled CuxZr1-x alloys by ab initio molecular dynamics. J. Appl. Phys. 2013, 114, 425. [Google Scholar] [CrossRef]
- Korkmaz and Korkmaz, S.D. Structure and Inter-Diffusion Coefficients of Liquid NaxK1-x Alloys. J. Phase Equilibria Diffus. 2010, 31, 15–21. [Google Scholar] [CrossRef]
- Liu, D.; Zhu, X.; Qin, J.; Wang, A.; Duan, J.; Gu, T. First-Principles Study of Chemical and Topological Short-Range Orders in the Mg-Si Liquid Alloys. Metals 2016, 6, 78. [Google Scholar] [CrossRef]
- Liu, D.; Qin, J.; Zhu, X.M.; Duan, J.P.; Gu, T.; Wang, A.M. Correlation between local structures and glass forming ability of liquid MgX-Zn(1-x) alloys. J. Non-Cryst. Solids 2016, 447, 262–266. [Google Scholar] [CrossRef]
- Hardy, H.K. A “sub-regular” solution model and its application to some binary alloy systems. J. Acta Metall. 1953, 1, 202–209. [Google Scholar] [CrossRef]
- Flemr, V. A note on excess Gibbs energy equations based on local composition concept. Collect. Czechoslov. Chem. Commun. 1976, 41, 3347–3349. [Google Scholar] [CrossRef]
- Franke, P.; Neusch, D. Elements and Binary Systems from Ag-AI to Au-TI; Springer: Berlin/Heidelberg, Germany, 2002; pp. 139–142. [Google Scholar]


| Type | ii | jj | ij |
|---|---|---|---|
| r0 | 1.74 | 1.57 | 1.59 |
| rm | 2.76 | 2.41 | 2.49 |
| r1 | 4.67 | 4.23 | 3.85 |
| g(rm) | 2.43 | 2.35 | 3.63 |
| u | 0.21 | 0.14 | 0.19 |
| v | 0.26 | 0.25 | 0.22 |
| ρ0 | 0.0625 | xi | 0.6 |
| Pair Potentials | Partial Coordination Numbers | ||||||
|---|---|---|---|---|---|---|---|
| εii/kT | εij/kT | εji/kT | εjj/kT | Zii | Zij | Zji | Zjj |
| −0.37 | −0.745 | −0.75 | −0.31 | 5.32 | 3.78 | 5.68 | 2.26 |
| MIVM | RSM | M-MIVM | |||||
| Bij | Bij | λji | λji | Z | w/ZkT | ψij | ψji |
| 1.66 | 0.43 | 0.43 | 0.38 | 8.63 | −0.86 | 5.38 | 3.67 |
| QCM | |||||||
| σ | β | ω/ZkT | |||||
| 0.53 | 1.04 | −2.09 | |||||
| Model | MIVM | Wilson | NRTL | RSM | QCM | M-MIVM | M-NRTL | M-RSM |
|---|---|---|---|---|---|---|---|---|
| 30.5 | 69.15 | 65.61 | 15.99 | 72.23 | 40.07 | 84.67 | 27.90 | |
| Activity | 28.40 | 504.02 | 459.87 | 24.56 | 605.14 | 33.99 | 47.56 | 29.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Chen, X.; Tao, D. Estimation of Component Activities and Molar Excess Gibbs Energy of 19 Binary Liquid Alloys from Partial Pair Distribution Functions in Literature. Metals 2023, 13, 996. https://doi.org/10.3390/met13050996
Wang C, Chen X, Tao D. Estimation of Component Activities and Molar Excess Gibbs Energy of 19 Binary Liquid Alloys from Partial Pair Distribution Functions in Literature. Metals. 2023; 13(5):996. https://doi.org/10.3390/met13050996
Chicago/Turabian StyleWang, Chunlong, Xiumin Chen, and Dongping Tao. 2023. "Estimation of Component Activities and Molar Excess Gibbs Energy of 19 Binary Liquid Alloys from Partial Pair Distribution Functions in Literature" Metals 13, no. 5: 996. https://doi.org/10.3390/met13050996
APA StyleWang, C., Chen, X., & Tao, D. (2023). Estimation of Component Activities and Molar Excess Gibbs Energy of 19 Binary Liquid Alloys from Partial Pair Distribution Functions in Literature. Metals, 13(5), 996. https://doi.org/10.3390/met13050996







