A Computational Fluid Dynamics Study on Physical Refining of Steel Melts by Filtration
Abstract
:1. Introduction
2. Theoretical Background
Summary of the Physical Steel Melt Refining Experiments
3. Methodology
3.1. Mathematical Modeling Modeling
- 1.
- The Navier–Stokes equations for incompressible fluids, containing continuity and conservation of momentum.
- 2.
- The Newton’s second law for the motion of particles in the fluid flow.
3.2. Assumptions
- Fluid Flow Simulations
- The fluid, filter, and particle properties were identical in all quarters of the whole filter setup.
- No fluid bypassing was considered. The filter was made as part of the alumina crucible.
- Temperature was assumed to be constant.
- The solution was independent of time, i.e., a steady-state solution.
- The gravitational force was considered.
- Incompressible Newtonian fluid with a constant fluid density and viscosity was considered.
- No heat transfer to/from the ambient medium was considered.
- There was no fluid–wall interaction.
- The walls were assumed to be straight and smooth using a no-slip boundary condition.
- Particle Tracing in Fluid Flow
- The fluid, filter, and particle properties were identical in all quarters of the whole filter setup.
- Fluid–particle interaction was not considered (unidirectional or one-way coupling).
- Particle–particle interaction was not considered.
- The particles were assumed to be spherical, following the findings of reference [13].
- Particles did not displace the fluid they occupied.
- Properties of the steel containing 0.012 pct. C, 0.04 Ni were assumed to be the same as iron at 1873 (K).
3.3. The Transport Equations
3.4. Boundary Conditions
4. Results
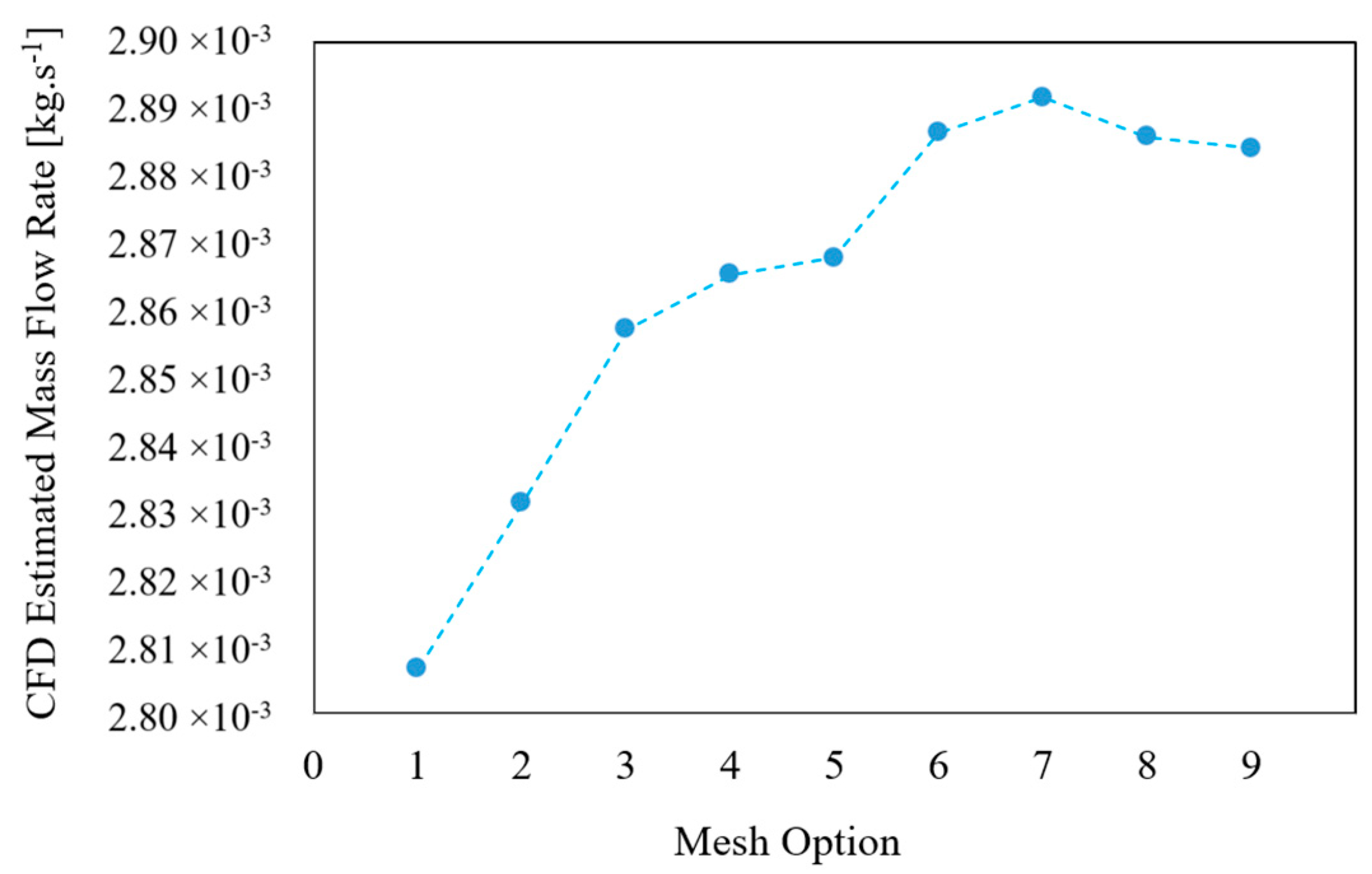
4.1. Mesh Independence
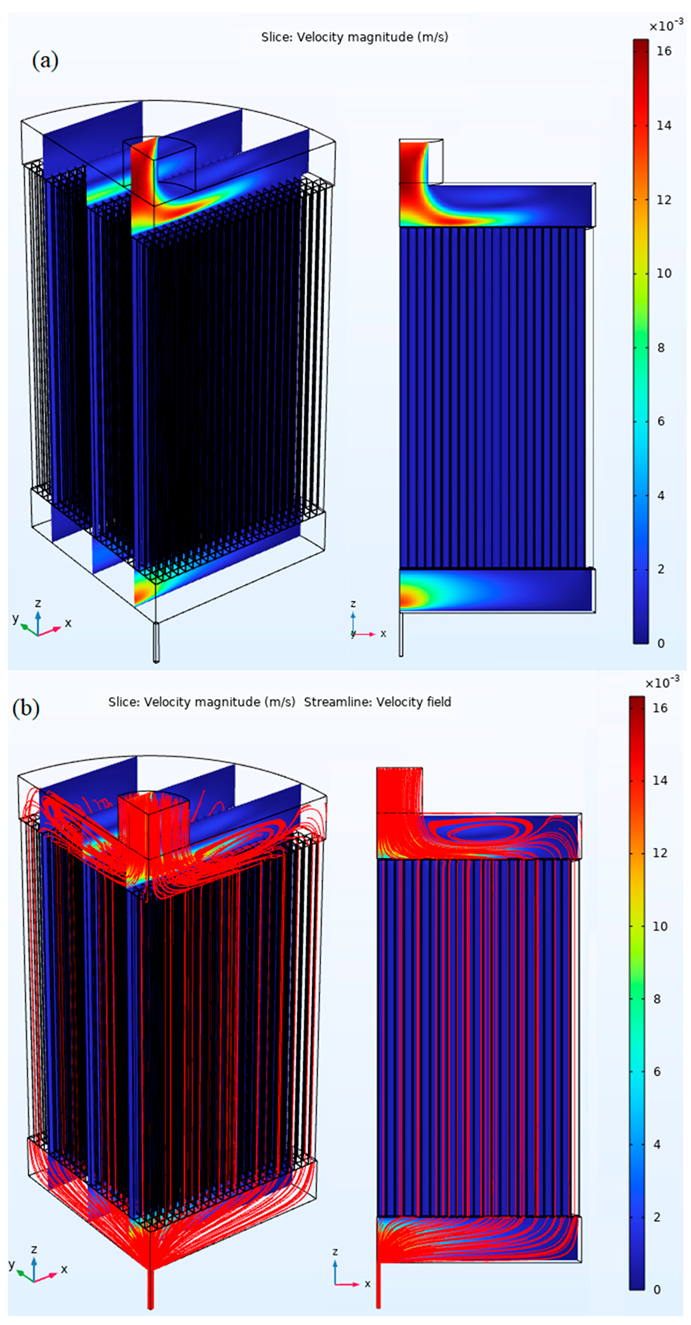
4.2. Fluid Flow Calculations
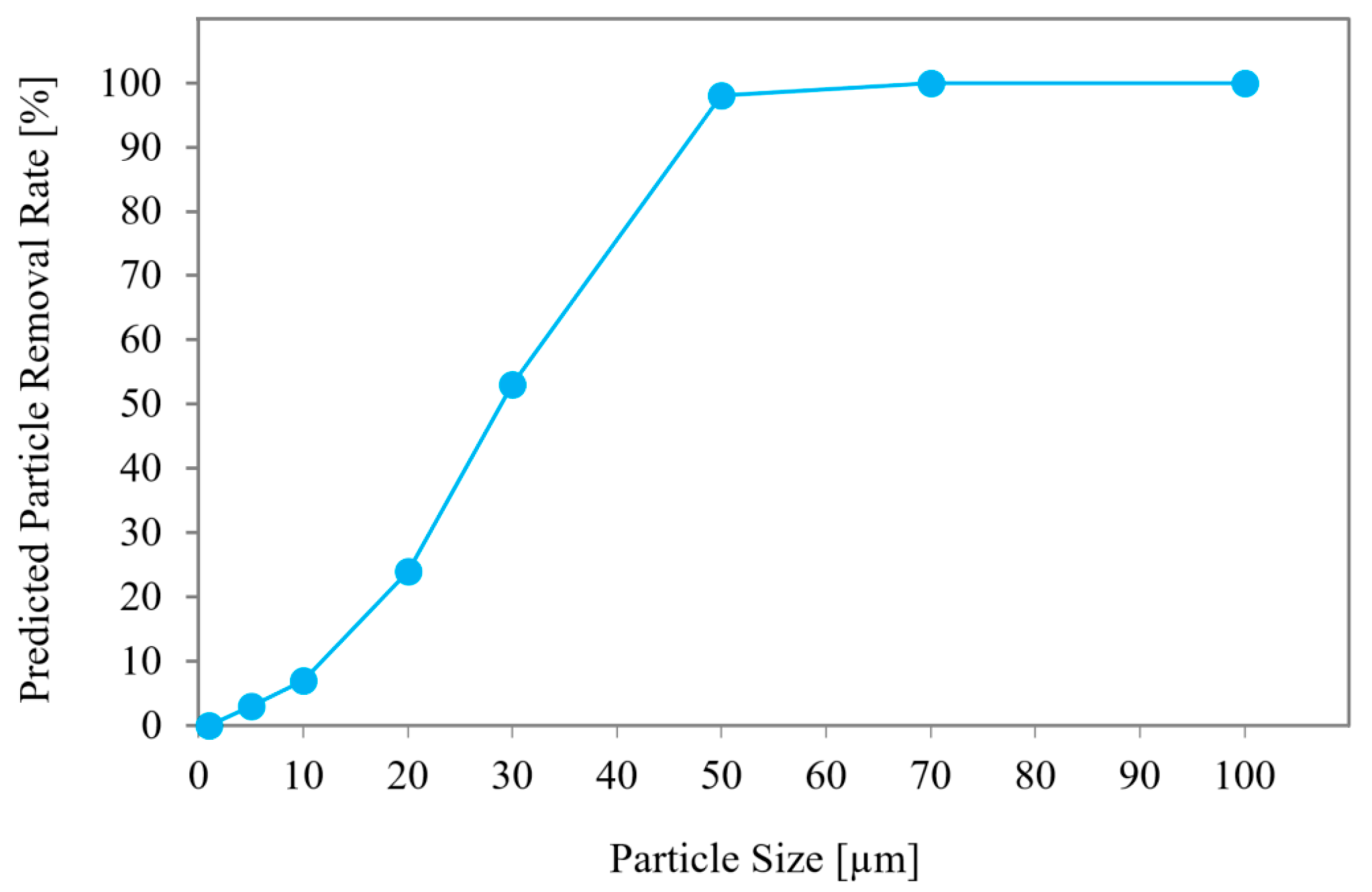
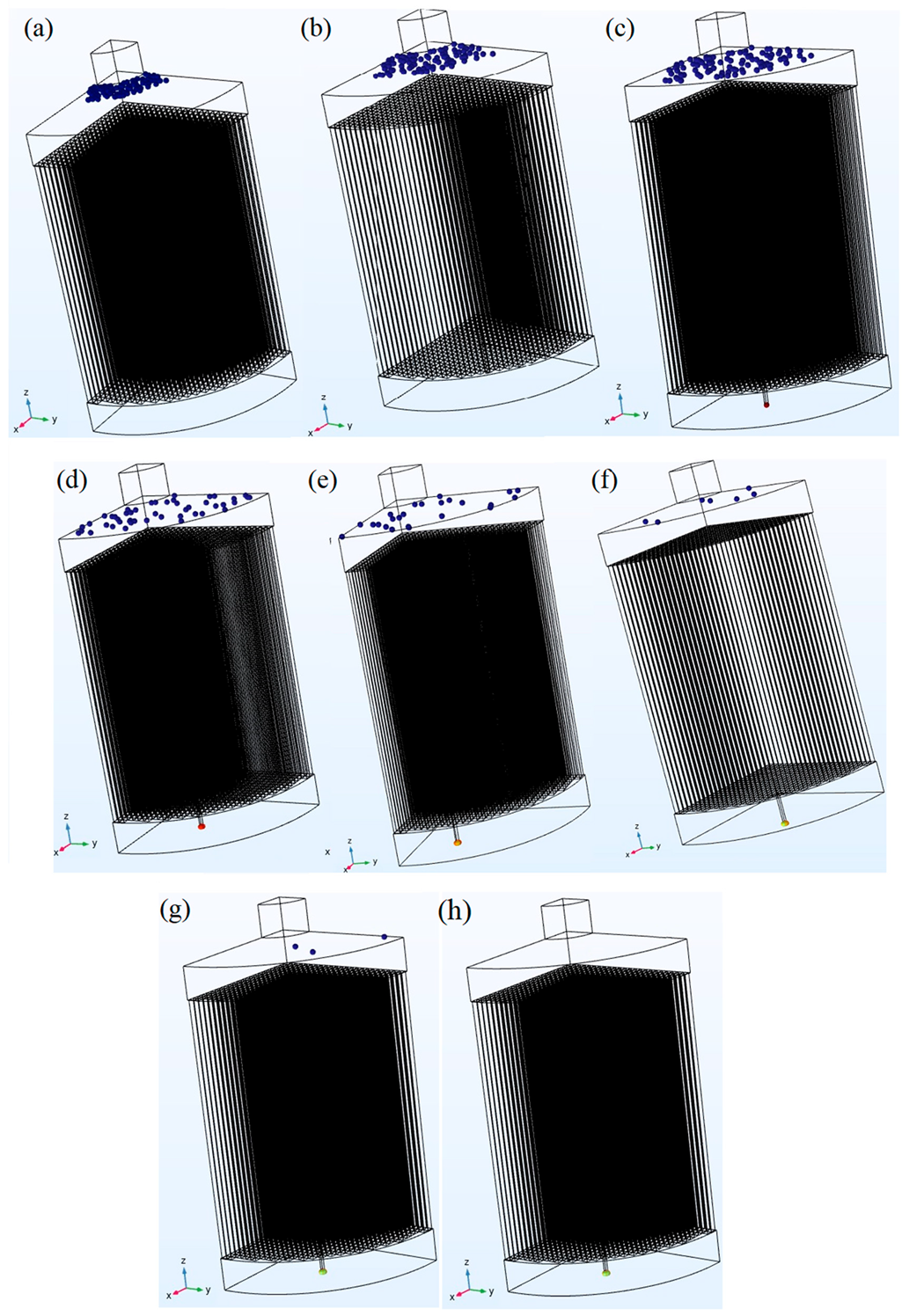
4.3. Particle Tracing in Fluid Flow
5. Discussions
6. Conclusions
- The modeled filtration setup could capture 100% of the particles larger than 50 µm.
- The percentage of the filtered particles decreased from 98% to 0% in the particle size range from 50 µm to 1 µm.
- The current model has a limitation in predicting particle filtration for particles in the size range of ≤5 µm.
- Further modeling development of physical filtration is required to include particle clustering and agglomeration which results in net or cake formation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Leonov, A.N.; Dechko, M.M. Theory of Design of Foam Ceramic Filters for Cleaning Molten Metals. Refract. Ind. Ceram. 1999, 40, 537. [Google Scholar] [CrossRef]
- Aneziris, C.G.; Dudczig, S.; Emmel, M.; Berek, H.; Schmidt, G.; Hubalkova, J. Reactive Ffilters for Steel Melt Filtration. Adv. Eng. Mater. 2013, 15, 46. [Google Scholar] [CrossRef]
- Akbarnejad, S.; Jonsson, L.; Kennedy, M.W.; Aune, R.E.; Jönsson, P. Analysis on Experimental Investigation and Mathematical Modeling of Incompressible Flow through Ceramic Foam Filter. Metall. Mater. Trans. B 2016, 47, 2229. [Google Scholar] [CrossRef]
- Yang, Y.; Maeda, Y.; Takita, M.; Nomura, H. Effect of Flow Behavior on the Removal of Inclusions by Filter. Int. J. Cast Metals Res. 1997, 10, 165. [Google Scholar] [CrossRef]
- Atkinson, H.V.; Shi, G. Characterization of Inclusions in Clean Steels: A Review Including the Statistics of Extremes Methods. Prog. Mater. Sci. 2003, 48, 457. [Google Scholar] [CrossRef]
- Smothers, W.J. Application of Refractories: Ceramic Engineering and Science Proceedings; The American Ceramic Society, Inc.: Columbus, OH, USA, 1987; Volume 8, p. 107. [Google Scholar]
- Zhang, L.; Thomas, B.G. State of the Art in Evaluation and Control of Steel Cleanliness. ISIJ Int. 2003, 43, 271. [Google Scholar] [CrossRef]
- Zhang, L.; Thomas, B.G. Inclusions in Continuous Casting of Steel. In Proceedings of the XXIV National Steelmaking Symposium, Morelia, Mexico, 26–28 November 2003; p. 138. [Google Scholar]
- Silva, A.L.V.d.C. Non-metallic Inclusions in Steels–Origin and Control. Mater. Res. Tech. 2018, 7, 283. [Google Scholar]
- Apelian, D.; Mutharasan, R.; Ali, S. Removal of Inclusions from Steel Melts by Filtration. Mater. Sci. 1985, 20, 3501. [Google Scholar] [CrossRef]
- Wang, Y.; Karasev, A.; Jönsson, P.G. Comparison of Nonmetallic Inclusion Characteristics in Metal Samples Using 2D and 3D Methods. Steel Res. Int. 2020, 91, 1900669. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, L.; Ren, Y.; Yang, W.; Wu, S. Metals, The Effect of Aluminum Addition on the Evolution of Inclusions in an Aluminum-Killed Calcium-Treated Steel. Metals 2022, 12, 181. [Google Scholar] [CrossRef]
- Ali, S.; Mutharasan, R.; Apelian, D. Physical Refining of Steel Melts by Filtration. Metall. Mater. Trans. B 1985, 16, 725. [Google Scholar] [CrossRef]
- Dippenaar, R Industrial Uses of Slag (the Use and Re-use of Iron and Steelmaking Slags). Ironmak. Steelmak. 2005, 32, 35. [CrossRef]
- Ali, S.; Apelian, D.; Mutharasant, R. Refining of Aluminum and Steel Melts by the Use of Multi-Cellular Extruded Ceramic Filters. Canad. Metall. Q. 1985, 24, 311. [Google Scholar] [CrossRef]
- Uemura, K.; Takahashi, M.; Koyama, S.; Nitta, M. Filtration Mechamism of Non-metallic Inclusions in Steel by Ceramic Loop Filter. ISIJ Int. 1992, 32, 150. [Google Scholar] [CrossRef]
- Scheffler, M.; Colombo, P. Cellular Ceramics: Structure, Manufacturing, Properties and Applications; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2005; p. 621. [Google Scholar]
- Damoah, L.N.W.; Zhang, L. Removal of Inclusions from Aluminum through Filtration. Metall. Mater. Trans. B 2010, 41, 886. [Google Scholar] [CrossRef]
- Kennedy, M.W.; Akhtar, S.; Bakken, J.A.; Aune, R.E. Electromagnetically Modified Filtration of Aluminum Melts—Part I: Electromagnetic Theory and 30 PPI Ceramic Foam Filter Experimental Results. Metall. Mater. Trans. B 2013, 44, 691. [Google Scholar] [CrossRef]
- Sahai, Y. Tundish Technology for Casting Clean Steel: A Review. Metall. Mater. Trans. B 2016, 47, 2095. [Google Scholar] [CrossRef]
- Ånmark, N.; Karasev, A.; Jönsson, P.G. The Effect of Different Non-Metallic Inclusions on the Machinability of Steels. Materials 2015, 8, 751. [Google Scholar] [CrossRef]
- Braun, T.B.; Elliott, J.F.; Flemings, M.C. The Clustering of Alumina Inclusions. Metall. Mater. Trans. B 1979, 10, 171. [Google Scholar] [CrossRef]
- McLean, A.; Ward, R.G.; Strathdee, B. Aluminum Deoxidation Products in Rimmed Steel. JOM 1965, 17, 526. [Google Scholar] [CrossRef]
- Wang, Y.; Karasev, A.; Jönsson, P.G. Non-metallic Inclusions in Different Ferroalloys and Their Effect on the Steel Quality: A Review. Metall. Mater. Trans. B 2021, 52, 2892. [Google Scholar] [CrossRef]
- Singh, S.N. Mechanism of Alumina Buildup in Tundish Nozzles During Continuous Casting of Aluminum-Killed Steels. Metall. Mater. Trans. B 1974, 5, 2165. [Google Scholar] [CrossRef]
- Debroy, T.; Sychterz, J.A. Numerical Calculation of Fluid Flow in a Continuous Casting Tundish. Metall. Mater. Trans. B 1985, 16, 497. [Google Scholar] [CrossRef]
- Zhang, L.; Pluschkell, W. Nucleation and Growth Kinetics of Inclusions during Liquid Steel Deoxidation. Ironmak. Steelmak. 2003, 30, 106. [Google Scholar] [CrossRef]
- Yin, H.B.; Shibata, H.; Emi, T.; Suzuki, M. “In-situ” Observation of Collision, Agglomeration and Cluster Formation of Alumina Inclusion Particles on Steel Melts. ISIJ Int. 1997, 37, 936. [Google Scholar] [CrossRef]
- Ende, M.A.V. Formation and Morphology of non-Metallic Inclusions in Aluminium Killed Steels. Ph.D. Thesis, Katholieke Universiteit, Leuven, Belgium, 2010. [Google Scholar]
- Lee, W.; Kim, J.G.; Jung, J., II; Huh, K.Y. Prediction of Nozzle Clogging through Fluid–Structure Interaction in the Continuous Steel Casting Process. Steel Res. Int. 2021, 92, 2000549. [Google Scholar] [CrossRef]
- Michelic, S.K.; Bernhard, C. Significance of Nonmetallic Inclusions for the Clogging Phenomenon in Continuous Casting of Steel––A Review. Steel Res. Int. 2022, 93, 2200086. [Google Scholar] [CrossRef]
- Wang, J.; Xia, M.; Wu, J.; Ge, C. Ladle Nozzle Clogging in Vacuum Induction Melting Gas Atomization: Influence of the Melt Viscosity. Metall. Mater. Trans. B 2022, 53, 2386. [Google Scholar] [CrossRef]
- Liang, W.; Li, J.; Lu, B.; Zhi, J.G.; Zhang, S.; Liu, Y. Analysis on Clogging of Submerged Entry Nozzle in Continuous Casting of High Strength Steel with Rare Earth. Iron and Steel Res. Int. 2022, 29, 34. [Google Scholar] [CrossRef]
- Bulkowski, L.; Galisz, U.; Kania, H.; Kudliński, Z.; Pieprzyca, J.; Barański, J. Industrial Tests of Steel Filtering Process. Arch. Metall. Mater. 2012, 57, 363. [Google Scholar] [CrossRef]
- Chakraborty, S.; Malley, R.J.O.; Bartlett, L.; Xu, M. Efficiency of Solid Inclusion Removal from the Steel Melt by Ceramic Foam Filter: Design and Experimental Validation. In Proceedings of the 122nd Metalcasting Congress, Forth Worth, TX, USA, 3–5 April 2018. [Google Scholar]
- Chakraborty, S. Removal of Non-metallic Inclusions from Molten Steel by Ceramic Foam Filtration. Ph.D. Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2020. [Google Scholar]
- Akbarnejad, S.; Pour, M.S.; Jonsson, L.T.I.; Jonsson, P.G. Effect of Fluid Bypassing on the Experimentally Obtained Darcy and Non-Darcy Permeability Parameters of Ceramic Foam Filters. Metall. Mater. Trans. B 2017, 48, 197. [Google Scholar] [CrossRef]
- Assael, M.J.; Kakosimos, K.; Banish, R.M.; Brillo, J.; Egry, I.; Brooks, R.; Quested, P.N.; Mills, K.C.; Nagashima, A.; Sato, Y.; et al. Reference Data for the Density and Viscosity of Liquid Aluminum and Liquid Iron. Phys. Chem. Ref. Data 2006, 35, 285. [Google Scholar] [CrossRef]
- Fox, R.W.; McDonald, A.T.; Pritchard, P.J. Introduction to Fluid Mechanics; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Johnson, R.W. The Handbook of Fluid Dynamics; CRC Press: Boca Raton, FL, USA; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- FD Module User’s Guide, COMSOL Multiphysics Version 6.0; Comsol: Stockholm, Sweden, 2021.
- Particle Tracing Module User’s Guide, COMSOL Multiphysics Version 6.0; Comsol: Stockholm, Sweden, 2021.
- White, F.M. Fluid Mechanics; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Haider, A.; Levenspiel, O. Drag Coefficient and Terminal Velocity of Spherical and Nonspherical Particles. Powder Technol. 1989, 58, 63. [Google Scholar] [CrossRef]
- Introduction to Particle Tracing Module, COMSOL Multiphysics Version 6.0; Comsol: Stockholm, Sweden, 2021.
- Saffman, P.G. The lift on a Small Sphere in a Slow Shear Flow. Fluid Mech. 1965, 22, 385. [Google Scholar] [CrossRef]
- Paladino, E.E.; Maliska, C.R. Virtual mass in accelerated bubbly flows. In Proceedings of the 4th European Thermal Sciences, National Exhibition Centre, Birmingham, UK, 29–31 March 2004. [Google Scholar]
- Maxey, M.R.; Riley, J.J. Equation of Motion for a Small Rigid Sphere in a Nonuniform Flow. Phys. Fluids 1983, 26, 883. [Google Scholar] [CrossRef]
- Ho, B.P.; Leal, L.G. Inertial Migration of Rigid Spheres in Two-dimensional Unidirectional Flows. Fluid Mech. 1974, 65, 365. [Google Scholar] [CrossRef]
- Li, A.; Ahmadi, G. Dispersion and Deposition of Spherical Particles from Point Sources in a Turbulent Channel Flow. Aero. Sci. Technol. 1992, 16, 209. [Google Scholar] [CrossRef]
- Apelian, D.; Mutharasan, R. Filtration: A Melt Refining Method. JOM 1980, 32, 14. [Google Scholar] [CrossRef]
- Raiber, K.; Hammerschmid, P.; Janke, D. Experimental Studies on Al2O3 Inclusion Removal from Steel Melts Using Ceramic Filters. ISIJ Int. 1995, 35, 380. [Google Scholar] [CrossRef]
- Gauckler, L.J.; Waeber, M.M.; Conti, C.; Jacob-Duliere, M. Ceramic Foam for Molten metal Filtration. JOM 1985, 37, 47. [Google Scholar] [CrossRef]
- Apelian, D.; Sutton, W.H. Utilization of Ceramic Filters to Produce Cleaner Superalloy Melts. In Proceedings of the 5th International Symposium on Superalloys, Champion, PA, USA, 7–11 October 1984; p. 421. [Google Scholar]


| Section | Diameter (mm) | Height (mm) | Length (mm) | Width (mm) |
|---|---|---|---|---|
| Inlet | 12.7 | 6.35 | N/A | N/A |
| Spacer between inlet & filter | 57.15 | 6.35 | N/A | N/A |
| Filter | 57.15 * | 50 | N/A | N/A |
| Filter pore | N/A | 50 | 1.15 | 1.15 |
| Alumina between 2 pores | N/A | 50 | 1.15 | 0.12 |
| Spacer between filter & outlet | 57.15 | 6.35 | N/A | N/A |
| outlet | 1 | 6.35 | N/A | N/A |
| Material | Density (kg.m−3) | Dynamic Viscosity (Pa.s) | Temperature (K) |
|---|---|---|---|
| Steel * | 6975 | 5.2 × 10−3 | 1873 |
| Alumina | 3900 | N/A |
| Particle Diameter (μm) | Relative Reynolds Number | ||
|---|---|---|---|
| Inlet | In a Pore | Outlet | |
| 100 | 1.8 | 0.1 | 287 |
| 70 | 1.2 | 0.8 | 200 |
| 50 | 0.9 | 0.05 | 143 |
| 30 | 0.5 | 0.03 | 86 |
| 20 | 0.4 | 0.02 | 57 |
| 10 | 0.2 | 0.01 | 29 |
| 5 | 0.1 | 0.005 | 14 |
| 1 | 0.02 | 0.001 | 3 |
| Section | Inlet | Interior Walls | Symmetry Walls | Outlet |
|---|---|---|---|---|
| Fluid | u = −nU0 (m.s−1) | u = 0 (m.s−1) | u. n = 0 (m.s−1) | Pref = 0 (Pa) |
| Particles | v = v0 (m.s−1) q = q0 (m) | v = 0 (m.s−1) | v = vc − 2(n. vc)n (m.s−1) | v = vc (m.s−1) |
| Mesh no. | Mesh Type | Element Size in Domains (mm) | Element Size in Boundaries (mm) | Total Mesh Element (millions) | Calculation Time (min) | |||
|---|---|---|---|---|---|---|---|---|
| Physics controlled | User controlled | Min. | Max. | Min. | Max. | |||
| 1 | Coarser | - | 6.82 | 1.7 | 3.41 | 1.02 | 0.26 | 8 |
| 2 | Coarse | - | 4.43 | 1.36 | 2.28 | 0.682 | 0.51 | 5 |
| 3 | Normal | - | 3.41 | 1.02 | 1.81 | 0.341 | 1.46 | 12 |
| 4 | - | √ | 2.28 | 0.682 | 1.81 | 0.341 | 1.6 | 14 |
| 5 | - | √ | 1.81 | 0.341 | 1.81 | 0.341 | 1.71 | 17 |
| 6 | - | √ | 1.26 | 0.136 | 1.26 | 0.136 | 10.2 | 308 |
| 7 | Finer | - | 1.81 | 0.341 | 0.784 | 0.0511 | 47.9 | 1502 |
| 8 | - | √ | 1.54 | 0.166 | 0.8 | 0.08 | 5.97 | 107 |
| 9 | - | √ | 1.54 | 0.166 | 0.784 | 0.0511 | 20.68 | 196 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbarnejad, S.; Sheng, D.-Y.; Jönsson, P.G. A Computational Fluid Dynamics Study on Physical Refining of Steel Melts by Filtration. Metals 2023, 13, 1022. https://doi.org/10.3390/met13061022
Akbarnejad S, Sheng D-Y, Jönsson PG. A Computational Fluid Dynamics Study on Physical Refining of Steel Melts by Filtration. Metals. 2023; 13(6):1022. https://doi.org/10.3390/met13061022
Chicago/Turabian StyleAkbarnejad, Shahin, Dong-Yuan Sheng, and Pär Göran Jönsson. 2023. "A Computational Fluid Dynamics Study on Physical Refining of Steel Melts by Filtration" Metals 13, no. 6: 1022. https://doi.org/10.3390/met13061022
APA StyleAkbarnejad, S., Sheng, D.-Y., & Jönsson, P. G. (2023). A Computational Fluid Dynamics Study on Physical Refining of Steel Melts by Filtration. Metals, 13(6), 1022. https://doi.org/10.3390/met13061022






